2. Theory
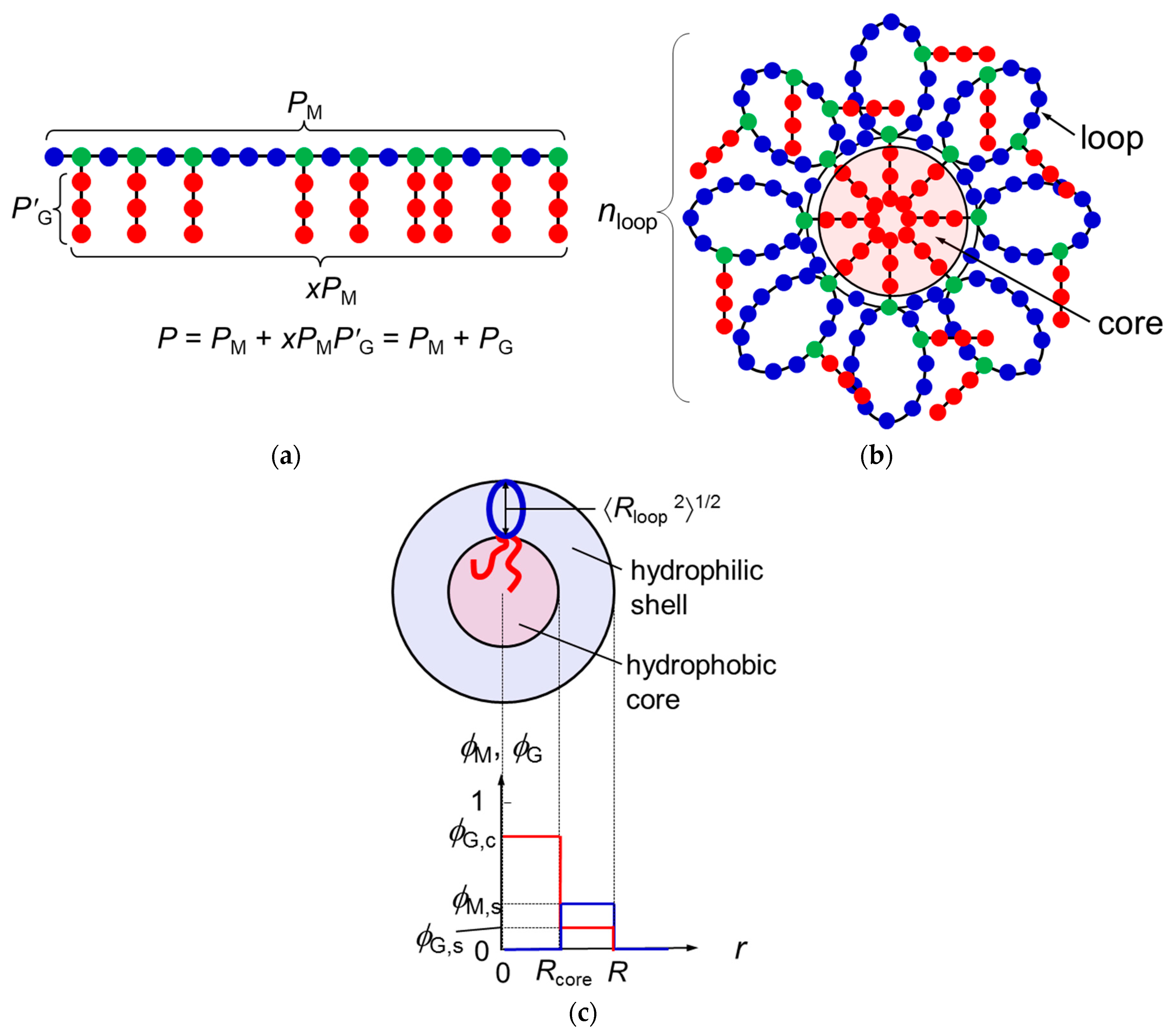
Let us consider the graft copolymer illustrated in
Figure 1a. The main chain and graft chains consist of
PM units and
P′
G units, respectively. The mole fraction of the branch units on the main chain is denoted as
x, and the distribution of the branch units along the main chain is assumed to be random or periodic (not block-like). The total number of the graft-chain units per copolymer chain is
PG =
xPMP′
G, and the total degree of polymerization of the graft copolymer chain is
P =
PM +
PG =
PM(1 +
xP′
G). It is assumed that the main-chain and graft-chain units as well as the solvent S molecule occupy lattice sites with a common size
a.
If the graft-chain unit is sufficiently hydrophobic, graft chains of the copolymer tend to aggregate to form a hydrophobic core, and the main chain tends to form loop chains in aqueous medium. As a result, the
m copolymer chains construct a flower micelle illustrated in
Figure 1b;
m is the copolymer-chain aggregation number of the micelle. Only graft chains attaching to roots of the loops can enter the hydrophobic core, and the remaining graft chains are outside the core.
According to the wormlike chain model [
13,
14,
15], the ring closure probability of the chain rapidly diminishes to zero at the chain contour length reducing to ca. 1.6
q, where
q is the persistence length. This means that the main chain portion shorter than 1.6
q cannot form the loop because of the chain stiffness. In what follows, we consider the flower micelle consisting of loop chains with this “minimum loop size” [
6]. The number of main-chain units per the minimum loop chain
Ploop, and the number of loop chains per chain
nloop are calculated by
The numbers of graft chains included in the hydrophobic core and outside of the core,
xcPM and
xsPM, respectively, are calculated by
where
λ is the number of side chains included in the core at each root of the loop. (
Figure 1b illustrates the case of
λ = 1). It has been assumed in Equation (2) that
nloop is much larger than unity.
In the previous paper [
12], we regarded the spherical micelle formed by di-block copolymer chains as a thermodynamic phase, assuming that the aggregation number of the micelle is sufficiently large. Similarly, the present study regards the flower micelle as a thermodynamic phase to demonstrate the micellization of the graft copolymer in a selective solvent. Furthermore, we use a simple model for the flower micellar phase, of which radial concentration profiles (volume fractions) of the main-chain and graft-chain units are given by
(cf.
Figure 1c). Here,
Rcore and
R are the radii of the micelle core and the whole micelle, respectively, and the solvent volume fraction is given by
S = 1 −
M −
G at each radial distance
r. Furthermore, using the wormlike chain model,
Rcore2 and the mean square distance from the end to the midpoint of the loop 〈
Rloop2〉 (cf.
Figure 1c) are expressed in terms of the persistence lengths of the graft chain (
qG) and of the copolymer main chain (
q), respectively, by [
15]
(cf.
Appendix A). The radius
R of the whole micelle is calculated by
The average volume fraction
ϕP of the copolymer in the flower micelle phase is given by
and the volume fractions
M,s,
G,s, and
G,c are related to
P by
From the last equation for
G,c in Equation (8), it can be seen that
P must be equal to or less than
PRcore3/xcPMP′
GR3, because
G,c does not exceed unity. Furthermore, since
m must be larger than unity,
PM must be smaller than 4π
R3P/3
a3(1 +
xP′
G) from Equation (7).
For amphiphilic random or periodic copolymers, the ionizable group or hydrophilic side-chain group of each hydrophilic monomer unit is substituted by the hydrophobic graft chain. Thus, the branch unit in the main chain (green circles in
Figure 1a,b) may be hydrophobic, having interaction parameters much different from those of the non-branch unit (i.e., the hydrophilic monomer unit) in the main chain but similar to those of the graft-chain unit. We refer to the non-branch unit in the main chain as the A unit and to the graft-chain unit as well as the branch unit in the main chain as the B unit, neglecting the difference in the interaction between the graft-chain unit and the branch unit in the main chain. The volume fractions of the A and B units in the shell and core phases are given by
and the mole fractions of the A and B units in the copolymer chain are written as
where
xB,s and
xB,c are the mole fractions of the B unit in the shell and core regions, respectively. The solvent volume fractions in the shell and core regions are given by
S,s = 1 −
A,s −
B,s and
S,c = 1 −
B,c, respectively.
We apply the Flory–Huggins theory [
16] to the flower micelle phase to formulate the mixing Gibbs energy per lattice site Δ
gm of the micelle phase, which consists of the mixing entropy Δ
S, the mixing enthalpy Δ
H, and the interfacial Gibbs energy 4π
Rcore2γ (
γ: the interfacial tension between the core and shell regions of the micelle). The formulation method is described in
Appendix B. The final result is written as
where
χAS,
χBS, and
χAB are the interaction parameters between S and A, between S and B, and between A and B, respectively,
κ is defined by Equation (B11), and (
a2/kBT)
γ is calculated by Equation (B13) with Equation (B14). The term ln
κ includes the conformational entropy loss at the formation of the flower micelle.
When the graft copolymer solution is homogeneous, the mixing Gibbs energy per lattice site Δ
gh is given by [
16]
with the average interaction parameter
between the graft copolymer chain and solvent, defined by [
17]
3. Results and Discussion
Because we did not consider above the interaction among flower micellar phases in the solution, the following discussion is limited to dilute solutions of random and periodic copolymers. Ueda et al. [
9] reported the molecular weight dependence of the micellization behavior for the amphiphilic alternating copolymer of sodium maleate and dodecyl vinyl ether, P(MAL/C12), in dilute aqueous solutions including 0.05 M NaCl. First, we examine theoretically the micellization behavior of an alternating copolymer mimicking P(MAL/C12).
In the lattice theory, the choice of the unit lattice site is rather arbitrary. Here, we assume the main-chain portion (the C
2 unit) of maleate or dodecyl vinyl ether monomer unit is chosen as the unit lattice site. Then, the hydrophobic dodecyl side chain is assumed to occupy six lattice sites, i.e.,
P′
G = 6. (The carboxy group and the ether oxygen atom in the maleate and dodecyl vinyl ether monomer units are not considered explicitly; they are assumed to be included in the main-chain portions). In aqueous solutions, a strong electrostatic repulsion acts among maleate units (the A unit), while a hydrophobic attraction acts among the C
2 units of the dodecyl group (the B unit). The strong electrostatic repulsion and hydrophobic attraction are expressed using a negative
χAS and positive
χBS, respectively. (To account for the long range electrostatic interaction, the unit lattice site may have to be larger than the C
2 unit, but the following results do not essentially change by the choice of the unit lattice site). Since we here focus on the amphiphilicity of the graft copolymer, we assume
χAB to be zero, as in the previous study [
12]. (The change of the
χAB value may be compensated by adjusting values of
χAS and
χBS).
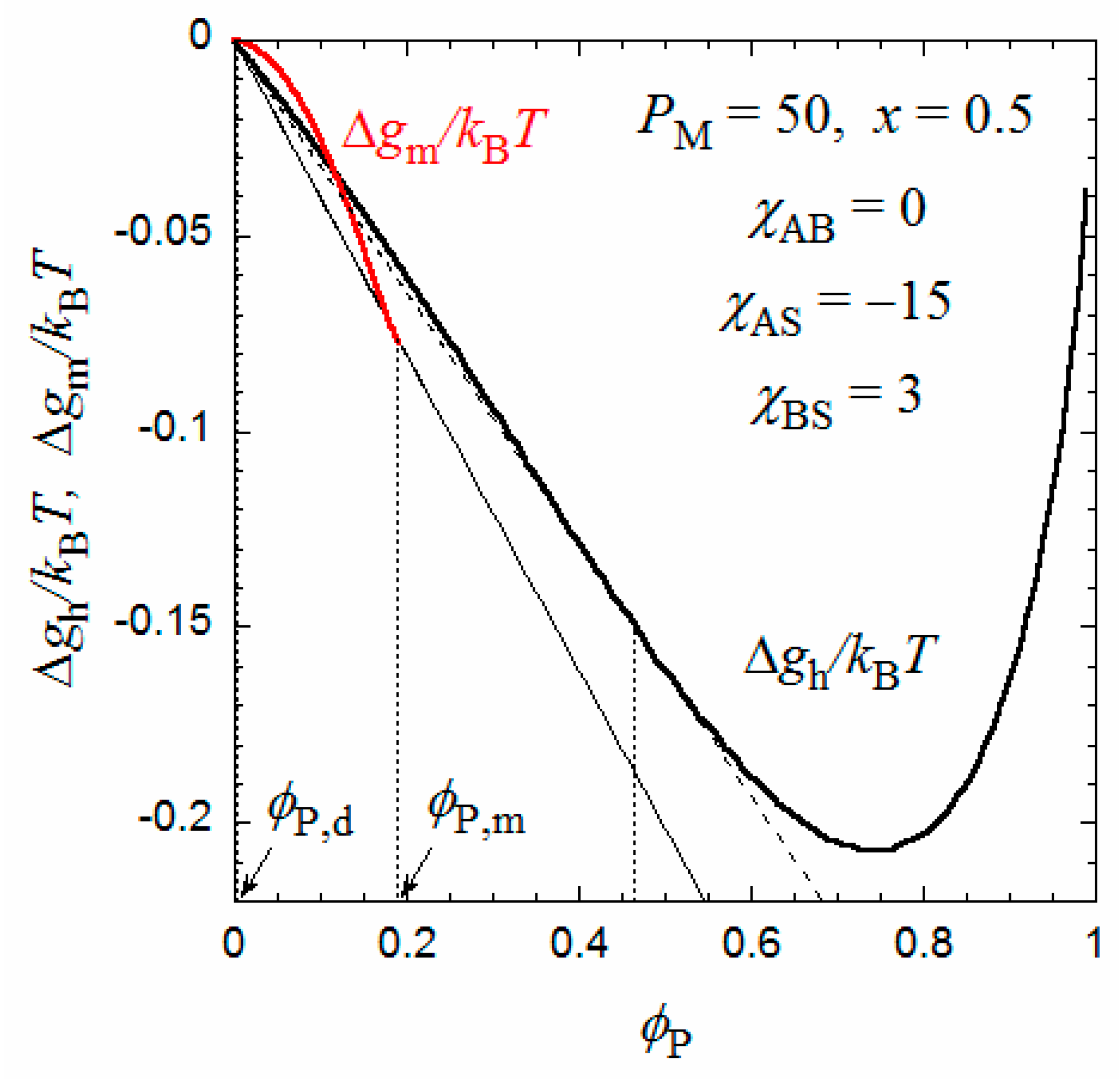
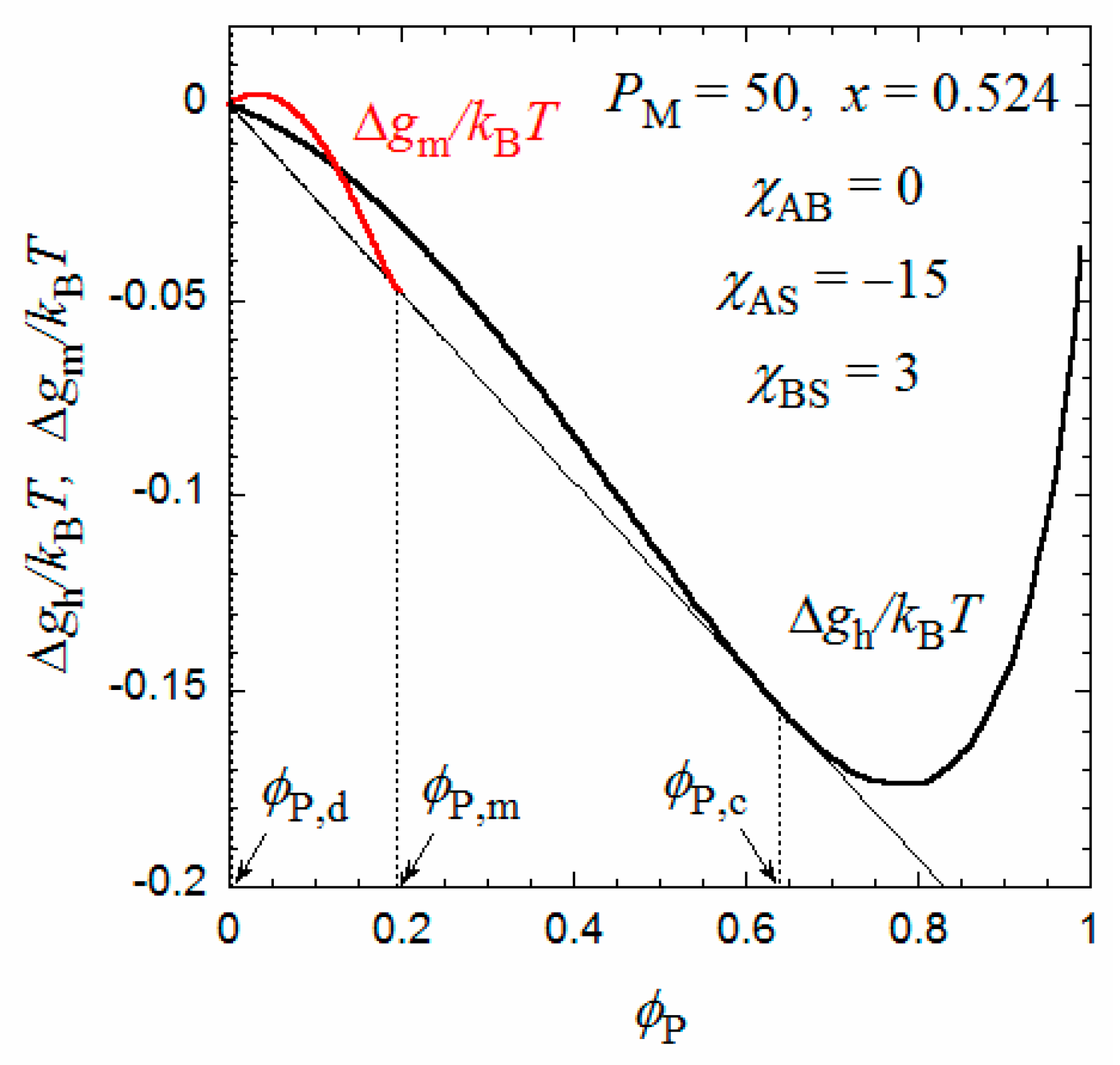
Figure 2 shows the copolymer concentration dependences of Δ
gm (red curve) and Δ
gh (black curve) calculated by Equations (11) and (12). We have chosen
PM = 50,
x = 0.5,
χAS = −15,
χBS = 3, and
χAB = 0 (
= 0.75). All remaining parameters included in Equation (11) can be calculated from
a = 0.25 nm (the contour length per the main-chain monomer (C
2) units), and
q = 3 nm,
qG = 0.53 nm, and
λ = 3 determined previously [
9]. We can draw a common tangent (the thin line) to the dilute side of the black curve and red curve. (It is seen that the black curve has a downward convex shape around
P = 0, if it is enlarged). The copolymer volume fractions at the two points of contact of the common tangent, denoted as
P,d and
P,m, are binodal concentrations of the coexisting dilute and micellar phases, respectively. The tangent line is below the common tangent line (the thin broken line) for the thick black curve for Δ
gh, indicating that the micellization is thermodynamically more stable than the phase separation into two homogeneous phases.
Similar curves for Δ
gm and Δ
gh were obtained for different
PM, and the volume fraction
P,m of the equilibrium micellar phase were determined by the above method. The aggregation number
m of the copolymer chains per micelle can be calculated from Equation (7), i.e.,
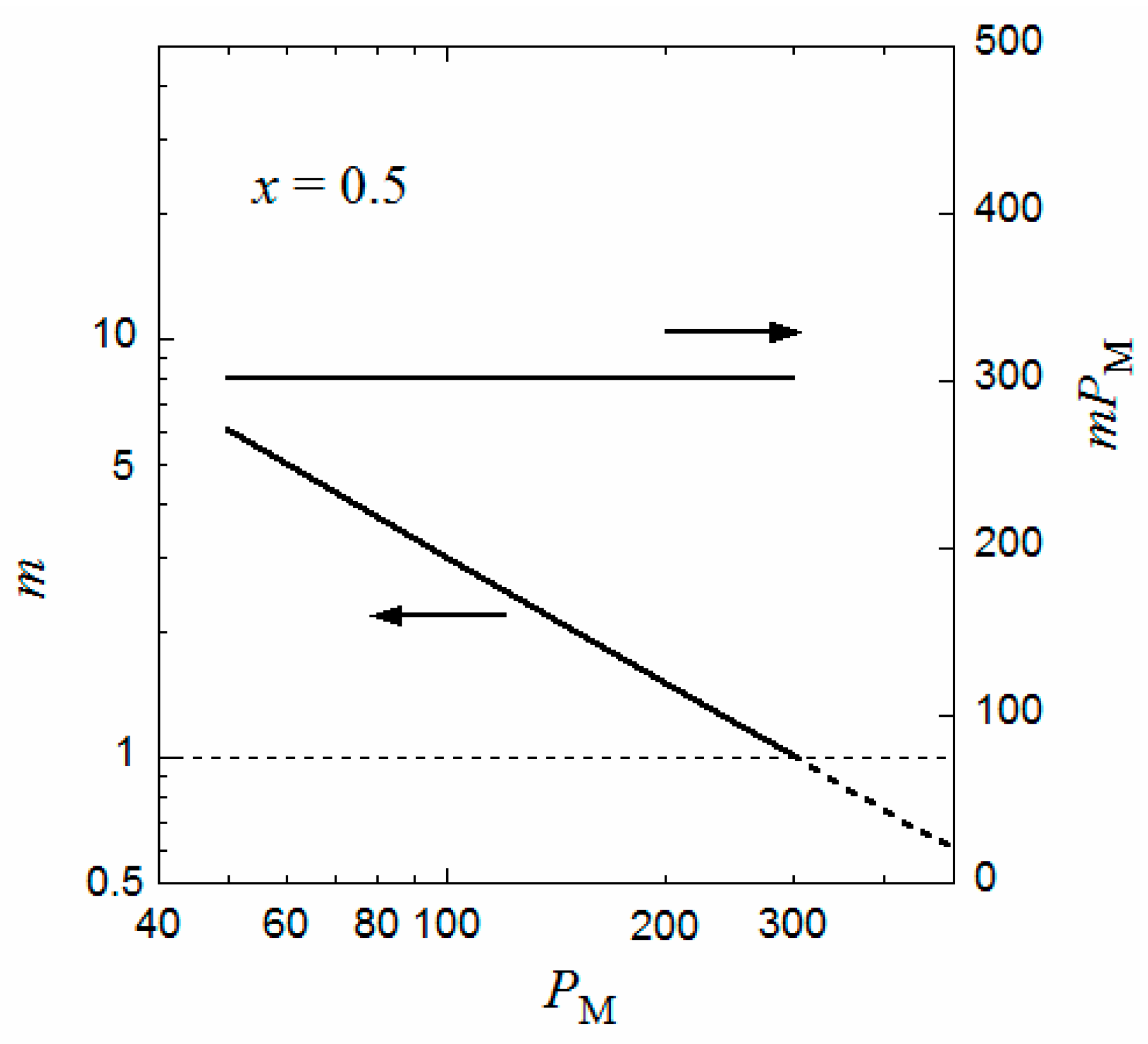
Figure 3 shows the degree of polymerization
PM dependence of
m such obtained as well as the product
mPM (the number of monomer units per micelle) at the interaction parameters identical to those in
Figure 2. It is seen that
m is inversely proportional to
PM, and the product
mPM is independent of
PM. (Because
P is proportional to
PM and
R is independent of
PM, the inverse proportionality of
m to
PM comes from the
PM independence of
P,m calculated from the comparison between of the Δ
gm and Δ
gh curves). This relation was observed experimentally for P(MAL/C12) in 0.05 M aqueous NaCl solution [
9] as well as for a random copolymer of poly(ethylene glycol) methyl ether methacrylate and dodecyl methacrylate, P(PEGMA/DMA), in water [
18]; however, for P(PEGMA/DMA) with
x = 0.5, the constant
mPM is slightly larger than 300. The value of
mPM changes by values of
q,
λ, and the interaction parameters. It is noted that the formulation of Δ
gm in the previous section can apply both to periodic and random copolymers.
When
PM approaches 300 in
Figure 3,
m tends to unity, and
P,d corresponding to the critical micelle concentration (cmc) of the coexisting dilute phase becomes very low (not shown). That is, when
PM approaches 300, the flower micelle is formed by one copolymer chain (the unimer micelle), and the cmc tends to zero. This situation resembles the liquid–liquid phase separation in a homopolymer polymer solution with an infinitely high-molecular-weight polymer, where the polymer volume fraction at the critical point is predicted to be zero by the conventional Flory–Huggins theory [
16].
When the same calculation of
m is performed where
PM > 300, the inverse proportionality of
m to
PM still holds even if
PM exceeds 300, as indicated by the dashed line in
Figure 3. However, because the aggregation number is less than unity, some portion of the main chain is not included in the flower micelle at
PM > 300. For example, at
PM = 600 where
m = 0.5, half of the main chain is not included in the flower micelle. This half main-chain portion may form another flower micelle. As a result, the whole copolymer chain forms a double-core flower necklace. (Strictly speaking, the double-core flower necklace needs a bridge chain connecting two unit flowers, so that
PM must be slightly larger than 600 to form the double-core flower necklace). In fact, Ueda et al. [
9] reported the transition from the flower micelle to the flower necklace at
PM exceeding 300.
The flower micelle is formed also by amphiphilic random copolymers with hydrophobic dodecyl side chains of
x < 0.5 in aqueous solutions. Next, we examine the hydrophobic monomer content dependence of the micellization for an aqueous solution of an amphiphilic random copolymer, calculated in the same way from the Δ
gm and Δ
gh curves as in
Figure 2. The number
λ of side chains included in the core at each root of the loop appearing in Equation (2) may be dependent on the monomer content
x. In the limit of
x = 1/
Ploop, each loop chain has only one hydrophobic side chain on average. Thus,
λ = 1 at
x = 1/
Ploop. When
x increases,
λ may first increase from unity and approach an asymptotic value. For a given value of
λ,
P,d and
P,m of the coexisting dilute and micellar phases can be calculated as functions of
x from the curves of Δ
gm and Δ
gh as mentioned above.
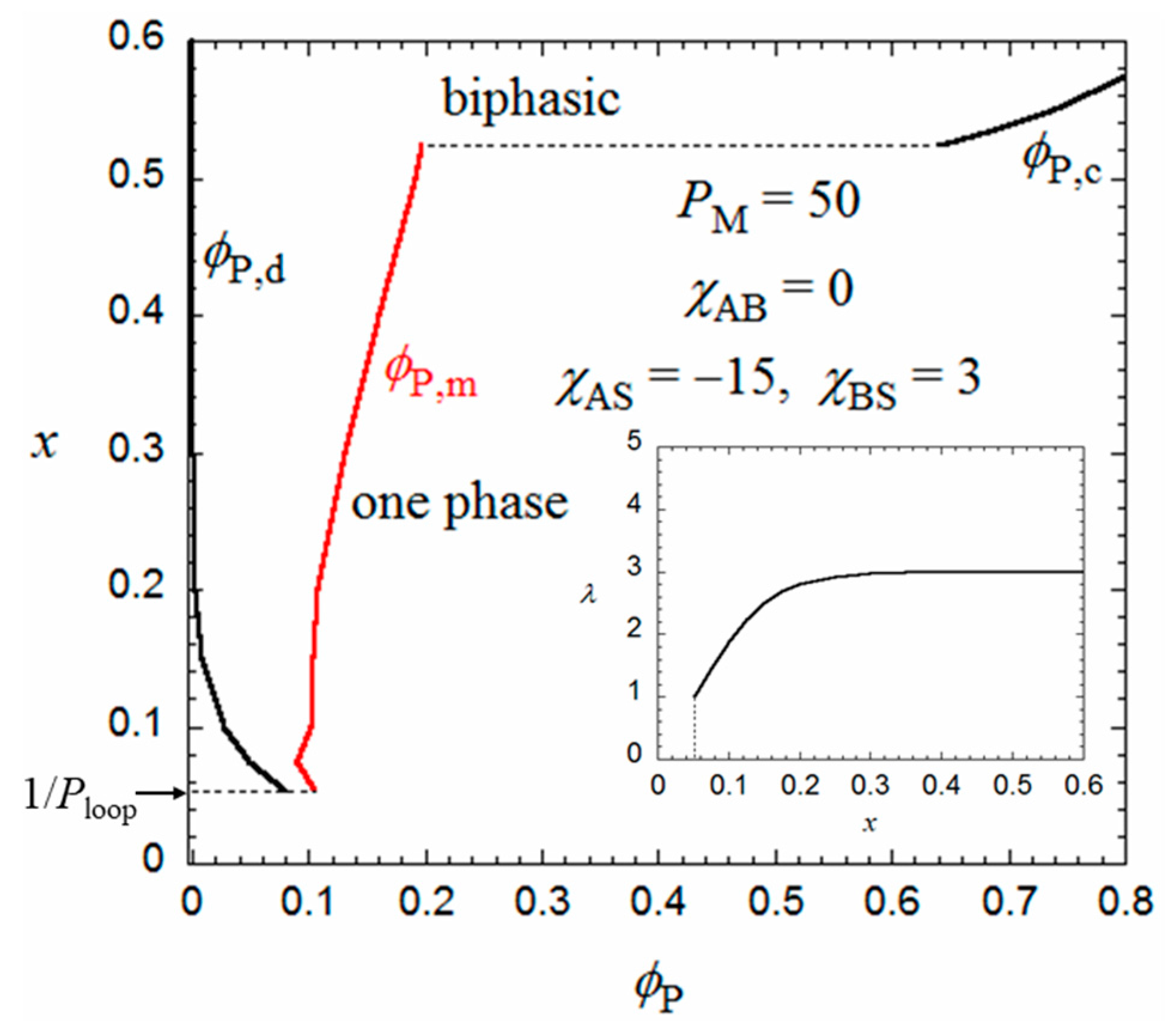
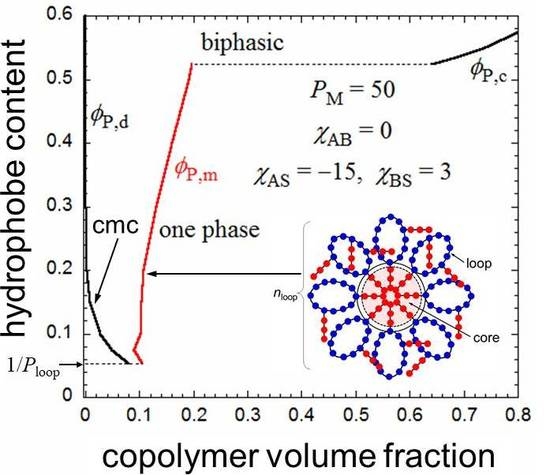
Figure 4 shows
ϕP,d and
ϕP,m obtained for the amphiphilic random copolymer with a
PM of 50 and the same interaction parameters used in
Figure 2 and
Figure 3, in the
x-
P phase diagram. The
x dependence of
λ used is shown in the insert of
Figure 4. When
x is decreased from 0.5,
P,d (cmc) increases, and the copolymer in a dilute solution (
P < 0.08) transforms from the flower micelle to the random coil at passing the bimodal curve for
P,d (cmc). At
x < 1/
Ploop, the loop size of the flower micelle should be larger than the minimum size given by Equation (1). We do not discuss such a loose flower micelle here.
On the other hand, when
x increases from 0.5, the Δ
gh −
P curve goes down relative to the Δ
gm −
P curve, and as shown in
Figure 5, at
x = 0.524, we can draw a common tangent (the thin line) to the dilute and concentrated sides of the black curve (Δ
gh) and the red curve (Δ
gm). When
x > 0.524, the phase separation into dilute and concentrated homogeneous phases with concentrations
P,d and
P,c becomes thermodynamically more stable than the micellization. As a result, the phase gap in the
x-
P phase diagram is abruptly enlarged when
x > 0.524, as shown in
Figure 4. To the best of my knowledge, there have hitherto been no reports of the corresponding crossover from micellization to liquid–liquid phase separation as the hydrophobic content
x increases.
Eisenberg et al. [
19] investigated the random copolymer of styrene and methacrylic acid with
x ~ 0.8, which was first dissolved in dioxane or tetrahydrofuran (THF), followed by the addition of water, and observed “large compound micelles” and “bowl-shaped aggregates” by transmission electronic microscopy (TEM). Here, the “large compound micelle” is the large homogeneous polymer-rich spheres, corresponding to the droplet of the concentrated homogeneous phase formed by the liquid–liquid phase separation, predicted in
Figure 4, and a “bowl-shaped aggregate” may be formed from the concentrated-phase droplet in which solvent bubbles are trapped [
19]. Wang et al. [
20] reported the formation of uniform colloidal spheres by an amphiphilic random copolymer, poly{2-[4-(phenylazo)phenoxy]ethyl acrylate-
co-acrylic acid}, where
x = 0.5 in THF–water mixtures with high water concentrations. This may be another example of the liquid–liquid phase separation of the amphiphilic random copolymer in solution. Zhang et al. [
21] studied the self-association of amphiphilic graft (periodic) copolymers in a hypothetical solution of the two-dimensional space by the self-consistent field theory. Although they assumed perfect flexibility and comparable chain lengths of the main and graft chains, being different conditions from the present study, they observed a “large compound micelle” at higher graft density (i.e., higher hydrophobic content
x) under weaker amphiphilicity (cf. Figure 8a in [
21], where the graft chain number = 5).
Yusa et al. [
22] found a transition from the unimer micelle to the single random coil chain of a random copolymer of hydrophilic sodium 2-(acrylamido)-2-methylpropanesulfonate and hydrophobic 11-acrylamidoundecanoic acid (AmU) where
x = 0.5 in 0.1 M aqueous NaCl solution by changing pH. At pH = 3, where the carboxy group is not ionized, AmU was strongly hydrophobic, and the copolymer formed a unimer micelle with
m = 1. The degree of polymerization
PM of the copolymer sample (= 475) was slightly larger than 300 (cf.
Figure 3), maybe due to the difference in the parameters, e.g.,
P’
G and
λ, from those used in
Figure 3. On the other hand, at pH = 9, where the carboxy group of AmU is ionized, the copolymer was transformed to a random coil. In
Figure 2, the Δ
gm curve goes up and the Δ
gh has no inflection point when
χBS is decreased from 3, i.e., AmU becomes more hydrophilic. As a result, the random coil conformation in the homogeneous phase becomes more stable than the flower micelle, which is consistent with Yusa et al.’s finding. The transition from the unimer micelle to the single random coil chain by decreasing
x, predicted in
Figure 4, was reported by Fujimoto and Sato [
11].
Recently, several authors have reported that amphiphilic random copolymers form vesicles in dilute solutions [
23,
24,
25,
26], which was not considered in the present study. Zhu and Liu [
24] investigated vinyl polymers bearing L-glutamic acid moieties and dodecyl groups in the random sequence to find the vesicle in water at a high hydrophobic content
x (>0.75). Their random copolymer samples possess low degrees of polymerization (<36). For these samples to form the flower micelle,
nloop should be less than 2 and one loop chain should bear many hydrophobes. The present theory may not be able to be applied to such random copolymers.
Tian et al. [
25] observed vesicles as well as hollow tubes and wormlike rods formed by poly(hydroxyethyl methacrylate) (PHEMA) partially and randomly modified by the hydrophobic 2-diazo-1,2-naphthoquinone in solution. These copolymer samples were dissolved in dimethyl- formamide, followed by the addition of water, and finally dialyzed against water to form the vesicle. Because even PHEMA is insoluble in water, the vesicle formed must not be in the thermodynamically stable state, which cannot be treated in the present statistical thermodynamic theory.
Ghosh et al. [
26] reported that an amphiphilic random copolymer of hydrophilic tri(oxyethylene) methacrylamide and hydrophobic
n-octyl methacrylate exhibited a thermally induced vesicle to spherical micelle transition. However, it should be noted that the illustration of the spherical micelle by these authors (cf. Scheme 1 in [
26]) was inconsistent with the experimental TEM observation of spherical aggregates (diameter in the range of 70–80 nm) at 60 °C. In the illustration, the hydrophilic and hydrophobic side chains were in the coronal and core regions of the micelle, respectively, and the whole copolymer main chain was confined to the corona-core interface. If this is the case, the diameter of the micelle must be equal to twice the sum of the hydrophilic and hydrophobic side chain lengths. Even if the side chains are fully extended, such an estimated diameter is as small as 6 nm, which is much smaller than the diameter of the spherical aggregate at 60 °C. Thus, the spherical aggregate at 60 °C may not be the spherical micelle indicated in their illustration, but the phase-separated concentrated phase droplet, because both kinds of side chains are hydrophobic at 60 °C above the lower critical solution temperature [
26].