A Numerical Method Charactering the Electromechanical Properties of Particle Reinforced Composite Based on Statistics
Abstract
:1. Introduction
2. Improved Visco-Hyperelastic Model
2.1. Strain Energy Potential and Viscoelasticity
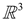 is introduced to illustrate the model. At the reference state t = 0, the undeformed stress-free configuration will be maintained. At time t, force field and electric field are applied on the outer space and , respectively. Meanwhile, the system has changed to current configuration . The deformation is described by function , which maps a reference particle X in to its deformed position in . The associated deformation gradient will be denoted by , and identifies its determinant, as shown in Figure 1.
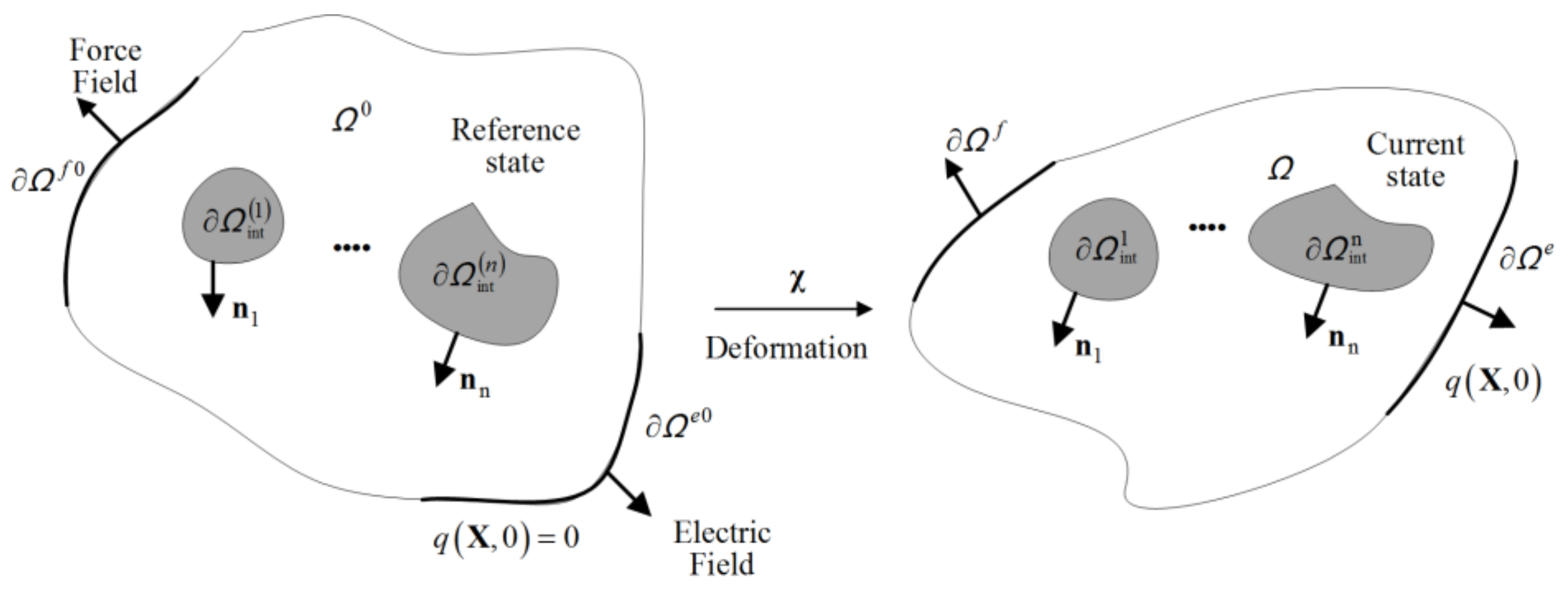
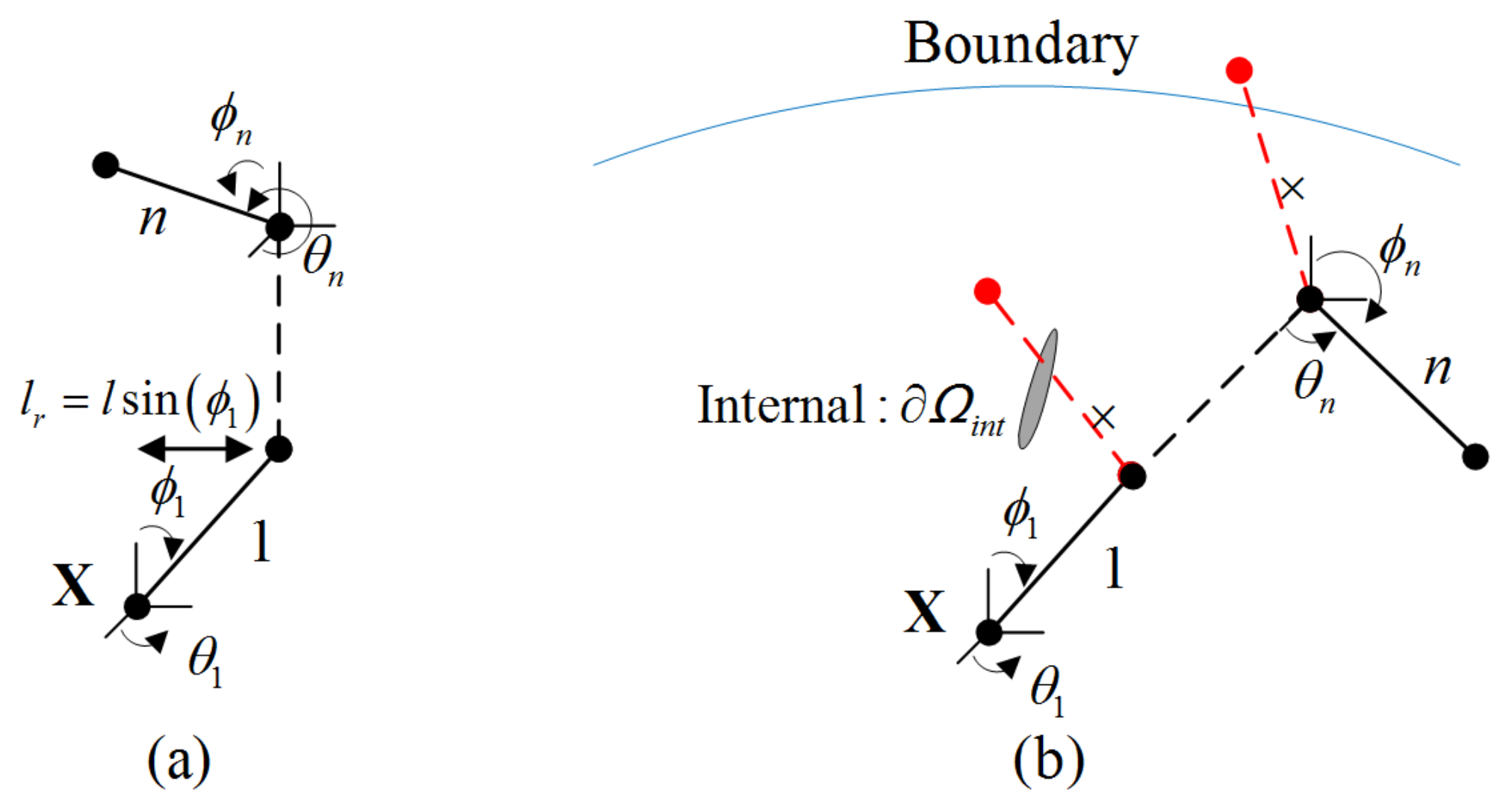
is introduced to illustrate the model. At the reference state t = 0, the undeformed stress-free configuration will be maintained. At time t, force field and electric field are applied on the outer space and , respectively. Meanwhile, the system has changed to current configuration . The deformation is described by function , which maps a reference particle X in to its deformed position in . The associated deformation gradient will be denoted by , and identifies its determinant, as shown in Figure 1.2.2. Distribution of Polymer Chain
2.3. The Mechanical Model of Soft Materials
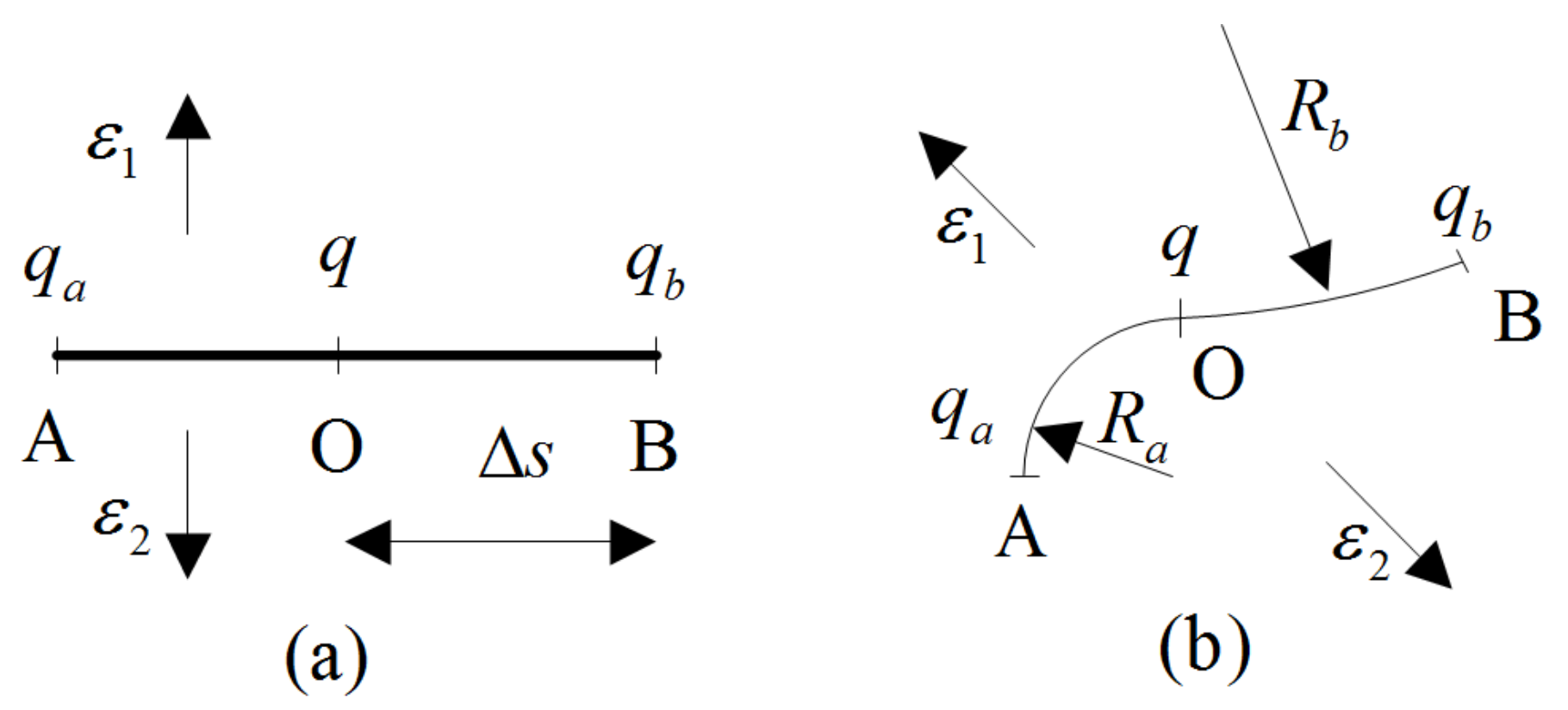
2.4. Re-Distribution of Charge on the Surface
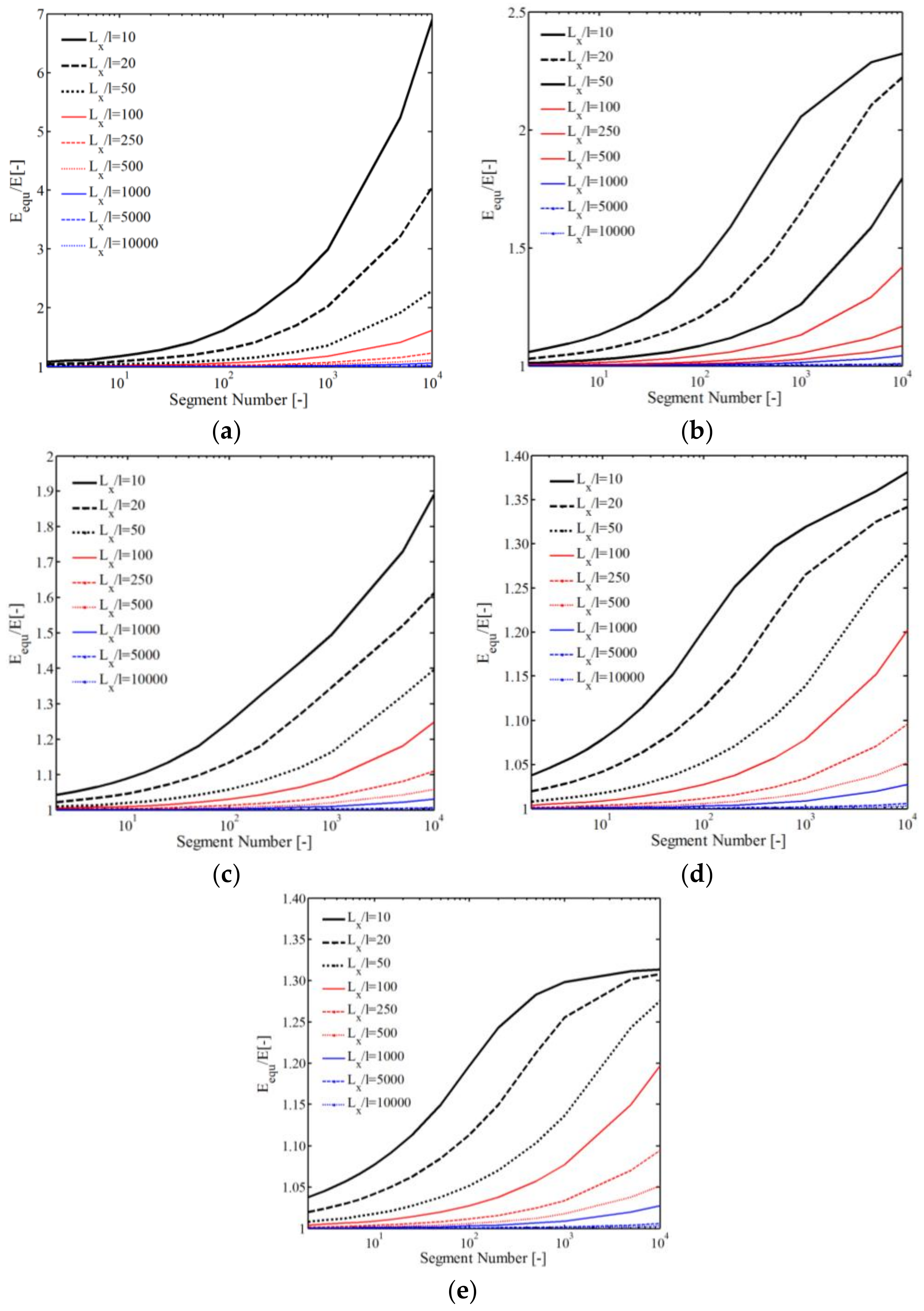
3. The Effect of External Structures on the Electromechanical Properties
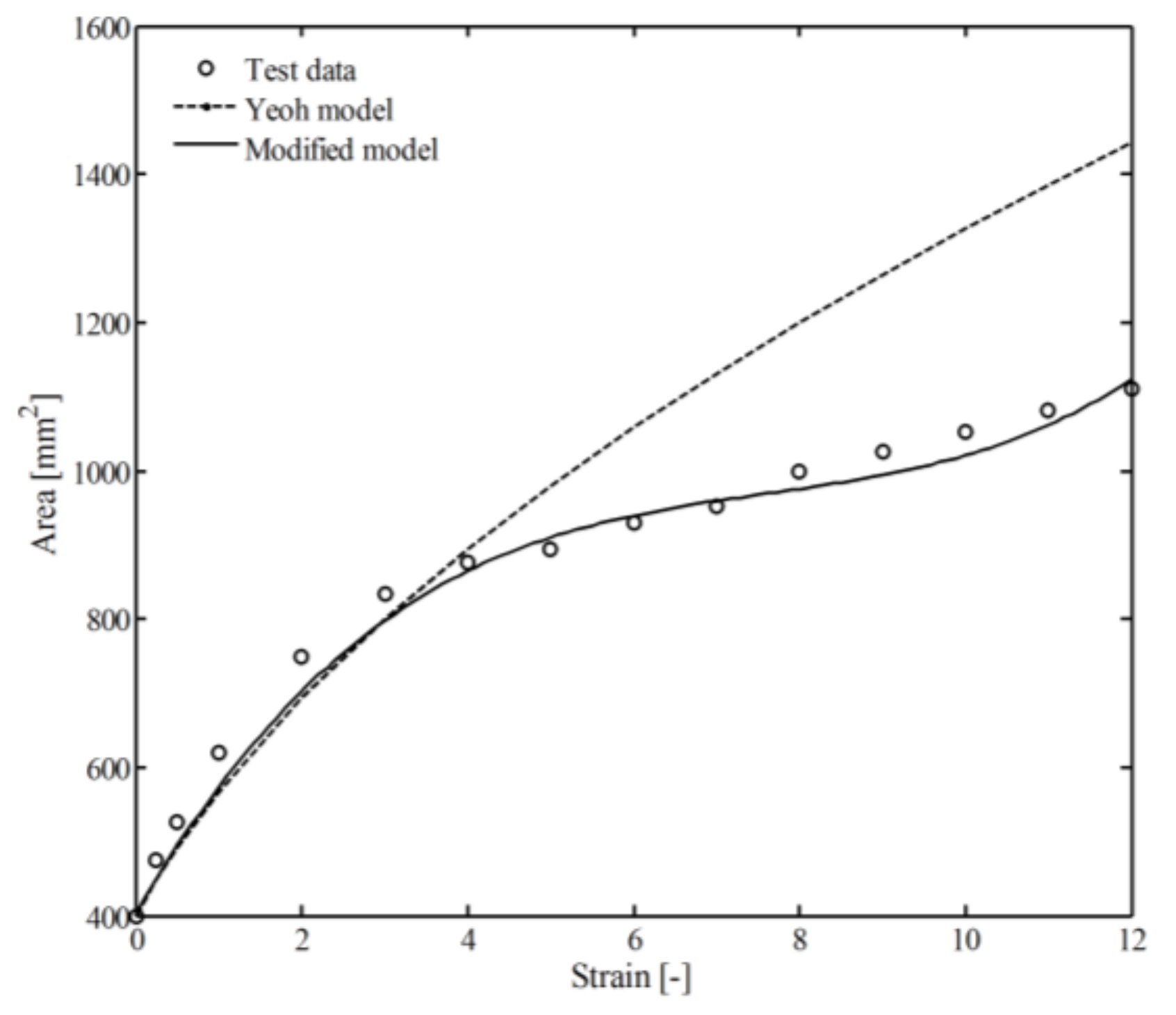
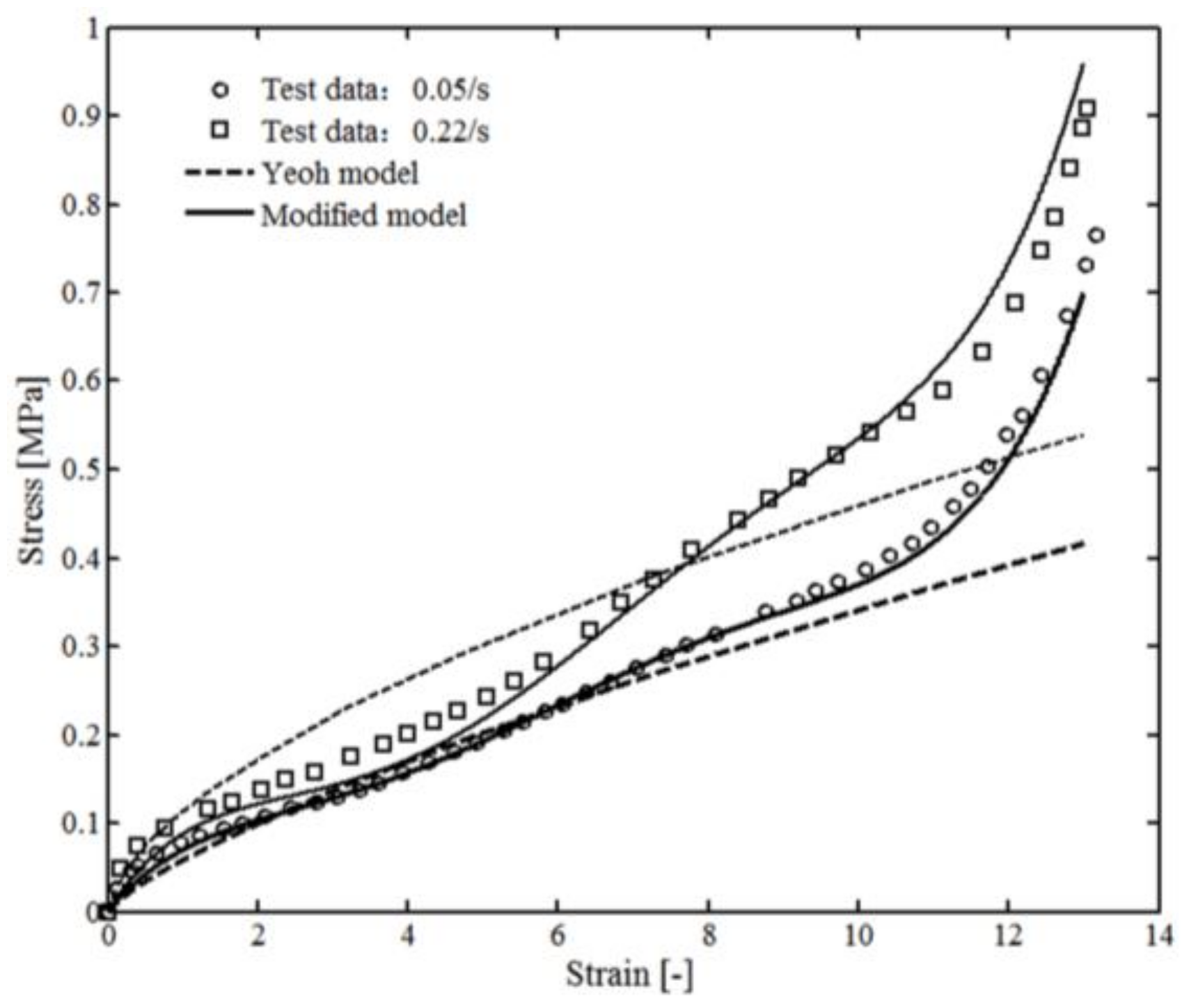
3.1. Determination of the Material Parameters
3.2. Simulation of Rectangle Sample
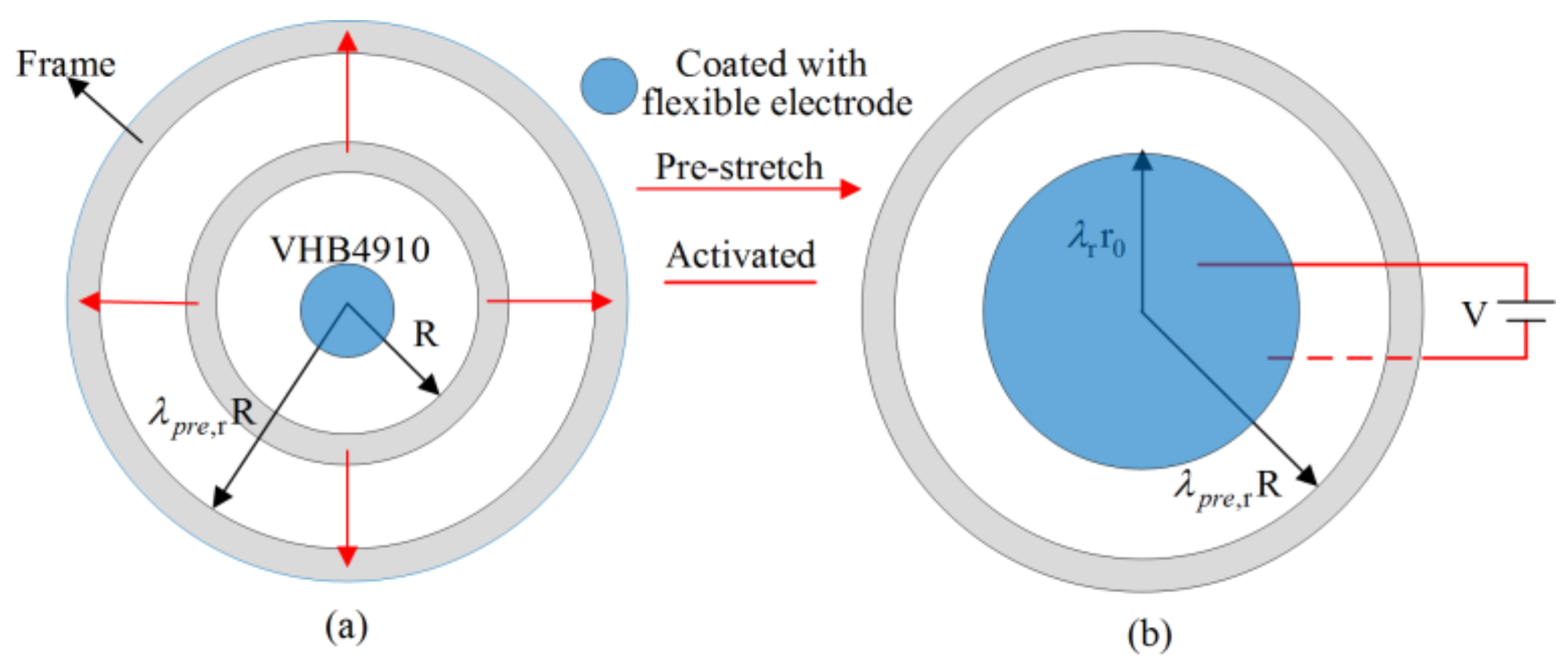
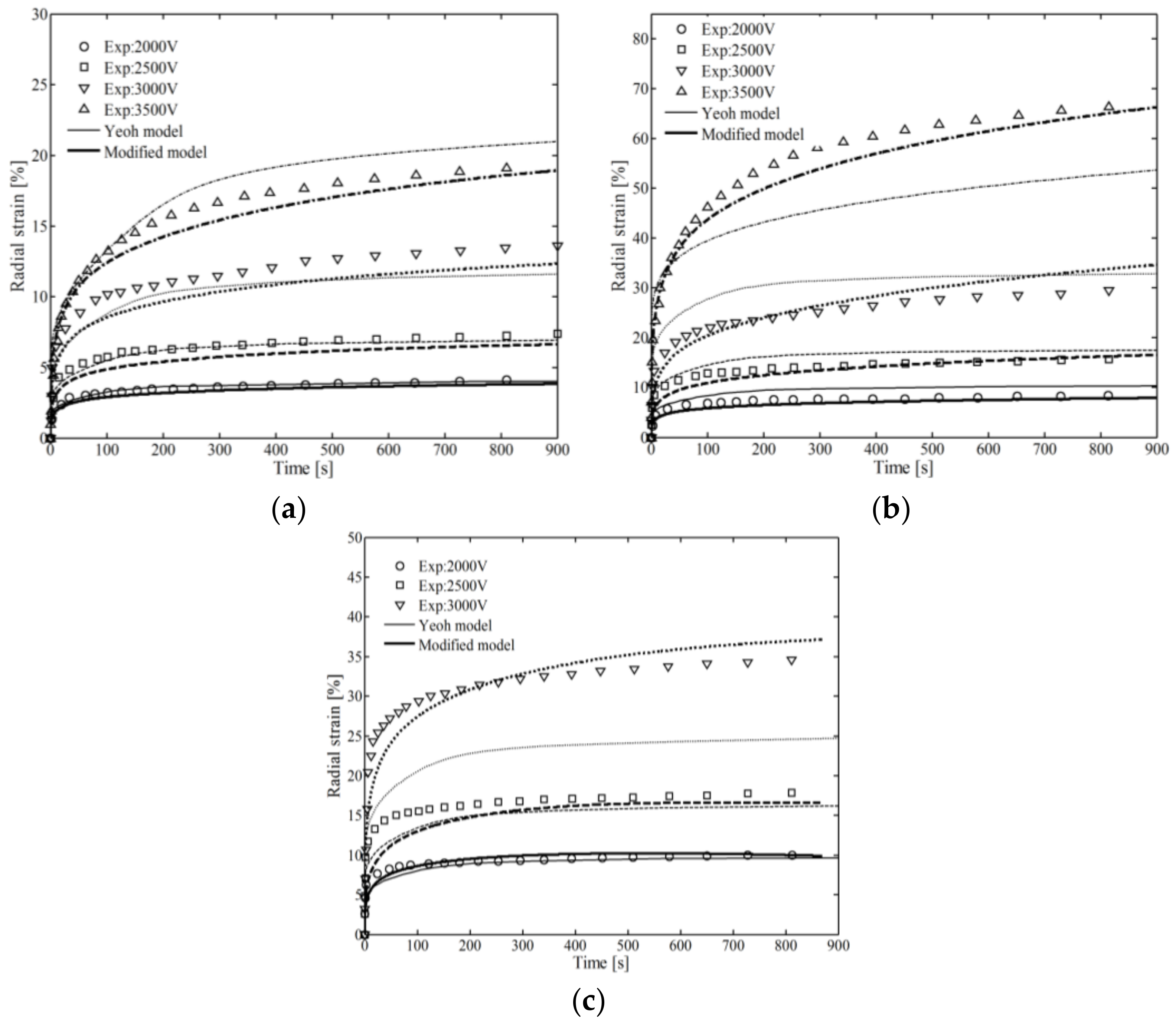
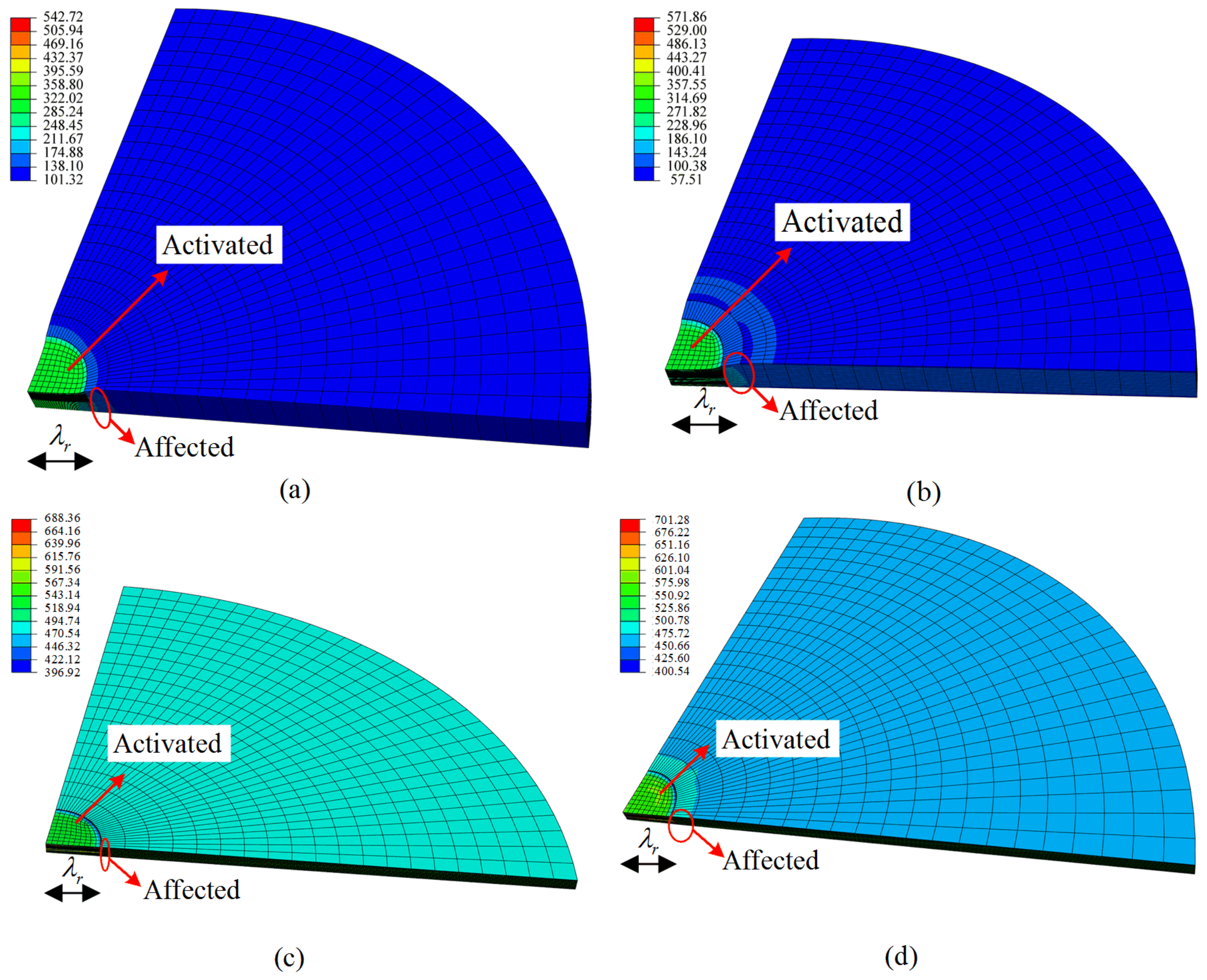
3.3. Simulation of Circular Dielectric Elastomer
4. The Effect of Internal Particles on the Electromechanical Properties
4.1. Determination of the Material Parameters: Local Density
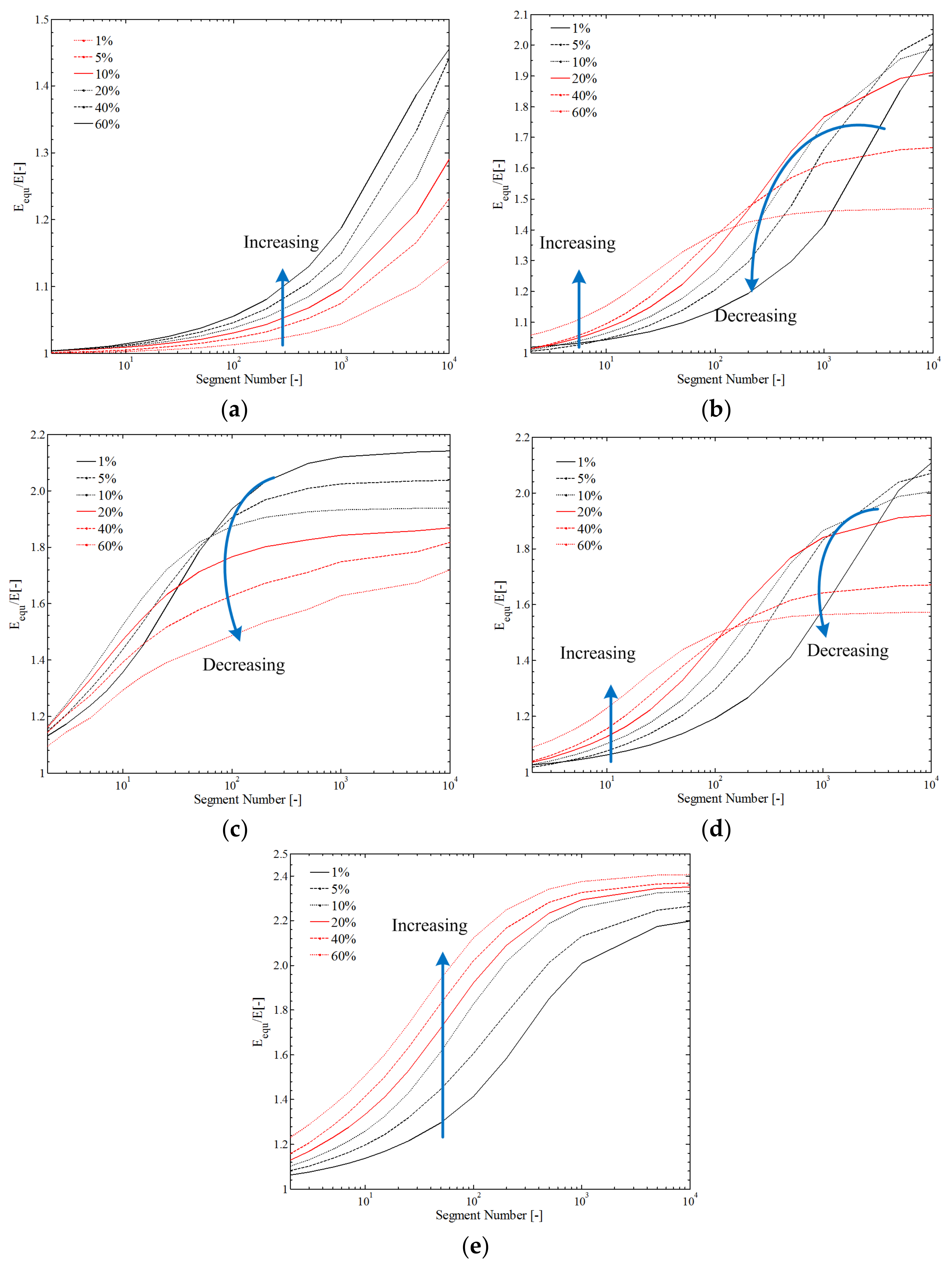
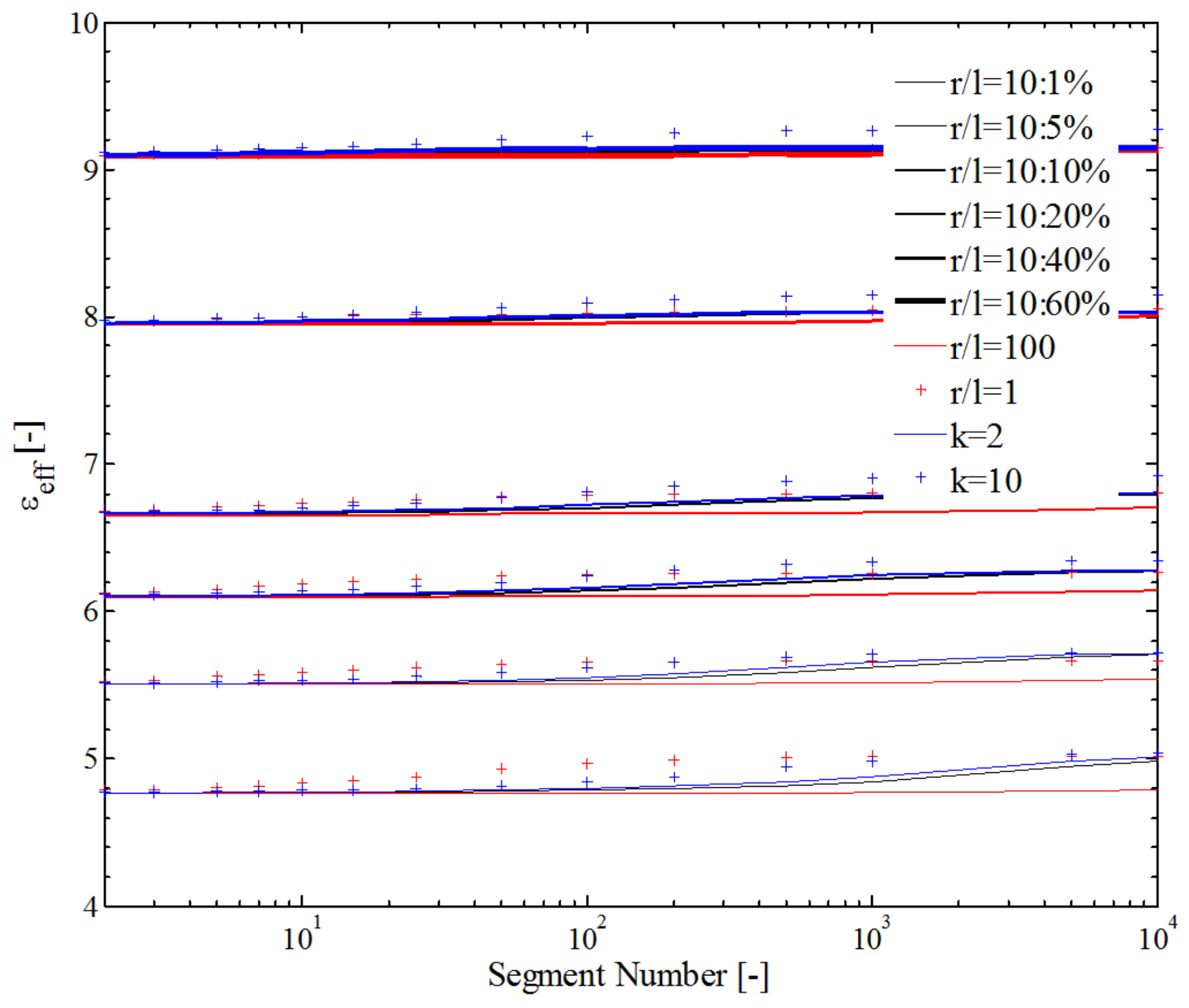
4.2. Simulation of the Physical Parameters
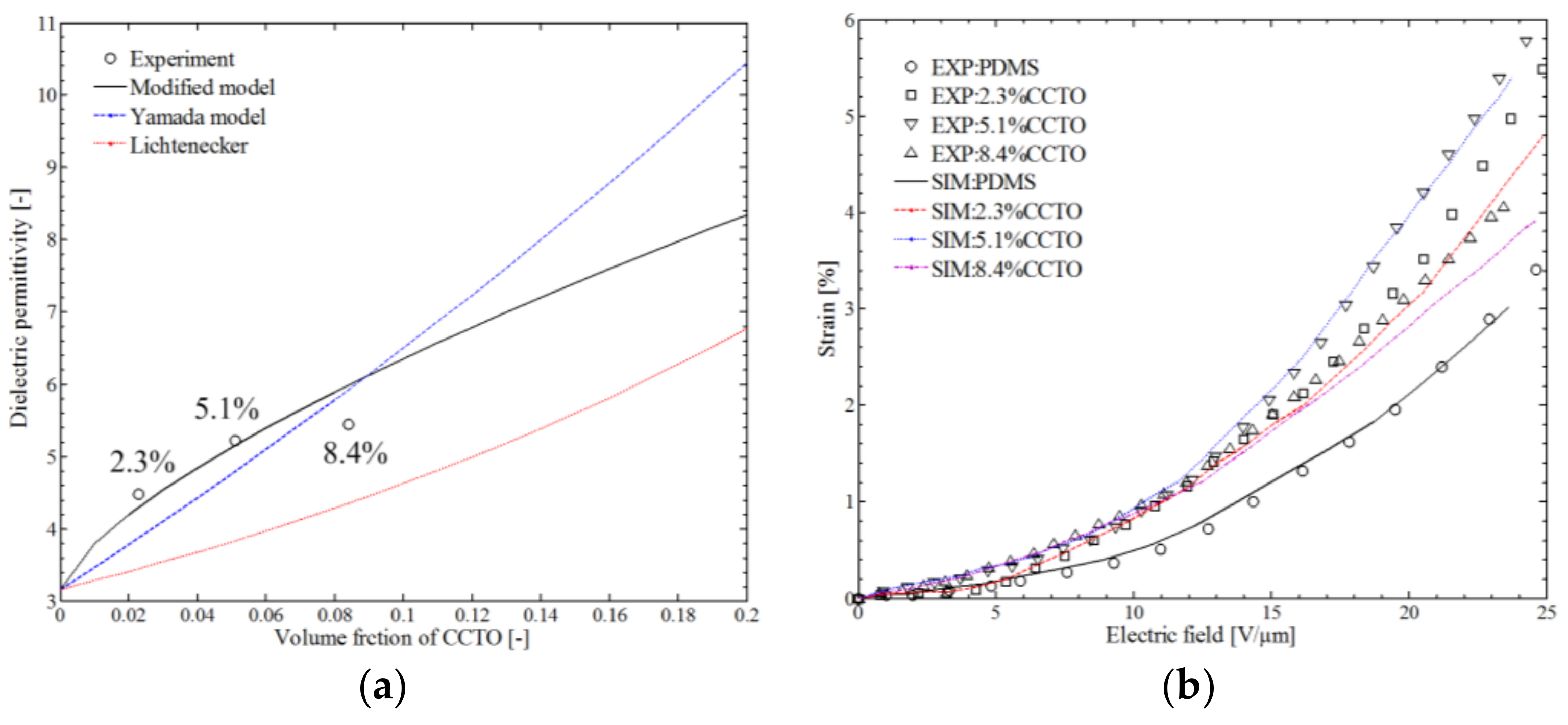
4.3. Simulation of CCTO-PDMS
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brochu, P.; Pei, Q. Advances in Dielectric Elastomers for Actuators and Artificial Muscles. Marcromol. Rapid Commun. 2010, 31, 10–36. [Google Scholar] [CrossRef] [PubMed]
- Bar-Cohen, Y. Actuation of biologically inspired intelligent robotics using artificial muscles. Ind. Robot Int. J. 2003, 30, 331–337. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Electromechanical coupling in dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 138, 384–393. [Google Scholar] [CrossRef]
- Koh, S.J.A.; Zhao, X.; Suo, Z.G. Maximal energy that can be converted by a dielectric elastomer generator. Appl. Phys. Lett. 2009, 94, 262902. [Google Scholar] [CrossRef]
- Kofod, G.; Sommer-Larsen, P.; Kornbluh, R.; Pelrine, R. Actuation response of polyacrylate dielectric elastomers. J. Intell. Mater. Syst. Struct. 2003, 14, 787–793. [Google Scholar] [CrossRef]
- Kofod, G. The static actuation of dielectric elastomer actuators: How does pre-stretch improve actuation? J. Phys. D Appl. Phys. 2008, 41, 215405. [Google Scholar] [CrossRef]
- Schmidt, A.; Bergamini, A.; Kovacs, G.; Mazza, E. Multiaxial mechanical characterization of interpenetrating polymer network reinforced acrylic elastomer. Exp. Mech. 2011, 51, 1421–1433. [Google Scholar] [CrossRef]
- Yang, S.; Benitez, R.; Fuentes, A.; Lozano, K. Dielectric analysis of VGCNF reinforced polyethylene composites. Compos. Sci. Technol. 2007, 67, 1159–1166. [Google Scholar] [CrossRef]
- Mishra, P.; Kumar, P. Dielectric properties of 0.25 (BZT–BCT)–0.75 [(1 − x) PVDF–xCCTO] (x = 0.02, 0.04, 0.06, 0.08 and 0.1) composites for embedded capacitor applications. Compos. Sci. Technol. 2013, 88, 26–32. [Google Scholar] [CrossRef]
- Lai, M.; Yu, S.; Sun, R.; Zeng, X.; Luo, S. Effects and mechanism of graft modification on the dielectric performance of polymer–matrix composites. Compos. Sci. Technol. 2013, 89, 127–133. [Google Scholar] [CrossRef]
- Qu, S.; Suo, Z. A finite element method for dielectric elastomer transducers. Acta Mech. Solida Sin. 2012, 25, 459–466. [Google Scholar] [CrossRef]
- Suo, Z.; Zhao, X.; Greene, W.H. A nonlinear field theory of deformable dielectrics. J. Mech. Phys. Solids 2008, 56, 467–486. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Yang, R. Effect of a metallic coating on the thermal conductivity of carbon nanofiber–dielectric matrix composites. Compos. Sci. Technol. 2015, 109, 18–24. [Google Scholar] [CrossRef]
- Ren, J.; Yu, D.; Feng, L.; Wang, G.; Lv, G. Nanocable-structured polymer/carbon nanotube composite with low dielectric loss and high impedance. Compos. Part. A Appl. Sci. Manuf. 2017, 98, 66–75. [Google Scholar] [CrossRef]
- Bai, J.B.; Allaoui, A. Effect of the length and the aggregate size of MWNTs on the improvement efficiency of the mechanical and electrical properties of nanocomposites—Experimental investigation. Compos. Part. A Appl. Sci. Manuf. 2003, 34, 689–694. [Google Scholar] [CrossRef]
- Liu, S.; Sun, H.; Ning, N.; Zhang, L.; Tian, M.; Zhu, W. Aligned carbon nanotubes stabilized liquid phase exfoliated graphene hybrid and their polyurethane dielectric elastomers. Compos. Sci. Technol. 2016, 125, 30–37. [Google Scholar] [CrossRef]
- Wang, B.; Jiao, Y.; Gu, A.; Liang, G.; Yuan, L. Dielectric properties and mechanism of composites by superposing expanded graphite/cyanate ester layer with carbon nanotube/cyanate ester layer. Compos. Sci. Technol. 2014, 91, 8–15. [Google Scholar] [CrossRef]
- Park, K.Y.; Han, J.H.; Lee, S.B.; Yi, J.W. Microwave absorbing hybrid composites containing Ni–Fe coated carbon nanofibers prepared by electroless plating. Compos. Part. A Appl. Sci. Manuf. 2011, 42, 573–578. [Google Scholar] [CrossRef]
- Ramajo, L.A.; Cristóbal, A.A.; Botta, P.M.; López, J.P.; Reboredo, M.M.; Castro, M.S. Dielectric and magnetic response of Fe3O4/epoxy composites. Compos. Part. A Appl. Sci. Manuf. 2009, 40, 388–393. [Google Scholar] [CrossRef]
- Tang, H.; Wang, P.; Zheng, P.; Liu, X. Core-shell structured BaTiO3@polymer hybrid nanofiller for poly (arylene ether nitrile) nanocomposites with enhanced dielectric properties and high thermal stability. Compos. Sci. Technol. 2016, 123, 134–142. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, M.; Li, H.; Wen, Y.; Wang, C.; Pu, Y. Enhanced dielectric properties in poly (vinylidene fluoride) composites by nanosized Ba(Fe0.5Nb0.5)O3 powders. Compos. Sci. Technol. 2015, 117, 410–416. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, F.; Hu, G.; Zhang, C.; Wang, M.; Qin, M.; Wang, L. Characterization and dielectric properties of modified Ba0.6Sr0.4TiO3/poly (vinylidene fluoride) composites with high dielectric tenability. Compos. Sci. Technol. 2015, 118, 94–100. [Google Scholar] [CrossRef]
- Prakash, B.S.; Varma, K.B.R. Dielectric behavior of CCTO/epoxy and Al-CCTO/epoxy composites. Compos. Sci. Technol. 2007, 67, 2363–2368. [Google Scholar] [CrossRef]
- Srivastava, A.; Maiti, P.; Kumar, D.; Parkash, O. Mechanical and dielectric properties of CaCu3Ti4O12 and La doped CaCu3Ti4O12 poly (vinylidene fluoride) composites. Compos. Sci. Technol. 2014, 93, 83–89. [Google Scholar] [CrossRef]
- Romasanta, L.J.; Leret, P.; Casaban, L.; Hernández, M.; de la Rubia, M.A.; Fernández, J.F.; Kenny, J.M.; Lopez-Manchado, M.A.; Verdejo, R. Towards materials with enhanced electro-mechanical response: CaCu3Ti4O12-polydimethylsiloxane composites. J. Mater. Chem. 2012, 22, 24705–24712. [Google Scholar] [CrossRef] [Green Version]
- Pukánszky, B. Interfaces and interphases in multicomponent materials: Past, present, future. Eur. Polym. J. 2005, 41, 645–662. [Google Scholar] [CrossRef]
- Romasanta, L.J.; Lopez-Manchado, M.A.; Verdejo, R. Increasing the performance of dielectric elastomer actuators: A review from the materials perspective. Prog. Polym. Sci. 2015, 51, 188–211. [Google Scholar] [CrossRef]
- Kuhn, W.; Grün, F. Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelastischer Stoffe. Kolloid Z. 1942, 101, 248–271. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J., Jr. Statistical mechanics of cross-linked polymer networks I. Rubberlike elasticity. J. Chem. Phys. 1943, 11, 512–520. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity; Oxford University Press: New York, NY, USA, 1975. [Google Scholar]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S.; Lulei, F. A micro-macro approach to rubber-like materials-Part I: The non-affine micro-sphere model of rubber elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S. A micro-macro approach to rubber-like materials. II. The micro-sphere model of finite rubber viscoelasticity. J. Mech. Phys. Solids 2005, 53, 2231–2258. [Google Scholar] [CrossRef]
- Göktepe, S.; Miehe, C. A micro–macro approach to rubber-like materials. Part III: The micro-sphere model of anisotropic Mullins-type damage. J. Mech. Phys. Solids 2005, 53, 2259–2283. [Google Scholar] [CrossRef]
- Dargazany, R.; Itskov, M. A network evolution model for the anisotropic Mullins effect in carbon black filled rubbers. Int. J. Solids Struct. 2009, 46, 2967–2977. [Google Scholar] [CrossRef]
- Itskov, M.; Knyazeva, A. A rubber elasticity and softening model based on chain length statistics. Int. J. Solids Struct. 2016, 80, 512–519. [Google Scholar] [CrossRef]
- Khiêm, V.N.; Itskov, M. Analytical network-averaging of the tube model: Rubber elasticity. J. Mech. Phys. Solids 2016, 95, 254–269. [Google Scholar] [CrossRef]
- Dargazany, R.; Itskov, M. Constitutive modeling of the Mullins effect and cyclic stress softening in filled elastomers. Phys. Rev. E 2013, 88, 012602. [Google Scholar] [CrossRef] [PubMed]
- Cohen, N.; Debotton, G. Multiscale analysis of the electromechanical coupling in dielectric elastomers. Eur. J. Mech. A Solids 2014, 48, 48–59. [Google Scholar] [CrossRef]
- Cohen, N.; Dayal, K.; Debotton, G. Electroelasticity of polymer networks. J. Mech. Phys. Solids 2016, 92, 105–126. [Google Scholar] [CrossRef]
- Trainito, C.I.; Bayart, E.; Subra, F.; Français, O.; Le Pioufle, B. The Electrorotation as a Tool to Monitor the Dielectric Properties of Spheroid during the Permeabilization. J. Membr. Biol. 2016, 249, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Schneider, G.A. A Griffith type energy release rate model for dielectric breakdown under space charge limited conductivity. J. Mech. Phys. Solids 2013, 61, 78–90. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics in: Mechanical Properties of Living Tissues, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Lochmatter, P.; Kovacs, G.; Wissler, M. Characterization of dielectric elastomer actuators based on a visco-hyperelastic film model. Smart Mater. Struct. 2007, 16, 477–486. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Mechanical behavior of an acrylic elastomer used in dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 134, 494–504. [Google Scholar] [CrossRef]
- Sahu, R.K.; Patra, K. Rate-dependent mechanical behavior of VHB 4910 elastomer. Mech. Adv. Mater. Struct. 2016, 23, 170–179. [Google Scholar] [CrossRef]
- Chang, M.; Wang, Z.; Tong, L.; Liang, W. Effect of geometric size on mechanical properties of dielectric elastomers based on an improved visco-hyperelastic film model. Smart Mater. Struct. 2017, 26, 035033. [Google Scholar] [CrossRef]
- Nalwa, H.S. Ferroelectric Polymers; Chapter 11; Marcel Dekker: New York, NY, USA, 1995. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.; Wang, Z. A Numerical Method Charactering the Electromechanical Properties of Particle Reinforced Composite Based on Statistics. Polymers 2018, 10, 426. https://doi.org/10.3390/polym10040426
Chang M, Wang Z. A Numerical Method Charactering the Electromechanical Properties of Particle Reinforced Composite Based on Statistics. Polymers. 2018; 10(4):426. https://doi.org/10.3390/polym10040426
Chicago/Turabian StyleChang, Mengzhou, and Zhenqing Wang. 2018. "A Numerical Method Charactering the Electromechanical Properties of Particle Reinforced Composite Based on Statistics" Polymers 10, no. 4: 426. https://doi.org/10.3390/polym10040426



