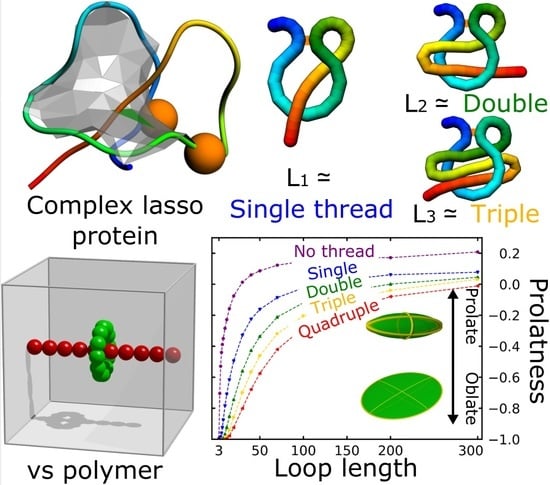
Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function
Abstract
:1. Introduction
2. Materials and Methods
2.1. Random Lassos Generation
2.2. Simulation Model
2.3. Data Analysis
2.4. Proteins Analyzed
2.5. Graphics
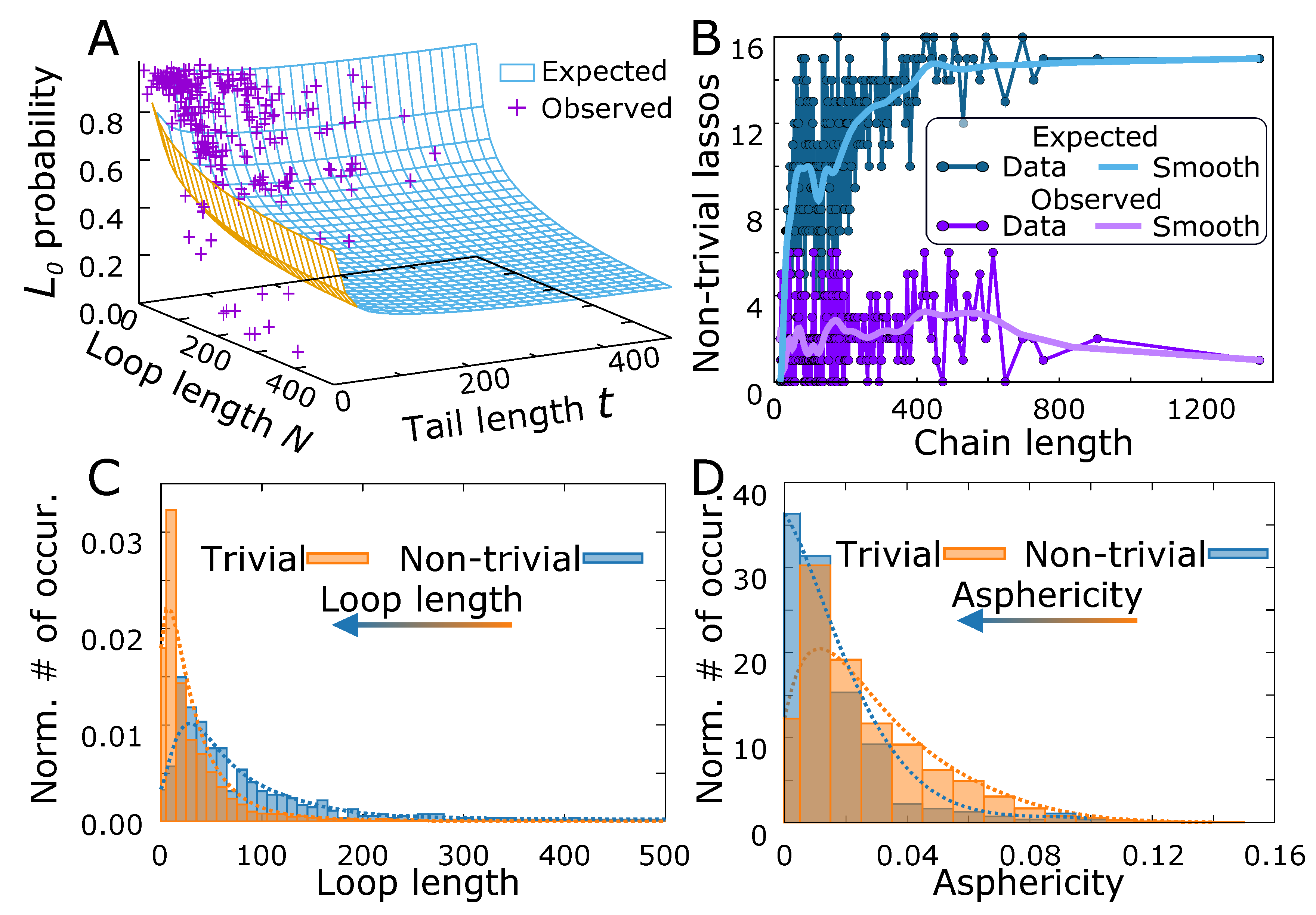
3. Results
3.1. Probability That a Lasso Is Complex
3.2. Shape Parameters of a Lasso Loop
3.3. Comparison Of Simulated Polymers with Complex Lasso Proteins
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flory, P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Flory, P.J. The configuration of real polymer chains. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reptation of a polymer chain in the presence of fixed obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Fukatsu, M.; Kurata, M. Hydrodynamic properties of flexible-ring macromolecules. J. Chem. Phys. 1966, 44, 4539–4545. [Google Scholar] [CrossRef]
- de Gennes, P. Conformations of polymers attached to an interface. Macromolecules 1980, 13, 1069–1075. [Google Scholar] [CrossRef]
- Deam, R.; Edwards, S.F. The theory of rubber elasticity. Philos. Trans. R. Soc. Lond. 1976, 280, 317–353. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Lagrangian theory for a self-avoiding random chain. Phys. Rev. 1974, 10, 1665. [Google Scholar] [CrossRef]
- Brás, A.R.; Pasquino, R.; Koukoulas, T.; Tsolou, G.; Holderer, O.; Radulescu, A.; Allgaier, J.; Mavrantzas, V.G.; Pyckhout-Hintzen, W.; Wischnewski, A.; et al. Structure and dynamics of polymer rings by neutron scattering: breakdown of the Rouse model. Soft Matter 2011, 7, 11169–11176. [Google Scholar] [CrossRef]
- Smrek, J.; Grosberg, A.Y. Understanding the dynamics of rings in the melt in terms of the annealed tree model. J. Phys. Condens. Matter 2015, 27, 064117. [Google Scholar] [CrossRef] [PubMed]
- Mirny, L.A. The fractal globule as a model of chromatin architecture in the cell. Chromosom. Res. 2011, 19, 37–51. [Google Scholar] [CrossRef]
- Obukhov, S.; Johner, A.; Baschnagel, J.; Meyer, H.; Wittmer, J. Melt of polymer rings: The decorated loop model. EPL (Europhys. Lett.) 2014, 105, 48005. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Annealed lattice animal model and Flory theory for the melt of non-concatenated rings: Towards the physics of crumpling. Soft Matter 2014, 10, 560–565. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. [Google Scholar] [CrossRef] [PubMed]
- Pasquino, R.; Vasilakopoulos, T.C.; Jeong, Y.C.; Lee, H.; Rogers, S.; Sakellariou, G.; Allgaier, J.; Takano, A.; Brás, A.R.; Chang, T.; et al. Viscosity of ring polymer melts. ACS Macro Lett. 2013, 2, 874–878. [Google Scholar] [CrossRef] [PubMed]
- Tsolou, G.; Stratikis, N.; Baig, C.; Stephanou, P.S.; Mavrantzas, V.G. Melt structure and dynamics of unentangled polyethylene rings: Rouse theory, atomistic molecular dynamics simulation, and comparison with the linear analogues. Macromolecules 2010, 43, 10692–10713. [Google Scholar] [CrossRef]
- Tsalikis, D.G.; Alatas, P.V.; Peristeras, L.D.; Mavrantzas, V.G. Scaling Laws for the Conformation and Viscosity of Ring Polymers in the Crossover Region around M e from Detailed Molecular Dynamics Simulations. ACS Macro Lett. 2018, 7, 916–920. [Google Scholar] [CrossRef]
- Alatas, P.V.; Tsalikis, D.G.; Mavrantzas, V.G. Detailed Molecular Dynamics Simulation of the Structure and Self-Diffusion of Linear and Cyclic n-Alkanes in Melt and Blends. Macromol. Theory Simul. 2017, 26, 1600049. [Google Scholar] [CrossRef]
- Papadopoulos, G.D.; Tsalikis, D.G.; Mavrantzas, V.G. Microscopic dynamics and topology of polymer rings immersed in a host matrix of longer linear polymers: Results from a detailed molecular dynamics simulation study and comparison with experimental data. Polymers 2016, 8, 283. [Google Scholar] [CrossRef]
- Witz, G.; Rechendorff, K.; Adamcik, J.; Dietler, G. Conformation of circular DNA in two dimensions. Phys. Rev. Lett. 2008, 101, 148103. [Google Scholar] [CrossRef]
- Grosberg, A.; Rabin, Y.; Havlin, S.; Neer, A. Crumpled globule model of the three-dimensional structure of DNA. EPL (Europhys. Lett.) 1993, 23, 373. [Google Scholar] [CrossRef]
- Halverson, J.D.; Smrek, J.; Kremer, K.; Grosberg, A.Y. From a melt of rings to chromosome territories: The role of topological constraints in genome folding. Rep. Prog. Phys. 2014, 77, 022601. [Google Scholar] [CrossRef]
- Lang, M.; Fischer, J.; Sommer, J.U. Effect of topology on the conformations of ring polymers. Macromolecules 2012, 45, 7642–7648. [Google Scholar] [CrossRef]
- Lang, M. Ring conformations in bidisperse blends of ring polymers. Macromolecules 2013, 46, 1158–1166. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Feigel, A.; Rabin, Y. Flory-type theory of a knotted ring polymer. Phys. Rev. E 1996, 54, 6618. [Google Scholar] [CrossRef]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E.; Summers, D. Knotting of random ring polymers in confined spaces. J. Chem. Phys. 2006, 124, 064903. [Google Scholar] [CrossRef]
- Marcone, B.; Orlandini, E.; Stella, A.; Zonta, F. Size of knots in ring polymers. Phys. Rev. E 2007, 75, 041105. [Google Scholar] [CrossRef] [PubMed]
- Tubiana, L.; Orlandini, E.; Micheletti, C. Multiscale entanglement in ring polymers under spherical confinement. Phys. Rev. Lett. 2011, 107, 188302. [Google Scholar] [CrossRef] [PubMed]
- Rosa, A.; Orlandini, E.; Tubiana, L.; Micheletti, C. Structure and dynamics of ring polymers: Entanglement effects because of solution density and ring topology. Macromolecules 2011, 44, 8668–8680. [Google Scholar] [CrossRef]
- Smrek, J.; Grosberg, A.Y. Minimal surfaces on unconcatenated polymer rings in melt. ACS Macro Lett. 2016, 5, 750–754. [Google Scholar] [CrossRef]
- Michieletto, D.; Turner, M.S. A topologically driven glass in ring polymers. Proc. Natl. Acad. Sci. USA 2016, 113, 5195–5200. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Turner, M.S. Ring Polymers: Threadings, Knot Electrophoresis and Topological Glasses. Polymers 2017, 9, 349. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Alexander, G.P.; Turner, M.S. Threading dynamics of ring polymers in a gel. ACS Macro Lett. 2014, 3, 255–259. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Alexander, G.P.; Turner, M.S. Dynamics of self-threading ring polymers in a gel. Soft Matter 2014, 10, 5936–5944. [Google Scholar] [CrossRef] [PubMed]
- Uehara, E.; Deguchi, T. Statistical properties of multi-theta polymer chains. J. Phys. A Math. Theor. 2018, 51, 134001. [Google Scholar] [CrossRef]
- Uehara, E.; Deguchi, T. Mean-square radius of gyration and the hydrodynamic radius for topological polymers expressed with graphs evaluated by the method of quaternions revisited. React. Funct. Polym. 2018, 133, 92–102. [Google Scholar] [CrossRef]
- Deguchi, T.; Uehara, E. Statistical and dynamical properties of topological polymers with graphs and ring polymers with knots. Polymers 2017, 9, 252. [Google Scholar] [CrossRef] [PubMed]
- Caraglio, M.; Micheletti, C.; Orlandini, E. Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation. Polymers 2017, 9, 327. [Google Scholar] [CrossRef] [PubMed]
- Tsalikis, D.G.; Mavrantzas, V.G.; Vlassopoulos, D. Analysis of slow modes in ring polymers: Threading of rings controls long-time relaxation. ACS Macro Lett. 2016, 5, 755–760. [Google Scholar] [CrossRef]
- Tsalikis, D.G.; Mavrantzas, V.G. Threading of ring poly (ethylene oxide) molecules by linear chains in the melt. ACS Macro Lett. 2014, 3, 763–766. [Google Scholar] [CrossRef]
- Harada, A.; Li, J.; Kamachi, M. The molecular necklace: A rotaxane containing many threaded α-cyclodextrins. Nature 1992, 356, 325–327. [Google Scholar] [CrossRef]
- Bruns, C.J.; Stoddart, J.F. Rotaxane-based molecular muscles. Acc. Chem. Res. 2014, 47, 2186–2199. [Google Scholar] [CrossRef] [PubMed]
- Valentina, S.; Ogawa, T.; Nakazono, K.; Aoki, D.; Takata, T. Efficient synthesis of cyclic block copolymers by rotaxane protocol by linear/cyclic topology transformation. Chem. Eur. J. 2016, 22, 8759–8762. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, T.; Usuki, N.; Nakazono, K.; Koyama, Y.; Takata, T. Linear—Cyclic polymer structural transformation and its reversible control using a rational rotaxane strategy. Chem. Commun. 2015, 51, 5606–5609. [Google Scholar] [CrossRef] [PubMed]
- Niemyska, W.; Dabrowski-Tumanski, P.; Kadlof, M.; Haglund, E.; Sułkowski, P.; Sulkowska, J.I. Complex lasso: New entangled motifs in proteins. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Niemyska, W.; Pasznik, P.; Sulkowska, J.I. LassoProt: Server to analyze biopolymers with lassos. Nucleic Acids Res. 2016, 44, W383–W389. [Google Scholar] [CrossRef]
- Haglund, E.; Pilko, A.; Wollman, R.; Jennings, P.A.; Onuchic, J.N. Pierced lasso topology controls function in leptin. J. Phys. Chem. B 2017, 121, 706–718. [Google Scholar] [CrossRef] [PubMed]
- Haglund, E.; Nguyen, L.; Schafer, N.P.; Lammert, H.; Jennings, P.A.; Onuchic, J.N. Uncovering the molecular mechanisms behind disease-associated leptin variants. J. Biol. Chem. 2018, 293, 12919–12933. [Google Scholar] [CrossRef] [PubMed]
- Rebuffat, S.; Blond, A.; Destoumieux-Garzón, D.; Goulard, C.; Peduzzi, J. Microcin J25, from the macrocyclic to the lasso structure: implications for biosynthetic, evolutionary and biotechnological perspectives. Curr. Protein Pept. Sci. 2004, 5, 383–391. [Google Scholar] [CrossRef]
- Pan, S.J.; Link, A.J. Sequence diversity in the lasso peptide framework: Discovery of functional microcin J25 variants with multiple amino acid substitutions. J. Am. Chem. Soc. 2011, 133, 5016–5023. [Google Scholar] [CrossRef] [PubMed]
- Ducasse, R.; Yan, K.P.; Goulard, C.; Blond, A.; Li, Y.; Lescop, E.; Guittet, E.; Rebuffat, S.; Zirah, S. Sequence determinants governing the topology and biological activity of a lasso peptide, microcin J25. ChemBioChem 2012, 13, 371–380. [Google Scholar] [CrossRef]
- Zimmermann, M.; Hegemann, J.D.; Xie, X.; Marahiel, M.A. The astexin-1 lasso peptides: Biosynthesis, stability, and structural studies. Chem. Biol. 2013, 20, 558–569. [Google Scholar] [CrossRef]
- Hegemann, J.D.; Zimmermann, M.; Xie, X.; Marahiel, M.A. Lasso peptides: An intriguing class of bacterial natural products. Acc. Chem. Res. 2015, 48, 1909–1919. [Google Scholar] [CrossRef]
- Braffman, N.R.; Piscotta, F.J.; Hauver, J.; Campbell, E.A.; Link, A.J.; Darst, S.A. Structural mechanism of transcription inhibition by lasso peptides microcin J25 and capistruin. Proc. Natl. Acad. Sci. USA 2019, 116, 1273–1278. [Google Scholar] [CrossRef]
- Allen, C.D.; Link, A.J. Self-assembly of catenanes from lasso peptides. J. Am. Chem. Soc. 2016, 138, 14214–14217. [Google Scholar] [CrossRef]
- Zong, C.; Maksimov, M.O.; Link, A.J. Construction of lasso peptide fusion proteins. ACS Chem. Biol. 2015, 11, 61–68. [Google Scholar] [CrossRef]
- Cantarella, J.; Duplantier, B.; Shonkwiler, C.; Uehara, E. A fast direct sampling algorithm for equilateral closed polygons. J. Phys. A Math. Theor. 2016, 49, 275202. [Google Scholar] [CrossRef]
- Clementi, C.; Nymeyer, H.; Onuchic, J.N. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? an investigation for small globular proteins1. J. Mol. Biol. 2000, 298, 937–953. [Google Scholar] [CrossRef]
- Weber, T.A.; Helfand, E. Time-correlation functions from computer simulations of polymers. J. Phys. Chem. 1983, 87, 2881–2889. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; Van Der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Topoly—A package to determine the topology of polymers. Under Construction. 2019.
- Ewing, B.; Millett, K.C. A load balanced algorithm for the calculation of the polynomial knot and link invariants. In The Mathematical Heritage of CF Gauss; World Scientific: Singapore, 1991; pp. 225–266. [Google Scholar]
- Gierut, A.M.; Niemyska, W.; Dabrowski-Tumanski, P.; Sułkowski, P.; Sulkowska, J.I. PyLasso: A PyMOL plugin to identify lassos. Bioinformatics 2017, 33, 3819–3821. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Orlandini, E.; Van Rensburg, E.J.; Tesi, M.; Whittington, S. Random linking of lattice polygons. J. Phys. A Math. Gen. 1994, 27, 335. [Google Scholar] [CrossRef]
- Soteros, C.; Sumners, D.; Whittington, S. Linking of random p-spheres in Zd. J. Knot Theory Its Ramif. 1999, 8, 49–70. [Google Scholar] [CrossRef]
- Diao, Y. Unsplittability of random links. In Random Knotting and Linking; World Scientific: Singapore, 1994; pp. 147–157. [Google Scholar]
- Diao, Y.; van Rensburg, E.J. Percolation of linked circles. In Topology and Geometry in Polymer Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 79–88. [Google Scholar]
- Rawdon, E.J.; Kern, J.C.; Piatek, M.; Plunkett, P.; Stasiak, A.; Millett, K.C. Effect of knotting on the shape of polymers. Macromolecules 2008, 41, 8281–8287. [Google Scholar] [CrossRef]
- Tsurusaki, K.; Deguchi, T. Fractions of particular knots in Gaussian random polygons. J. Phys. Soc. Jpn. 1995, 64, 1506–1518. [Google Scholar] [CrossRef]
- Shimamura, M.K.; Deguchi, T. Knot complexity and the probability of random knotting. Phys. Rev. E 2002, 66, 040801. [Google Scholar] [CrossRef] [PubMed]
- Orlandini, E.; Tesi, M.; Van Rensburg, E.J.; Whittington, S.G. Asymptotics of knotted lattice polygons. J. Phys. A Math. Gen. 1998, 31, 5953. [Google Scholar] [CrossRef]
- Kuhn, W. The shape of fibrous molecules in solution. Kolloid-Zeitschrift 1934, 68, 2. [Google Scholar] [CrossRef]
- Drube, F.; Alim, K.; Witz, G.; Dietler, G.; Frey, E. Excluded volume effects on semiflexible ring polymers. Nano Lett. 2010, 10, 1445–1449. [Google Scholar] [CrossRef]
- Alim, K.; Frey, E. Shapes of semiflexible polymer rings. Phys. Rev. Lett. 2007, 99, 198102. [Google Scholar] [CrossRef]
- Bishop, M.; Michels, J. Scaling in two-dimensional linear and ring polymers. J. Chem. Phys. 1986, 85, 1074–1076. [Google Scholar] [CrossRef]
- Bishop, M.; Saltiel, C.J. Polymer shapes in two, four, and five dimensions. J. Chem. Phys. 1988, 88, 3976–3980. [Google Scholar] [CrossRef]
- Millett, K.C.; Plunkett, P.; Piatek, M.; Rawdon, E.J.; Stasiak, A. Effect of knotting on polymer shapes and their enveloping ellipsoids. J. Chem. Phys. 2009, 130, 04B623. [Google Scholar] [CrossRef]
- Diehl, H.; Eisenriegler, E. Universal shape ratios for open and closed random walks: Exact results for all d. J. Phys. A Math. Gen. 1989, 22, L87. [Google Scholar] [CrossRef]
- Jagodzinski, O.; Eisenriegler, E.; Kremer, K. Universal shape properties of open and closed polymer chains: Renormalization group analysis and Monte Carlo experiments. J. Phys. I 1992, 2, 2243–2279. [Google Scholar] [CrossRef]
- Jagodzinski, O. The asphericity of star polymers: A renormalization group study. J. Phys. A Math. Gen. 1994, 27, 1471. [Google Scholar] [CrossRef]
- Prellberg, T. Scaling of self-avoiding walks and self-avoiding trails in three dimensions. J. Phys. A Math. Gen. 2001, 34, L599. [Google Scholar] [CrossRef]
- Lua, R.C.; Grosberg, A.Y. Statistics of knots, geometry of conformations, and evolution of proteins. PLoS Comput. Biol. 2006, 2, e45. [Google Scholar] [CrossRef]
- Ostermeir, K.; Alim, K.; Frey, E. Buckling of stiff polymer rings in weak spherical confinement. Phys. Rev. E 2010, 81, 061802. [Google Scholar] [CrossRef] [PubMed]
- Soler, M.A.; Rey, A.; Faísca, P.F. Steric confinement and enhanced local flexibility assist knotting in simple models of protein folding. Phys. Chem. Chem. Phys. 2016, 18, 26391–26403. [Google Scholar] [CrossRef] [PubMed]
- Niewieczerzal, S.; Sulkowska, J.I. Knotting and unknotting proteins in the chaperonin cage: Effects of the excluded volume. PLoS ONE 2017, 12, e0176744. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Dabrowski-Tumanski, P.; Niewieczerzal, S.; Sulkowska, J.I. The exclusive effects of chaperonin on the behavior of proteins with 52 knot. PLoS Comput. Biol. 2018, 14, e1005970. [Google Scholar] [CrossRef]
- Micheletti, C.; Orlandini, E. Knotting and unknotting dynamics of DNA strands in nanochannels. ACS Macro Lett. 2014, 3, 876–880. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sulkowska, J.I. KnotProt 2.0: A database of proteins with knots and other entangled structures. Nucleic Acids Res. 2018, 47, D367–D375. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Stasiak, A.; Sulkowska, J.I. In search of functional advantages of knots in proteins. PLoS ONE 2016, 11, e0165986. [Google Scholar] [CrossRef] [PubMed]
- Allen, C.D.; Chen, M.Y.; Trick, A.Y.; Le, D.T.; Ferguson, A.L.; Link, A.J. Thermal unthreading of the lasso peptides astexin-2 and astexin-3. ACS Chem. Biol. 2016, 11, 3043–3051. [Google Scholar] [CrossRef]





| Thread | Radius of Gyration | Asphericity | Prolatness | |||||
|---|---|---|---|---|---|---|---|---|
| Thickness | ratio | |||||||
| 0 | 0.154 | −0.102 | 1.00 | 0.0342 | −0.186 | 0.0708 | −1.37 | 0.300 |
| 1 | 0.164 | −0.0825 | 1.06 | 0.188 | −0.753 | 0.0853 | −3.07 | 0.315 |
| 2 | 0.164 | −0.0162 | 1.06 | 0.353 | −0.822 | 0.0858 | −4.57 | 0.384 |
| 3 | 0.164 | 0.0376 | 1.06 | 0.845 | −0.993 | 0.0869 | −5.53 | 0.420 |
| 4 | 0.164 | 0.106 | 1.06 | 1.05 | −0.969 | 0.0856 | −6.10 | 0.413 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabrowski-Tumanski, P.; Gren, B.; Sulkowska, J.I. Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function. Polymers 2019, 11, 707. https://doi.org/10.3390/polym11040707
Dabrowski-Tumanski P, Gren B, Sulkowska JI. Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function. Polymers. 2019; 11(4):707. https://doi.org/10.3390/polym11040707
Chicago/Turabian StyleDabrowski-Tumanski, Pawel, Bartosz Gren, and Joanna I. Sulkowska. 2019. "Statistical Properties of Lasso-Shape Polymers and Their Implications for Complex Lasso Proteins Function" Polymers 11, no. 4: 707. https://doi.org/10.3390/polym11040707