A Full Range Experimental Study of Amplitude- and Frequency-Dependent Characteristics of Rubber Springs
Abstract
:1. Introduction
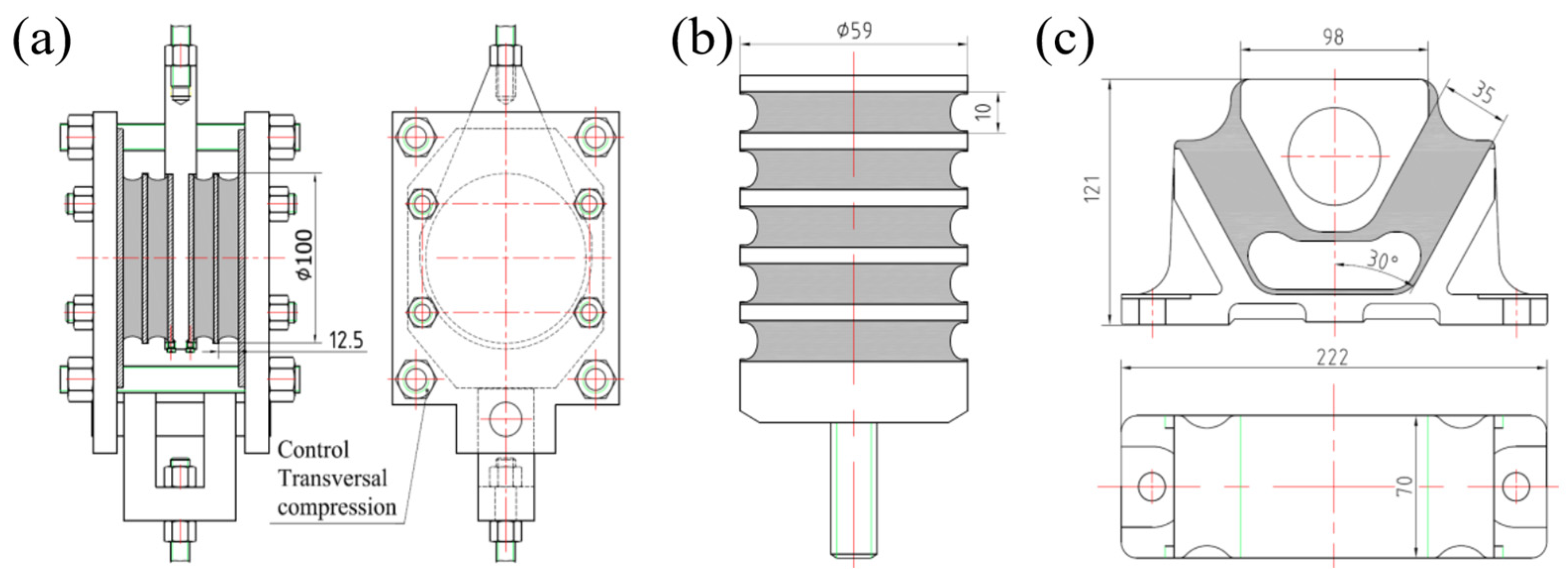
2. Rubber Spring Samples
3. Experiments
- ST rubber spring:
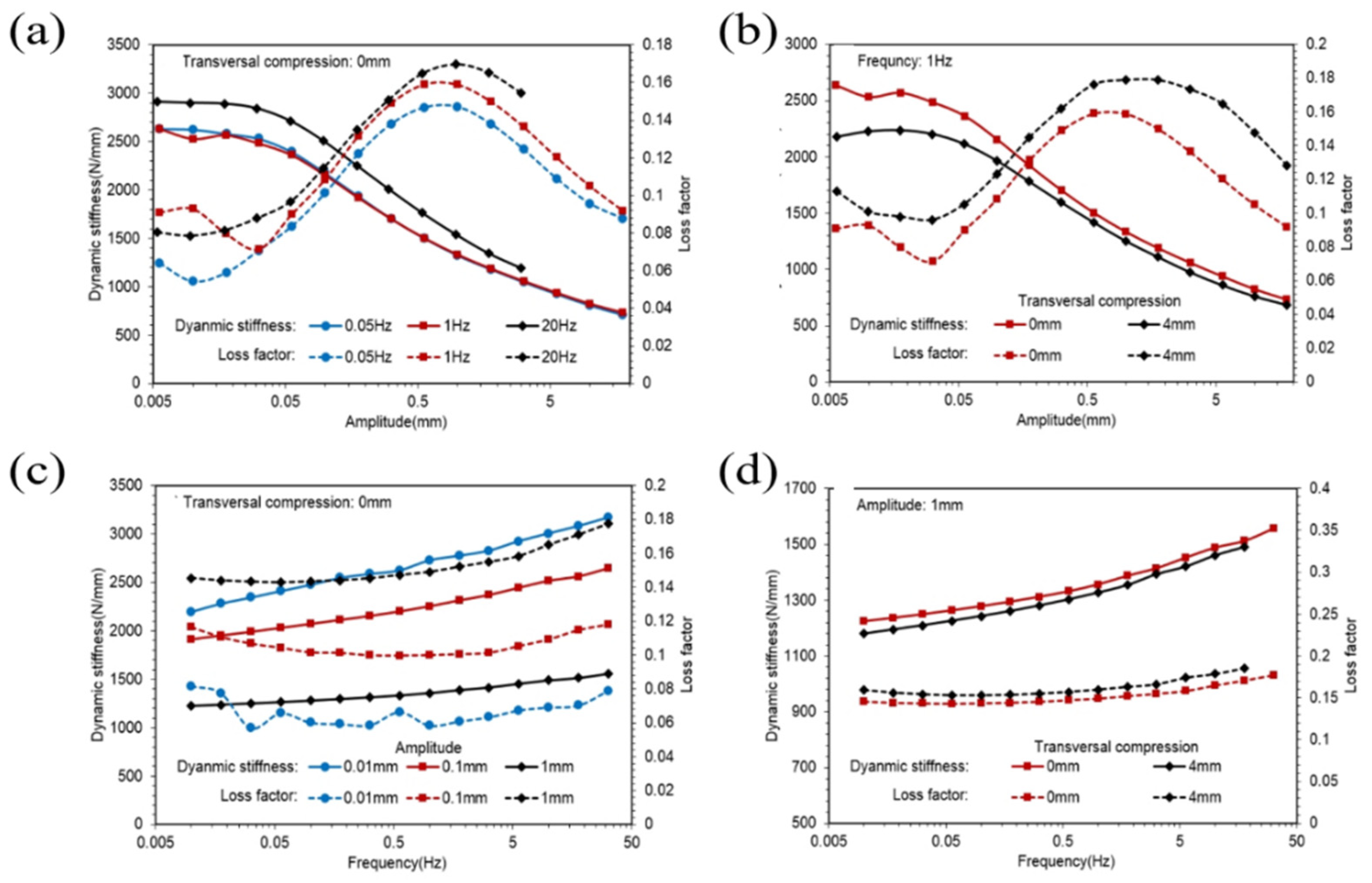
- Amplitude sweeps from 0 to the maximum of 17.8 mm with 0.05, 1 and 20 Hz frequencies under 0 and 4 mm transversal compression.
- Frequency sweeps from 0 to the maximum of 31.6 Hz with 0.01, 0.1 and 1 mm amplitudes under 0 and 4 mm transversal compression.
- CT rubber spring:
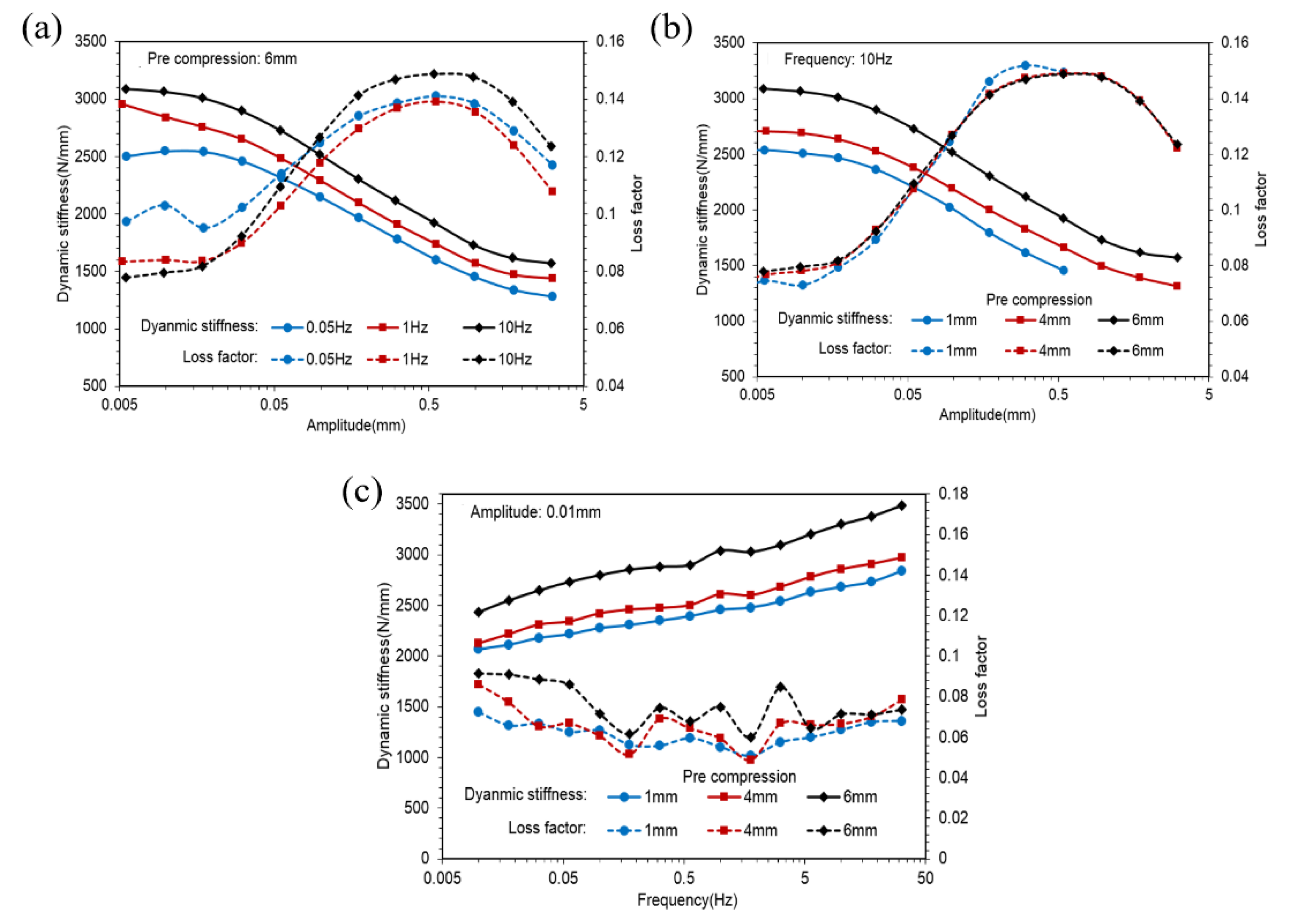
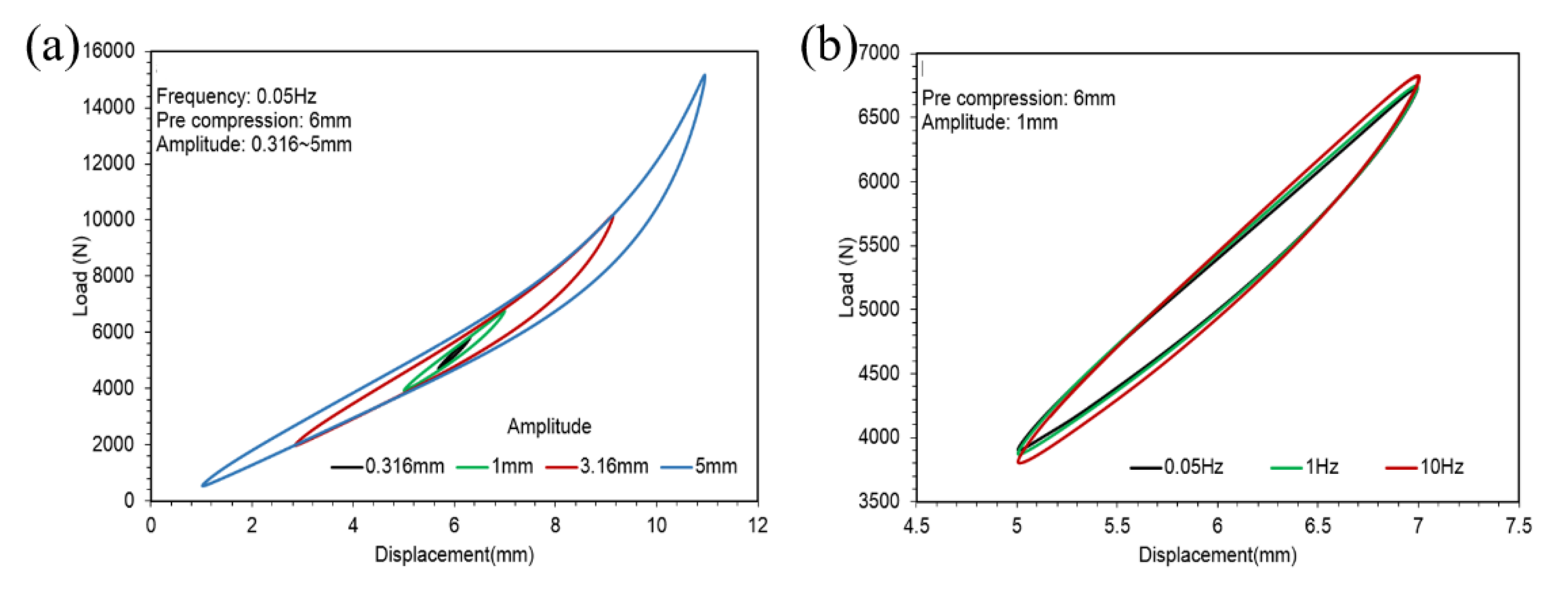
- Amplitude sweeps from 0 to the maximum of 3.15 mm with 0.05, 1 and 10 Hz frequencies under 1, 4 and 6 mm pre-compression.
- Frequency sweeps from 0 to the maximum of 31.6 Hz with a 0.01 mm amplitude under 1, 4 and 6 mm pre-compression.
- SCCT rubber spring:
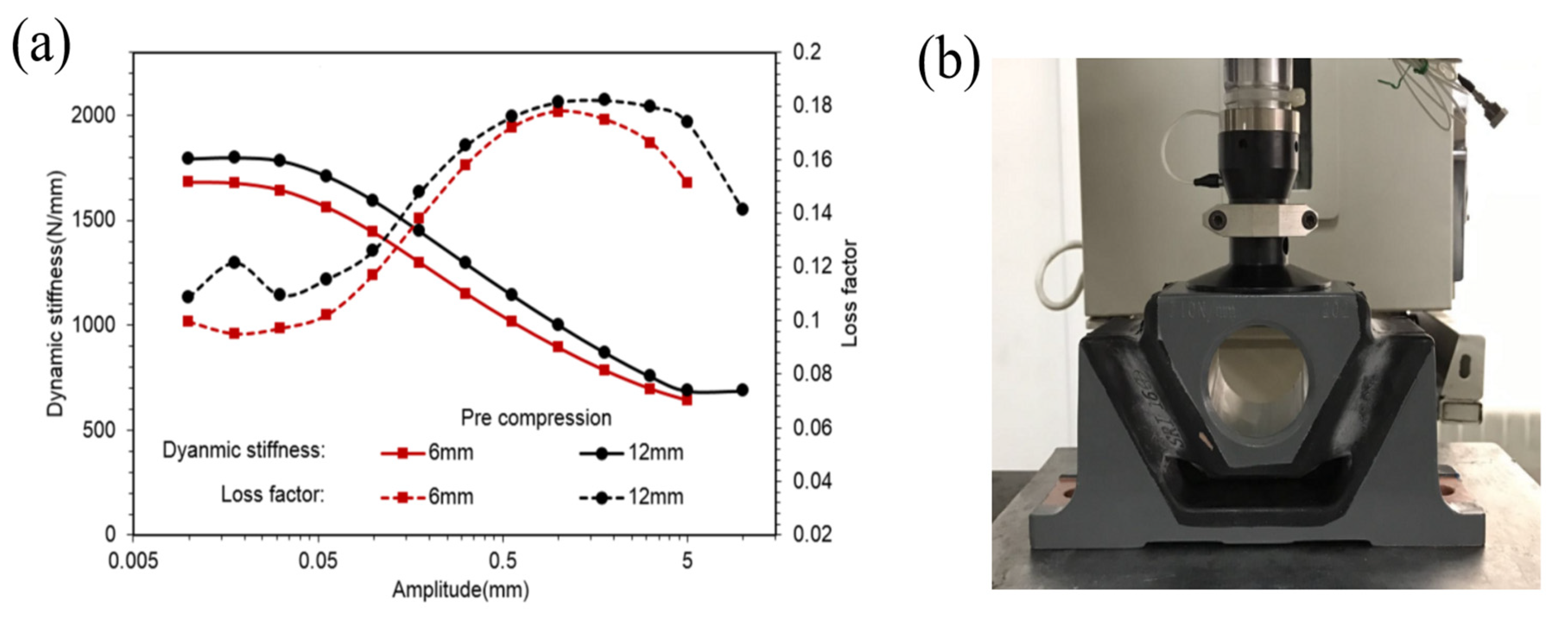
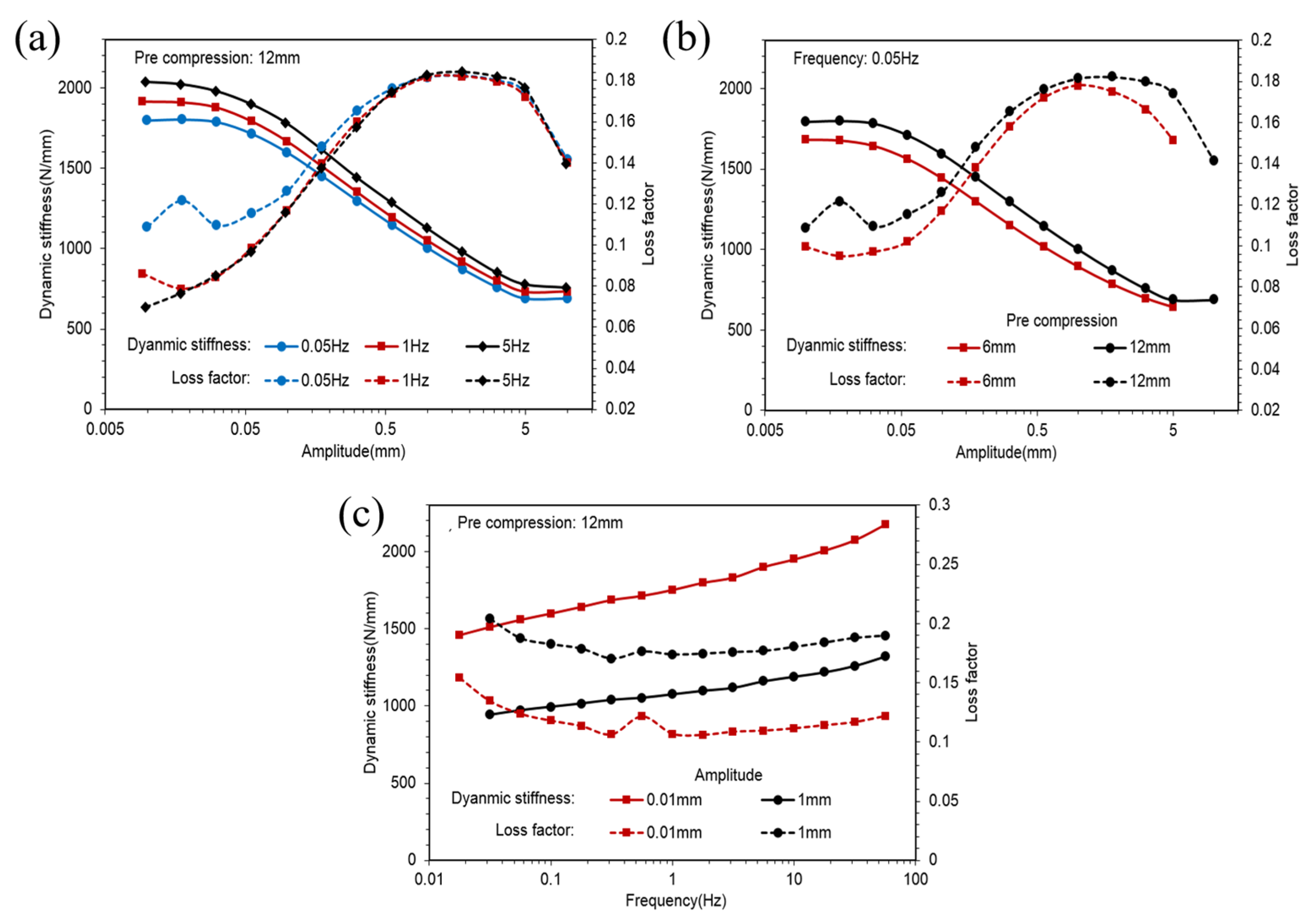
- Amplitude sweeps from 0 to the maximum of 10 mm with 0.05, 1 and 5 Hz frequencies under 6 and 12 mm pre-compression.
- Frequency sweeps from 0 to the maximum of 31.6 Hz with 0.01 and 1 mm amplitudes under 12 mm pre-compression.
4. Experimental Results
5. Research Ideas Regarding Model Establishment
5.1. Research Questions/Hypotheses
- (a)
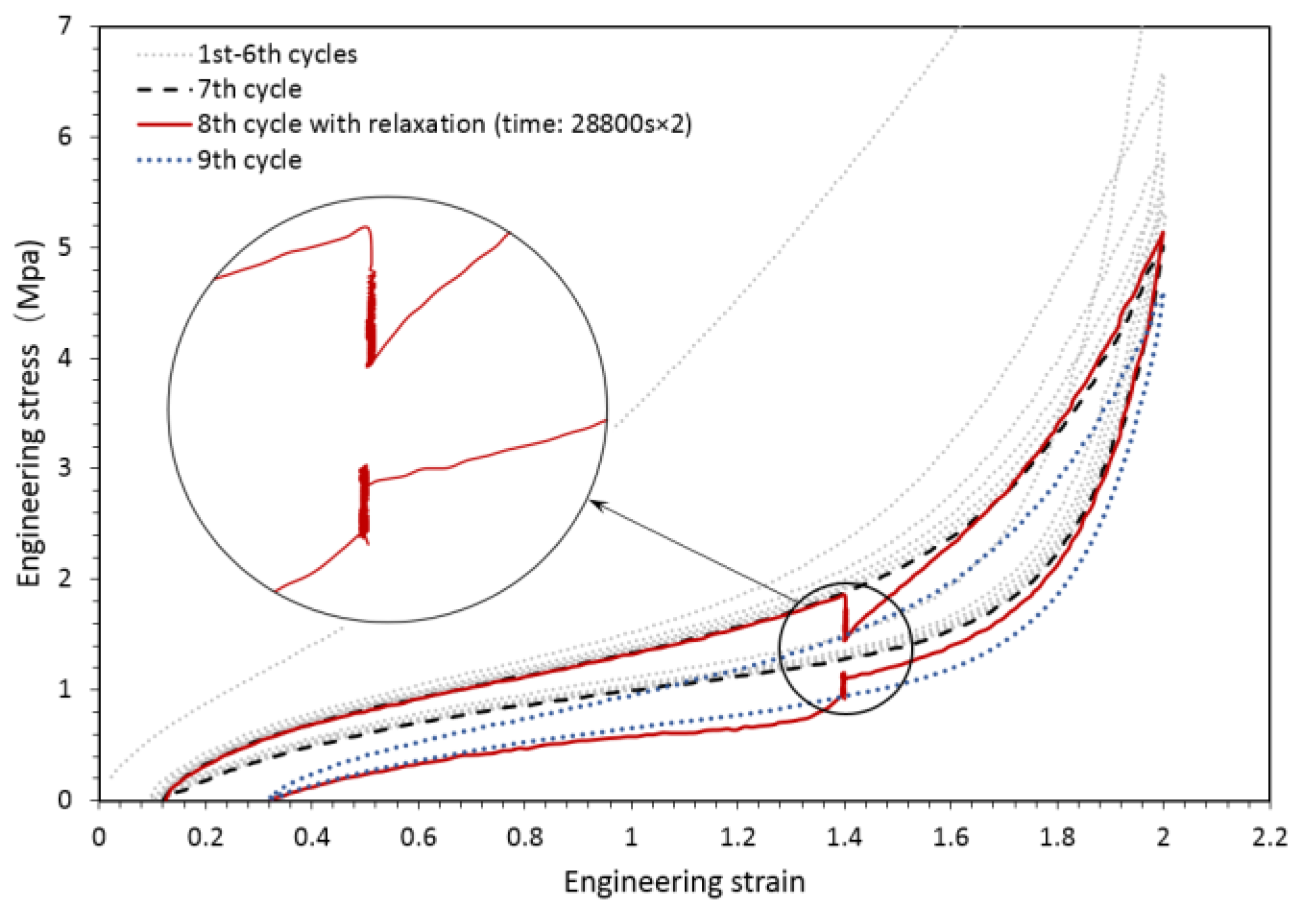
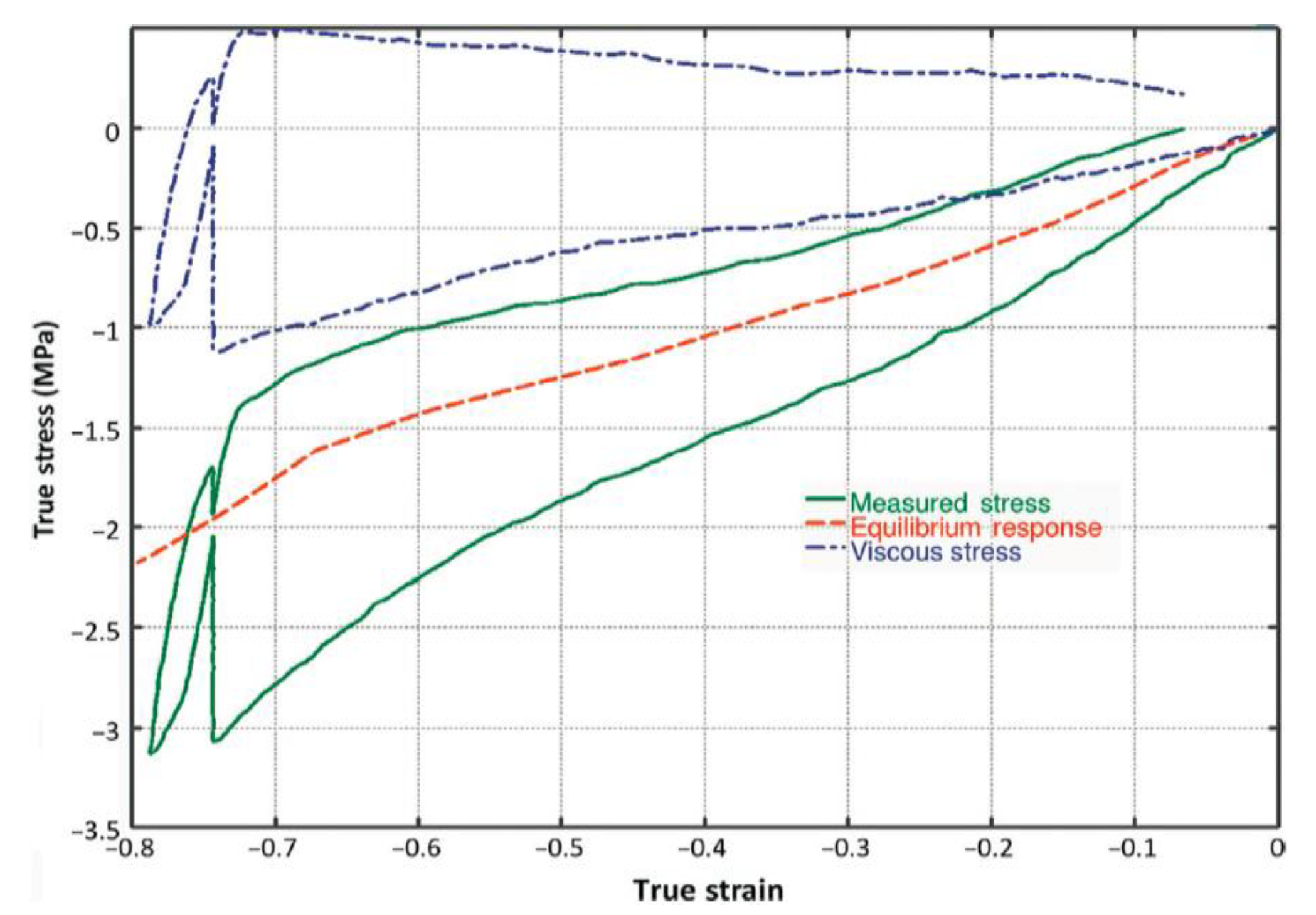
- Internal friction evolves differently with respect to the deformation level for large strains, which was the major difference compared with that of small strains.
- (b)
- A governing equation describing the dependence of internal friction on specific evolution variables needs to be developed to determine which variables (e.g., strain energy density, maximum largest principal stretch, invariants or maximal principal stress, etc.) will dominate the evolution of internal friction in different deformation levels.
- (c)
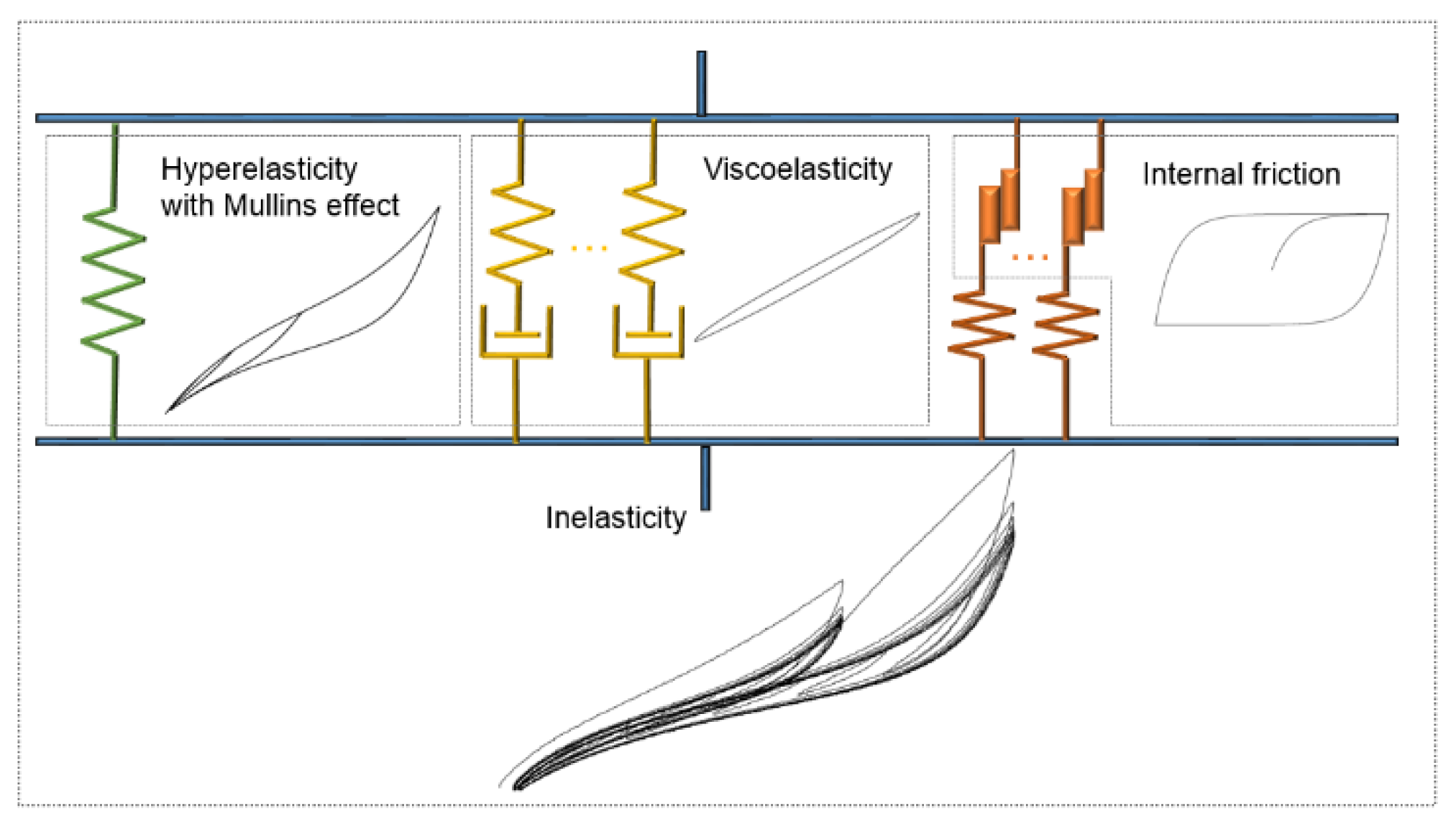
- The constitutive framework of CBFR’s complicated inelasticity can be established by incorporating comprehensive factors of hyperelasticity, the Mullins effect, viscoelasticity and internal friction. Numerical implementation can be realized using the finite element method based on the user subroutine of commercial finite element software.
5.2. Research Design
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sebeșan, I.; Țurcanu, I. Conical Rubber Suspension Springs in the Construction of Railway Vehicles. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012113. [Google Scholar] [CrossRef]
- Wang, L.; Shi, B.; Zhao, H.; Qi, X.; Chen, J.; Li, J.; Shang, Y.; Fu, K.K.; Zhang, X.; Tian, M.; et al. 3D-Printed Parahydrophobic Functional Textile with a Hierarchical Nanomicroscale Structure. ACS Nano 2022. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Chi, M.; Liang, S.; Dai, L.; Jiang, Y. Research on Non-Hyperelastic Mechanical Model of EMU Rubber Spring Based on Experimental Data. J. Strain Anal. Eng. Des. 2022, 57, 255–265. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, J. Test and simulation study of the effect of transverse impact stress on the rosette 19-hole gun propellant under low temperature. FirePhysChem 2022, 2, 147–153. [Google Scholar] [CrossRef]
- Pang, W.; Wang, K.; Trache, D.; Fan, X.; Li, J.; Li, H. Experiments and simulations on interactions between 2,3-bis(hydroxymethyl)-2,3-dinitro-1,4-butanediol tetranitrate (DNTN) with some energetic components and inert materials. FirePhysChem 2021, 1, 166–173. [Google Scholar] [CrossRef]
- Payne, A.R. The Dynamic Properties of Carbon Black-Loaded Natural Rubber Vulcanizates. Part I. J. Appl. Polym. Sci. 1962, 6, 57–63. [Google Scholar] [CrossRef]
- Payne, A.R. The Dynamic Properties of Carbon Black Loaded Natural Rubber Vulcanizates. Part II. J. Appl. Polym. Sci. 1962, 6, 368–372. [Google Scholar] [CrossRef]
- Payne, A.R. Strainwork Dependence of Filler-Loaded Vulcanizates. J. Appl. Polym. Sci. 1964, 8, 2661–2686. [Google Scholar] [CrossRef]
- Pintado, P.; Ramiro, C.; Berg, M.; Morales, A.L.; Nieto, A.J.; Chicharro, J.M.; Miguel de Priego, J.C.; García, E. On the Mechanical Behavior of Rubber Springs for High Speed Rail Vehicles. J. Vib. Control 2018, 24, 4676–4688. [Google Scholar] [CrossRef]
- Heinrich, G.; Klüppel, M. Recent Advances in the Theory of Filler Networking in Elastomers. Fill. Elastomers Drug Deliv. Syst. 2002, 160, 1–44. [Google Scholar]
- Shi, B.H.; Zhang, M.; Liu, S.K.; Sun, B.Z.; Gu, B.H. Multi-Scale Ageing Mechanisms of 3D Four Directional and Five Directional Braided Composites’ Impact Fracture Behaviors under Thermo-Oxidative Environment. Int. J. Mech. Sci. 2019, 155, 50–65. [Google Scholar] [CrossRef]
- Shi, B.; Shang, Y.; Zhang, P.; Cuadros, A.P.; Qu, J.; Sun, B.; Gu, B.; Chou, T.-W.; Fu, K.K. Dynamic Capillary-Driven Additive Manufacturing of Continuous Carbon Fiber Composite. Matter 2020, 2, 1594–1604. [Google Scholar] [CrossRef]
- Höfer, P.; Lion, A. Modelling of Frequency-and Amplitude-Dependent Material Properties of Filler-Reinforced Rubber. J. Mech. Phys. Solids 2009, 57, 500–520. [Google Scholar] [CrossRef]
- Rendek, M.; Lion, A. Amplitude Dependence of Filler-Reinforced Rubber: Experiments, Constitutive Modelling and FEM–Implementation. Int. J. Solids Struct. 2010, 47, 2918–2936. [Google Scholar] [CrossRef] [Green Version]
- Bergström, J.S.; Boyce, M. Constitutive Modeling of the Large Strain Time-Dependent Behavior of Elastomers. J. Mech. Phys. Solids 1998, 46, 931–954. [Google Scholar] [CrossRef]
- Ayoub, G.; Zaïri, F.; Naït-Abdelaziz, M.; Gloaguen, J.-M.; Kridli, G. A Visco-Hyperelastic Damage Model for Cyclic Stress-Softening, Hysteresis and Permanent Set in Rubber Using the Network Alteration Theory. Int. J. Plast. 2014, 54, 19–33. [Google Scholar] [CrossRef]
- Dal, H.; Kaliske, M. Bergström–Boyce Model for Nonlinear Finite Rubber Viscoelasticity: Theoretical Aspects and Algorithmic Treatment for the FE Method. Comput. Mech. 2009, 44, 809–823. [Google Scholar] [CrossRef]
- Österlöf, R.; Wentzel, H.; Kari, L.; Diercks, N.; Wollscheid, D. Constitutive Modelling of the Amplitude and Frequency Dependency of Filled Elastomers Utilizing a Modified Boundary Surface Model. Int. J. Solids Struct. 2014, 51, 3431–3438. [Google Scholar] [CrossRef] [Green Version]
- Österlöf, R.; Wentzel, H.; Kari, L. A Finite Strain Viscoplastic Constitutive Model for Rubber with Reinforcing Fillers. Int. J. Plast. 2016, 87, 1–14. [Google Scholar] [CrossRef]
- Coveney, V.A.; Johnson, D.E. Rate-Dependent Modeling of a Highly Filled Vulcanizate. Rubber Chem. Technol. 2000, 73, 565–577. [Google Scholar] [CrossRef]
- Berg, M. A Non-Linear Rubber Spring Model for Rail Vehicle Dynamics Analysis. Veh. Syst. Dyn. 1998, 30, 197–212. [Google Scholar] [CrossRef]
- Berg, M. A Model for Rubber Springs in the Dynamic Analysis of Rail Vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1997, 211, 95–108. [Google Scholar] [CrossRef]
- Scheffer, T.; Diebels, S. Comparison of Two Different Modeling Approaches to Describe the Non-Linear Viscoelastic Behavior of Filled Rubber Material. PAMM 2016, 16, 389–390. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Liang, Y.; Xue, W.; Zhang, Z.; Jia, X.; Huang, H.; Qiao, Z.; Mei, D.; Zhong, C. Polymer-Supported Ultra-Thin ZIF-67 Membrane through in Situ Interface Self-Repair. J. Membr. Sci. 2021, 625, 119139. [Google Scholar] [CrossRef]
- Donner, H.; Kanzenbach, L.; Ihlemann, J.; Naumann, C. Efficiency of Rubber Material Modelling and Characterisation. In Constitutive Models for Rubber X; CRC Press: Boca Raton, FL, USA, 2017; pp. 19–29. [Google Scholar]
- Polach, O. Modelling of Rubber Components Using Estimated Parameters. In Proceedings of the 24th International Symposium on Dynamics of Vehicles on Roads and Tacks, Graz, Austria, 17–21 August 2015; pp. 17–21. [Google Scholar]
- Sjöberg, M. Rubber Isolators-Measurements and Modelling Using Fractional Derivatives and Friction; SAE Technical Paper; SAE: Warrendale, PA, USA, 2000. [Google Scholar]
- Sjöberg, M.M.; Kari, L. Non-Linear Behavior of a Rubber Isolator System Using Fractional Derivatives. Veh. Syst. Dyn. 2002, 37, 217–236. [Google Scholar] [CrossRef]
- Gil-Negrete, N.; Vinolas, J.; Kari, L. A Nonlinear Rubber Material Model Combining Fractional Order Viscoelasticity and Amplitude Dependent Effects. J. Appl. Mech. 2009, 76, 011009. [Google Scholar] [CrossRef]
- Bedük, M.D.; Çalışkan, K.; Henze, R.; Küçükay, F. Effects of Damper Failure on Vehicle Stability. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1024–1039. [Google Scholar] [CrossRef]
- Shi, H.; Wu, P. A Nonlinear Rubber Spring Model Containing Fractional Derivatives for Use in Railroad Vehicle Dynamic Analysis. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 1745–1759. [Google Scholar] [CrossRef]
- Sedlaczek, K.; Dronka, S.; Rauh, J. Advanced Modular Modelling of Rubber Bushings for Vehicle Simulations. Veh. Syst. Dyn. 2011, 49, 741–759. [Google Scholar] [CrossRef]
- Alonso, A.; Gil-Negrete, N.; Nieto, J.; Gimenez, J.G. Development of a Rubber Component Model Suitable for Being Implemented in Railway Dynamic Simulation Programs. J. Sound Vib. 2013, 332, 3032–3048. [Google Scholar] [CrossRef]
- Dzierżek, S. Experiment-Based Modeling of Cylindrical Rubber Bushings for the Simulation of Wheel Suspension Dynamic Behavior. SAE Trans. 2000, 109, 78–85. [Google Scholar]
- Bao, P.; Li, J.; Han, Z.; Ma, H.; Wang, B. Comparing the impact safety between two HMX-based PBX with different binders. FirePhysChem 2021, 1, 139–145. [Google Scholar] [CrossRef]
- Kong, L.; Dong, K.; Li, G.; Yang, C.; Lai, S.; Qu, Y. Molecular simulation study on the protective mechanism of three kinds of HTPB propellant antioxidants. FirePhysChem 2022, 2, 4–13. [Google Scholar] [CrossRef]
- Bergstrom, J.S. Mechanics of Solid Polymers: Theory and Computational Modeling; William Andrew: Norwich, NY, USA, 2015. [Google Scholar]
- Chagnon, G.; Verron, E.; Gornet, L.; Marckmann, G.; Charrier, P. On the Relevance of Continuum Damage Mechanics as Applied to the Mullins Effect in Elastomers. J. Mech. Phys. Solids 2004, 52, 1627–1650. [Google Scholar] [CrossRef]




| Item | |
|---|---|
| SMR20 | 70 |
| CB24 | 30 |
| N550 | 30 |
| Si69 | 3 |
| ZnO | 5 |
| MgO | 0.3 |
| SA | 3 |
| 4020 | 1.5 |
| RD | 1.5 |
| Vulcanizing agent | 2 |
| Sulfur promoter | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Li, J.; Wang, Y.; Li, X.; Gao, Y.; Zhao, D.; Shi, B.; Zou, L.; Song, X.; Shang, Y. A Full Range Experimental Study of Amplitude- and Frequency-Dependent Characteristics of Rubber Springs. Polymers 2022, 14, 4662. https://doi.org/10.3390/polym14214662
Shi Y, Li J, Wang Y, Li X, Gao Y, Zhao D, Shi B, Zou L, Song X, Shang Y. A Full Range Experimental Study of Amplitude- and Frequency-Dependent Characteristics of Rubber Springs. Polymers. 2022; 14(21):4662. https://doi.org/10.3390/polym14214662
Chicago/Turabian StyleShi, Yanping, Juanjuan Li, Yuan Wang, Xuebing Li, Yuanjing Gao, Dong Zhao, Baohui Shi, Lihua Zou, Xiuduo Song, and Yuanyuan Shang. 2022. "A Full Range Experimental Study of Amplitude- and Frequency-Dependent Characteristics of Rubber Springs" Polymers 14, no. 21: 4662. https://doi.org/10.3390/polym14214662





