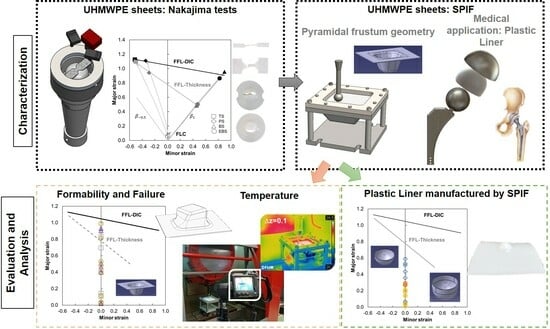
Assessing Formability and Failure of UHMWPE Sheets through SPIF: A Case Study in Medical Applications
Abstract
:1. Introduction
2. Methods
2.1. Formability Limits
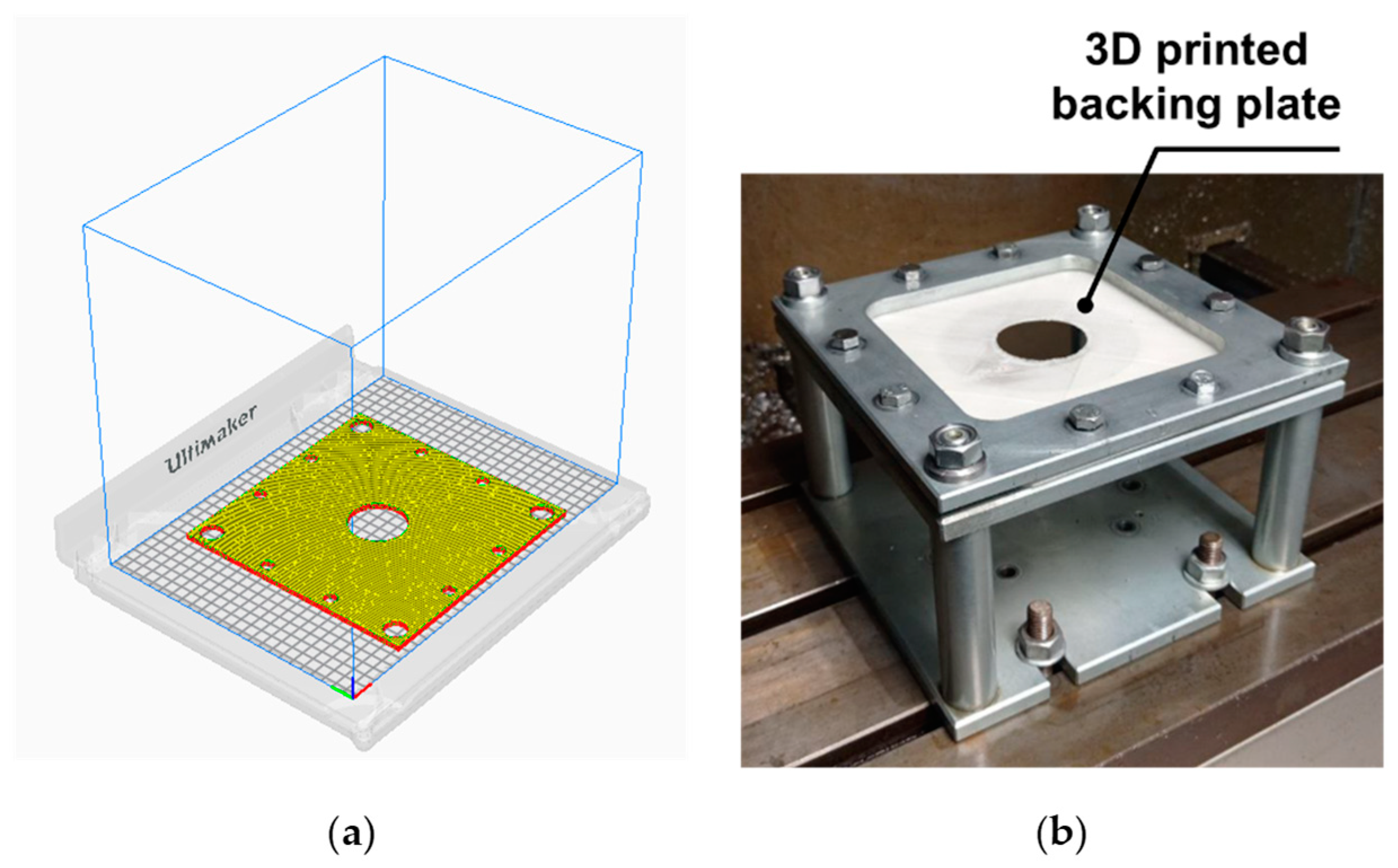
2.2. SPIF Tests
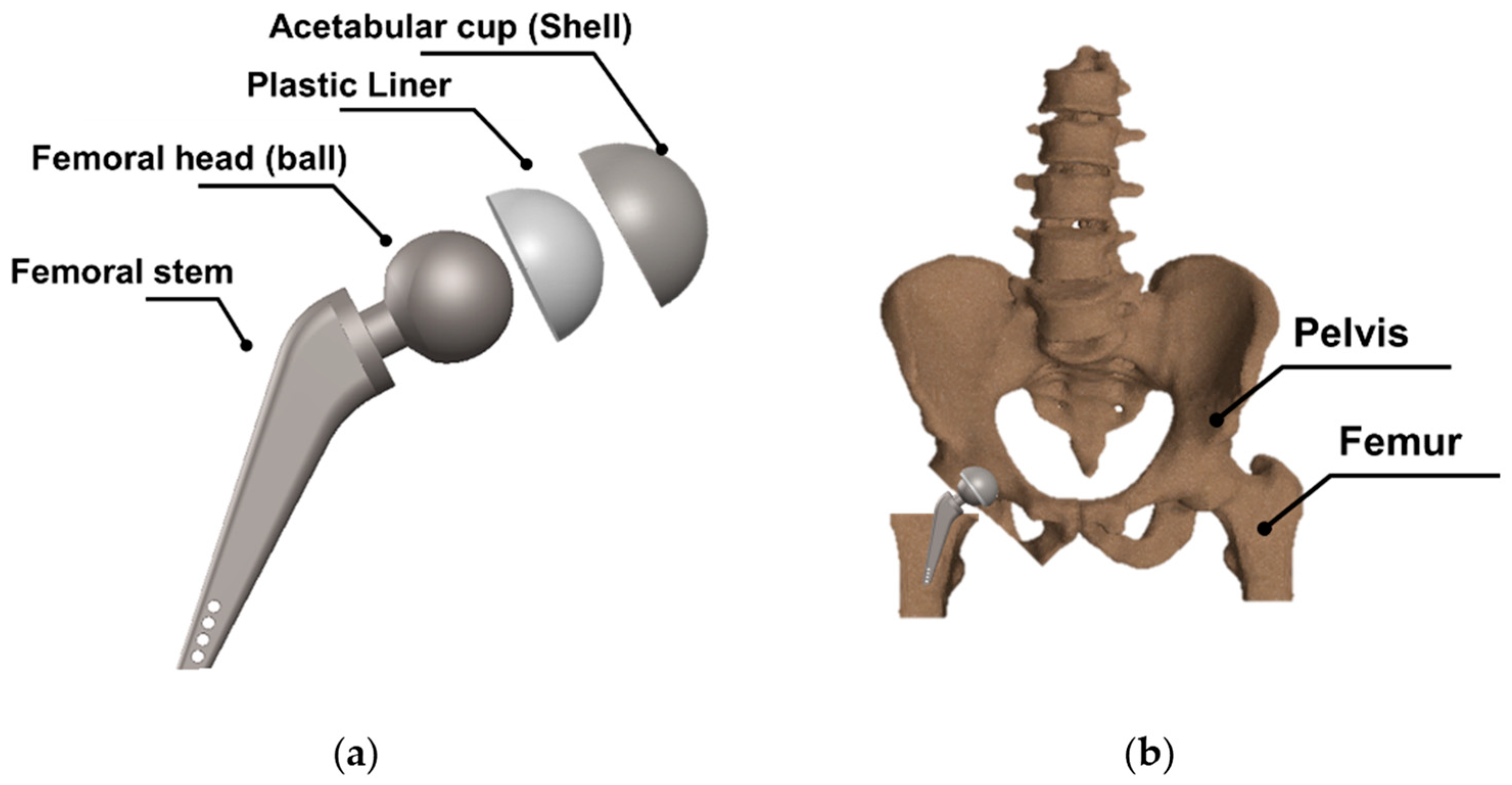
2.3. Medical Application
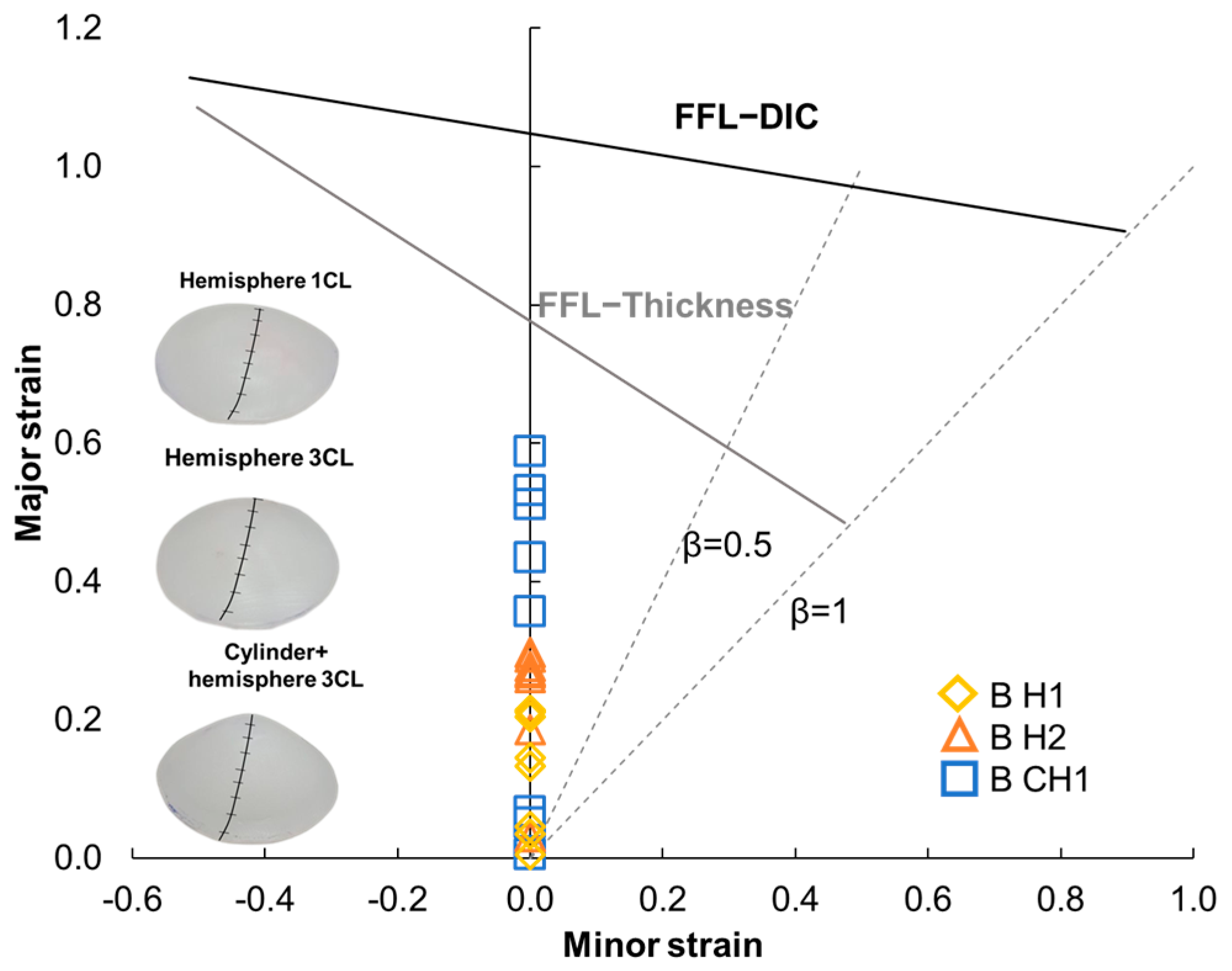
3. Results and Discussion
3.1. SPIF Tests
3.1.1. SPIF Analysis
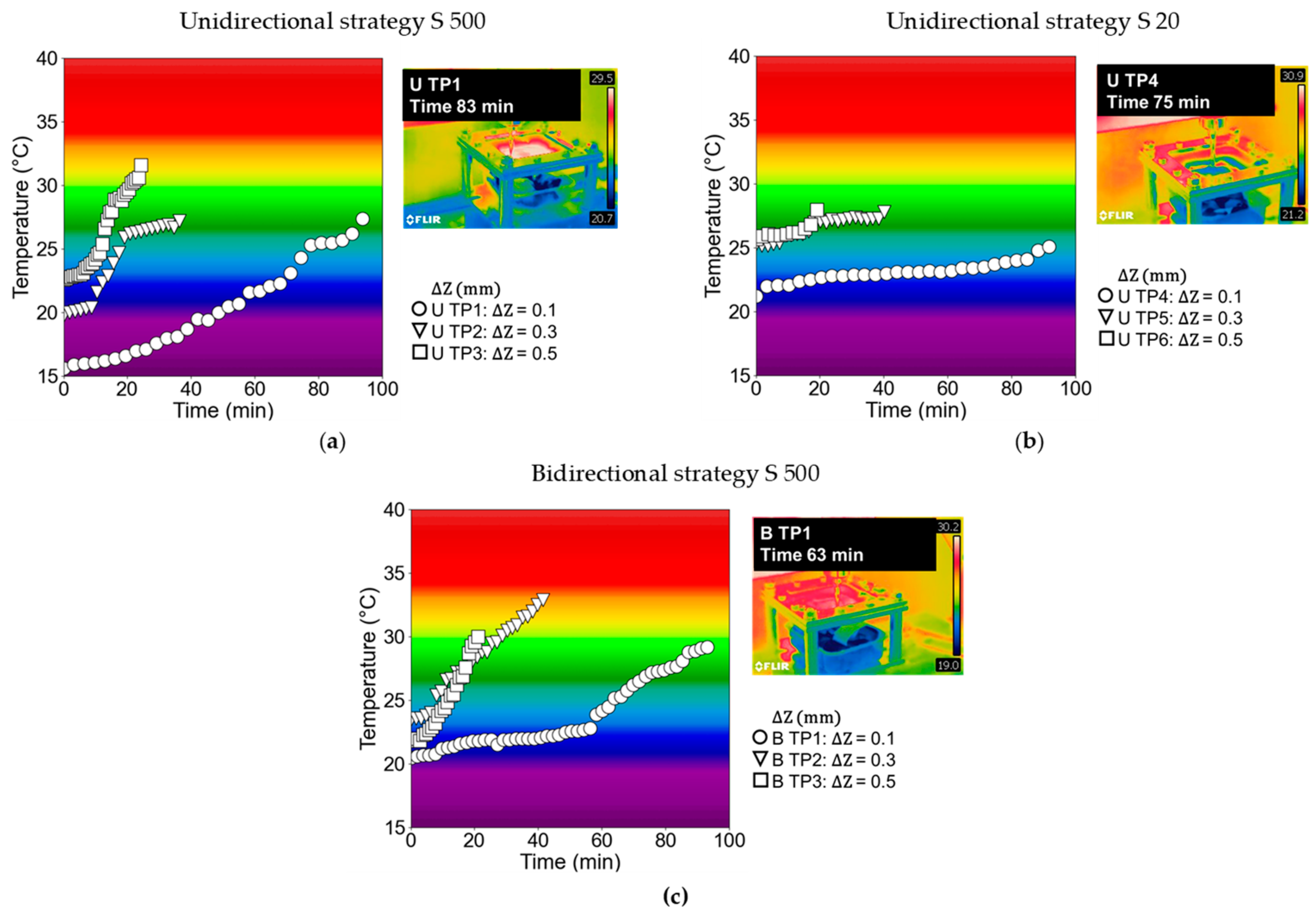
3.1.2. Temperature Analysis
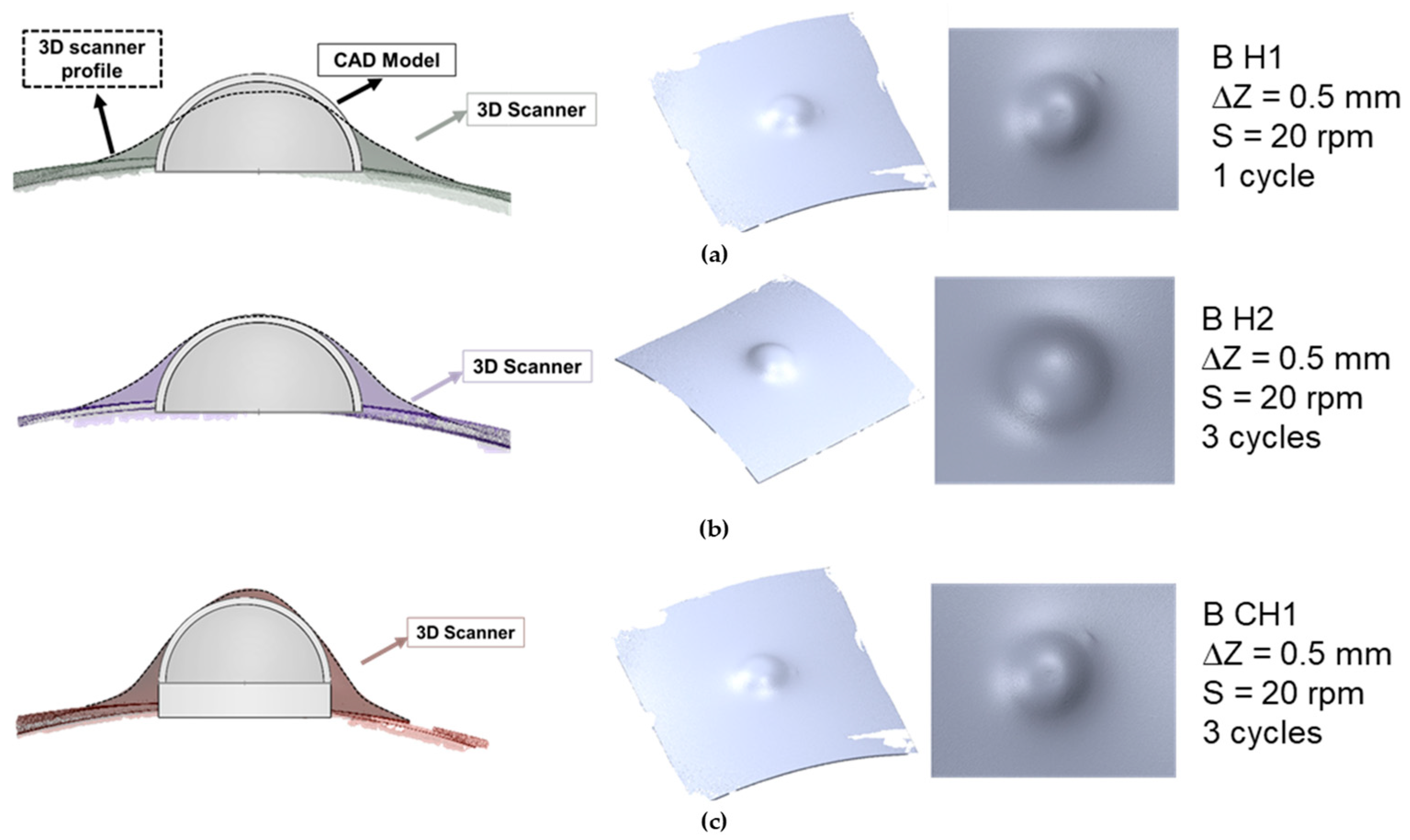
3.2. Plastic Liner Device
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Popkova, E.G.; Ragulina, Y.V.; Bogovix, A.V. (Eds.) The Industrial Revolution of the 21st Century; Springer: Berlin/Heidelberg, Germany, 2006; Volume 169, p. 249. [Google Scholar] [CrossRef]
- Marques, T.A.; Silva, M.B.; Martins, P.A.F. On the Potential of Single Point Incremental Forming of Sheet Polymer Parts. Int. J. Adv. Manuf. Technol. 2012, 60, 75–86. [Google Scholar] [CrossRef]
- Bagudanch, I.; Garcia-Romeu, M.L.; Centeno, G.; Elías-Zúñiga, A.; Ciurana, J. Forming Force and Temperature Effects on Single Point Incremental Forming of Polyvinylchloride. J. Mater. Process. Technol. 2015, 219, 221–229. [Google Scholar] [CrossRef]
- Centeno, G.; Morales-Palma, D.; Gonzalez-Perez-Somarriba, B.; Bagudanch, I.; Egea-Guerrero, J.J.; Gonzalez-Perez, L.M.; García-Romeu, M.L.; Vallellano, C. A Functional Methodology on the Manufacturing of Customized Polymeric Cranial Prostheses from CAT Using SPIF. Rapid Prototyp. J. 2017, 23, 771–780. [Google Scholar] [CrossRef]
- Martins, P.A.F.; Kwiatkowski, L.; Franzen, V.; Tekkaya, A.E.; Kleiner, M. Single Point Incremental Forming of Polymers. CIRP Ann. Manuf. Technol. 2009, 58, 229–232. [Google Scholar] [CrossRef]
- Rosa-Sainz, A.; Centeno, G.; Silva, M.B.; López-Fernández, J.A.; Martínez-Donaire, A.J.; Vallellano, C. On the Determination of Forming Limits in Polycarbonate Sheets. Materials 2020, 13, 928. [Google Scholar] [CrossRef] [PubMed]
- Rosa-Sainz, A.; Centeno, G.; Silva, M.B.; Vallellano, C. Experimental Failure Analysis in Polycarbonate Sheet Deformed by Spif. J. Manuf. Process. 2021, 64, 1153–1168. [Google Scholar] [CrossRef]
- Rosa-Sainz, A.; García-Romeu, M.L.; Ferrer, I.; Silva, M.B.; Centeno, G. On the Effective Peek Application for Customized Cranio-Maxillofacial Prostheses: An Experimental Formability Analysis. J. Manuf. Process. 2023, 86, 66–84. [Google Scholar] [CrossRef]
- Le, V.S.; Ghiotti, A.; Lucchetta, G. Preliminary Studies on Single Point Incremental Forming for Thermoplastic Materials. Int. J. Mater. Form. 2008, 1, 1179–1182. [Google Scholar] [CrossRef]
- Davarpanah, M.A.; Mirkouei, A.; Yu, X.; Malhotra, R.; Pilla, S. Effects of Incremental Depth and Tool Rotation on Failure Modes and Microstructural Properties in Single Point Incremental Forming of Polymers. J. Mater. Process. Technol. 2015, 222, 287–300. [Google Scholar] [CrossRef]
- Tathe, A.; Ghodke, M.; Nikalje, A.P. A Brief Review: Biomaterials and Their Apllication. Available online: https://www.semanticscholar.org/paper/A-BRIEF-REVIEW%3A-BIOMATERIALS-AND-THEIR-APLLICATION-Tathe-Ghodke/a807e0f8fcebf4c0defc9f832a38533f9c80ac0d (accessed on 2 September 2022).
- Bagudanch, I.; García-Romeu, M.L.; Ferrer, I.; Ciurana, J. Customized Cranial Implant Manufactured by Incremental Sheet Forming Using a Biocompatible Polymer. Rapid Prototyp. J. 2018, 24, 120–129. [Google Scholar] [CrossRef]
- Centeno, G.; Bagudanch, I.; Morales-Palma, D.; García-Romeu, M.L.; Gonzalez-Perez-Somarriba, B.; Martinez-Donaire, A.J.; Gonzalez-Perez, L.M.; Vallellano, C. Recent Approaches for the Manufacturing of Polymeric Cranial Prostheses by Incremental Sheet Forming. Proc. Procedia Eng. 2017, 183, 180–187. [Google Scholar] [CrossRef]
- Clavijo-Chaparro, S.L.; Iturbe-Ek, J.; Lozano-Sánchez, L.M.; Sustaita, A.O.; Elías-Zúñiga, A. Plasticized and Reinforced Poly(Methyl Methacrylate) Obtained by a Dissolution-Dispersion Process for Single Point Incremental Forming: Enhanced Formability towards the Fabrication of Cranial Implants. Polym. Test. 2018, 68, 39–45. [Google Scholar] [CrossRef]
- Chen, L.F.; Chen, F.; Gatea, S.; Ou, H. PEEK Based Cranial Reconstruction Using Thermal Assisted Incremental Sheet Forming. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 236, 997–1004. [Google Scholar] [CrossRef]
- Fiorentino, A.; Marenda, G.P.; Marzi, R.; Ceretti, E.; Kemmoku, D.T.; Lopes Da Silva, J.V. Rapid Prototyping Techniques for Individualized Medical Prosthesis Manufacturing. In Innovative Developments in Virtual and Physical Prototyping, Proceedings of the 5th International Conference on Advanced Research in Virtual and Rapid Prototyping, Leiria, Portugal, 28 September–1 October 2011; CRC Press: Boca Raton, FL, USA, 2012; Volume 1, pp. 589–594. [Google Scholar] [CrossRef]
- Chilukoti, G.R.; Periyasam, A.P. Ultra High Molecular Weight Polyethylene for Medical Applications. Available online: https://www.researchgate.net/publication/298626009_Ultra_high_molecular_weight_polyethylene_for_medical_applications (accessed on 31 August 2022).
- Kurtz, S.M. From Ethylene Gas to UHMWPE Component: The Process of Producing Orthopedic Implants. In UHMWPE Biomaterials Handbook: Ultra High Molecular Weight Polyethylene in Total Joint Replacement and Medical Devices: Third Edition; William Andrew Publishing: Norwich, NY, USA, 2016; pp. 7–20. ISBN 9780323354011. [Google Scholar]
- Musib, M.K. A Review of the History and Role of UHMWPE as A Component in Total Joint Replacements. Int. J. Biol. Eng. 2011, 1, 6–10. [Google Scholar] [CrossRef]
- Ardestani, M.M.; Amenábar Edwards, P.P.; Wimmer, M.A. Prediction of Polyethylene Wear Rates from Gait Biomechanics and Implant Positioning in Total Hip Replacement. Clin. Orthop. Relat. Res. 2017, 475, 2027–2042. [Google Scholar] [CrossRef]
- Kurtz, S.M.; Gawel, H.A.; Patel, J.D. History and Systematic Review of Wear and Osteolysis Outcomes for First-Generation Highly Crosslinked Polyethylene. Clin. Orthop. Relat. Res. 2011, 469, 2262. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.; Naqvi, R.A.; Abbas, N.; Khan, S.M.; Nawaz, S.; Hussain, A.; Zahra, N.; Khalid, M.W. Ultra-High-Molecular-Weight-Polyethylene (UHMWPE) as a Promising Polymer Material for Biomedical Applications: A Concise Review. Polymers 2020, 12, 323. [Google Scholar] [CrossRef]
- Wang, M.; Fu, J.; Jin, Z.-M.; Wang, J.-W. UHMWPE Biomaterials for Joint Implants: Structures, Properties and Clinical Performance; Springer: Berlin/Heidelberg, Germany, 2019; Volume 13. [Google Scholar] [CrossRef]
- Rosa-Sainz, A.; Centeno, G.; Silva, M.B.; López-Fernández, J.A.; Martínez-Donaire, A.J.; Vallellano, C. On the Determination of the Forming Limits by Necking and Fracture of Polycarbonate Sheet. Miner. Met. Mater. Ser. 2021, 2597–2608. [Google Scholar] [CrossRef]
- Goodfellow UHMWPE Sheet 2 mm Thick |Properties. Available online: https://www.goodfellow.com/p/et30-sh-000100/uhmwpe-sheet (accessed on 19 July 2023).
- ISO12004-2; Metallic Materials-Sheet and Strip-Determination of Forming Limit Curves Part 2: Determination of Forming Limit Curves in Laboratory. International Organization of Standards: Geneva, Switzerland, 2008.
- Martínez-Donaire, A.J.; García-Lomas, F.J.; Vallellano, C. New Approaches to Detect the Onset of Localised Necking in Sheets under Through-Thickness Strain Gradients. Mater. Des. 2014, 57, 135–145. [Google Scholar] [CrossRef]
- Centeno, G.; Bagudanch, I.; Martínez-Donaire, A.J.; García-Romeu, M.L.; Vallellano, C. Critical Analysis of Necking and Fracture Limit Strains and Forming Forces in Single-Point Incremental Forming. Mater. Des. 2014, 63, 20–29. [Google Scholar] [CrossRef]
- Franzen, V.; Kwiatkowski, L.; Martins, P.A.F.; Tekkaya, A.E. Single Point Incremental Forming of PVC. J. Mater. Process. Technol. 2009, 209, 462–469. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, F. Mechanism of Twist in Incremental Sheet Forming of Thermoplastic Polymer. Mater. Des. 2020, 195, 108997. [Google Scholar] [CrossRef]
- Rosa-Sainz, A.; Centeno, G.; Silva, M.B.; Vallellano, C. Experimental Investigation of Polycarbonate Sheets Deformed by SPIF: Formability, Micro-Mechanisms of Failure and Temperature Analysis. J. Mater. Res. Technol. 2023, 25, 7546–7565. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Ma, Y.; Geng, Y.; Tan, J. Rheological and Mechanical Properties of Ultrahigh Molecular Weight Polyethylene/High Density Polyethylene/Polyethylene Glycol Blends. Adv. Ind. Eng. Polym. Res. 2019, 2, 51–60. [Google Scholar] [CrossRef]
- Hallab, N.J.; Jacobs, J.J. Orthopedic Applications. In Biomaterials Science, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 841–882. [Google Scholar] [CrossRef]
- Biomet, Z. Acetabular System. Available online: https://www.zimmerbiomet.com/en/products-and-solutions/specialties/hip/g7-acetabular-system.html (accessed on 5 September 2022).
- Medina-Sánchez, G.; Torres-Jimenez, E.; Lopez-Garcia, R.; Dorado-Vicente, R.; Cazalla-Moral, R. Temperature Influence on Single Point Incremental Forming of PVC Parts. Procedia Manuf. 2017, 13, 335–342. [Google Scholar] [CrossRef]
- Bagudanch, I.; Vives-Mestres, M.; Sabater, M.; Garcia-Romeu, M.L. Polymer Incremental Sheet Forming Process: Temperature Analysis Using Response Surface Methodology. Mater. Manuf. Process. 2017, 32, 44–53. [Google Scholar] [CrossRef]
- Formisano, A.; Boccarusso, L.; Durante, M. Optimization of Single-Point Incremental Forming of Polymer Sheets through FEM. Materials 2023, 16, 451. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, F.; Gatea, S.; Ou, H. Design of the Novel Hot Incremental Sheet Forming Experimental Setup, Characterization of Formability Behavior of Polyether-Ether-Ketone (PEEK). Int. J. Adv. Manuf. Technol. 2020, 106, 5365–5381. [Google Scholar] [CrossRef]
- Lozano-Sánchez, L.M.; Bagudanch, I.; Sustaita, A.O.; Iturbe-Ek, J.; Elizalde, L.E.; Garcia-Romeu, M.L.; Elías-Zúñiga, A. Single-Point Incremental Forming of Two Biocompatible Polymers: An Insight into Their Thermal and Structural Properties. Polym. 2018, 10, 391. [Google Scholar] [CrossRef]
- Bagudanch, I.; Garcia-Romeu, M.L.; Sabater, M. Incremental Forming of Polymers: Process Parameters Selection from the Perspective of Electric Energy Consumption and Cost. J. Clean. Prod. 2016, 112, 1013–1024. [Google Scholar] [CrossRef]
- Formisano, A.; Lambiase, F.; Durante, M. Polymer Self-Heating during Incremental Forming. J. Manuf. Process. 2020, 58, 1189–1199. [Google Scholar] [CrossRef]
- Matplotlib Python v3.4.2. Available online: https://matplotlib.org/ (accessed on 25 June 2021).
- NumPy Library Python. Available online: https://numpy.org/doc/stable/ (accessed on 22 December 2022).
- Hagan, E.; Jeswiet, J. A Review of Conventional and Modern Single-Point Sheet Metal Forming Methods. Proc. Inst. Mech. Eng. 2005, 217, 213–225. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, Y.; Xu, C.; Liu, Y.; Ghafoor, S.; Li, F. Incremental Sheet Forming towards Biomedical Implants: A Review. J. Mater. Res. Technol. 2020, 9, 7225–7251. [Google Scholar] [CrossRef]








| Geometry | Dimensions | Wall Angle | |||||
|---|---|---|---|---|---|---|---|
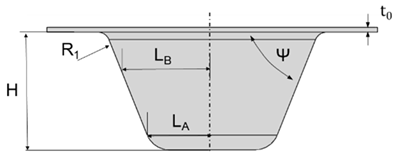 | LA (mm) | LB (mm) | R1 (mm) | H (mm) | ψ | t0 (mm) | Fixed |
| 25 | 40 | 5 | 50 | 20 | 2 | ||
| Test Condition | (mm) | (rpm) | (mm/min) | (mm) |
|---|---|---|---|---|
| U TP1 | 10 | 500 | 1000 | 0.5 |
| U TP2 | 10 | 500 | 1000 | 0.3 |
| U TP3 | 10 | 500 | 1000 | 0.1 |
| U TP4 | 10 | 20 | 1000 | 0.5 |
| U TP5 | 10 | 20 | 1000 | 0.3 |
| U TP6 | 10 | 20 | 1000 | 0.1 |
| B TP1 | 10 | 500 | 1000 | 0.5 |
| B TP2 | 10 | 500 | 1000 | 0.3 |
| B TP3 | 10 | 500 | 1000 | 0.1 |
| Geometry | Parameters (mm) | ||||
|---|---|---|---|---|---|
| Hemispherical Geometry | Dimensions | ||||
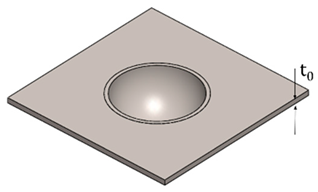 | 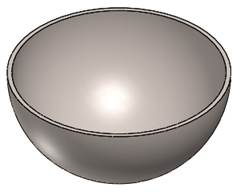 | 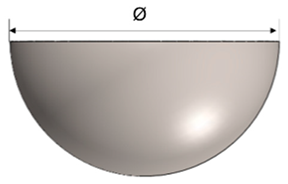 | Ø | t0 | |
| 44 | 2 | ||||
| Cylindrical and a hemispherical zone | H | Ø | t0 | ||
 | 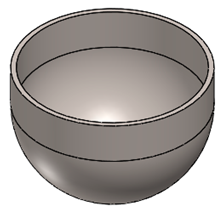 | 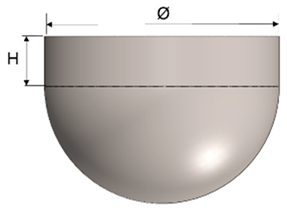 | 10 | 44 | 2 |
| Test Condition | (mm) | (rpm) | (mm/min) | (mm) | Cycles |
|---|---|---|---|---|---|
| B H1 | 10 | 20 | 1000 | 0.5 | 1 |
| B H2 | 10 | 20 | 1000 | 0.5 | 3 |
| B CH1 | 10 | 20 | 1000 | 0.5 | 3 |
| Test Condition | (mm) | (rpm) | (mm/min) | (mm) | Failure | Fracture Depth (mm) |
|---|---|---|---|---|---|---|
| U TP1 | 10 | 500 | 1000 | 0.1 | T + F | 29.7 |
| U TP2 | 10 | 500 | 1000 | 0.3 | T + F | 36.3 |
| U TP3 | 10 | 500 | 1000 | 0.5 | T + F | 39 |
| U TP4 | 10 | 20 | 1000 | 0.1 | T + F | 29.4 |
| U TP5 | 10 | 20 | 1000 | 0.3 | T + F | 40 |
| U TP6 | 10 | 20 | 1000 | 0.5 | T + F | 32 |
| B TP1 | 10 | 500 | 1000 | 0.1 | F | 28.1 |
| B TP2 | 10 | 500 | 1000 | 0.3 | F | 39 |
| B TP3 | 10 | 500 | 1000 | 0.5 | F | 37.5 |
| Test Condition | (mm) | (rpm) | Failure | Time (min) | Number of Cycles |
|---|---|---|---|---|---|
| B H1 | 0.5 | 20 | no | 5 | 1 |
| B H2 | 0.5 | 20 | no | 16 | 3 |
| B CH1 | 0.5 | 20 | no | 21 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosa-Sainz, A.; Silva, M.B.; Beltrán, A.M.; Centeno, G.; Vallellano, C. Assessing Formability and Failure of UHMWPE Sheets through SPIF: A Case Study in Medical Applications. Polymers 2023, 15, 3560. https://doi.org/10.3390/polym15173560
Rosa-Sainz A, Silva MB, Beltrán AM, Centeno G, Vallellano C. Assessing Formability and Failure of UHMWPE Sheets through SPIF: A Case Study in Medical Applications. Polymers. 2023; 15(17):3560. https://doi.org/10.3390/polym15173560
Chicago/Turabian StyleRosa-Sainz, Ana, M. Beatriz Silva, Ana M. Beltrán, Gabriel Centeno, and Carpóforo Vallellano. 2023. "Assessing Formability and Failure of UHMWPE Sheets through SPIF: A Case Study in Medical Applications" Polymers 15, no. 17: 3560. https://doi.org/10.3390/polym15173560
APA StyleRosa-Sainz, A., Silva, M. B., Beltrán, A. M., Centeno, G., & Vallellano, C. (2023). Assessing Formability and Failure of UHMWPE Sheets through SPIF: A Case Study in Medical Applications. Polymers, 15(17), 3560. https://doi.org/10.3390/polym15173560