Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints
Abstract
:1. Introduction
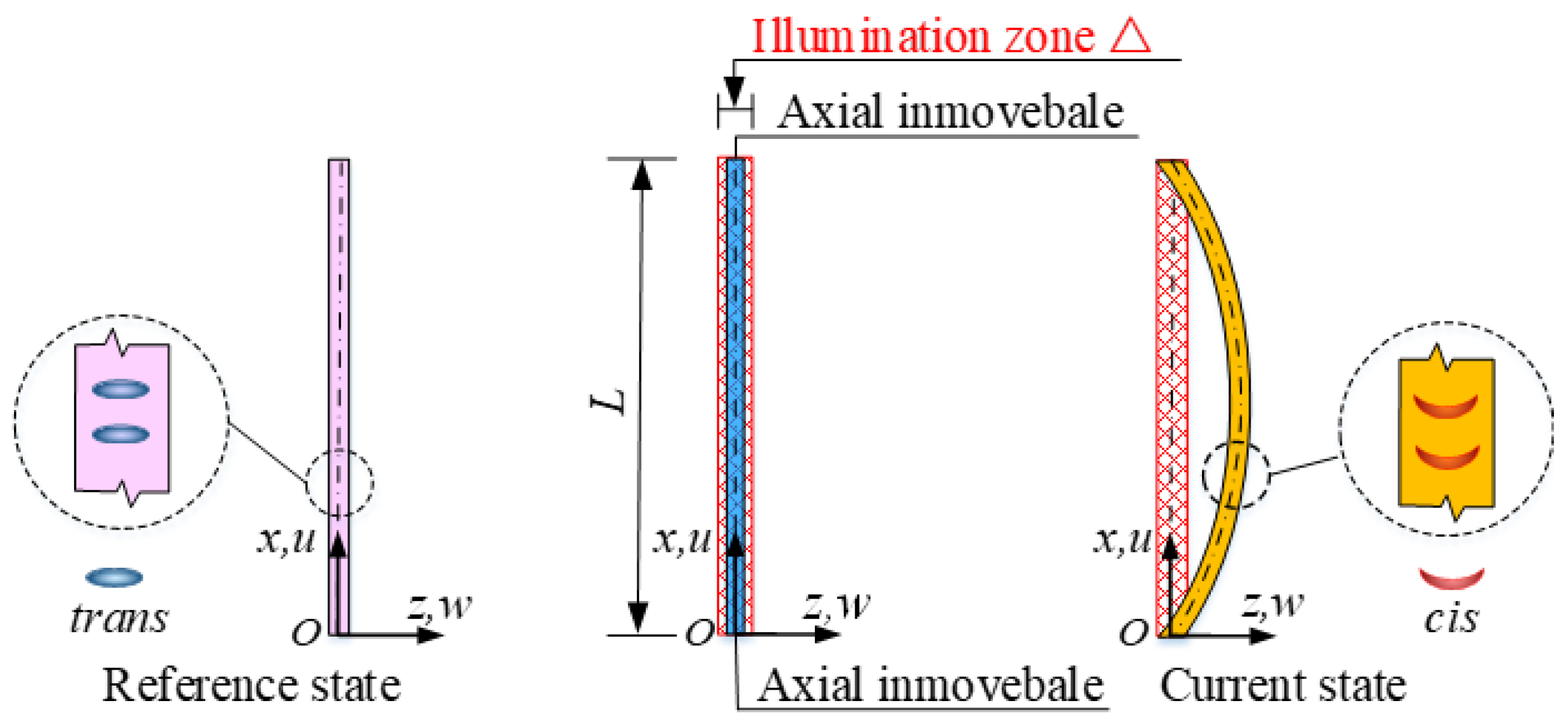
2. Theoretical Model and Formulation
2.1. Governing Equations for Dynamic Euler Buckling of a LCE Rod
2.2. Evolution of the Number Fraction in the LCE Rod
2.3. Nondimensionalization
2.4. Solution to the Dynamic Euler Buckling of the LCE Rods
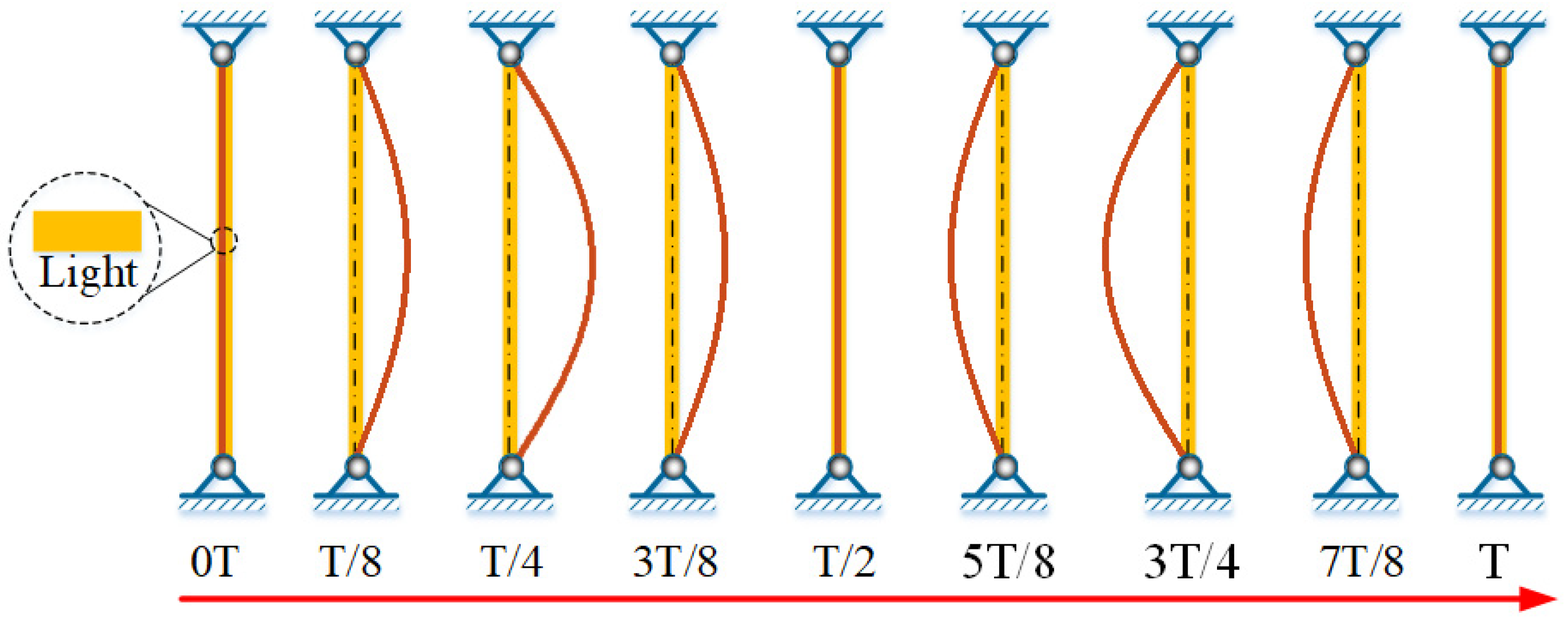
3. Two Motion Modes and Their Mechanisms
3.1. Two Motion Modes
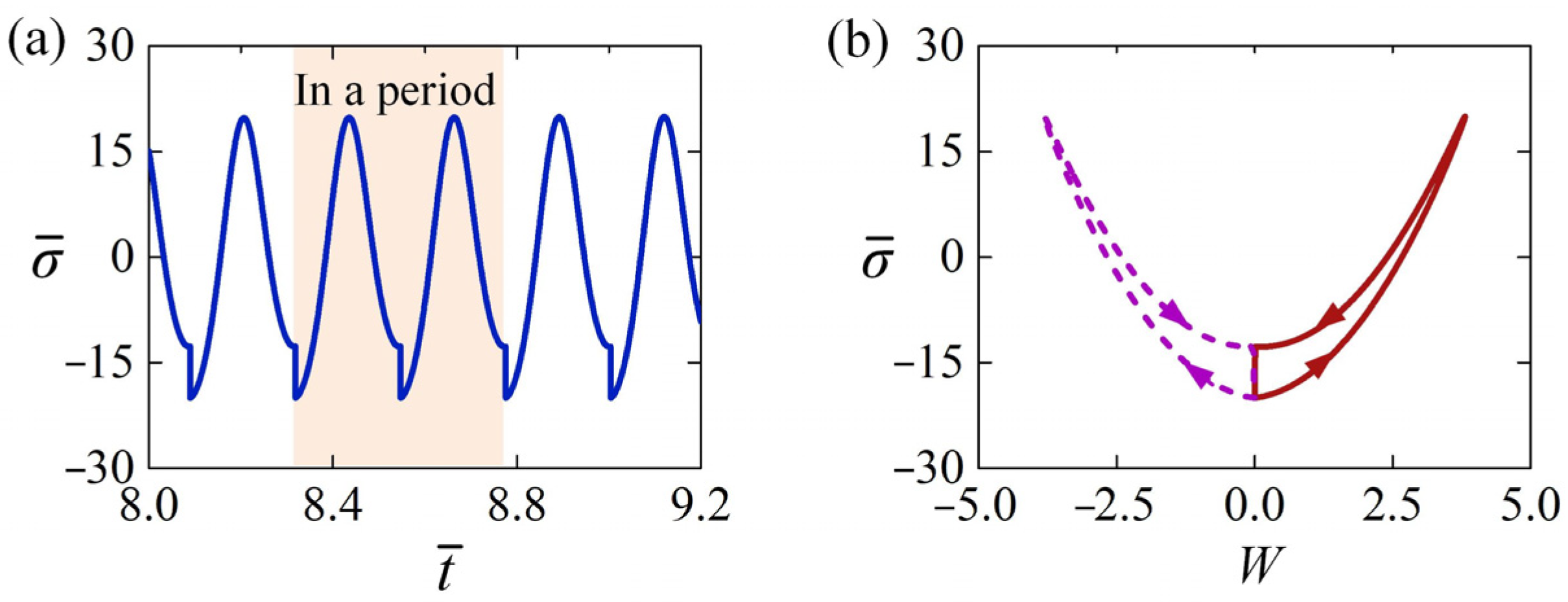
3.2. Evolution of Key Physical Quantities
3.3. Mechanism of the Self-Sustained Euler Buckling
4. Influence of System Parameters
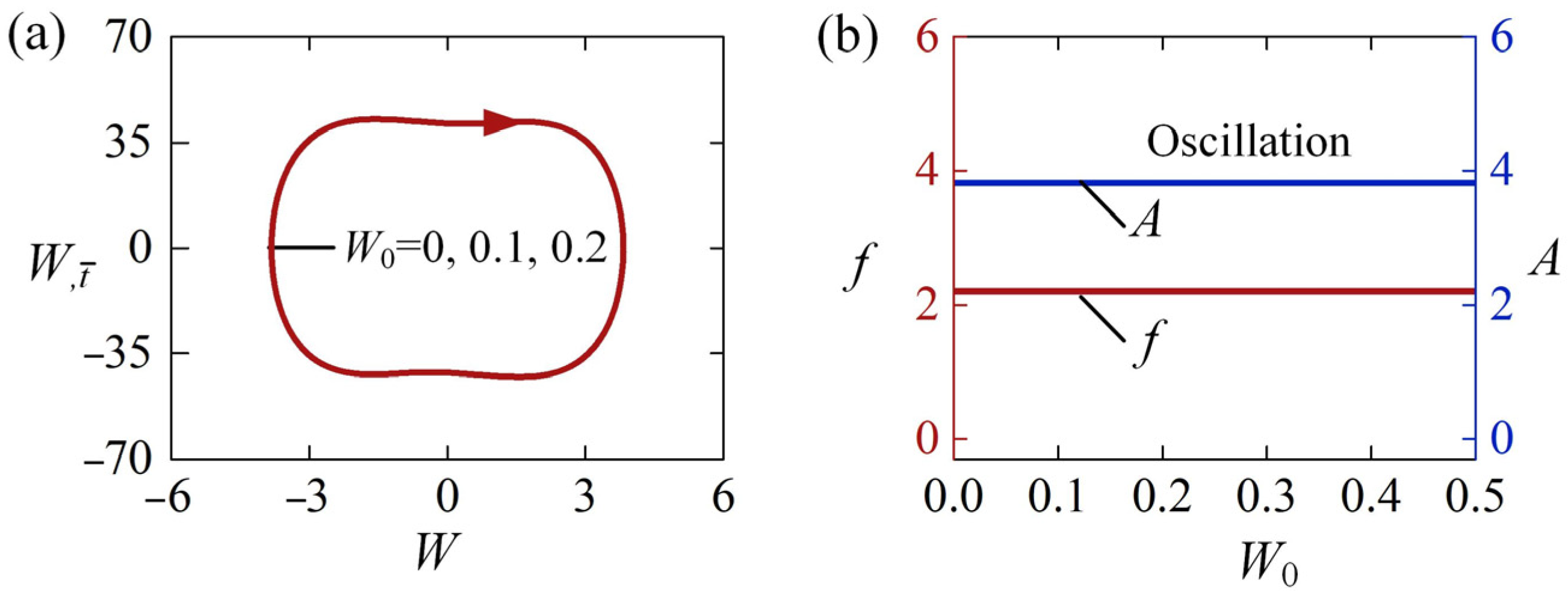
4.1. Effect of the Initial Condition
4.2. Effect of the Light-Induced Expansion Loading
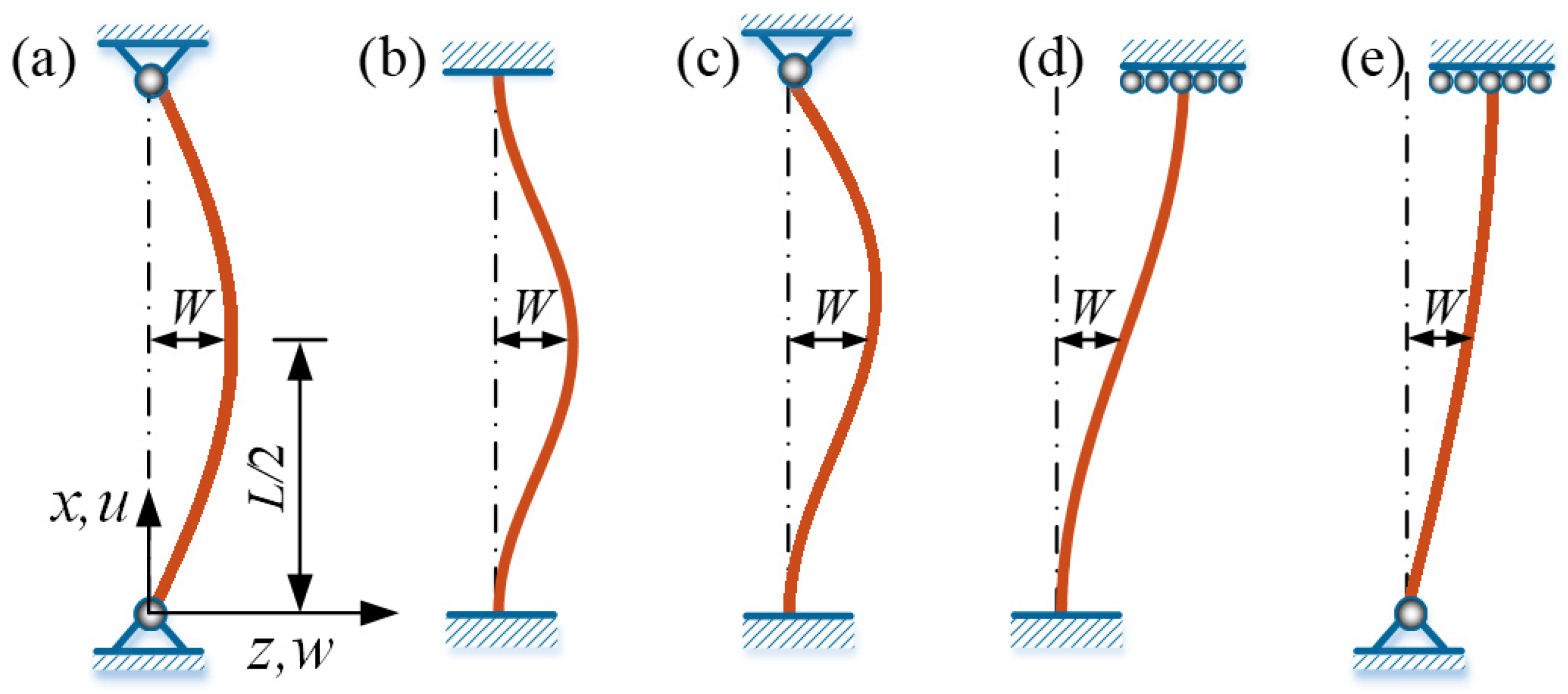
5. Self-Buckling Mode: Different Boundary Conditions
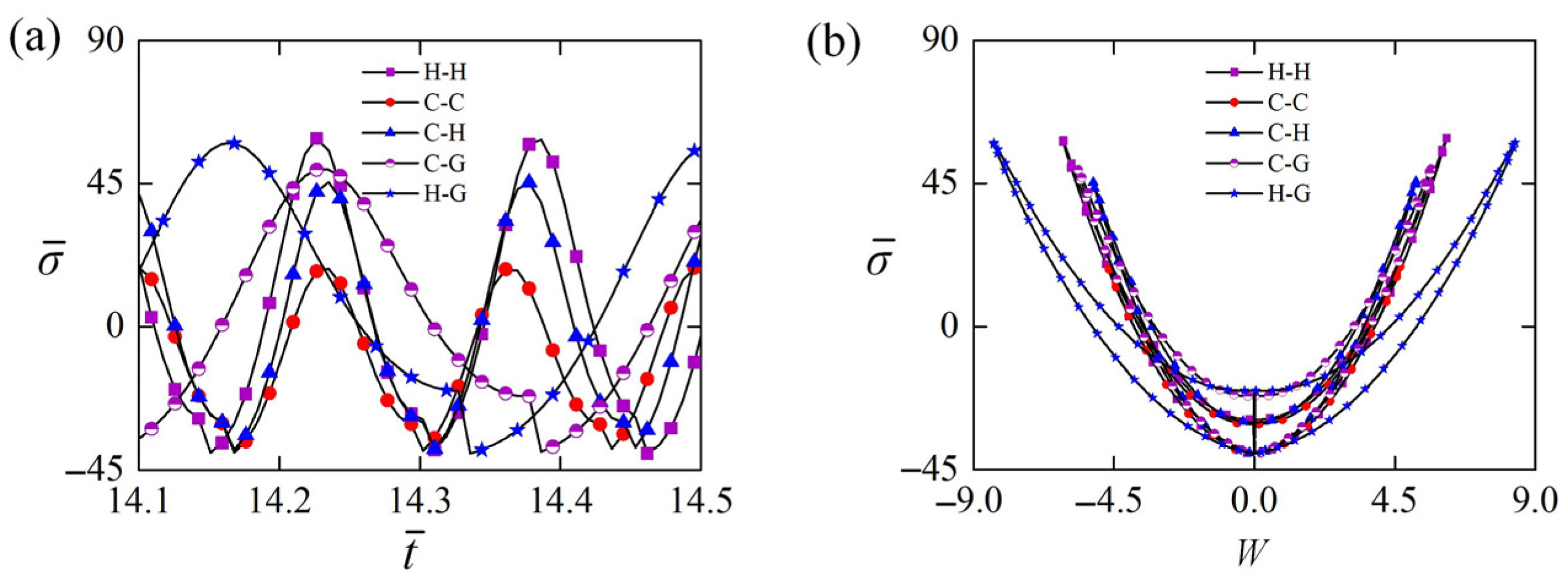
5.1. Normal Stress for Different Constraint Configurations
5.2. Equivalent Force for Different Constraint Configurations
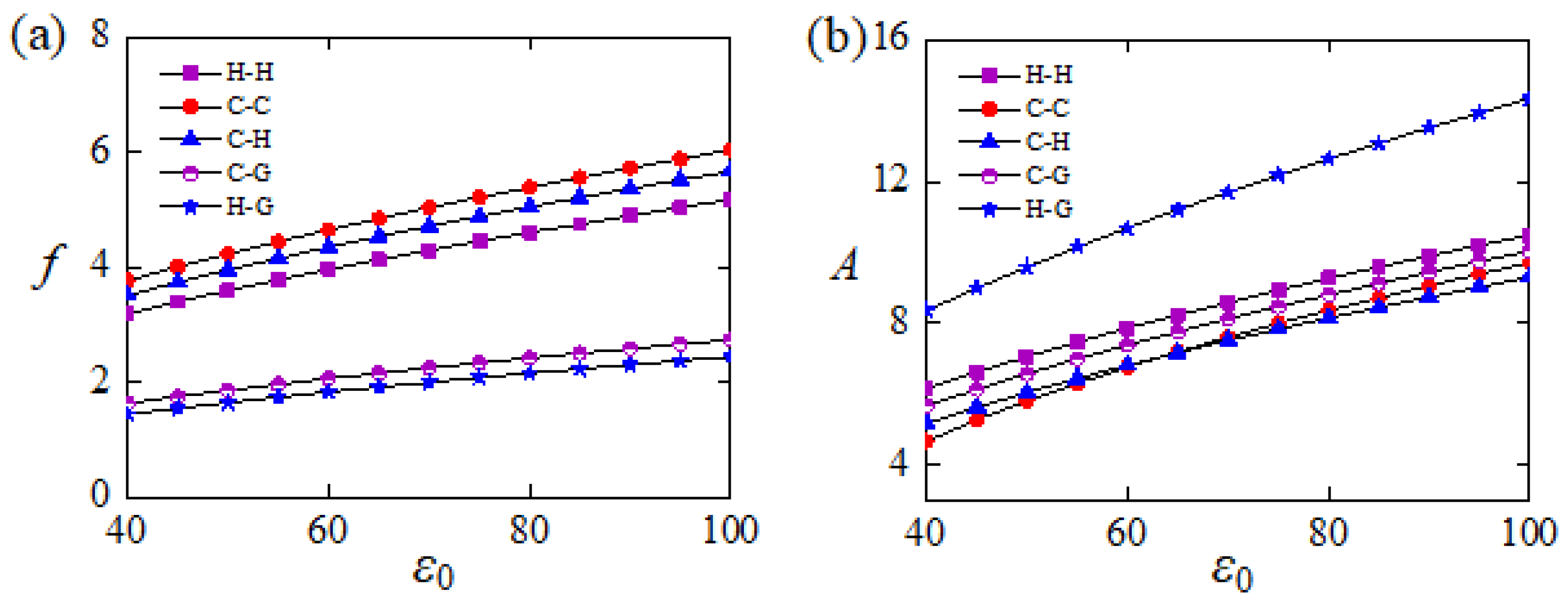
5.3. Frequency and Amplitude for Different Constraint Configurations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ding, W. Self-Excited Vibration; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81–85. [Google Scholar] [CrossRef]
- Cheng, Q.; Cheng, W.; Dai, Y.; Li, K. Self-oscillating floating of a spherical liquid crystal elastomer balloon under steady illumination. Int. J. Mech. Sci. 2023, 241, 107985. [Google Scholar] [CrossRef]
- Sangwan, V.; Taneja, A.; Mukherjee, S. Design of a robust self-excited biped walking mechanism. Mech. Mach. Theory 2004, 39, 1385–1397. [Google Scholar] [CrossRef]
- Shin, B.; Ha, J.; Lee, M.; Park, K.; Park, G.H.; Choi, T.H.; Cho, K.-J.; Kim, H.-Y. Hygrobot: A self-locomotive ratcheted actuator powered by environmental humidity. Sci. Robot. 2018, 3, eaar2629. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Chen, Z.; Xu, P. Light-propelled self-sustained swimming of a liquid crystal elastomer torus at low Reynolds number. Int. J. Mech. Sci. 2022, 219, 107128. [Google Scholar] [CrossRef]
- Liao, B.; Zang, H.; Chen, M.; Wang, Y.; Lang, X.; Zhu, N.; Yang, Z.; Yi, Y. Soft Rod-Climbing Robot Inspired by Winding Locomotion of Snake. Soft Robot. 2020, 7, 500–511. [Google Scholar] [CrossRef]
- Chun, S.; Pang, C.; Cho, S.B. A Micropillar-Assisted Versatile Strategy for Highly Sensitive and Efficient Triboelectric Energy Generation under In-Plane Stimuli. Adv. Mater. 2019, 32, e1905539. [Google Scholar] [CrossRef] [PubMed]
- Wie, J.J.; Shankar, M.R.; White, T.J. Photomotility of polymers. Nat. Commun. 2016, 7, 13260. [Google Scholar] [CrossRef]
- Tang, Y.; Li, M.; Wang, T.; Dong, X.; Hu, W.; Sitti, M. Wireless Miniature Magnetic Phase-Change Soft Actuators. Adv. Mater. 2022, 34, 2204185. [Google Scholar] [CrossRef]
- White, T.J.; Broer, D.J. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087–1098. [Google Scholar] [CrossRef]
- Preston, D.J.; Rothemund, P.; Jiang, H.J.; Nemitz, M.P.; Rawson, J.; Suo, Z.; Whitesides, G.M. Digital logic for soft devices. Proc. Natl. Acad. Sci. USA 2019, 116, 7750–7759. [Google Scholar] [CrossRef] [Green Version]
- Xia, M.; Pan, N.; Zhang, C.; Zhang, C.; Fan, W.; Xia, Y.; Wang, Z.; Sui, K. Self-Powered Multifunction Ionic Skins Based on Gradient Polyelectrolyte Hydrogels. ACS Nano 2022, 16, 4714–4725. [Google Scholar] [CrossRef] [PubMed]
- Shen, Q.; Trabia, S.; Stalbaum, T.; Palmre, V.; Kim, K.; Oh, I. A multiple-shape memory polymer-metal composite actuator capable of programmable control, creating complex 3D motion of bending, twisting, and oscillation. Sci. Rep. 2016, 6, 24462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, B.; Jia, R.; Yang, H.; Chen, X.; Tan, K.; Deng, Q.; Tang, J. Magnetic arthropod millirobots fabricated by 3D-printed hydrogels. Adv. Intell. Syst. 2022, 4, 2100139. [Google Scholar] [CrossRef]
- Zhu, Q.L.; Dai, C.F.; Wagner, D.; Khoruzhenko, O.; Hong, W.; Breu, J.; Zheng, Q.; Wu, Z.L. Patterned Electrode Assisted One-Step Fabrication of Biomimetic Morphing Hydrogels with Sophisticated Anisotropic Structures. Adv. Sci. 2021, 8, 2102353. [Google Scholar] [CrossRef] [PubMed]
- Jin, B.; Liu, J.; Shi, Y.; Chen, G.; Zhao, Q.; Yang, S. Solvent-Assisted 4D Programming and Reprogramming of Liquid Crystalline Organogels. Adv. Mater. 2021, 34, 2107855. [Google Scholar] [CrossRef]
- Wu, J.; Yao, S.; Zhang, H.; Man, W.; Bai, Z.; Zhang, F.; Wang, X.; Fang, D.; Zhang, Y. Liquid crystal elastomer metamaterials with giant biaxial thermal shrinkage for enhancing skin regeneration. Adv. Mater. 2021, 33, 2106175. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, J.; Yang, S. Multi-functional liquid crystal elastomer composites. Appl. Phys. Rev. 2022, 9, 011301. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, H.; Lee, X.; Zeng, H.; Priimagi, A. Kirigami-based light-induced shape-morphing and locomotion. Adv. Mater. 2020, 32, 1906233. [Google Scholar] [CrossRef] [Green Version]
- Bazir, A.; Baumann, A.; Ziebert, F.; Kulić, I.M. Dynamics of fiberboids. Soft Matter 2020, 16, 5210–5223. [Google Scholar] [CrossRef]
- Hu, Y.; Ji, Q.; Huang, M.; Chang, L.; Zhang, C.; Wu, G.; Zi, B.; Bao, N.; Chen, W.; Wu, Y. Light-driven self-oscillating actuators with pototactic locomotion based on black phosphorus heterostructure. Angew. Chem. Int. Ed. 2021, 60, 20511–20517. [Google Scholar] [CrossRef]
- Sun, J.; Hu, W.; Zhang, L.; Lan, R.; Yang, H.; Yang, D. Light-Driven Self-Oscillating Behavior of Liquid-Crystalline Networks Triggered by Dynamic Isomerization of Molecular Motors. Adv. Funct. Mater. 2021, 31, 2103311. [Google Scholar] [CrossRef]
- Xu, T.; Pei, D.; Yu, S.; Zhang, X.; Yi, M.; Li, C. Design of MXene Composites with Biomimetic Rapid and Self-Oscillating Actuation under Ambient Circumstances. ACS Appl. Mater. Interfaces 2021, 13, 31978–31985. [Google Scholar] [CrossRef] [PubMed]
- Zeng, H.; Lahikainen, M.; Liu, L.; Ahmed, Z.; Wani, O.M.; Wang, M.; Yang, H.; Priimagi, A. Light-fuelled freestyle self-oscillators. Nat. Commun. 2019, 10, 5057. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Li, Y.; Lv, J.-A. Phototunable self-oscillating system driven by a self-winding fiber actuator. Nat. Commun. 2021, 12, 3211. [Google Scholar] [CrossRef]
- He, Q.; Wang, Z.; Wang, Y.; Wang, Z.; Li, C.; Annapooranan, R.; Zeng, J.; Chen, R.; Cai, S. Electrospun liquid crystal elastomer microfiber actuator. Sci. Robot. 2021, 6, eabi9704. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Du, C.; Wang, W.; Li, K. A thermally-responsive fiber engine in a linear temperature field. Int. J. Mech. Sci. 2022, 225, 107391. [Google Scholar] [CrossRef]
- Ge, D.; Dai, Y.; Li, K. Light-powered self-spinning of a button spinner. Int. J. Mech. Sci. 2023, 238, 107824. [Google Scholar] [CrossRef]
- Liang, X.; Chen, Z.; Zhu, L.; Li, K. Light-powered self-excited oscillation of a liquid crystal elastomer pendulum. Mech. Syst. Signal Process. 2021, 163, 108140. [Google Scholar] [CrossRef]
- Gelebart, A.H.; Mulder, D.J.; Varga, M.; Konya, A.; Ghislaine, V.; Meijer, E.W.; Selinger, R.L.B.; Broer, D.J. Making waves in a photoactive polymer film. Nature 2017, 546, 632–636. [Google Scholar] [CrossRef]
- Kuenstler, A.S.; Chen, Y.; Bui, P.; Kim, H.; DeSimone, A.; Jin, L.; Hayward, R.C. Blueprinting Photothermal Shape-Morphing of Liquid Crystal Elastomers. Adv. Mater. 2020, 32, e2000609. [Google Scholar] [CrossRef]
- Zhao, T.; Fan, Y.; Lv, J.-A. Photomorphogenesis of Diverse Autonomous Traveling Waves in a Monolithic Soft Artificial Muscle. ACS Appl. Mater. Interfaces 2022, 14, 23839–23849. [Google Scholar] [CrossRef]
- Ge, D.; Li, K. Self-oscillating buckling and postbuckling of a liquid crystal elastomer disk under steady illumination. Int. J. Mech. Sci. 2022, 221, 107233. [Google Scholar] [CrossRef]
- Xu, P.; Jin, J.; Li, K. Light-powered self-excited bouncing of a liquid crystal elastomer ball. Int. J. Mech. Sci. 2021, 208, 106686. [Google Scholar] [CrossRef]
- Kim, Y.; Berg, J.v.D.; Crosby, A.J. Autonomous snapping and jumping polymer gels. Nat. Mater. 2021, 20, 1695–1701. [Google Scholar] [CrossRef]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.M.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 1727. [Google Scholar] [CrossRef] [PubMed]
- Lv, X.; Yu, M.; Wang, W.; Yu, H. Photothermal pneumatic wheel with high loadbearing capacity. Compos. Commun. 2021, 24, 100651. [Google Scholar] [CrossRef]
- Ge, D.; Li, K. Pulsating self-snapping of a liquid crystal elastomer bilayer spherical shell under steady illumination. Int. J. Mech. Sci. 2022, 233, 107646. [Google Scholar] [CrossRef]
- Baumann, A.; Sánchez-Ferrer, A.; Jacomine, L.; Martinoty, P.; Le Houerou, V.; Ziebert, F.; Kulić, I.M. Motorizing fibres with geometric zero-energy modes. Nat. Mater. 2018, 17, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Zhou, L.; Du, C.; Li, K. A light-fueled self-oscillating liquid crystal elastomer balloon with self-shading effect. Chaos Solitons Fractals 2022, 155, 111646. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, W.; Sun, J.; Nandi, R.; Yang, Z. Bioinspired Construction of Artificial Cardiac Muscles Based on Liquid Crystal Elastomer Fibers. Adv. Mater. Technol. 2021, 7, 2100934. [Google Scholar] [CrossRef]
- Hou, K.; Guan, D.; Li, H.; Sun, Y.; Long, Y.; Song, K. Programmable light-driven swimming actuators via wavelength signal switching. Sci. Adv. 2021, 7, eabh3051. [Google Scholar] [CrossRef]
- Zhao, Y.; Xuan, C.; Qian, X.; Alsaid, Y.; Hua, M.; Jin, L.; He, X. Soft phototactic swimmer based on self-sustained hydrogel oscillator. Sci. Robot. 2019, 4, eaax7112. [Google Scholar] [CrossRef] [PubMed]
- Vantomme, G.; Elands, L.C.M.; Gelebart, A.H.; Meijer, E.W.; Pogromsky, A.Y.; Nijmeijer, H.; Broer, D.J. Coupled liquid crystalline oscillators in Huygens’ synchrony. Nat. Mater. 2021, 20, 1702–1706. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Yan, H.; Zhong, Z. Deep neural networks for large deformation of photo-thermo-pH responsive cationic gels. Appl. Math. Model 2021, 100, 549–563. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Choi, G.P.T.; Mahadevan, L. Self-Excited Motions of Volatile Drops on Swellable Sheets. Phys. Rev. Lett. 2020, 124, 258002. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Chang, L.; Hu, Y.; Huang, M.; Ji, Q.; Lu, P.; Liu, J.; Chen, W.; Wu, Y. An Autonomous Soft Actuator with Light-Driven Self-Sustained Wavelike Oscillation for Phototactic Self-Locomotion and Power Generation. Adv. Funct. Mater. 2020, 30, 1908842. [Google Scholar] [CrossRef]
- Lan, R.; Sun, J.; Shen, C.; Huang, R.; Zhang, Z.; Zhang, L.; Wang, L.; Yang, H. Near-Infrared Photodriven Self-Sustained Oscillation of Liquid-Crystalline Network Film with Predesignated Polydopamine Coating. Adv. Mater. 2020, 32, e1906319. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Fu, C.; Xia, Z.; Hurren, C.; Nilghaz, A.; Wang, X. Textiles in soft robots: Current progress and future trends. Biosens. Bioelectron. 2021, 196, 113690. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, Y. Photomechanical vibration energy harvesting based on liquid crystal elastomer cantilever. Smart Mater. Struct. 2019, 28, 075017. [Google Scholar] [CrossRef]
- Sapountzakis, E.; Tsiatas, G. Elastic flexural buckling analysis of composite beams of variable cross-section by BEM. Eng. Struct. 2006, 29, 675–681. [Google Scholar] [CrossRef]
- Korner, K.; Kuenstler, A.S.; Hayward, R.C.; Audoly, B.; Bhattacharya, K. A nonlinear beam model of photomotile structures. Proc. Natl. Acad. Sci. USA 2020, 117, 9762–9770. [Google Scholar] [CrossRef]
- Timoshenko, S.; Gere, J. Theory of Elastic Stability, 2nd ed.; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Camacho-Lopez, M.; Finkelmann, H.; Palffy-Muhoray, P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. [Google Scholar] [CrossRef]
- Serak, S.; Tabiryan, N.; Vergara, R.; White, T.J.; Vaia, R.A.; Bunning, T.J. Liquid crystalline polymer cantilever oscillators fueled by light. Soft Matter 2010, 6, 779–783. [Google Scholar] [CrossRef]
- Braun, L.B.; Hessberger, T.; Pütz, E.; Müller, C.; Giesselmann, F.; Serra, C.A.; Zentel, R. Actuating thermo- and photo-responsive tubes from liquid crystalline elastomers. J. Mater. Chem. C 2018, 6, 9093–9101. [Google Scholar] [CrossRef]
- Emam. S.A.; Nayfeh, A.H. Post-buckling and free vibrations of composite beams. Comput. Struct. 2009, 88, 636–642. [Google Scholar] [CrossRef]
- Corbett, D.; Xuan, C.; Warner, M. Deep optical penetration dynamics in photo-bending. Phys. Rev. E 2015, 92, 013206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gupta, R.; Gunda, J.B.; Janardhan, G.R.; Rao, G.V. Thermal post-buckling analysis of slender columns using the concept of coupled displacement field. Int. J. Mech. Sci. 2010, 52, 590–594. [Google Scholar] [CrossRef]
- Fung, Y.C.; Drucker, D.C. Foundation of Solid Mechanics. J. Appl. Mech. 1966, 33, 238. [Google Scholar] [CrossRef]
- Yu, Y.; Nakano, M.; Ikeda, T. Photomechanics: Directed bending of a polymer film by light. Nature 2003, 425, 145. [Google Scholar] [CrossRef]
- Bartholomew, A.K.; Stone, I.B.; Steigerwald, M.L.; Lambert, T.H.; Roy, X. Highly Twisted Azobenzene Ligand Causes Crystals to Continuously Roll in Sunlight. J. Am. Chem. Soc. 2022, 144, 16773–16777. [Google Scholar] [CrossRef] [PubMed]
- Nayfeh, A.H.; Emam, S.A. Exact solution and stability of postbuckling configurations of beams. Nonlinear Dyn. 2008, 54, 395–408. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behavior, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]





| Parameter | Definition | Value | Units |
|---|---|---|---|
| Contraction coefficient | 0–0.5 | / | |
| trans-to-cis thermal relaxation time | 0.1 | s | |
| Light intensity | 0–1 | kW/m2 | |
| Light-absorption constant | 0.0003 | m2/(s∙W) | |
| Elastic modulus of LCE balloon | 1–10 | MPa | |
| Mass density | 103 | kg/m3 | |
| Length of LCE rod | 10–50 | mm | |
| Cross-sectional area of LCE rod | 0–0.1 | mm2 | |
| Area moment of inertia of LCE rod | (0–1) × 10−6 | mm4 | |
| Damping coefficient | 0–0.001 | mg∙mm2/s |
| Parameter | |||||
|---|---|---|---|---|---|
| Value | 0–0.5 | 0–1 | 0–100 | 0–0.1 | 0–2 |
| Maximum () | |||||
|---|---|---|---|---|---|
| Case H-H | 6.16 | 59.41 | 2084.97 | 78.72 | 1761 |
| Case C-C | 4.67 | 18.91 | 2139.81 | 75.72 | 1254 |
| Case C-H | 5.18 | 45.59 | 2099.59 | 73.75 | 1393 |
| Case C-G | 5.66 | 49.64 | 506.85 | 37.40 | 754 |
| Case H-G | 8.36 | 57.98 | 590.86 | 48.60 | 1435 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, D.; Dai, Y.; Li, K. Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints. Polymers 2023, 15, 316. https://doi.org/10.3390/polym15020316
Ge D, Dai Y, Li K. Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints. Polymers. 2023; 15(2):316. https://doi.org/10.3390/polym15020316
Chicago/Turabian StyleGe, Dali, Yuntong Dai, and Kai Li. 2023. "Self-Sustained Euler Buckling of an Optically Responsive Rod with Different Boundary Constraints" Polymers 15, no. 2: 316. https://doi.org/10.3390/polym15020316







