In-Plane Elastic Properties of 3D-Printed Graded Hierarchical Hexagonal Honeycombs
Abstract
:1. Introduction
2. Geometric Description of Graded Hierarchical Hexagonal Honeycomb
3. Theory of Effective Elastic Modulus and Poisson’s Ratio
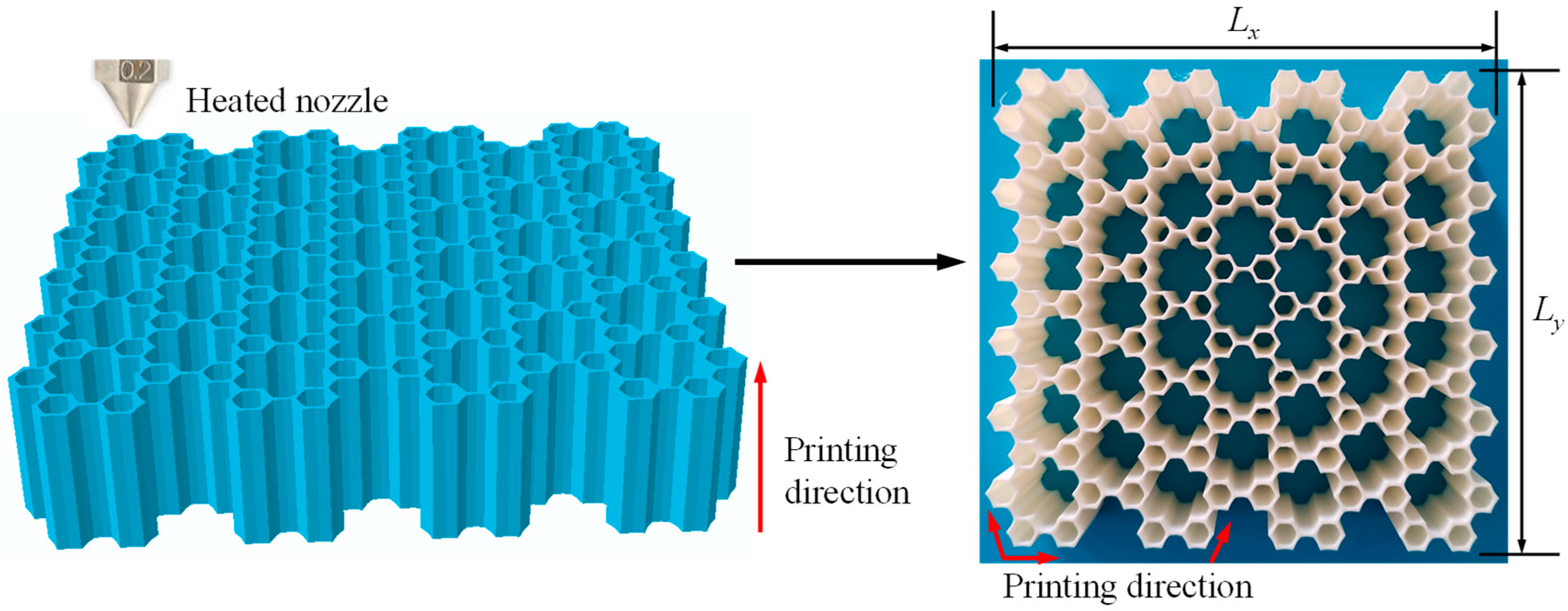
4. Experimental and Numerical Methods
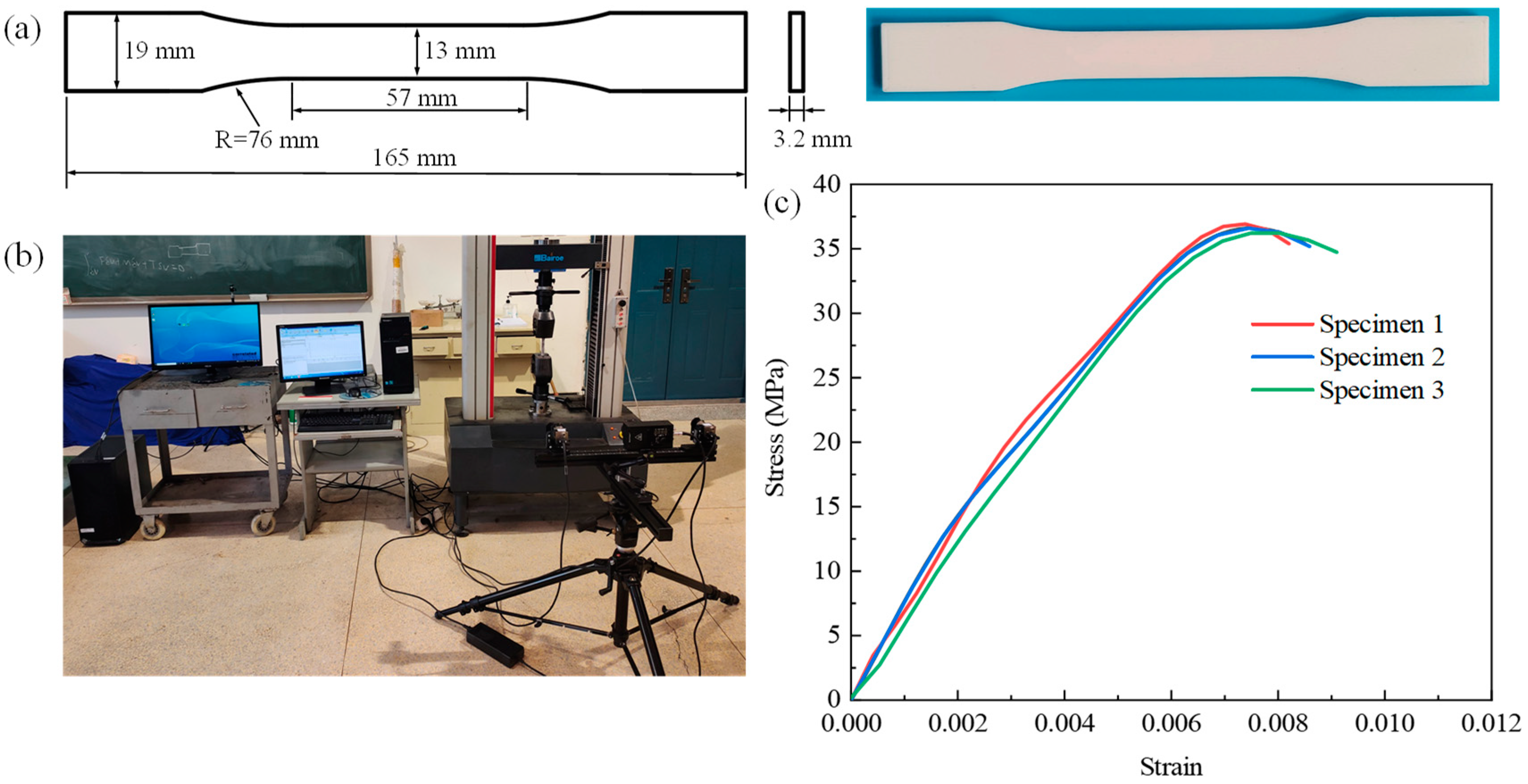
4.1. Experimental Test
4.2. Finite Element Modeling
4.3. Validation of Finite Element Modeling Method
5. Results and Discussion
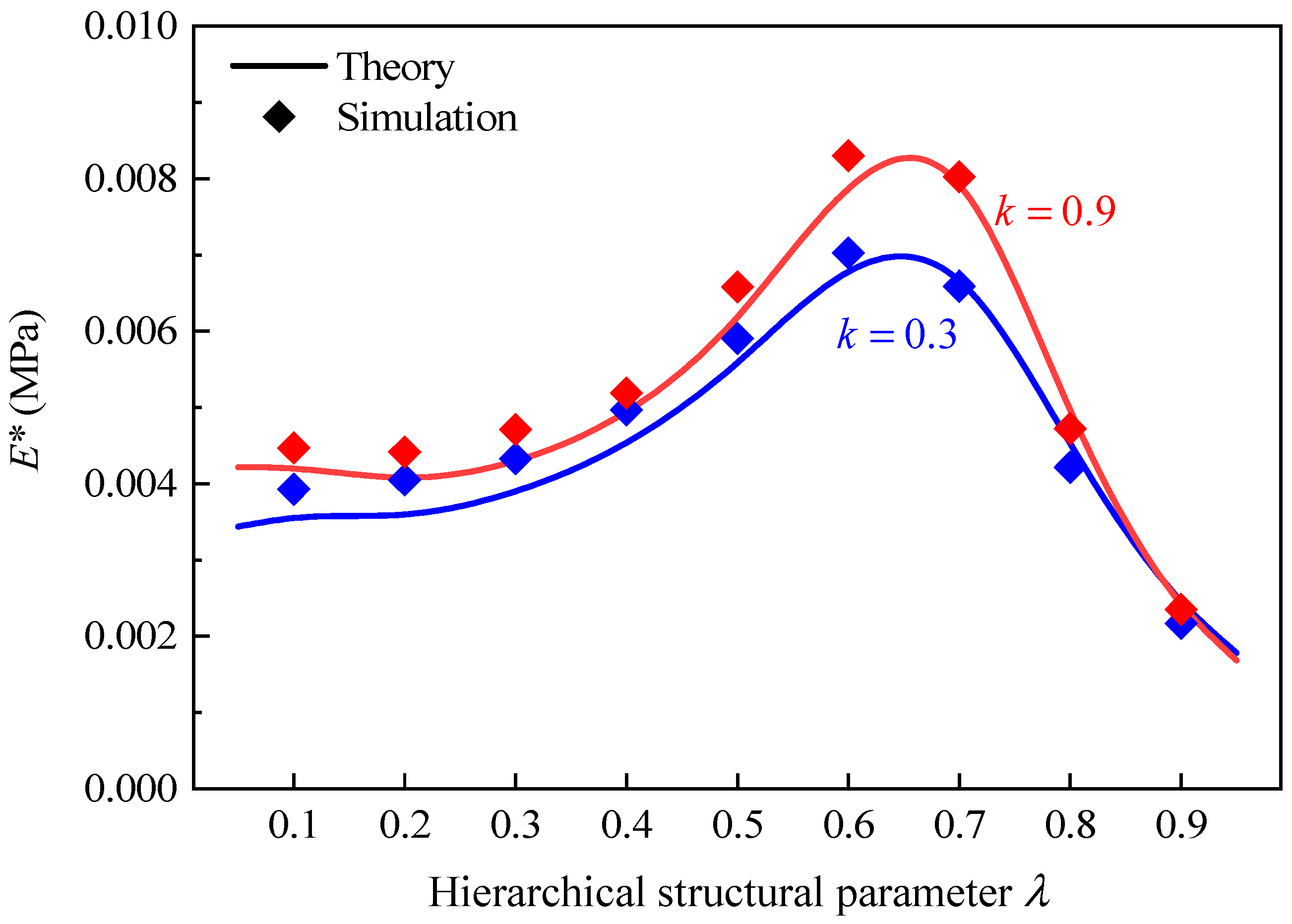
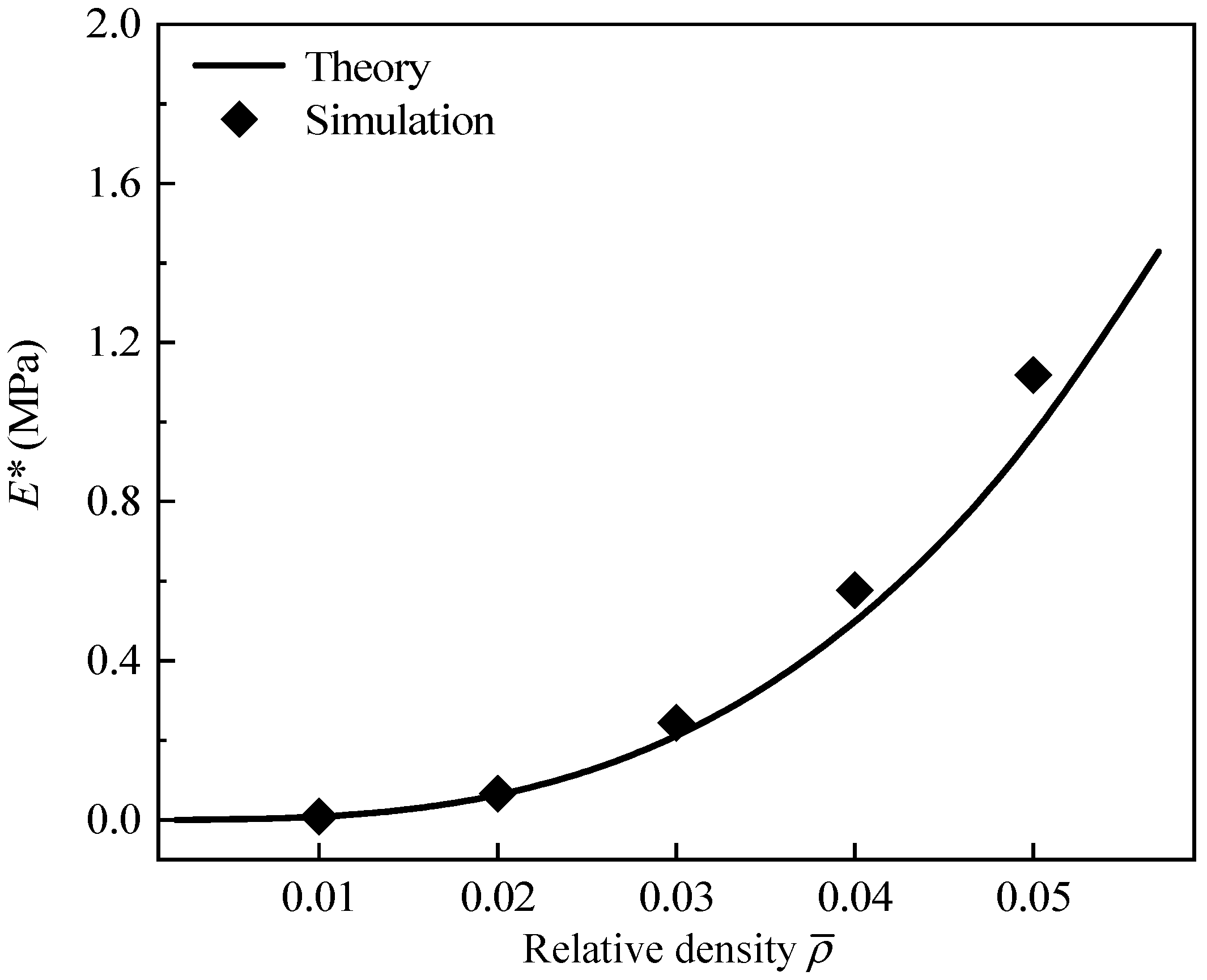
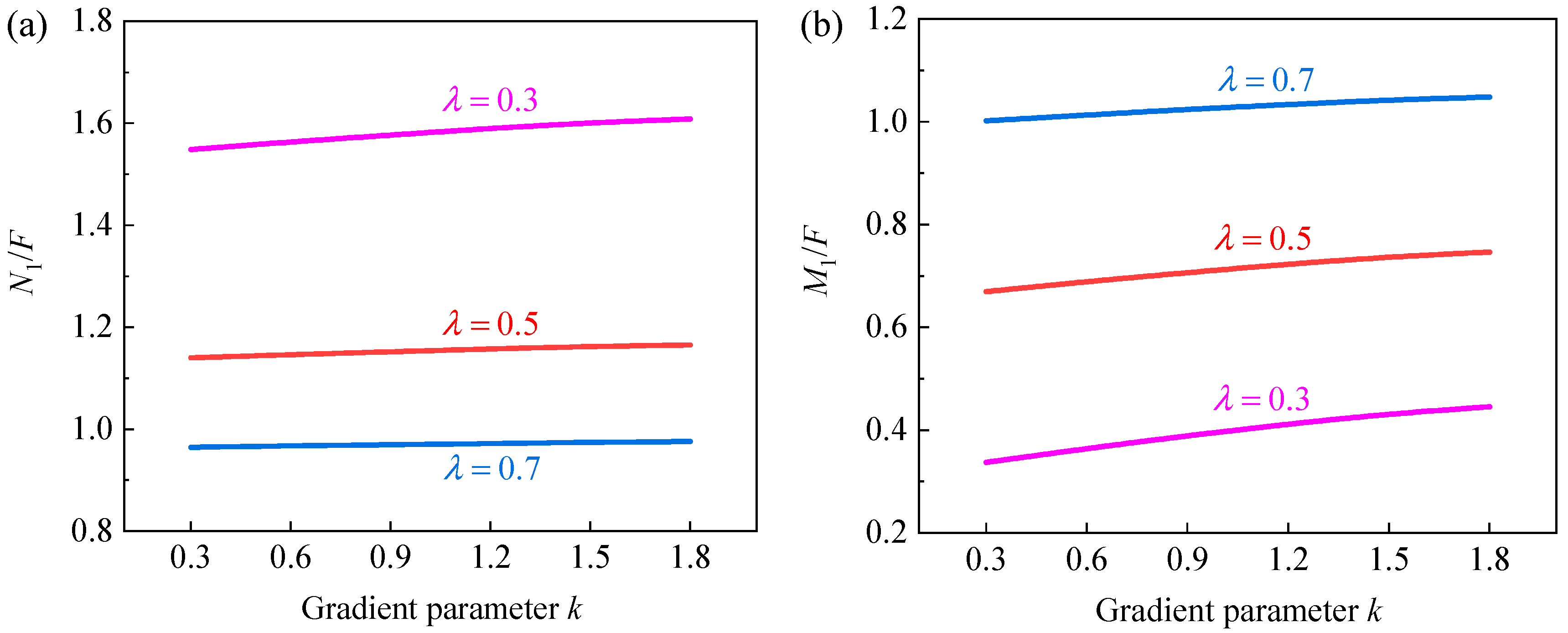
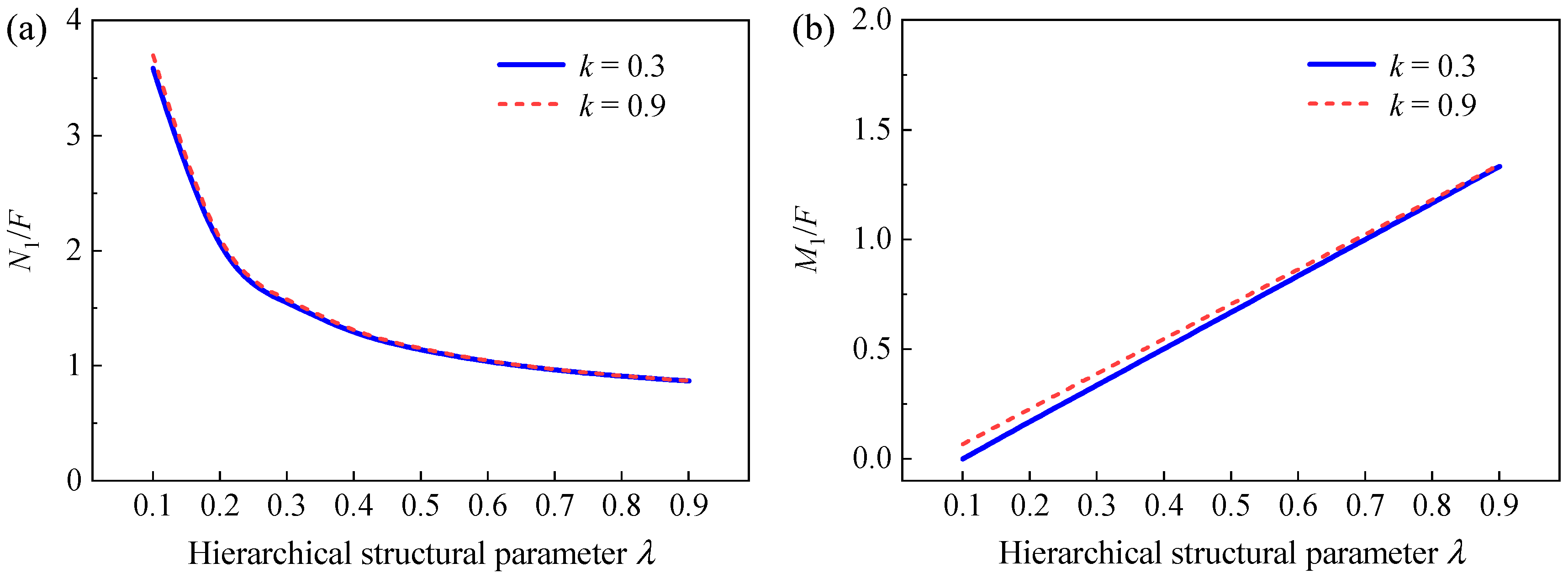
5.1. Effective Elastic Modulus
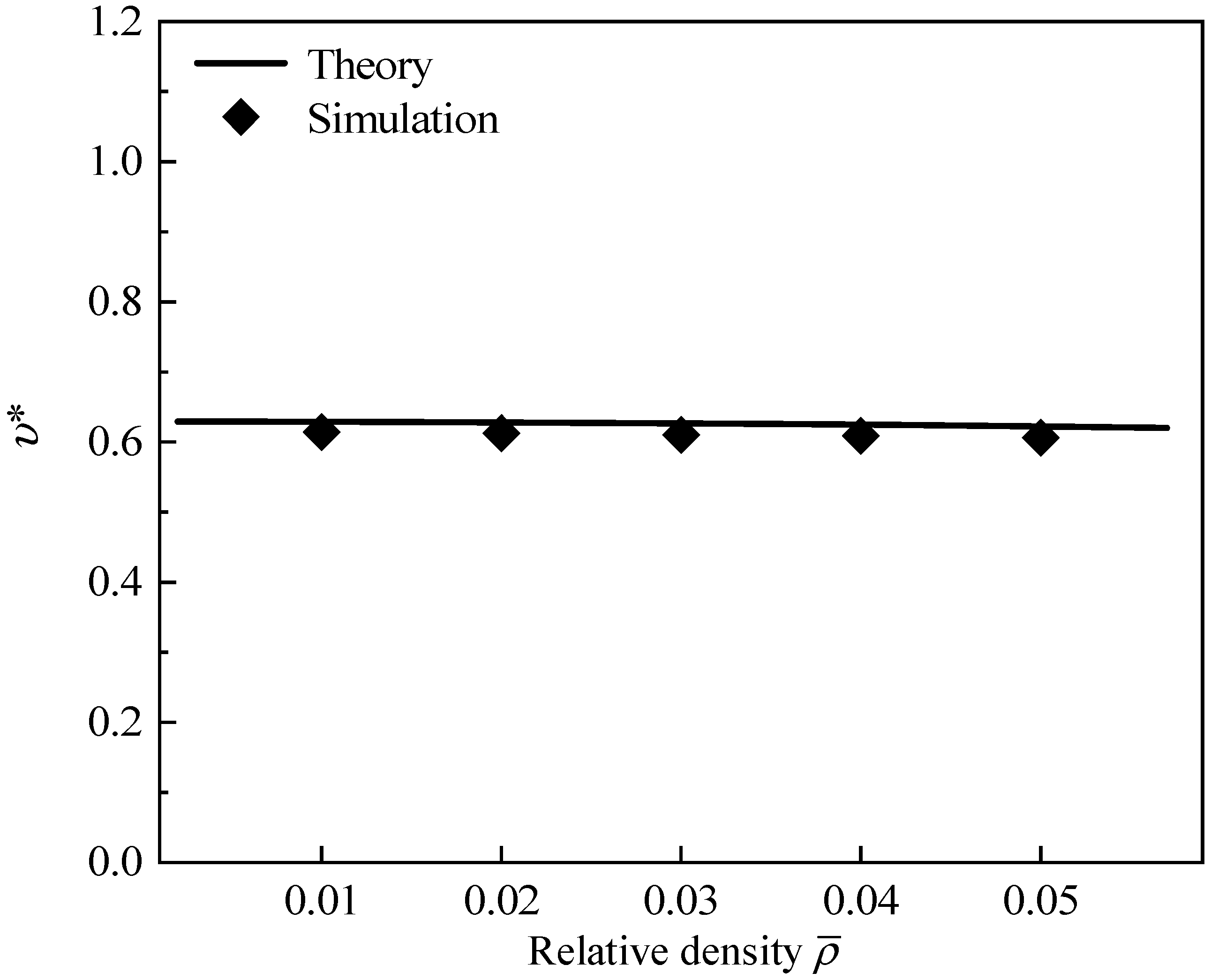
5.2. Poisson’s Ratio
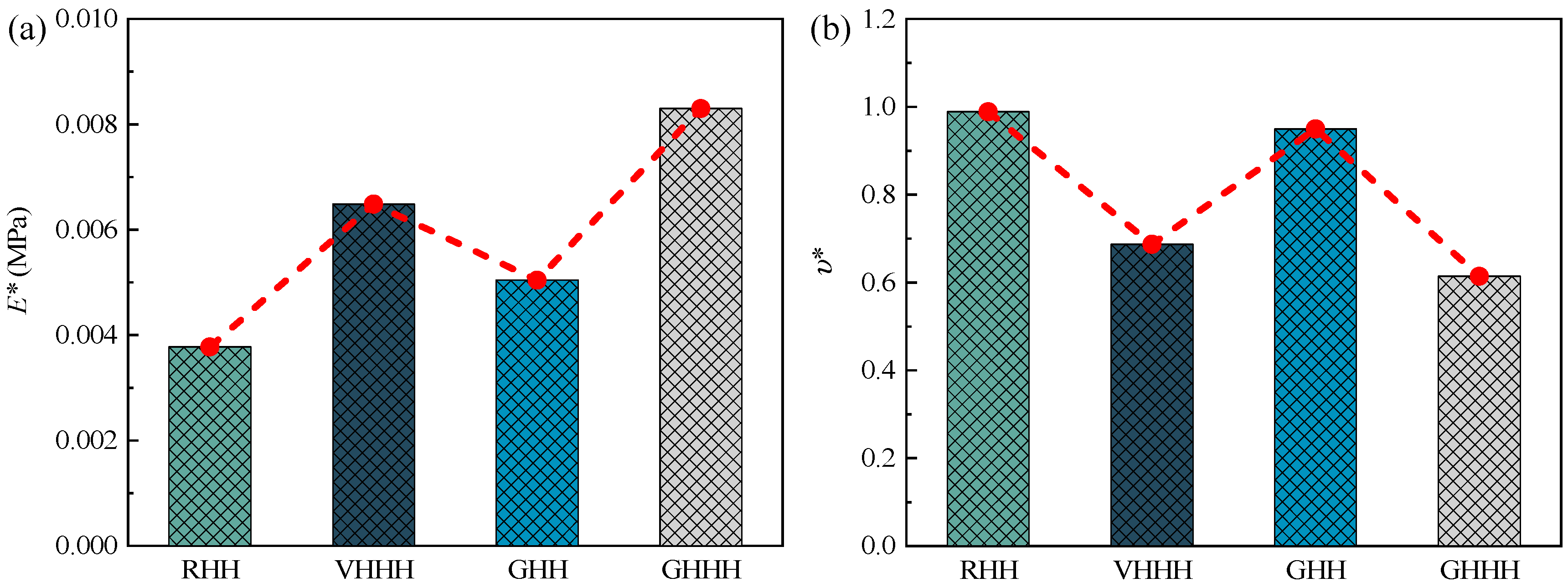
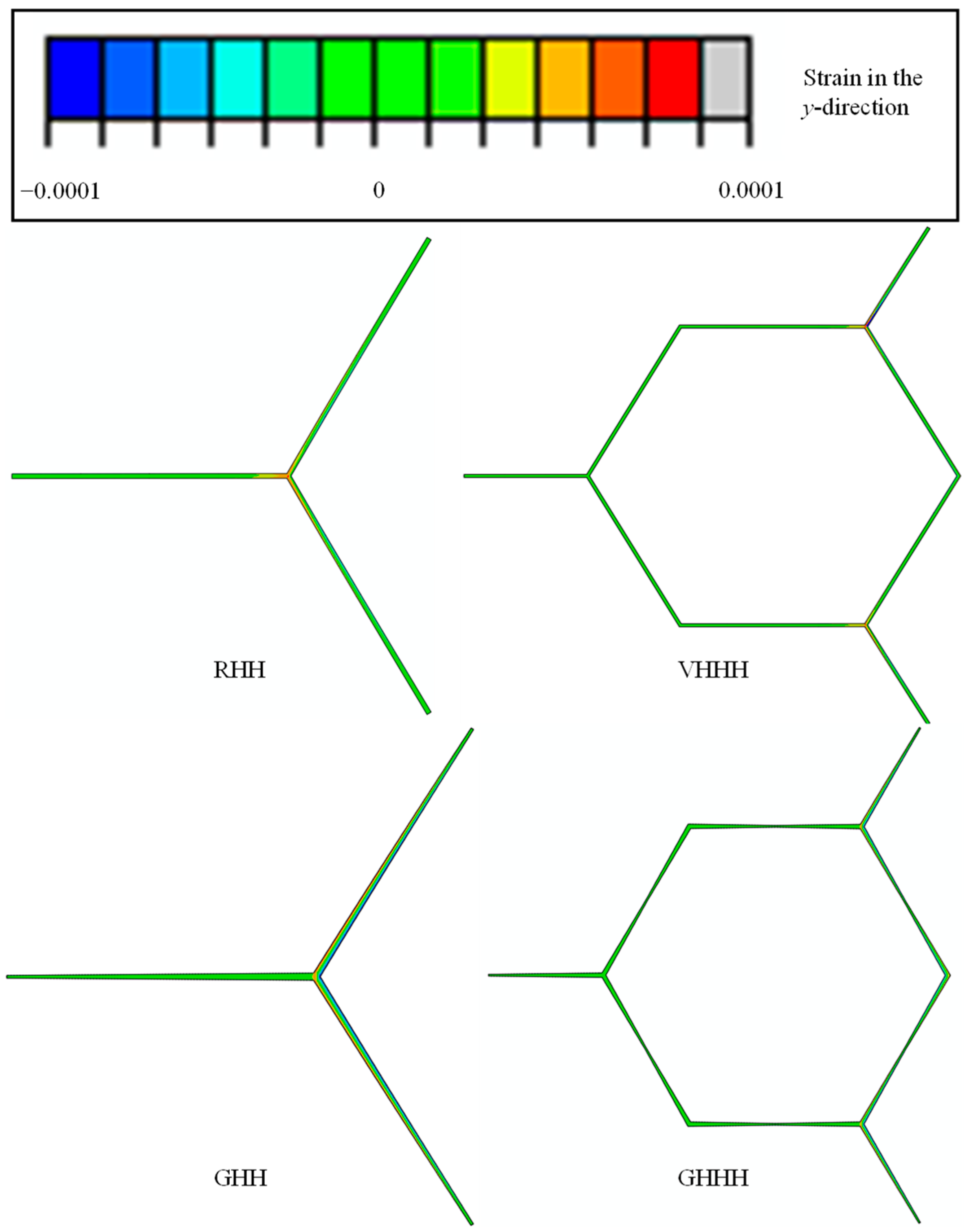
5.3. Effect of Integrating Hierarchical and Gradient Designs
6. Conclusions
- (1)
- Theoretical models to predict the effective elastic modulus and Poisson’s ratio of GHHH were developed based on Euler beam theory, and theoretical results were in good agreement with experimental and numerical results.
- (2)
- The gradient parameter and hierarchical structural parameter have an important effect on the effective elastic modulus and Poisson’s ratio of GHHH. In addition, Poisson’s ratio is less sensitive to the relative density.
- (3)
- The effect of gradient design and hierarchical design on the in-plane elastic properties of GHHH has been analyzed and compared. Compared to gradient design, hierarchical design shows a more pronounced effect on Poisson’s ratio and adjusting the internal forces of GHHH.
- (4)
- The effective elastic modulus of GHHH is higher than that of RHH, VHHH, and GHH when the relative density is fixed. The effective elastic modulus of GHHH can be up to 2.2 times that of RHH. However, Poisson’s ratio of GHHH is lower than that of RHH, VHHH, and GHH.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Liu, J.; Jia, L.; Chen, Z. Recent Advances in Woven Spacer Fabric Sandwich Composite Panels: A Review. Polymers 2022, 14, 3537. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Sun, R.; Scarpa, F.; Wang, J. In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers 2019, 11, 1132. [Google Scholar] [CrossRef]
- Gao, Z.; Li, H.; Zhao, J.; Guan, J.; Wang, Q. Analyses of dynamic characteristics of functionally graded porous (FGP) sandwich plates with viscoelastic materials-filled square-celled core. Eng. Struct. 2021, 248, 113242. [Google Scholar] [CrossRef]
- Ma, Q.; Kuai, T.; Rejab, M.; Kumar, N.M.; Idris, M.; Abdullah, M. Effect of boundary factor and material property on single square honeycomb sandwich panel subjected to quasi-static compression loading. J. Mech. Eng. Sci. 2020, 14, 7348–7360. [Google Scholar] [CrossRef]
- Fan, J.; Li, P.; Guo, W.; Zhao, X.; Su, C.; Xu, X. Experimental Investigation on the Low-Velocity Impact Response of Tandem Nomex Honeycomb Sandwich Panels. Polymers 2023, 15, 456. [Google Scholar] [CrossRef]
- Wei, K.; Chen, H.; Pei, Y.; Fang, D. Planar lattices with tailorable coefficient of thermal expansion and high stiffness based on dual-material triangle unit. J. Mech. Phys. Solids 2016, 86, 173–191. [Google Scholar] [CrossRef]
- Wang, Z. Recent advances in novel metallic honeycomb structure. Compos. Part B Eng. 2019, 166, 731–741. [Google Scholar] [CrossRef]
- Murray, C.M.; Mao, M.; Park, J.; Howard, J.; Wereley, N.M. Visco-Elastic Honeycomb Structures with Increased Energy Absorption and Shape Recovery Performance Using Buckling Initiators. Polymers 2023, 15, 3350. [Google Scholar] [CrossRef]
- Cui, Z.; Qi, J.; Duan, Y.; Tie, Y.; Zheng, Y.; Yang, J.; Li, C. Low-Velocity Impact Resistance of 3D Re-Entrant Honeycomb Sandwich Structures with CFRP Face Sheets. Polymers 2023, 15, 1092. [Google Scholar] [CrossRef]
- Wen, W.; Lei, M.; Tao, Y.; Lian, Y. Out-of-plane crashworthiness of bio-inspired hierarchical diamond honeycombs with variable cell wall thickness. Thin-Walled Struct. 2022, 176, 109347. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yang, S. Advanced honeycomb designs for improving mechanical properties: A review. Compos. Part B Eng. 2021, 227, 109393. [Google Scholar] [CrossRef]
- Yao, R.; Pang, T.; He, S.; Li, Q.; Zhang, B.; Sun, G. A bio-inspired foam-filled multi-cell structural configuration for energy absorption. Compos. Part B Eng. 2022, 238, 109801. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, R.; Chen, B. Energy absorption properties of multi-cell thin-walled tubes with a double surface gradient. Thin-Walled Struct. 2019, 145, 106386. [Google Scholar] [CrossRef]
- Tao, Y.; Duan, S.; Wen, W.; Pei, Y.; Fang, D. Enhanced out-of-plane crushing strength and energy absorption of in-plane graded honeycombs. Compos. Part B Eng. 2017, 118, 33–40. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, L.; Yang, P.; Fang, J.; Li, W. Energy absorption of additively manufactured functionally bi-graded thickness honeycombs subjected to axial loads. Thin-Walled Struct. 2021, 164, 107810. [Google Scholar] [CrossRef]
- Zou, Z.; Xu, F.; Xu, Z.; Niu, X.; Fang, T. Parametric design and energy absorption of non-uniform classic honeycombs mapped by topology optimization. Mech. Adv. Mater. Struct. 2023, 1–15. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Liu, Y. In-plane crushing behavior of density graded cross-circular honeycombs with zero Poisson’s ratio. Thin-Walled Struct. 2020, 151, 106767. [Google Scholar] [CrossRef]
- Li, Z.; Sun, H.; Wang, T.; Wang, L.; Su, X. Modularizing honeycombs for enhancement of strength and energy absorption. Compos. Struct. 2022, 279, 114744. [Google Scholar] [CrossRef]
- Sahu, S.K.; Sreekanth, P.S.R. Experimental investigation of in-plane compressive and damping behavior anisotropic graded honeycomb structure. Arab. J. Sci. Eng. 2022, 47, 15741–15753. [Google Scholar] [CrossRef]
- Tao, Y.; Li, W.; Cheng, T.; Wang, Z.; Chen, L.; Pei, Y.; Fang, D. Out-of-plane dynamic crushing behavior of joint-based hierarchical honeycombs. J. Sandw. Struct. Mater. 2021, 23, 2832–2855. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z.; Shim, V.; Guo, Y.; Sun, Z.; Li, X.; Wang, Z. In-plane compression of 3D-printed self-similar hierarchical honeycombs—Static and dynamic analysis. Thin-Walled Struct. 2020, 157, 106990. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Shi, C.; Zhou, W. Theoretical and numerical analysis of the folding mechanism of vertex-based hierarchical honeycomb structure. Mech. Adv. Mater. Struct. 2020, 27, 789–799. [Google Scholar] [CrossRef]
- Yao, R.; Pang, T.; Zhang, B.; Fang, J.; Li, Q.; Sun, G. On the crashworthiness of thin-walled multi-cell structures and materials: State of the art and prospects. Thin-Walled Struct. 2023, 189, 110734. [Google Scholar] [CrossRef]
- Ajdari, A.; Jahromi, B.H.; Papadopoulos, J.; Nayeb-Hashemi, H.; Vaziri, A. Hierarchical honeycombs with tailorable properties. Int. J. Solids Struct. 2012, 49, 1413–1419. [Google Scholar] [CrossRef]
- Hong, H.; Hu, M.; Dai, L. Dynamic Mechanical Behavior of Hierarchical Resin Honeycomb by 3D Printing. Polymers 2021, 13, 19. [Google Scholar] [CrossRef]
- Tao, Y.; Li, W.; Wei, K.; Duan, S.; Wen, W.; Chen, L.; Pei, Y.; Fang, D. Mechanical properties and energy absorption of 3D printed square hierarchical honeycombs under in-plane axial compression. Compos. Part B Eng. 2019, 176, 107219. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, J.; Liu, K.; Tao, Y. Hybrid hierarchical square honeycomb with widely tailorable effective in-plane elastic modulus. Thin-Walled Struct. 2022, 171, 108816. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, J.; He, K.; Tao, Y. Out-of-plane crushing behavior of hybrid hierarchical square honeycombs. Thin-Walled Struct. 2022, 181, 110051. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, G.; Ha, N.S.; Wang, L. In-plane compression of graded hierarchical honeycombs. Adv. Struct. Eng. 2022, 25, 1483–1504. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, E.T.; Wang, G.; Ng, B.F. In-plane crushing behavior and energy absorption of a novel graded honeycomb from hierarchical architecture. Int. J. Mech. Sci. 2022, 221, 107202. [Google Scholar] [CrossRef]
- Wen, W.; Lei, M.; Tao, Y. The effect of material distribution on the out-of-plane elastic properties of hierarchical diamond honeycombs. Eng. Struct. 2022, 272, 115000. [Google Scholar] [CrossRef]
- Taylor, C.; Smith, C.; Miller, W.; Evans, K. Functional grading in hierarchical honeycombs: Density specific elastic performance. Compos. Struct. 2012, 94, 2296–2305. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, E.T.; Ng, B.F. In-plane dynamic crushing of a novel honeycomb with functionally graded fractal self-similarity. Compos. Struct. 2021, 270, 114106. [Google Scholar] [CrossRef]
- Liu, H.; Chen, L.; Cao, J.; Chen, L.; Du, B.; Guo, Y.; Li, W.; Fang, D. Axial compression deformability and energy absorption of hierarchical thermoplastic composite honeycomb graded structures. Compos. Struct. 2020, 254, 112851. [Google Scholar] [CrossRef]
- Zhao, R.; Yuan, B.; Zhou, D.; Li, Z.; Zhao, M.; Tao, Y. On the out-of-plane crashworthiness of incorporating hierarchy and gradient into hexagonal honeycomb. Mech. Adv. Mater. Struct. 2023, 1–15. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Sun, Z.; Guo, Y.; Shim, V. Characterisation and modeling of additively-manufactured polymeric hybrid lattice structures for energy absorption. Int. J. Mech. Sci. 2021, 191, 106101. [Google Scholar] [CrossRef]
- Isaac, C.W.; Duddeck, F. Recent progress in 4D printed energy-absorbing metamaterials and structures. Virtual Phys. Prototyp. 2023, 18, e2197436. [Google Scholar] [CrossRef]
- Isaac, C.W.; Sokołowski, A.; Duddeck, F.; Adamiak, M.; Pakieła, W.; Aremu, A. Mechanical characterisation and crashworthiness performance of additively manufactured polymer-based honeycomb structures under in-plane quasi-static loading. Virtual Phys. Prototyp. 2023, 18, e2273296. [Google Scholar] [CrossRef]
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2022.
- Johnston, R.; Kazancı, Z. Analysis of additively manufactured (3D printed) dual-material auxetic structures under compression. Addit. Manuf. 2021, 38, 101783. [Google Scholar] [CrossRef]
- Chuang, C.H.; Huang, J.S. Elastic moduli and plastic collapse strength of hexagonal honeycombs with plateau borders. Int. J. Mech. Sci. 2002, 44, 1827–1844. [Google Scholar] [CrossRef]
- Rahman, K.M.; Hu, Z.; Letcher, T. In-Plane Stiffness of Additively Manufactured Hierarchical Honeycomb Metamaterials with Defects. J. Manuf. Sci. Eng. 2018, 140, 011007. [Google Scholar] [CrossRef]
- Sun, Y.; Pugno, N.M. In plane stiffness of multifunctional hierarchical honeycombs with negative Poisson’s ratio sub-structures. Compos. Struct. 2013, 106, 681–689. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, B.; Pugno, N.; Wang, B.; Ding, Q. In-plane stiffness of the anisotropic multifunctional hierarchical honeycombs. Compos. Struct. 2015, 131, 616–624. [Google Scholar] [CrossRef]





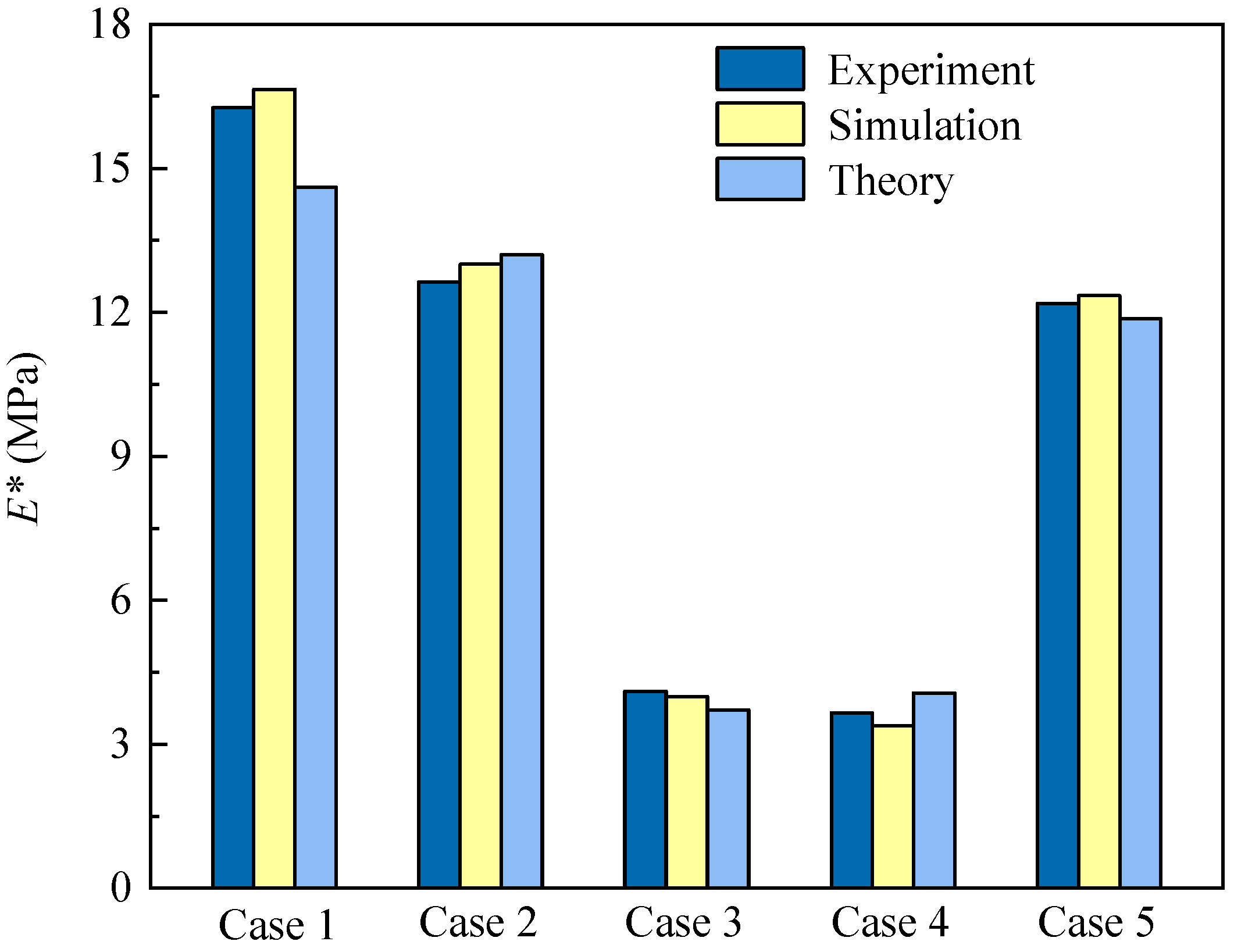



| Specimen | (mm) | (mm) | (mm) | h (mm) | (mm) | |||
|---|---|---|---|---|---|---|---|---|
| Case 1 | 141.32 | 132.78 | 12 | 30 | 0.8 | 2/3 | 0.5 | 0.1283 |
| Case 2 | 141.04 | 132.54 | 12 | 30 | 0.8 | 2/3 | 0.25 | 0.1283 |
| Case 3 | 136.64 | 128.73 | 12 | 30 | 0.8 | 0.3 | 0.25 | 0.1001 |
| Case 4 | 136.99 | 129.03 | 12 | 30 | 0.8 | 0.3 | 1 | 0.1001 |
| Case 5 | 142.99 | 134.22 | 12 | 30 | 0.8 | 0.8 | 1 | 0.1386 |
| Element Size (mm) | Effective Elastic Modulus (10−4 MPa) | Error (%) |
|---|---|---|
| 0.01 | 45.18 | - |
| 0.02 | 43.28 | −4.21 |
| 0.04 | 5.21 | −87.95 |
| 0.08 | 0.14 | −97.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Zhao, R.; Shi, J.; Zhou, D.; Han, Y. In-Plane Elastic Properties of 3D-Printed Graded Hierarchical Hexagonal Honeycombs. Polymers 2024, 16, 859. https://doi.org/10.3390/polym16060859
Tao Y, Zhao R, Shi J, Zhou D, Han Y. In-Plane Elastic Properties of 3D-Printed Graded Hierarchical Hexagonal Honeycombs. Polymers. 2024; 16(6):859. https://doi.org/10.3390/polym16060859
Chicago/Turabian StyleTao, Yong, Ruochao Zhao, Jun Shi, De Zhou, and Yanqun Han. 2024. "In-Plane Elastic Properties of 3D-Printed Graded Hierarchical Hexagonal Honeycombs" Polymers 16, no. 6: 859. https://doi.org/10.3390/polym16060859






