Reverse Engineering of Radical Polymerizations by Multi-Objective Optimization
Abstract
1. Introduction
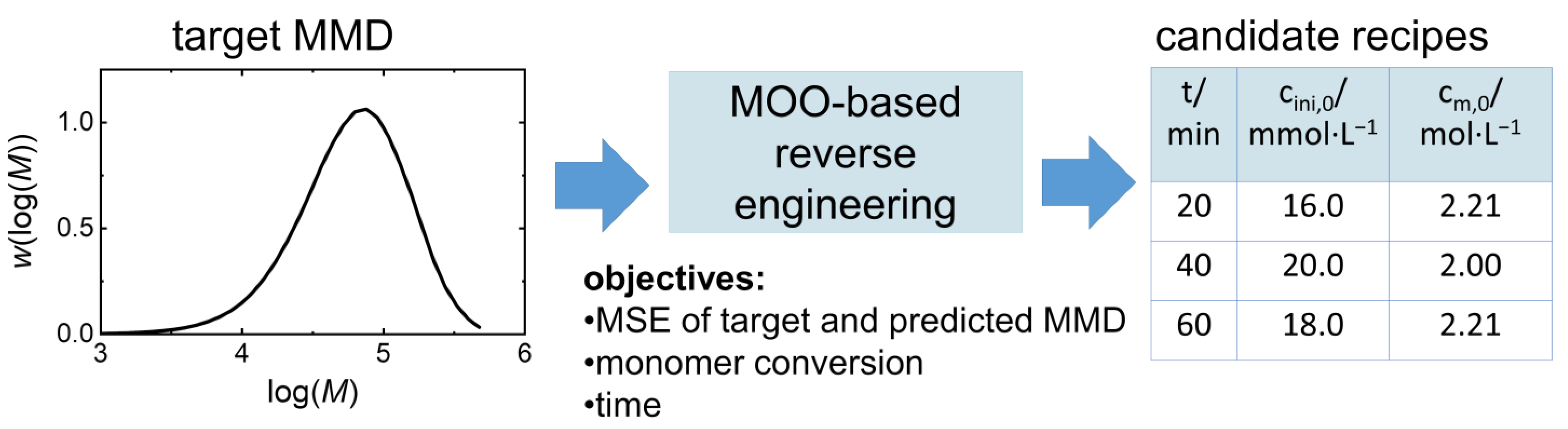
2. Reverse Engineering Modeling Approach
2.1. Model Development
2.2. Data Acquisition and Processing
3. Results and Discussion
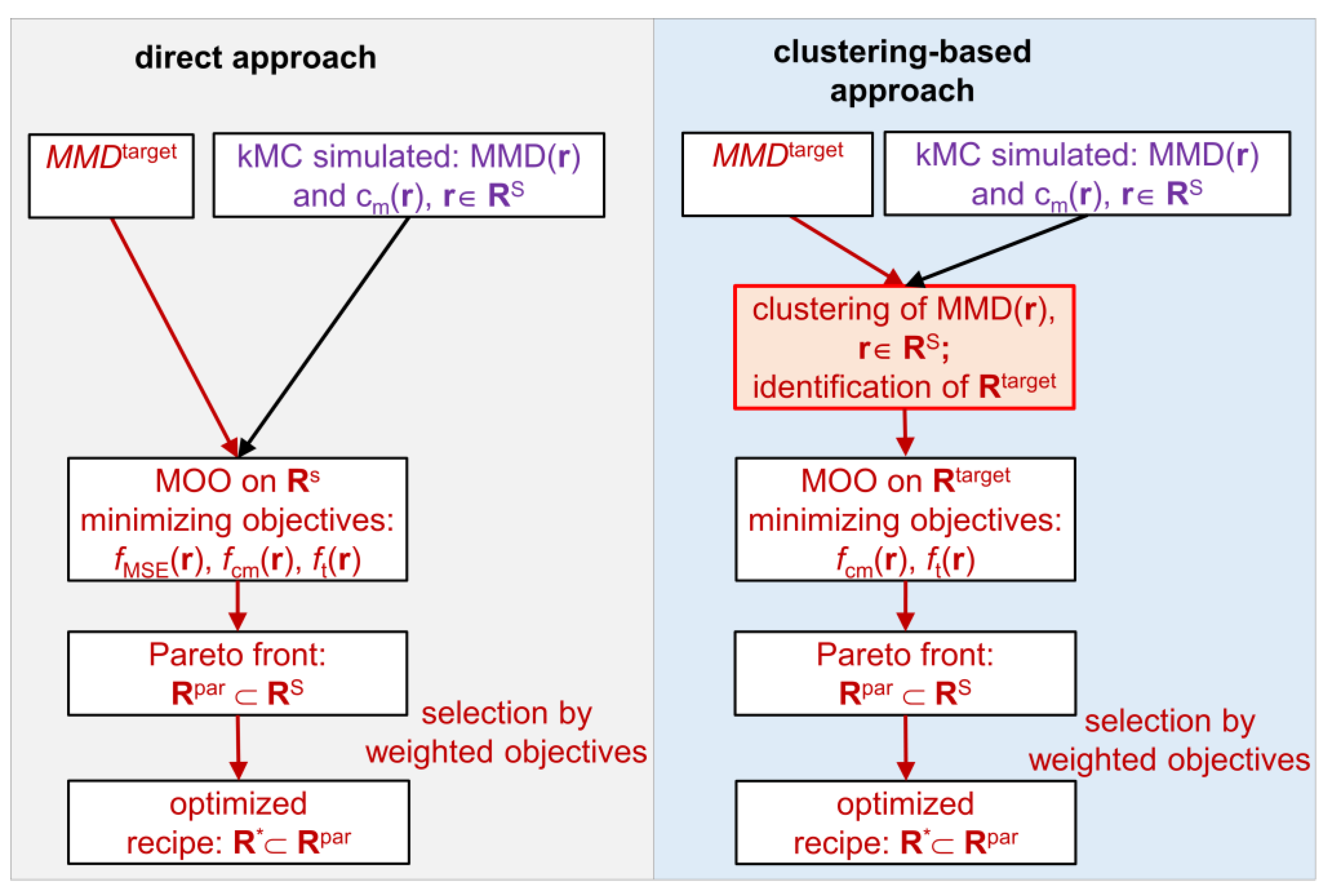
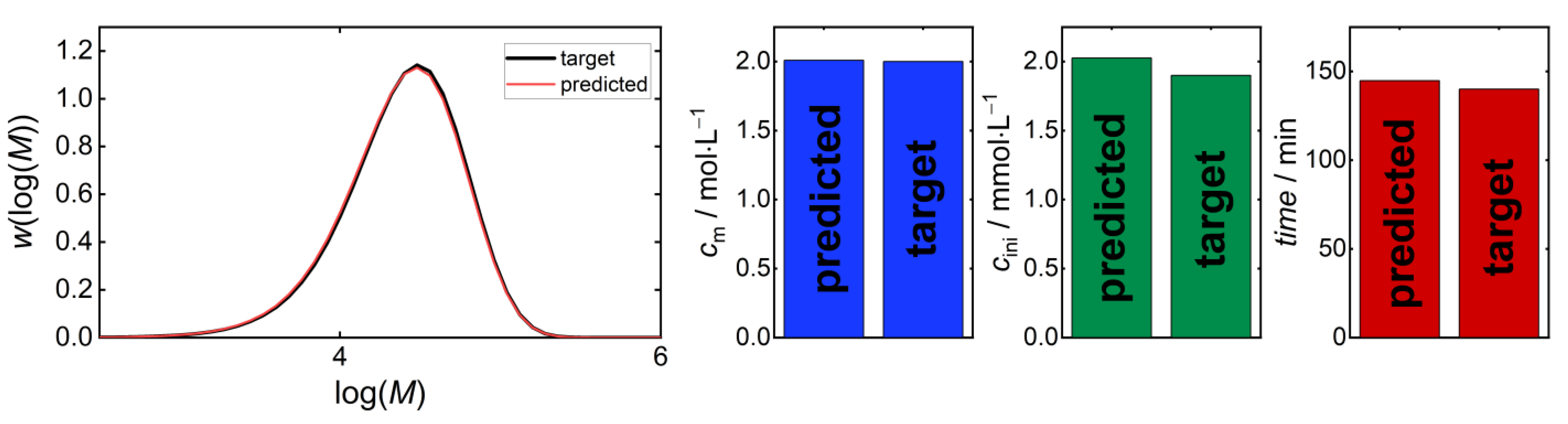
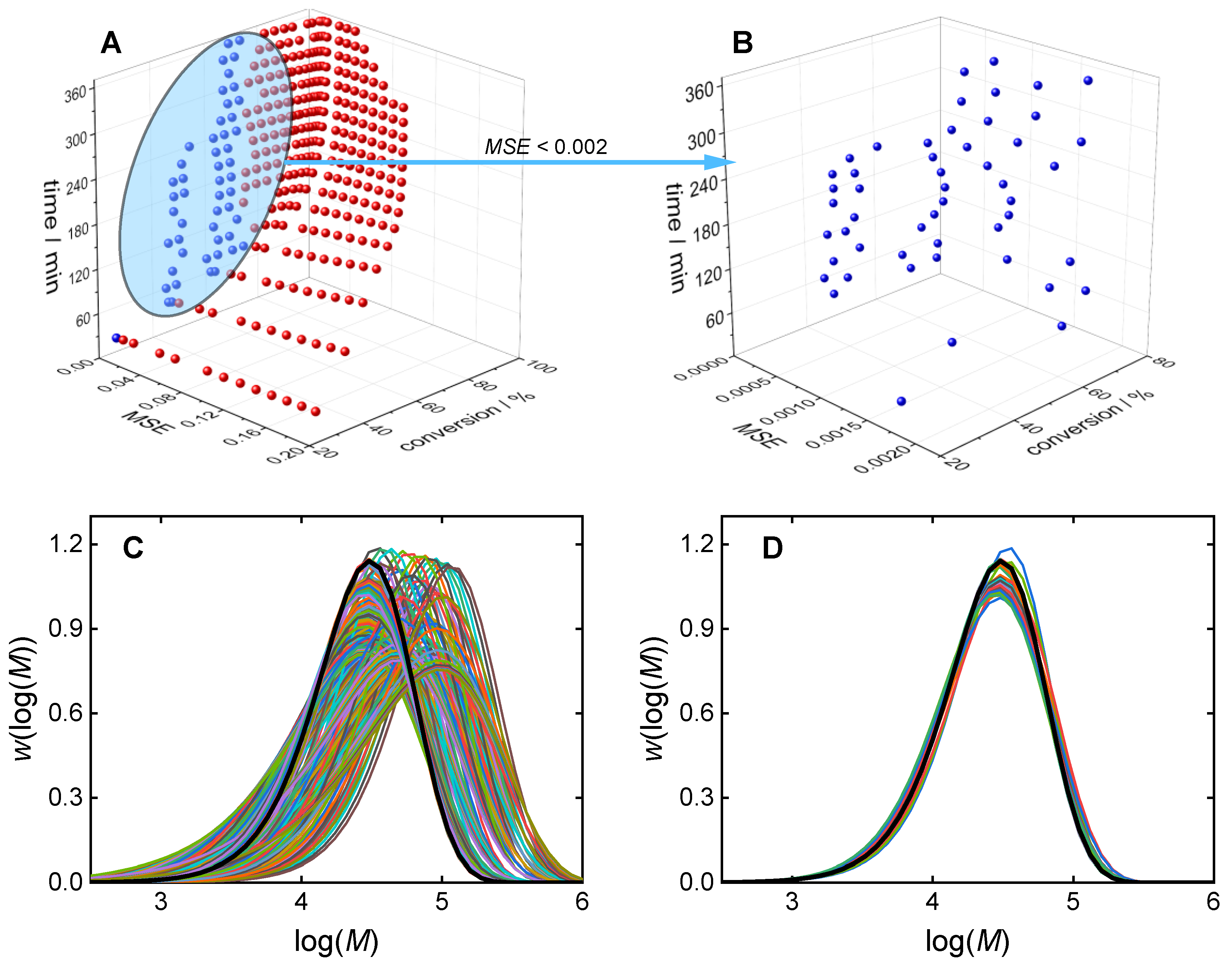
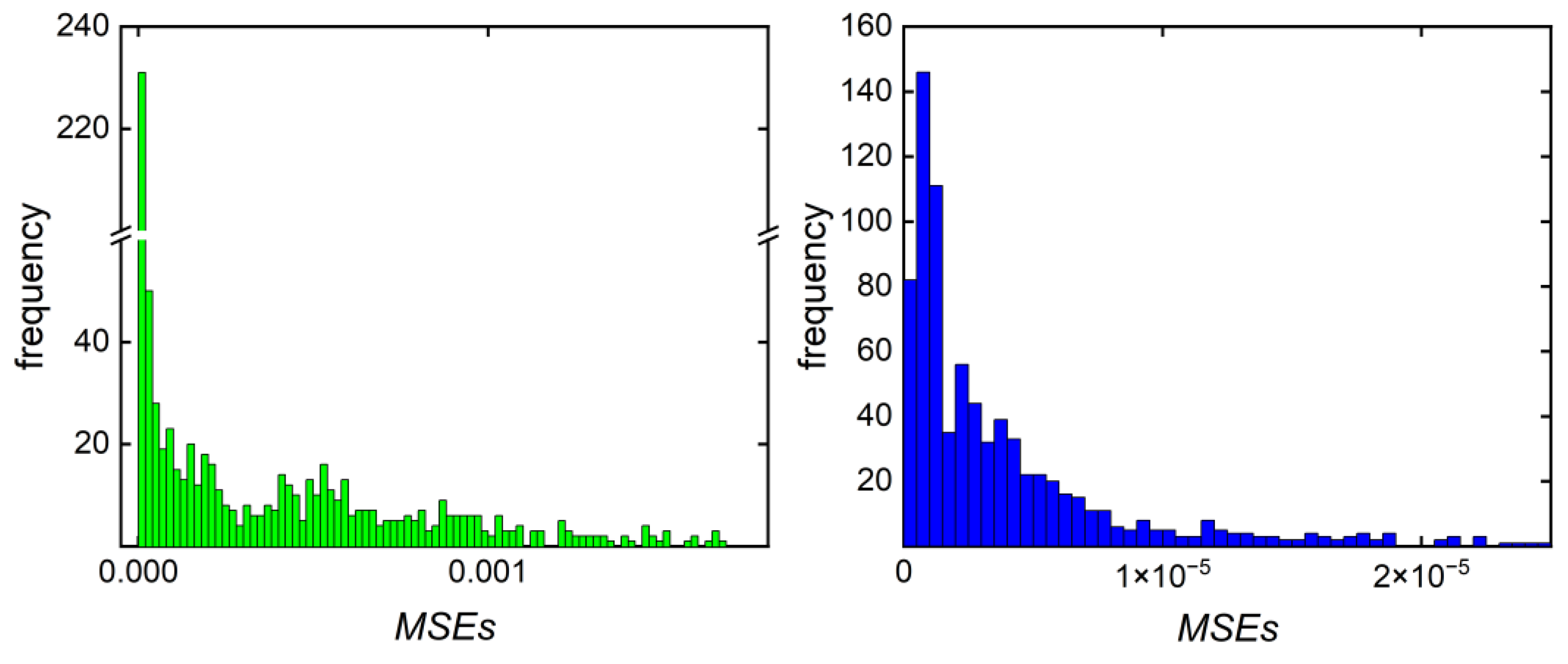
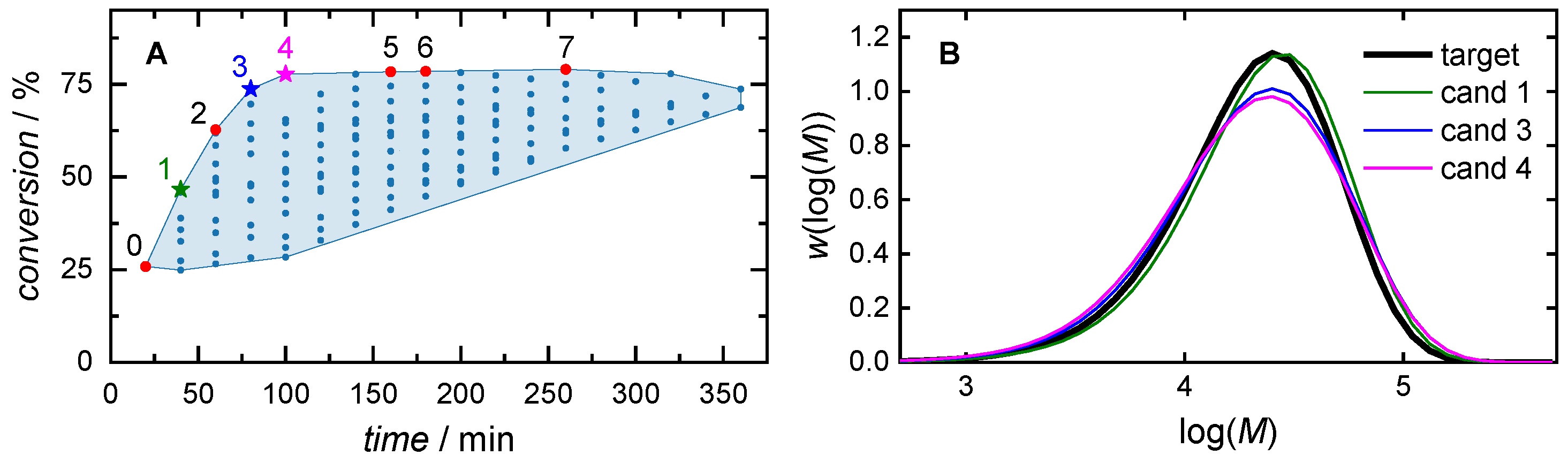
3.1. Direct Pareto Optimization
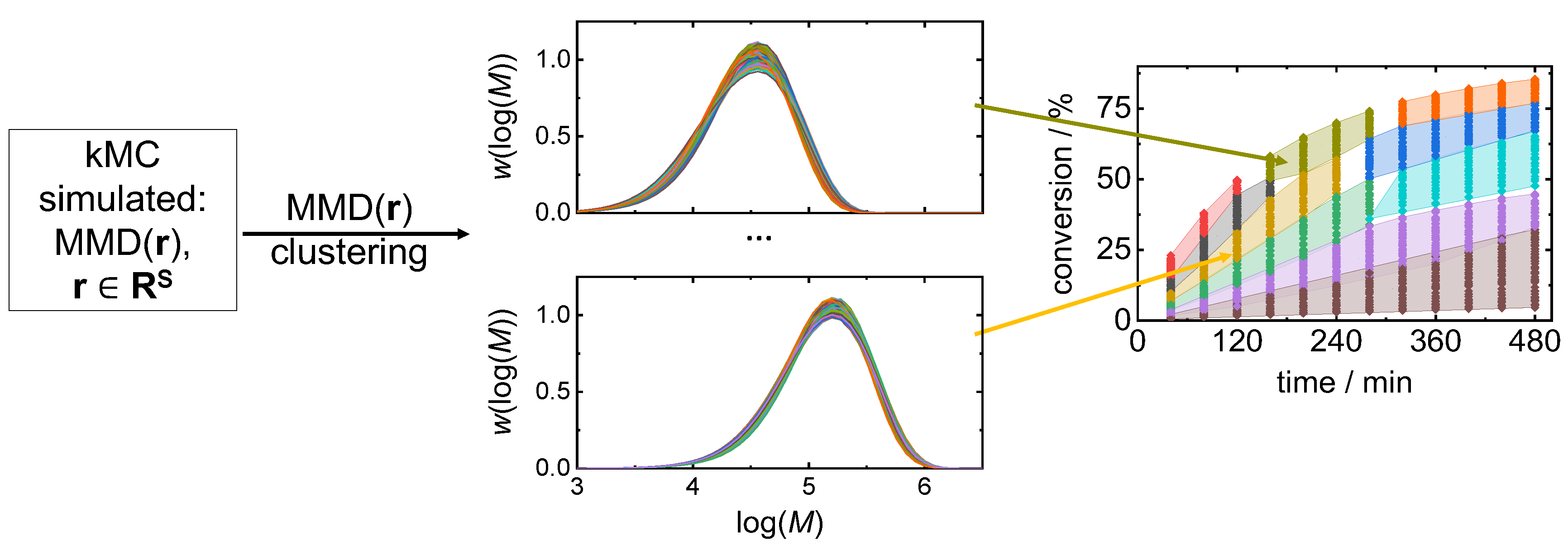
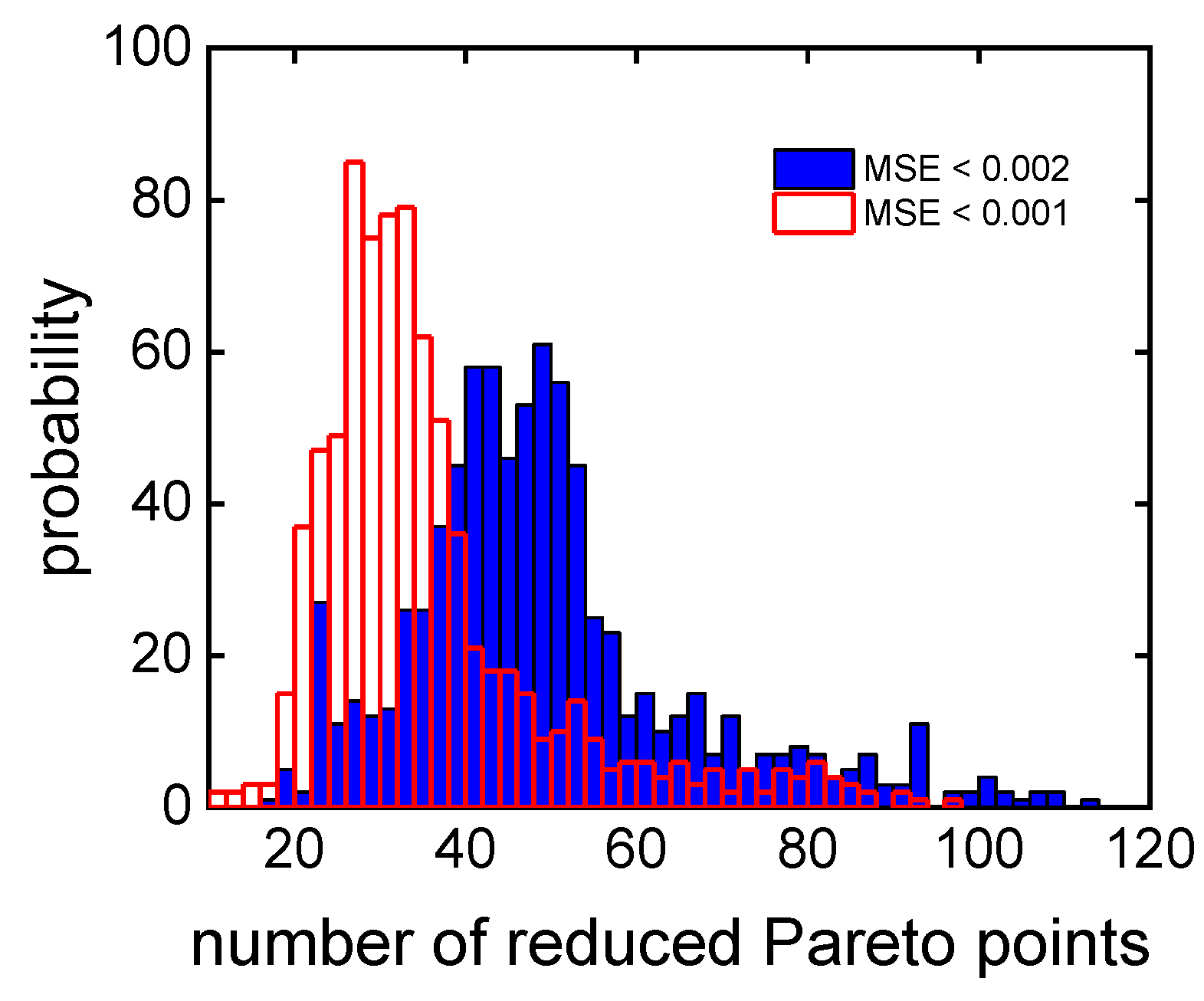
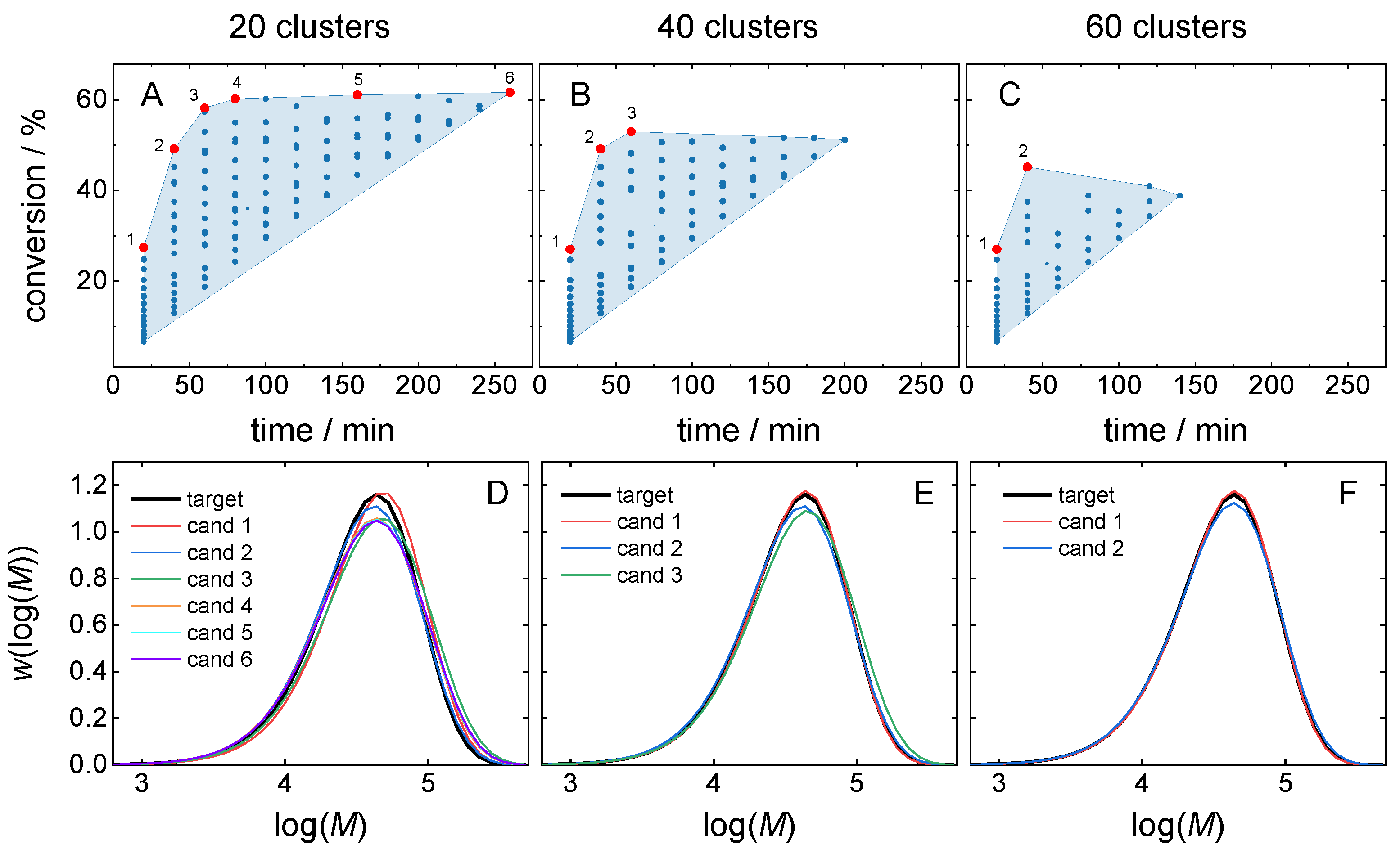
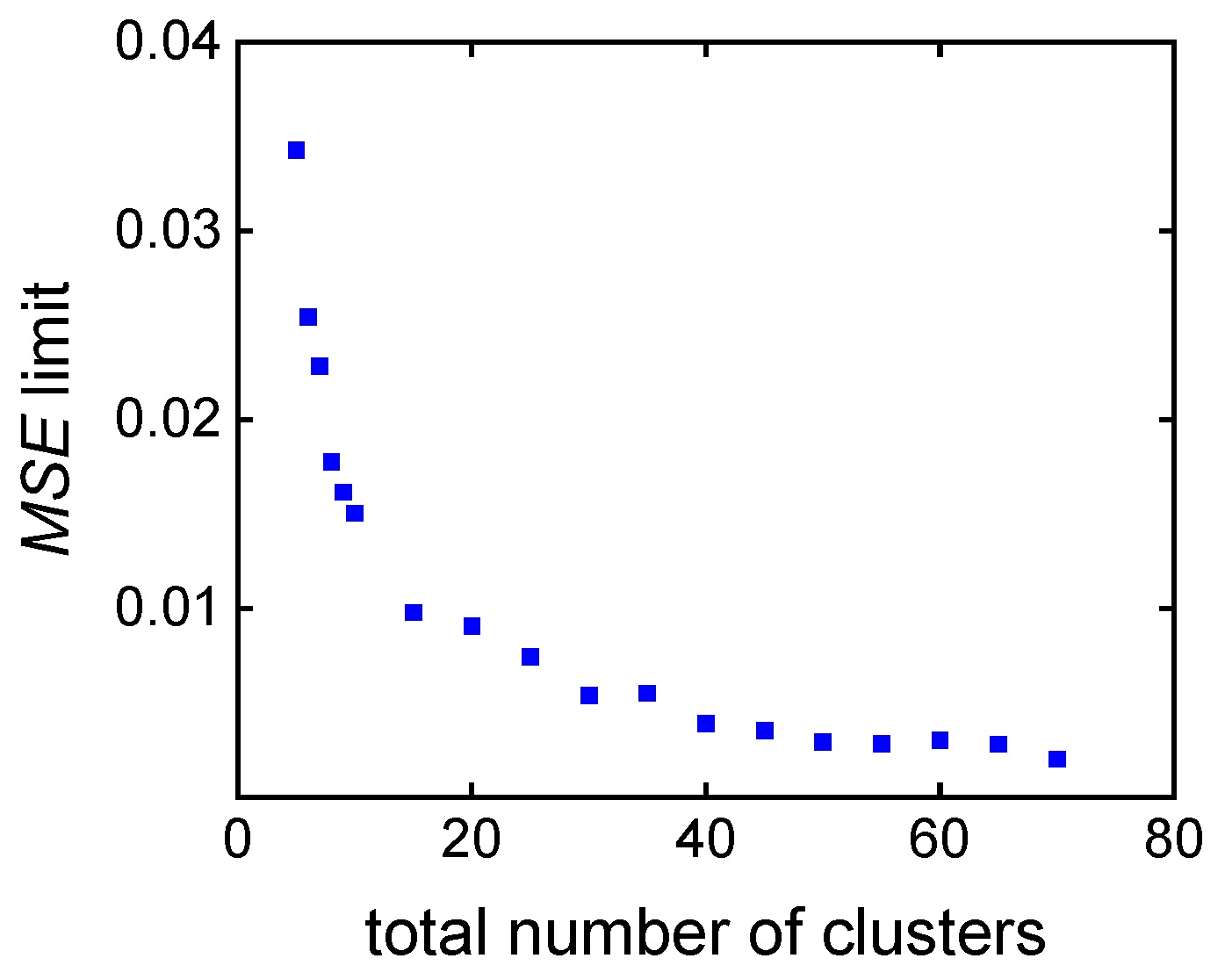
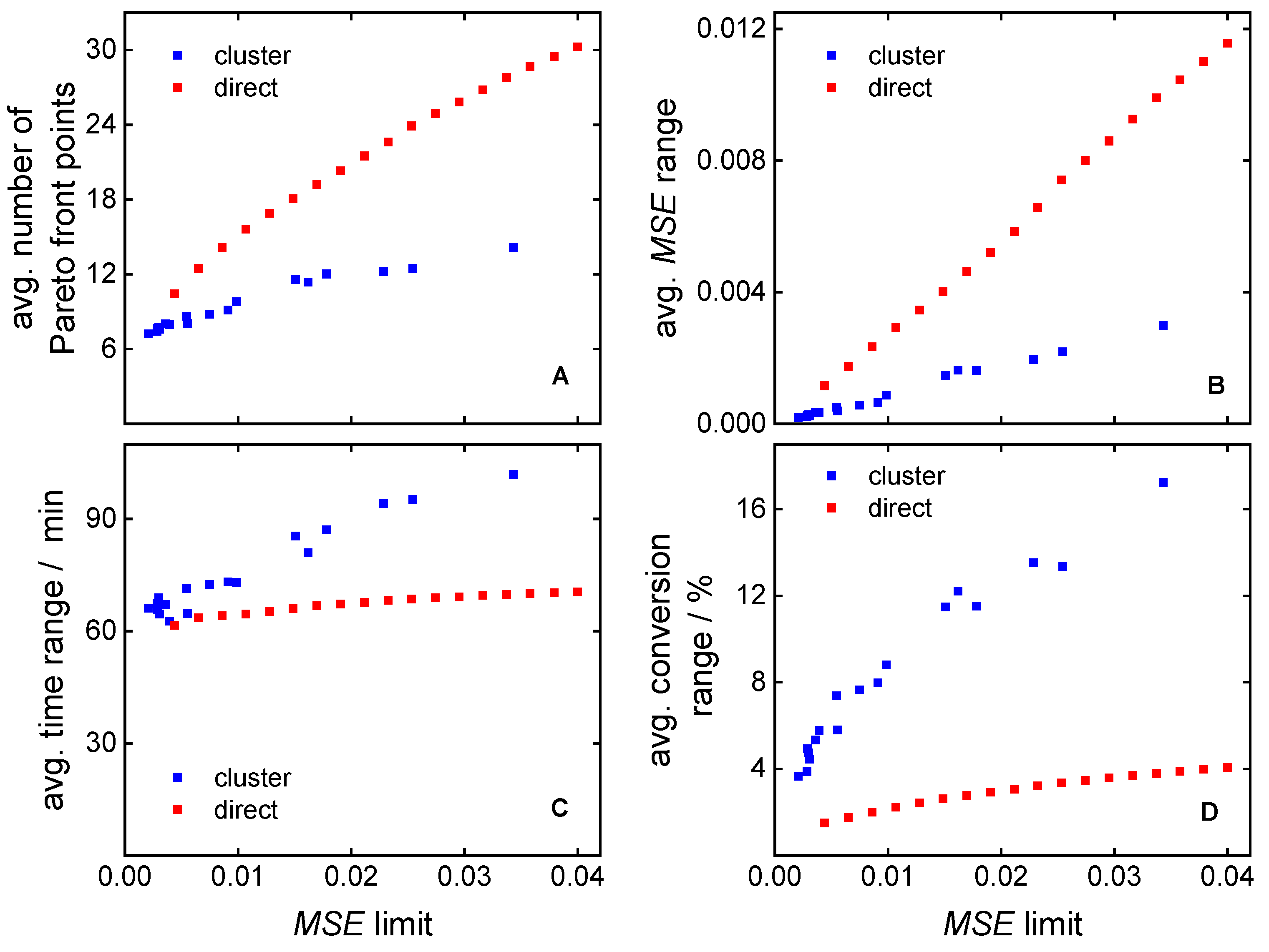
3.2. Clustering-Supported Pareto Optimization
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ballard, N.; Asua, J.M. Radical polymerization of acrylic monomers: An overview. Prog. Polym. Sci. 2018, 79, 40–60. [Google Scholar] [CrossRef]
- Meszena, Z.G.; Johnson, A.F. Modelling and simulation of polymerisation processes. Comput. Chem. Eng. 1999, 23, 375–378. [Google Scholar] [CrossRef]
- Saldívar-Guerra, E. Numerical Techniques for the Solution of the Molecular Weight Distribution in Polymerization Mechanisms, State of the Art. Macromol. React. Eng. 2020, 14, 2000010. [Google Scholar] [CrossRef]
- Gómez-Reguera, J.A.; Vivaldo-Lima, E.; Gabriel, V.A.; Dubé, M.A. Modeling of the Free Radical Copolymerization Kinetics of n-Butyl Acrylate, Methyl Methacrylate and 2-Ethylhexyl Acrylate Using PREDICI®. Processes 2019, 7, 395. [Google Scholar] [CrossRef]
- Trigilio, A.D.; Marien, Y.W.; Van Steenberge, P.H.M.; D’hooge, D.R. Gillespie-Driven kinetic Monte Carlo Algorithms to Model Events for Bulk or Solution (Bio)Chemical Systems Containing Elemental and Distributed Species. Ind. Eng. Chem. Res. 2020, 59, 18357–18386. [Google Scholar] [CrossRef]
- Peikert, P.; Pflug, K.M.; Busch, M. Modeling of High-Pressure Ethene Homo- and Copolymerization. Chem. Ing. Tech. 2019, 91, 673–677. [Google Scholar] [CrossRef]
- Trigilio, A.D.; Marien, Y.W.; Van Steenberge, P.H.M.; D’hooge, D.R. Toward an Automated Convergence Tool for Kinetic Monte Carlo Simulation of Conversion, Distributions, and Their Averages in Non-dispersed Phase Linear Chain-Growth Polymerization. Ind. Eng. Chem. Res. 2023, 62, 2583–2593. [Google Scholar] [CrossRef]
- Brandão, A.L.T.; Soares, J.B.P.; Pinto, J.C.; Alberton, A.L. When Polymer Reaction Engineers Play Dice: Applications of Monte Carlo Models in PRE. Macromol. React. Eng. 2015, 9, 141–185. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Saeb, M.R.; Penlidis, A.; Jabbari, E.; Stadler, F.J.; Zinck, P.; Matyjaszewski, K. Intelligent Machine Learning: Tailor-Making Macromolecules. Polymers 2019, 11, 579. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, Y.; Penlidis, A. Polymerization Data Mining: A Perspective. Adv. Theory Simul. 2019, 2, 1800144. [Google Scholar] [CrossRef]
- Fiosina, J.; Sievers, P.; Drache, M.; Beuermann, S. Polymer reaction engineering meets explainable machine learning. Comput. Chem. Eng. 2023, 177, 108356. [Google Scholar] [CrossRef]
- Spyromitros-Xioufis, E.; Tsoumakas, G.; Groves, W.; Vlahavas, I. Multi-target regression via input space expansion: Treating targets as inputs. Mach. Learn. 2016, 104, 55–98. [Google Scholar] [CrossRef]
- Ngatchou, P.; Zarei, A.; El-Sharkawi, A. Pareto Multi Objective Optimization. In Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, Arlington, VA, USA, 6–10 November 2005; IEEE/Institute of Electrical and Electronics Engineers Incorporated: Piscataway, NJ, USA, 2005; pp. 84–91, ISBN 1-59975-174-7. [Google Scholar]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Doumpos, M.; Zopounidis, C. Multi-objective optimization models in finance and investments. J. Glob. Optim. 2020, 76, 243–244. [Google Scholar] [CrossRef]
- Gupta, S.; Haq, A.; Ali, I.; Sarkar, B. Significance of multi-objective optimization in logistics problem for multi-product supply chain network under the intuitionistic fuzzy environment. Complex. Intell. Syst. 2021, 7, 2119–2139. [Google Scholar] [CrossRef]
- Bhaskar, V.; Gupta, S.K.; Ray, A.K. Applications of multiobjective optimization in chemical engineering. Rev. Chem. Eng. 2000, 16, 1–54. [Google Scholar] [CrossRef]
- Murugan, C.; Subbaian, S. Multi-Objective Optimization for Enhanced Ethanol Production during Whey Fermentation. In Proceedings of the 2022 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 8–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7, ISBN 978-1-6654-6275-4. [Google Scholar]
- Fiandaca, G.; Fraga, E.S.; Brandani, S. A multi-objective genetic algorithm for the design of pressure swing adsorption. Eng. Optim. 2009, 41, 833–854. [Google Scholar] [CrossRef]
- Ganesan, T.; Elamvazuthi, I.; Ku Shaari, K.Z.; Vasant, P. Swarm intelligence and gravitational search algorithm for multi-objective optimization of synthesis gas production. Appl. Energy 2013, 103, 368–374. [Google Scholar] [CrossRef]
- Charoenpanich, T.; Anantawaraskul, S.; Soares, J.B.P. Using Artificial Intelligence Techniques to Design Ethylene/1-Olefin Copolymers. Macromol. Theory Simul. 2020, 29, 2000048. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Curteanu, S. The use of differential evolution algorithm for solving chemical engineering problems. Rev. Chem. Eng. 2016, 32, 149–180. [Google Scholar] [CrossRef]
- Fernandes, F.A.N.; Lona, L.M. Neural network applications in polymerization processes. Braz. J. Chem. Eng. 2005, 22, 401–418. [Google Scholar] [CrossRef]
- Fierens, S.; D’hooge, D.; van Steenberge, P.; Reyniers, M.-F.; Marin, G. Exploring the Full Potential of Reversible Deactivation Radical Polymerization Using Pareto-Optimal Fronts. Polymers 2015, 7, 655–679. [Google Scholar] [CrossRef]
- Mannodi-Kanakkithodi, A.; Pilania, G.; Ramprasad, R.; Lookman, T.; Gubernatis, J.E. Multi-objective optimization techniques to design the Pareto front of organic dielectric polymers. Comput. Mater. Sci. 2016, 125, 92–99. [Google Scholar] [CrossRef]
- Theis, A.; Davis, T.P.; Stenzel, M.H.; Barner-Kowollik, C. Probing the reaction kinetics of vinyl acetate free radical polymerization via living free radical polymerization (MADIX). Polymer 2006, 47, 999–1010. [Google Scholar] [CrossRef]
- Niu, L.; Xia, Z. Comparison of the different emulsion polymerization routes between acrylic and vinyl acetate monomers using poly(vinyl alcohol) as the sole stabilizer. Colloid Polym. Sci. 2012, 290, 699–707. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidisc. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Algorithm. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Nielsen, F.; Nock, R.; Amari, S. On Clustering Histograms with k-Means by Using Mixed α-Divergences. Entropy 2014, 16, 3273–3301. [Google Scholar] [CrossRef]
- Henderson, K.; Gallagher, B.; Eliassi-Rad, T. EP-MEANS: An Efficient Nonparametric Clustering of Empirical Probability Distributions. In Proceedings of the 30th Annual ACM Symposium on Applied Computing, SAC 2015: Symposium on Applied Computing, Salamanca, Spain, 13–17 April 2015; Wainwright, R.L., Corchado, J.M., Bechini, A., Hong, J., Eds.; ACM: New York, NY, USA, 2015; pp. 893–900, ISBN 9781450331968. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman Divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Drache, M.; Drache, G. Simulating Controlled Radical Polymerizations with mcPolymer—A Monte Carlo Approach. Polymers 2012, 4, 1416–1442. [Google Scholar] [CrossRef]
- Feuerpfeil, A.; Drache, M.; Jantke, L.-A.; Melchin, T.; Rodríguez-Fernández, J.; Beuermann, S. Modeling Semi-Batch Vinyl Acetate Polymerization Processes. Ind. Eng. Chem. Res. 2021, 60, 18256–18267. [Google Scholar] [CrossRef]
- Mätzig, J.; Drache, M.; Drache, G.; Beuermann, S. Kinetic Monte Carlo Simulations as a Tool for Unraveling the Impact of Solvent and Temperature on Polymer Topology for Self-Initiated Butyl Acrylate Radical Polymerizations at High Temperatures. Macromol. Theory Simul. 2023, 32, 2300007. [Google Scholar] [CrossRef]
| Variables | Description | Restrictions |
|---|---|---|
| cm,0 | initial monomer concentration | cm,0(min) ≤ cm,0 ≤ cm,0(max) |
| cini,0 | initial initiator concentration | cini,0(min) ≤ cini,0 ≤ cini,0(max) |
| t | reaction time | tmin ≤ t ≤ tmax |
| r = [cm,0, cini,0, t] | initial recipe |
| Objectives | Description |
|---|---|
| fMSE(r)= | minimal MSE, where MMD(r) is simulated |
| fcm(r)= | minimal relative monomer concentration |
| ft(r) = t | minimal reaction time (directly from r) |
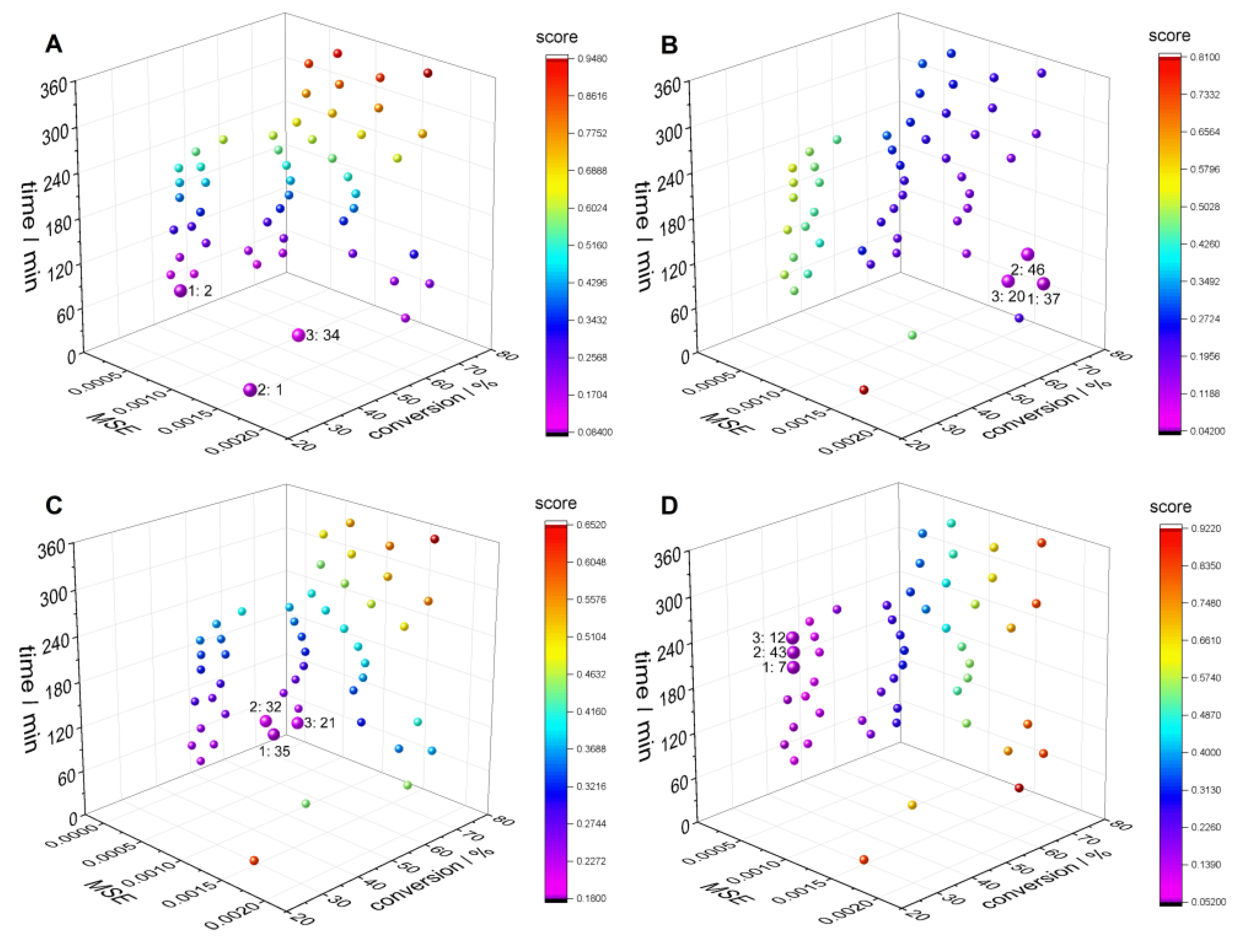
| IDs of the Best Recipe | 1 | 34 | 2 | 46 | 20 | 37 | ||
|---|---|---|---|---|---|---|---|---|
| wi | Time Focus (A) | wi | Conversion Focus (B) | |||||
| cm,0/mol∙L−1 | 2.0 | 2.21 | 2.0 | 2.21 | 2.43 | 2.43 | ||
| cini,0/mmol∙L−1 | 20 | 20 | 20 | 8.4 | 16.1 | 20 | ||
| time/min | 0.9 | 20 | 40 | 40 | 0.19 | 120 | 80 | 80 |
| MSE/×10−3 | 0.05 | 1.63 | 1.37 | 0.08 | 0.01 | 1.72 | 1.58 | 1.81 |
| conversion/% | 0.05 | 25.9 | 46.6 | 45.9 | 0.8 | 71.3 | 69.6 | 73.7 |
| IDs of the Best Recipe | 35 | 32 | 21 | 43 | 12 | 7 | ||
| wi | Equal Weights (C) | wi | MSE Focus (D) | |||||
| cm,0/mol∙L−1 | 2.21 | 2.21 | 2.21 | 2.0 | 2.0 | 2.0 | ||
| cini,0/mmol∙L−1 | 20.0 | 10.5 | 13.0 | 12.4 | 10.0 | 1.5 | ||
| time/min | 1/3 | 60 | 80 | 80 | 0.01 | 180 | 200 | 160 |
| MSE/×10−5 | 1/3 | 35 | 31 | 54 | 0.9 | 0.086 | 0.032 | 0.15 |
| conversion/% | 1/3 | 61.8 | 60.2 | 64.4 | 0.09 | 48.3 | 48.2 | 48.2 |
| Objective Weights | Cand. ID | cm,0/mol∙L−1 | cini,0/mmol∙L−1 | Time/min | MSE/10−3 | Conversion/% |
|---|---|---|---|---|---|---|
| 0 | 2.00 | 20.0 | 20 | 1.63 | 25.9 | |
| time focus: (wcm = 0.2, wt = 0.8) | 1 | 2.21 | 20.0 | 40 | 1.37 | 46.6 |
| 2 | 2.43 | 20.0 | 60 | 1.94 | 62.7 | |
| equal weights: (wcm = 0.5, wt = 0.5) | 3 | 2.43 | 20.0 | 80 | 1.81 | 73.7 |
| conversion focus: (wcm = 0.8, wt = 0.2) | 4 | 2.43 | 16.1 | 100 | 2.61 | 77.7 |
| 5 | 2.43 | 6.86 | 160 | 2.79 | 78.3 | |
| 6 | 2.43 | 5.54 | 180 | 2.83 | 78.5 | |
| 7 | 2.43 | 2.91 | 260 | 2.98 | 79.0 |
| Number of Clusters | 20 | 40 | 60 | |
|---|---|---|---|---|
| Cand. ID/ | 3 | 2 | 1 | |
| property | wi | |||
| cm,0/mol∙L−1 | 3.50 | 3.07 | 2.86 | |
| cini,0/mmol∙L−1 | 13.0 | 20.0 | 20.0 | |
| time/min | 0.5 | 60.0 | 40.0 | 20.0 |
| MSE/×10−3 | 3.04 | 0.32 | 0.03 | |
| conversion/% | 0.5 | 58.2 | 49.2 | 27.0 |
| score (wt = 0.5, wcm = 0.5) | 0.50 | 0.39 | 0.50 | |
| score (wMSE = 1/3, wcm = 1/3, wt = 1/3) | 0.67 | 0.30 | 0.33 |
| Approach | Direct | Clustering-Supported Approach | ||||
|---|---|---|---|---|---|---|
| 20 Clusters | 40 Clusters | 60 Clusters | 80 Clusters | 100 Clusters | ||
| execution time, s | 679 | 56 | 25 | 18 | 14 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiosina, J.; Sievers, P.; Kanagaraj, G.; Drache, M.; Beuermann, S. Reverse Engineering of Radical Polymerizations by Multi-Objective Optimization. Polymers 2024, 16, 945. https://doi.org/10.3390/polym16070945
Fiosina J, Sievers P, Kanagaraj G, Drache M, Beuermann S. Reverse Engineering of Radical Polymerizations by Multi-Objective Optimization. Polymers. 2024; 16(7):945. https://doi.org/10.3390/polym16070945
Chicago/Turabian StyleFiosina, Jelena, Philipp Sievers, Gavaskar Kanagaraj, Marco Drache, and Sabine Beuermann. 2024. "Reverse Engineering of Radical Polymerizations by Multi-Objective Optimization" Polymers 16, no. 7: 945. https://doi.org/10.3390/polym16070945
APA StyleFiosina, J., Sievers, P., Kanagaraj, G., Drache, M., & Beuermann, S. (2024). Reverse Engineering of Radical Polymerizations by Multi-Objective Optimization. Polymers, 16(7), 945. https://doi.org/10.3390/polym16070945










