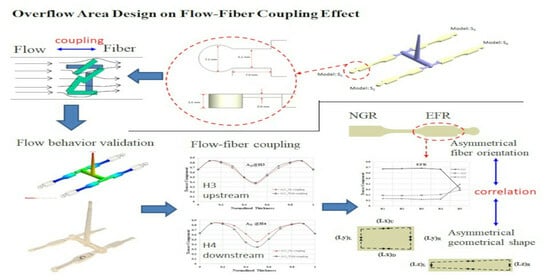
Study on the Influence of Runner and Overflow Area Design on Flow–Fiber Coupling in a Multi-Cavity System
Abstract
1. Introduction
2. Theoretical Background
2.1. Model for Polymer Melt Flow
2.2. Models for Fiber Orientations
2.3. Model for Viscosity by Flow–Fiber Coupling
3. Systems and Information
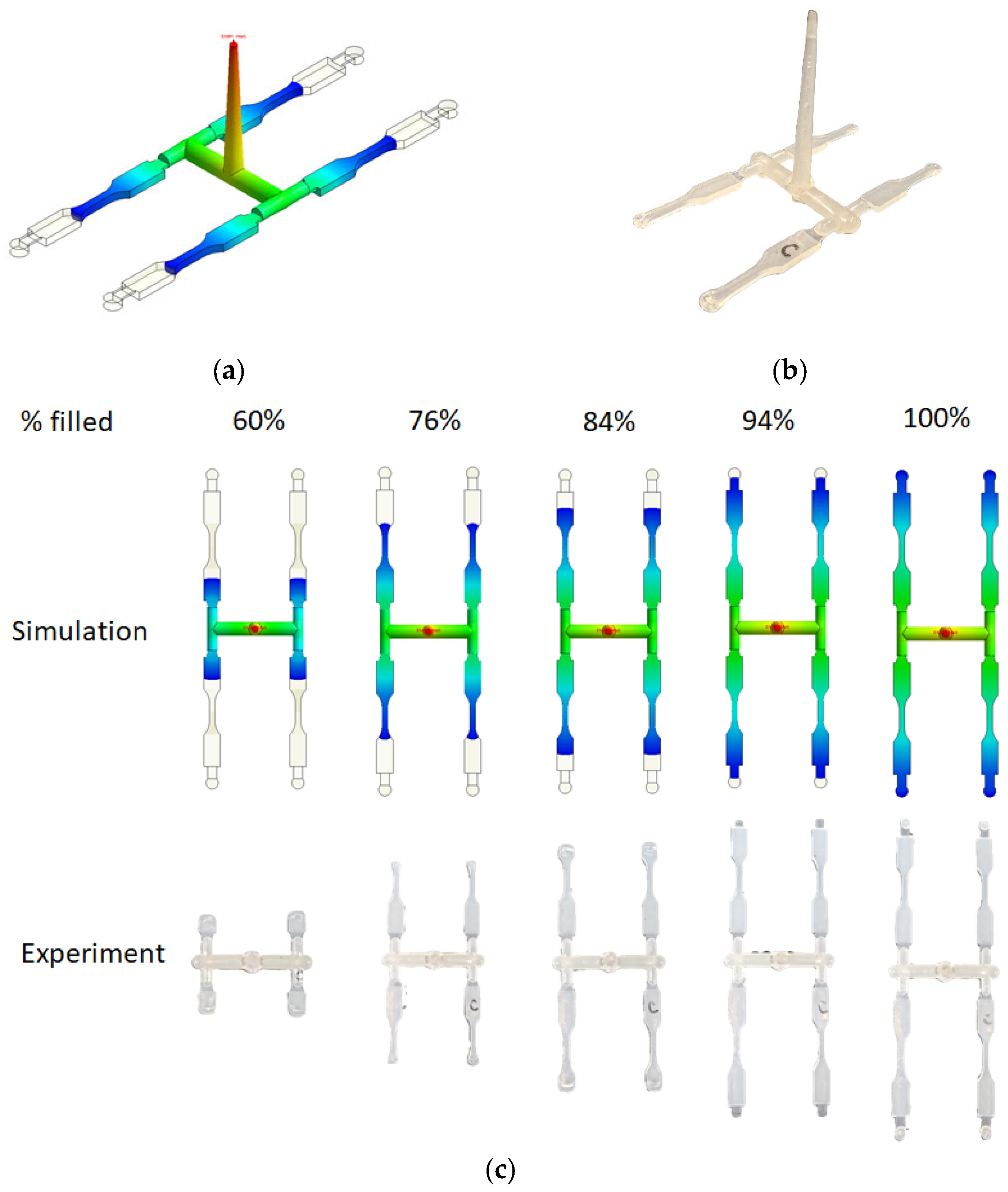
3.1. System of Simulation
3.2. System of Experimentation
3.3. Dimensional Measurement of the Injected Parts
4. Results
4.1. Flow Behavior Validation
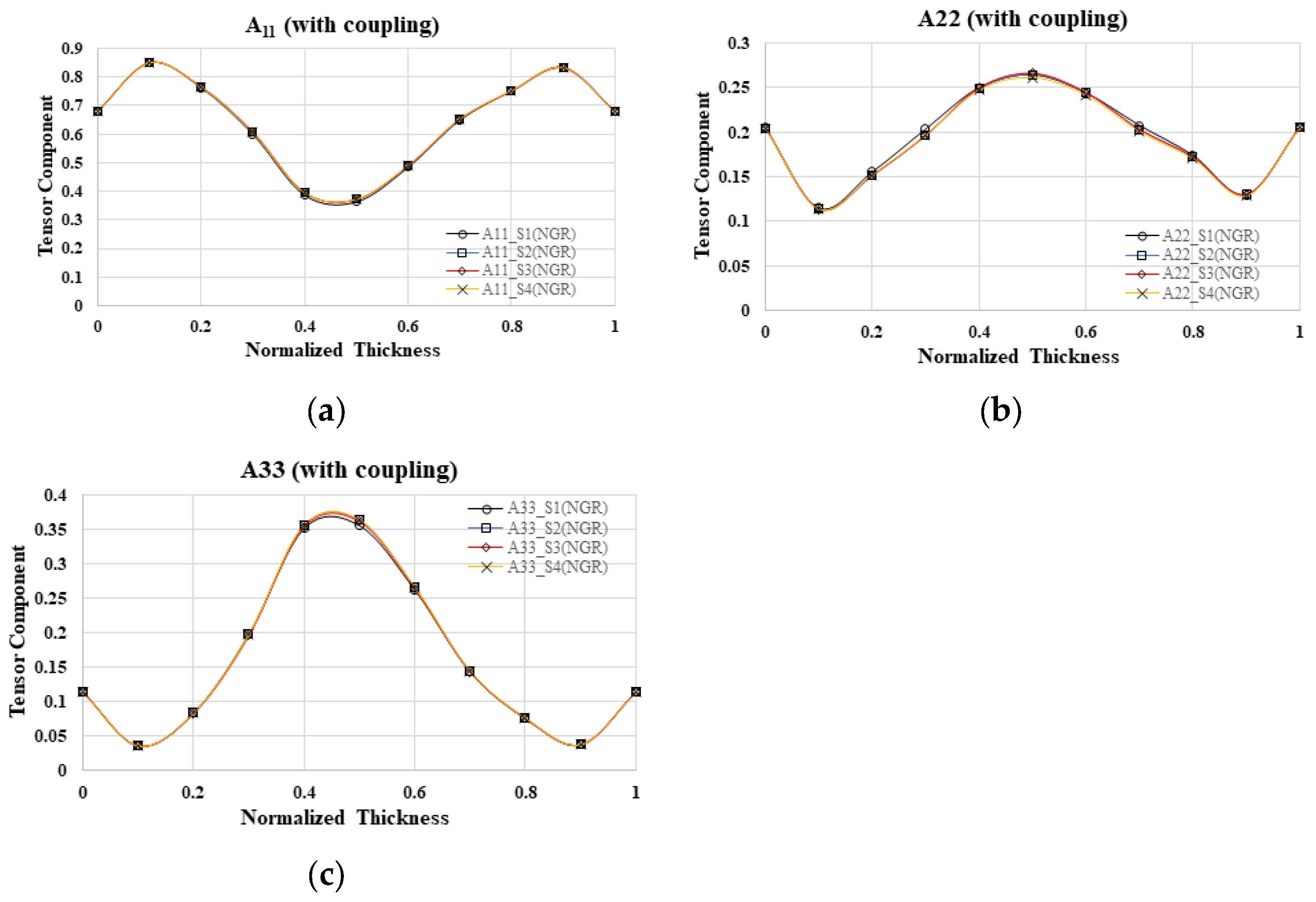
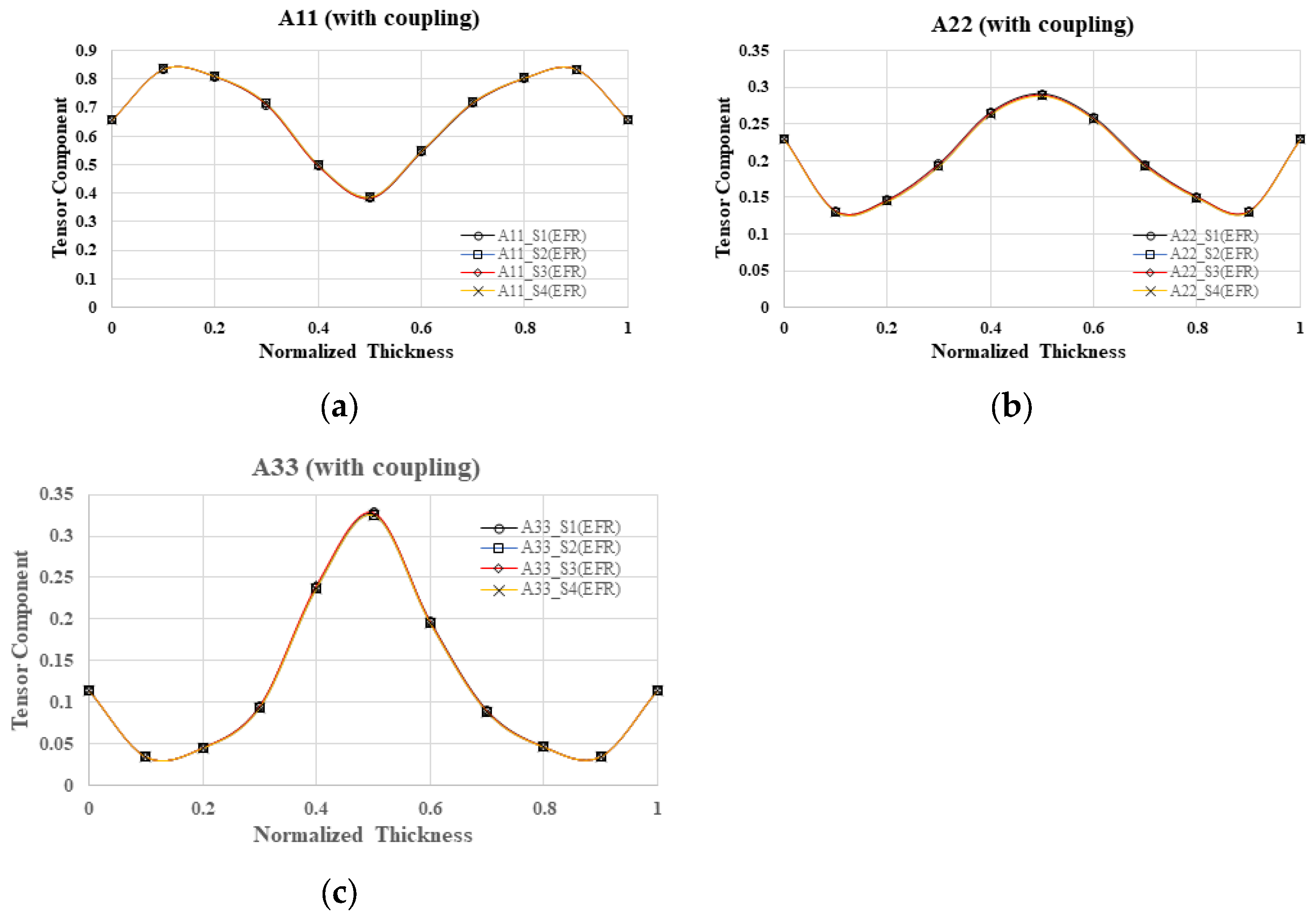
4.2. Fiber Orientation Distribution from Cavity to Cavity
4.2.1. Simulation Result with Flow–Fiber Coupling Effect
4.2.2. Simulation Result without Flow–Fiber Coupling Effect
4.3. Discover the Evidence of the Flow–Fiber Coupling Effect in a Single Cavity S1
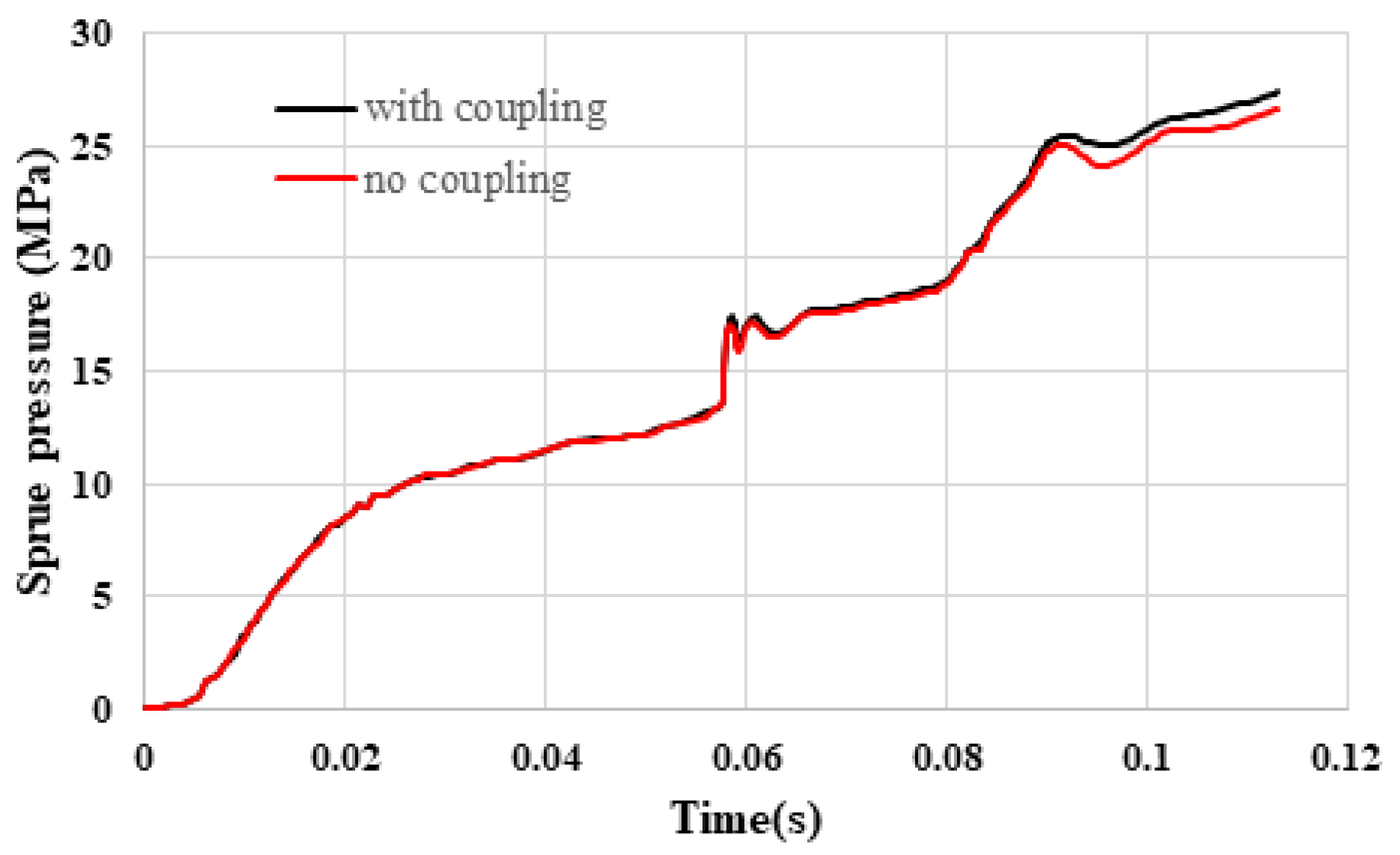
4.3.1. Sprue Pressure
4.3.2. Theoretical Investigation into the Impact of the Overflow Area on the Flow–Fiber Coupling Effect
4.4. The Relationship between Fiber Orientations and Geometrical Shrinkage
4.4.1. Numerical Prediction of the Average Fiber Orientation along Flow Direction
4.4.2. Numerical prediction of the geometrical shrinkage
4.4.3. Experimental Validation of the Geometrical Shrinkage
5. Discussion
5.1. Flow–Fiber Coupling Effect Validation
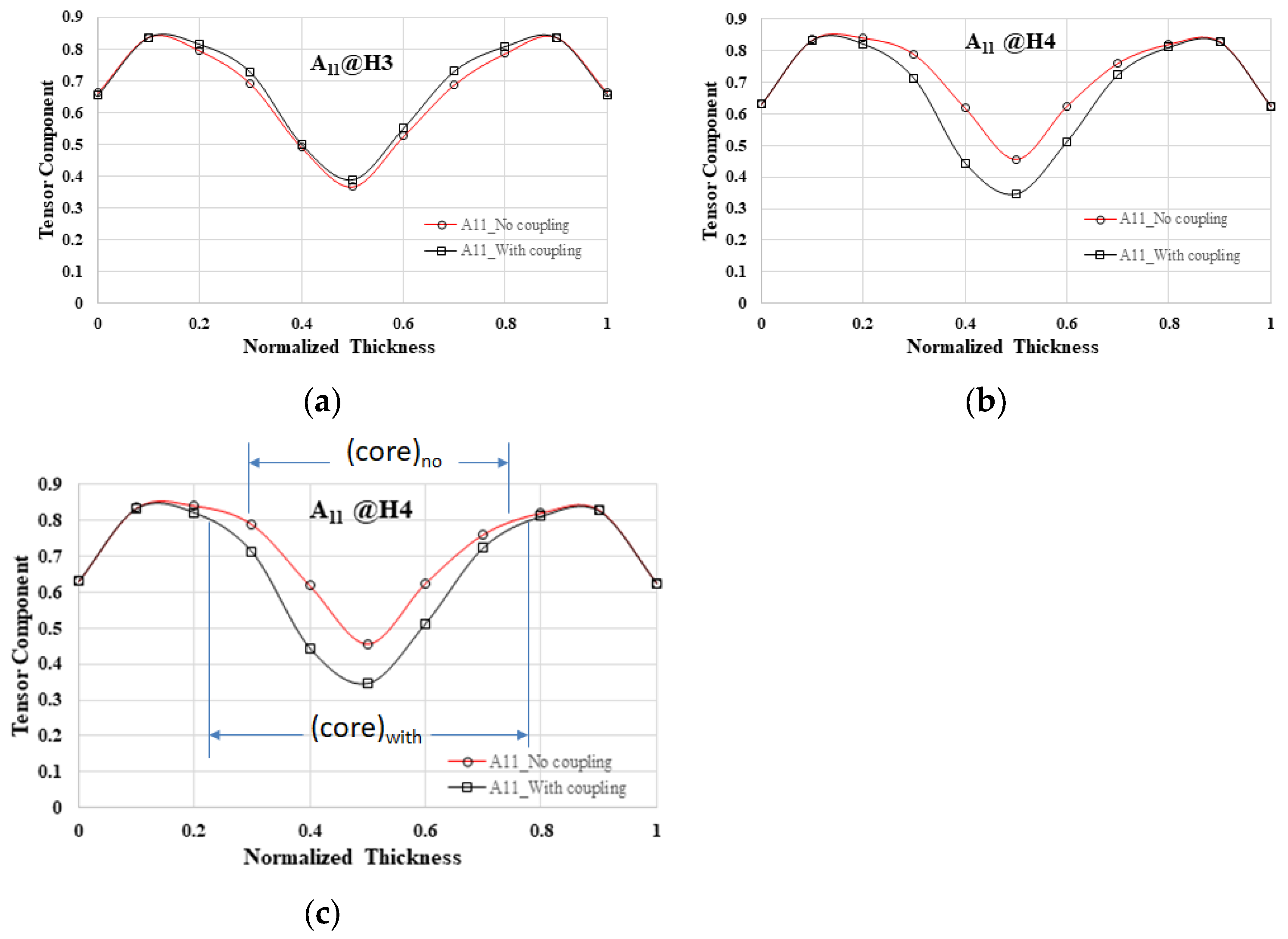
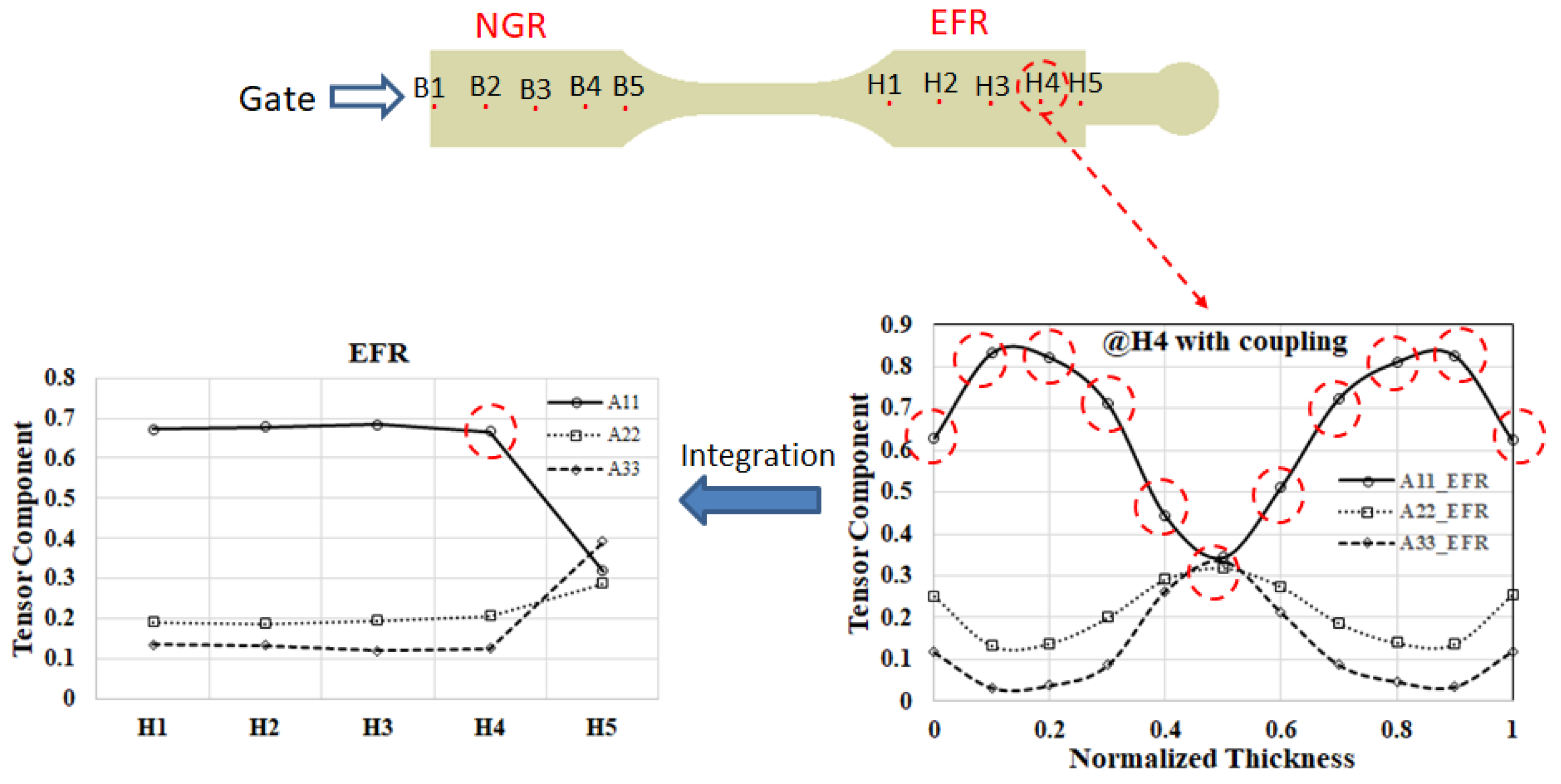
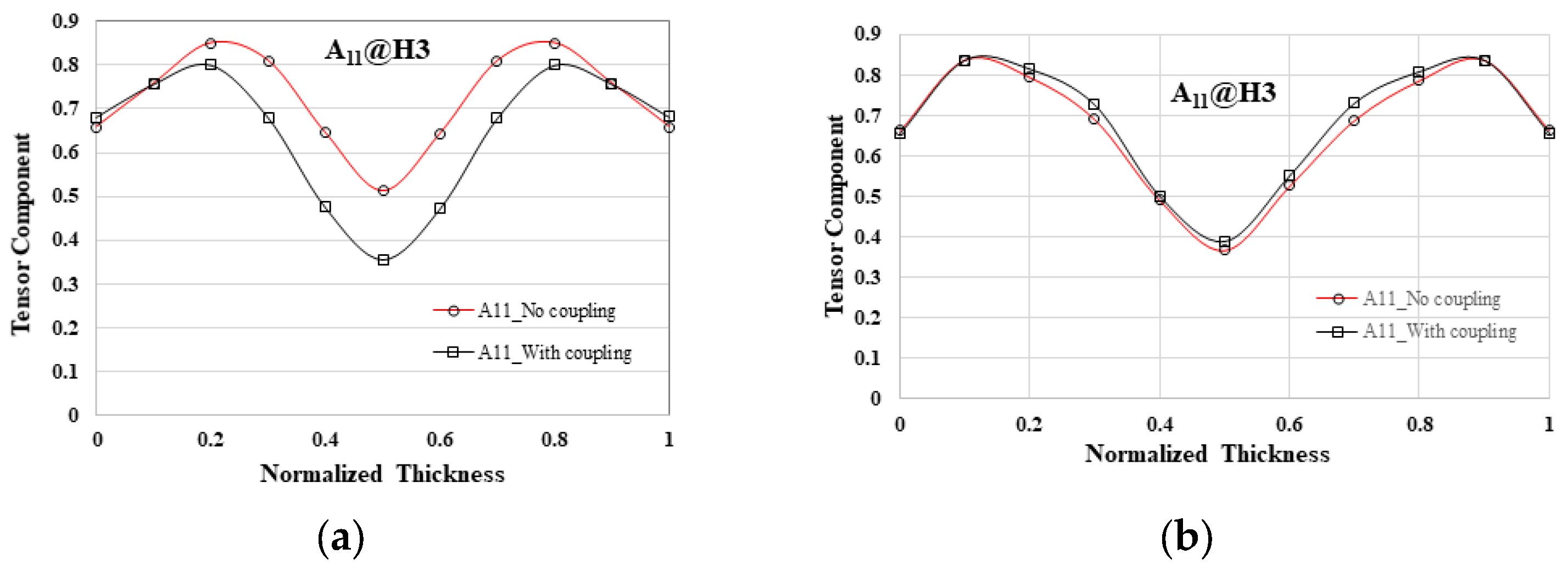
5.2. The Influence of Overflow Area on the Occurrence of Flow–Fiber Coupling
5.3. Validation of the Flow–Fiber Coupling Effect on the Asymmetrical Shrikange Behavior from Upstream to Downstream
6. Conclusions
- Irrespective of the consideration of the flow–fiber coupling effect, the theoretical fiber orientation of each cavity remains consistent.
- When examining the flow–fiber coupling effect, two observations can demonstrate this phenomenon: (1) the sprue pressure in the system exhibiting flow–fiber coupling was higher than in the system without this coupling, and (2) the core layer area in the system with flow–fiber coupling was observed to be enlarged compared to the system lacking such coupling.
- In a geometric system featuring an overflow area design, the presence of these overflow areas serves to postpone the onset of the flow–fiber coupling effect in contrast to a system lacking such design elements.
- Through the integration of fiber orientation distribution data, it is possible to examine the consequences of the delayed flow–fiber coupling effect in the overflow area, particularly in the EFR. This phenomenon leads to a significant transfer of A11 fiber orientation to A22 and A33 in the final filling zone (H4 to H5), resulting in an asymmetrical arrangement of fiber orientation.
- By analyzing the geometric dimensions of the final part from the 1 × 4 multi-cavity system with overflow area, it is evident that there are noticeable variations in size and shrinkage between the upstream and downstream sections within the EFR. These differences align with the asymmetrical distribution of fiber orientation induced by the flow–fiber coupling effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Composites World Report. Composites End Markets: Automotive. 2022. Available online: https://www.compositesworld.com/articles/composites-end-markets-automotive-2022 (accessed on 2 February 2022).
- Othman, R.; Ismail, N.I.; Pahmi, M.A.A.H.; Basri, M.H.M.; Sharudin, H.; Hemdi, A.R. Application of carbon fiber reinforced plastics in automotive industry: A review. J. Mech. Manuf. 2018, 1, 144–154. [Google Scholar]
- Office of Energy Efficiency and Renewable Energy. U. S. Department of Energy Report, Materials 2018 Annual Progress Report; Office of Energy Efficiency and Renewable Energy: Washington, DC, USA, 2018.
- Der, A.; Kaluza, A.; Reimer, L.; Herrmann, C.; Thiede, S. Integration of energy oriented manufacturing simulation into the life cycle evaluation of lightweight body parts. Int. J. Precis. Eng. Manuf.-Green Technol. 2022, 9, 899–918. [Google Scholar] [CrossRef]
- Garate, J.; Solovitz, S.A.; Kim, D. Fabrication and performance of segmented thermoplastic composite wind turbine blades. Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 271–277. [Google Scholar] [CrossRef]
- Thomason, J.L.; Vlug, M.A. Influence of fiber length and concentration on the properties of glass fiber-reinforced polypropylene: Part 1-Tensile and flexural modulus. Composites 1996, 27 Pt A, 477–484. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: Interface strength and fibre strain in injection moulded long fibre PP at high fibre content. Compost. Part A Appl. Sci. Manuf. 2007, 38, 210–216. [Google Scholar] [CrossRef]
- Wang, C.; Yang, S. Thermal, tensile and dynamic mechanical properties of short carbon fibre reinforced polypropylene composites. Polym. Polym. Compos. 2013, 21, 65–71. [Google Scholar] [CrossRef]
- Cilleruelo, L.; Lafranche, E.; Krawczak, P.; Pardo, P.; Lucas, P. Injection moulding of long glass fibre reinforced poly(ethylene terephtalate): Influence of carbon black and nucleating agents on impact properties. Express Polym. Lett. 2012, 6, 706–718. [Google Scholar] [CrossRef]
- Rohde, M.; Ebel, A.; Wolff-Fabris, F.; Altstädt, V. Influence of processing parameters on the fiber length and impact properties of injection molded long glass fiber reinforced polypropylene. Int. Polym. Process. 2011, 26, 292–303. [Google Scholar] [CrossRef]
- Goris, S.; Back, T.; Yanev, A.; Brands, D.; Drummer, D.; Osswald, T.A. A novel fiber length measurement technique for discontinuous fiber-reinforced composites: A comparative study with existing methods. Polym. Compos. 2018, 39, 4058–4070. [Google Scholar] [CrossRef]
- Nguyen, B.N.; Bapanapalli, S.K.; Holbery, J.D.; Smith, M.T.; Kunc, V.; Frame, B.J.; Phelps, J.H.; Tucker, C.L. Fiber length and orientation in long-fiber injection-molded thermoplastics-Part I: Modeling of microstructure and elastic Properties. J. Compos. Mater. 2008, 42, 1003–1029. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C.L. Orientation behavior of fibers in concentrated suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Ortman, K.; Baird, D.; Wapperom, P.; Aning, A. Prediction of fiber orientation in the iInjection molding of long fiber suspensions. Polym. Compos. 2012, 33, 1360–1367. [Google Scholar] [CrossRef]
- Phelps, J.H.; Tucker, C.L., III. An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non-Newton. Fluid Mech. 2009, 56, 165–176. [Google Scholar] [CrossRef]
- Wang, J.; O’Gara, J.F.; Tucker, C.L., III. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Wang, J.; Jin, X. Comparison of recent fiber orientation models in autodesk moldflow insight simulations with measured fiber orientation data. In Proceedings of the Polymer Processing Society 26th Annual Meeting (PPS-26), Banff, AB, Canada, 4–8 July 2010. [Google Scholar]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Phenomenological improvements to predictive models of fiber orientation in concentrated suspensions. J. Rheol. 2013, 57, 1597–1631. [Google Scholar] [CrossRef]
- Libscomb, G.G.; Denn, M.M.; Hur, D.U.; Boger, D.V. The flow of fiber suspensions in complex geometries. J. Non-Newton. Fluid Mech. 1988, 26, 297–325. [Google Scholar] [CrossRef]
- VerWeyst, B.E.; Tucker, C.L., III. Fiber suspensions in complex geometries: Flow/orientation coupling. Can. J. Chem. Eng. 2002, 80, 1093–1106. [Google Scholar] [CrossRef]
- Tseng, H.C.; Su, T.H. Coupled flow and fiber orientation analysis for 3D injection molding simulations of fiber composites. In Proceedings of the Polymer Processing Society 34th Annual Meeting (PPS-34). AIP Conf. Proc. 2019, 2065, 030021. [Google Scholar] [CrossRef]
- Favaloro, A.J.; Tseng, H.C.; Pipes, R.B. A new anisotropic viscous constitutive model or composite molding simulation. Compos. Part A 2018, 115, 112–122. [Google Scholar] [CrossRef]
- Tseng, H.C.; Favaloro, A.J. The use of informed isotropic constitutive equation to simulate anisotropic rheological behaviors in fiber suspensions. J. Rheol. 2019, 63, 263–274. [Google Scholar] [CrossRef]
- Huang, C.T.; Lai, C.H. Investigation on the coupling effects between flow and fibers on fiber-reinforced plastic (FRP) injection parts. Polymers 2020, 12, 2274. [Google Scholar] [CrossRef] [PubMed]
- Bernasconi, A.; Cosmi, F.; Hine, P.J. Analysis of fibre orientation distribution in short fibre reinforced polymers: A comparison between optical and tomographic methods. Compos. Sci. Technol. 2012, 72, 2002–2008. [Google Scholar] [CrossRef]
- Gandhi, U.; Goris, S.D.B.; Kunc, V.; Song, Y.Y. Method to measure orientation of discontinuous fiber embedded in the polymer matrix from computerized tomography scan data. J. Thermoplast. Compos. Mater. 2015, 29, 1696–1709. [Google Scholar] [CrossRef]
- Teuwsen, J.; Goris, S.; Osswald, T.A. Impact of the process-induced microstructure on the mechanical performance of injection molded long glass fiber reinforced polypropylene. In SPE ANTEC Annual Tech Paper; SPE: Danbury, CT, USA, 2017; pp. 626–635. [Google Scholar]
- Huang, C.T.; Chu, J.H.; Fu, W.W.; Hsu, C.; Hwang, S.J. Flow-induced orientations of fibers and their influences on warpage and mechanical property in injection fiber reinforced plastic (FRP) Parts. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 917–934. [Google Scholar] [CrossRef]
- Huang, C.T.; Wang, J.Z.; Lai, C.H.; Hwang, S.J.; Huang, P.W.; Peng, H.S. Correlation Between Fiber Orientation and Geometrical Shrinkage of Injected Parts Under the Influence of Flow-Fiber Coupling Effect. Int. J. Precis. Eng. Manuf.-Green Technol. 2023, 10, 1039–1060. [Google Scholar] [CrossRef]
- Beaumont, J.P.; Young, J.H.; Jaworski, M.J. Solving Mold Filling Imbalances in Multi-Cavity Injection Molds. J. Inject. Molding Technol. 1998, 2, 47–58. [Google Scholar]
- Beaumont, J.P.; Young, J.H. Mold filling imbalances in Geometrically Balanced Runner Systems. J. Reinf. Plast. Compos. 1999, 18, 572–590. [Google Scholar] [CrossRef]
- Beaumont, J.P. Runner and Gating Design Handbook, 2nd ed.; Hanser: Munich, Germany, 2004. [Google Scholar]
- Chiang, G.; Chien, J.; Hsu, D.; Tsai, V.; Yang, A. True 3D CAE visualization of filling imbalance in geometry-balanced runners. In Proceedings of the SPE Annual Tech Meeting (ANTEC2005), Boston, MA, USA, 1–5 May 2005; pp. 55–59. [Google Scholar]
- Chien, J.; Huang, C.; Yang, W.; Hsu, D. True 3D CAE Visualization of “Intra-Cavity” Filling Imbalance in Injection. In Proceedings of the SPE Annual Tech Meeting (ANTEC2006), Charlotte, NC, USA, 7–11 May 2006; pp. 1153–1157. [Google Scholar]
- Petzold, F.; Thornagel, M.; Manek, K. Complex Thermal Hot-Runner Balancing: A Method to Optimize Filling Pattern and Product Quality. In Proceedings of the SPE Annual Tech Meeting (ANTEC2009), Chicago, IL, USA, 22–24 June 2009; pp. 291–295. [Google Scholar]
- Wilczyński, K.; Narowski, P. A Strategy for Problem Solving of Filling Imbalance in Geometrically Balanced Injection Molds. Polymers 2020, 12, 805. [Google Scholar] [CrossRef]



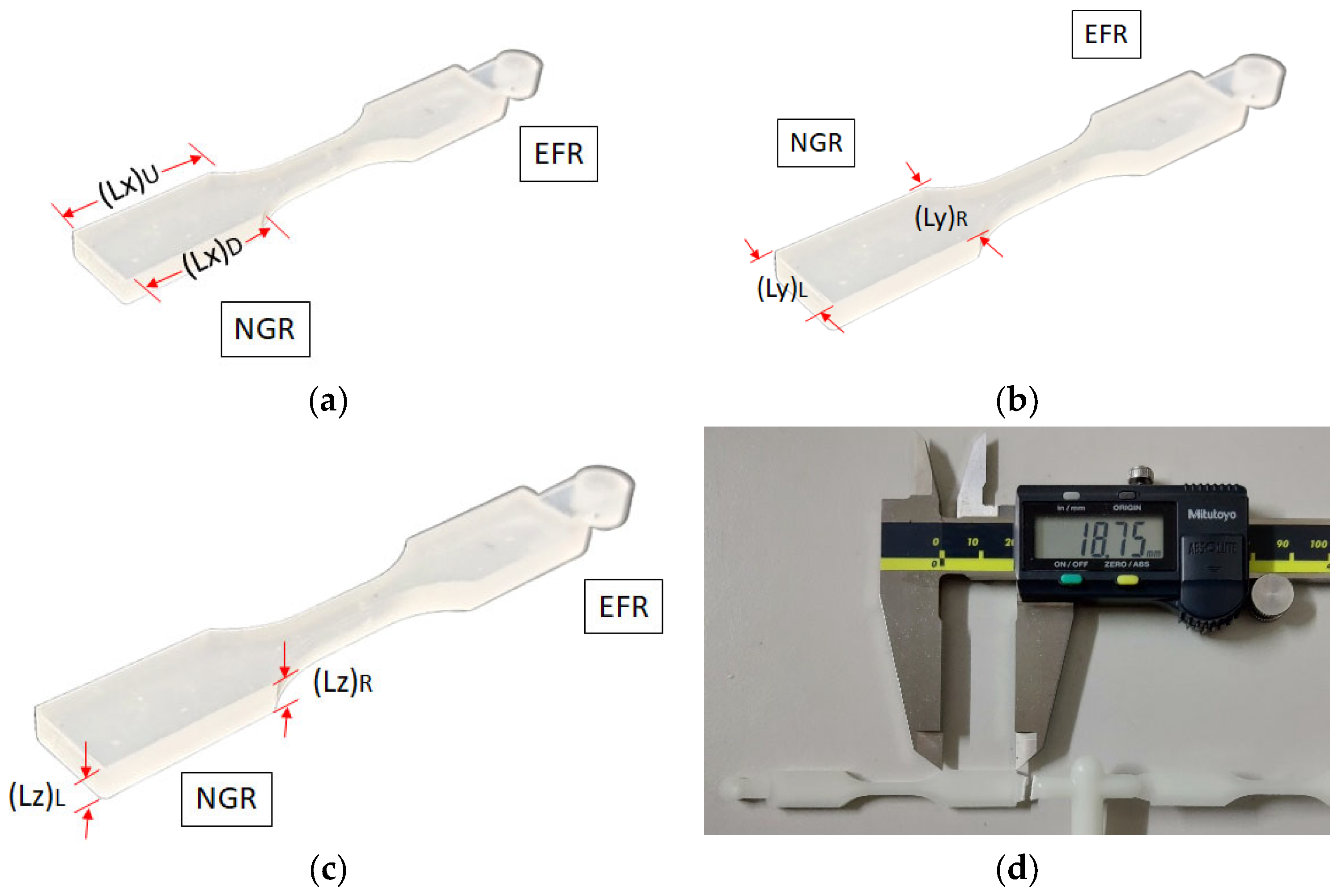


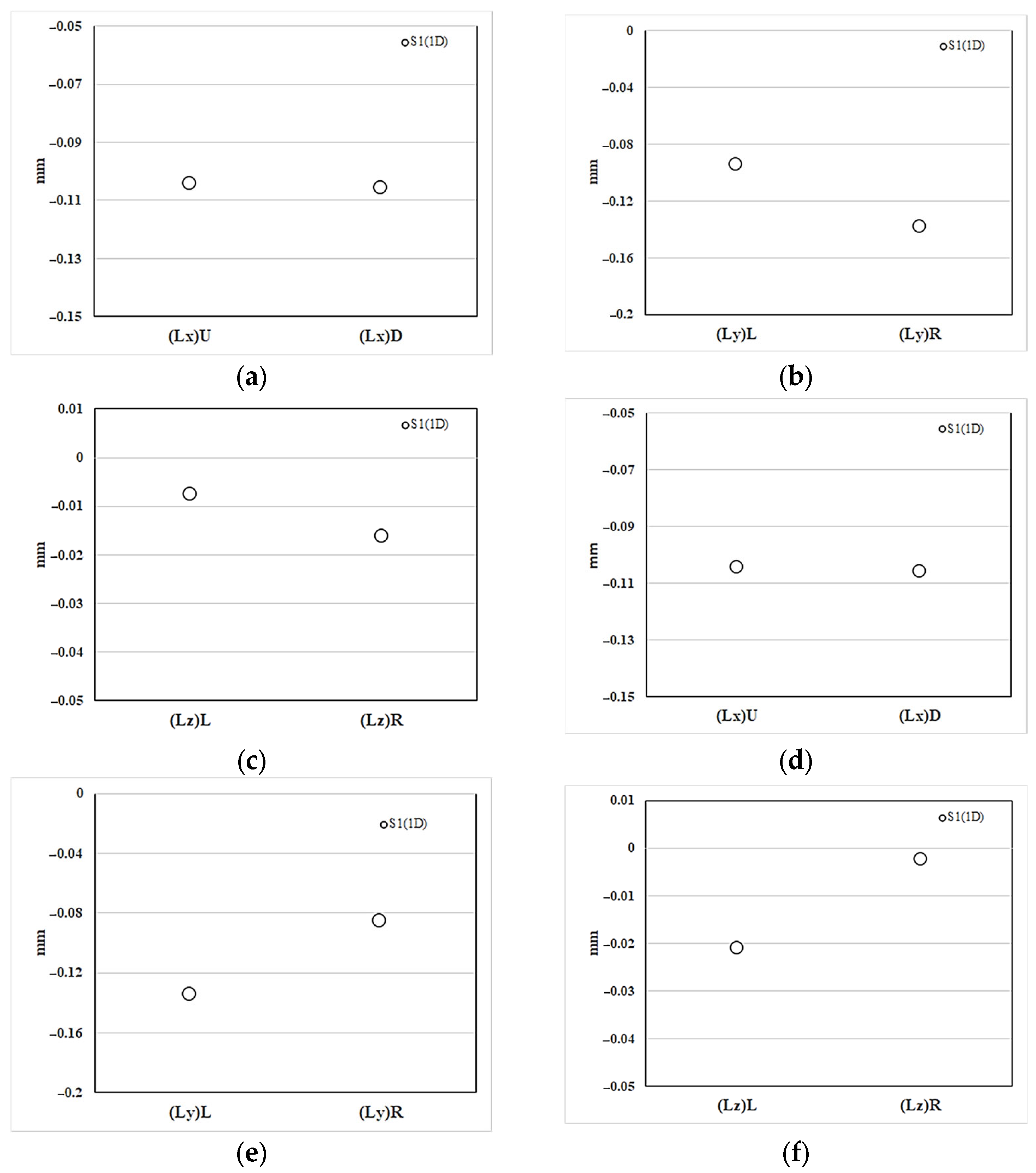
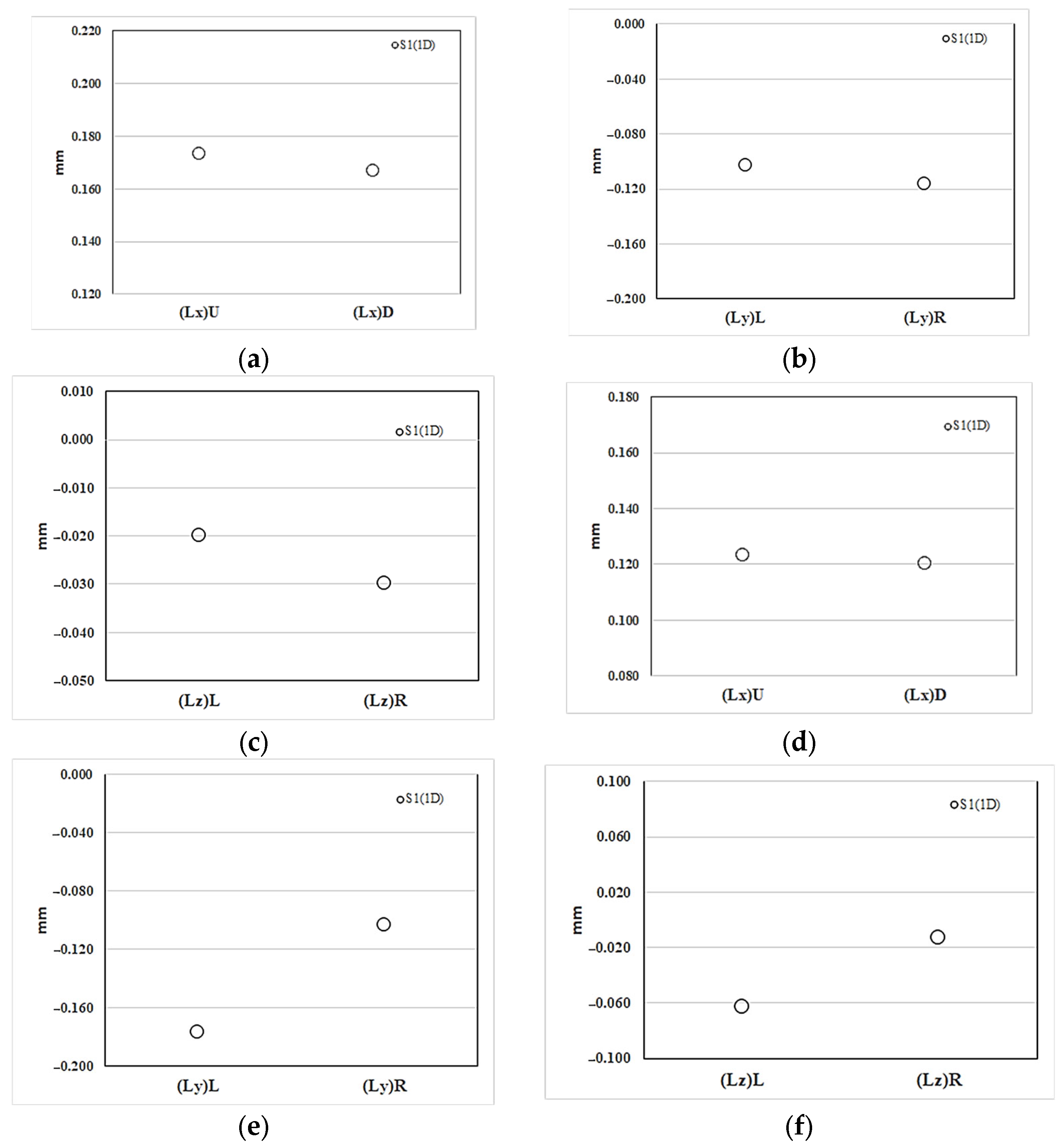
| Region | Material | Shrinkage | ||||||
|---|---|---|---|---|---|---|---|---|
| Unit | (Lx)U | (Lx)D | (Ly)L | (Ly)R | (Lz)L | (Lz)R | ||
| EFR | PP | mm | 18.440 | 18.440 | 9.317 | 9.333 | 3.440 | 3.450 |
| ±0.000 | ±0.000 | ±0.006 | ±0.006 | ±0.010 | ±0.010 | |||
| % | −0.753 | −0.753 | −2.239 | −2.064 | −1.714 | −1.429 | ||
| 30SFPP | mm | 18.703 | 18.700 | 9.353 | 9.427 | 3.437 | 3.487 | |
| ±0.006 | ±0.000 | ±0.006 | ±0.006 | ±0.006 | ±0.006 | |||
| % | 0.664 | 0.646 | −1.854 | −1.084 | −1.810 | −0.381 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, F.-L.; Chen, C.-T.; Hwang, S.-S.; Hwang, S.-J.; Huang, P.-W.; Peng, H.-S.; Jien, M.-Y.; Huang, C.-T. Study on the Influence of Runner and Overflow Area Design on Flow–Fiber Coupling in a Multi-Cavity System. Polymers 2024, 16, 1279. https://doi.org/10.3390/polym16091279
Hsieh F-L, Chen C-T, Hwang S-S, Hwang S-J, Huang P-W, Peng H-S, Jien M-Y, Huang C-T. Study on the Influence of Runner and Overflow Area Design on Flow–Fiber Coupling in a Multi-Cavity System. Polymers. 2024; 16(9):1279. https://doi.org/10.3390/polym16091279
Chicago/Turabian StyleHsieh, Fang-Lin, Chuan-Tsen Chen, Shyh-Shin Hwang, Sheng-Jye Hwang, Po-Wei Huang, Hsin-Shu Peng, Ming-Yuan Jien, and Chao-Tsai Huang. 2024. "Study on the Influence of Runner and Overflow Area Design on Flow–Fiber Coupling in a Multi-Cavity System" Polymers 16, no. 9: 1279. https://doi.org/10.3390/polym16091279
APA StyleHsieh, F.-L., Chen, C.-T., Hwang, S.-S., Hwang, S.-J., Huang, P.-W., Peng, H.-S., Jien, M.-Y., & Huang, C.-T. (2024). Study on the Influence of Runner and Overflow Area Design on Flow–Fiber Coupling in a Multi-Cavity System. Polymers, 16(9), 1279. https://doi.org/10.3390/polym16091279