RC Beams Strengthened with Mechanically Fastened Composites: Experimental Results and Numerical Modeling
Abstract
:1. Introduction

2. Outline of the Proposed 1D-FE Model
2.1. Assumptions and Formulation of the Finite Element
- -
- a 1D element that represents the behavior of Euler–Bernoulli’s RC beam;
- -
- a rod element that simulates the mechanical behavior of an FRP laminate;
- -
- two springs that simulate the behavior of the fasteners and are only translational in the direction of the beam axis.

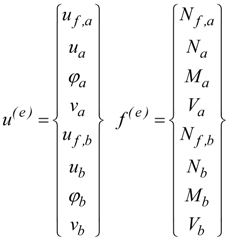
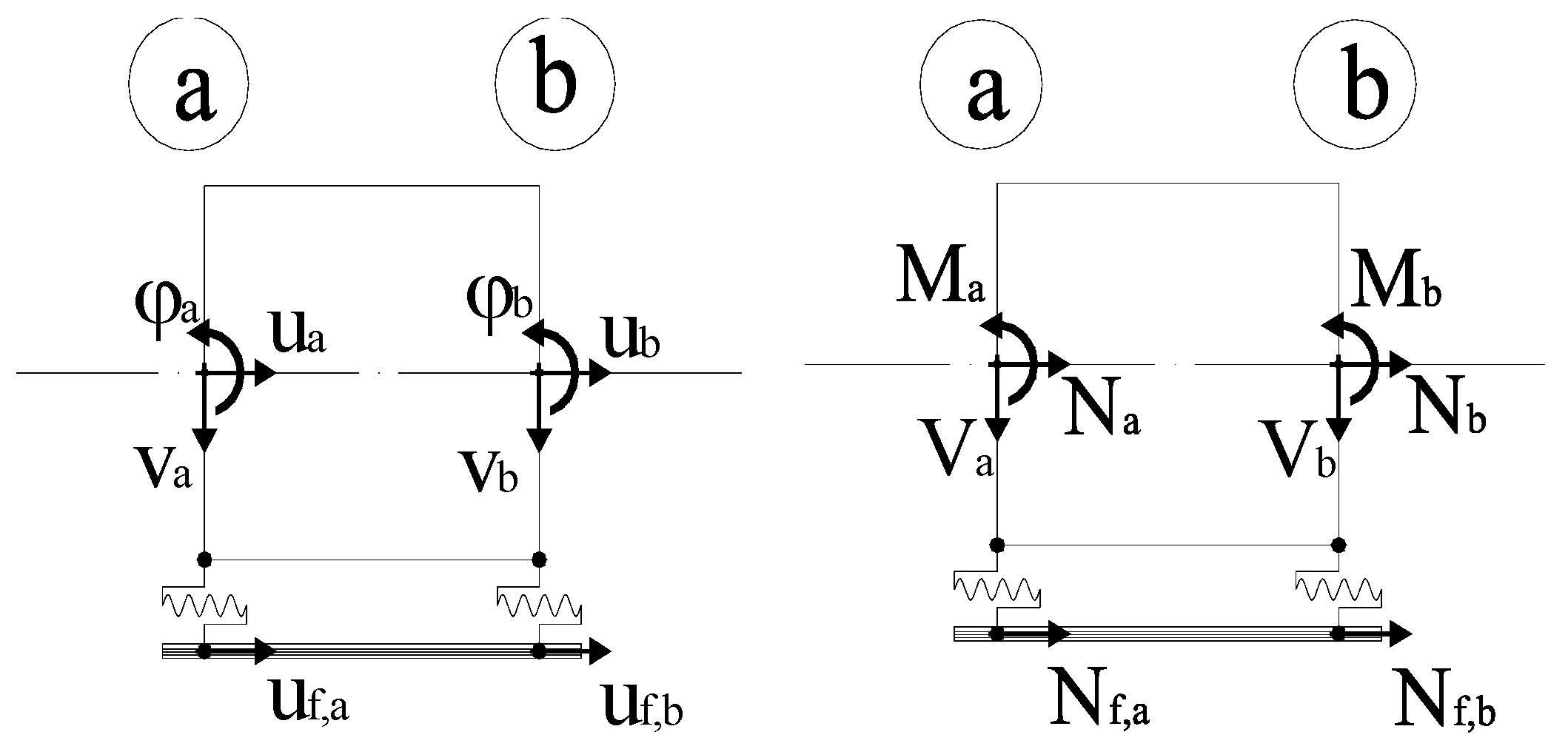
2.2. Nonlinear Analysis Procedure
- -
- the flexural stiffness of the FRP laminate is neglected, and only the axial one is considered;
- -
- equal vertical displacements occur in the connected RC slab and FRP laminate elements;
- -
- shear deformations of the RC slab are neglected.

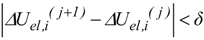
3. The Database
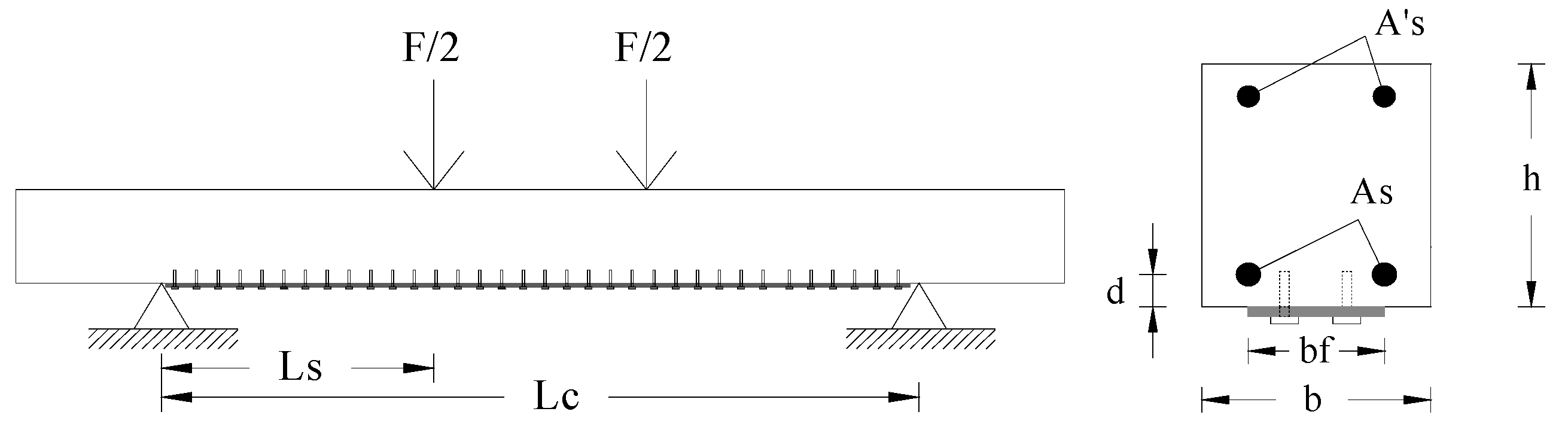
- -
- fc = average value of concrete cylinder compressive strength;
- -
- fy = average value of yield strength of longitudinal steel reinforcement, when obtained by tensile tests (alternatively, information about the steel grade is provided);
- -
- Fy = experimental value of the force measured at the beam yielding during the test;
- -
- Fmax = experimental value of the peak force measured during the test;
- -
- Lf, Ef, ff = length, elastic modulus and tensile strength of the employed FRP strip, respectively;
- -
- da, La = diameter and shank length of the employed fasteners (shot, screw or wedge), respectively, which were provided or not with steel washer.
| Source | Test | Lc | Ls | b × h | A’s | As | d | fc | Steel type | Fy 1 | Fmax 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm2) | (mm2) | (mm2) | (mm) | (MPa) | fy (MPa) | KN | KN | ||
| Borowicz (2002) [18] | U-W-2 | 3505 | 1372 | 305 × 305 | 143 | 1013 | 51 | 44.7 | Grade 60 | 186 | 210 |
| U-W-4 | 2134 | 686 | 377 | 427 | |||||||
| U-W-5 | 2642 | 940 | 268 | 344 | |||||||
| U-W-6 | 3353 | 1295 | 193 | 243 | |||||||
| U-W-7 | 3454 | 1346 | 185 | 234 | |||||||
| U-W-8 | 3505 | 1372 | 182 | 233 | |||||||
| U-W-9 | 3505 | 1372 | 202 | 257 | |||||||
| Ebead (2011) [19] | M-F-D10-1 | 2250 | 850 | 150 × 250 | 101 | 157 | 25 | 41 | 540 | 51 | 70 |
| M-F-D10-2 | 157 | 25 | 38 | 540 | 70 | 77 | |||||
| M-F-D12-1 | 226 | 26 | 38 | 550 | 79 | 99 | |||||
| M-F-D12-2 | 226 | 26 | 39 | 550 | 75 | 105 | |||||
| M-F-D16-1 | 402 | 28 | 40 | 530 | 106 | 130 | |||||
| M-F-D16-2 | 402 | 28 | 39 | 530 | 110 | 132 | |||||
| M-P-D10-1 | 157 | 25 | 37 | 540 | 44 | 55 | |||||
| M-P-D10-2 | 157 | 25 | 38 | 540 | 39 | 60 | |||||
| M-P-D12-1 | 226 | 26 | 36 | 550 | 68 | 79 | |||||
| M-P-D12-2 | 226 | 26 | 39 | 550 | 68 | 81 | |||||
| M-P-D16-1 | 402 | 28 | 36 | 530 | 101 | 105 | |||||
| M-P-D16-2 | 402 | 28 | 41 | 530 | - | 110 | |||||
| Ekenel et al. (2005) [20] | S-4-F | 1829 | 304 | 254 × 165 | 143 | 214 | 45 | 27.6 | 414 | 57 | 72 |
| El-Maaddawy (2013) [5] | C0-PAF-32 | 2800 | 1200 | 250 × 275 | 339 | 100 | 34 | 30.5 | 500 | 85 | 122 |
| C0-PAF-52 | 85 | 134 | |||||||||
| C0-EAB | 90 | 132 | |||||||||
| C0-TAB | 90 | 135 | |||||||||
| C1-PAF-32 | 80 | 95 | |||||||||
| C1-PAF-52 | 80 | 109 | |||||||||
| C1-EAB | 85 | 125 | |||||||||
| C1-TAB | 85 | 129 | |||||||||
| C2-PAF-32 | 75 | 84 | |||||||||
| C2-PAF-52 | 75 | 87 | |||||||||
| C2-EAB | 75 | 110 | |||||||||
| C2-TAB | 75 | 128 | |||||||||
| El-Maaddawy et al. (2013) [21] | C0-F50-32 | 1250 | 550 | 150 × 210 | 226 | 100 | 30 | 32 | 538 | 80 | 86 |
| C0-F100-32 | 85 | 87 | |||||||||
| C0-F100-32-2 | 85 | 88 | |||||||||
| C0-F50-52 | 85 | 94 | |||||||||
| C0-F100-52 | 85 | 90 | |||||||||
| C1-F50-32 | 80 | 90 | |||||||||
| C1-F100-32 | 80 | 87 | |||||||||
| C1-F100-32-2 | 80 | 88 | |||||||||
| C1-F50-52 | 80 | 90 | |||||||||
| C1-F100-52 | 70 | 81 | |||||||||
| C2-F50-32 | 70 | 80 | |||||||||
| C2-F100-32 | 75 | 81 | |||||||||
| C2-F100-32-2 | 80 | 84 | |||||||||
| C2-F50-52 | 70 | 76 | |||||||||
| C2-F100-52 | 70 | 78 | |||||||||
| C3-F50-52 | 65 | 74 | |||||||||
| C3-F100-52 | 70 | 83 | |||||||||
| Galati et al. (2007) [22] | M-F-P-2 | 2200 | 600 | 200 × 250 | 226 | 226 | 29 | 31.5 | 462 | 87 | 131 |
| Lamanna (2002) [23] | D-1 | 1168 | 483 | 153 × 153 | 143 | 254 | 50 | 42 | Grade 60 | 52 | 61 |
| D-2 | 1168 | 483 | 42 | 52 | 58 | ||||||
| E-1 | 1168 | 483 | 42 | 51 | 55 | ||||||
| E-2 | 1168 | 483 | 42 | 51 | 61 | ||||||
| J-1 | 1168 | 483 | 42 | 50 | 54 | ||||||
| L-1 | 1067 | 432 | 42 | 55 | 56 | ||||||
| T-1 | 1067 | 432 | 42 | 56 | 62 | ||||||
| T-2 | 1067 | 432 | 42 | 59 | 67 | ||||||
| T-3 | 1067 | 432 | 42 | 54 | 61 | ||||||
| F-1 | 1168 | 483 | 21 | 48 | 52 | ||||||
| G-1 | 1168 | 483 | 21 | 49 | 50 | ||||||
| K-1 | 1168 | 483 | 21 | 47 | 50 | ||||||
| M-1 | 1067 | 432 | 21 | 53 | 55 | ||||||
| N-1 | 1067 | 432 | 21 | 57 | 57 | ||||||
| P-1 | 1067 | 432 | 21 | 60 | 62 | ||||||
| Q-1 | 1067 | 432 | 21 | 56 | 56 | ||||||
| R-1 | 1067 | 432 | 21 | 56 | 62 | ||||||
| R-2 | 1067 | 432 | 21 | 56 | 59 | ||||||
| U-1 | 1067 | 432 | 21 | 53 | 55 | ||||||
| Lamanna et al. (2001) [24] | F-42-S-102-1R | 1067 | 432 | 153 × 153 | 143 | 254 | 39 | 42 | Grade 60 | 59 | 67 |
| F-21-S-102-2R | 21 | 56 | 59 | ||||||||
| Bank et al. (2002) Lamanna et al.(2004) [25,26] | S-4-Y-AL32 | 3353 | 1118 | 305 × 305 | 143 | 1013 | 51 | 35.3 | Grade 60 | 225 | 255 |
| I-4-N-AL32 | 233 | 253 | |||||||||
| I-4-Y-AL32 | 239 | 269 | |||||||||
| I-4-Y-AL32-R | 234 | 279 | |||||||||
| I-8-Y-AL32 | 248 | 273 | |||||||||
| H1.5-4-YAL32 | 249 | 262 | |||||||||
| H1.5-4-Y-AL42D | 244 | 273 | |||||||||
| H1.5-4-Y-AL47D | 249 | 293 | |||||||||
| H1.5-4-Y-AL47D-3 | 249 | 285 | |||||||||
| H1.5-4-Y-AL47D-3R | 249 | 283 | |||||||||
| H1.5-8-Y-AL32 | 266 | 266 | |||||||||
| H1.0-4-Y-AL47D-5 | 219 | 243 | |||||||||
| Lee et al. (2007) [27] | 1 | 1370 | 610 | 200 × 150 | 157 | 226 | 40 | 34.5 | Grade 60 | 79 | 84 |
| 2 | 1370 | 610 | 200 × 150 | 157 | 226 | 40 | 34.5 | Grade 60 | 78 | 92 | |
| Martin and Lamanna (2008) [28] | 6-L | 3353 | 1219 | 305 × 305 | 143 | 1013 | 51 | 48 | Grade 60 | 185 | 203 |
| 6-S | 196 | 211 | |||||||||
| 10-L | 182 | 206 | |||||||||
| 12-L | 192 | 213 | |||||||||
| Napoli et al. (2008) [11] | MF-1-L | 3048 | 1219 | 305 × 152 | - | 380 | 25 | 26.7 | Grade 60 | 42 | 61 |
| MF-1-S | 41 | 56 | |||||||||
| MF-2-L | 36 | 56 | |||||||||
| MF-2-S | 35 | 50 |
| Source | Test | bf | tf | Lf | Ef | ff | Fastener type | da | La | Washer | # rows |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (GPa) | (MPa) | (mm) | (mm) | |||||
| Borowicz (2002) [18] | U-W-2 | 102 | 3.2 | 3404 | 56.5 | 494 | PAF | 4.5 | 47 | YES | 2-a |
| U-W-4 | 2134 | 494 | 2-a | ||||||||
| U-W-5 | 2642 | 494 | 2-a | ||||||||
| U-W-6 | 3251 | 743 | 2-a | ||||||||
| U-W-7 | 3048 | 743 | 2-a | ||||||||
| U-W-8 | 2997 | 743 | 2-a | ||||||||
| U-W-9 | 6.4 | 3404 | 743 | 2-a | |||||||
| Ebead (2011) [19] | M-F-D10-1 | 102 | 3.2 | 2200 | 72 | 1003 | Screw | 4.76 | 37 | YES | 2-a |
| M-F-D10-2 | 2200 | 1-a/2-a | |||||||||
| M-F-D12-1 | 2200 | 2-a | |||||||||
| M-F-D12-2 | 2200 | 1-a/2-a | |||||||||
| M-F-D16-1 | 2200 | 2-a | |||||||||
| M-F-D16-2 | 2200 | 1-a/2-a | |||||||||
| M-P-D10-1 | 1350 | 2-a | |||||||||
| M-P-D10-2 | 1350 | 1-a/2-a | |||||||||
| M-P-D12-1 | 1350 | 2-a | |||||||||
| M-P-D12-2 | 1350 | 1-a/2-a | |||||||||
| M-P-D16-1 | 1350 | 2-a | |||||||||
| M-P-D16-2 | 1350 | 1-a/2-a | |||||||||
| Ekenel et al. (2005) [20] | S-4-F | 102 | 3.2 | 1778 | 62 | 531 | Wedge anchor | 9.5 | 40.3 | YES | 1-s |
| El-Maaddawy (2013) [5] | C0-PAF-32 | 102 | 3.2 | 2600 | 62 | 852 | PAF | 4 | 32 | NO | 2-a |
| C0-PAF-52 | PAF | 4 | 52 | NO | 2-a | ||||||
| C0-EAB | Wedge | 8 | 55 | YES | 1-s | ||||||
| C0-TAB | Screw | 8 | 55 | NO | 1-s | ||||||
| C1-PAF-32 | PAF | 4 | 32 | NO | 2-a | ||||||
| C1-PAF-52 | PAF | 4 | 52 | NO | 2-a | ||||||
| C1-EAB | Wedge | 8 | 55 | YES | 1-s | ||||||
| C1-TAB | Screw | 8 | 55 | NO | 1-s | ||||||
| C1-PAF-32 | PAF | 4 | 32 | NO | 2-a | ||||||
| C1-PAF-52 | PAF | 4 | 52 | NO | 2-a | ||||||
| C1-EAB | Wedge | 8 | 55 | YES | 1-s | ||||||
| C1-TAB | Screw | 8 | 55 | NO | 1-s | ||||||
| El-Maaddawy et al. (2013) [21] | C0-F50-32 | 51 | 3.2 | 1050 | 62 | 852 | PAF | 4 | 32 | NO | 1-a |
| C0-F100-32 | 102 | 32 | 1-a | ||||||||
| C0-F100-32-2 | 102 | 32 | 2-a | ||||||||
| C0-F50-52 | 51 | 52 | 1-a | ||||||||
| C0-F100-52 | 102 | 52 | 1-a | ||||||||
| C1-F50-32 | 51 | 32 | 1-a | ||||||||
| C1-F100-32 | 102 | 32 | 1-a | ||||||||
| C1-F100-32-2 | 102 | 32 | 2-a | ||||||||
| C1-F50-52 | 51 | 52 | 1-a | ||||||||
| C1-F100-52 | 102 | 52 | 1-a | ||||||||
| C2-F50-32 | 51 | 32 | 1-a | ||||||||
| C2-F100-32 | 102 | 32 | 1-a | ||||||||
| C2-F100-32-2 | 102 | 32 | 2-a | ||||||||
| C2-F50-52 | 51 | 52 | 1-a | ||||||||
| C2-F100-52 | 102 | 52 | 1-a | ||||||||
| C3-F50-52 | 51 | 52 | 1-a | ||||||||
| C3-F100-52 | 102 | 52 | 1-a | ||||||||
| Galati et al. (2007) [22] | M-F-P-2 | 102 | 3.2 | 2100 | 62 | 835 | Wedge anchor | 12 | 100 | YES | 1-s/2-a |
| Lamanna (2002) [23] | D-1 | 102 | 3.2 | 1117 | 13.8 | 232 | PAF | 4 | 22 | YES | 2-a |
| D-2 | 1117 | 13.8 | 232 | 4 | 22 | 2-a | |||||
| E-1 | 1117 | 13.8 | 232 | 4 | 22 | 2-a | |||||
| E-2 | 1117 | 13.8 | 232 | 4 | 22 | 2-a | |||||
| J-1 | 1117 | 13.8 | 232 | 3.7 | 27 | 1-a | |||||
| L-1 | 1016 | 13.8 | 232 | 4.5 | 32 | 1-a | |||||
| T-1 | 1016 | 13.8 | 232 | 3.7 | 32 | 1-a | |||||
| T-2 | 1016 | 13.8 | 232 | 3.7 | 32 | 1-a | |||||
| T-3 | 1016 | 13.8 | 232 | 3.7 | 32 | 1-a | |||||
| F-1 | 1117 | 13.8 | 232 | 3.7 | 27 | 1-a | |||||
| G-1 | 1117 | 13.8 | 232 | 3.7 | 27 | 2-a | |||||
| K-1 | 1117 | 13.8 | 232 | 3.7 | 32 | 1-a | |||||
| M-1 | 1016 | 13.8 | 232 | 3.7 | 32 | 1-a | |||||
| N-1 | 1016 | 17.0 | 351 | 3.7 | 32 | 1-a | |||||
| P-1 | 6.4 | 1016 | 15.5 | 204 | 3.7 | 27 | 1-a | ||||
| Q-1 | 3.2 | 1016 | 27.3 | 561 | 3.7 | 32 | 1-a | ||||
| R-1 | 1016 | 13.8 | 232 | 3.5 | 27 | 2-a | |||||
| R-2 | 1016 | 13.8 | 232 | 3.5 | 27 | 2-a | |||||
| U-1 | 51 | 1016 | 13.8 | 232 | 3.7 | 32 | 1-a | ||||
| Lamanna et al. (2001) [24] | F-42-S-102-1R | 102 | 3.2 | 1016 | 13.8 | 232 | PAF | 3.5 | 27 | YES | 2-a |
| F-21-S-102-2R | 3.7 | 32 | 1-a | ||||||||
| Bank et al. (2002) Lamanna et al.(2004) [25,26] | S-4-Y-AL32 | 102 | 3.2 | 3048 | 15.2 | 325 | PAF | 4.5 | 32 | YES | 2-a |
| I-4-N-AL32 | 102 | 26.3 | 695 | 32 | 2-a | ||||||
| I-4-Y-AL32 | 102 | 26.3 | 695 | 32 | 2-a | ||||||
| I-4-Y-AL32-R | 102 | 26.3 | 695 | 32 | 2-a | ||||||
| I-8-Y-AL32 | 204 | 26.3 | 695 | 32 | 4-a | ||||||
| H1.5-4-YAL32 | 102 | 57.2 | 828 | 32 | 2-a | ||||||
| H1.5-4-Y-AL42D | 102 | 57.2 | 828 | 42 | 2-a | ||||||
| H1.5-4-Y-AL47D | 102 | 57.2 | 828 | 47 | 2-a | ||||||
| H1.5-4-Y-AL47D-3 | 102 | 57.2 | 828 | 47 | 2-a | ||||||
| H1.5-4-Y-AL47D-3R | 102 | 57.2 | 828 | 47 | 2-a | ||||||
| H1.5-8-Y-AL32 | 102 | 57.2 | 828 | 32 | 4-a | ||||||
| H1.0-4-Y-AL47D-5 | 102 | 56.9 | 916 | 47 | 2-a | ||||||
| Lee et al. (2007) [27] | 1 | 102 | 3.2 | 1370 | 68.3 | 848 | PAF | 3.5 | 25 | YES | 2-a |
| 2 | 102 | 3.2 | 1370 | 68.3 | 848 | PAF | 3.5 | 32 | YES | 2-a | |
| Martin and Lamanna (2008) [28] | 6-L | 102 | 3.2 | 3251 | 57.7 | 805 | Screw | 12.7 | 50.8 | YES | 1-a |
| 6-S | 1-s | ||||||||||
| 10-L | 1-a | ||||||||||
| 12-L | 1-a | ||||||||||
| Napoli et al. (2008) [11] | MF-1-L | 102 | 3.2 | 2718 | 62 | 852 | Screw | 9.5 | 44.5 | NO | 1-s |
| MF-1-S | 2108 | 1-s | |||||||||
| MF-2-L | 2718 | 1-s | |||||||||
| MF-2-S | 2413 | 1-s |
4. Application of the FE Model
- (a)
- uncertainty on the actual mechanical properties of steel rebars and mainly on the fy value, which is not always provided in the literature papers, and the choice of the stress-strain law to use for simulating the response of such rebars;
- (b)
- selection of the bearing stress-slip interface law to model the effect of the partial interaction between concrete and FRP laminate; and
- (c)
- the cracking process in RC members, related to the different tensile response of concrete, which is generally neglected in modeling methods.
4.1. Influence of Mechanical Properties and Stress-Strain Behavior of Steel Rebars

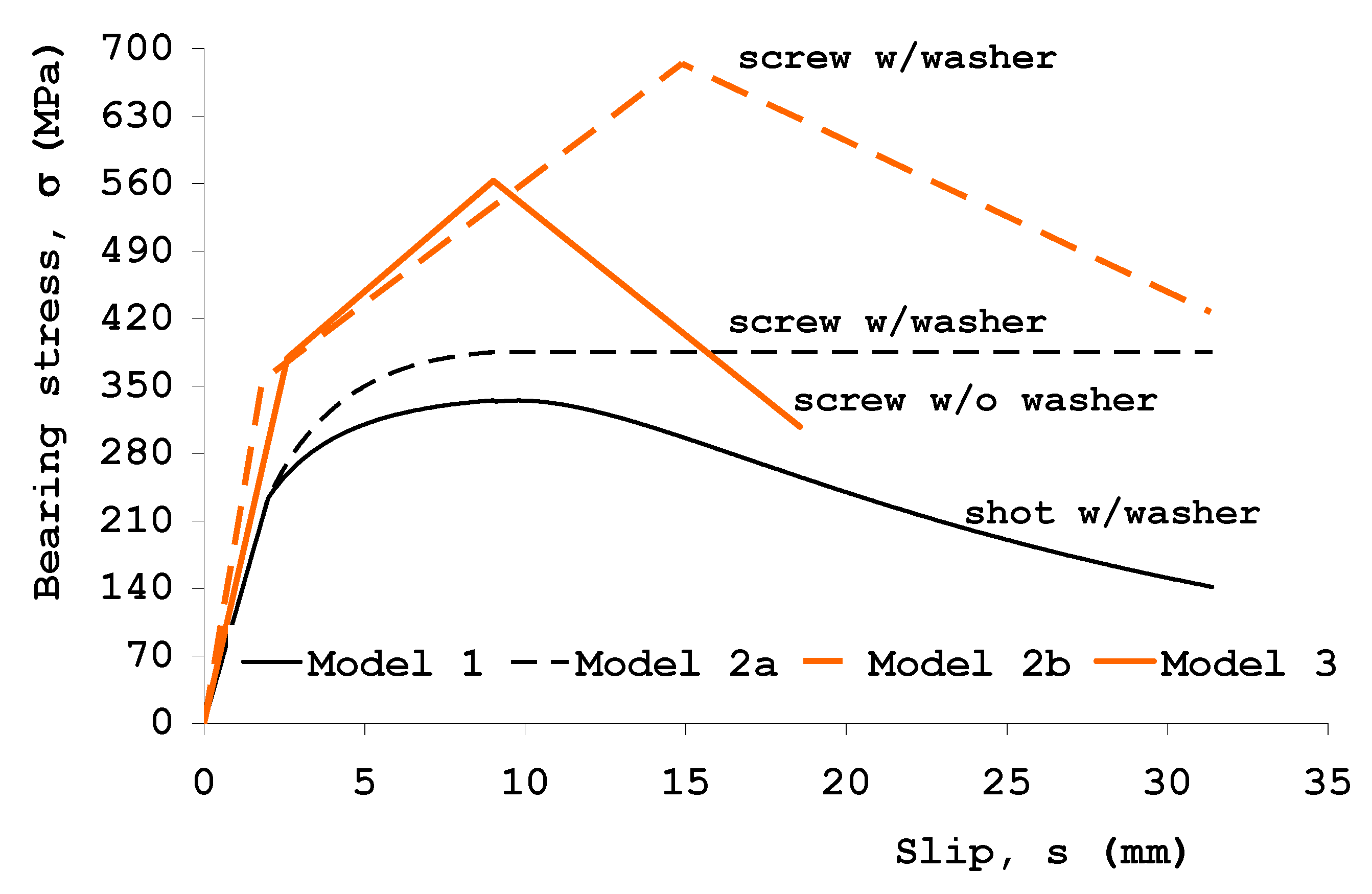
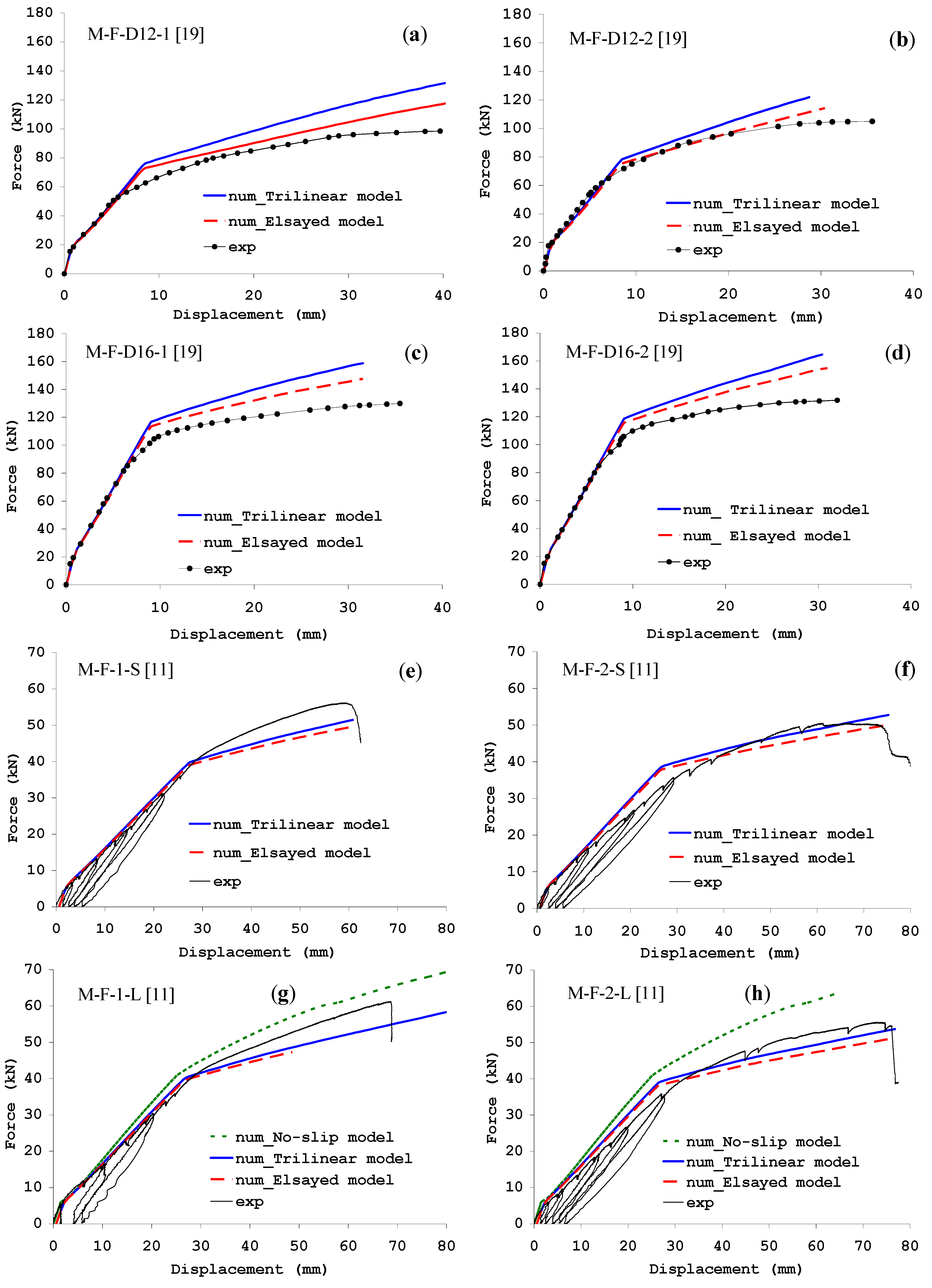
4.2. Influence of the Bearing Stress–Slip Interface Law
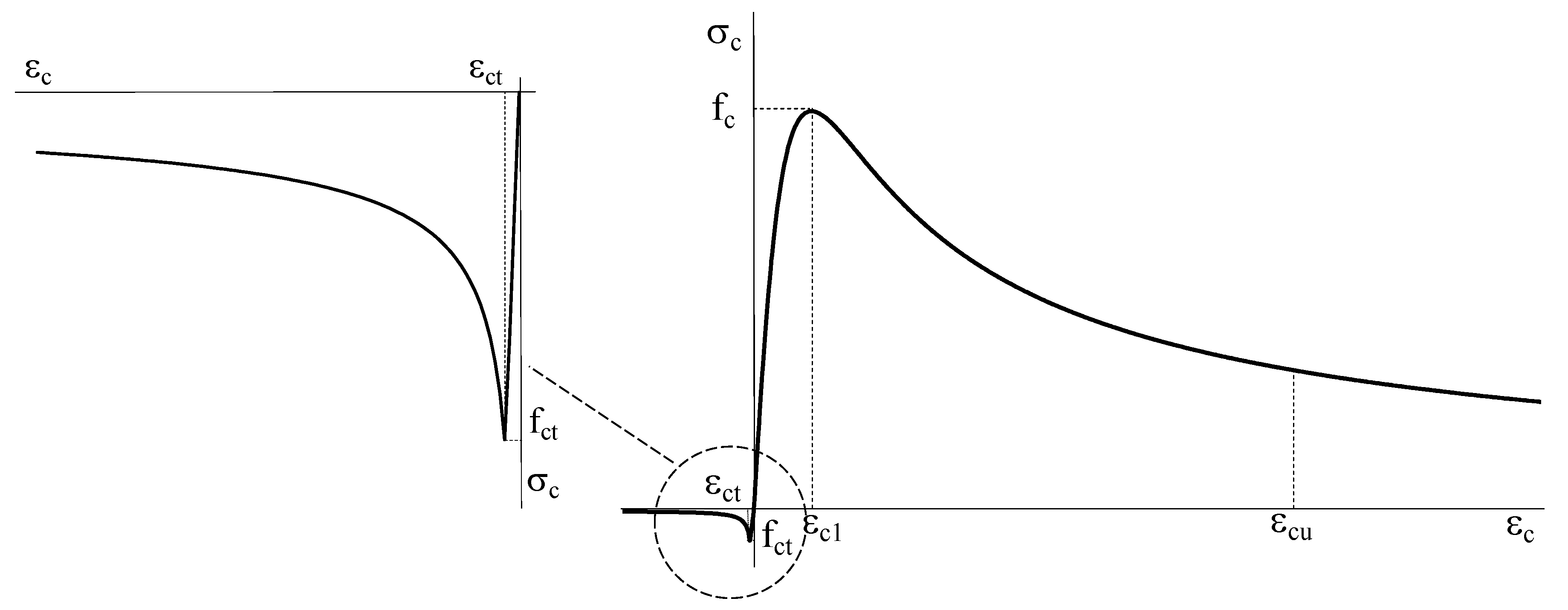
4.3. Influence of the Tension-Stiffening Effect
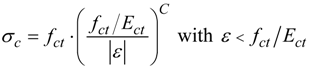
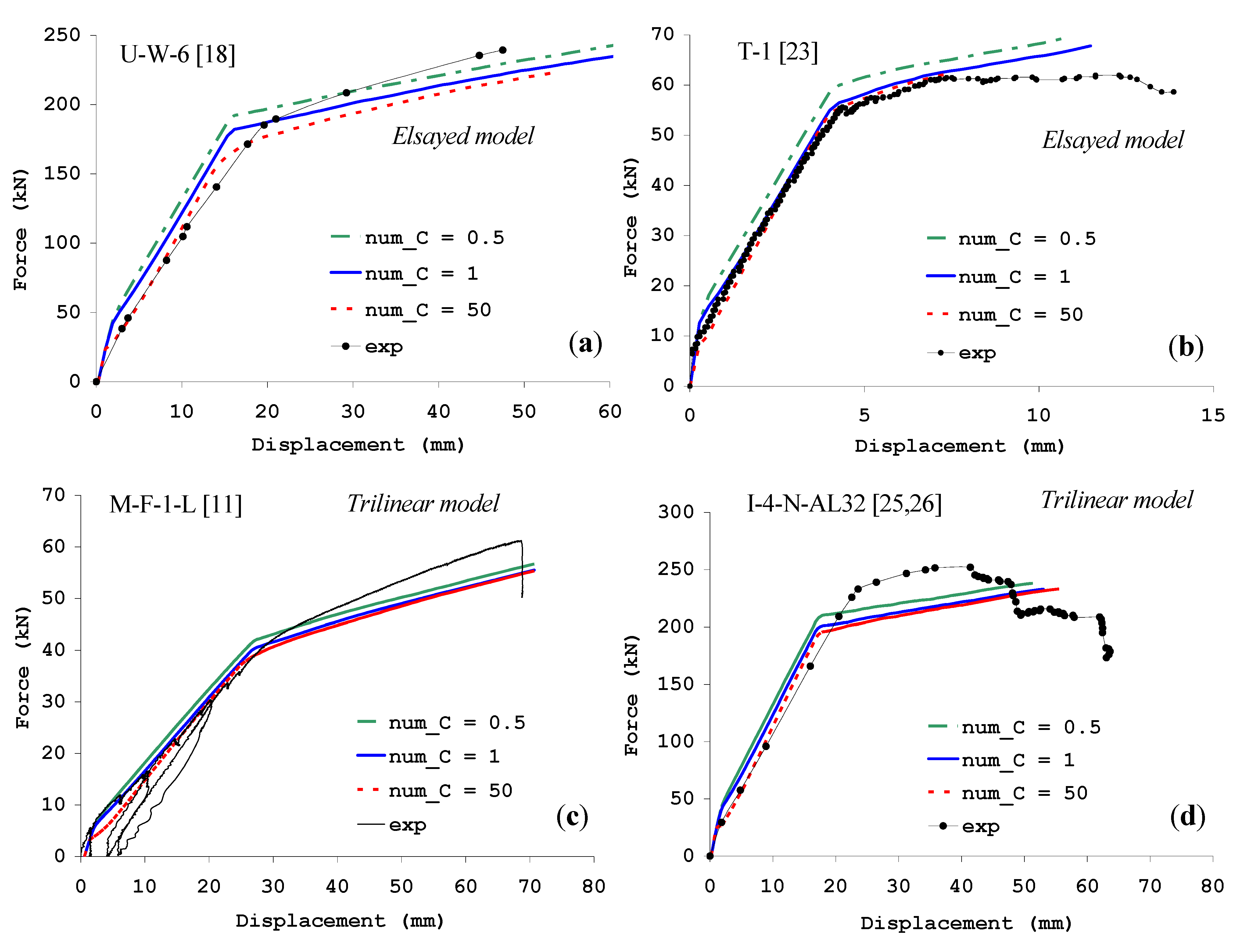
5. Conclusions
- (a)
- as expected, a rather slight dependence of the performed analyses on the stress-strain model used for steel rebars is observed; thus, a simplified elastic-plastic law can be successfully chosen in the simulation of tests;
- (b)
- since small values of interfacial slips are activated in the case of MF-FRP-strengthened beams, the numerical simulations do not significantly change with the use of two different bearing stress-slip relationships, thus implying that both of them are suitable in the modeling of these members;
- (c)
- the use of a lower tension-stiffening effect has an influence on the bending moment of the beam at yielding and provides the most accurate simulations in terms of initial stiffness when shot fasteners are used. In fact, the installation of such a connector type generally induces significant pre-cracking in the concrete, which is well reproduced by a lower contribution of the tension-stiffening effect. For the case of fastening with concrete screws or wedge anchors, instead, the implementation of the tension-stiffening effect with the C exponent equal to one generally provides the most accurate simulation of the experimental results.
Conflicts of Interest
References
- Strongwell. 2010. Available online: http://www.strongwell.com (accessed on 27 January 14).
- Bank, L.C. Mechanically-Fastened FRP (MF-FRP)—A Viable Alternative for Strengthening RC Members. In Proceedings of the FRP Composites in Civil Engineering (CICE 2004), Adelaide, Australia, 8–10 December 2004.
- Rizzo, A.; Galati, N.; Nanni, A.; Bank, L.C. Strengthening Concrete Structures with Mechanically Fastened Pultruded Strips. In Proceedings of the Composites 2005, Columbus, OH, USA, 28–30 September 2005.
- Brown, V.L.; Bank, L.C.; Arora, D.; Borowicz, D.T.; Godat, A.; Lamanna, A.J.; Lee, J.; Matta, F.; Napoli, A.; Tan, K.H. Experimental studies of mechanically-fastened FRP systems: State-of-the-art. In ACI Special Publication SP-275-48, Proceedings of the FRPRCS-10, Tampa Bay, FL, USA, 2–4 April 2011; pp. 841–886.
- El-Maaddawy, T. Mechanically fastened composites for retrofitting corrosion-damaged reinforced-concrete beams: Experimental investigation. J. Compos. Constr. 2013. [Google Scholar] [CrossRef]
- Dempsey, D.D.; Scott, D.W. Wood members strengthened with mechanically fastened FRP strips. J. Compos. Constr. 2006, 10, 392–398. [Google Scholar] [CrossRef]
- Schorer, A.E.; Bank, L.C.; Oliva, M.G.; Wacker, J.P.; Rammer, D.C. Feasibility of Rehabilitating Timber Bridges Using Mechanically Fastened FRP Strips. In Proceedings of the ASCE SEI Structures 2008 Conference, Crossing Borders, Vancouver, BC, Canada, 24–26 April 2008.
- Napoli, A.; Bank, L.C.; Brown, V.L.; Martinelli, E.; Matta, F.; Realfonzo, R. Analysis and design of RC structures strengthened with mechanically fastened FRP laminates: A review. Compos. B Eng. 2013, 55, 386–399. [Google Scholar] [CrossRef]
- Lee, J.H.; Lopez, M.M.; Bakis, C.E. Slip effects in reinforced concrete beams with mechanically fastened FRP strip. Cem. Concr. Compos. 2009, 31, 496–504. [Google Scholar] [CrossRef]
- Nardone, F.; Lignola, G.P.; Prota, A.; Manfredi, G.; Nanni, A. Modeling of flexural behavior of RC beams strengthened with mechanically fastened FRP strips. Compos. Struct. 2011, 93, 1973–1985. [Google Scholar] [CrossRef]
- Napoli, A.; Matta, F.; Martinelli, E.; Nanni, A.; Realfonzo, R. Modelling and verification of response of RC slabs strengthened in flexure with mechanically fastened FRP laminates. Mag. Concr. Res. 2010, 62, 593–605. [Google Scholar] [CrossRef]
- Martinelli, E.; Napoli, A.; Nunziata, B.; Realfonzo, R. A 1D finite element model for the flexural behaviour of RC beams strengthened with MF-FRP strips. Compos. Struct. 2014, 107, 190–204. [Google Scholar] [CrossRef]
- Faella, C.; Martinelli, E.; Nigro, E. Formulation and validation of a theoretical model for intermediate debonding in FRP strengthened RC beams. Compos. B Eng. 2008, 39, 645–655. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress strain curve for concrete. Cem. Concr. Res. 1973, 3, 583–559. [Google Scholar] [CrossRef]
- Okamura, H.; Maekawa, K.; Sivasubramaniyam, S. Verification of Modeling for Reinforced Concrete Finite Element. In Finite Element Analysis of Reinforced Concrete Structures, Proceedings of the Seminar ASCE, Tokyo, Japan, 21–24 May 1985; pp. 528–543.
- Realfonzo, R.; Martinelli, E.; Napoli, A.; Nunziata, B. Experimental investigation of the mechanical connection between FRP laminates and concrete. Compos. B: Eng. 2013, 45, 341–355. [Google Scholar] [CrossRef]
- Elsayed, W.E.; Ebead, U.A.; Neale, K.W. Studies on mechanically fastened fiber-reinforced polymer strengthening systems. ACI Struct. J. 2009, 106, 49–59. [Google Scholar]
- Borowicz, D.T. Rapid Strengthening of Concrete Beams with Powder-Actuated Fastening Systems and Fiber Reinforced Polymer (FRP) Composite Materials. MSc Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2002. [Google Scholar]
- Ebead, U. Hybrid externally bonded/mechanically fastened fiber-reinforced polymer for RC beam strengthening. ACI Struct. J. 2011, 108, 669–678. [Google Scholar]
- Ekenel, M.; Rizzo, A.; Myers, J.J.; Nanni, A. Flexural fatigue behavior of reiforced concrete beams strengthened with FRP fabric and precured laminate systems. J. Comp. Constr. 2006, 10, 433–442. [Google Scholar] [CrossRef]
- El-Maaddawy, T.; Nessabi, A.; El-Dieb, A. Flexural response of corroded reinforced concrete beams strengthened with powder-actuated fastened composites. J. Compos. Constr. 2013. [Google Scholar] [CrossRef]
- Galati, D.; Rizzo, A.; Micelli, F. Comparison of reinforced concrete beams strengthened with FRP pre-cured laminate systems and tested under flexural loading. In Proceedings of the FRPRCS-8, Patras, Greece, 16–18 July 2007.
- Lamanna, A.J. Flexural Strengthening of Reinforced Concrete Beams with Mechanically Fastened Fiber Reinforced Polymer Strips. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2002. [Google Scholar]
- Lamanna, A.J.; Bank, L.C.; Scott, D.W. Flexural strengthening of reinforced concrete beams using fasteners and fiber-reinforced polymer strips. ACI Struct. J. 2001, 98, 368–376. [Google Scholar]
- Bank, L.C.; Lamanna, A.J.; Ray, J.C.; Velazquez, G.I. Rapid Strengthening of Reinforced Concrete Beams with Mechanically Fastened, Fiber Reinforced Polymeric Composites Materials; Report ERDC/GSL TR-02-4; US Army Corps of Engineers: Madison, WI, USA, 2002; pp. 1–99. [Google Scholar]
- Lamanna, A.J.; Bank, L.C.; Scott, D.W. Flexural strengthening of reinforced concrete beams by mechanically attaching fiber-reinforced polymer strips. J. Compos. Constr. 2004, 8, 203–210. [Google Scholar] [CrossRef]
- Lee, H.L.; Lopez, M.M.; Bakis, C.E. Flexural behavior of reinforced concrete beams strengthened with mechanically fastened FRP strip. In Proceedings of the FRPRCS-8, Patras, Greece, 16–18 July 2007.
- Martin, J.A.; Lamanna, A.J. Performance of mechanically fastened FRP strengthened concrete beams in flexure. J. Compos. Constr. 2008, 12, 257–265. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Martinelli, E.; Napoli, A.; Nunziata, B.; Realfonzo, R. RC Beams Strengthened with Mechanically Fastened Composites: Experimental Results and Numerical Modeling. Polymers 2014, 6, 613-633. https://doi.org/10.3390/polym6030613
Martinelli E, Napoli A, Nunziata B, Realfonzo R. RC Beams Strengthened with Mechanically Fastened Composites: Experimental Results and Numerical Modeling. Polymers. 2014; 6(3):613-633. https://doi.org/10.3390/polym6030613
Chicago/Turabian StyleMartinelli, Enzo, Annalisa Napoli, Bruno Nunziata, and Roberto Realfonzo. 2014. "RC Beams Strengthened with Mechanically Fastened Composites: Experimental Results and Numerical Modeling" Polymers 6, no. 3: 613-633. https://doi.org/10.3390/polym6030613





