The Effect of Heat Transfer and Polymer Concentration on Non-Newtonian Fluid from Pore-Scale Simulation of Rock X-ray Micro-CT
Abstract
:1. Introduction
2. Pore-Scale Governing Equations
2.1. Mass and Momentum Conservations
2.2. Energy Conservation
2.3. Temperature-Concentration Power-Law Viscosity Model
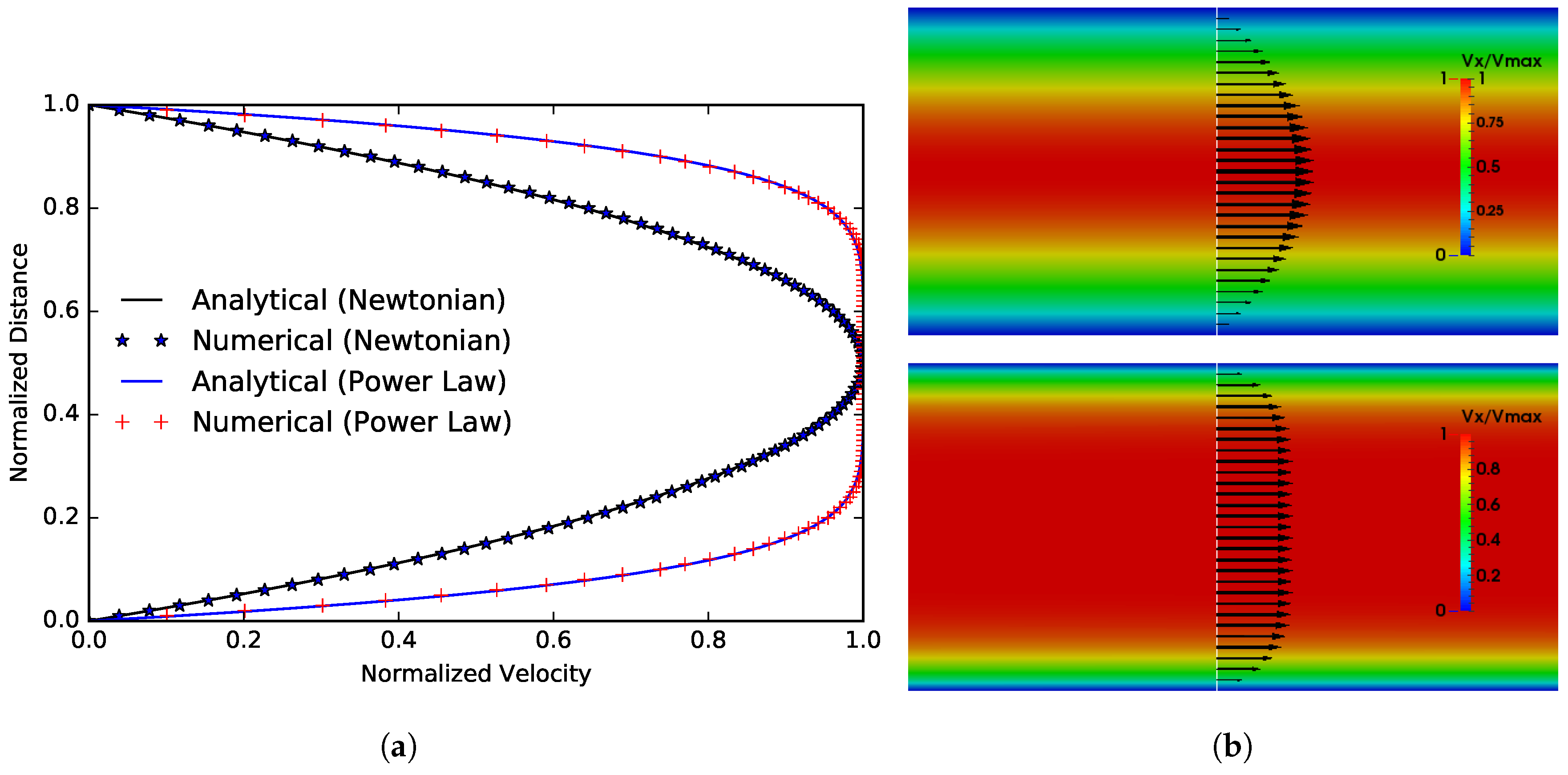
3. Numerical Approach and Validation
3.1. Flow between Two Parallel Plates
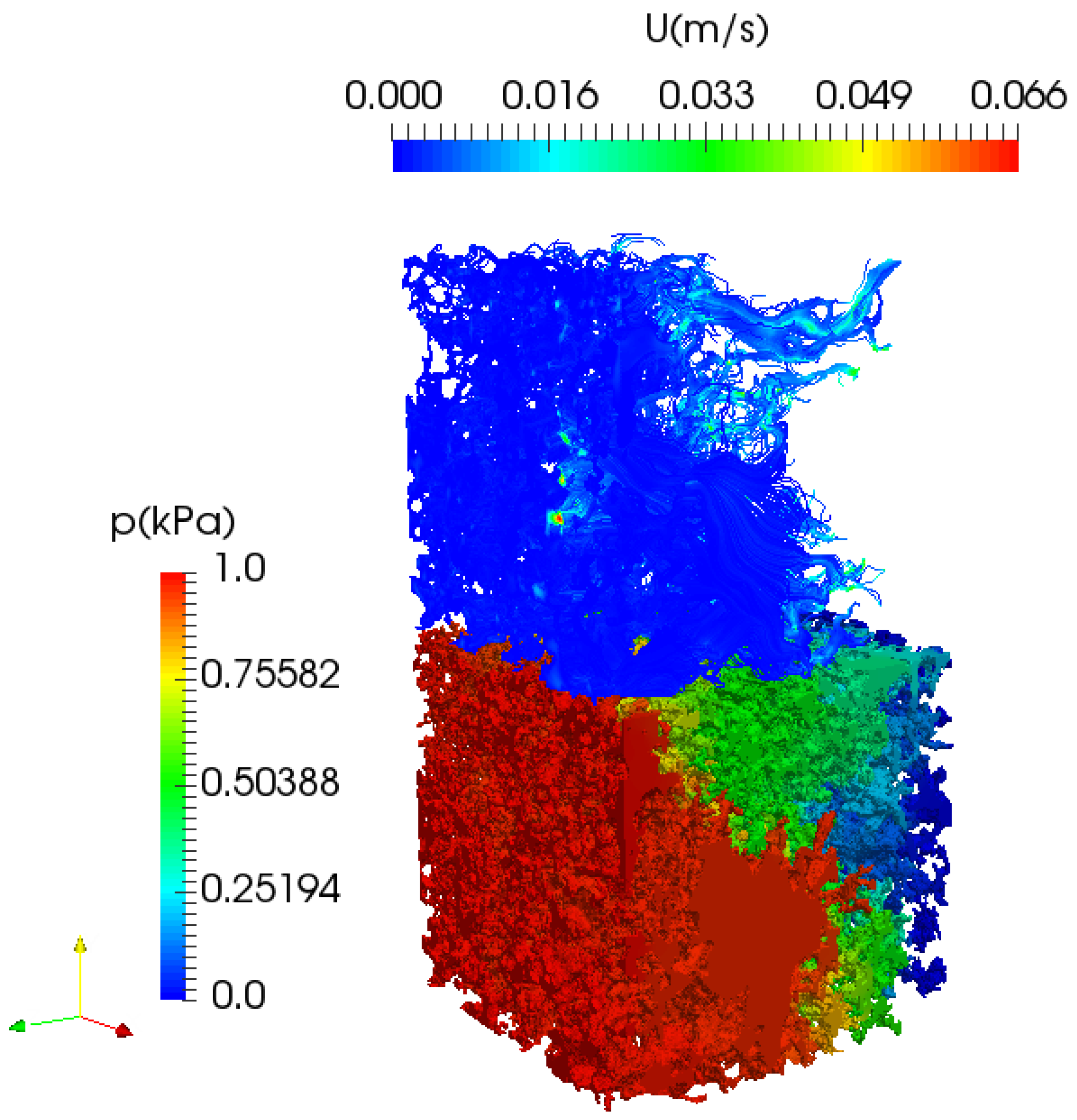
3.2. Flow in Porous Media
4. Pore-Scale Non-Newtonian and Non-Isothermal Fluid Flow Simulation
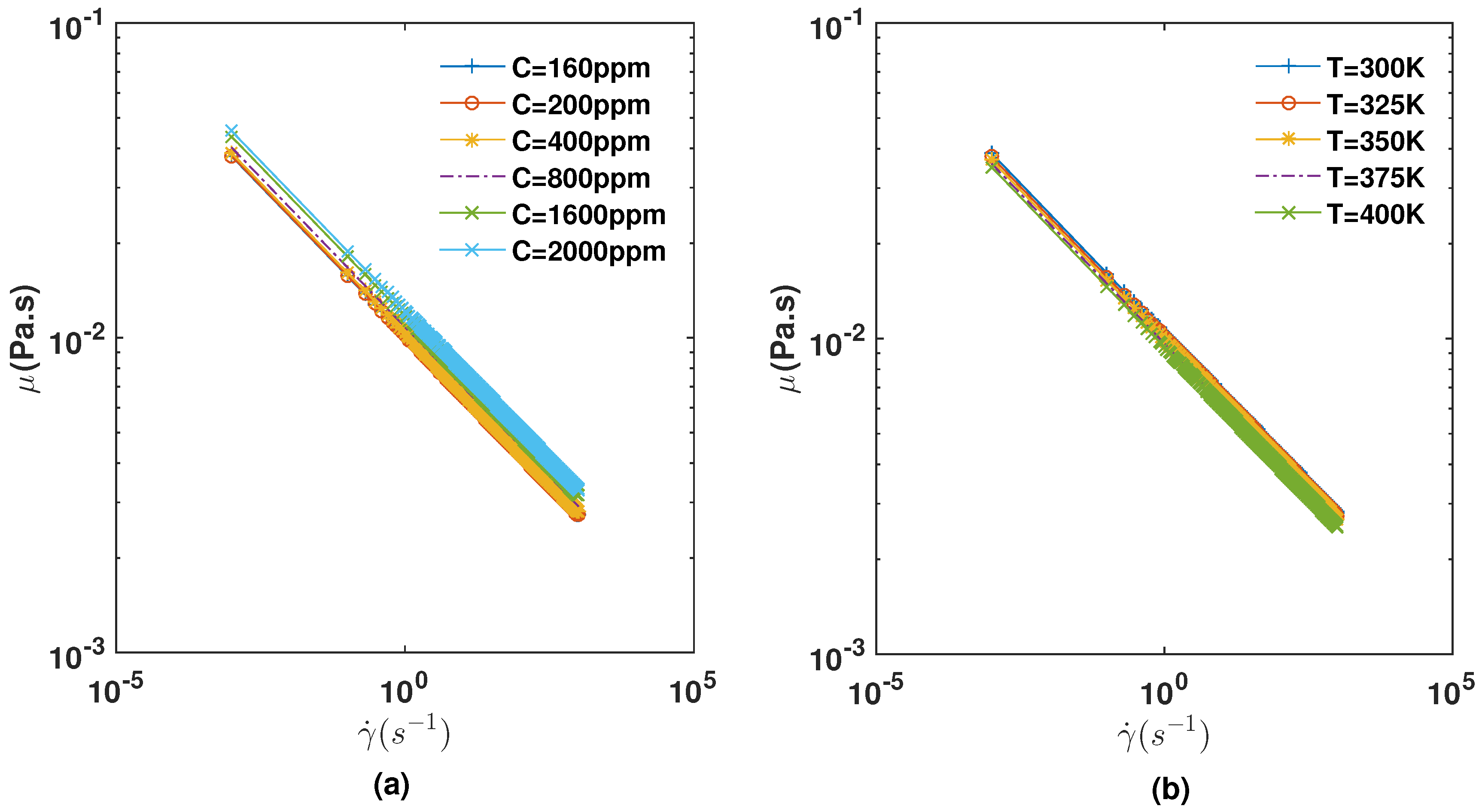
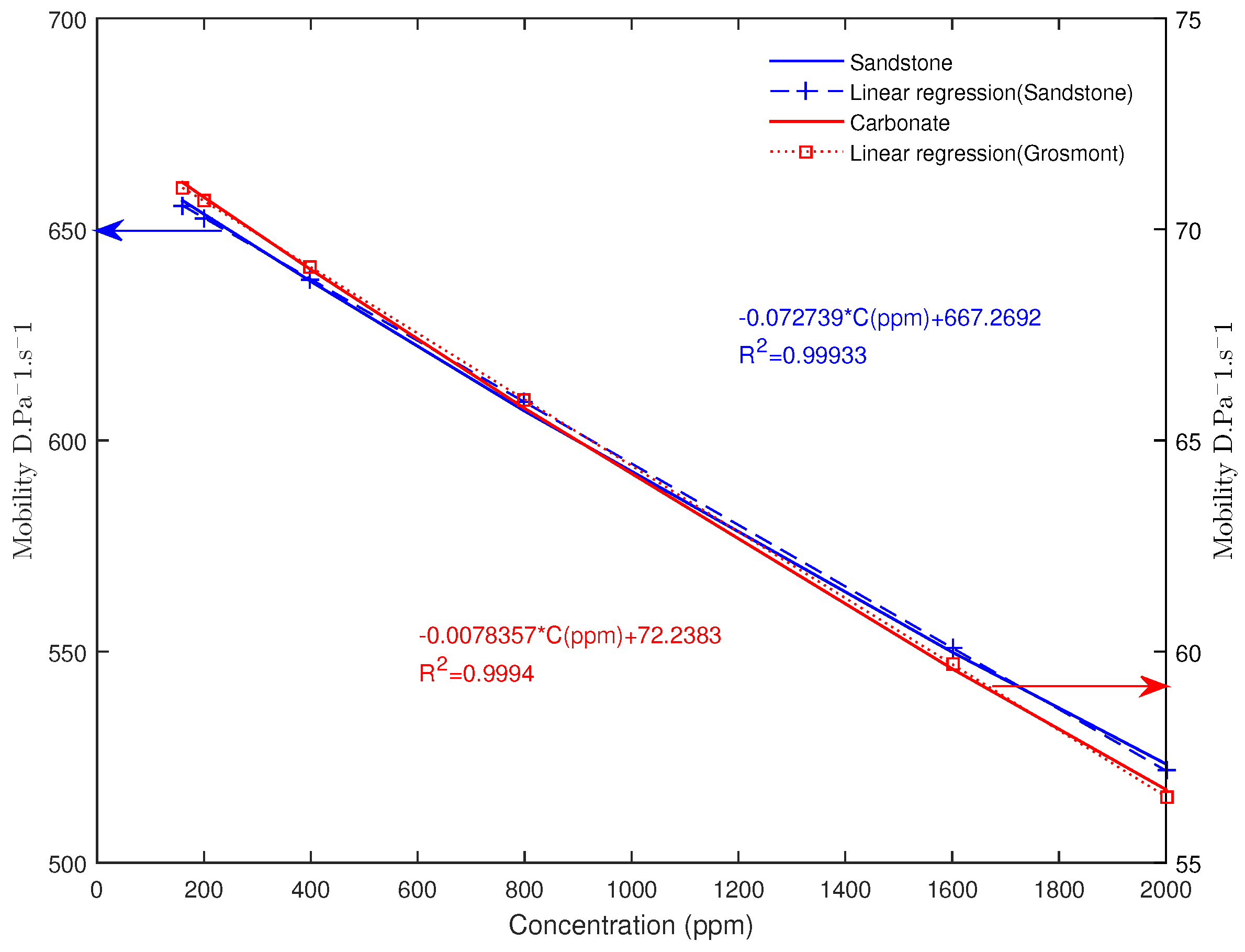
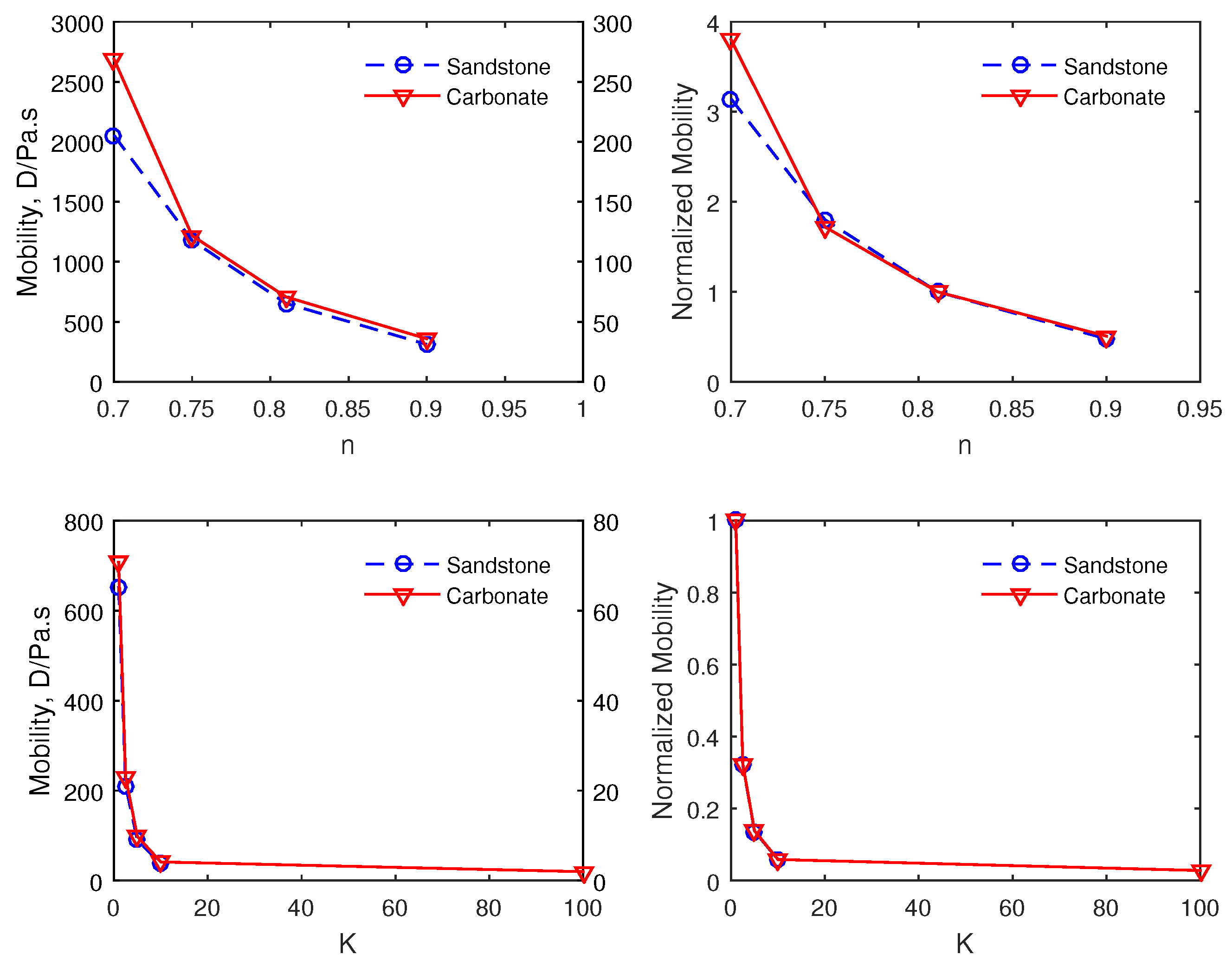
4.1. Effect of the Polymer Concentration on the Mobility
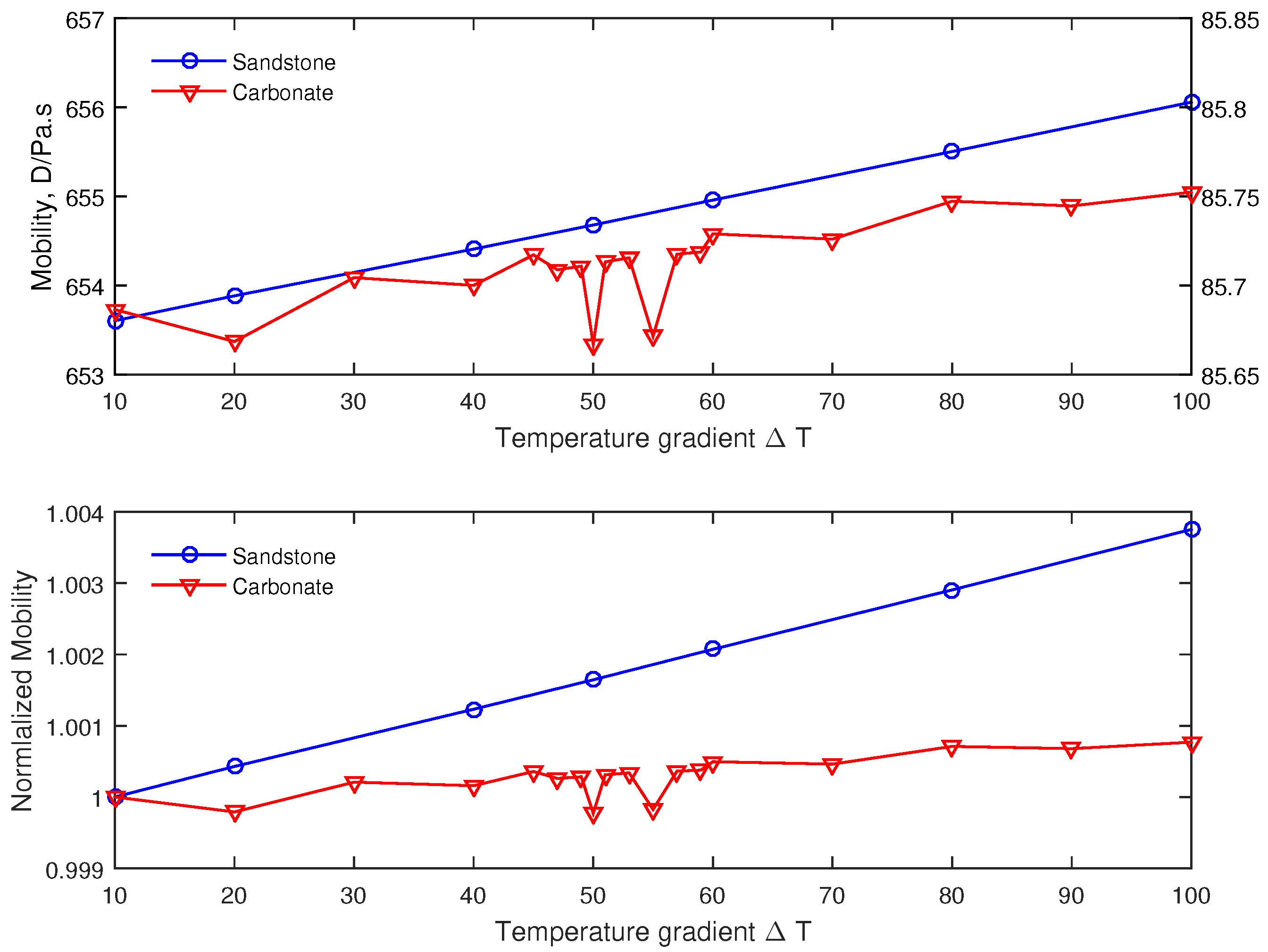
4.2. Effect of Temperature Gradient on the Mobility
4.3. Effect of the Fluid Rheological Parameters on the Mobility
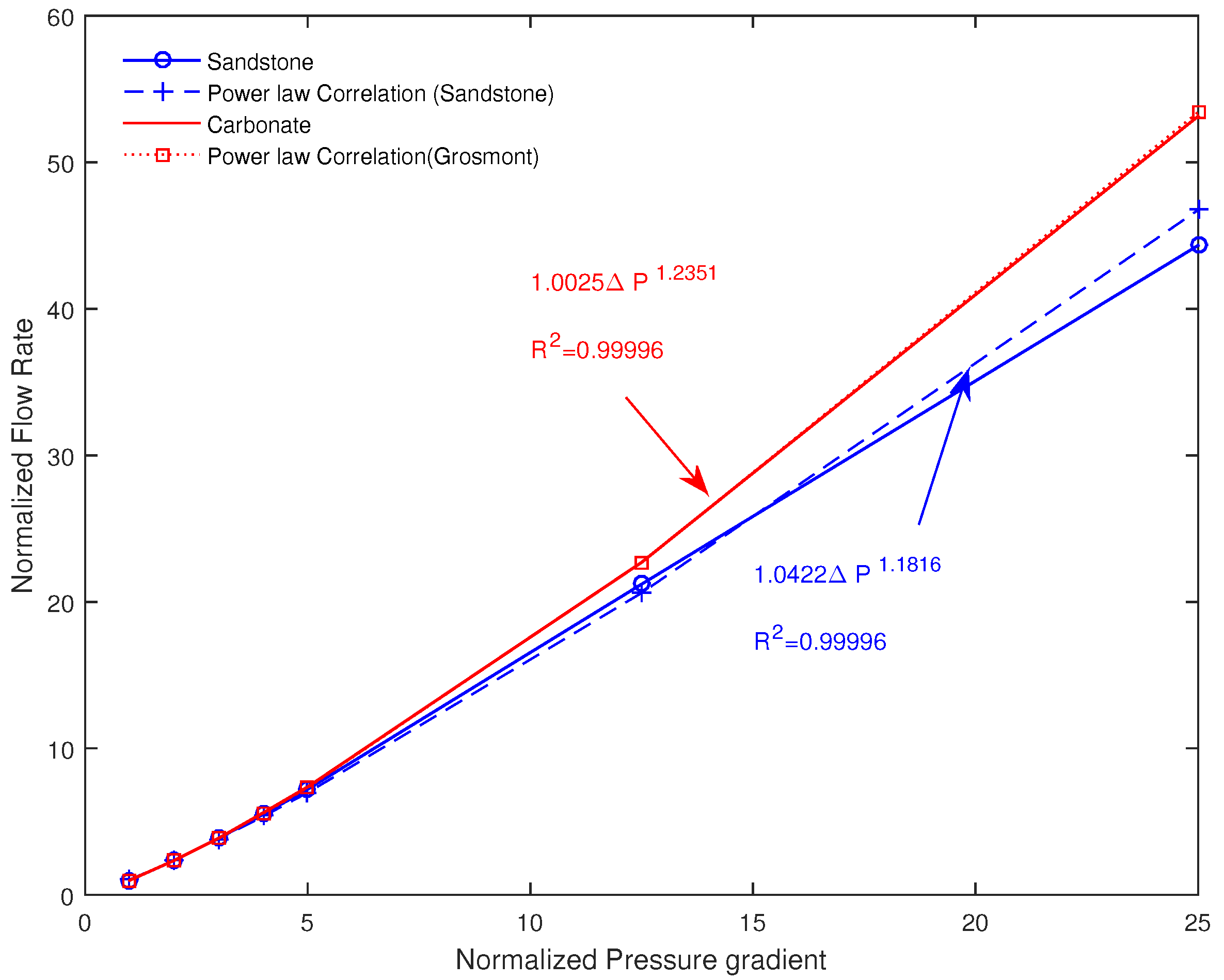
4.4. Effect of the Pressure Gradient
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef]
- Jouini, M.S.; Vega, S.; Al-Ratrout, A. Numerical estimation of carbonate rock properties using multiscale images. Geophys. Prospect. 2015, 63, 405–421. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C.; et al. Digital rock physics benchmarks-part II: Computing effective properties. Comput. Geosci. 2013, 50, 33–43. [Google Scholar] [CrossRef]
- Guibert, R.; Nazarova, M.; Horgue, P.; Hamon, G.; Creux, P.; Debenest, G. Computational Permeability Determination from Pore-Scale Imaging: Sample Size, Mesh and Method Sensitivities. Transp. Porous Media 2015, 107, 641–656. [Google Scholar] [CrossRef] [Green Version]
- Mostaghimi, P.; Blunt, M.J.; Bijeljic, B. Computations of Absolute Permeability on Micro-CT Images. Math. Geosci. 2013, 45, 103–125. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Z.; Shen, J.; Liu, W. Lattice Boltzmann simulation of effective thermal conductivity of porous media with multiphase. J. Porous Media 2015, 18, 929–939. [Google Scholar] [CrossRef]
- Sochi, T. Non-Newtonian flow in porous media. Polymer 2010, 51, 5007–5023. [Google Scholar] [CrossRef]
- Fayed, H.E.; Sheikh, N.A.; Iliev, O. On Laminar Flow of Non-Newtonian Fluids in Porous Media. Transp. Porous Media 2016, 111, 253–264. [Google Scholar] [CrossRef]
- Celli, M.; Barletta, A.; Longo, S.; Chiapponi, L.; Ciriello, V.; Di Federico, V.; Valiani, A. Thermal Instability of a Power-Law Fluid Flowing in a Horizontal Porous Layer with an Open Boundary: A Two-Dimensional Analysis. Transp. Porous Media 2017, 118, 449–471. [Google Scholar] [CrossRef]
- Tembely, M.; Vadillo, D.; Mackley, M.R.; Soucemarianadin, A. The matching of a “one-dimensional” numerical simulation and experiment results for low viscosity Newtonian and non-Newtonian fluids during fast filament stretching and subsequent break-up. J. Rheol. 2012, 56, 159–183. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Kuznetsov, A.V. Flow in a Curved Porous Channel with a Rectangular Cross Section. J. Porous Media 2008, 11, 241–246. [Google Scholar]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Longo, S.; DiFederico, V. Unsteady Flow of Shear-Thinning Fluids in Porous Media with Pressure-Dependent Properties. Transp. Porous Media 2015, 110, 429–447. [Google Scholar] [CrossRef]
- Longo, S.; Di Federico, V.; Chiapponi, L.; Archetti, R. Experimental verification of power-law non-Newtonian axisymmetric porous gravity currents. J. Fluid Mech. 2013, 731. [Google Scholar] [CrossRef]
- Di Federico, V. Estimates of equivalent aperture for non-Newtonian flow in a rough-walled fracture. J. Rock Mech. Min. Sci. 1997, 34, 1133–1137. [Google Scholar] [CrossRef]
- Lavrov, A. Numerical modeling of steady-state flow of a non-Newtonian power-law fluid in a rough-walled fracture. Comput. Geotech. 2013, 50, 101–109. [Google Scholar] [CrossRef]
- Lavrov, A. Radial Flow of Non-Newtonian Power-Law Fluid in a Rough-Walled Fracture: Effect of Fluid Rheology. Transp. Porous Media 2014, 105, 559–570. [Google Scholar] [CrossRef]
- Nowak, Z.; Gryglaszewski, P.; Stacharska-Targosz, J. Laminar heat transfer to power law fluids in flat gaps with various thermal wall conditions. Acta Mech. 1982, 44, 223–236. [Google Scholar] [CrossRef]
- Di Federico, V.; Longo, S.; King, S.E.; Chiapponi, L.; Petrolo, D.; Ciriello, V. Gravity-driven flow of Herschel–Bulkley fluid in a fracture and in a 2D porous medium. J. Fluid Mech. 2017, 821, 59–84. [Google Scholar] [CrossRef]
- Lake, L.W. Enhanced Oil Recovery; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Katime, I.; Ochoa, J.R. Viscosity–temperature relationships for dilute solutions of poly(cyclohexyl methacrylate) in methyl isobutyl ketone. J. Appl. Polym. Sci. 1984, 29, 4427–4431. [Google Scholar]
- Van Velzen, D.; Cardozo, R.L.; Langenkamp, H. A Liquid Viscosity-Temperature-Chemical Constitution Relation for Organic Compounds. Ind. Eng. Chem. Fundam. 1972, 11, 20–25. [Google Scholar] [CrossRef]
- Quadri, S.M.R.; Shoaib, M.; AlSumaiti, A.M.; Alhassan, S. Screening of Polymers for EOR in High Temperature, High Salinity and Carbonate Reservoir Conditions. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 6–9 December 2015. [Google Scholar]
- Pancharoen, M. Physical Properties of Associative Polymer Solutions. Master’s Thesis, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Madonna, C.; Almqvist, B.S.; Saenger, E.H. Digital rock physics: numerical prediction of pressure-dependent ultrasonic velocities using micro-CT imaging. Geophys. J. Int. 2012, 189, 1475–1482. [Google Scholar] [CrossRef]
- Di Federico, V.; Pinelli, M.; Ugarelli, R. Estimates of effective permeability for non-Newtonian fluid flow in randomly heterogeneous porous media. Stoch. Environ. Res. Risk Assess. 2010, 24, 1067–1076. [Google Scholar] [CrossRef]
- Pascal, H. Nonsteady flow of non-Newtonian fluids through a porous medium. Int. J. Eng. Sci. 1983, 21, 199–210. [Google Scholar]
- Bourgeat, A.; Mikelić, A. Homogenization of a polymer flow through a porous medium. Nonlinear Anal. Theory Methods Appl. 1996, 26, 1221–1253. [Google Scholar] [CrossRef]
- Chevalier, T.; Chevalier, C.; Clain, X.; Dupla, J.; Canou, J.; Rodts, S.; Coussot, P. Darcy’s law for yield stress fluid flowing through a porous medium. J. Non-Newton. Fluid Mech. 2013, 195, 57–66. [Google Scholar] [CrossRef]




| Parameters | (Pa s) | (-) | (K) | Tref (K) | n (-) |
|---|---|---|---|---|---|
| Values (SI) | 10 | 100 | 10 | 293 | 0.81 |
| Boundaries | Pressures | Velocity | Temperature |
|---|---|---|---|
| Inlet | fixed value, P = 1000 Pa | normal gradient, = 0 | fixed value, T |
| Outlet | fixes value, P = 0 Pa | normal gradient, = 0 | fixes value, T = 300 K |
| Sides | normal gradient, = 0 | fixed valued, V = 0 | normal gradient, = 0 |
| Pore/rock interface | normal gradient, = 0 | No-slip, V = 0 | normal gradient, = 0 |
| Sample | Image Size | Voxel Size (m) | Porosity (%) | FVM (mD) | LBM (mD) | Relative Errors (%) |
|---|---|---|---|---|---|---|
| Fontainebleau Sandstone | × 300 | 7.5 | 14.5 | 1614 | 1610 | 0.2 |
| Grosmont Carbonate | × 400 | 2.02 | 24.7 | 217 | 214 | 1.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tembely, M.; AlSumaiti, A.M.; Jouini, M.S.; Rahimov, K. The Effect of Heat Transfer and Polymer Concentration on Non-Newtonian Fluid from Pore-Scale Simulation of Rock X-ray Micro-CT. Polymers 2017, 9, 509. https://doi.org/10.3390/polym9100509
Tembely M, AlSumaiti AM, Jouini MS, Rahimov K. The Effect of Heat Transfer and Polymer Concentration on Non-Newtonian Fluid from Pore-Scale Simulation of Rock X-ray Micro-CT. Polymers. 2017; 9(10):509. https://doi.org/10.3390/polym9100509
Chicago/Turabian StyleTembely, Moussa, Ali M. AlSumaiti, Mohamed S. Jouini, and Khurshed Rahimov. 2017. "The Effect of Heat Transfer and Polymer Concentration on Non-Newtonian Fluid from Pore-Scale Simulation of Rock X-ray Micro-CT" Polymers 9, no. 10: 509. https://doi.org/10.3390/polym9100509
APA StyleTembely, M., AlSumaiti, A. M., Jouini, M. S., & Rahimov, K. (2017). The Effect of Heat Transfer and Polymer Concentration on Non-Newtonian Fluid from Pore-Scale Simulation of Rock X-ray Micro-CT. Polymers, 9(10), 509. https://doi.org/10.3390/polym9100509





