Predicting Soil Textural Classes Using Random Forest Models: Learning from Imbalanced Dataset
Abstract
:1. Introduction
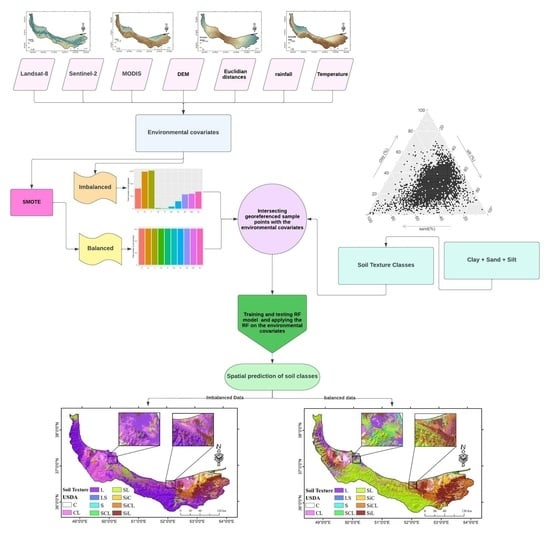
2. Materials and Methods
2.1. Study Area
2.2. Soil Data
2.3. Balanced Data
2.4. Environmental Covariates
2.5. Machine Learning
2.6. Accuracy Assessment
3. Results and Discussion
3.1. Balanced and Imbalanced Datasets
3.2. Accuracy Assessment
3.3. Covariate Importance
3.4. Predicted Maps
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yolcubal, I.; Brusseau, M.L.; Artiola, J.F.; Wierenga, P.; Wilson, L.G. Environmental Physical Properties and Processes. In Environmental Monitoring and Characterization; Elsevier: Amsterdam, The Netherlands, 2004; pp. 207–239. ISBN 978-0-12-064477-3. [Google Scholar]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; NRCS-USDA: Washington, DC, USA, 2014. [Google Scholar]
- USDA. USDA. USDA Textural Soil Classification. In Soil Mechanics Level I Module 3; United States Department of Agriculture, National Employee Staff, Soil Conservation Service: Washington, DC, USA, 1987. [Google Scholar]
- Borrelli, P.; Paustian, K.; Panagos, P.; Jones, A.; Schütt, B.; Lugato, E. Effect of Good Agricultural and Environmental Conditions on Erosion and Soil Organic Carbon Balance: A National Case Study. Land Use Policy 2016, 50, 408–421. [Google Scholar] [CrossRef]
- Gomes, L.C.; Faria, R.M.; de Souza, E.; Veloso, G.V.; Schaefer, C.E.G.R.; Filho, E.I.F. Modelling and Mapping Soil Organic Carbon Stocks in Brazil. Geoderma 2019, 340, 337–350. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, G.-L.; Song, X.; Li, D.; Zhao, Y.; Yang, J.; Wu, H.; Yang, F. High-Resolution and Three-Dimensional Mapping of Soil Texture of China. Geoderma 2020, 361, 114061. [Google Scholar] [CrossRef]
- Hengl, B.D.; Heuvelink, T.; Kempen, G.; Mulder, B.; Olmedo, T.; Poggio, G.; Ribeiro, L.; Thine, E.; Omuto, C.; Yigini, Y. Soil Organic Carbon Mapping Cookbook; FAO: Rome, Italy, 2017; p. 180. [Google Scholar]
- Mahmoudzadeh, H.; Matinfar, H.R.; Taghizadeh-Mehrjardi, R.; Kerry, R. Spatial Prediction of Soil Organic Carbon Using Machine Learning Techniques in Western Iran. Geoderma Reg. 2020, 21, e00260. [Google Scholar] [CrossRef]
- Arrouays, D.; Grundy, M.G.; Hartemink, A.E.; Hempel, J.W.; Heuvelink, G.B.M.; Hong, S.Y.; Lagacherie, P.; Lelyk, G.; McBratney, A.B.; McKenzie, N.J.; et al. GlobalSoilMap. In Advances in Agronomy; Elsevier: Amsterdam, The Netherlands, 2014; Volume 125, pp. 93–134. ISBN 978-0-12-800137-0. [Google Scholar]
- Adhikari, K.; Kheir, R.B.; Greve, M.B.; Bøcher, P.K.; Malone, B.P.; Minasny, B.; McBratney, A.B.; Greve, M.H. High-Resolution 3-D Mapping of Soil Texture in Denmark. Soil Sci. Soc. Am. J. 2013, 77, 860–876. [Google Scholar] [CrossRef]
- ViscarraRossel, R.A.; Chen, C.; Grundy, M.J.; Searle, R.; Clifford, D.; Campbell, P.H. The Australian Three-Dimensional Soil Grid: Australia’s Contribution to the GlobalSoilMap Project. Soil Res. 2015, 53, 845. [Google Scholar] [CrossRef] [Green Version]
- Mulder, V.L.; Lacoste, M.; Richer-de-Forges, A.C.; Arrouays, D. GlobalSoilMap France: High-Resolution Spatial Modelling the Soils of France up to Two Meter Depth. Sci. Total Environ. 2016, 573, 1352–1369. [Google Scholar] [CrossRef]
- Padarian, J.; Minasny, B.; McBratney, A.B. Chile and the Chilean Soil Grid: A Contribution to GlobalSoilMap. Geoderma Reg. 2017, 9, 17–28. [Google Scholar] [CrossRef]
- Ramcharan, A.; Hengl, T.; Nauman, T.; Brungard, C.; Waltman, S.; Wills, S.; Thompson, J. Soil Property and Class Maps of the Conterminous United States at 100-Meter Spatial Resolution. Soil Sci. Soc. Am. J. 2018, 82, 186–201. [Google Scholar] [CrossRef] [Green Version]
- Tóth, B.; Weynants, M.; Nemes, A.; Makó, A.; Bilas, G.; Tóth, G. New Generation of Hydraulic Pedotransfer Functions for Europe: New Hydraulic Pedotransfer Functions for Europe. Eur. J. Soil Sci. 2015, 66, 226–238. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Li, M.; Wijewardane, N.K.; Ge, Y.; Xu, Z.; Wilkins, M.R. Visible/near Infrared Spectroscopy and Machine Learning for Predicting Polyhydroxybutyrate Production Cultured on Alkaline Pretreated Liquor from Corn Stover. Bioresour. Technol. Rep. 2020, 9, 100386. [Google Scholar] [CrossRef]
- Hamel, Z.; Ababou, A.; Saidi, D.; Kemassi, A. Evaluation of Soil Aggregate Stability in Algerian Northwestern Soils Using Pedotransfer Functions and Artificial Neural Networks. Acta Ecol. Sin. 2021, 41, 235–242. [Google Scholar] [CrossRef]
- Singh, G.; Panda, R.K.; Bisht, D.S. Improved Generalized Calibration of an Impedance Probe for Soil Moisture Measurement at Regional Scale Using Bayesian Neural Network and Soil Physical Properties. J. Hydrol. Eng. 2021, 26, 04020068. [Google Scholar] [CrossRef]
- Elbisy, M.S. Support Vector Machine and Regression Analysis to Predict the Field Hydraulic Conductivity of Sandy Soil. KSCE J. Civ. Eng. 2015, 19, 2307–2316. [Google Scholar] [CrossRef]
- Sihag, P.; Tiwari, N.K.; Ranjan, S. Support Vector Regression-Based Modeling of Cumulative Infiltration of Sandy Soil. ISHJ. Hydraul. Eng. 2018, 26, 1–7. [Google Scholar] [CrossRef]
- Kovačević, M.; Bajat, B.; Gajić, B. Soil Type Classification and Estimation of Soil Properties Using Support Vector Machines. Geoderma 2010, 154, 340–347. [Google Scholar] [CrossRef]
- Barman, U.; Choudhury, R.D. Soil Texture Classification Using Multi Class Support Vector Machine. Inf. Process. Agric. 2020, 7, 318–332. [Google Scholar] [CrossRef]
- Martin, M.P.; Lo Seen, D.; Boulonne, L.; Jolivet, C.; Nair, K.M.; Bourgeon, G.; Arrouays, D. Optimizing Pedotransfer Functions for Estimating Soil Bulk Density Using Boosted Regression Trees. Soil Sci. Soc. Am. J. 2009, 73, 485–493. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a Generic Framework for Predictive Modeling of Spatial and Spatio-Temporal Variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef]
- Dharumarajan, S.; Hegde, R. Digital Mapping of Soil Texture Classes Using Random Forest Classification Algorithm. Soil Use Manag. 2022, 38, 135–149. [Google Scholar] [CrossRef]
- Szabó, B.; Szatmári, G.; Takács, K.; Laborczi, A.; Makó, A.; Rajkai, K.; Pásztor, L. Mapping Soil Hydraulic Properties Using Random-Forest-Based Pedotransfer Functions and Geostatistics. Hydrol. Earth Syst. Sci. 2019, 23, 2615–2635. [Google Scholar] [CrossRef] [Green Version]
- Kardani, N.; Bardhan, A.; Gupta, S.; Samui, P.; Nazem, M.; Zhang, Y.; Zhou, A. Predicting Permeability of Tight Carbonates Using a Hybrid Machine Learning Approach of Modified Equilibrium Optimizer and Extreme Learning Machine. Acta Geotech. 2022, 17, 1239–1255. [Google Scholar] [CrossRef]
- Provost, F. Machine Learning from Imbalanced Data Sets 101. In Proceedings of the AAAI’2000 Workshop on Imbalanced Data Sets, Austin, TX, USA, 31 July 2000; Volume 68, pp. 1–3. [Google Scholar]
- Zhu, B.; Baesens, B.; vandenBroucke, S.K.L.M. An Empirical Comparison of Techniques for the Class Imbalance Problem in Churn Prediction. Inf. Sci. 2017, 408, 84–99. [Google Scholar] [CrossRef] [Green Version]
- Abdi, L.; Hashemi, S. To Combat Multi-Class Imbalanced Problems by Means of Over-Sampling Techniques. IEEE Trans. Knowl. Data Eng. 2016, 28, 238–251. [Google Scholar] [CrossRef]
- Sharififar, A.; Sarmadian, F.; Minasny, B. Mapping Imbalanced Soil Classes Using Markov Chain Random Fields Models Treated with Data Resampling Technique. Comput. Electron. Agric. 2019, 159, 110–118. [Google Scholar] [CrossRef]
- Baaghideh, M.; Dadashi-Roudbari, A.; Beiranvand, F. Analysis of Precipitation Variation in the Northern Strip of Iran. Model. Earth Syst. Environ. 2020, 6, 567–574. [Google Scholar] [CrossRef]
- Ziarati, P.; Zendehdel, T.; Bidgoli, S.A. Nitrate Content in Drinking Water in Gilan and Mazandaran Provinces, Iran. J. Environ. Anal. Toxicol. 2014, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Gee, G.W.; Bauder, J.W. Particle Size Analysis. In Methods of Soil Analysis, Part 1 (Second Ed.), 9th ed.; Klute, A., Ed.; Soil Science Society of America: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar]
- Taghizadeh-Mehrjardi, R.; Mahdianpari, M.; Mohammadimanesh, F.; Behrens, T.; Toomanian, N.; Scholten, T.; Schmidt, K. Multi-Task Convolutional Neural Networks Outperformed Random Forest for Mapping Soil Particle Size Fractions in Central Iran. Geoderma 2020, 376, 114552. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Dimensionality Reduction for Imbalanced Learning. In Learning from Imbalanced Data Sets; Springer International Publishing: Cham, Switzerland, 2018; pp. 227–251. ISBN 978-3-319-98073-7. [Google Scholar]
- Grunwald, S. Multi-Criteria Characterization of Recent Digital Soil Mapping and Modeling Approaches. Geoderma 2009, 152, 195–207. [Google Scholar] [CrossRef]
- Chawla, N.V.; Cieslak, D.A.; Hall, L.O.; Joshi, A. Automatically Countering Imbalance and Its Empirical Relationship to Cost. Data Min. Knowl. Disc. 2008, 17, 225–252. [Google Scholar] [CrossRef] [Green Version]
- Estabrooks, A.; Jo, T.; Japkowicz, N. A Multiple Resampling Method for Learning from Imbalanced Data Sets. Comput. Intell. 2004, 20, 18–36. [Google Scholar] [CrossRef] [Green Version]
- García, V.; Sánchez, J.S.; Martín-Félez, R.; Mollineda, R.A. Surrounding Neighborhood-Based SMOTE for Learning from Imbalanced Data Sets. Prog. Artif. Intell. 2012, 1, 347–362. [Google Scholar] [CrossRef] [Green Version]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Møller, A.B.; Beucher, A.M.; Pouladi, N.; Greve, M.H. Oblique Geographic Coordinates as Covariates for Digital Soil Mapping. SOIL 2020, 6, 269–289. [Google Scholar] [CrossRef]
- Behrens, T.; Schmidt, K.; ViscarraRossel, R.A.; Gries, P.; Scholten, T.; MacMillan, R.A. Spatial Modelling with Euclidean Distance Fields and Machine Learning: Spatial Modelling with Euclidean Distance Fields. Eur. J. Soil Sci. 2018, 69, 757–770. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Ishwaran, H.; Kogalur, U.B. Consistency of Random Survival Forests. Stat. Probab. Lett. 2010, 80, 1056–1064. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Behrens, T.; Zhu, A.-X.; Schmidt, K.; Scholten, T. Multi-Scale Digital Terrain Analysis and Feature Selection for Digital Soil Mapping. Geoderma 2010, 155, 175–185. [Google Scholar] [CrossRef]
- Brazil, I.N.P.E. Monitoramento da F/floresta Amaz6nica Brasileira por Satelite. Monit. Braz. Amazon For. Satel. 1999, 1999, 20011. [Google Scholar]
- da Silva, A.F.; Barbosa, A.P.; Zimback, C.R.L.; Landim, P.M.B.; Soares, A. Estimation of Croplands Using Indicator Kriging and Fuzzy Classification. Comput. Electron. Agric. 2015, 111, 1–11. [Google Scholar] [CrossRef]
- Lantz, B. Machine Learning with R: Expert Techniques for Predictive Modeling; Packt Publishing Ltd.: Birrmingham, UK, 2019. [Google Scholar]
- Landis, J.R.; Koch, G.G. An Application of Hierarchical Kappa-Type Statistics in the Assessment of Majority Agreement among Multiple Observers. Biom. 1977, 33, 363–374. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C. Machine Learning for Predicting Soil Classes in Three Semi-Arid Landscapes. Geoderma 2015, 239–240, 68–83. [Google Scholar] [CrossRef] [Green Version]
- Jafari, A.; Finke, P.A.; VandeWauw, J.; Ayoubi, S.; Khademi, H. Spatial Prediction of USDA- Great Soil Groups in the Arid Zarand Region, Iran: Comparing Logistic Regression Approaches to Predict Diagnostic Horizons and Soil Types. Eur. J. Soil Sci. 2012, 63, 284–298. [Google Scholar] [CrossRef]
- Neyestani, M.; Sarmadian, F.; Jafari, A.; Keshavarzi, A.; Sharififar, A. Digital Mapping of Soil Classes Using Spatial Extrapolation with Imbalanced Data. Geoderma Reg. 2021, 26, e00422. [Google Scholar] [CrossRef]
- Silva, B.P.C.; Silva, M.L.N.; Avalos, F.A.P.; de Menezes, M.D.; Curi, N. Digital Soil Mapping Including Additional Point Sampling in Posses Ecosystem Services Pilot Watershed, Southeastern Brazil. Sci. Rep. 2019, 9, 13763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akpa, S.I.C.; Odeh, I.O.A.; Bishop, T.F.A.; Hartemink, A.E. Digital Mapping of Soil Particle-Size Fractions for Nigeria. Soil Sci. Soc. Am. J. 2014, 78, 1953–1966. [Google Scholar] [CrossRef] [Green Version]
- Taghizadeh-Mehrjardi, R.; Emadi, M.; Cherati, A.; Heung, B.; Mosavi, A.; Scholten, T. Bio-Inspired Hybridization of Artificial Neural Networks: An Application for Mapping the Spatial Distribution of Soil Texture Fractions. Remote Sens. 2021, 13, 1025. [Google Scholar] [CrossRef]
- Amirian-Chakan, A.; Minasny, B.; Taghizadeh-Mehrjardi, R.; Akbarifazli, R.; Darvishpasand, Z.; Khordehbin, S. Some Practical Aspects of Predicting Texture Data in Digital Soil Mapping. Soil Tillage Res. 2019, 194, 104289. [Google Scholar] [CrossRef]
- Malone, B.P.; Minasny, B.; McBratney, A.B. Using R for Digital Soil Mapping. In Progress in Soil Science; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-44325-6. [Google Scholar]
- Gallant, J.C.; Dowling, T.I. A Multiresolution Index of Valley Bottom Flatness for Mapping Depositional Areas: MULTIRESOLUTION VALLEY BOTTOM FLATNESS. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Umali, B.P.; Oliver, D.P.; Forrester, S.; Chittleborough, D.J.; Hutson, J.L.; Kookana, R.S.; Ostendorf, B. The Effect of Terrain and Management on the Spatial Variability of Soil Properties in an Apple Orchard. Catena 2012, 93, 38–48. [Google Scholar] [CrossRef]
- Tyagi, S.; Mittal, S. Sampling Approaches for Imbalanced Data Classification Problem in Machine Learning. In Proceedings of the ICRIC 2019, Jammu, India, March 2019; Singh, P.K., Kar, A.K., Singh, Y., Kolekar, M.H., Tanwar, S., Eds.; Lecture Notes in Electrical Engineering. Springer International Publishing: Cham, Switzerland, 2020; Volume 597, pp. 209–221. [Google Scholar]
- Kamal, A.H.M.; Zhu, X.; Pandya, A.; Hsu, S.; Narayanan, R. Feature Selection for Datasets with Imbalanced Class Distributions. Int. J. Soft. Eng. Knowl. Eng. 2010, 20, 113–137. [Google Scholar] [CrossRef]
- Wadoux, A.M.C.; Samuel-Rosa, A.; Poggio, L.; Mulder, V.L. A Note on Knowledge Discovery and Machine Learning in Digital Soil Mapping. Eur. J. Soil Sci. 2020, 71, 133–136. [Google Scholar] [CrossRef]
- Sáez, J.A.; Krawczyk, B.; Woźniak, M. Analyzing the Oversampling of Different Classes and Types of Examples in Multi-Class Imbalanced Datasets. Pattern Recognit. 2016, 57, 164–178. [Google Scholar] [CrossRef]
- Loyola-González, O.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A.; García-Borroto, M. Study of the Impact of Resampling Methods for Contrast Pattern Based Classifiers in Imbalanced Databases. Neurocomputing 2016, 175, 935–947. [Google Scholar] [CrossRef]
- Kehl, M.; Vlaminck, S.; Köhler, T.; Laag, C.; Rolf, C.; Tsukamoto, S.; Frechen, M.; Sumita, M.; Schmincke, H.-U.; Khormali, F. Pleistocene Dynamics of Dust Accumulation and Soil Formation in the Southern Caspian Lowlands—New Insights from the Loess-Paleosol Sequence at Neka-Abelou, Northern Iran. Quat. Sci. Rev. 2021, 253, 106774. [Google Scholar] [CrossRef]





| Soil Texture | C | CL | L | LS | S | SCL | SL | ZC | ZCL | ZL |
|---|---|---|---|---|---|---|---|---|---|---|
| Percentage (%) in the original dataset | 13/27 | 24/40 | 25/09 | 0/39 | 0/20 | 4/28 | 4/86 | 9/38 | 9/81 | 11/21 |
| Source | Covariate | Abbreviation | |
|---|---|---|---|
| DEM | Aspect | - | |
| Catchment area | Cat.Area | ||
| Catchment slope | Cat.Slope | ||
| Channel network-based level | CNBL | ||
| Channel network distance index | CNDI | ||
| Convergence index | Con.Index | ||
| Elevation | - | ||
| Length-slope factor | LS.Factor | ||
| Mid slope position | Mid.Slope.P | ||
| Modified catchment area | M.Cat.Area | ||
| Multiresolution ridge top flatness | MRRTF | ||
| Multiresolution valley bottom flatness | MRVBF | ||
| Normalized height | N.Height | ||
| Plan curvature | Plan.Cur | ||
| Profile curvature | Prof.Cur | ||
| Relative slope position | R.Slope.P | ||
| Slope height | Slope.Height | ||
| Slope | - | ||
| Standard height | S.Height | ||
| Topographic wetness index | TWI | ||
| Total catchment area | Total.Cat.Area | ||
| Valley depth | Valley.Depth | ||
| Wind effect | Wind.Effect | ||
| Remote sensing images a | Sentinel-2 | Sentinel-2 spectral bands (B2.S, B3.S, B4.S, B5.S, B6.S, B7.S, B8.S, B11.S, B12.S) | |
| Normalized difference vegetation index | NDVI | ||
| Soil adjusted vegetation index | SAVI | ||
| Brightness index | BrightnessIndex | ||
| Clay index | ClayIndex | ||
| Landsat 8 | Landsat 8 spectral bands (B2.L, B3.L, B4.L, B5.L, B6.L, B7.L, B10.L, B11.L) NDVI, SAVI, brightness index, clay index | ||
| MODIS | MODIS spectral bands (B1.M, B2.M, B3.M, B4.M, B5.M, B6.M, B7.M) NDVI, SAVI, brightness index, clay index | ||
| Bioclimatic data | Rainfall Temperature | Bio12 Bio01 | |
| Distance layers | Distance to different parts of the study area | dis.1, … dis.15 |
| Soil Texture | Imbalanced | Balanced | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | F-Score | Precision | Recall | F-Score | |
| C | 0.45 | 0.38 | 0.41 | 0.61 | 0.68 | 0.64 |
| CL | 0.41 | 0.51 | 0.46 | 0.75 | 0.52 | 0.62 |
| L | 0.46 | 0.60 | 0.52 | 0.75 | 0.59 | 0.66 |
| LS | 0.15 | 0.04 | 0.07 | 0.30 | 0.71 | 0.42 |
| S | 0.00 | 0.00 | 0.00 | 0.20 | 0.53 | 0.29 |
| SCL | 0.56 | 0.08 | 0.14 | 0.25 | 0.51 | 0.33 |
| SL | 0.29 | 0.08 | 0.13 | 0.36 | 0.59 | 0.45 |
| ZC | 0.45 | 0.40 | 0.43 | 0.57 | 0.67 | 0.61 |
| ZCL | 0.44 | 0.32 | 0.37 | 0.48 | 0.64 | 0.55 |
| ZL | 0.46 | 0.35 | 0.40 | 0.53 | 0.54 | 0.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallah, S.; Delsouz Khaki, B.; Davatgar, N.; Scholten, T.; Amirian-Chakan, A.; Emadi, M.; Kerry, R.; Mosavi, A.H.; Taghizadeh-Mehrjardi, R. Predicting Soil Textural Classes Using Random Forest Models: Learning from Imbalanced Dataset. Agronomy 2022, 12, 2613. https://doi.org/10.3390/agronomy12112613
Mallah S, Delsouz Khaki B, Davatgar N, Scholten T, Amirian-Chakan A, Emadi M, Kerry R, Mosavi AH, Taghizadeh-Mehrjardi R. Predicting Soil Textural Classes Using Random Forest Models: Learning from Imbalanced Dataset. Agronomy. 2022; 12(11):2613. https://doi.org/10.3390/agronomy12112613
Chicago/Turabian StyleMallah, Sina, Bahareh Delsouz Khaki, Naser Davatgar, Thomas Scholten, Alireza Amirian-Chakan, Mostafa Emadi, Ruth Kerry, Amir Hosein Mosavi, and Ruhollah Taghizadeh-Mehrjardi. 2022. "Predicting Soil Textural Classes Using Random Forest Models: Learning from Imbalanced Dataset" Agronomy 12, no. 11: 2613. https://doi.org/10.3390/agronomy12112613
APA StyleMallah, S., Delsouz Khaki, B., Davatgar, N., Scholten, T., Amirian-Chakan, A., Emadi, M., Kerry, R., Mosavi, A. H., & Taghizadeh-Mehrjardi, R. (2022). Predicting Soil Textural Classes Using Random Forest Models: Learning from Imbalanced Dataset. Agronomy, 12(11), 2613. https://doi.org/10.3390/agronomy12112613