Assessment of the Spatial Variability and Uncertainty of Shreddable Pruning Biomass in an Olive Grove Based on Canopy Volume and Tree Projected Area
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Field Sampling
2.2. Geostatistical Analysis
2.3. Software
3. Results and Discussion
3.1. Statistics of Field and Laboratory Variables
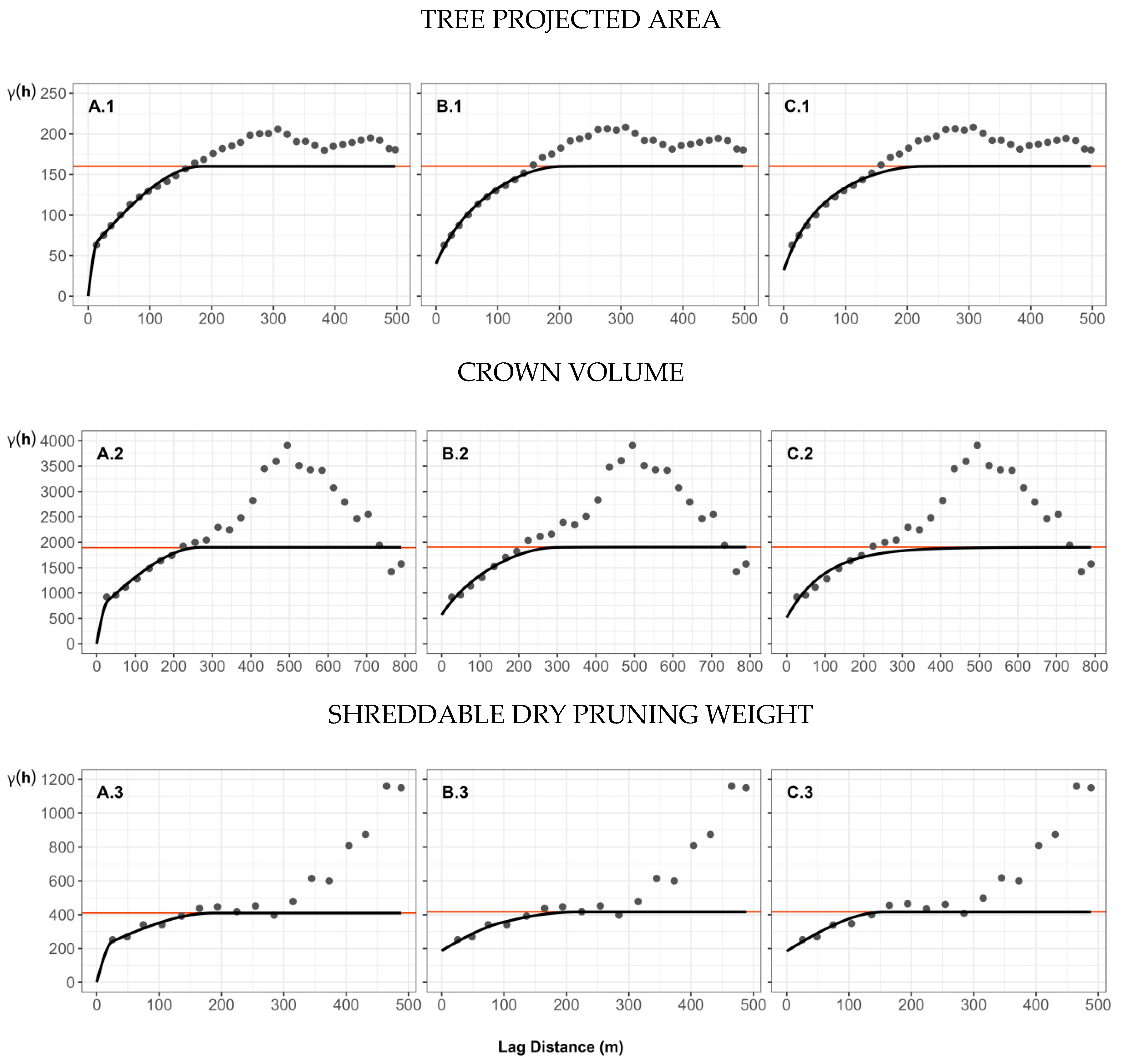
3.2. Spatial Autocorrelation of Field and Laboratory Variables
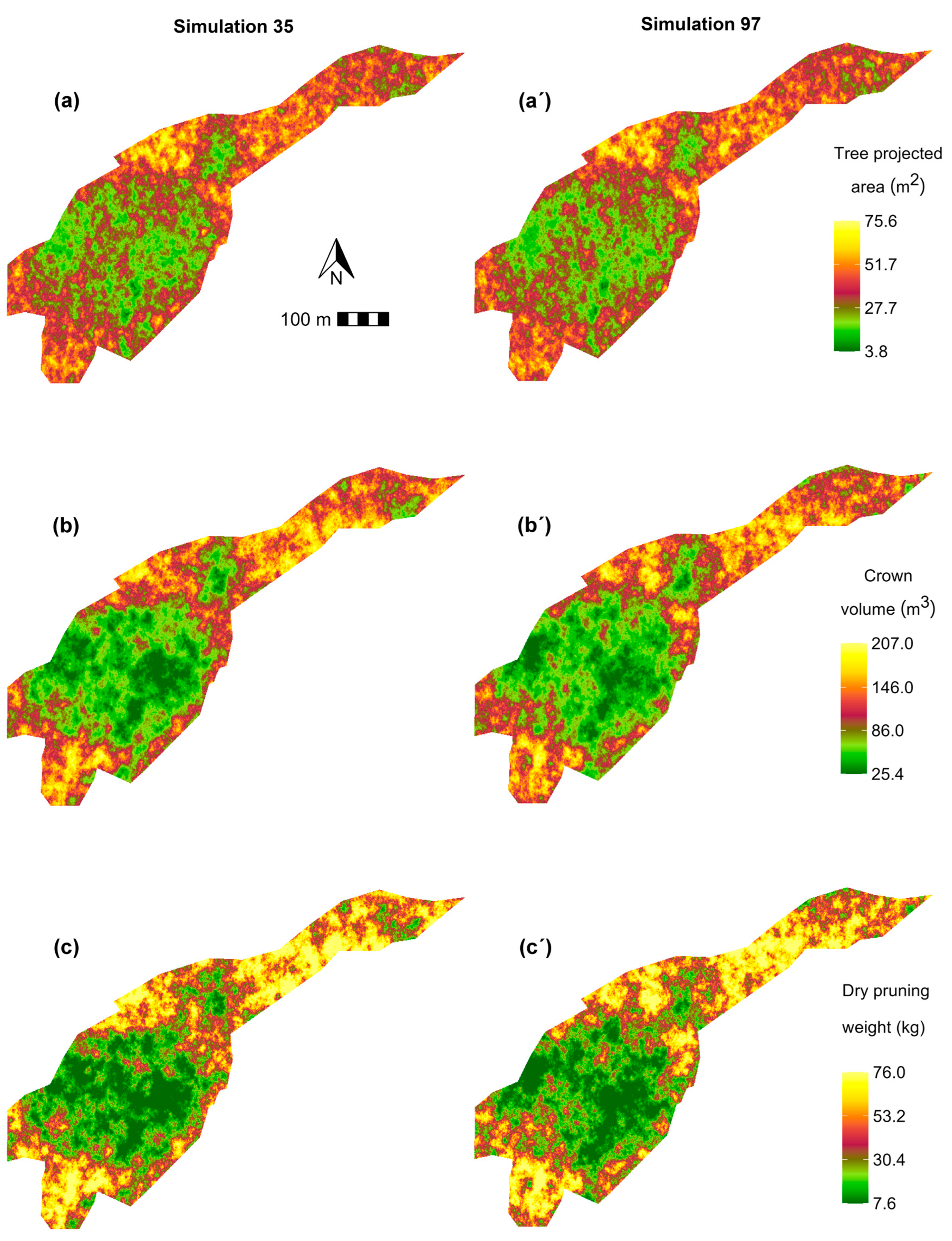
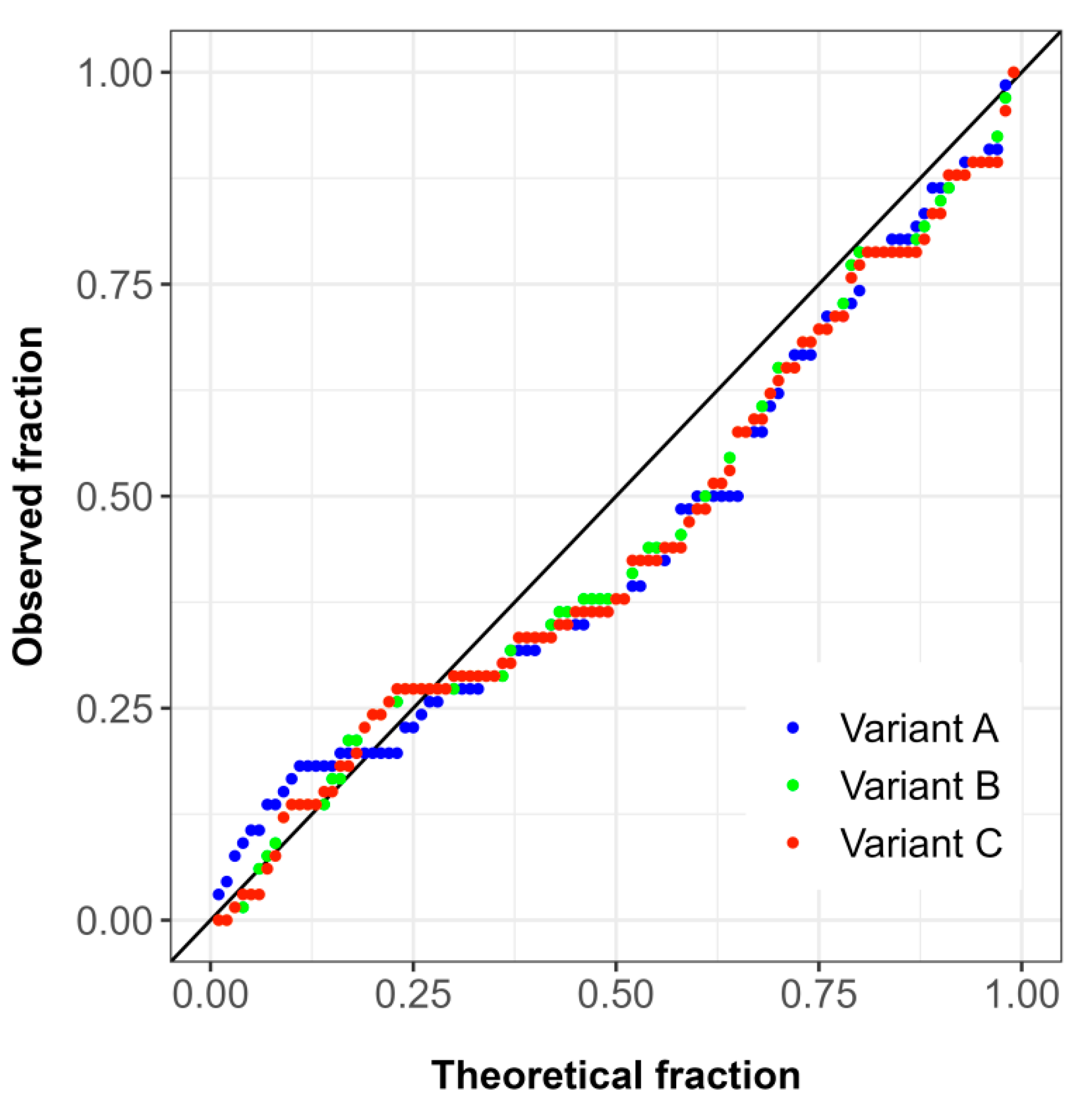
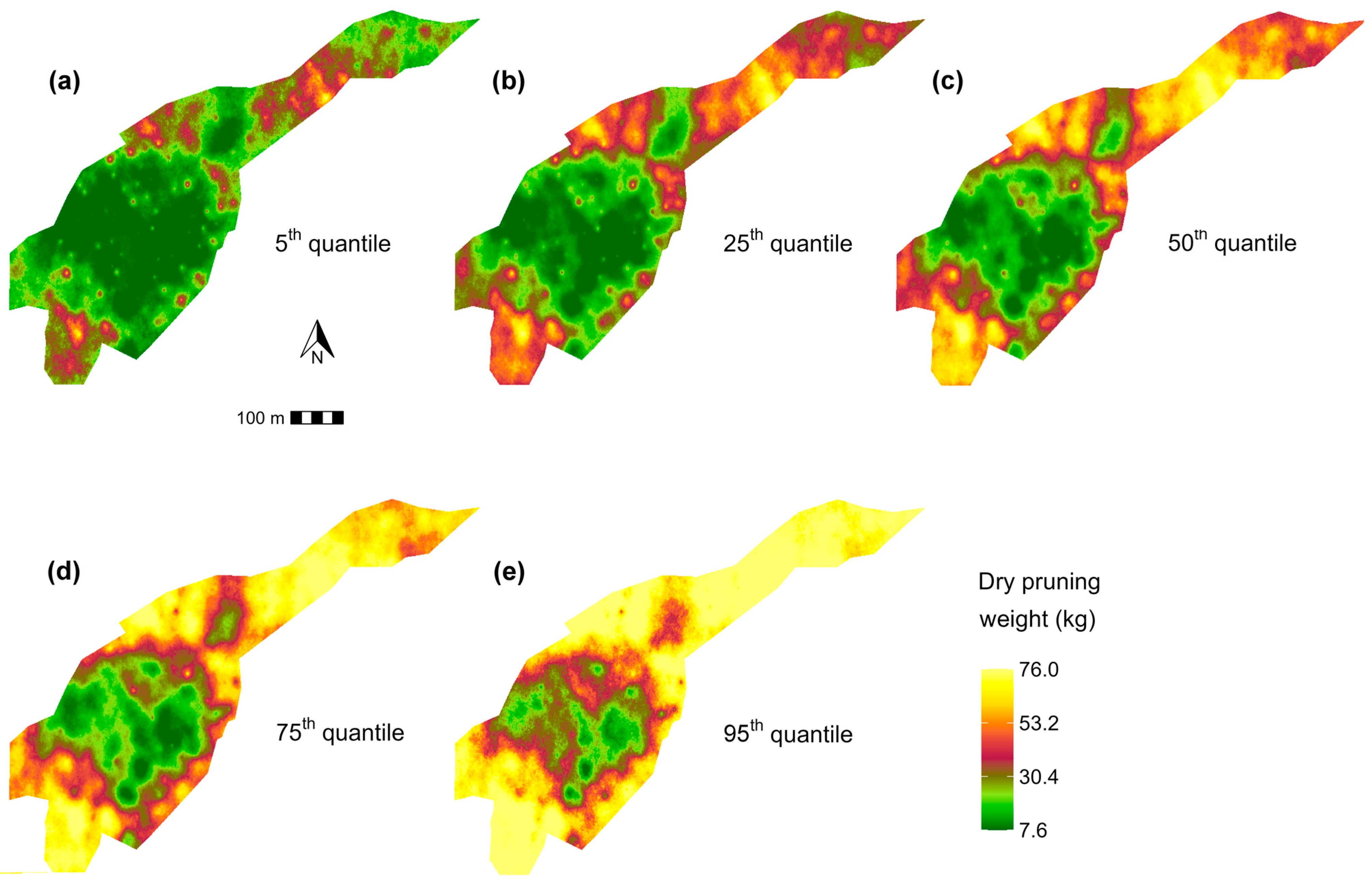
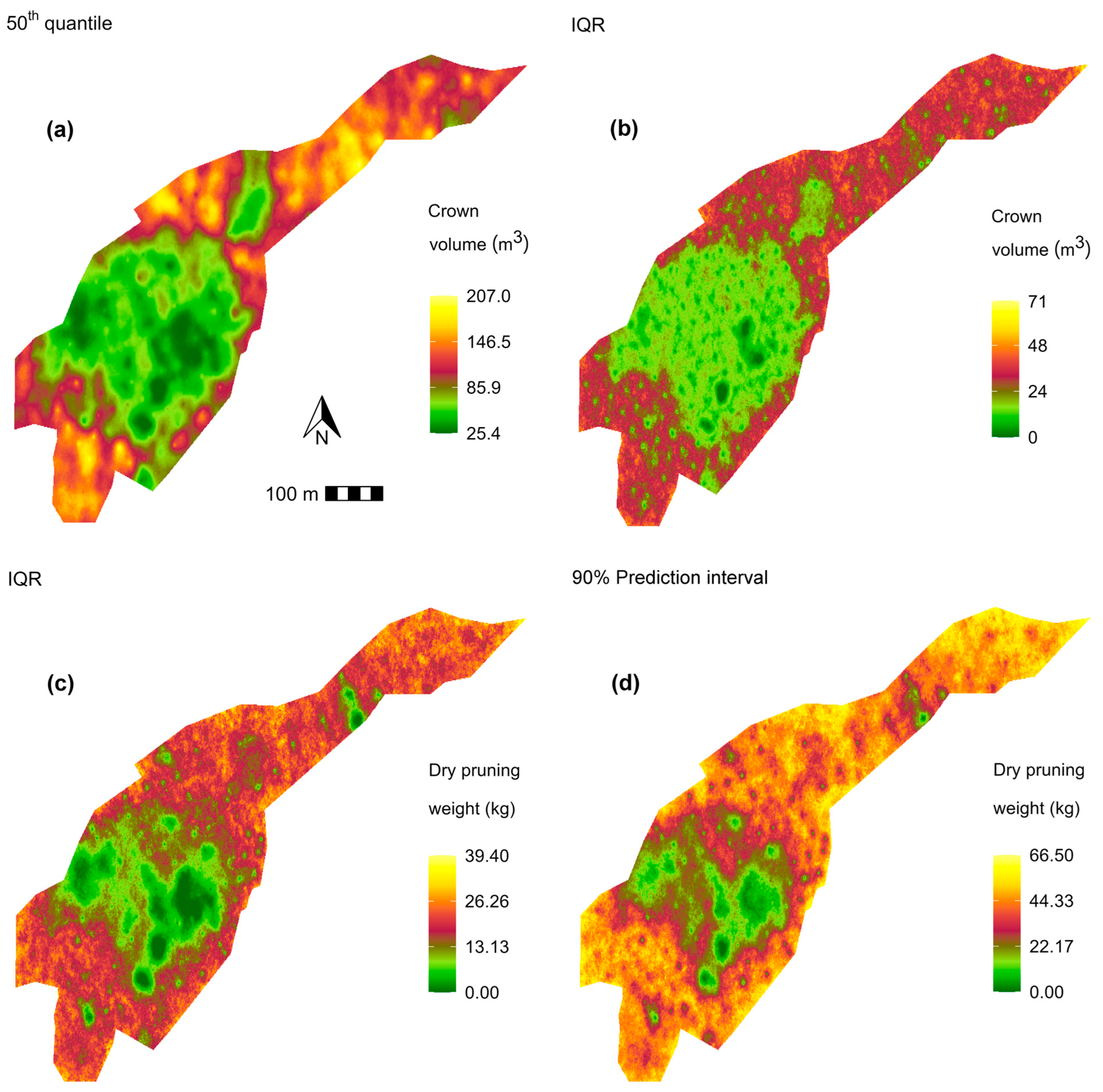
3.3. Spatial Uncertainty of Variables and Validation of Results
3.4. Agronomic and Energy Implications of the Spatial Distribution and Uncertainty of the Canopy Volume and Shreddable Pruning Material
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO Agricultural Statistics. Available online: http://faostat.fao.org (accessed on 23 January 2023).
- Ministerio de Agricultura, Pesca y Alimentación. Anuario de Estadística. 2020. Available online: https://www.mapa.gob.es/es/estadistica/temas/publicaciones/anuario-de-estadistica/2020/default.aspx?parte=3&capitulo=07&grupo=12 (accessed on 3 June 2023).
- Lucena, B.; Manrique, T.; Méndez, M.A. La olivicultura en el mundo y en España. In El Cultivo Del Olivo; Barranco, D., Fernández-Escobar, R., Rallo, L., Eds.; Ediciones MundiPrensa: Madrid, Spain, 2017; pp. 1–34. ISBN 9788484767145. [Google Scholar]
- Parra, M.A. Suelo. In El Cultivo Del Olivo; Barranco, D., Fernández Escobar, R., Rallo, L., Eds.; Mundi-Prensa: Madrid, Spain, 2017; pp. 251–288. ISBN 9788484767145. [Google Scholar]
- Fernández-Escobar, R.; de la Rosa, R.; León, L.; Gómez, J.A.; Testi, L.; Orgaz, F.; Gil-Ribes, J.A.; Quesada-Moraga, E.; Trapero, A.; Msallem, M. Sistemas de producción en olivicultura. Olivae Rev. Of. Cons. Oleícola Int. 2012, 118, 55–68. [Google Scholar]
- Ministerio de Agricultura, Pesca y Alimentación. ESYRCE. Available online: https://www.mapa.gob.es/es/estadistica/temas/estadisticas-agrarias/agricultura/esyrce/ (accessed on 19 March 2023).
- Saavedra, M.M.; Pastor, M. Sistemas de Cultivo en Olivar. Manejo de Malas Hierbas y Herbicidas; Editorial Agrícola Española: Madrid, Spain, 2002; ISBN 84-85441-65-6. [Google Scholar]
- Espejo-Pérez, A.J.; Rodríguez-Lizana, A.; Ordóñez, R.; Giráldez, J.V. Soil Loss and Runoff Reduction in Olive-Tree Dry-Farming with Cover Crops. Soil Sci. Soc. Am. J. 2013, 77, 2140–2148. [Google Scholar] [CrossRef] [Green Version]
- Cerdà, A.; Lavee, H.; Romero-Díaz, A.; Hooke, J.; Montanarella, L. Soil erosion and degradation in Mediterranean-type ecosystems. L. Degrad. Dev. 2010, 21, 71–74. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Ordóñez-Fernández, R.; Repullo-Ruibérriz de Torres, M.A.; Márquez-García, J.; Moreno-García, M.; Carbonell-Bojollo, R.M. Legumes used as cover crops to reduce fertilisation problems improving soil nitrate in an organic orchard. Eur. J. Agron. 2018, 95, 1–13. [Google Scholar] [CrossRef]
- Torrús-Castillo, M.; Domouso, P.; Herrera-Rodríguez, J.M.; Calero, J.; García-Ruiz, R. Aboveground Carbon Fixation and Nutrient Retention in Temporary Spontaneous Cover Crops in Olive Groves of Andalusia. Front. Environ. Sci. 2022, 10, 868410. [Google Scholar] [CrossRef]
- Rodríguez-Lizana, A.; Repullo-Ruibérriz De Torres, M.A.; Carbonell-Bojollo, R.; Alcántara, C.; Ordóñez-Fernández, R. Brachypodium distachyon, Sinapis alba, and controlled spontaneous vegetation as groundcovers: Soil protection and modeling decomposition. Agric. Ecosyst. Environ. 2018, 265, 62–72. [Google Scholar] [CrossRef]
- Alcántara, C.; Pujadas, A.; Saavedra, M. Management of cruciferous cover crops by mowing for soil and water conservation in southern Spain. Agric. Water Manag. 2011, 98, 1071–1080. [Google Scholar] [CrossRef]
- Rodríguez-Lizana, A.; Repullo-Ruibérriz de Torres, M.A.; Carbonell-Bojollo, R.M.; Moreno-García, M.; Ordóñez-Fernández, R. Study of C, N, P and K Release from Residues of Newly Proposed Cover Crops in a Spanish Olive Grove. Agronomy 2020, 10, 1041. [Google Scholar] [CrossRef]
- Repullo-Ruibérriz de Torres, M.A.; Carbonell-Bojollo, R.M.; Moreno-García, M.; Ordóñez-Fernández, R.; Rodríguez-Lizana, A. Soil organic matter and nutrient improvement through cover crops in a Mediterranean olive orchard. Soil Tillage Res. 2021, 210, 104977. [Google Scholar] [CrossRef]
- Hao, X.; Abou, M.; Steenwerth, K.L.; Nocco, M.A.; Basset, C.; Daccache, A. Are there universal soil responses to cover cropping? A systematic review. Sci. Total Environ. 2023, 861, 160600. [Google Scholar] [CrossRef]
- Rodríguez-Lizana, A.; Espejo-Pérez, A.J.; González-Fernández, P.; Ordóñez-Fernández, R. Pruning residues as an alternative to traditional tillage to reduce erosion and pollutant dispersion in olive groves. Water Air Soil Pollut. 2008, 193, 165–173. [Google Scholar] [CrossRef]
- Rodríguez-Lizana, A.; Pereira, M.J.; Ribeiro, M.C.; Soares, A.; Márquez-García, F.; Ramos, A.; Gil-Ribes, J. Assessing Local Uncertainty of Soil Protection in an Olive Grove Area with Pruning Residues Cover: A Geostatistical Cosimulation Approach. Land Degrad. Dev. 2017, 28, 2086–2097. [Google Scholar] [CrossRef]
- Repullo, M.A.; Carbonell, R.; Hidalgo, J.; Rodríguez-Lizana, A.; Ordóñez, R. Using olive pruning residues to cover soil and improve fertility. Soil Tillage Res. 2012, 124, 36–46. [Google Scholar] [CrossRef]
- Ordóñez-Fernández, R.; Repullo-Ruibérriz de Torres, M.A.; Román-Vázquez, J.; González-Fernández, P.; Carbonell-Bojollo, R. Macronutrients released during the decomposition of pruning residues used as plant cover and their effect on soil fertility. J. Agric. Sci. 2015, 153, 615–630. [Google Scholar] [CrossRef]
- Henry, G.M.; Hoyle, J.A.; Beck, L.L.; Cooper, T.; Montague, T.; Mckenney, C. Evaluation of Mulch and Preemergence Herbicide Combinations for Weed Control in High-density Olive (Olea europaea L.) Production. HortScience 2015, 50, 1338–1341. [Google Scholar] [CrossRef]
- López-Escudero, F.J.; Mercado-Blanco, J. Verticillium wilt of olive: A case study to implement an integrated strategy to control a soil-borne pathogen. Plant Soil 2011, 344, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Mairech, H.; López-Bernal, Á.; Moriondo, M.; Dibari, C.; Regni, L.; Proietti, P.; Villalobos, F.J.; Testi, L. Is new olive farming sustainable? A spatial comparison of productive and environmental performances between traditional and new olive orchards with the model OliveCan. Agric. Syst. 2020, 181, 102816. [Google Scholar] [CrossRef]
- Gómez-Muñoz, B.; Valero-Valenzuela, J.D.; Hinojosa, M.B.; García-Ruiz, R. Management of tree pruning residues to improve soil organic carbon in olive groves. Eur. J. Soil Biol. 2016, 74, 104–113. [Google Scholar] [CrossRef]
- Nieto, O.M.; Castro, J.; Fernández, E.; Smith, P. Simulation of soil organic carbon stocks in a Mediterranean olive grove under different soil-management systems using the RothC model. Soil Use Manag. 2010, 26, 118–125. [Google Scholar] [CrossRef]
- González-Ruiz, R.; Gómez-Guzmán, A.; Martínez-Rojas, M.; García-Fuentes, A.; Cordovilla, M.; Sainz-Pérez, M.; Sánchez-Solana, A.; Rodríguez-Lizana, A. The Influence of Mixed Green Covers, a New Trend in Organic Olive Growing, on the Efficiency of Predatory Insects. Agriculture 2023, 13, 785. [Google Scholar] [CrossRef]
- Calatrava, J.; Franco, J.A. Using pruning residues as mulch: Analysis of its adoption and process of diffusion in Southern Spain olive orchards. J. Environ. Manag. 2011, 92, 620–629. [Google Scholar] [CrossRef]
- Boletín Oficial del Estado. Ley 7/2022, de 8 de Abril, de Residuos y Suelos Contaminados Para Una Economía Circular; State Agency Official State Gazette: Madrid, Spain, 2022; pp. 1–136. [Google Scholar]
- Moreno-García, M.; Repullo-Ruibérriz de Torres, M.A.; Carbonell-Bojollo, R.M.; Ordóñez-Fernández, R. Management of pruning residues for soil protection in olive orchards. Land Degrad. Dev. 2018, 29, 2975–2984. [Google Scholar] [CrossRef]
- Manzanares, P.; Ruiz, E.; Ballesteros, M.; Negro, M.J. Residual biomass potential in olive tree cultivation and olive oil industry in Spain: Valorization proposal in a biorefinery context. Span. J. Agric. Res. 2017, 15, 6. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Li, Q.; Pan, L. Review of organic mulching effects on soil and water loss. Arch. Agron. Soil Sci. 2021, 67, 136–151. [Google Scholar] [CrossRef]
- Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; López-Cortés, I.; Salazar, D.; Fernández-Sarría, A. Estimation of pruning biomass of olive trees using airborne discrete-return LiDAR data. Biomass Bioenergy 2015, 81, 315–321. [Google Scholar] [CrossRef]
- Rodríguez-Lizana, A.; Pereira, M.J.; Ribeiro, M.C.; Soares, A.; Azevedo, L.; Miranda-Fuentes, A.; Llorens, J. Spatially variable pesticide application in olive groves: Evaluation of potential pesticide-savings through stochastic spatial simulation algorithms. Sci. Total Environ. 2021, 778, 146111. [Google Scholar] [CrossRef]
- Jiménez-Brenes, F.M.; López-Granados, F.; Castro, A.I.; Torres-Sánchez, J.; Serrano, N.; Peña, J.M. Quantifying pruning impacts on olive tree architecture and annual canopy growth by using UAV-based 3D modelling. Plant Methods 2017, 13, 55. [Google Scholar] [CrossRef] [Green Version]
- Velàzquez-Martì, B.; Cortès, I.L.; Salazar-Hernàndez, D.M. Dendrometric analysis of olive trees for wood biomass quantification in Mediterranean orchards. Agrofor. Syst. 2014, 88, 755–765. [Google Scholar] [CrossRef]
- Assirelli, A.; Romano, E.; Bisaglia, C.; Lodolini, E.M.; Neri, D.; Brambilla, M. Canopy Index Evaluation for Precision Management in an Intensive Olive Orchard. Sustainability 2021, 13, 8266. [Google Scholar] [CrossRef]
- Fernández-Sarría, A.; López-Cortés, I.; Estornell, J.; Velázquez-Martí, B.; Salazar, D. Estimating residual biomass of olive tree crops using terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 163–170. [Google Scholar] [CrossRef]
- Torquati, B.; Marino, D.; Venanzi, S.; Porceddu, P.R.; Chiorri, M. Using tree crop pruning residues for energy purposes: A spatial analysis and an evaluation of the economic and environmental sustainability. Biomass Bioenergy 2016, 95, 124–131. [Google Scholar] [CrossRef]
- Fernández-Sarría, A.; López-Cortés, I.; Martí, J.; Estornell, J. Estimation of Walnut Structure Parameters Using Terrestrial Photogrammetry Based on Structure-from-Motion (SfM). J. Indian Soc. Remote Sens. 2022, 50, 1931–1944. [Google Scholar] [CrossRef]
- Méndez, V.; Pérez-Romero, A.; Sola-Guirado, R.R.; Miranda-Fuentes, A.; Manzano-Agugliaro, F.; Zapata-Sierra, A.; Rodríguez-Lizana, A. In-Field Estimation of Orange Number and Size by 3D Laser Scanning. Agronomy 2019, 9, 885. [Google Scholar] [CrossRef] [Green Version]
- Escolà, A.; Martínez-Casasnovas, J.A.; Rufat, J.; Arnó, J.; Arbonés, A.; Sebé, F.; Pascual, M.; Gregorio, E.; Rosell-Polo, J.R. Mobile terrestrial laser scanner applications in precision fruticulture/horticulture and tools to extract information from canopy point clouds. Precis. Agric. 2017, 18, 111–132. [Google Scholar] [CrossRef] [Green Version]
- Dalla Corte, A.P.; Rex, F.E.; Roberti, D.; De Almeida, A.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Maria, A.; Zambrano, A.; et al. Measuring Individual Tree Diameter and Height Using GatorEye High-Density UAV-Lidar in an Integrated Crop-Livestock-Forest System. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef] [Green Version]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in Central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Soares, A. Direct Sequential Simulation and Cosimulation. Math. Geol. 2001, 33, 911–926. [Google Scholar] [CrossRef]
- Horta, A.; Soares, A. Direct sequential Co-simulation with joint probability distributions. Math. Geosci. 2010, 42, 269–292. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.; Brus, D.J.; Heuvelink, G.B.M. Accounting for non-stationary variance in geostatistical mapping of soil properties. Geoderma 2018, 324, 138–147. [Google Scholar] [CrossRef]
- Peel, M.; Fynlaison, B.; McMahon, T. Updated world map of the Köppen-Geiger classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Agencia Estatal de Meteorología. Valores Climáticos Normales. Available online: https://www.aemet.es/es/serviciosclimaticos/datosclimatologicos/valoresclimatologicos (accessed on 15 June 2023).
- Panagiotou, C.F.; Kyriakidis, P.; Tziritis, E. Application of geostatistical methods to groundwater salinization problems: A review. J. Hydrol. 2022, 615, 128566. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Deutsch, C. V Direct assessment of local accuracy and precision. In Proceedings of the Geostatistics Wollongong ’96, Wollongong, Australia, 2–6 September 1996; Baafi, E.Y., Schofield, N.A., Eds.; Kluwer Academic Publishing: Dordrecht, The Netherlands, 1997; pp. 115–125. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing 2019; R Foundation for Statistical Computing: Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 3 June 2023).
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. Historical commentary NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Miranda-Fuentes, A.; Llorens, J.; Gamarra-Diezma, J.; Gil-Ribes, J.; Gil, E. Towards an Optimized Method of Olive Tree Crown Volume Measurement. Sensors 2015, 15, 3671–3687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schumman, A.; Hostler, K.; Buchanon, S.; Zaman, Q. Relating citrus canopy size and yield to precision fertilization. Proc. Fla. State Hortic. Soc. 2006, 119, 148–154. [Google Scholar]
- Jopaul, G.; Panzou, L.; Fayolle, A.; Jucker, T.; Phillips, O.L.; Bohlman, S.; Banin, L.F.; Lewis, S.L.; Luciana, K.A.; Cécile, F.A.; et al. Pantropical variability in tree crown allometry. Glob. Ecol. Biogeogr. 2021, 30, 459–475. [Google Scholar]
- Velázquez-Martí, B.; Fernández-González, E.; López-Cortés, I.; Salazar-Hernández, D.M. Quantification of the residual biomass obtained from pruning of trees in Mediterranean olive groves. Biomass Bioenergy 2011, 35, 3453–3464. [Google Scholar] [CrossRef]
- Castillo-Ruiz, F.J.; Sola-Guirado, R.; Castro-García, S.; González-Sánchez, E.J.; Colmenero-Martínez, J.T.; Blanco-Roldán, G.L. Scientia Horticulturae Pruning systems to adapt traditional olive orchards to new integral harvesters. Sci. Hortic. 2017, 220, 122–129. [Google Scholar] [CrossRef]
- Colaço, A.F.; Molin, J.P.; Rosell-Polo, J.R.; Escolà, A. Spatial variability in commercial orange groves. Part 1: Canopy volume and height. Precis. Agric. 2019, 20, 805–822. [Google Scholar] [CrossRef] [Green Version]
- Goovaerts, P. Geostatistical modelling of uncertainty in soil science. Geoderma 2001, 103, 3–26. [Google Scholar] [CrossRef]
- Chilès, J.-P.; Delfiner, P. Geostatistics. Modelling Spatial Uncertainty, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 978-0-470-18315-1. [Google Scholar]
- Szatmári, G.; Bakacsi, Z.; Laborczi, A.; Petrik, O.; Pataki, R.; Tóth, T.; Pásztor, L. Elaborating Hungarian Segment of the Global Map of Salt-Affected Soils (GSSmap): National Contribution to an International Initiative. Remote Sens. 2020, 12, 4073. [Google Scholar] [CrossRef]
- Szatmári, G.; Pásztor, L.; Heuvelink, G.B.M. Estimating soil organic carbon stock change at multiple scales using machine learning and multivariate geostatistics. Geoderma 2021, 403, 115356. [Google Scholar] [CrossRef]
- Sun, X.L.; Zhao, Y.G.; Wu, Y.J.; Zhao, M.S.; Wang, H.L.; Zhang, G.L. Spatio-temporal change of soil organic matter content of Jiangsu Province, China, based on digital soil maps. Soil Use Manag. 2012, 28, 318–328. [Google Scholar] [CrossRef]
- Allocca, C.; Castrignanò, A.; Nasta, P.; Romano, N. Geoderma Regional-scale assessment of soil functions and resilience indicators: Accounting for change of support to estimate primary soil properties and their uncertainty. Geoderma 2023, 431, 116339. [Google Scholar] [CrossRef]
- Miranda-Fuentes, A.; Llorens, J.; Rodríguez-Lizana, A.; Cuenca, A.; Gil, E.; Blanco-Roldán, G.L.; Gil-Ribes, J.A. Assessing the optimal liquid volume to be sprayed on isolated olive trees according to their canopy volumes. Sci. Total Environ. 2016, 568, 296–305. [Google Scholar] [CrossRef]
- Örn, S. Estimating Light Interception of Orchard Trees Using LiDAR and Solar Models; Linköoping University: Linköping, Sweden, 2016. [Google Scholar]
- Underwood, J.P.; Hung, C.; Whelan, B.; Sukkarieh, S. Mapping almond orchard canopy volume, flowers, fruit and yield using lidar and vision sensors. Comput. Electron. Agric. 2016, 130, 83–96. [Google Scholar] [CrossRef]
- Maldera, F.; Vivaldi, G.A.; Iglesias-castellarnau, I.; Camposeo, S. Two Almond Cultivars Trained in a Super-High Density Orchard Show Different Growth, Yield Efficiencies and Damages by Mechanical Harvesting. Agronomy 2021, 11, 1406. [Google Scholar] [CrossRef]
- Sola-Guirado, R.R.; Bayano-Tejero, S.; Rodríguez-Lizana, A.; Gil-Ribes, J.A.; Miranda-Fuentes, A. Assessment of the Accuracy of a Multi-Beam LED Scanner Sensor for Measuring Olive Canopies. Sensors 2018, 18, 4406. [Google Scholar] [CrossRef] [Green Version]
- Libutti, A.; Rita, A.; Cammerino, B.; Monteleone, M. Management of Residues from Fruit Tree Pruning: A Trade-Off between Soil Quality and Energy Use. Agronomy 2021, 11, 236. [Google Scholar] [CrossRef]
- De Andalucía, J. La bioenergia en Andalucía; Sevilla, Spain. 2020. Available online: https://www.agenciaandaluzadelaenergia.es/sites/default/files/Documentos/3_2_0068_20_LA_BIOENERGIA_EN_ANDALUCIA.PDF (accessed on 23 January 2023).
- Adeleke, A.A.; Ikubanni, P.P.; Orhadahwe, T.A.; Christopher, C.T.; Akano, J.M.; Agboola, O.O.; Adegoke, S.O.; Balogun, A.O.; Ibikunle, R.A. Heliyon Sustainability of multifaceted usage of biomass: A review. Heliyon 2021, 7, e08025. [Google Scholar] [CrossRef]
- Oyegoke, T.; Obadiah, E.; Mohammed, S.Y.; Bamigbala, O.A.; Owolabi, O.A.; Oyegoke, A.; Onadeji, A.; Mantu, A.I. Papers of the 29th European Biomass Conference Setting the course for a biobased economy. In Proceedings of the Exploration Of Biomass for the Production of Bioethanol: “Economic Feasibility and Optimization Studies of Transforming Maize Cob into Bioethanol as a Substitute for Fossil Fuels” Conference, Online, 26–29 April 2021; Mauguin, P., Scarlat, N., Grassi, A., Eds.; pp. 1270–1275. [Google Scholar]
- Palmieri, N.; Suardi, A.; Alfano, V.; Pari, L. Circular Economy Model: Insights from a Case Study in South Italy. Sustainability 2020, 12, 3466. [Google Scholar] [CrossRef] [Green Version]
- Jordán, A.; Zavala, L.M.; Gil, J. Catena Effects of mulching on soil physical properties and runoff under semi-arid conditions in southern Spain. Catena 2010, 81, 77–85. [Google Scholar] [CrossRef]
- Rodrigues, M.Â.; Ferreira, I.Q.; Marília, A.; Arrobas, M. Scientia Horticulturae Fertilizer recommendations for olive based upon nutrients removed in crop and pruning. Sci. Hortic. 2012, 142, 205–211. [Google Scholar] [CrossRef]
- Silveira, C.; Almeida, A.; Ribeiro, C. Technological Innovation in the Traditional Olive Orchard Management: Advances and Opportunities to the Northeastern Region of Portugal. Water 2022, 14, 4081. [Google Scholar] [CrossRef]
- Taguas, V.; Marín-Moreno, V.; Barranco, D.; Rafael, P.; García-ferrer, A. Opportunities of super high-density olive orchard to improve soil quality: Management guidelines for application of pruning residues. J. Environ. Manage. 2021, 293, 112785. [Google Scholar] [CrossRef]
- Ortí, E. Determinación y Análisis de Las Condiciones Óptimas de Trabajo de Una Trituradora de eje Horizontal Sobre Restos de Poda de Cítricos; Universidad Politécnica de Valéncia: València, Spain, 2001. [Google Scholar]
- Pari, L.; Suardi, A.; Santangelo, E.; García-galindo, D.; Scarfone, A.; Alfano, V. Biomass and Bioenergy Current and innovative technologies for pruning harvesting: A review. Biomass Bioenergy 2017, 107, 398–410. [Google Scholar] [CrossRef]
- Conservation Tillage Information Center Tillage Type Definitions. Available online: https://www.extension.purdue.edu/extmedia/ct/ct-1.html (accessed on 27 March 2023).
- Buttafuoco, G.; Caloiero, T.; Coscarelli, R. Spatial uncertainty assessment in modelling reference evapotranspiration at regional scale. Hydrol. Earth Syst. Sci. 2010, 14, 2319–2327. [Google Scholar] [CrossRef] [Green Version]

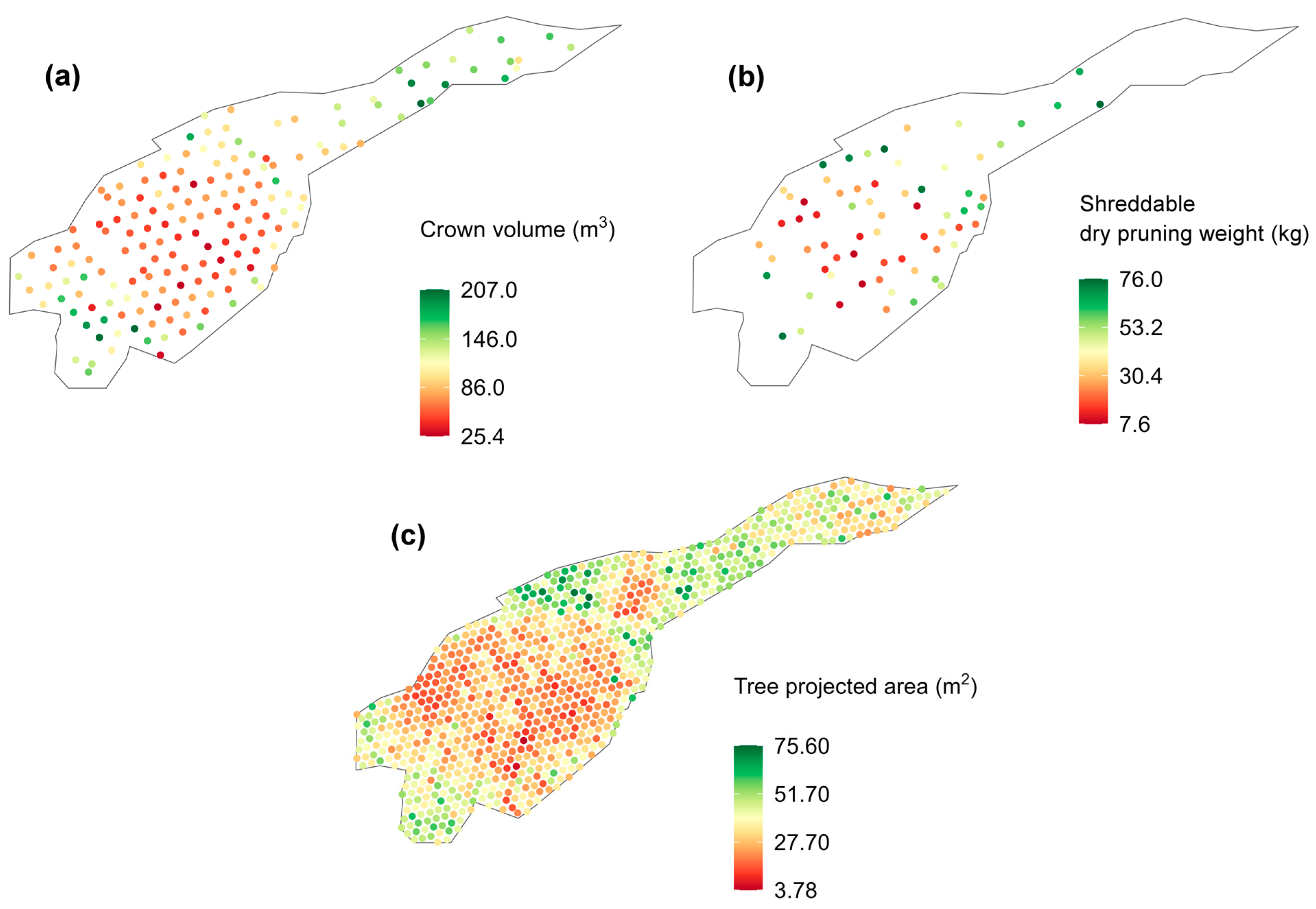
| Depth (cm) | pH (H2O) | pH (Cl2Ca) | Sand (%) | Silt (%) | Clay (%) | OC (g kg−1) | CaCO3 (%) | CEC (cmolc kg−1) |
|---|---|---|---|---|---|---|---|---|
| 0–10 | 8.2 | 7.8 | 6.2 | 44.7 | 49.1 | 7.7 | 28.6 | 25 |
| 10–20 | 8.2 | 7.8 | 10.3 | 40.4 | 49.3 | 6.8 | 28.9 | 22 |
| 20–40 | 8.4 | 7.8 | 8.1 | 42.9 | 49.0 | 6.1 | 30.7 | 24 |
| 40–60 | 8.5 | 7.8 | 8.5 | 43.0 | 48.5 | 5.7 | 32.5 | 22 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rainfall (mm) | 49.1 | 51.8 | 70.7 | 51.8 | 36.0 | 6.0 | 0.5 | 5.0 | 22.2 | 64.5 | 71.7 | 77.6 |
| Monthly temperature (°C) | ||||||||||||
| Maximum | 14.6 | 16.4 | 19.4 | 22.6 | 27.4 | 32.7 | 36.5 | 36.2 | 30.9 | 25.6 | 18.4 | 15.5 |
| Mean | 9.2 | 10.6 | 13.0 | 15.8 | 19.9 | 24.4 | 27.5 | 27.5 | 23.4 | 19.0 | 12.9 | 10.3 |
| Minimum | 4.2 | 5.1 | 7.3 | 9.8 | 12.8 | 16.2 | 18.6 | 19.2 | 16.8 | 13.4 | 7.9 | 5.7 |
| Mean ± SE | Coefficient of Variation | Minimum | Lower Quartile | Median | Upper Quartile | Maximum | |
|---|---|---|---|---|---|---|---|
| Shreddable dry pruning weight (kg) | 37.2 ± 2.51 | 0.55 | 7.6 | 19.3 | 32.6 | 50.1 | 76 |
| Tree projected area (m2 tree−1) | 34.9 ± 0.41 | 0.36 | 3.8 | 25.2 | 33.4 | 44.1 | 75.6 |
| Crown volume (m3 tree−1) | 94.5 ± 3.37 | 0.46 | 25.4 | 61.8 | 81.4 | 123.5 | 207 |
| Shreddable Dry Pruning Weight (kg) | Tree Projected Area (m2 tree−1) | Crown Volume (m3 tree−1) | ||
|---|---|---|---|---|
| Variant A | Variogram sill | C1 = 0.49; C2 = 0.51 | C1 = 0.34; C2 = 0.66 | C1 = 0.34; C2 = 0.66 |
| Variogram range (m) | a1 = 25; a2 = 188 | a1 = 15; a2 = 185 | a1 = 28; a2 = 271 | |
| Model | Sph 1; Sph | Sph; Sph | Sph; Sph | |
| Variant B | Variogram sill | Co = 0.45; C1 = 0.15; C2 = 0.40 | Co = 0.25; C1 = 0.30; C2 = 0.45 | Co = 0.30; C1 = 0.25; C2 = 0.45 |
| Variogram range (m) | ao = 0 3; a1 = 100; a2 = 200 | ao = 0; a1 = 15; a2 = 185 | ao = 0; a1 = 28; a2 = 271 | |
| Model | Sph; Sph | Sph; Sph | Sph; Exp 2 | |
| Variant C | Variogram sill | Co = 0.45; C1 = 0.15; C2 = 0.40 | Co = 0.20; C1 = 0.45; C2 = 0.35 | Co = 0.45; C1 = 0.40; C2 = 0.15 |
| Variogram range (m) | ao = 0; a1 = 50; a2 = 157 | ao = 0; a1 = 50; a2 = 180 | ao = 0; a1 = 15, a2 = 100 | |
| Model | Exp; Sph | Exp; Sph | Exp; Exp |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Lizana, A.; Ramos, A.; Pereira, M.J.; Soares, A.; Ribeiro, M.C. Assessment of the Spatial Variability and Uncertainty of Shreddable Pruning Biomass in an Olive Grove Based on Canopy Volume and Tree Projected Area. Agronomy 2023, 13, 1697. https://doi.org/10.3390/agronomy13071697
Rodríguez-Lizana A, Ramos A, Pereira MJ, Soares A, Ribeiro MC. Assessment of the Spatial Variability and Uncertainty of Shreddable Pruning Biomass in an Olive Grove Based on Canopy Volume and Tree Projected Area. Agronomy. 2023; 13(7):1697. https://doi.org/10.3390/agronomy13071697
Chicago/Turabian StyleRodríguez-Lizana, Antonio, Alzira Ramos, María João Pereira, Amílcar Soares, and Manuel Castro Ribeiro. 2023. "Assessment of the Spatial Variability and Uncertainty of Shreddable Pruning Biomass in an Olive Grove Based on Canopy Volume and Tree Projected Area" Agronomy 13, no. 7: 1697. https://doi.org/10.3390/agronomy13071697





