Flanking Variation Influences Rates of Stutter in Simple Repeats
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples, Sequencing, and Haplotype Identification
2.2. Repeat and Flanking Region Characterization
2.3. Identifying Simple Repeats and Their −1 Stutter Products
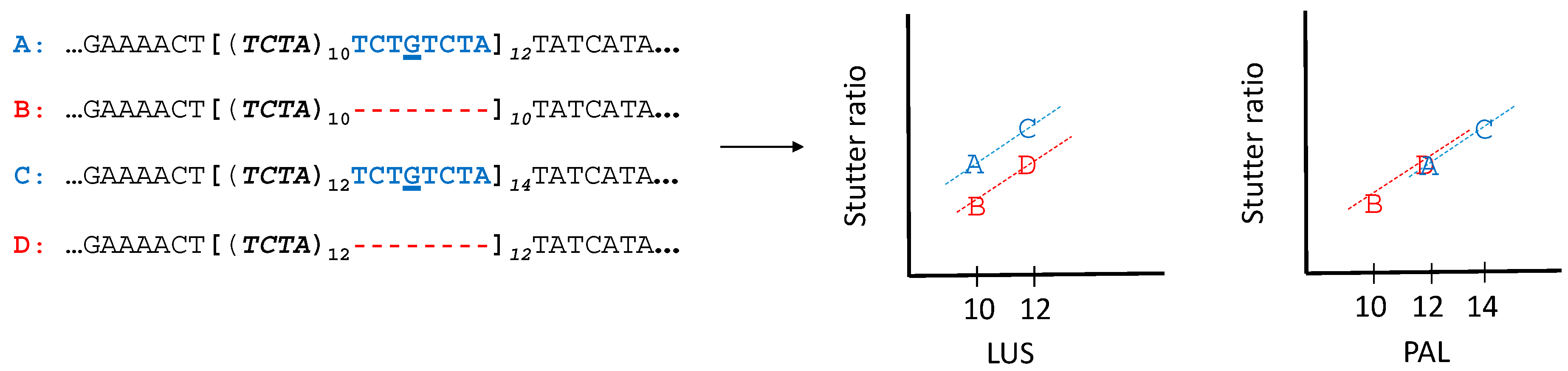
2.4. Modelling of Stutter Ratios
3. Results
3.1. The Distribution of Flanking Haplotypes
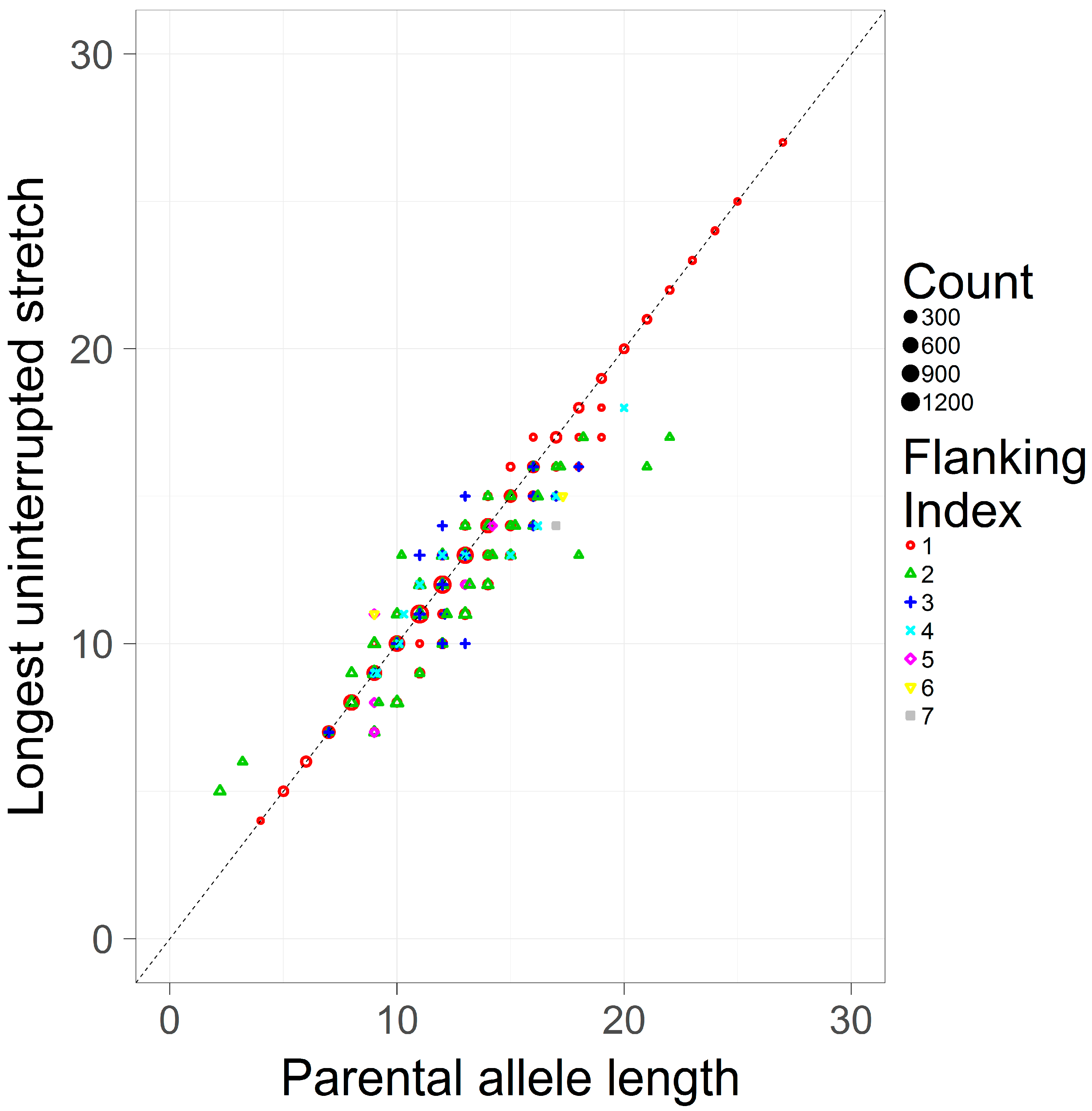
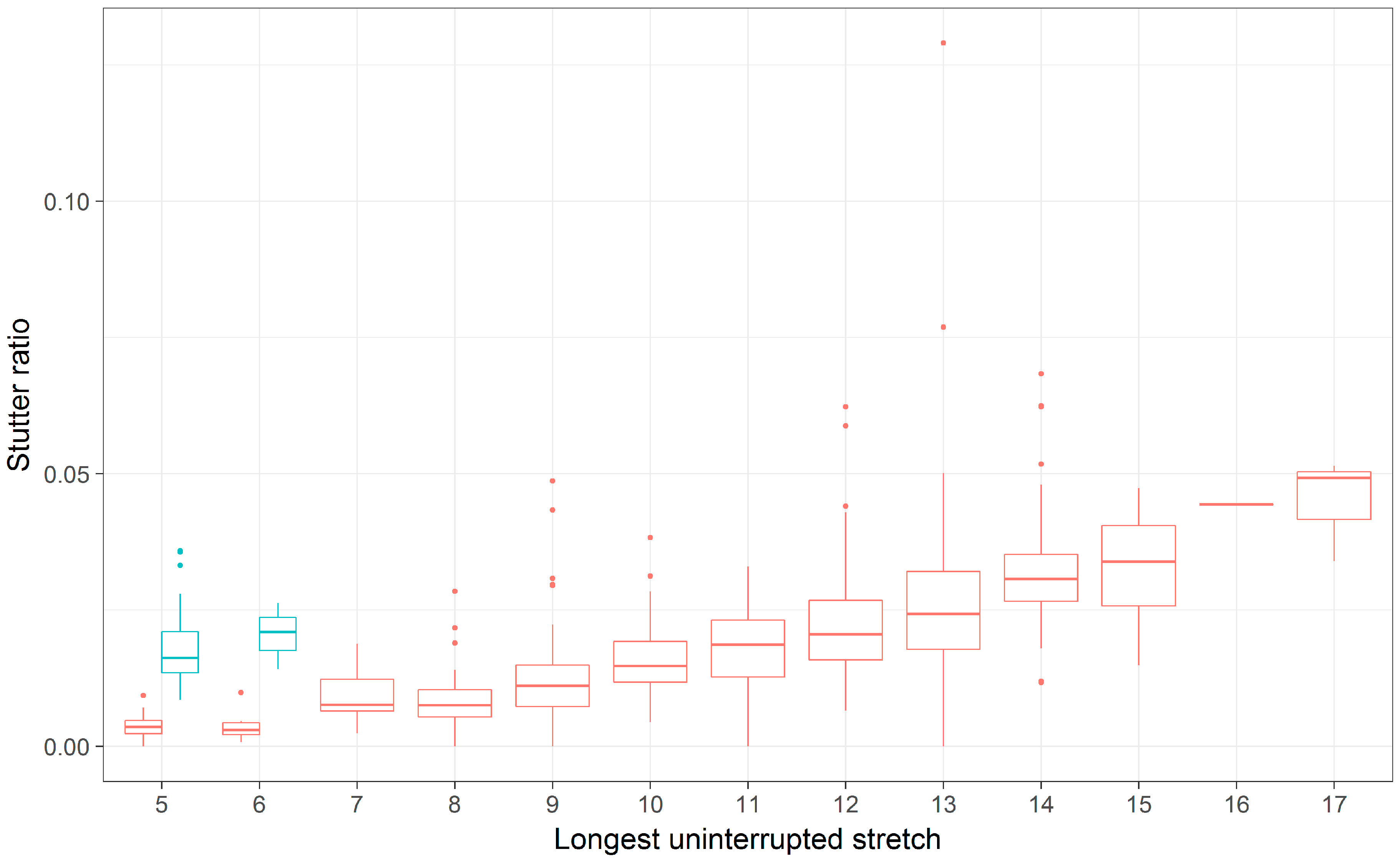
3.2. Comparing the Longest Uninterrupted Stretch to the Parental Allele Length
3.3. Coverage and the Stutter Ratio
3.4. Characterizing Flanking Sequence Variation
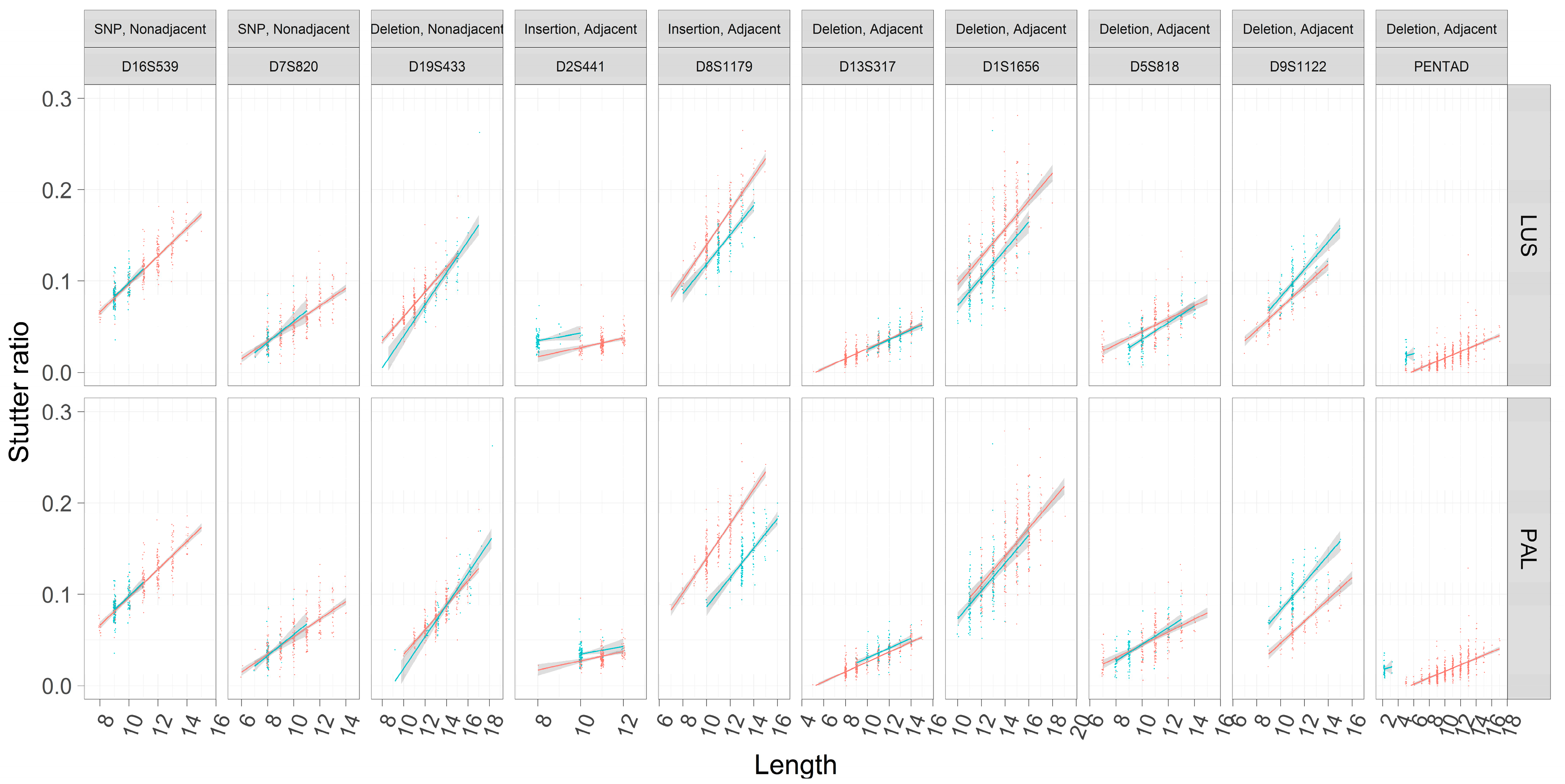
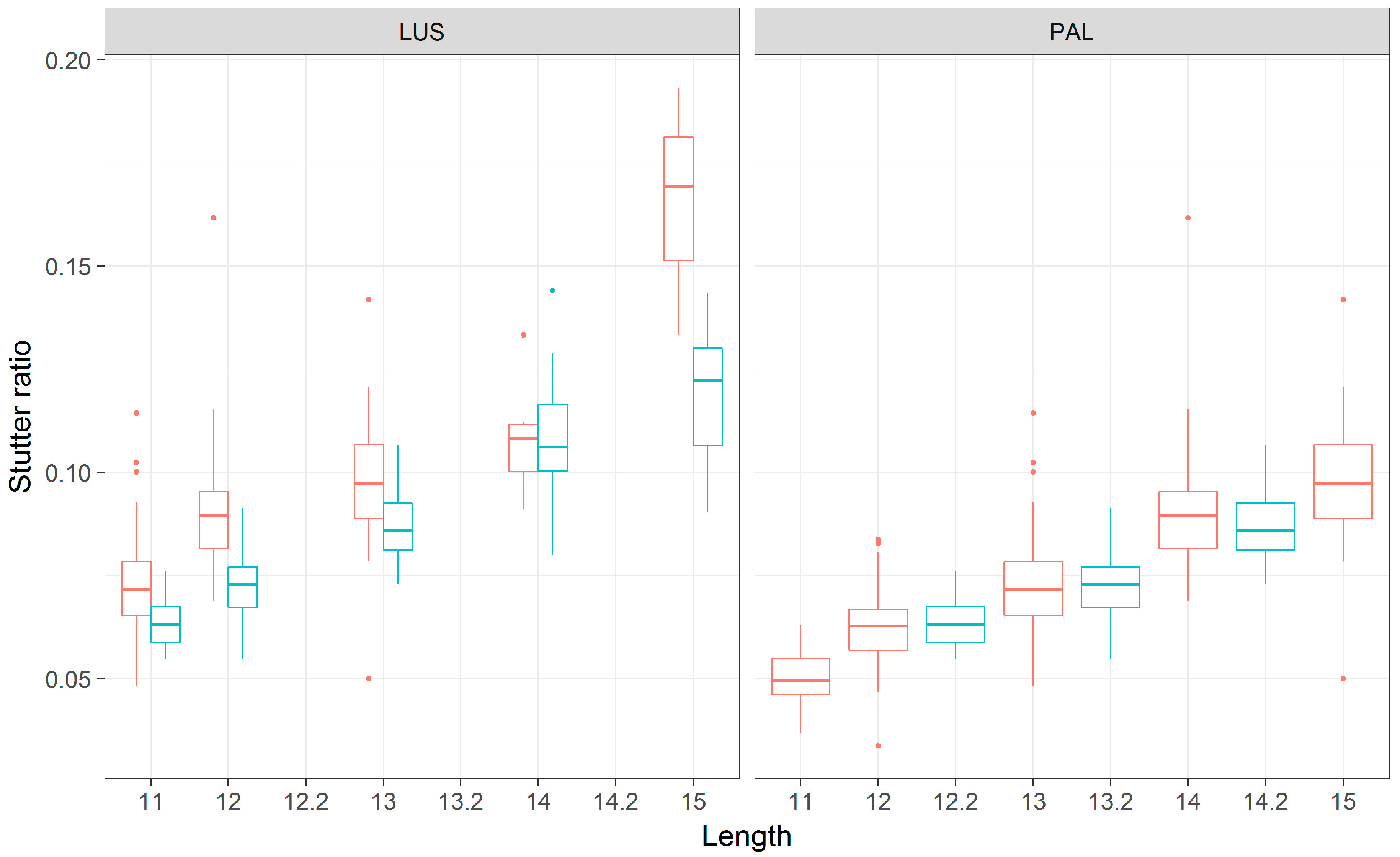
3.5. Stutter Ratios and Flanking Sequence Variation
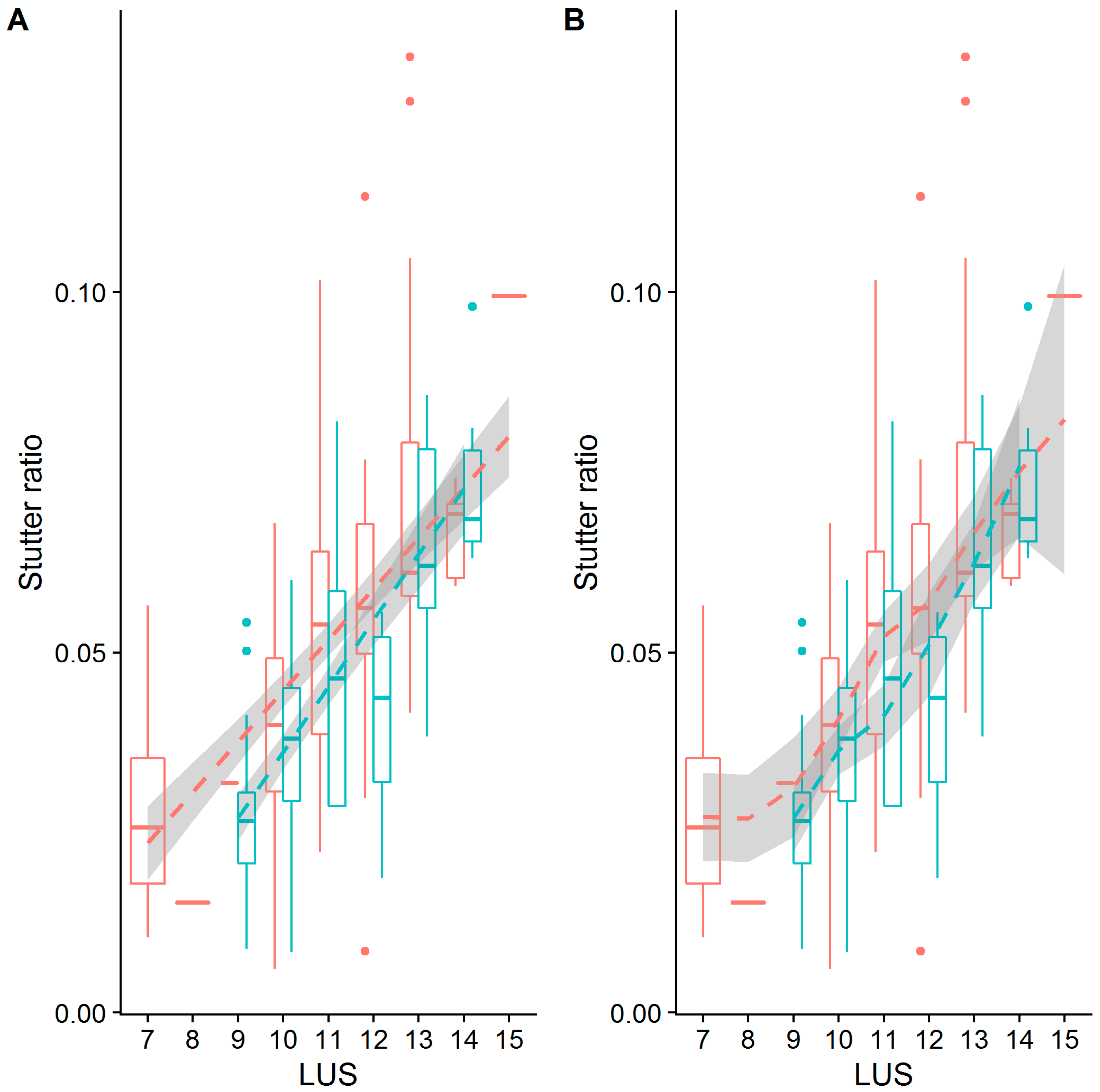
3.6. Linear Models of Stutter Ratios
4. Discussion
4.1. Nonadjacent Flanking Mutations and Stutter
4.2. Adjacent Flanking Mutations and Stutter
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Vilsen, S.B.; Tvedebrink, T.; Mogensen, H.S.; Morling, N. Statistical modelling of Ion PGM HID STR 10-plex MPS data. Forensic Sci. Int. Genet. 2017, 28, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Brookes, C.; Bright, J.A.; Harbison, S.; Buckleton, J. Characterising stutter in forensic STR multiplexes. Forensic Sci. Int. Genet. 2012, 6, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Walsh, P.S.; Fildes, N.J.; Reynolds, R. Sequence analysis and characterization of stutter products at the tetranucleotide repeat locus vWA. Nucleic Acids Res. 1996, 24, 2807–2812. [Google Scholar] [CrossRef] [PubMed]
- Bright, J.A.; Stevenson, K.E.; Coble, M.D.; Hill, C.R.; Curran, J.M.; Buckleton, J.S. Characterising the STR locus D6S1043 and examination of its effect on stutter rates. Forensic Sci. Int. Genet. 2014, 8, 20–23. [Google Scholar] [CrossRef] [PubMed]
- Bright, J.A.; Taylor, D.; Curran, J.M.; Buckleton, J.S. Developing allelic and stutter peak height models for a continuous method of DNA interpretation. Forensic Sci. Int. Genet. 2013, 7, 296–304. [Google Scholar] [CrossRef] [PubMed]
- Aponte, R.A.; Gettings, K.B.; Duewer, D.L.; Coble, M.D.; Vallone, P.M. Sequence-based analysis of stutter at STR loci: Characterization and utility. Forensic Sci. Int. Genet. Suppl. Ser. 2015, 5, e456–e458. [Google Scholar] [CrossRef]
- Bright, J.A.; Curran, J.M.; Buckleton, J.S. Modelling PowerPlex Y stutter and artefacts. Forensic Sci. Int. Genet. 2014, 11, 126–136. [Google Scholar] [CrossRef] [PubMed]
- Novroski, N.M.M.; King, J.L.; Churchill, J.D.; Seah, L.H.; Budowle, B. Characterization of genetic sequence variation of 58 STR loci in four major population groups. Forensic Sci. Int. Genet. 2016, 25, 214–226. [Google Scholar] [CrossRef] [PubMed]
- King, J.L.; Wendt, F.R.; Sun, J.; Budowle, B. STRait Razor v2s: Advancing sequence-based STR allele reporting and beyond to other marker systems. Forensic Sci. Int. Genet. 2017, 29, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; King, L.; Budowle, B. Investigation of the STR loci noise distributions of PowerSeqTM Auto System. Croat. Med. J. 2017, 58, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Parson, W.; Ballard, D.; Budowle, B.; Butler, J.M.; Gettings, K.B.; Gill, P.; Gusmão, L.; Hares, D.R.; Irwin, J.A.; King, J.L.; et al. Massively parallel sequencing of forensic STRs: Considerations of the DNA commission of the International Society for Forensic Genetics (ISFG) on minimal nomenclature requirements. Forensic Sci. Int. Genet. 2016, 22, 54–63. [Google Scholar] [CrossRef] [PubMed]
- R Core Team R: A Language and Environment for Statistical Computing. 2017. Available online: http://www.r-project.org/ (accessed on 16 November 2017).
- Yohai, V.J. High Breakdown-Point and High Efficiency Robust Estimates for Regression. Ann. Stat. 1987, 15, 642–656. [Google Scholar] [CrossRef]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis. 2009. Available online: http://ggplot2.org (accessed on 29 September 2017).
- Weusten, J.; Herbergs, J. A stochastic model of the processes in PCR based amplification of STR DNA in forensic applications. Forensic Sci. Int. Genet. 2012, 6, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Gill, P. Application of low copy number DNA profiling. Croat. Med. J. 2001, 42, 229–232. [Google Scholar] [PubMed]
- Balding, D.J.; Buckleton, J. Interpreting low template DNA profiles. Forensic Sci. Int. Genet. 2009, 4, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Caragine, T.; Mikulasovich, R.; Tamariz, J.; Bajda, E.; Sebestyen, J.; Baum, H.; Prinz, M. Validation of testing and interpretation protocols for low template DNA samples using AmpFISTR Identifiler. Croat. Med. J. 2009, 50, 250–267. [Google Scholar] [CrossRef] [PubMed]
- Klintschar, M.; Wiegand, P. Polymerase slippage in relation to the uniformity of tetrameric repeat stretches. Forensic Sci. Int. 2003, 135, 163–166. [Google Scholar] [CrossRef]
- Schlötterer, C.; Tautz, D. Slippage syntesis of simple sequence DNA. Nucleic Acids Res. 1992, 20, 211–215. [Google Scholar] [CrossRef] [PubMed]
- Lazaruk, K.; Wallin, J.; Holt, C.; Nguyen, T.; Walsh, P.S. Sequence variation in humans and other primates at six short tandem repeat loci used in forensic identity testing. Forensic Sci. Int. 2001, 119, 1–10. [Google Scholar] [CrossRef]
- Kelly, H.; Bright, J.A.; Buckleton, J.S.; Curran, J.M. Identifying and modelling the drivers of stutter in forensic DNA profiles. Aust. J. Forensic Sci. 2014, 46, 194–203. [Google Scholar] [CrossRef]
- Fisher, R.A. Combining independent tests of significance. Am. Stat. 1948, 2, 30. [Google Scholar]
- Heinrich, M.; Felske-Zech, H.; Brinkmann, B.; Hohoff, C. Characterisation of variant alleles in the STR systems D2S1338, D3S1358 and D19S433. Int. J. Leg. Med. 2005, 119, 310–313. [Google Scholar] [CrossRef] [PubMed]
- Olofsson, J.; Andersen, M.M.; Mogensen, H.S.; Eriksen, P.S.; Morling, N. Sequence variants of allele 22 and 23 of DYS635 causing different stutter rates. Forensic Sci. Int. Genet. 2012, 6, e161–e162. [Google Scholar] [CrossRef] [PubMed]
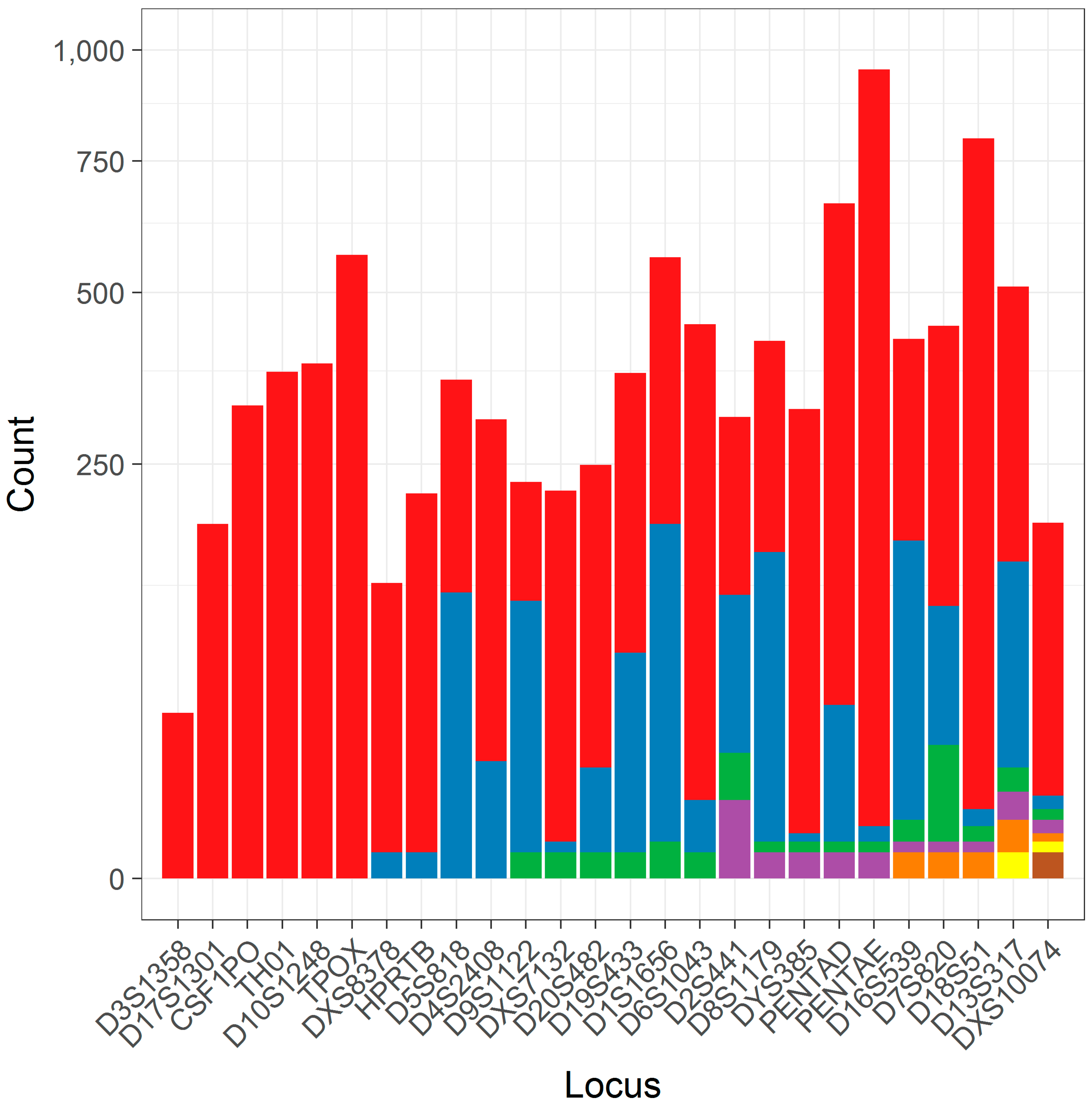

| Locus | Number of Alleles Considered (Total) | Number of Unique Flanking Haplotypes |
|---|---|---|
| D3S1358 | 40 | 1 |
| D17S1301 | 183 | 1 |
| CSF1PO | 326 | 1 |
| TH01 | 374 | 1 |
| D10S1248 | 386 | 1 |
| TPOX | 566 | 1 |
| DXS8378 | 127 | 2 |
| HPRTB | 216 | 2 |
| D4S2408 | 307 | 2 |
| D5S818 | 362 | 2 |
| DXS7132 | 219 | 3 |
| D9S1122 | 229 | 3 |
| D20S482 | 249 | 3 |
| D19S433 | 372 | 3 |
| D6S1043 | 447 | 3 |
| D1S1656 | 562 | 3 |
| D2S441 | 310 | 4 |
| DYS385 | 321 | 4 |
| D8S1179 | 421 | 4 |
| PENTA D | 664 | 4 |
| PENTA E | 953 | 4 |
| D16S539 | 424 | 5 |
| D7S820 | 445 | 5 |
| D18S51 | 798 | 5 |
| D13S317 | 510 | 6 |
| DXS10074 | 184 | 7 |
| Type of Change | Location of Change | Locus | Repeat Motif | Plausible Evolutionary Explanation |
|---|---|---|---|---|
| CT Deletion | Nonadjacent | D19S433 | CCTT | Indel in flank |
| A → C | Nonadjacent | D16S539 | GATA | SNP in flank |
| G → A | Nonadjacent | D7S820 | TATC | SNP in flank |
| AAAGAAAAAAAAG Deletion | Adjacent | PENTAD | AAAGA | Indel (non-slippage) |
| TCTGTCTA Insertion | Adjacent | D2S441 | TCTA | SNP in repeat |
| TCTATCTG Insertion | Adjacent | D8S1179 | TCTA | SNP in repeat |
| TAGATCGA Deletion | Adjacent | D9S1122 | TAGA | SNP in repeat |
| AATC Deletion | Adjacent | D13S317 | TATC | SNP in repeat or indel |
| CCTA Deletion | Adjacent | D1S1656 | TCTA | SNP in repeat or indel |
| CTCT Deletion | Adjacent | D5S818 | ATCT | SNP in repeat or indel |
| Locus | Max VIF | R2 | Intercept, Haplotype 1 | Intercept, Haplotype 2 | p-Value (Same Intercept) | PAL Slope, Haplotype 1 | PAL Slope, Haplotype 2 | p-Value (Same Slope) | Slope, Correct | p-Value (Correct) |
|---|---|---|---|---|---|---|---|---|---|---|
| D13S317 | 1.2 | 0.761 | −0.031 | −0.028 | 5.7 × 10−06 | 0.006 | -- | -- | 7.69 × 10−07 | 0.263 |
| D16S539 | 1.2 | 0.794 | −0.053 | −0.051 | 0.173 | 0.015 | -- | -- | −1.41 × 10−06 | 0.277 |
| D19S433 | 1.2 | 0.735 | −0.083 | −0.083 | 0.995 | 0.013 | -- | -- | −2.24 × 10−06 | 0.025 |
| D1S1656 | 1.7 | 0.606 | −0.063 | −0.072 | 0.005 | 0.015 | -- | -- | −1.38 × 10−05 | 0.154 |
| D2S441 | 1.4 | 0.221 | −0.035 | −0.027 | 6.6 × 10−13 | 0.006 | -- | -- | 2.66 × 10−06 | 0.008 |
| D5S818 | 1.6 | 0.445 | −0.023 | −0.047 | 0.009 | 0.007 | 0.009 | 0.008 | 3.80 × 10−06 | 0.466 |
| D7S820 | 1.2 | 0.654 | −0.040 | −0.042 | 0.125 | 0.009 | -- | -- | 1.36 × 10−07 | 0.952 |
| D8S1179 | 1.9 | 0.695 | −0.045 | −0.105 | 1.2 × 10−88 | 0.018 | -- | -- | 1.30 × 10−06 | 0.514 |
| D9S1122 | 1.1 | 0.684 | −0.078 | −0.038 | 5.5 × 10−48 | 0.013 | -- | -- | −4.06 × 10−06 | 0.287 |
| PENTAD | 2.3 | 0.481 | −0.017 | 0.010 | 2.0 × 10−55 | 0.003 | -- | -- | 5.31 × 10−07 | 0.602 |
| Locus | Max VIF | R2 | Intercept, Haplotype 1 | Intercept, Haplotype 2 | p-Value (Same Intercept) | LUS Slope, Haplotype 1 | LUS Slope, Haplotype 2 | p-Value (Same Slope) | Slope, Correct | p-Value (Correct) |
|---|---|---|---|---|---|---|---|---|---|---|
| D13S317 | 1.4 | 0.761 | −0.031 | −0.033 | 0.024 | 0.006 | -- | -- | 7.69 × 10−07 | 0.263 |
| D16S539 | 1.2 | 0.794 | −0.053 | −0.051 | 0.173 | 0.015 | -- | -- | −1.41 × 10−06 | 0.277 |
| D19S433 | 1.2 | 0.735 | −0.059 | −0.069 | 2.7 × 10−08 | 0.012 | -- | -- | −2.24 × 10−06 | 0.025 |
| D1S1656 | 1.2 | 0.606 | −0.049 | −0.072 | 6.4 × 10−19 | 0.015 | -- | -- | −1.38 × 10−05 | 0.154 |
| D2S441 | 6.4 | 0.221 | −0.035 | −0.016 | 4.6 × 10−17 | 0.006 | -- | -- | 2.66 × 10−06 | 0.008 |
| D5S818 | 1.4 | 0.445 | −0.023 | −0.056 | 0.001 | 0.007 | 0.009 | 0.008 | 3.80 × 10−06 | 0.466 |
| D7S820 | 1.2 | 0.654 | −0.040 | −0.042 | 0.125 | 0.009 | -- | -- | 1.36 × 10−07 | 0.952 |
| D8S1179 | 1.1 | 0.695 | −0.045 | −0.068 | 1.2 × 10−35 | 0.018 | -- | -- | 1.30 × 10−06 | 0.514 |
| D9S1122 | 1.3 | 0.684 | −0.053 | −0.038 | 2.4 × 10−10 | 0.013 | -- | -- | −4.06 × 10−06 | 0.287 |
| PENTAD | 1.5 | 0.481 | −0.017 | 0.001 | 5.7 × 10−41 | 0.003 | -- | -- | 5.31 × 10−07 | 0.602 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woerner, A.E.; King, J.L.; Budowle, B. Flanking Variation Influences Rates of Stutter in Simple Repeats. Genes 2017, 8, 329. https://doi.org/10.3390/genes8110329
Woerner AE, King JL, Budowle B. Flanking Variation Influences Rates of Stutter in Simple Repeats. Genes. 2017; 8(11):329. https://doi.org/10.3390/genes8110329
Chicago/Turabian StyleWoerner, August E., Jonathan L. King, and Bruce Budowle. 2017. "Flanking Variation Influences Rates of Stutter in Simple Repeats" Genes 8, no. 11: 329. https://doi.org/10.3390/genes8110329
APA StyleWoerner, A. E., King, J. L., & Budowle, B. (2017). Flanking Variation Influences Rates of Stutter in Simple Repeats. Genes, 8(11), 329. https://doi.org/10.3390/genes8110329





