A Polarized Atmospheric Radiative Transfer Model for Calculations of Spectra of the Stokes Parameters of Shortwave Radiation Based on the Line-by-Line and Monte Carlo Methods
Abstract
:1. Introduction
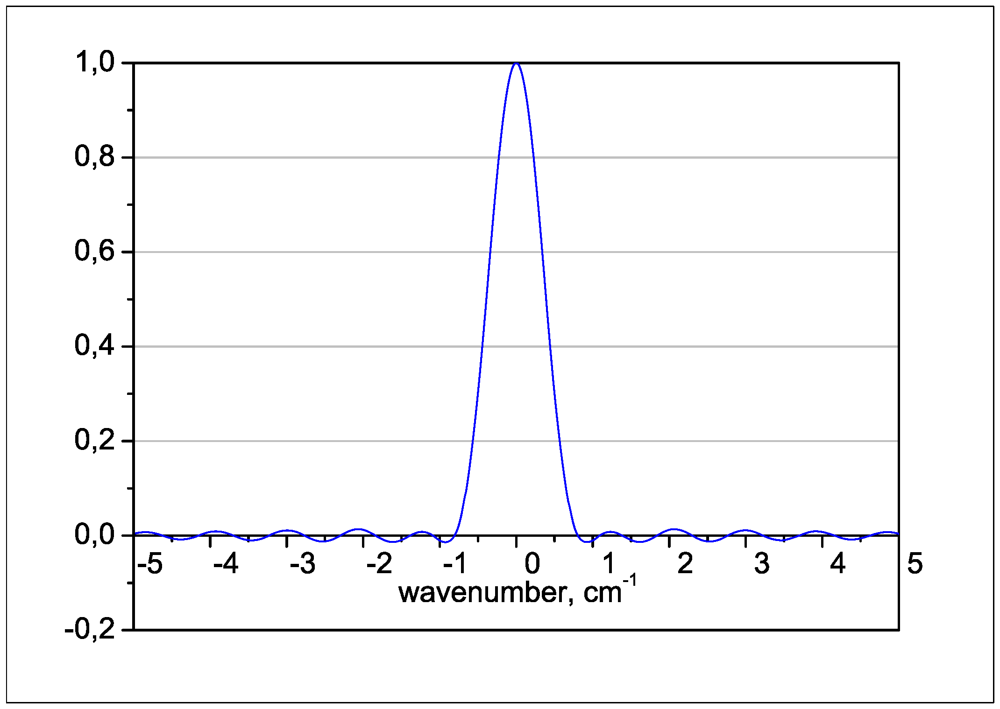
2. Description of the Model
2.1. Computation of the Parameters of Electromagnetic Scattering on Spherical Polydispersions
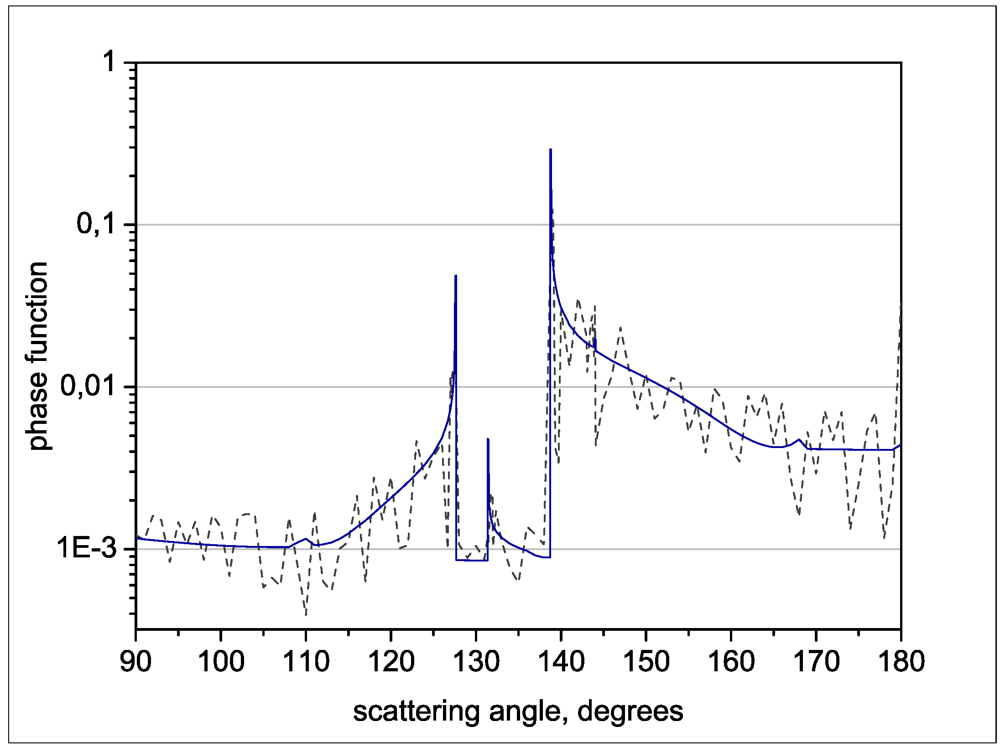
2.2. Computation of the Molecular Spectra

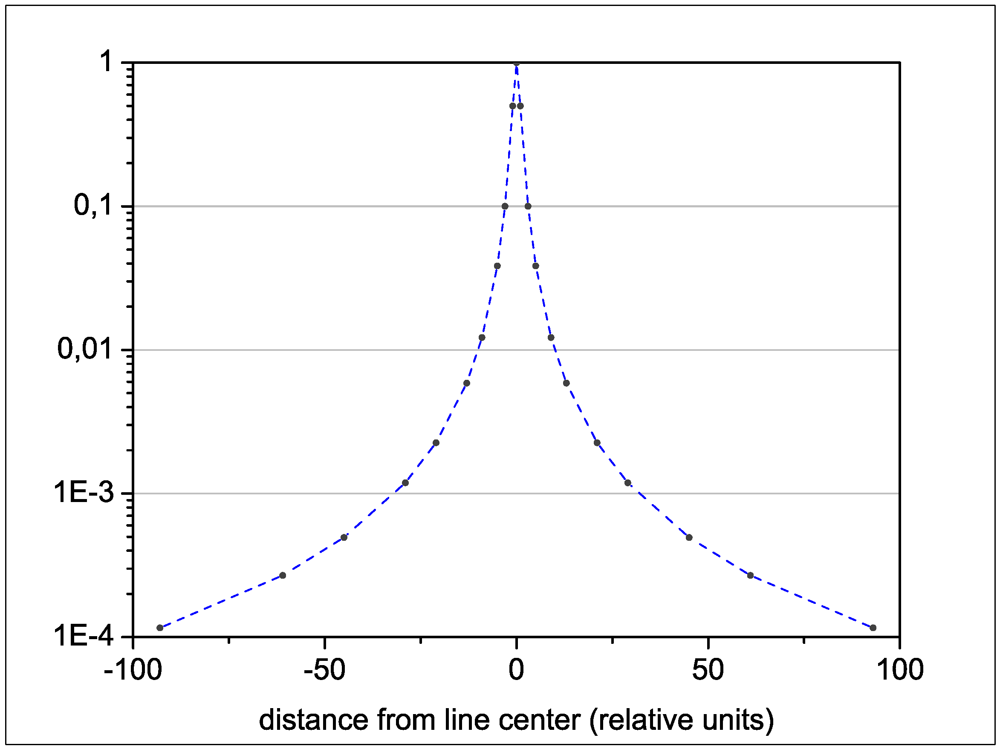

2.3. Applied MC Technique
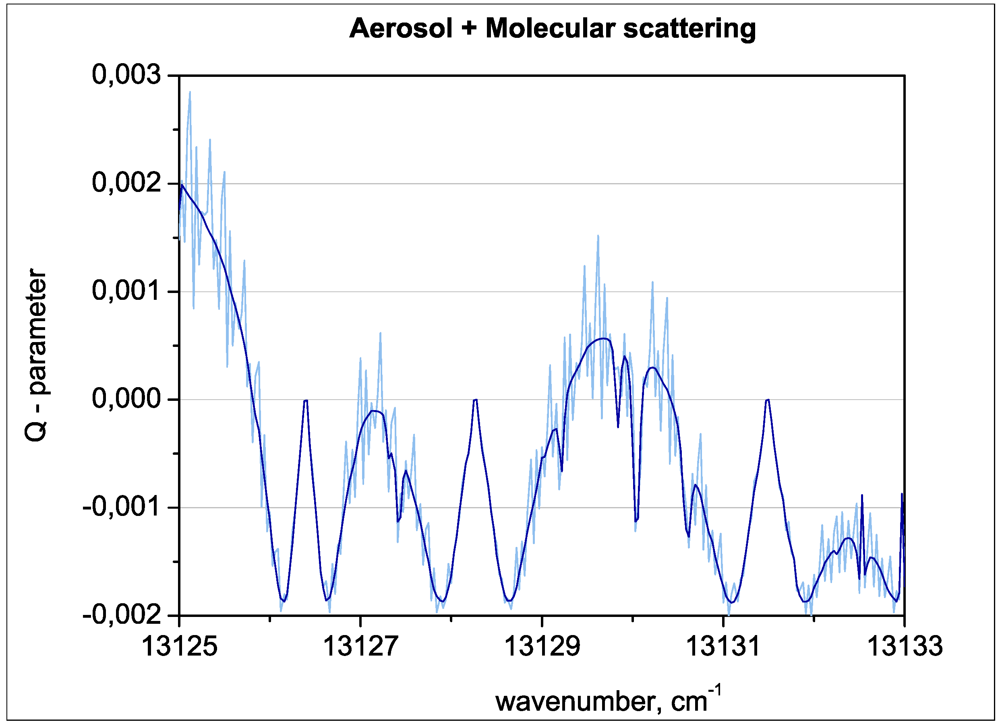
3. Validations against Benchmark Results

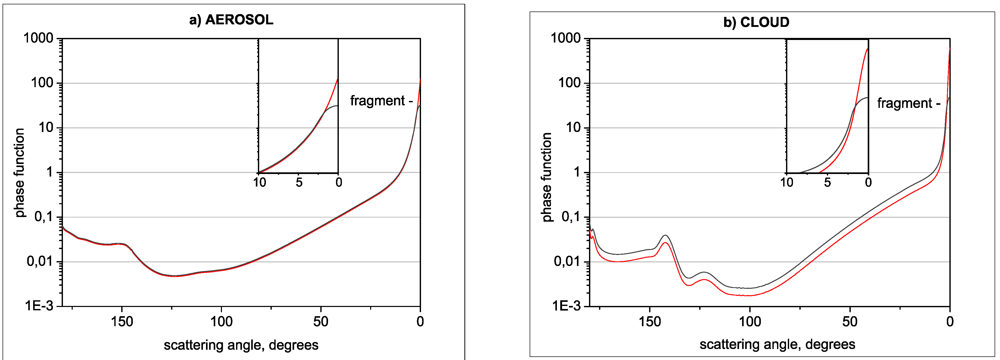
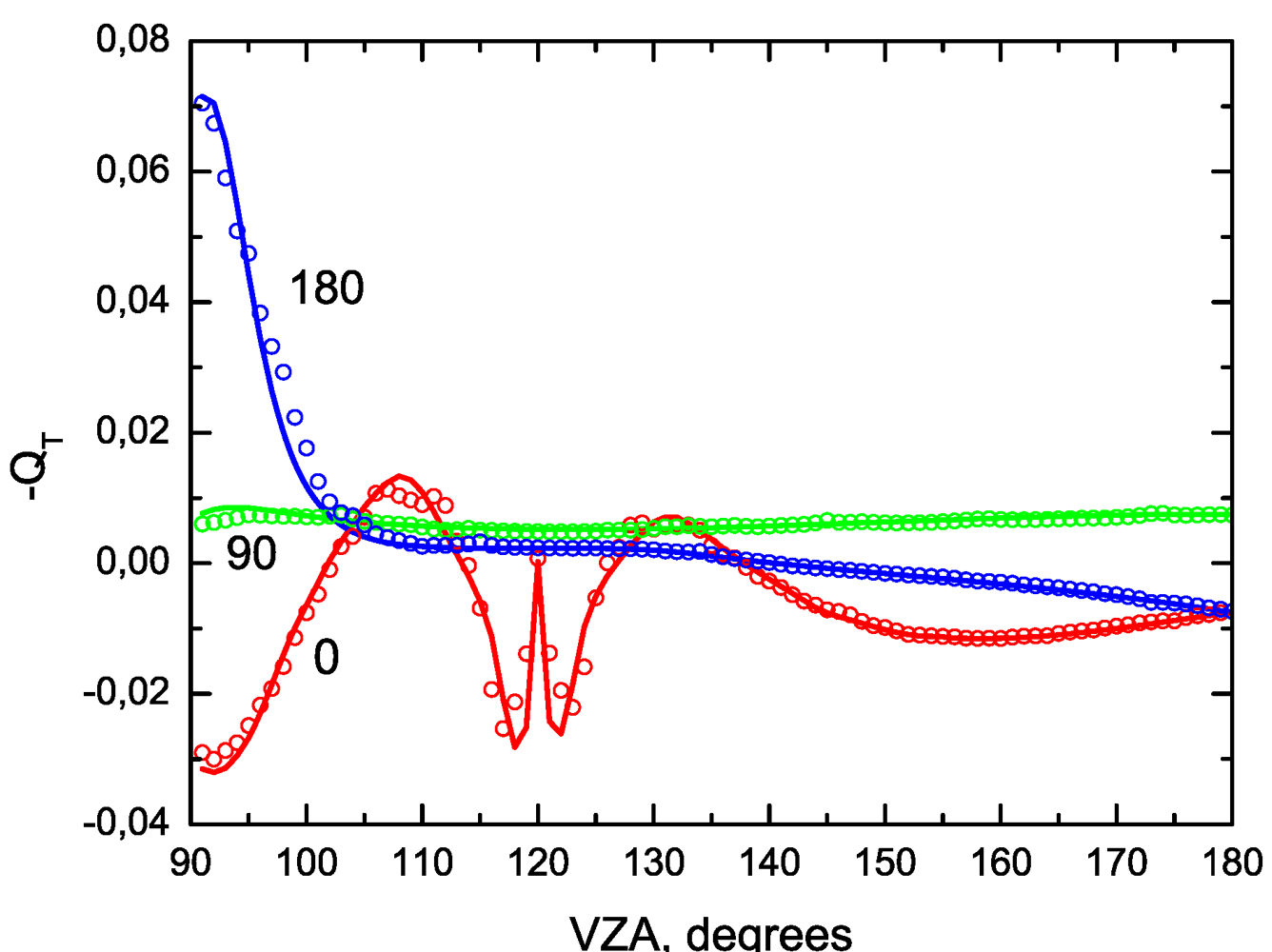
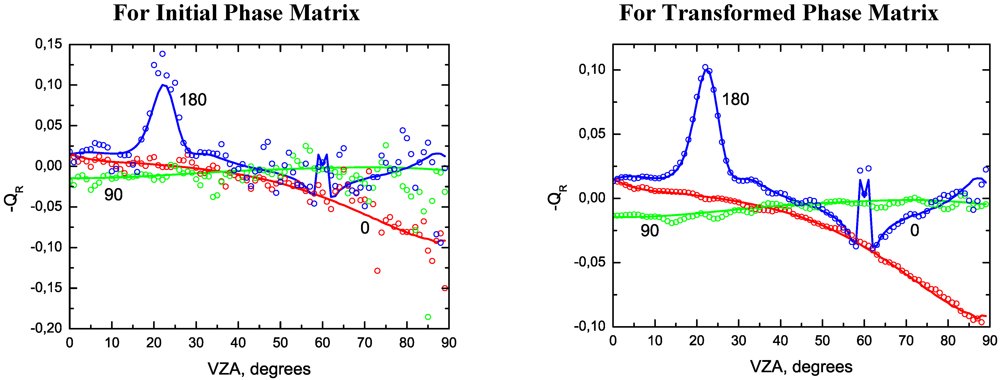
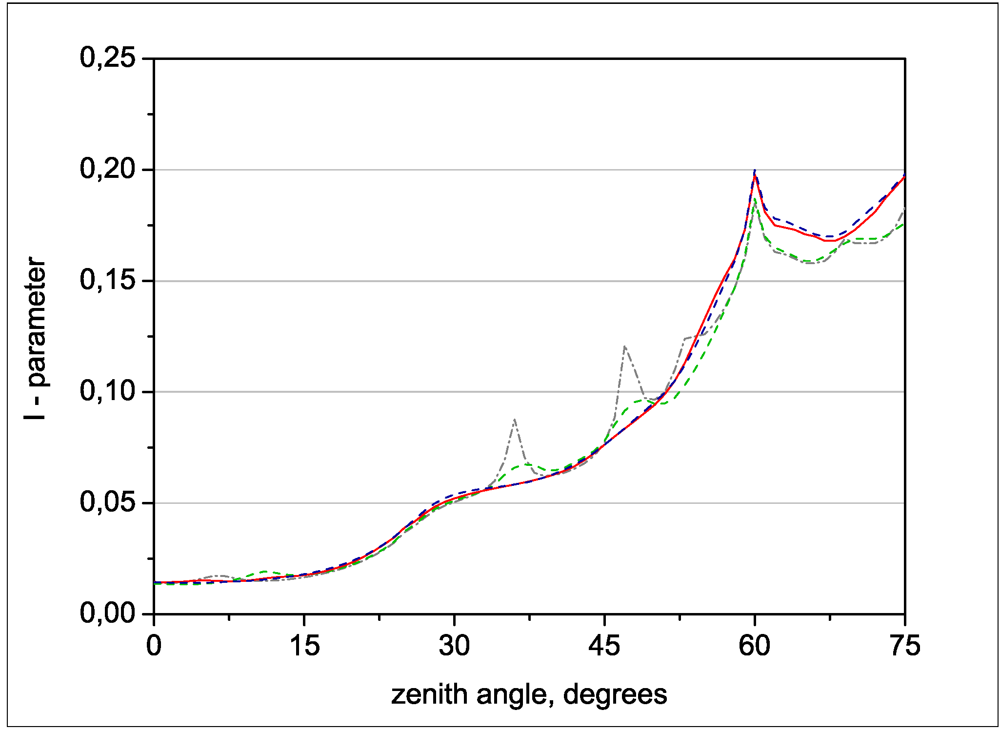
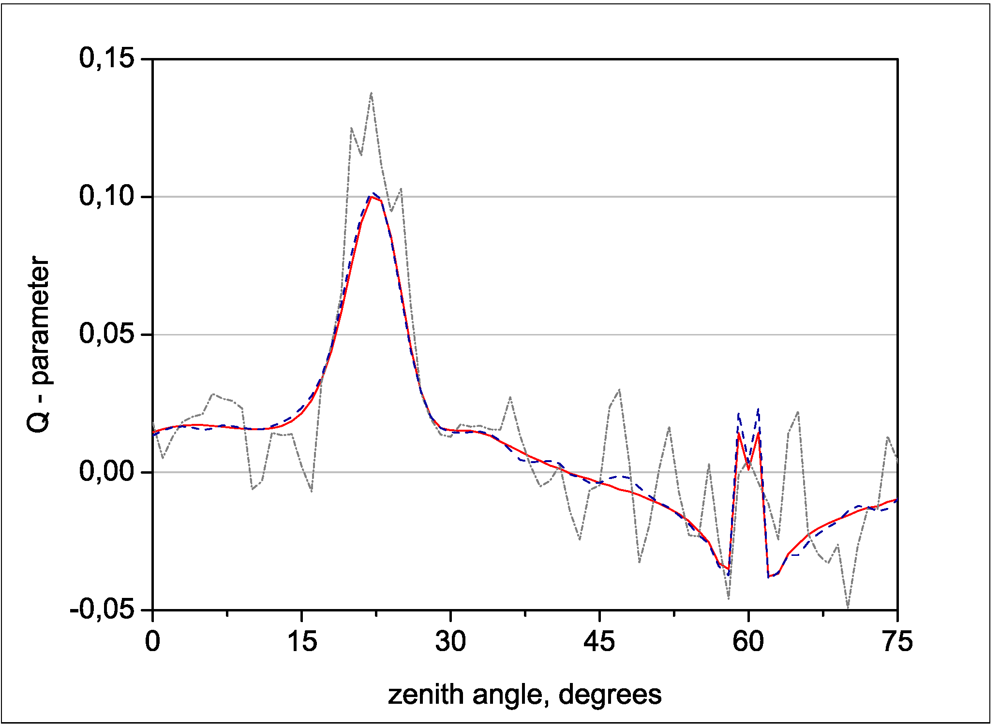
4. Application to Remote Sensing
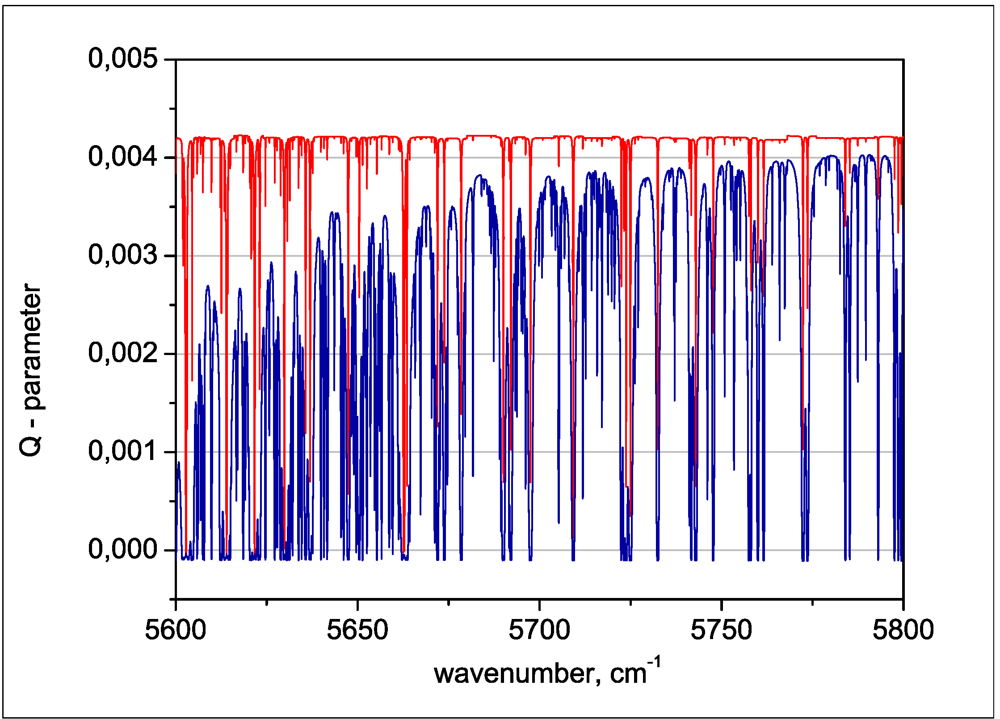
4.1. Retrieval of the Structure of Clouds and Aerosols





| X1 = 0.04 | X2 = 0.03 | X3 = 0.02 | X4 = 0.01 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNR | N = 6,400 | 800 | 200 | N = 6,400 | 800 | 200 | N = 6,400 | 800 | 200 | N = 6,400 | 800 | 200 |
| 1,000 | 1.7 | 5 | 10 | 5 | 16 | 30 | 7 | 21 | 40 | 5 | 16 | 30 |
| 333 | 5 | 15 | 30 | 16 | 47 | 91 | 21 | 64 | 121 | 16 | 48 | 89 |
| 100 | 17 | 52 | 102 | 53 | 156 | 305 | 71 | 213 | 402 | 53 | 160 | 297 |
| X1=0.04 | X2=0.03 | X3=0.02 | X4=0.01 | |||||
|---|---|---|---|---|---|---|---|---|
| SNR | 1/32 | 1.0 | 1/32 | 1.0. | 1/32 | 1.0. | 1/32 | 1.0 |
| 1,000 | 7.9 | 10 | 20 | 30 | 21 | 40 | 14 | 30 |
| 333 | 24 | 30 | 59 | 91 | 63 | 121 | 41 | 89 |
| 100 | 79 | 102 | 196 | 305 | 211 | 402 | 137 | 297 |
4.2. Time Considerations for High Resolution Spectra Calculations
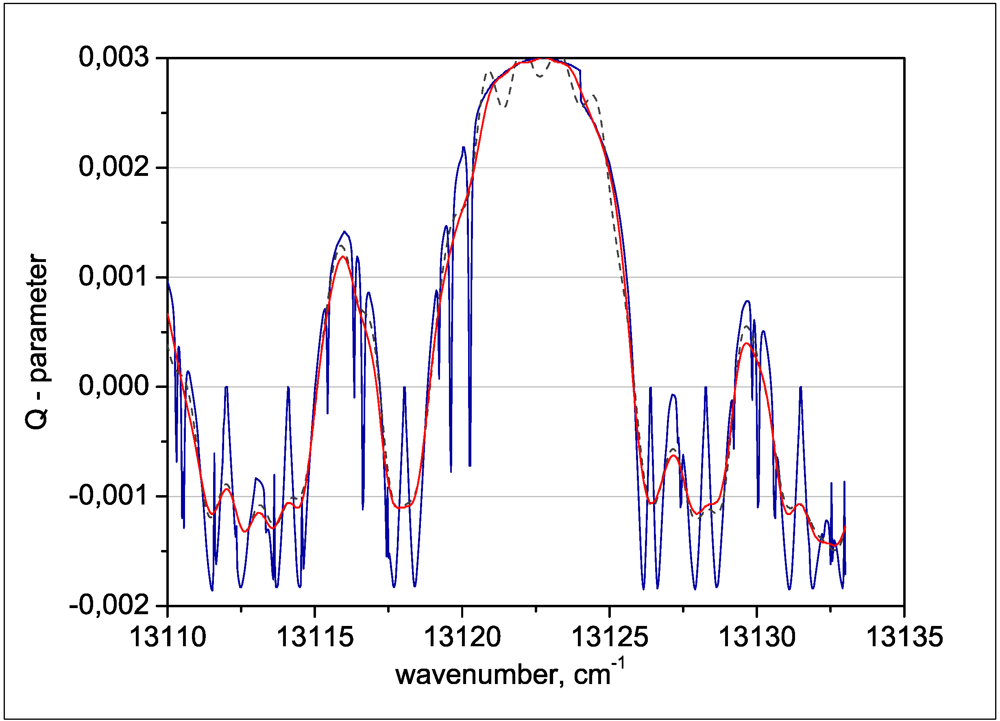
5. Conclusions
Acknowledgments
References
- IPCC. Summary for Policymakers. Available online: http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-spm.pdf (accessed on 15 December 2007).
- King, M.D.; Menzel, P.W.; Kaufman, Y.J.; Tanre, D.; Gao, B.C.; Platnick, S.; Ackerman, S.A.; Remer, L.A.; Pincus, R.; Hubanks, P.A. Cloud and aerosol properties, precipitable water, profiles of temperature and water vapor from MODIS. IEEE Trans. Geosci. Remote Sens. 2003, 41, 442–458. [Google Scholar] [CrossRef]
- Bizzari, B. The space-based global observing system in 2011 (GOS-2011). Available online: ftp://ftp.wmo.int/Documents/PublicWeb/sat/DossierGOS (accessed on 1 September 2011).
- Chang, F.L.; Li, Z. Estimating the vertical variation of cloud droplet effective radius using multispectral near-infrared satellite measurements. J. Geophys. Res. 2002, 107, 1–12. [Google Scholar]
- Fisher, J.; Grassl, H. Detection of cloud top-height from backscattered radiances within the oxygen A-band. Part 1: Theoretical study. J. Appl. Meteorol. 1991, 30, 1245–1259. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. Reference. In Cloud Optics; Springer: Berlin, Germany, 2006. [Google Scholar]
- Liou, K.N.; Goody, R.M.; West, R. CIRRUS: A Low Cost Cloud/Climate Mission. Office of Space Science NASA: Washington, DC, USA, 1996. [Google Scholar]
- Mishchenko, M.I.; Hovenier, J.W.; Travis, L.D. Reference. In Light Scattering by Nonspherical Particles; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Kokhanovsky, A.A.; Budak, V.P.; Cornet, C.; Duan, M.; Emde, C.; Katsev, I.L.; Klyukov, D.A.; Korkin, S.V.; C-Labonnote, L.; Mayer, B.; Min, Q.; Nakajima, T.; Ota, Y.; Prikhach, A.S.; Rozanov, V.V.; Yokota, T.; Zege, E.P. Benchmark results in vector atmospheric radiative transfer. J. Quant. Spectrosc. Rad. Transfer. 2010, 111, 1931–1946. [Google Scholar] [CrossRef]
- Fomin, B.A.; Correa, M.P. A k-distribution technique for radiative transfer simulation in inhomogeneous atmosphere: 2. FKDM, fast k-distribution model for the shortwave. J. Geophys. Res. 2005. [Google Scholar] [CrossRef]
- Tarasova, T.A.; Fomin, B.A. The use of new parameterizations for gaseous absorption in the CLIRAD-SW solar radiation code for models. J. Atmos. Ocean. Technol. 2007, 24, 1157–1163. [Google Scholar] [CrossRef]
- Fomin, B.A.; Mazin, I.P. Model for an investigation of radiative transfer in cloudy atmosphere. Atmos. Res. 1998. [Google Scholar] [CrossRef]
- Halthore, R.N.; Crisp, D.; Schwartz, S.E.; Anderson, G.P.; Berk, A.; Bonnel, B.; Boucher, O.; Chang, F.-L.; Chou, M.-D.; Clothiax, E.E.; Dubuisson, P.; Fomin, B.; Fouquart, Y.; Freidenreich, S.; Gautier, C.; Kato, S.; Lazlo, I.; Li, Z.; Plana-Fattori, A.; Ramaswamy, V.; Ricchiazzi, P.; Shiren, Y.; Trischenko, A.; Wiscombe, W. Intercomparison of shortwave radiative transfer codes and measurements. J. Geophys. Res. 2005. [Google Scholar] [CrossRef]
- Forster, P.; Fomichev, V.; Rozanov, E.; Cagnazzo, C.; Jonsson, A.; Langematz, U.; Fomin, B.; Iacono, M.; Mayer, B.; Mlawer, E.; Myhre, G.; Portmann, R.; Akiyoshi, H.; Falaleeva, V.; Gillett, N.; Karpechko, A.; Li, J.; Lemennais, P.; Morgenstern, O.; Oberländer, S.; Sigmond, M.; Shibata, K. Evaluation of radiation scheme performance within chemistry climate models. J. Geophys. Res. 2011. [Google Scholar] [CrossRef]
- Oreopulos, L.; Mlawer, E.; Delamere, J.; Shippert, T.; Cole, J.; Fomin, B.; Iacono, M.; Jin, Z.; Manners, J.; Raisanen, P.; Rose, F.; Zhang, Y.; Wilson, M.; Rossow, W. The continual intercomparison of radiation codes: Results from phase I. J. Geophys.Res. 2012. [Google Scholar] [CrossRef]
- Cornet, C.; C-Labonnote, L.; Szcap, F. Three-dimensional polarized Monte Carlo atmospheric radiative transfer model (3DMCPOL): 3D effects on polarized visible reflectances of a cirrus cloud. J. Quant. Spectrosc. Rad. Transfer. 2010, 111, 174–186. [Google Scholar] [CrossRef]
- Fomin, B.A. Effective interpolation technique for line-by-line calculations of radiation absorption in gases. J. Quant. Spectrosc. Rad. Transfer. 1995, 53, 663–669. [Google Scholar] [CrossRef]
- Kuntz, M.; Hopfner, M. Efficient line-by-line calculation of absorbing coefficients. J. Quant. Spectrosc. Rad. Transfer. 1999, 110, 97–104. [Google Scholar] [CrossRef]
- Rothman, L.S.; Gordon, I. E.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Boudon, V.; Brown, L.R.; Campargue, A.; Champion, J.-P.; Chance, K.; Coudert, L.H.; Dana, V.; Devi, V.M.; Fally, S.; Flaud, J.-M.; Gamache, R.R.; Goldman, A.; Jacquemart, D.; Kleiner, I.; Lacome, N.; Lafferty, W.J.; Mandin, J.-Y.; Massie, S.T.; Mikhailenko, S.N.; Miller, C.E.; Moazzen-Ahmadi, N.; Naumenko, O.V.; Nikitin, A.V.; Orphal, J.; Perevalov, V.I.; Perrin, A.; Predoi-Cross, A.; Rinsland, C.P.; Rotger, M.; Šimečková, M.; Smith, M.A.H.; Sung, K.; Tashkun, S.A.; Tennyson, J.; Toth, R.A.; Vandaele, A.C.; Vander Auwera, J. The HITRAN 2008 molecular spectroscopic database. J. Quant. Spectrosc. Rad. Transfer. 2009, 110, 533–572. [Google Scholar]
- Clough, S.A.; Shepard, M.W.; Mlawer, E.J.; Delamere, J.S.; Jacono, M.J.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Rad. Transfer. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Marchuk, G.I.; Mikhailov, G.A.; Nazaraliev, M.A.; Darbijan, R.A.; Kargin, B.A.; Elepov, B.S. Reference. In The Monte Carlo Method in Atmospheric Optics; Springer: New York, NY, USA, 1980. [Google Scholar]
- Evans, K.F.; Marshak, A. Numerical Methods. In 3D Radiative Transfer in Cloudy Atmospheres; Springer: Berlin, Germany, 2005. [Google Scholar]
- Fomin, B.A.; Rublev, A.N.; Trotsenko, A.N. Line-by-line Procedures to Compute Radiative Transfer Parameters in Scattering Atmosphere. In Proceeding of IRS’92: Current Problems in Atmospheric Radiation. A.DEEPAK Publishing: Hampton, VA, USA, 1993. [Google Scholar]
- Chandrasekhar, S. Reference. In Radiative Transfer; Dover: New York, NY, USA, 1960. [Google Scholar]
- Sushkevich, T.A. Reference. In Mathematical Models of Radiation Transfer; BINOM: Moscow, Russia, 2005. (in Russian) [Google Scholar]
- Romanov, S.V.; Trotsenko, A.N.; Fomin, B.A. Reference. In Application of the Numerical Methods to Describe the Transfer of Solar Radiation in The Scattering Atmosphere with Accurate Treatment of The Selective Gas Absorption; Preprint Institute of Atomic Energy: Moscow, Russia, 1991. (in Russian) [Google Scholar]
- Rodgers, C.D. Reference. In Inverse Method for Atmospheric Sounding; World Scientific: River Edge, NJ, USA, 2000. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fomin, B.; Falaleeva, V. A Polarized Atmospheric Radiative Transfer Model for Calculations of Spectra of the Stokes Parameters of Shortwave Radiation Based on the Line-by-Line and Monte Carlo Methods. Atmosphere 2012, 3, 451-467. https://doi.org/10.3390/atmos3040451
Fomin B, Falaleeva V. A Polarized Atmospheric Radiative Transfer Model for Calculations of Spectra of the Stokes Parameters of Shortwave Radiation Based on the Line-by-Line and Monte Carlo Methods. Atmosphere. 2012; 3(4):451-467. https://doi.org/10.3390/atmos3040451
Chicago/Turabian StyleFomin, Boris, and Victoria Falaleeva. 2012. "A Polarized Atmospheric Radiative Transfer Model for Calculations of Spectra of the Stokes Parameters of Shortwave Radiation Based on the Line-by-Line and Monte Carlo Methods" Atmosphere 3, no. 4: 451-467. https://doi.org/10.3390/atmos3040451




