Comparative Spectral Analysis and Correlation Properties of Observed and Simulated Total Column Ozone Records
Abstract
:1. Introduction
2. Data and Methods
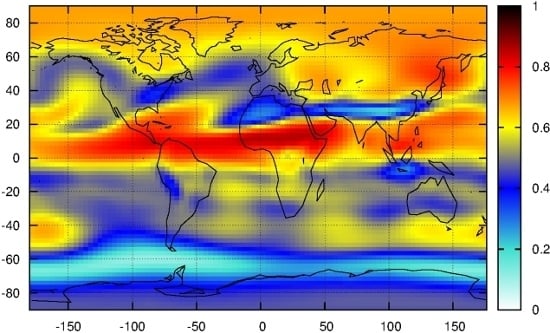
2.1. Spectral Weight Analysis

2.2. Detrended Fluctuation Analysis
3. Results and Discussion
3.1. Spectral Peak Maps
3.2. DFA Exponent Maps

4. Conclusions
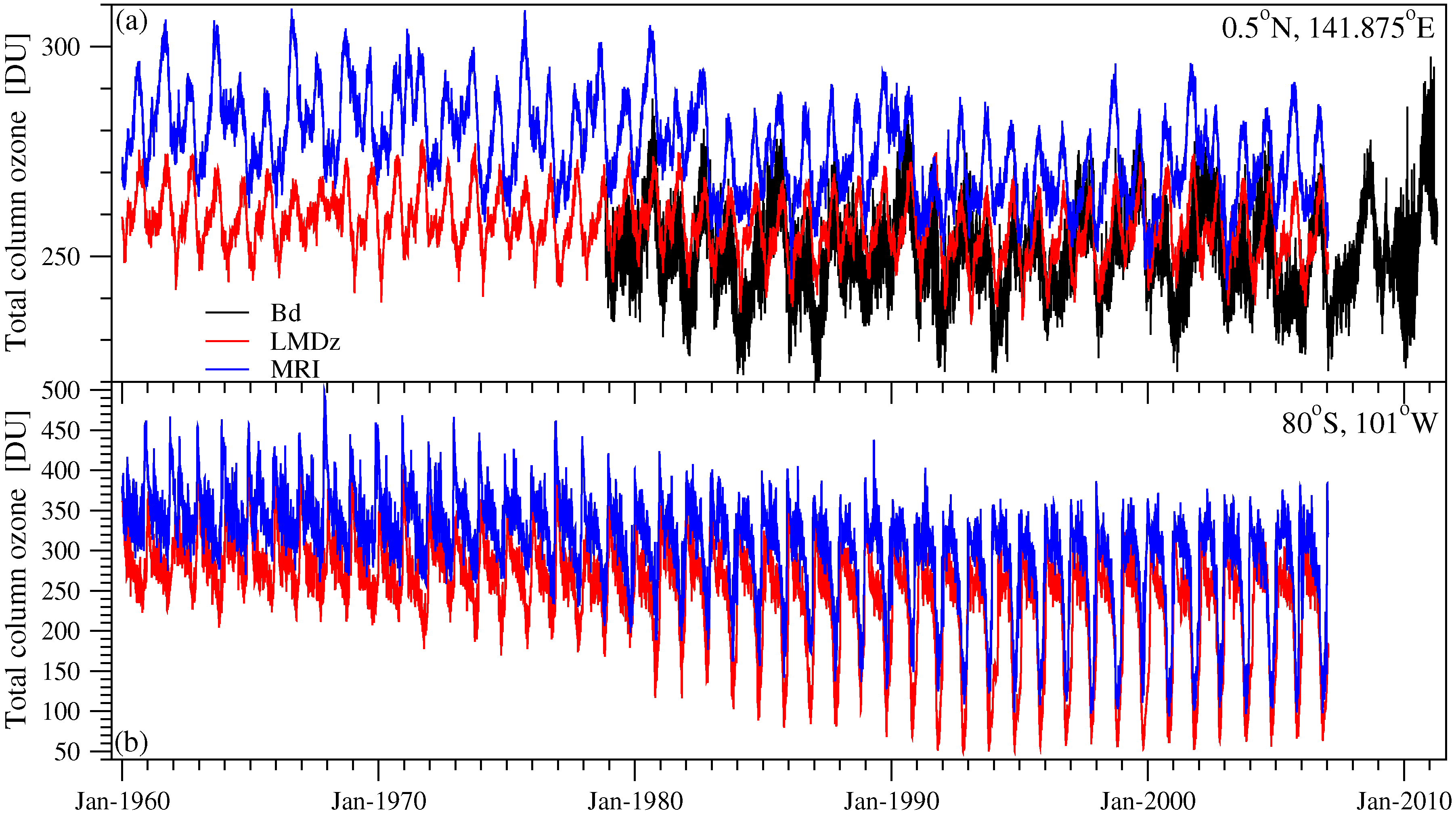
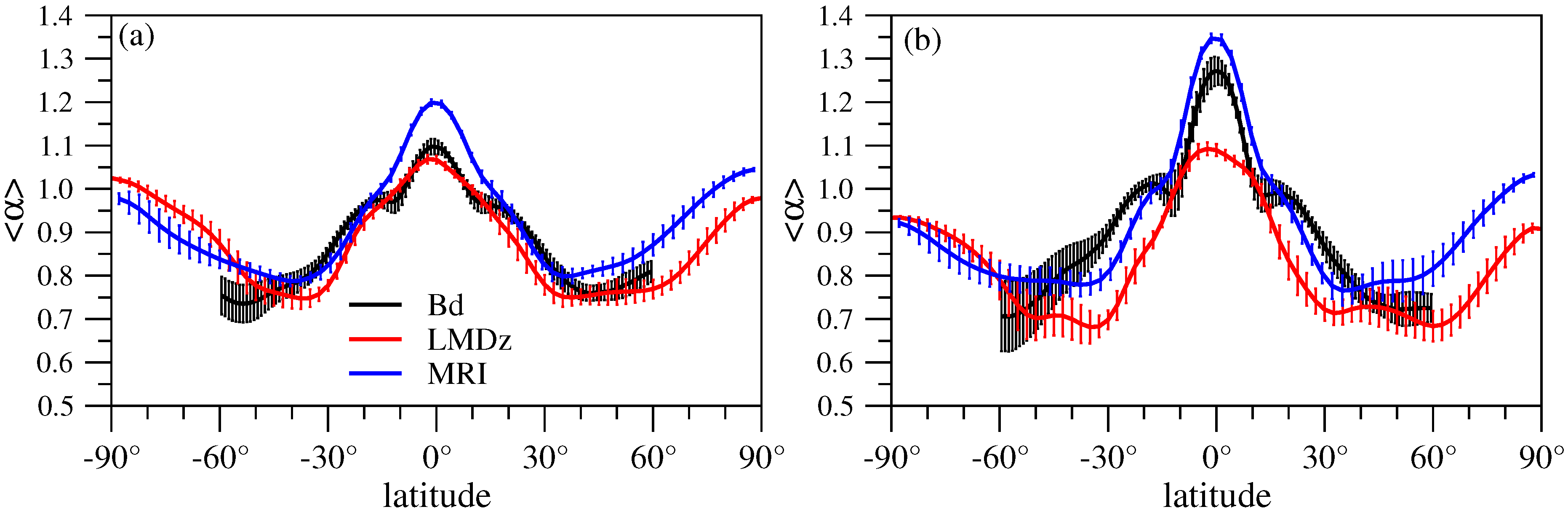
- Both the LMDz and MRI models provide an adequate reproduction of empirical data in the period of comparison (see Figure 1), however the latter seems to slightly overestimate total column ozone values.
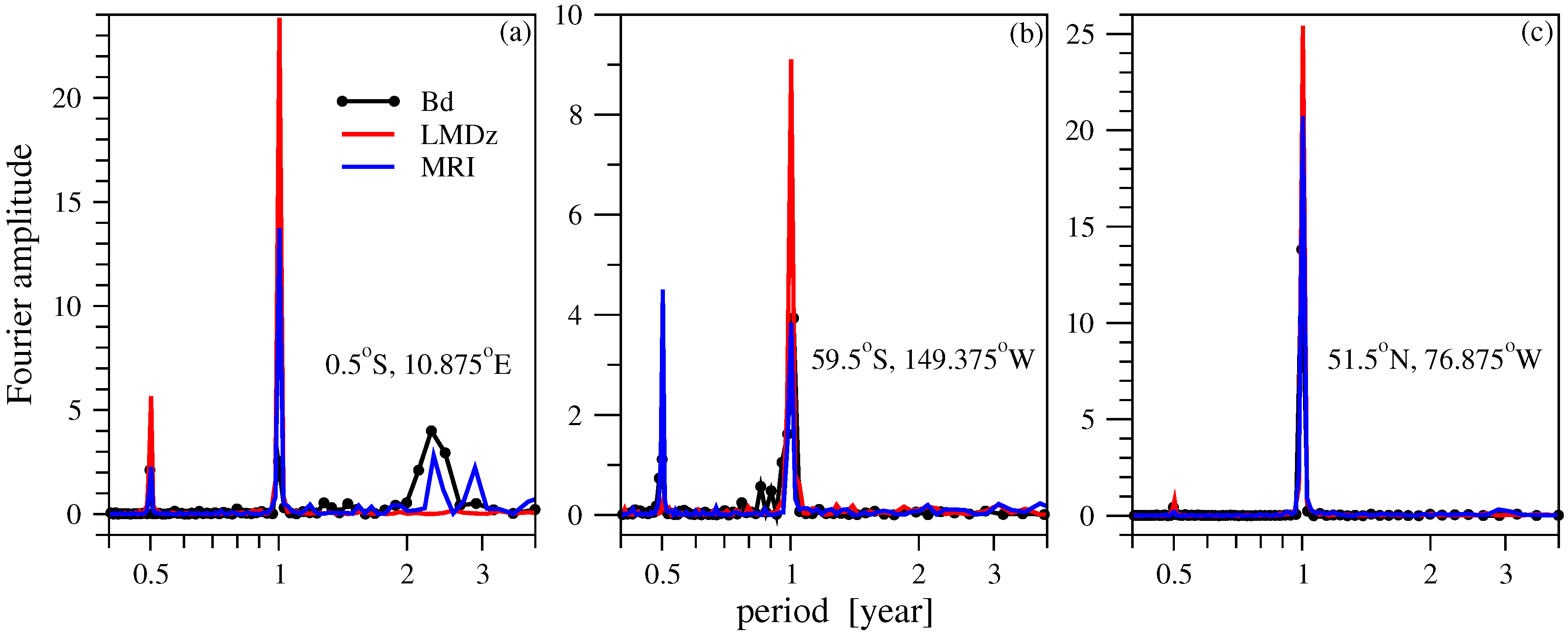
- Spectral analysis reveals that both models underestimate high frequency (daily) variability (see Figure 3), MRI performs better from this point of view. Such deficiency might have a rather complex origin, because several dynamical processes (advection, diffusion and mixing) contribute to short time fluctuations.
- Spectral weight analysis indicates some anomalies in the dynamical core of both CCMs. The geographic locations of semiannual oscillations are shifted in the models. MRI is known to reproduce the QBO mode along the equator (albeit it is definitely weaker than in the empirical records), however it underperforms with respect of the annual component.
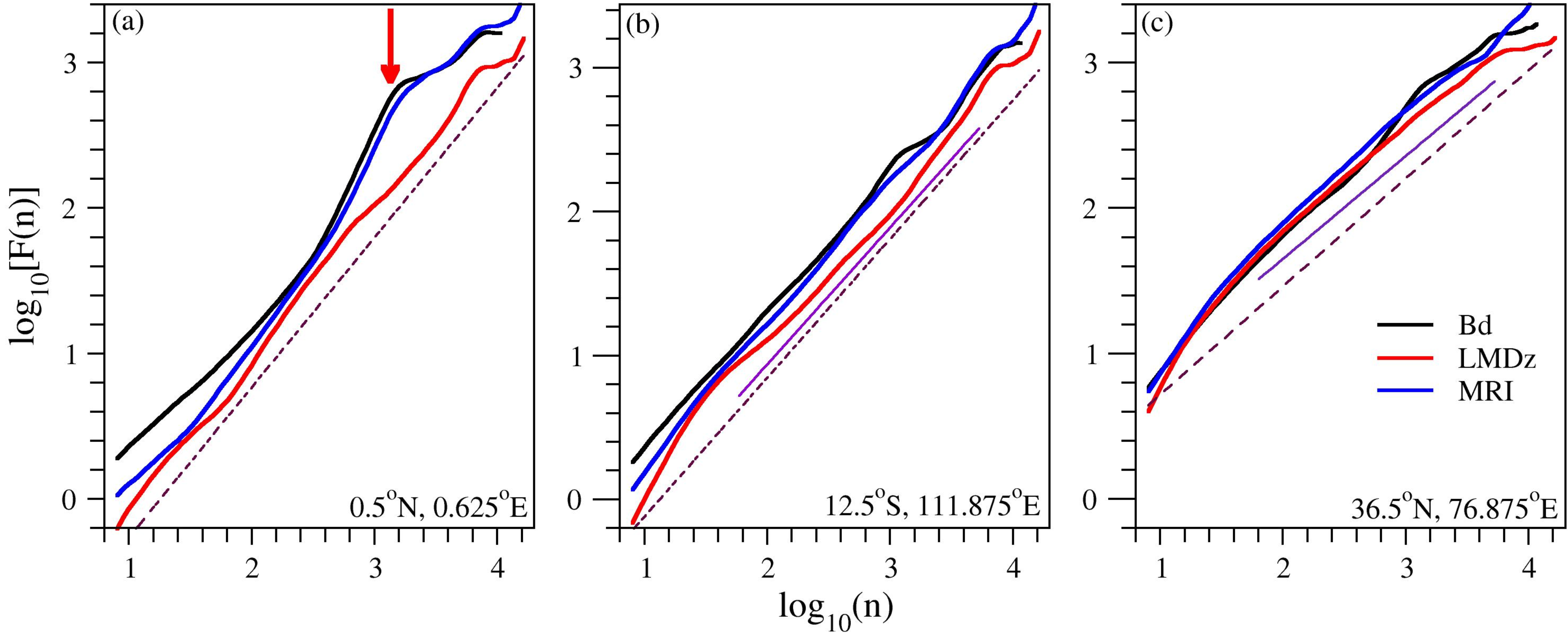
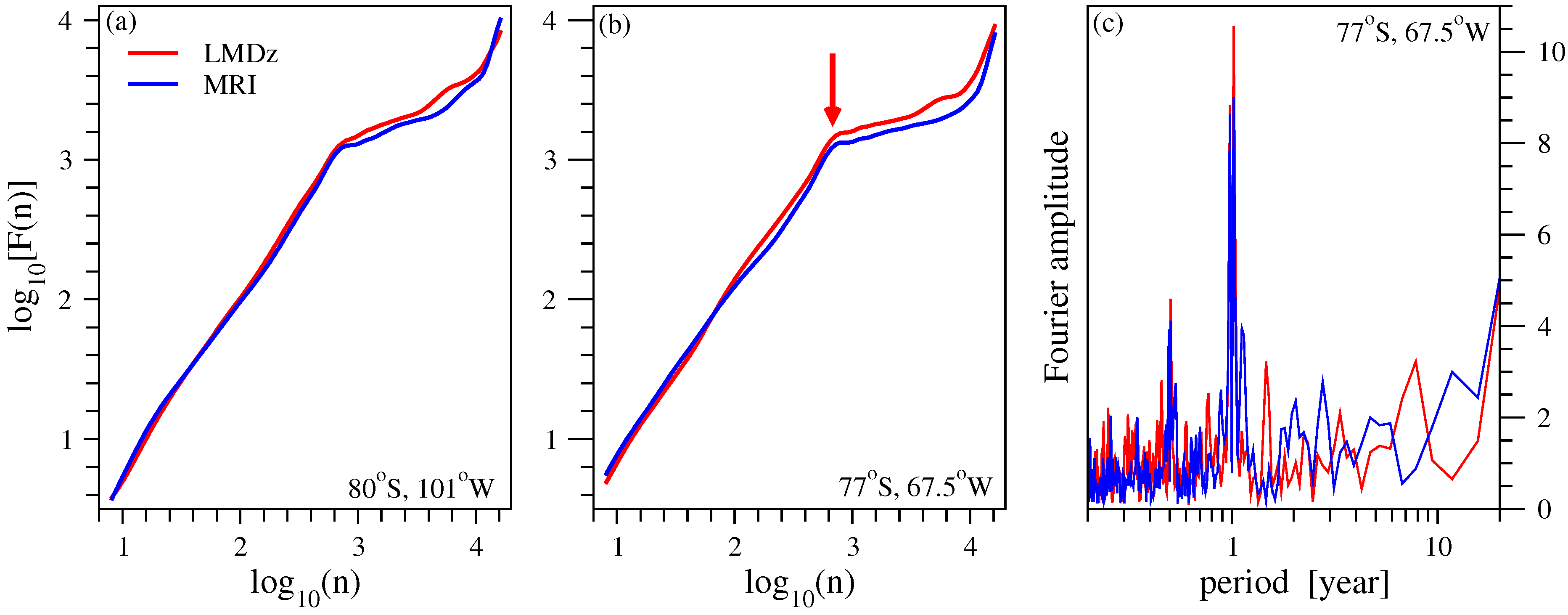
- The presence of quasi-biennial oscillations decreases the accuracy of DFA analysis (see Figure 4(a)). Band pass Fourier filtering can remove such spectral component (see [22]), however one should be careful, because the DFA method is based on residual (anomaly) analysis. Specifically, the standard Wiener filtering consists of two steps: firstly, the Fourier transform of a given time series is produced and the amplitudes are set to be zero or to some assumed (practically interpolated) base line values in the required frequency ranges, and secondly, an inverse Fourier transform produces the filtered time series. When this method is applied on a global scale, obviously the filtered components disappear everywhere, also from signals where QBO oscillations are not present. Care should be taken especially when the target is to detect long range correlations, because such procedure might distort the original properties of the time series. Too strong filtering can yield (geographically) inconsistent results as probably demonstrated in [35,36].Note that the low model values of high frequency variabilities are reflected by the fact that the initial parts of fluctuation functions remain systematically below the curve for empirical data (Figure 4).
- The DFA3 fluctuation functions are adequately reproduced by both CCMs (see Figure 6 and Figure 7). We do not claim that the curves represent pure power law behavior (see Figure 4); still the overall trends are close to linear on log-log scale, indicating the presence of long range correlations. (The appearance of clean power laws is not even expected, because many processes of various characteristic time scales contribute to the instantaneous value of any atmospheric variable at a given location.)
- Since the reproduction of correlation properties in the models is quite satisfactory in the overlapping geographic latitude band between −60 and 60, we can have a strong confidence in the prediction of both models that correlations are stronger over both polar regions. This observations is also supported by considering the role of polar vortices in the meridional transport processes.
- Classical methods of time series analysis have a limited applicability over the polar regions, especially over the Antarctic. Such strong nonstationary signals as represented by the total ozone level during the decades of ozone hole make any residual (anomaly) analysis very difficult. Standard methods to remove semiannual and annual oscillations fail when the amplitudes change strongly (see Figure 9), however an over-filtering might yield information loss about correlation properties.
Acknowledgements
Conflicts of Interest
References
- Von Hobe, M.; Bekki, S.; Borrmann, S.; Cairo, F.; D’Amato, F.; Di Donfrancesco, G.; Dönbrack, A.; Ebersoldt, A.; Ebert, M.; Emde, C.; et al. Reconciliation of essential process parameters for an enhanced predictability of Arctic stratospheric ozone loss and its climate interactions. Atmos. Chem. Phys. Discuss. 2012, 12, 30661–30754. [Google Scholar] [CrossRef]
- Butchart, N.A.; Charlton-Perez, A.J.; Cionni, I.; Hardiman, S.C.; Haynes, P.H.; Krüer, K.; Kushner, P.J.; Newman, P.A.; Osprey, S.M.; Perlwitz, J.; et al. Multimodel climate and variability of the stratosphere. J. Geophys. Res. 2011, 116, D05102. [Google Scholar] [CrossRef]
- Douglass, A.R.; Stolarski, R.S.; Strahan, S.E.; Oman, L.D. Understanding differences in upper stratospheric ozone response to changes in chlorine and temperature as computed using CCMVal-2 models. J. Geophys. Res. 2012, 117, D16306. [Google Scholar] [CrossRef]
- Gettelman, A.; Eyring, V.; Fischer, C.; Shiona, H.; Cionni, I.; Neish, M.; Morgenstern, O.; Wood, S.W.; Li, Z. A community diagnostic tool for chemistry climate model validation. Geosci. Model Dev. 2012, 5, 1061–1073. [Google Scholar] [CrossRef]
- Hourdin, F.; Musat, I.; Bony, S.; Braconnot, P.; Codron, F.; Dufresne, J.-L.; Fairhead, L.; Filiberti, M.-A.; Friedlingstein, P.; Grandpeix, J.-Y.; et al. The LMDz4 general circulation model: Climate performance and sensitivity to parametrized physics with emphasis on tropical convection. Clim. Dyn. 2006, 27, 787–813. [Google Scholar] [CrossRef] [Green Version]
- Jourdain, L.; Bekki, S.; Lott, F.; Lefèvre, F. The coupled chemistry climate model LMDz-REPROBUS: Description and evaluation of a transient simulation of the period 1980–1999. Ann. Geophys. 2008, 26, 1391–1413. [Google Scholar] [CrossRef]
- Marchand, M.; Keckhut, P.; Lefebvre, S.; Claud, C.C.D.; Hauchecorne, A.; Lefèvre, F.; Lefebvre, M.-P.; Jumelet, J.; Lott, F.; Hourdin, F.; et al. Dynamical amplification of the stratospheric solar response simulated with the Chemistry-Climate model LMDz-Reprobus. J. Atmos. Solar-Terrest. Phys. 2012, 75–76, 147–160. [Google Scholar] [CrossRef]
- Austin, J.; Scinocca, J.; Plummer, D.; Oman, L.; Waugh, D.; Akiyoshi, H.; Bekki, S.; Braesicke, P.; Butchart, N.; Chipperfield, M.; et al. The decline and recovery of total column ozone using a multi-model time series analysis. J. Geophys. Res. 2010, 115, D00M10. [Google Scholar] [CrossRef]
- Gettelman, A.; Hegglin, M.I.; Son, S.-W.; Kim, J.; Fujiwara, M.; Birner, T.; Kremser, S.; Rex, M.; Añel, J.A.; Akiyoshi, H.; et al. Multimodel assessment of the upper troposphere and lower stratosphere: Tropics and global trends. J. Geophys. Res. 2010, 115, D00M08. [Google Scholar] [CrossRef]
- Hegglin, M.I.; Gettelman, A.; Hoor, P.; Krichevsky, R.; Manney, G.L.; Pan, L.L.; Son, S.W.; Stiller, G.; Tilmes, S.; Walkeret, K.A.; et al. Multimodel assessment of the upper troposphere and lower stratosphere: Extratropics. J. Geophys. Res. 2010, 115, D00M09. [Google Scholar] [CrossRef]
- Hourdin, F.; Foujols, M.-A.; Codron, F.; Guemas, V.; Dufresne, J.-L.; Bony, S.; Denvil, S.; Guez, L.; Lott, F.; Ghattas, J.; et al. Impact of the LMDZ atmospheric grid configuration on the climate and sensitivity of the IPSL-CM5A coupled model. Clim. Dyn. 2012. [Google Scholar] [CrossRef]
- Eyring, V.; Shepherd, T.G.; Waugh, D.W. (Eds.) SPARC Report No. 5; WCRP-132; WMO/TD-No. 1526. SPARC CCMVal. SPARC Report on the Evaluation of Chemistry-Climate Models. 2010. Available online: http://www.sparc-climate.org/publications/ (accessed on 15 June 2010).
- Bodeker, G.E.; Shiona, H.; Eskes, H. Indicators of Antarctic ozone depletion. Atmos. Chem. Phys. 2005, 5, 2603–2615. [Google Scholar] [CrossRef]
- Müller, R.; Grooß, J.-U.; Lemmen, C.; Heinze, D.; Dameris, M.; Bodeker, G.E. Simple measures of ozone depletion in the polar stratosphere. Atmos. Chem. Phys. 2008, 8, 251–264. [Google Scholar] [CrossRef]
- Struthers, H.; Bodeker, G.E.; Austin, J.; Bekki, S.; Cionni, I.; Dameris, M.; Giorgetta, M.A.; Grewe, V.; Lefèvre, F.; Lott, F.; et al. The simulation of the Antarctic ozone hole by chemistry-climate models. Atmos. Chem. Phys. 2009, 9, 6363–6376. [Google Scholar] [CrossRef] [Green Version]
- Shibata, K.; Deushi, M.; Sekiyama, T.T.; Yoshimura, H. Development of an MRI chemical transport model for the study of stratospheric chemistry. Papers Meteorol. Geophys. 2005, 55, 75–119. [Google Scholar] [CrossRef]
- Shibata, K.; Deushi, M. Long-term variations and trends in the simulation of the middle atmosphere 1980–2004 by the chemistry-climate model of the Meteorological Research Institute. Ann. Geophys. 2010, 26, 1299–1326. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Manzini, E.; Roeckner, E. Forcing of the quasi-biennial oscillation from a broad spectrum of atmospheric waves. Geophys. Res. Lett. 2002, 29, 86:1–86:4. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Manzini, E.; Roeckner, E.; Esch, M.; Bengtsson, L. Climatology and forcing of the Quasi-Biennial Oscillation in the MAECHAM5 model. J. Clim. 2006, 19, 3882–3901. [Google Scholar] [CrossRef]
- Bodeker, G.E.; Scott, J.C.; Kreher, K.; McKenzie, R.L. Global ozone trends in potential vorticity coordinates using TOMS and GOME intercompared against the Dobson network: 1978–1998. J. Geophys. Res. 2001, 106, 23029–23042. [Google Scholar] [CrossRef]
- Bodeker, G.E.; Connor, B.J.; Liley, J.B.; Matthews, W.A. The global mass of ozone: 1978–1998. Geophys. Res. Lett. 2001, 28, 2819–2822. [Google Scholar] [CrossRef]
- Kiss, P.; Müller, R.; Jánosi, I.M. Long-range correlations of extrapolar total ozone are determined by the global atmospheric circulation. Nonlin. Proc. Geophys. 2007, 14, 435–442. [Google Scholar] [CrossRef]
- Jánosi, I.M.; Müller, R. Empirical mode decomposition and correlation properties of long daily ozone records. Phys. Rev. E 2005, 71, 056126. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Derby, N.B. Assessing the Detrended Fluctuation Analysis Method of Estimating the Hurst Coefficient; University of Washington: Seattle, WA, USA, 2004. [Google Scholar]
- Lowen, S.B.; Teich, M.C. Fractal-Based Point Processes; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Hu, K.; Ivanov, P.Ch.; Chen, Z.; Carpena, P.; Stanley, H.E. Effect of trends on detrended fluctuation analysis. Phys. Rev. E 2001, 64, 011114. [Google Scholar] [CrossRef]
- Király, A.; Jánosi, I.M. Stochastic modeling of daily temperature fluctuations. Phys. Rev. E 2002, 65, 051102. [Google Scholar] [CrossRef]
- Xu, L.; Ivanov, P.Ch.; Hu, K.; Chen, Z.; Carbone, A.; Stanley, H.E. Quantifying signals with power-law correlations: A comparative study of detrended fluctuation analysis and detrended moving average techniques. Phys. Rev. E 2005, 71, 051101. [Google Scholar] [CrossRef]
- Pattantyús-Ábrahám, M.; Király, A.; Jánosi, I.M. Nonuniversal atmospheric persistence: Different scaling of daily minimum and maximum temperatures. Phys. Rev. E 2004, 69, 021110. [Google Scholar] [CrossRef]
- Khosrawi, F.; Müller, R.; Urban, J.; Proffitt, M.H.; Stiller, G.; Kiefer, M.; Lossow, S.; Kinnison, D.; Olschewski, F.; Riese, M.; Murtagh, D. Assessment of the interannual variability and impact of the QBO and upwelling on tracer-tracer distributions of N2O and O3 in the tropical lower stratosphere. Atmos. Chem. Phys. 2013, 13, 3619–3641. [Google Scholar] [CrossRef]
- Gerber, E.P.; Butler, A.; Calvo Fernandez, N.; Charlton-Perez, A.; Giorgetta, M.; Manzini, E.; Perlwitz, J.; Polvani, L.M.; Sassi, F.; Scaife, A.A.; et al. Assessing and understanding the impact of stratospheric dynamics and variability on the Earth system. Bull. Am. Meteor. Soc. 2012, 93, 845–859. [Google Scholar] [CrossRef]
- Farman, J.C.; Gardiner, B.G.; Shanklin, J.D. Large losses of total ozone in Antarctica reveal seasonal ClOx/NOx interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- Solomon, S. Stratospheric ozone depletion: A review of concepts and history. Rev. Geophys. 1999, 37, 275–316. [Google Scholar] [CrossRef]
- Vyushin, D.I.; Fioletov, V.E.; Shepherd, T.G. Impact of long-range correlations on trend detection in total ozone. J. Geophys. Res. 2007, 112, D14307. [Google Scholar] [CrossRef]
- Vyushin, D.I.; Shepherd, T.G.; Fioletov, V.E. On the statistical modeling of persistence in total ozone anomalies. J. Geophys. Res. 2010, 115, D16306. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Homonnai, V.; Jánosi, I.M.; Lefèvre, F.; Marchand, M. Comparative Spectral Analysis and Correlation Properties of Observed and Simulated Total Column Ozone Records. Atmosphere 2013, 4, 198-213. https://doi.org/10.3390/atmos4020198
Homonnai V, Jánosi IM, Lefèvre F, Marchand M. Comparative Spectral Analysis and Correlation Properties of Observed and Simulated Total Column Ozone Records. Atmosphere. 2013; 4(2):198-213. https://doi.org/10.3390/atmos4020198
Chicago/Turabian StyleHomonnai, Viktória, Imre M. Jánosi, Franck Lefèvre, and Marion Marchand. 2013. "Comparative Spectral Analysis and Correlation Properties of Observed and Simulated Total Column Ozone Records" Atmosphere 4, no. 2: 198-213. https://doi.org/10.3390/atmos4020198
APA StyleHomonnai, V., Jánosi, I. M., Lefèvre, F., & Marchand, M. (2013). Comparative Spectral Analysis and Correlation Properties of Observed and Simulated Total Column Ozone Records. Atmosphere, 4(2), 198-213. https://doi.org/10.3390/atmos4020198