The Copula Function-Based Probability Characteristics Analysis on Seasonal Drought & Flood Combination Events on the North China Plain
Abstract
:1. Introduction
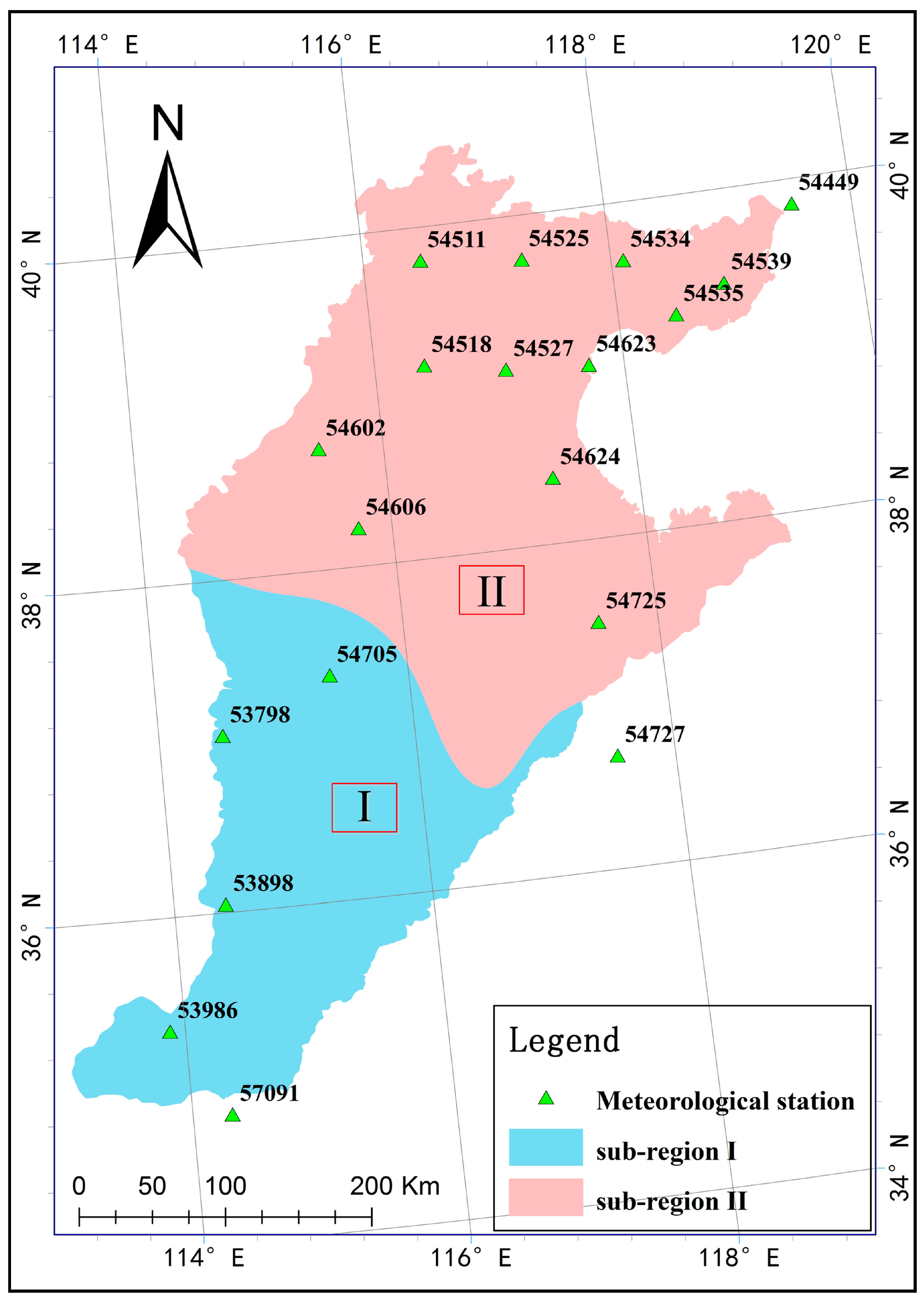
2. Study Area and Data
2.1. Overview of the Region of Interest
2.2. Data Sources

3. Methodology
3.1. Theory of L-Moments
3.2. Identification and Test of Homogenous Regions Based on the L-Moments
3.2.1. Identification of Homogenous Regions
3.2.2. Screening Data Using the Discordancy Measure Test
| Number of Sites | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Critical value | 1.333 | 1.648 | 1.917 | 2.140 | 2.329 | 2.491 | 2.632 | 2.757 | 2.869 | 2.971 | 3.000 |
3.2.3. Regional Heterogeneity Test
3.2.4. Selection of Best-Fit Distribution Function
3.3. Precipitation Anomaly Percentage
3.4. Bivariate Copula Joint Distribution Function

| Copula Function | C(u,v) | Parameter Space | τ and θ |
|---|---|---|---|
| Gumbel | |||
| Clayton | |||
| Frank |
3.5. Goodness of Fit Test
3.5.1. Kolmogorov-Smirnov (K-S) Test
3.5.2. Graphic Test
4. Results and Discussion
4.1. Seasonal Distribution of Regional Precipitation
| Sub-Region | Meteorological Stations | Mean Annual Precipitation/mm | Seasonal Distribution of Precipitation/% | |||
|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | |||
| I | 53798 | 516 | 13.72 | 64.61 | 18.81 | 2.86 |
| 53898 | 561 | 14.64 | 62.56 | 19.43 | 3.36 | |
| 53986 | 567 | 15.88 | 60.33 | 20.71 | 3.09 | |
| 54727 | 637 | 15.14 | 63.69 | 17.93 | 3.24 | |
| 57091 | 630 | 17.92 | 56.45 | 21.35 | 4.28 | |
| 54705 | 479 | 14.07 | 63.95 | 18.79 | 3.19 | |
| 54511 | 556 | 11.74 | 71.72 | 14.68 | 1.86 | |
| II | 54534 | 611 | 11.87 | 71.60 | 14.53 | 2.00 |
| 54602 | 518 | 11.76 | 70.24 | 15.92 | 2.08 | |
| 54606 | 521 | 12.14 | 69.01 | 16.40 | 2.45 | |
| 54449 | 644 | 12.82 | 70.74 | 14.74 | 1.70 | |
| 54518 | 514 | 10.58 | 72.08 | 15.46 | 1.88 | |
| 54525 | 586 | 10.40 | 73.07 | 14.79 | 1.74 | |
| 54527 | 540 | 11.87 | 71.20 | 14.92 | 2.01 | |
| 54535 | 611 | 11.79 | 72.02 | 14.13 | 2.06 | |
| 54539 | 610 | 12.93 | 70.67 | 14.27 | 2.13 | |
| 54623 | 582 | 11.40 | 71.51 | 14.95 | 2.14 | |
| 54624 | 591 | 11.70 | 71.73 | 14.34 | 2.23 | |
| 54725 | 572 | 13.34 | 67.70 | 15.94 | 3.02 | |
4.2. Results of Homogenous Regional Identification Based on L-moments
| Sub-Region I | Sub-Region II | ||||||
|---|---|---|---|---|---|---|---|
| Meteorological Stations | Discordancy Measure D | Meteorological Stations | Discordancy Measure D | ||||
| Spring | Summer | Autumn | Spring | Summer | Autumn | ||
| 53798 | 1.08 | 1.47 | 0.36 | 54511 | 0.62 | 1.12 | 1.15 |
| 54534 | 2.03 | 1.32 | 0.15 | ||||
| 53898 | 1.64 | 0.1 | 0.95 | 54602 | 2.07 | 2.69 | 1.40 |
| 54606 | 0.8 | 0.16 | 0.56 | ||||
| 53986 | 0.81 | 0.22 | 0.95 | 54449 | 0.49 | 0.66 | 0.43 |
| 54518 | 0.09 | 1.46 | 2.11 | ||||
| 54727 | 1.32 | 1.64 | 1.13 | 54525 | 0.94 | 0.57 | 1.50 |
| 54527 | 0.29 | 0.41 | 0.75 | ||||
| 57091 | 0.48 | 1.61 | 1.38 | 54535 | 0.67 | 0.09 | 1.05 |
| 54539 | 0.34 | 0.41 | 1.72 | ||||
| 54705 | 0.65 | 0.95 | 1.25 | 54623 | 0.45 | 0.42 | 1.61 |
| 54624 | 1.92 | 2.02 | 0.20 | ||||
| 54725 | 2.30 | 1.68 | 0.36 | ||||
| Sub-Region | Seasons | Heterogeneity Measure | ||
|---|---|---|---|---|
| H1 | H2 | H3 | ||
| I | Spring | 0.86 | −0.88 | −1.69 |
| Summer | 0.41 | 0.23 | 0.44 | |
| Autumn | −0.23 | −1.03 | −0.88 | |
| II | Spring | −1.01 | −2.10 | −2.54 |
| Summer | −0.25 | 0.24 | 0.10 | |
| Autumn | −1.85 | −2.24 | −1.54 | |
| Sub-Region | Distribution | Spring | Summer | Autumn |
|---|---|---|---|---|
| I | GLO | 2.11 | 1.00 | 4.15 |
| GEV | 0.59 | −1.50 | 2.38 | |
| GNO | 0.14 | −1.25 | 1.87 | |
| P-III | −0.75 | −1.45 | 0.87 | |
| GPA | −3.01 | −6.48 | −1.81 | |
| II | GLO | 4.13 | 5.84 | 2.15 |
| GEV | 1.76 | 2.07 | −0.48 | |
| GNO | 1.11 | 2.16 | −0.79 | |
| P-III | −0.20 | 1.59 | −1.64 | |
| GPA | −3.81 | −5.75 | −6.30 | |
| Best fit | Sub-region I | GNO | GLO | P-III |
| Sub-region II | P-III | P-III | GEV |


| Seasons | Spring | Summer | Autumn | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sub-region I | Best-fit distribution | GNO | GLO | P-III | ||||||||||
| Parameter/Statistic | ξ | α | k | K-S | ξ | α | k | K-S | ξ | β | α | K-S | ||
| Meteorological stations | 53798 | −18.0588 | 58.4344 | −0.5694 | 0.0688 | −9.1975 | 21.9138 | −0.2385 | 0.0550 | −139.5923 | 0.0373 | 5.2070 | 0.0693 | |
| 53898 | −9.2467 | 48.2550 | −0.3702 | 0.0565 | −3.8273 | 21.4678 | −0.1070 | 0.0563 | −182.1496 | 0.0471 | 8.5867 | 0.1006 | ||
| 53986 | −11.1264 | 47.9706 | −0.4416 | 0.0759 | −3.5532 | 21.7771 | −0.0981 | 0.0645 | −145.0157 | 0.0408 | 5.9120 | 0.0830 | ||
| 54727 | −9.1277 | 51.0613 | −0.3469 | 0.0712 | −0.5261 | 18.1884 | −0.0176 | 0.0653 | −100.7213 | 0.0247 | 2.4881 | 0.0898 | ||
| 57091 | −12.3213 | 50.2480 | −0.4644 | 0.0337 | −0.9850 | 21.1229 | −0.0283 | 0.0715 | −146.8917 | 0.0535 | 7.8616 | 0.0890 | ||
| 54705 | −14.4809 | 57.8962 | −0.4728 | 0.0697 | −1.6266 | 20.8702 | −0.0472 | 0.0797 | −103.6220 | 0.0219 | 2.2695 | 0.0649 | ||
| Sub-region II | Best-fit distribution | P-III | P-III | GEV | ||||||||||
| Parameter/ Statistic | ξ | β | α | K-S | ξ | β | α | K-S | ξ | α | k | K-S | ||
| Meteorological stations | 54511 | −88.8633 | 0.0227 | 2.0169 | 0.0507 | −373.1322 | 0.2892 | 107.9153 | 0.0743 | −23.3955 | 48.5116 | 0.1051 | 0.0614 | |
| 54534 | −104.9823 | 0.0384 | 4.0270 | 0.0559 | −207.6734 | 0.2079 | 43.1766 | 0.0677 | −24.5054 | 41.0608 | −0.0195 | 0.0506 | ||
| 54602 | −88.1920 | 0.0179 | 1.5810 | 0.0603 | −159.0345 | 0.0771 | 12.2663 | 0.0863 | −27.3803 | 42.1948 | −0.0679 | 0.0584 | ||
| 54606 | −123.6783 | 0.0317 | 3.9160 | 0.0551 | −177.7901 | 0.1282 | 22.7881 | 0.0561 | −23.6675 | 44.2714 | 0.0448 | 0.0644 | ||
| 54449 | −127.4946 | 0.0452 | 5.7573 | 0.0413 | −75.7425 | 0.0524 | 3.9695 | 0.0600 | −23.7160 | 38.0654 | −0.0444 | 0.0557 | ||
| 54518 | −126.5779 | 0.0397 | 5.0303 | 0.0473 | −87.5464 | 0.0524 | 4.5891 | 0.0600 | −28.1047 | 47.1006 | −0.0194 | 0.0419 | ||
| 54525 | −120.2312 | 0.0368 | 4.4193 | 0.0403 | −220.0703 | 0.1549 | 34.0958 | 0.0712 | −22.4098 | 47.3171 | 0.1156 | 0.0688 | ||
| 54527 | −123.3882 | 0.0409 | 5.0426 | 0.0598 | −153.9328 | 0.1290 | 19.8613 | 0.0660 | −22.1711 | 41.8291 | 0.0499 | 0.0746 | ||
| 54535 | −89.4351 | 0.0222 | 1.9896 | 0.0638 | −142.8562 | 0.1001 | 14.3053 | 0.0729 | −23.4979 | 35.9935 | −0.0714 | 0.0661 | ||
| 54539 | −104.3600 | 0.0304 | 3.1702 | 0.0797 | −150.9863 | 0.1161 | 17.5369 | 0.0731 | −23.2573 | 40.0777 | −0.0031 | 0.0918 | ||
| 54623 | −125.3790 | 0.0322 | 4.0405 | 0.0458 | −94.3140 | 0.0638 | 6.0195 | 0.0824 | −24.5883 | 39.9580 | −0.0372 | 0.0689 | ||
| 54624 | −128.0802 | 0.0353 | 4.5151 | 0.0886 | −88.6065 | 0.0532 | 4.7131 | 0.0616 | −24.0894 | 39.3210 | −0.0347 | 0.0506 | ||
| 54725 | −144.6437 | 0.0514 | 7.4316 | 0.0755 | −82.7962 | 0.0570 | 4.7227 | 0.0595 | −22.4426 | 40.9570 | 0.0304 | 0.0703 | ||
4.3. Parameter Estimation and Goodness of Fit Test of the Best-Fit Distribution
4.4. Bivariate Copula Distribution Parameter Estimation and Fitting Test
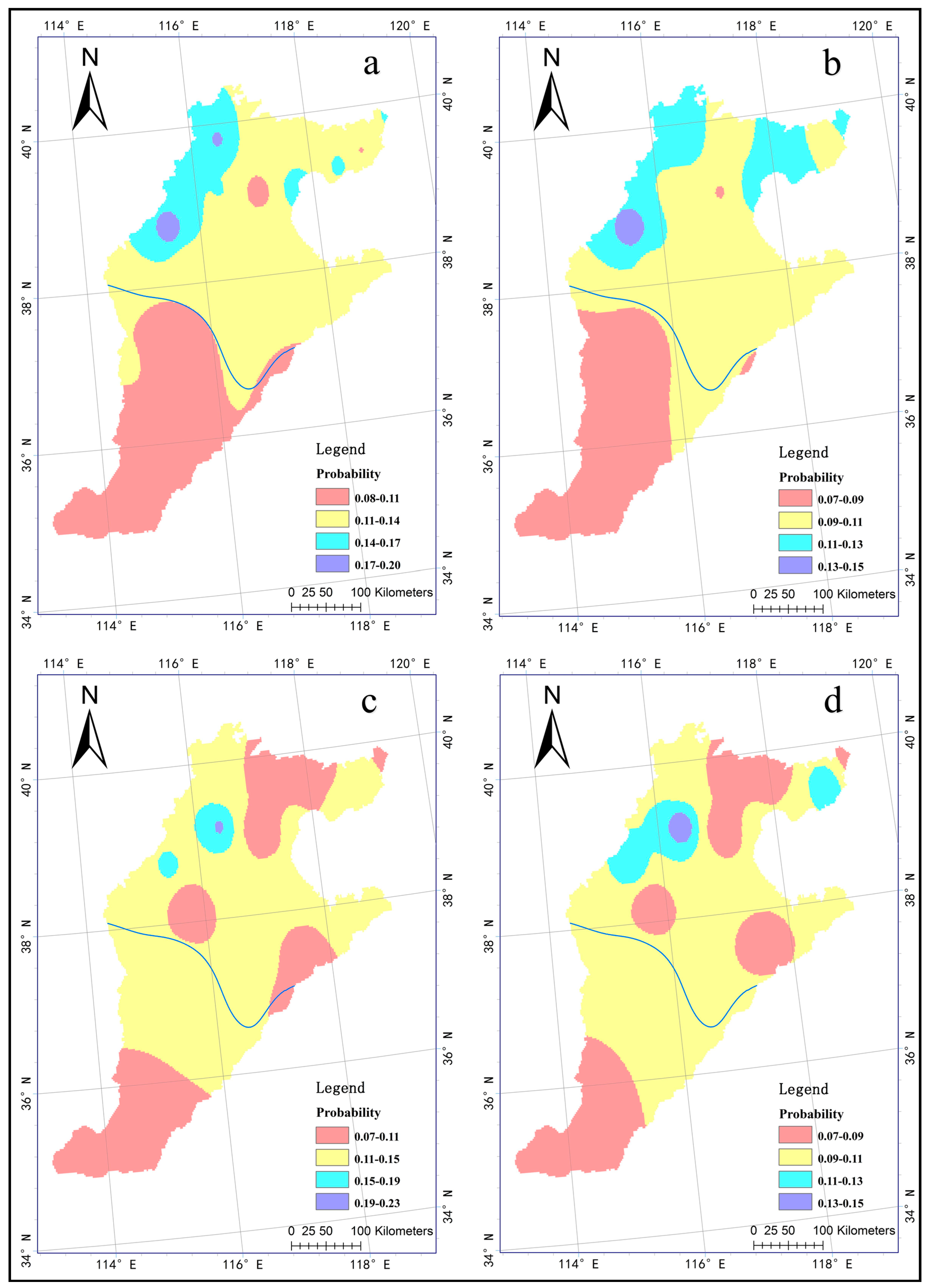
4.5. Analysis of the Occurrence Frequency of DFCEs

| Sub-Regions | Meteorological Stations | Spring-Summer | Summer-Autumn | ||||
|---|---|---|---|---|---|---|---|
| τ | θ | K-S | τ | θ | K-S | ||
| I | 53798 | −0.1176 | −1.0701 | 0.1010 | 0.0261 | 0.2354 | 0.0633 |
| 53898 | −0.0225 | −0.2026 | 0.0893 | −0.0530 | −0.4780 | 0.1352 | |
| 53986 | 0.0094 | 0.0849 | 0.1025 | −0.0290 | −0.2616 | 0.0691 | |
| 54727 | 0.0261 | 0.2353 | 0.0728 | 0.0987 | 0.8953 | 0.0750 | |
| 57091 | −0.0044 | −0.0392 | 0.0835 | 0.0225 | 0.2026 | 0.1053 | |
| 54705 | −0.1001 | −0.9087 | 0.0604 | 0.0290 | 0.2616 | 0.0802 | |
| II | 54511 | 0.0624 | 0.5635 | 0.0901 | −0.0131 | −0.1177 | 0.0617 |
| 54534 | 0.1713 | 1.5792 | 0.0814 | −0.0377 | −0.3400 | 0.0886 | |
| 54602 | 0.1046 | 0.9496 | 0.0842 | 0.1089 | 0.9892 | 0.0667 | |
| 54606 | 0.0203 | 0.1829 | 0.0606 | −0.0690 | −0.6231 | 0.0611 | |
| 54449 | 0.1880 | 1.7425 | 0.0697 | −0.0566 | −0.5108 | 0.1033 | |
| 54518 | 0.0639 | 0.5771 | 0.0563 | 0.2890 | 2.7943 | 0.0607 | |
| 54525 | 0.0501 | 0.4521 | 0.0643 | −0.0298 | −0.2681 | 0.0883 | |
| 54527 | 0.0124 | 0.1112 | 0.0941 | −0.0145 | −0.1306 | 0.0969 | |
| 54535 | 0.1147 | 1.0431 | 0.0734 | 0.1220 | 1.1115 | 0.0758 | |
| 54539 | 0.0145 | 0.1306 | 0.0554 | 0.2395 | 2.2619 | 0.1014 | |
| 54623 | 0.1611 | 1.4813 | 0.0818 | 0.0726 | 0.6559 | 0.0669 | |
| 54624 | −0.0065 | −0.0588 | 0.0758 | 0.0363 | 0.3269 | 0.0903 | |
| 54725 | 0.0922 | 0.8355 | 0.0643 | 0.0276 | 0.2483 | 0.0842 | |
| Grade | Anomaly Percentage | Type of Drought & Flood |
|---|---|---|
| 1 | M ≥ 75% | Serious flood |
| 2 | 50% ≤ M < 75% | Heavy flood |
| 3 | 25% ≤ M < 50% | Relatively heavy flood |
| 4 | −25% ≤ M < 25% | Normal |
| 5 | −50% ≤ M < −25% | Relatively heavy drought |
| 6 | −75% ≤ M < −50% | Heavy drought |
| 7 | M < −75% | Serious drought |
| Sub-Region | Meteorological Stations | Seasonal Drought & Flood Joint Distribution Probability | Probability of Spring-Summer DFCEs | Probability of Summer-Autumn DFCEs | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SSD | SDSF | SFSD | SSF | SAD | SDAF | SFAD | SAF | ||||
| I | 53798 | 0.1128 | 0.0732 | 0.0624 | 0.0401 | 0.1340 | 0.0944 | 0.0907 | 0.0640 | 0.2885 | 0.3831 |
| 53898 | 0.0904 | 0.0767 | 0.0651 | 0.0553 | 0.0970 | 0.0659 | 0.0820 | 0.0557 | 0.2875 | 0.3006 | |
| 53986 | 0.1011 | 0.0871 | 0.0691 | 0.0596 | 0.1016 | 0.0682 | 0.0872 | 0.0585 | 0.3169 | 0.3155 | |
| 54727 | 0.0802 | 0.0786 | 0.0597 | 0.0586 | 0.1039 | 0.0719 | 0.1020 | 0.0706 | 0.2771 | 0.3484 | |
| 57091 | 0.0935 | 0.0898 | 0.0620 | 0.0595 | 0.0905 | 0.0705 | 0.0869 | 0.0677 | 0.3048 | 0.3156 | |
| 54705 | 0.0823 | 0.0765 | 0.0508 | 0.0472 | 0.1173 | 0.0700 | 0.1097 | 0.0655 | 0.2568 | 0.3625 | |
| II | 54511 | 0.1727 | 0.1269 | 0.1190 | 0.0877 | 0.1313 | 0.1084 | 0.0946 | 0.0780 | 0.5063 | 0.4123 |
| 54534 | 0.1174 | 0.1115 | 0.0859 | 0.0817 | 0.0746 | 0.0530 | 0.0704 | 0.0500 | 0.3965 | 0.2480 | |
| 54602 | 0.1832 | 0.1419 | 0.1128 | 0.0880 | 0.1578 | 0.1103 | 0.1227 | 0.0862 | 0.5259 | 0.4770 | |
| 54606 | 0.1208 | 0.1055 | 0.0792 | 0.0691 | 0.0833 | 0.0633 | 0.0720 | 0.0547 | 0.3746 | 0.2733 | |
| 54449 | 0.1451 | 0.1217 | 0.1106 | 0.0932 | 0.0868 | 0.0599 | 0.0708 | 0.0487 | 0.4706 | 0.2662 | |
| 54518 | 0.1406 | 0.1020 | 0.1015 | 0.0738 | 0.1946 | 0.1495 | 0.1461 | 0.1141 | 0.4179 | 0.6043 | |
| 54525 | 0.1157 | 0.1044 | 0.0857 | 0.0774 | 0.0884 | 0.0737 | 0.0793 | 0.0661 | 0.3832 | 0.3075 | |
| 54527 | 0.0969 | 0.0885 | 0.0702 | 0.0641 | 0.0820 | 0.0640 | 0.0748 | 0.0584 | 0.3197 | 0.2792 | |
| 54535 | 0.1437 | 0.1247 | 0.0968 | 0.0842 | 0.1232 | 0.0877 | 0.1071 | 0.0765 | 0.4494 | 0.3945 | |
| 54539 | 0.1096 | 0.0977 | 0.0731 | 0.0652 | 0.1406 | 0.1101 | 0.1270 | 0.0998 | 0.3456 | 0.4775 | |
| 54623 | 0.1584 | 0.1267 | 0.1135 | 0.0914 | 0.1216 | 0.0878 | 0.0963 | 0.0698 | 0.4900 | 0.3755 | |
| 54624 | 0.1177 | 0.0905 | 0.0880 | 0.0677 | 0.1176 | 0.0844 | 0.0912 | 0.0656 | 0.3639 | 0.3588 | |
| 54725 | 0.1316 | 0.1014 | 0.0978 | 0.0756 | 0.1072 | 0.0828 | 0.0817 | 0.0632 | 0.4064 | 0.3349 | |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IPCC. Climate Change 2007: Synthesis Report; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- IPCC. Summary for Policymakers of Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Shahabfar, A.; Eitzinger, J. Spatio-Temporal analysis of droughts in semi-arid regions by using meteorological drought indices. Atmosphere 2013, 4, 94–112. [Google Scholar] [CrossRef]
- Liepert, B.G.; Romanou, A. Global dimming and brightening and the water cycle. Bull. Amer. Meteorol. Soc. 2005, 86, 622–623. [Google Scholar]
- Wu, Z.W.; Li, J.P.; He, J.H.; Jiang, Z.H. Large-scale atmospheric singularities and summer long-cycle droughts-floods abrupt alternation in the middle and lower reaches of the Yangtze River. Chin. Sci. Bull. 2006, 51, 2027–2034. [Google Scholar] [CrossRef]
- Wu, Z.W.; Li, J.P.; He, J.H.; Jiang, Z.H. Occurrence of droughts and floods during the normal summer monsoons in the mid- and lower reaches of the Yangtze River. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Shiau, J.; Modarres, R. Copula-based drought severity-duration-frequency analysis in Iran. Meteorol. Appl. 2009, 16, 481–489. [Google Scholar] [CrossRef]
- Ibrahim, K.; Wan Zin, W.Z.; Jemain, A.A. Evaluating the dry conditions in Peninsular Malaysia using bivariate copula. ANZIAM J. 2010, 51, C555–C569. [Google Scholar]
- Mirabbasi, R.; Fakheri-Fard, A.; Dinpashoh, Y. Bivariate drought frequency analysis using the copula method. Theor. Appl. Climatol. 2012, 108, 191–206. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Sraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the Litija station on the Sava River. Hydrol. Process. 2014. [Google Scholar] [CrossRef]
- Li, T.Y.; Guo, S.L.; Chen, L.; Guo, J. Bivariate flood frequency analysis with historical information based on copula. J. Hydrol. Eng. 2012, 18, 1018–1030. [Google Scholar] [CrossRef]
- Mirabbasi, R.; Anagnostou, E.N.; Fakheri-Fard, A.; Dinpashoh, Y.; Eslamian, S. Analysis of meteorological drought in northwest Iran using the joint deficit index. J. Hydrol. 2013, 492, 35–48. [Google Scholar]
- Madadgar, S.; Moradkhani, H. Drought analysis under climate change using copula. J. Hydrol. Eng. 2011, 18, 746–759. [Google Scholar] [CrossRef]
- Ma, M.; Song, S.; Ren, L.; Jiang, S.; Song, J. Multivariate drought characteristics using trivariate Gaussian and Student copulas. Hydrol. Process. 2013, 27, 1175–1190. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate flood frequency analysis using the Gumbel–Hougaard copula. J. Hydrol. Eng. 2007, 12, 431–439. [Google Scholar] [CrossRef]
- Grimaldi, S.; Serinaldi, F. Asymmetric copula in multivariate flood frequency analysis. Adv. Water Resour. 2006, 29, 1155–1167. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. The intrinsic dependence structure of peak, volume, duration, and average intensity of hyetographs and hydrographs. Water Resour. Res. 2013, 49, 3423–3442. [Google Scholar] [CrossRef]
- Bezak, N.; Mikoš, M.; Šraj, M. Trivariate frequency analyses of peak discharge, hydrograph volume and suspended sediment concentration data using copulas. Water Resour. Manag. 2014, 28, 2195–2212. [Google Scholar] [CrossRef]
- Liu, C.M.; Yu, J.J.; Kendy, E. Groundwater exploitation and its impact on the environment in the North China Plain. Water Int. 2001, 26, 265–272. [Google Scholar] [CrossRef]
- Ren, X.S. Water Resources Assessment of Haihe River Basin; China Water Power Press: Beijing, China, 1997. (in Chinese) [Google Scholar]
- Haihe River Water Resources Conservancy Commission. Flood and Drought Disasters in Haihe River Basin; Tianjin Science and Technology Press: Tianjin, China, 2009. (in Chinese) [Google Scholar]
- Committee for Haihe River Records Compilation. Haihe River Records (Volume One); China Water Power Press: Beijing, China, 1997. (in Chinese) [Google Scholar]
- China Meteorological Data Sharing Service System. Available online: http://cdc.cma.gov.cn/home.do (accessed on 12 August 2014).
- Qian, W.; Lin, X. Regional trends in recent precipitation indices in China. Meteorol. Atmos. Phys. 2005, 90, 193–207. [Google Scholar] [CrossRef]
- Du, H.; Xia, J.; Zeng, S.D. Regional frequency analysis of extreme precipitation and its spatio-temporal characteristics in the Huai River Basin, China. Nat. Hazards 2014, 70, 195–215. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. B 1990, 52, 105–124. [Google Scholar]
- Sankarasubramanian, A.; Srinivasan, K. Investigation and comparison of sampling properties of L-moments and conventional moments. J. Hydrol. 1999, 218, 13–34. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Xiong, L.H.; Guo, S.L.; Wang, C.J. Advance in regional flood frequency analysis from abroad. Adv. Water Sci. 2004, 15, 261–267. (In Chinese) [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Sangati, M.; Zanon, F. Regional frequency analysis of extreme precipitation in the eastern Italian Alps and the August 29, 2003 flash flood. J. Hydrol. 2007, 345, 149–166. [Google Scholar] [CrossRef]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L. Statistical inference procedures for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika. 1938, 30, 81–89. [Google Scholar] [CrossRef]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Research Report: Fortran Routines for Use with the Method of L-Moments, Version 3.04. Available online: http://btr0xq.rz.uni-bayreuth.de/math/statlib/general/lmoments.pdf (accessed on 13 November 2014).
- Ju, X.S.; Yang, X.W.; Chen, L.J.; Wang, Y.M. Research on determination of station indexes and division of regional flood/drought grades in China. Q. J. Appl. Meteorol. 1997, 8, 26–33. (In Chinese) [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, W.; Yu, F.; Xie, Y.; Liu, J.; Li, C.; Zhao, N. The Copula Function-Based Probability Characteristics Analysis on Seasonal Drought & Flood Combination Events on the North China Plain. Atmosphere 2014, 5, 847-869. https://doi.org/10.3390/atmos5040847
Mu W, Yu F, Xie Y, Liu J, Li C, Zhao N. The Copula Function-Based Probability Characteristics Analysis on Seasonal Drought & Flood Combination Events on the North China Plain. Atmosphere. 2014; 5(4):847-869. https://doi.org/10.3390/atmos5040847
Chicago/Turabian StyleMu, Wenbin, Fuliang Yu, Yuebo Xie, Jia Liu, Chuanzhe Li, and Nana Zhao. 2014. "The Copula Function-Based Probability Characteristics Analysis on Seasonal Drought & Flood Combination Events on the North China Plain" Atmosphere 5, no. 4: 847-869. https://doi.org/10.3390/atmos5040847
APA StyleMu, W., Yu, F., Xie, Y., Liu, J., Li, C., & Zhao, N. (2014). The Copula Function-Based Probability Characteristics Analysis on Seasonal Drought & Flood Combination Events on the North China Plain. Atmosphere, 5(4), 847-869. https://doi.org/10.3390/atmos5040847






