Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations
Abstract
:1. Introduction
2. Model
2.1. Governing Equation
2.2. Analytical Solution
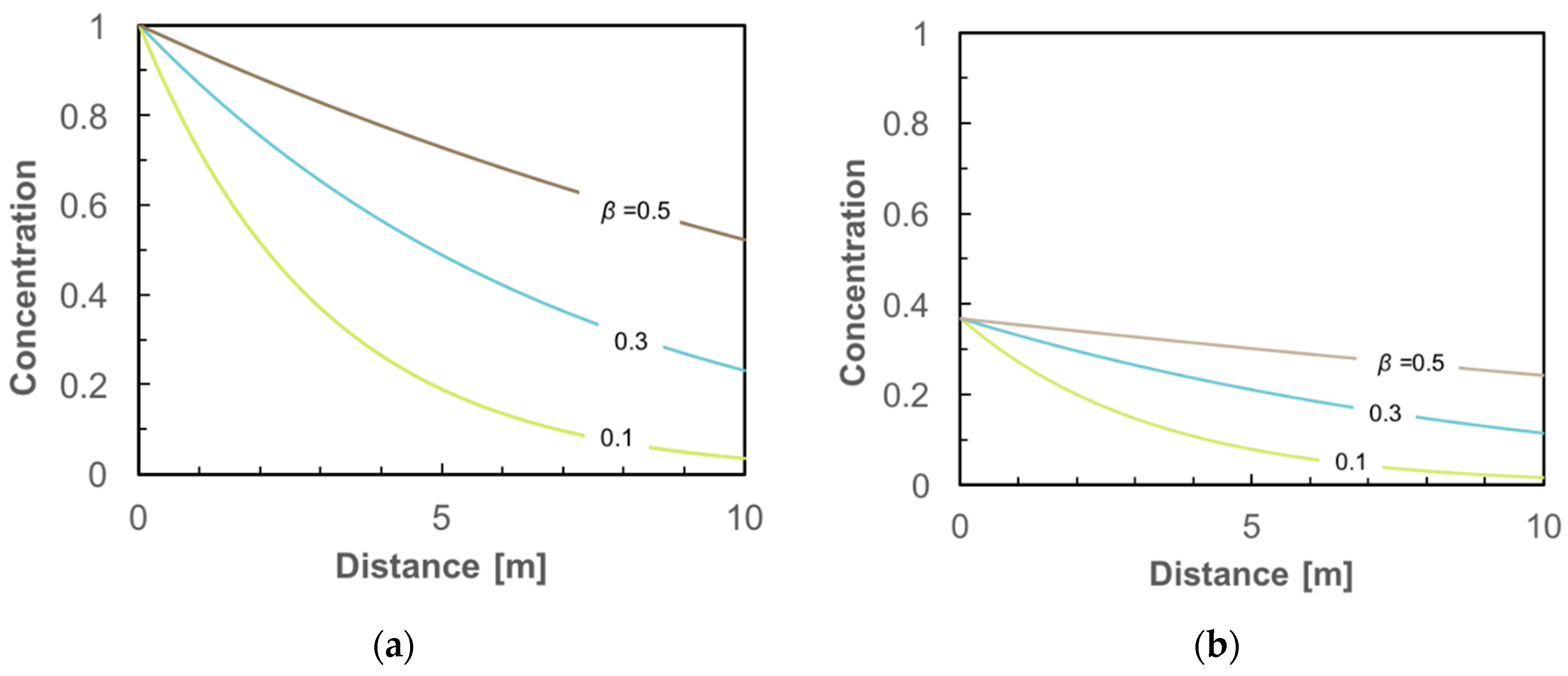
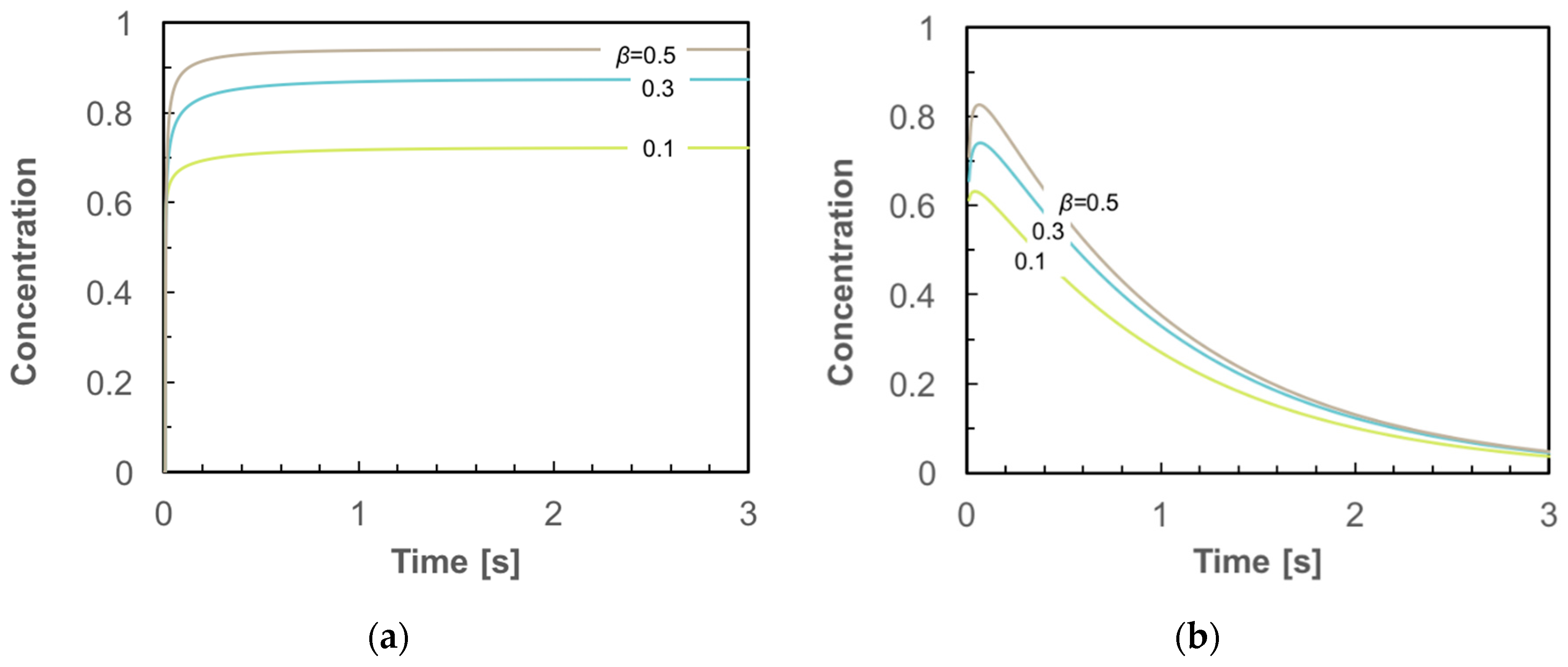
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Coats, K.; Smith, B.D. Dead-end pore volume and dispersion in porous media. Soc. Petrol. Eng. J. 1964, 4, 73–84. [Google Scholar] [CrossRef]
- Long, J.C.S.; Remer, J.S.; Wilson, C.R.; Witherspoon, P.A. Porous media equivalents for network of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef]
- Sahimi, M. Flow phenomena in rocks: From continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Mod. Phys. 1993, 65, 1395–1534. [Google Scholar]
- Edery, Y.; Guadagnini, A.; Scher, H.; Berkowitz, B. Origins of anomalous transport in heterogeneous media: Structural and dynamic controls. Water Resour. Res. 2014, 50, 1490–1505. [Google Scholar] [CrossRef]
- Hatano, Y.; Hatano, N. Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resour. Res. 1998, 34, 1027–1033. [Google Scholar] [CrossRef]
- Haggerty, R.; Wondzell, S.M.; Johnson, M.A. Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream. Geophys. Res. Lett. 2002, 29, 1640. [Google Scholar] [CrossRef]
- Radilla, G.; Sausse, J.; Sanjuan, B.; Fourar, M. Interpreting tracer tests in the enhanced geothermal system (EGS) of Soultz-sous-Forêts using the equivalent stratified medium approach. Geothermics 2012, 44, 43–51. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M., Jr. Navier-Stokes flow and transport simulations using real fractures shows heavy tailing due to eddies. Geophys. Res. Lett. 2007, 34, L14404. [Google Scholar] [CrossRef]
- Hodgkinson, D.; Benabderrahmane, H.; Elert, M.; Hautojärvi, A.; Selroos, J.O.; Tanaka, Y.; Uchida, M. An overview of Task 6 of the Aspö Task Force: Modelling groundwater and solute transport: Improved understanding of radionuclide transport in fractured rock. Hydrogeol. J. 2009, 17, 1035–1049. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Interpreting tracer breakthrough tailing from different forced-gradient tracer experiment configurations in fractured bedrock. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Tsang, Y.W. Study of alternative tracer tests in characterizing transport in fractured rocks. Geophys. Res. Lett. 1995, 22, 1421–1424. [Google Scholar] [CrossRef]
- Tang, D.H.; Frind, E.O.; Sudicky, E.A. Contaminant transport in fractured porous media: Analytical solution for a single fracture. Water Resour. Res. 1981, 17, 555–564. [Google Scholar] [CrossRef]
- Sudicky, E.; Frind, E. Contaminant transport in fractured porous media: Analytical solutions for a system of parallel fractures. Water Resour. Res. 1982, 18, 1634–1642. [Google Scholar] [CrossRef]
- Neretnieks, I. A note on fracture flow dispersion mechanisms in the ground. Water Resour. Res. 1983, 19, 364–370. [Google Scholar] [CrossRef]
- Becker, M.W.; Shapiro, A.M. Tracer transport in fractured crystalline rock: Evidence of nondiffusive breakthrough tailing. Water Resour. Res. 2000, 36, 1677–1686. [Google Scholar] [CrossRef]
- Yates, S.R. An analytical solution for one-dimensional transport in heterogeneous porous media. Water Resour. Res. 1990, 26, 2331–2338. [Google Scholar]
- Haggerty, R.; Gorelick, S.M. Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 1995, 31, 2383–2400. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44, RG2003. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.S.W.; Meerschaert, M.M. Application of a fractional advection-dispersion equation. Water Resour. Res. 2000, 36, 1403–1412. [Google Scholar] [CrossRef]
- Morales-Casique, E.; Neuman, S.P.; Guadagnini, A. Non-local and localized analyses of non-reactive solute transport in bounded randomly heterogeneous porous media: Theoretical framework. Adv. Water Resour. 2006, 29, 1238–1255. [Google Scholar] [CrossRef]
- Schumer, R.; Meerschaert, M.M.; Baeumer, B. Fractional advection-dispersion equations for modeling transport at the Earth surface. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.V.; Turner, I.; Zhuang, P. Time fractional advection-dispersion equation. J. Appl. Math. Comput. 2003, 13, 233–245. [Google Scholar] [CrossRef] [Green Version]
- Fomin, S.; Chugunov, V.; Hashida, T. The effect of non-Fickian diffusion into surrounding rocks on contaminant transport in a fractured porous aquifer. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2923–2939. [Google Scholar] [CrossRef]
- Suzuki, A.; Fomin, S.A.; Chugunov, V.A.; Niibori, Y.; Hashida, T. Fractional diffusion modeling of heat transfer in porous and fractured media. Int. J. Heat Mass Transf. 2016, 103, 611–618. [Google Scholar] [CrossRef]
- Zumofen, G.; Klafter, J. Scale-invariant motion in intermittent chaotic systems. Phys. Rev. E 1993, 47, 851–863. [Google Scholar] [CrossRef]
- Penttinen, L.; Siitari-kauppi, M.; Ikonen, J. Forsmark Site Investigation Determination of Porosity and Micro Fracturing Using the C-PMMA Technique in Samples Taken from Forsmark Area; Technical Report; Svensk Kärnbränslehantering AB: Stockholm, Sweden, 2006. [Google Scholar]
- Fomin, S.A.; Chugunov, V.A.; Hashida, T. Non-Fickian mass transport in fractured porous media. Adv. Water Resour. 2011, 34, 205–214. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar] [CrossRef]
- Grisak, G.; Pickens, J. An analytical solution for solute transport through fractured media with matrix diffusion. J. Hydrol. 1981, 52, 47–57. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations: Volume 2: Applications in Engineering and Physical Sciences; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, A.; Fomin, S.; Chugunov, V.; Hashida, T. Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations. Water 2018, 10, 123. https://doi.org/10.3390/w10020123
Suzuki A, Fomin S, Chugunov V, Hashida T. Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations. Water. 2018; 10(2):123. https://doi.org/10.3390/w10020123
Chicago/Turabian StyleSuzuki, Anna, Sergei Fomin, Vladimir Chugunov, and Toshiyuki Hashida. 2018. "Mathematical Modeling of Non-Fickian Diffusional Mass Exchange of Radioactive Contaminants in Geological Disposal Formations" Water 10, no. 2: 123. https://doi.org/10.3390/w10020123



