Discharge Coefficient of Rectangular Short-Crested Weir with Varying Slope Coefficients
Abstract
:1. Introduction
2. Theoretical Analysis of Influential Factors of Discharge Coefficient
3. Numerical Modeling
3.1. Governing Equations
3.2. Disposal of Free Water Surface
3.3. Boundary Conditions
3.4. Grids Layout
3.5. Numerical Simulation
4. Results and Discussion
4.1. Validation of Numerical Models
4.2. Calculation Formula of Discharge Coefficient
4.3. Effects of Slope Coefficients on Discharge Coefficient
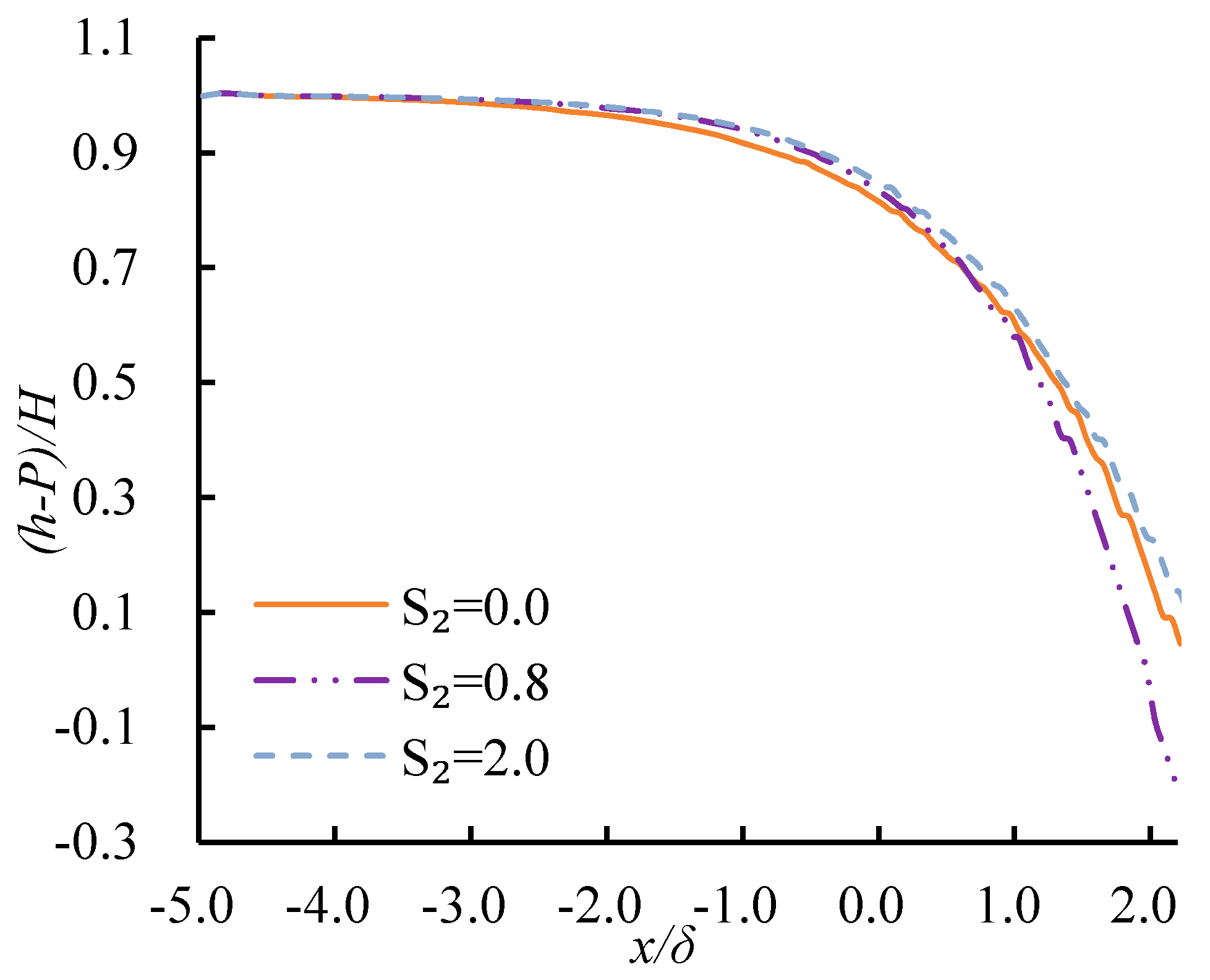
4.4. Effects of Slope Coefficients on Free Surface Profiles
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| B | width of weir |
| Fr | Froude number |
| g | acceleration of gravity |
| hf | frictional head loss |
| hj | local head loss |
| hw | total head loss |
| H | overflow piezometric head upstream of weir |
| H0 | upstream overflow total energy head, H0 = H + U2/2g |
| m | discharge coefficient |
| m′ | fitting discharge coefficient |
| P | height of weir |
| Q | inflow discharge |
| R | correlation coefficient |
| S1 | upstream slope coefficient (the ratio of horizontal to vertical) |
| S2 | downstream slope coefficient (the ratio of horizontal to vertical) |
| U | approaching velocity |
| α | nondimensional coefficient |
| β | nondimensional coefficient |
| δ | length of weir |
| ξ | relative total energy head over the crest, ξ = H0/(P + δ) |
| ρ | mass density of water |
| σ | surface tension of water |
| μ | dynamic viscosity of water |
References
- Govinda Rao, N.S.; Muralidhar, D. Discharge characteristics of weirs of finite-crest width. La Houille Blanche 1963, 5, 537–545. [Google Scholar] [CrossRef]
- Li, J.X.; Zhao, Z.X. Hydraulics; Hohai University Press: Nanjing, China, 2001. (In Chinese) [Google Scholar]
- Inozemtsev, Y.P. Cavitation destruction of concrete and protective facings under natural conditions. Power Technol. Eng. 1969, 3, 35–42. [Google Scholar] [CrossRef]
- Bos, M.G. Discharge Measurement Structures; NASA Sti/recon Technical Report N; National Aeronautics and Space Administration: Washington, DC, USA, 1989; Volume 78, pp. 120–122.
- Ramamurthy, A.; Tim, U.; Rao, M. Characteristics of square-edged and round-nosed broad-crested weirs. J. Irrig. Drain. Eng. 1988, 114, 61–73. [Google Scholar] [CrossRef]
- Tong, H.H.; Lan, F.R. Analysis of the effect of weir height on discharge capacity of low weirs. Yangtze River 2002, 11, 20–21. (In Chinese) [Google Scholar]
- Singer, J. Square-edged broad-crested weir as a flow measurement device. Water Water Eng. 1964, 68, 229–235. [Google Scholar]
- Kiselef, P.G.; Zhou, P.; Hua, Z. Hydraulics: Principle of Fluid Mechanics; China Water & Power Press: Beijing, China, 1983. (In Chinese) [Google Scholar]
- Li, W. Hydraulic Reckoner; China Water & Power Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Tong, H.H.; Ai, K.M.; Ding, X.Q. Discharge capacity of broken-line practical weir. J. Yangtze River Sci. Res. Inst. 2002, 19, 19–22. (In Chinese) [Google Scholar]
- Farhoudi, J.; Shokri, N. Flow from Broad Crested Rectangular Weirs with Sloped Downstream Face, 32nd ed.; IAHR Congress: Venice, Italy, 2007. [Google Scholar]
- Badr, K.; Mowla, D. Development of rectangular broad-crested weirs for flow characteristics and discharge measurement. KSCE J. Civ. Eng. 2015, 19, 136–141. [Google Scholar] [CrossRef]
- Azimi, A.H.; Rajaratnam, N. Discharge characteristics of weirs of finite crest length. J. Irrig. Drain. Eng. 2009, 139, 1081–1085. [Google Scholar] [CrossRef]
- Goodarzi, E.; Farhoudi, J.; Shokri, N. Flow Characteristics of rectangular broad-crested weirs with sloped upstream face. J. Hydrol. Hydromech 2012, 60, 87. [Google Scholar] [CrossRef]
- Farhoudi, J.; Shah Alami, H. Slope effect on discharge efficiency in rectangular broad crested weir with sloped upstream face. Int. J. Civ. Eng. 2005, 3, 58–65. [Google Scholar]
- Sargison, J.E.; Percy, A. Hydraulics of broad-crested weirs with varying slopes. J. Irrig. Drain. Eng. ASCE 2009, 135, 115–118. [Google Scholar] [CrossRef]
- Tong, H.H.; Li, M.C.; Ding, X.Q. Relation between low weir shape and discharge capacity. J. Yangtze River Sci. Res. Inst. 2011, 28, 25–28. (In Chinese) [Google Scholar]
- Chen, Y.J.; Gu, X.F.; Fu, Z.F.; Cui, Z. Effects of varying upstream side slope coefficients on discharge coefficient of broken-line practical weirs. J. Hohai Univ. (Nat. Sci.) 2018. in press (In Chinese) [Google Scholar]
- Chen, Y.J.; Fu, Z.F.; Cui, Z. Effects of varying upstream side slopes on discharge coefficient of rectangular profile short-crested weirs. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
- Li, W. Hydraulic Calculation Mannual; China Water & Power Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Haun, S.; Olsen, N.R.B.; Feurich, R. Numerical modeling of flow over trapezoidal broad-crested weir. Eng. Appl. Comp. Fluid 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Flow Science Inc. Flow-3D User Manual Version 11.0.3; Flow Science Inc.: Santa Fe, NM, USA, 2015. [Google Scholar]
- Paik, J.; Lee, N.J. Numerical modeling of free surface flow over a broad-crested rectangular weir. J. Korea Water Resour. Assoc. 2015, 48, 281–290. (In Korean) [Google Scholar] [CrossRef]
- Vaccine, D.V.; Wang, S.X. Model scale and discharge coefficient. Adv. Sci. Technol. Water Resour. 1981, 2, 37–44. (In Chinese) [Google Scholar]
- Isaacs, L.T. Effects of Laminar Boundary Layer on a Model Broad-Crested Weir; NASA Sti/recon Technical Report N; National Aeronautics and Space Administration: Washington, DC, USA, 1981; Volume 83, pp. 1–20.
- Ranga Raju, K.G.; Srivastava, R.; Porey, P.D. Scale effects in modelling flow over broad-crested weirs. Irrig. Power 1990, 47, 101–106. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Wang, F.J. Analysis of Computational Fluid Dynamics: Theory and Application of CFD Software; Tsinghua University Press: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Azimi, H.; Shabanlou, S.; Ebtehaj, I.; Bonakdari, H. Discharge Coefficient of rectangular side weirs on circular channels. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
















| Meshing | Number of Cells | RMSE | MAPE |
|---|---|---|---|
| 1 | 195,600 | 8.30% | 7.53% |
| 2 | 283,360 | 6.21% | 4.97% |
| 3 | 568,800 | 2.93% | 0.57% |
| 4 | 652,500 | 2.75% | 0.45% |
| Configuration | Scheme | Upstream Side Slope Coeff. S1 | Downstream Slope Coeff. S2 | No. of Models | Interpretation |
|---|---|---|---|---|---|
| VRV | Mij i = 1, j = 1 | 0.0 | 0.0 | 1 | Rectangular short-crested weir |
| URV | Mij i ≠ 1, j = 1 | 0.3, 0.5, 0.8, 1.0, 1.5, 2.0 | 0.0 | 6 | Only study the effect of the varying S1 on the discharge coefficient of rectangular short-crested weir |
| VRD | Mij i = 1, j ≠ 1 | 0.0 | 0.4, 0.8, 1.0, 1.3, 1.5, 1.8, 2.0, 3.0 | 8 | Only study the effect of the varying S2 on the discharge coefficient of short-crested weir |
| URD | Mij i ≠ 1, j ≠ 1 | 0.3, 0.5, 0.8, 1.0, 1.5, 2.0 | 0.4, 0.8, 1.0, 1.3, 1.5, 1.8, 2.0, 3.0 | 48 | Study the combinational effect of the varying S1 and S2 on discharge coefficient of rectangular short-crested weir |
| Scheme | Upstream Slope Coeff. S1 | Downstream Slope Coeff. S2 | Weir Height P (cm) | Crest Length δ (cm) | Weir Width B (cm) | Total crest Head H0 (cm) |
|---|---|---|---|---|---|---|
| M11 | 0.0 | 0.0 | 24.0 | 16.0 | 30.0 | 8.0, 12.0, 16.0, 20.0, 24.0 |
| M71 | 2.0 | 0.0 | ||||
| M73 | 2.0 | 0.8 |
| Statistical Object | ξ | Scheme | RMSE | MAPE |
|---|---|---|---|---|
| Discharge coefficient | 0.2–0.6 | S1 = 0.0, S2 = 0.0 | 0.37% | 0.91% |
| S1 = 2.0, S2 = 0.0 | 0.49% | 1.11% | ||
| S1 = 2.0, S2 = 0.8 | 0.36% | 0.85% | ||
| Free surface profile | 0.6 | S1 = 0.0, S2 = 0.0 | 2.95% | 2.80% |
| S1 = 2.0, S2 = 0.0 | 2.68% | 2.86% | ||
| S1 = 2.0, S2 = 0.8 | 1.84% | 2.20% |
| Parameter | Upstream Slope Coefficient | Downstream Slope Coefficient | ||||||
|---|---|---|---|---|---|---|---|---|
| S1 = 0.0 | S1 = 0.3 | S1 = 0.5 | S1 = 0.8 | S1 = 1.0 | S1 = 1.5 | S1 = 2.0 | ||
| α | S2 = 0.0 | 0.0619 | 0.0596 | 0.0586 | 0.0546 | 0.0524 | 0.0468 | 0.0421 |
| S2 = 0.4 | 0.0679 | 0.0678 | 0.0657 | 0.0626 | 0.0588 | 0.0529 | 0.0481 | |
| S2 = 0.8 | 0.0794 | 0.0774 | 0.0751 | 0.0719 | 0.0682 | 0.0609 | 0.0546 | |
| S2 = 1.0 | 0.0770 | 0.0746 | 0.0734 | 0.0694 | 0.0663 | 0.0594 | 0.0540 | |
| S2 = 1.3 | 0.0712 | 0.0693 | 0.0676 | 0.0647 | 0.0620 | 0.0559 | 0.0499 | |
| S2 = 1.5 | 0.0676 | 0.0658 | 0.0649 | 0.0615 | 0.0591 | 0.0529 | 0.0477 | |
| S2 = 1.8 | 0.0594 | 0.0606 | 0.0573 | 0.0576 | 0.0525 | 0.0469 | 0.0426 | |
| S2 = 2.0 | 0.0593 | 0.0584 | 0.0574 | 0.0551 | 0.0529 | 0.0480 | 0.0439 | |
| S2= 3.0 | 0.0458 | 0.0476 | 0.0466 | 0.0456 | 0.0421 | 0.0381 | 0.0339 | |
| β | S2 = 0.0 | 0.4697 | 0.4725 | 0.4740 | 0.4727 | 0.4716 | 0.4656 | 0.4591 |
| S2 = 0.4 | 0.4786 | 0.4845 | 0.4852 | 0.4845 | 0.4814 | 0.4750 | 0.4692 | |
| S2 = 0.8 | 0.4925 | 0.4957 | 0.4959 | 0.4955 | 0.4920 | 0.4843 | 0.4757 | |
| S2 = 1.0 | 0.4883 | 0.4913 | 0.4929 | 0.4913 | 0.4894 | 0.4817 | 0.4743 | |
| S2 = 1.3 | 0.4798 | 0.4828 | 0.4849 | 0.4839 | 0.4832 | 0.4767 | 0.4689 | |
| S2 = 1.5 | 0.4736 | 0.4776 | 0.4798 | 0.4791 | 0.4780 | 0.4715 | 0.4650 | |
| S2 = 1.8 | 0.4606 | 0.4692 | 0.4674 | 0.4723 | 0.4669 | 0.4617 | 0.4562 | |
| S2 = 2.0 | 0.4602 | 0.4652 | 0.4676 | 0.4683 | 0.4676 | 0.4630 | 0.4578 | |
| S2 = 3.0 | 0.4377 | 0.4467 | 0.4490 | 0.4516 | 0.4486 | 0.4460 | 0.4407 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Fu, Z.; Chen, Q.; Cui, Z. Discharge Coefficient of Rectangular Short-Crested Weir with Varying Slope Coefficients. Water 2018, 10, 204. https://doi.org/10.3390/w10020204
Chen Y, Fu Z, Chen Q, Cui Z. Discharge Coefficient of Rectangular Short-Crested Weir with Varying Slope Coefficients. Water. 2018; 10(2):204. https://doi.org/10.3390/w10020204
Chicago/Turabian StyleChen, Yuejun, Zongfu Fu, Qingsheng Chen, and Zhen Cui. 2018. "Discharge Coefficient of Rectangular Short-Crested Weir with Varying Slope Coefficients" Water 10, no. 2: 204. https://doi.org/10.3390/w10020204
APA StyleChen, Y., Fu, Z., Chen, Q., & Cui, Z. (2018). Discharge Coefficient of Rectangular Short-Crested Weir with Varying Slope Coefficients. Water, 10(2), 204. https://doi.org/10.3390/w10020204





