Wave Height Attenuation and Flow Resistance Due to Emergent or Near-Emergent Vegetation
Abstract
:1. Introduction
2. Materials and Methods
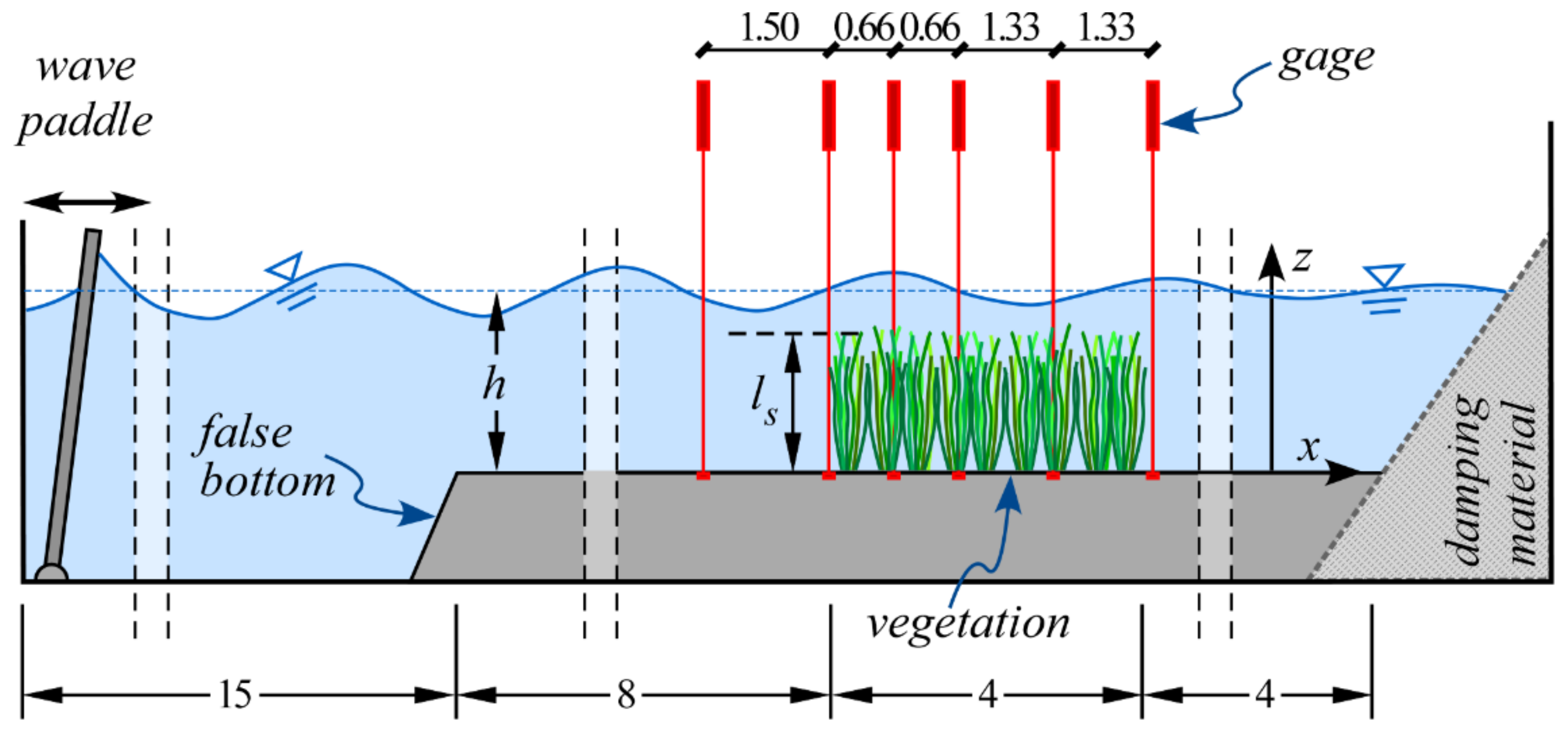
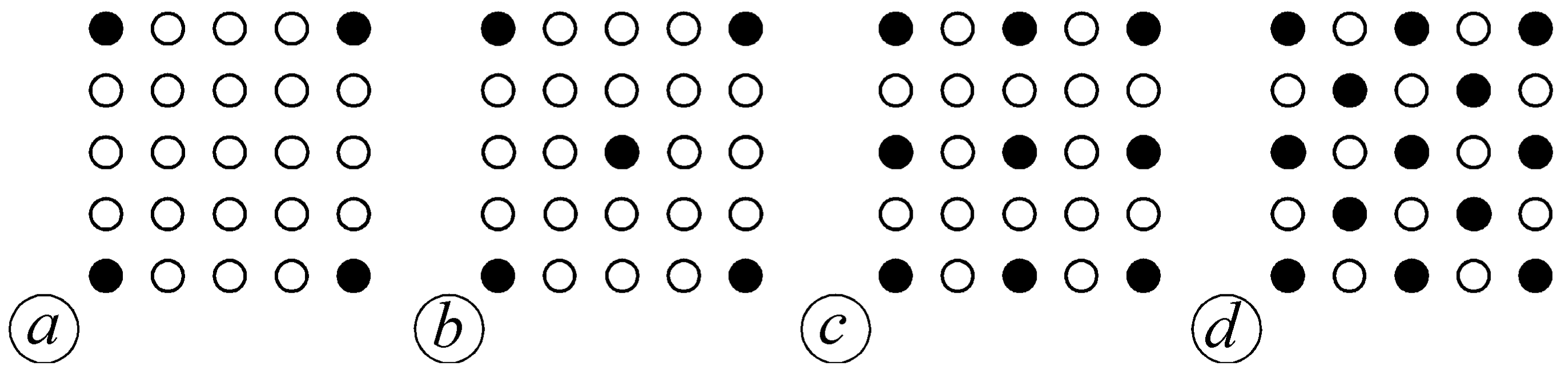
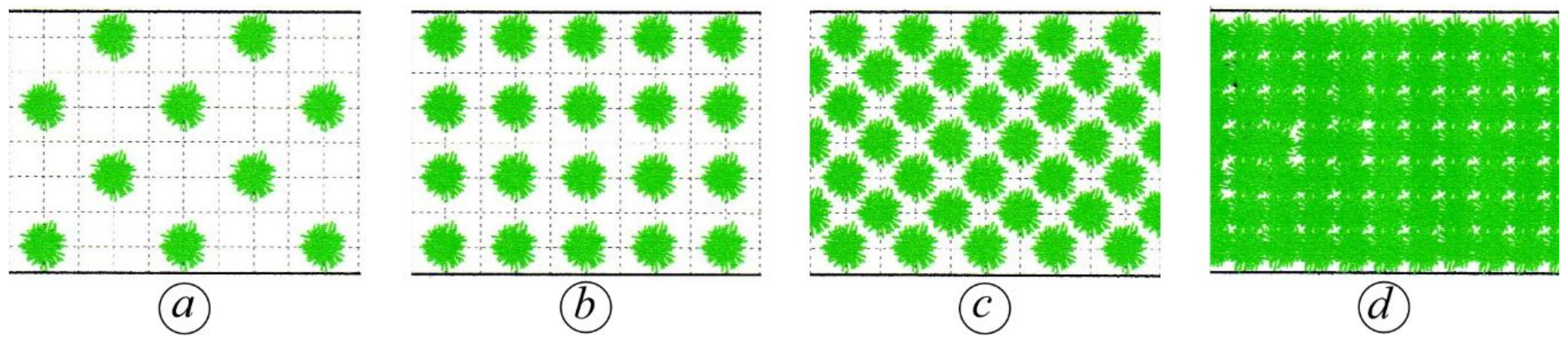
2.1. Experimental Setup
2.2. The Theoretical Model
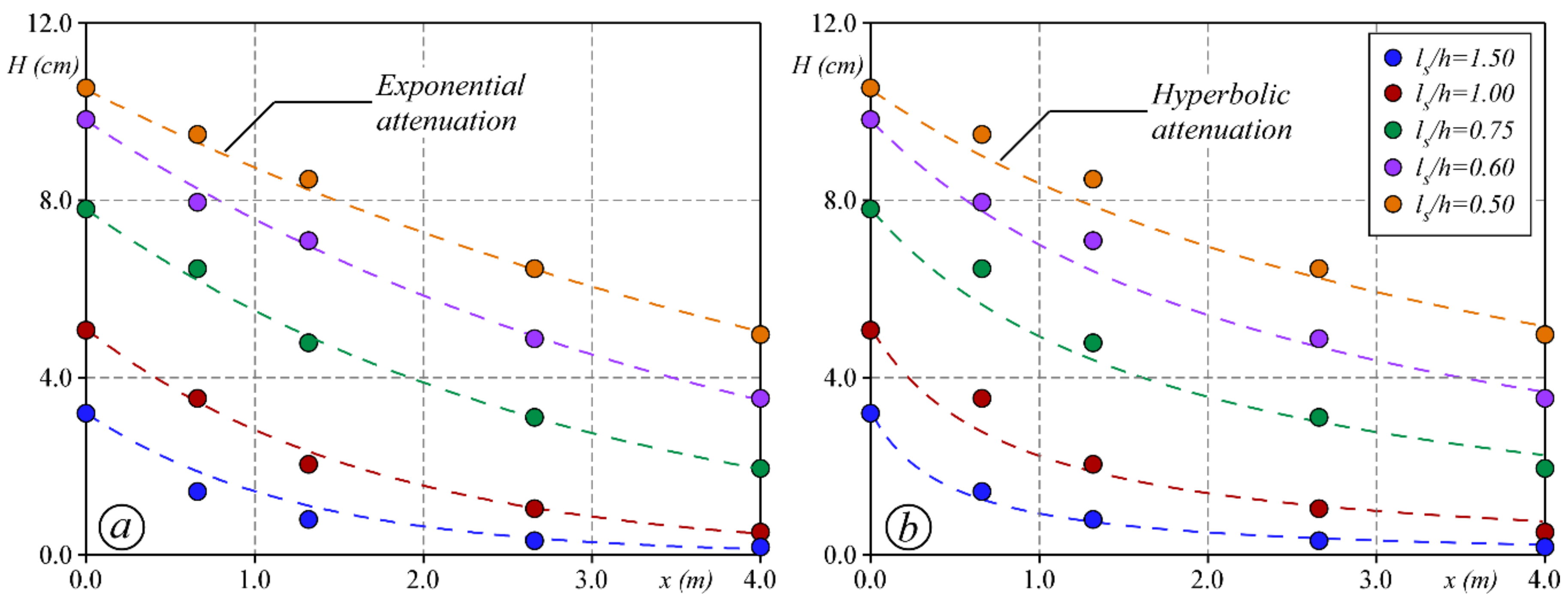
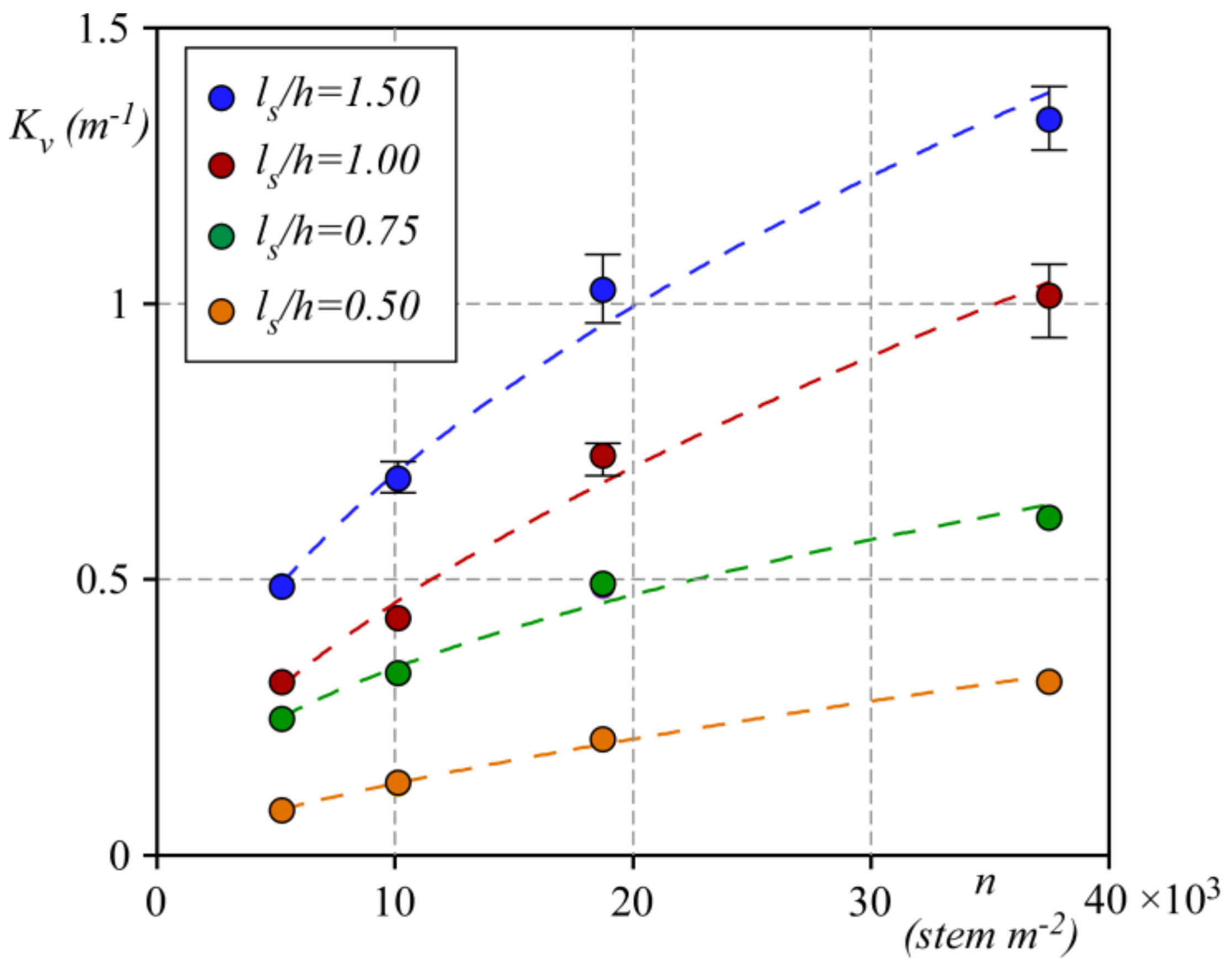
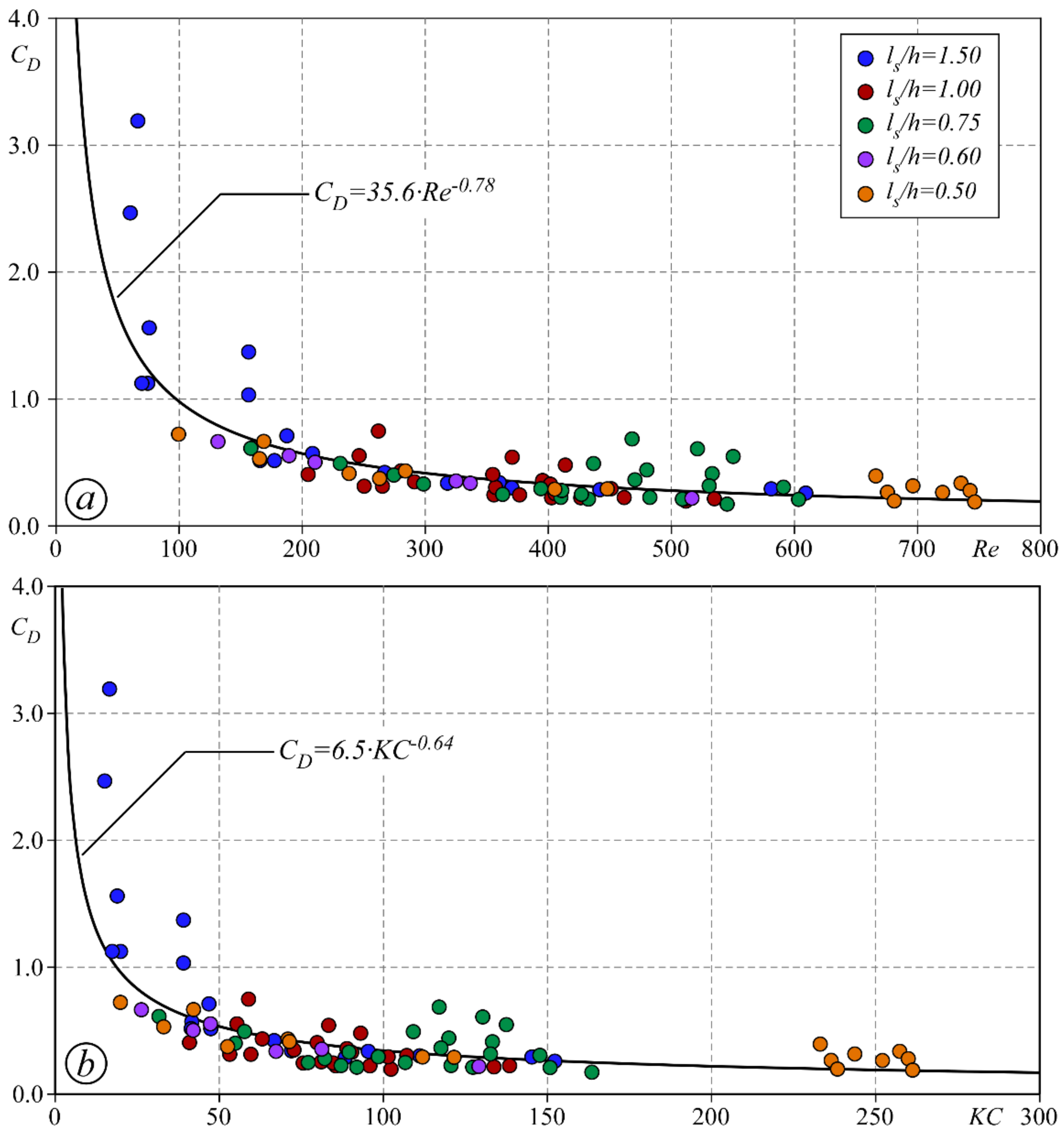
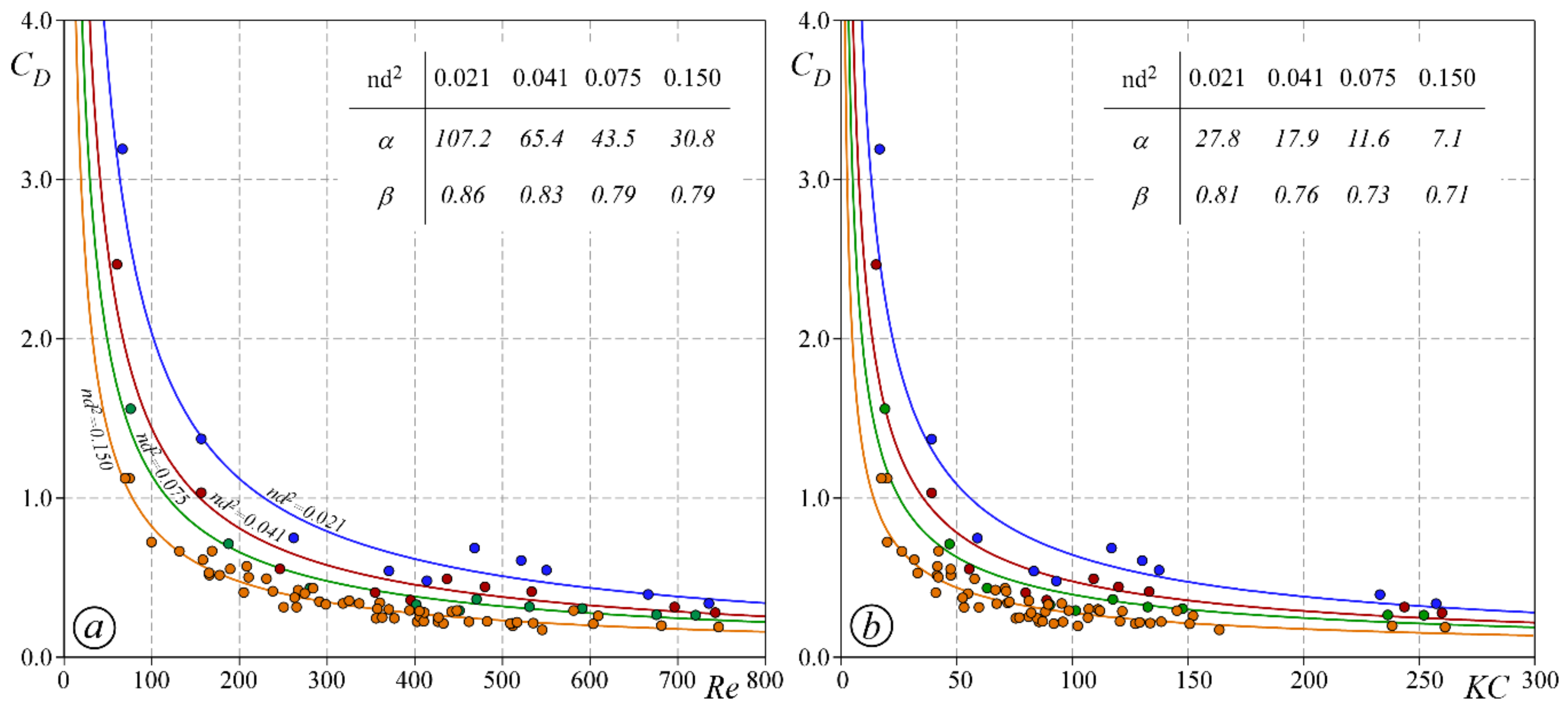
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Costanza, R.; d’Arge, R.; De Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Fisher, J.S.; Zieman, J.C.; Thayer, G.W. Influence of the seagrass, Zostera marina L., on current flow. Estuar. Coast. Shelf Sci. 1982, 15, 351–364. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Cahalan, J.A. A preliminary evaluation of wave attenuation by four species of seagrass. Estuar. Coast. Shelf Sci. 1992, 35, 565–576. [Google Scholar] [CrossRef]
- Titus, J.G. Rising seas, coastal erosion, and the takings clause: How to save wetlands and beaches without hurting property owners. MD Law Rev. 1998, 57, 1279–1399. [Google Scholar]
- Carniello, L.; Defina, A.; D’Alpaos, L. Morphological evolution of the Venice lagoon: Evidence from the past and trend for the future. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W.; Asano, T. Wave attenuation by vegetation. J. Waterw. Port Coast. Ocean Eng. 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Mork, M. Wave attenuation due to bottom vegetation. Waves Nonlinear Process. Hydrodyn. 1996, 371–382. [Google Scholar]
- Möller, I.; Spencer, T. Wave dissipation over macro-tidal saltmarshes: Effects of marsh edge typology and vegetation change. J. Coast. Res. 2002, 36, 506–521. [Google Scholar]
- Ghisalberti, M.; Nepf, H.M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. Ocean. 2002, 107. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H. The structure of the shear layer in flows over rigid and flexible canopies. Environ. Fluid Mech. 2006, 6, 277–301. [Google Scholar] [CrossRef]
- Palmer, M.R.; Nepf, H.M.; Pettersson, T.J.R. Accumulation and Removal in Aquatic Systems. Limnol. Oceanogr. 2004, 49, 76–85. [Google Scholar] [CrossRef]
- Hendriks, I.E.; Sintes, T.; Bouma, T.J.; Duarte, C.M. Experimental assessment and modeling evaluation of the effects of the seagrass Posidonia oceanica on flow and particle trapping. Mar. Ecol. Prog. Ser. 2008, 356, 163–173. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Musumeci, R.E.; Cavallaro, L.; Foti, E. A small scale Pressure Retarded Osmosis power plant: Dynamics of the brackish effluent discharge along the coast. Ocean Eng. 2017, 130, 417–428. [Google Scholar] [CrossRef]
- Peruzzo, P.; Defina, A.; Nepf, H. Capillary trapping of buoyant particles within regions of emergent vegetation. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Chang, E.R.; Veeneklaas, R.M.; Buitenwerf, R.; Bakker, J.P.; Bouma, T.J. To move or not to move: Determinants of seed retention in a tidal marsh. Funct. Ecol. 2008, 22, 720–727. [Google Scholar] [CrossRef]
- Peruzzo, P.; Defina, A.; Nepf, H.M.; Stocker, R. Capillary interception of floating particles by surface-piercing vegetation. Phys. Rev. Lett. 2013, 111, 164501. [Google Scholar] [CrossRef] [PubMed]
- Peruzzo, P.; Pietro Viero, D.; Defina, A. A semi-empirical model to predict the probability of capture of buoyant particles by a cylindrical collector through capillarity. Adv. Water Resour. 2016, 97, 168–174. [Google Scholar] [CrossRef]
- Gacia, E.; Granata, T.; Duarte, C. An approach to measurement of particle flux and sediment retention within seagrass (Posidonia oceanica) meadows. Aquat. Bot. 1999, 65, 255–268. [Google Scholar] [CrossRef]
- Gacia, E.; Duarte, C.M. Sediment retention by a Mediterranean Posidonia oceanica meadow: The balance between deposition and resuspension. Estuar. Coast. Shelf Sci. 2001, 52, 505–514. [Google Scholar] [CrossRef]
- Fauria, K.E.; Kerwin, R.E.; Nover, D.; Schladow, S.G. Suspended particle capture by synthetic vegetation in a laboratory flume. Water Resour. Res. 2015, 51, 9112–9126. [Google Scholar] [CrossRef]
- De Serio, F.; Meftah, M.B.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2017. [Google Scholar] [CrossRef]
- Mossa, M.; De Serio, F. Rethinking the process of detrainment: Jets in obstructed natural flows. Sci. Rep. 2016, 6, 39103. [Google Scholar] [CrossRef] [PubMed]
- Mossa, M.; Meftah, M.B.; De Serio, F.; Nepf, H.M. How vegetation in flows modifies the turbulent mixing and spreading of jets. Sci. Rep. 2017, 7, 6587. [Google Scholar] [CrossRef] [PubMed]
- Dalrymple, R.A.; Kirby, J.T.; Hwang, P.A. Wave diffraction due to areas of energy dissipation. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 67–79. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Manca, E.; Cáceres, I.; Alsina, J.M.; Stratigaki, V.; Townend, I.; Amos, C.L. Wave energy and wave-induced flow reduction by full-scale model Posidonia oceanica seagrass. Cont. Shelf Res. 2012, 50, 100–116. [Google Scholar] [CrossRef]
- Anderson, M.E.; Smith, J.M. Wave attenuation by flexible, idealized salt marsh vegetation. Coast. Eng. 2014, 83, 82–92. [Google Scholar] [CrossRef]
- Ifuku, M.; Hayashi, H. Development of eelgrass (Zostera marina) bed utilizing sand drift control mats. Coast. Eng. J. 1998, 40, 223–239. [Google Scholar] [CrossRef]
- Moeller, I.; Spencert, T.; French, J.R. Wind wave attenuation over saltmarsh surfaces: Preliminary results from Norfolk, England. J. Coast. Res. 1996, 12, 1009–1016. [Google Scholar]
- Moller, I.; Spencer, T.; French, J.R.; Leggett, D.J.; Dixon, M. Wave transformation over salt marshes: A field and numerical modelling study from north Norfolk, England. Estuar. Coast. Shelf Sci. 1999, 49, 411–426. [Google Scholar] [CrossRef]
- Mazda, Y.; Kobashi, D.; Okada, S. Tidal-scale hydrodynamics within mangrove swamps. Wetl. Ecol. Manag. 2005, 13, 647–655. [Google Scholar] [CrossRef]
- Cassan, L.; Roux, H.; Garambois, P.-A. A Semi-Analytical Model for the Hydraulic Resistance Due to Macro-Roughnesses of Varying Shapes and Densities. Water 2017, 9, 637. [Google Scholar] [CrossRef]
- Dubi, A.; Tørum, A. Wave damping by kelp vegetation. Coast. Eng. 1994, 142–156. [Google Scholar] [CrossRef]
- Knutson, P.L.; Brochu, R.A.; Seelig, W.N.; Inskeep, M. Wave damping in Spartina alterniflora marshes. Wetlands 1982, 2, 87–104. [Google Scholar] [CrossRef]
- Elwany, M.H.S.; O’Reilly, W.C.; Guza, R.T.; Flick, R.E. Effects of Southern California kelp beds on waves. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 143–150. [Google Scholar] [CrossRef]
- Möller, I. Quantifying saltmarsh vegetation and its effect on wave height dissipation: Results from a UK East coast saltmarsh. Estuar. Coast. Shelf Sci. 2006, 69, 337–351. [Google Scholar] [CrossRef]
- Silvestri, S.; Defina, A.; Marani, M. Tidal regime, salinity and salt marsh plant zonation. Estuar. Coast. Shelf Sci. 2005, 62, 119–130. [Google Scholar] [CrossRef]
- Beach, W.P.; Neumeier, U.; Ciavola, P. Flow Resistance and Associated Sedimentary Processes in a Spartina maritima Salt-Marsh. J. Coast. Res. 2004, 20, 435–447. [Google Scholar]
- Defina, A.; Peruzzo, P. Floating particle trapping and diffusion in vegetated open channel flow. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Defina, A.; Peruzzo, P. Diffusion of floating particles in flow through emergent vegetation: Further experimental investigation. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Yan, N.I. Drag Forces on Vegetation Due to Waves and Currents. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Koch, D.L.; Ladd, A.J.C. Moderate Reynolds number flows through periodic and random arrays of aligned cylinders. J. Fluid Mech. 1997, 349, 31–66. [Google Scholar] [CrossRef]
- Poggi, D.; Katul, G.G.; Albertson, J.D. A note on the contribution of dispersive fluxes to momentum transfer within canopies. Boundary-Layer Meteorol. 2004, 111, 615–621. [Google Scholar] [CrossRef]
- Meftah, M.B.; Mossa, M. Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 2013, 25, 45102. [Google Scholar] [CrossRef]
- Meftah, M.B.; De Serio, F.; Mossa, M. Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 2014, 26, 65102. [Google Scholar] [CrossRef]
- Defina, A.; Bixio, A.C. Mean flow and turbulence in vegetated open channel flow. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Poggi, D.; Krug, C.; Katul, G.G. Hydraulic resistance of submerged rigid vegetation derived from first-order closure models. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Blevins, R.D. Forces on and Stability of a Cylinder in a Wake. ASME J. Offshore Mech. Arct. Eng. 2005, 127, 39–45. [Google Scholar] [CrossRef]
- Zdravkovich, M.M.; Pridden, D.L. Interference between two circular cylinders; series of unexpected discontinuities. J. Wind Eng. Ind. Aerodyn. 1977, 2, 255–270. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [Google Scholar] [CrossRef]
- Trimble, S.; Houser, C.; Trimble, S.; Morales, B. Influence of Blade Flexibility on the Drag Coefficient of Aquatic Vegetation. Estuar. Coast. 2015, 38, 569–577. [Google Scholar]
- White, F.M. Viscous Fluid Flow; McGraw-Hill Education: New York, NY, USA, 1991; pp. 335–393. [Google Scholar]



| Series 1 | ||||
| np | n | h | T | H0/L |
| (plant/m2) | (stem/m2) | (cm) | (s) | |
| 43.75 | 5250 | 10 ÷ 30 | 0.7 ÷ 1.4 | 0.01 ÷ 0.09 |
| 84.50 | 10,140 | |||
| 156.25 | 18,750 | |||
| 312.50 | 37,500 | |||
| Series 2 | ||||
| 312.50 | 37,500 | 10 ÷ 30 | 0.8; 1.0; 1.2 | 0.03; 0.05; 0.08 |
| Uniform Flow Test | |||
|---|---|---|---|
| np | n | h | T |
| (plant/m2) | (stem/m2) | (cm) | (s) |
| 78.125 | 9375 | 5; 10: 15 | ~6.7 |
| 156.25 | 18,750 | ||
| 312.50 | 37,500 | ||
| 625.00 | 75,000 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peruzzo, P.; De Serio, F.; Defina, A.; Mossa, M. Wave Height Attenuation and Flow Resistance Due to Emergent or Near-Emergent Vegetation. Water 2018, 10, 402. https://doi.org/10.3390/w10040402
Peruzzo P, De Serio F, Defina A, Mossa M. Wave Height Attenuation and Flow Resistance Due to Emergent or Near-Emergent Vegetation. Water. 2018; 10(4):402. https://doi.org/10.3390/w10040402
Chicago/Turabian StylePeruzzo, Paolo, Francesca De Serio, Andrea Defina, and Michele Mossa. 2018. "Wave Height Attenuation and Flow Resistance Due to Emergent or Near-Emergent Vegetation" Water 10, no. 4: 402. https://doi.org/10.3390/w10040402






