Considering Abrupt Change in Rainfall for Flood Season Division: A Case Study of the Zhangjia Zhuang Reservoir, Based on a New Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. New Technique
2.1.1. Opposite Difference Function
2.1.2. Variable Set
2.1.3. Discriminant Model Based on Variable Set
2.2. Application of the New Method Based on the Technique
2.3. Abrupt Change over a Year of Rainfall
2.4. Fisher Optimal Segmentation Method
2.5. Evaluation Index of Flood Season Division Results
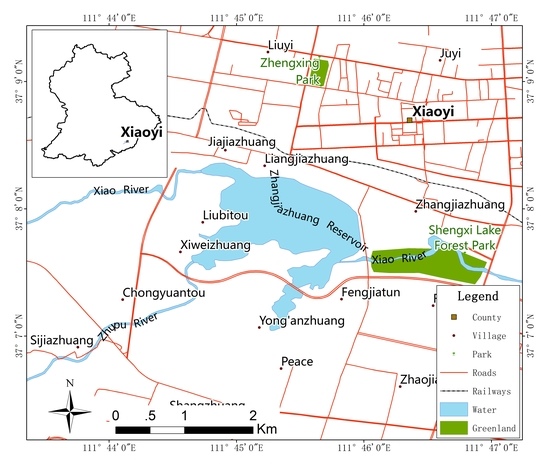
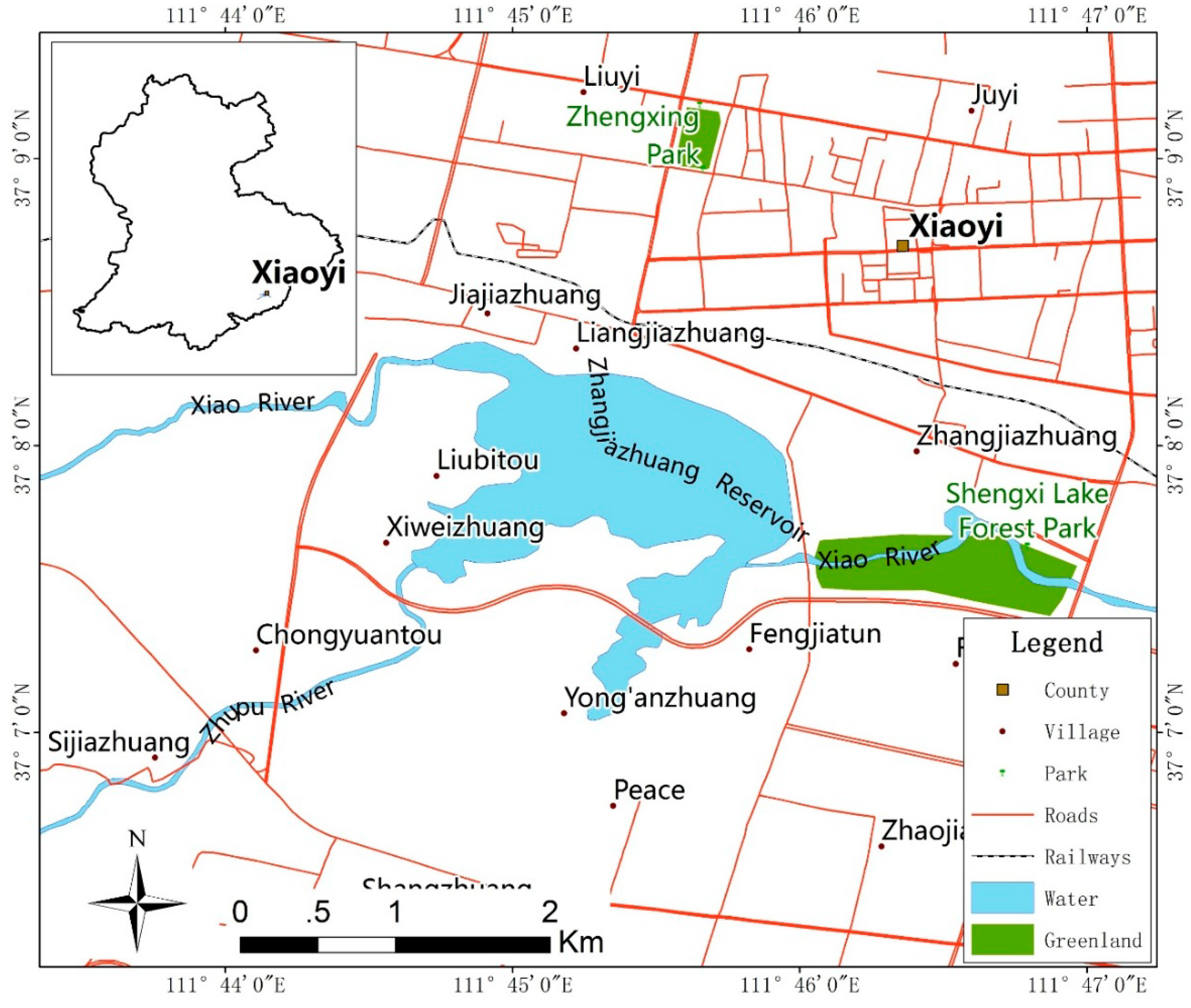
2.6. Case Study Area
3. Results
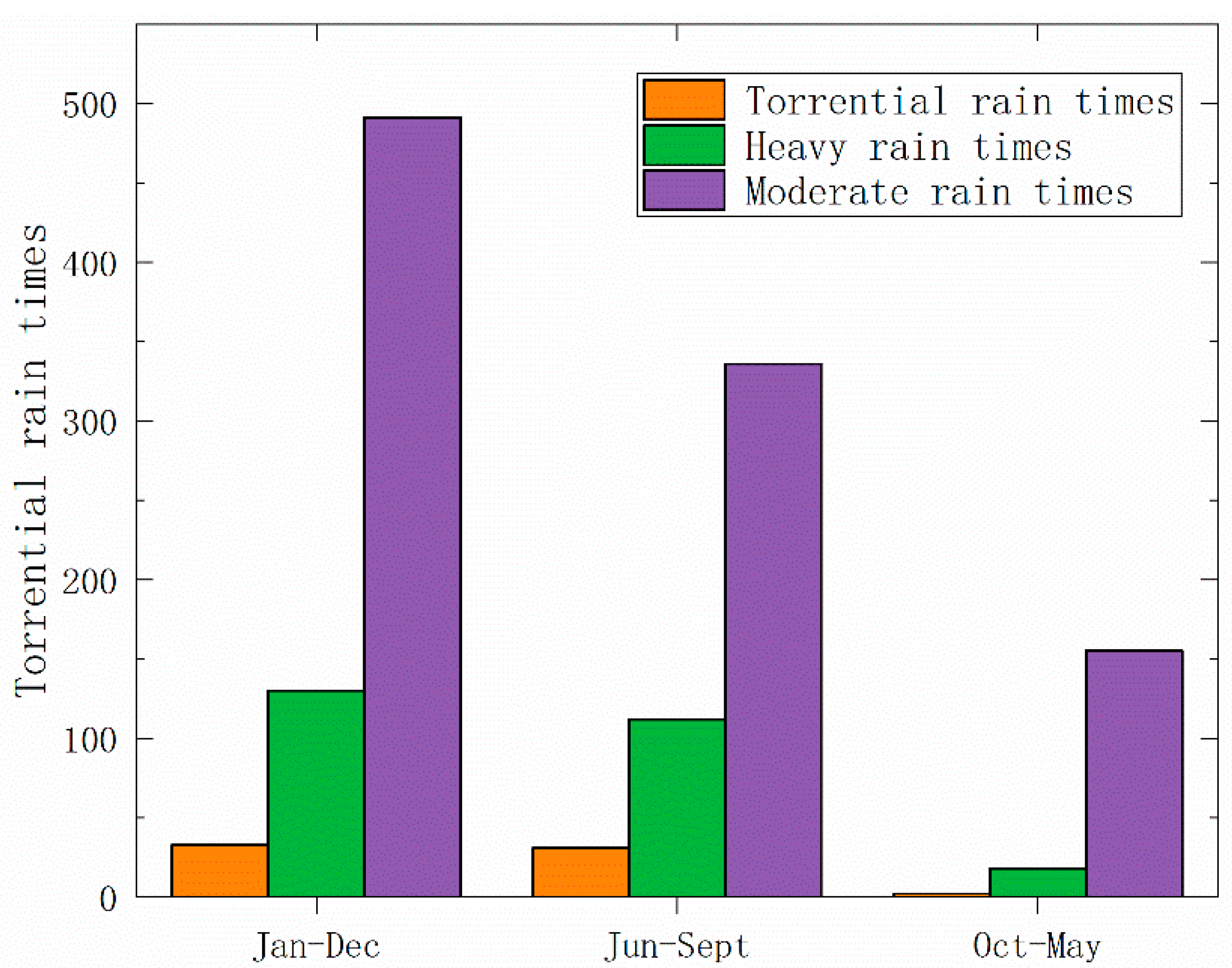
3.1. Temporal Distribution of Rainfall
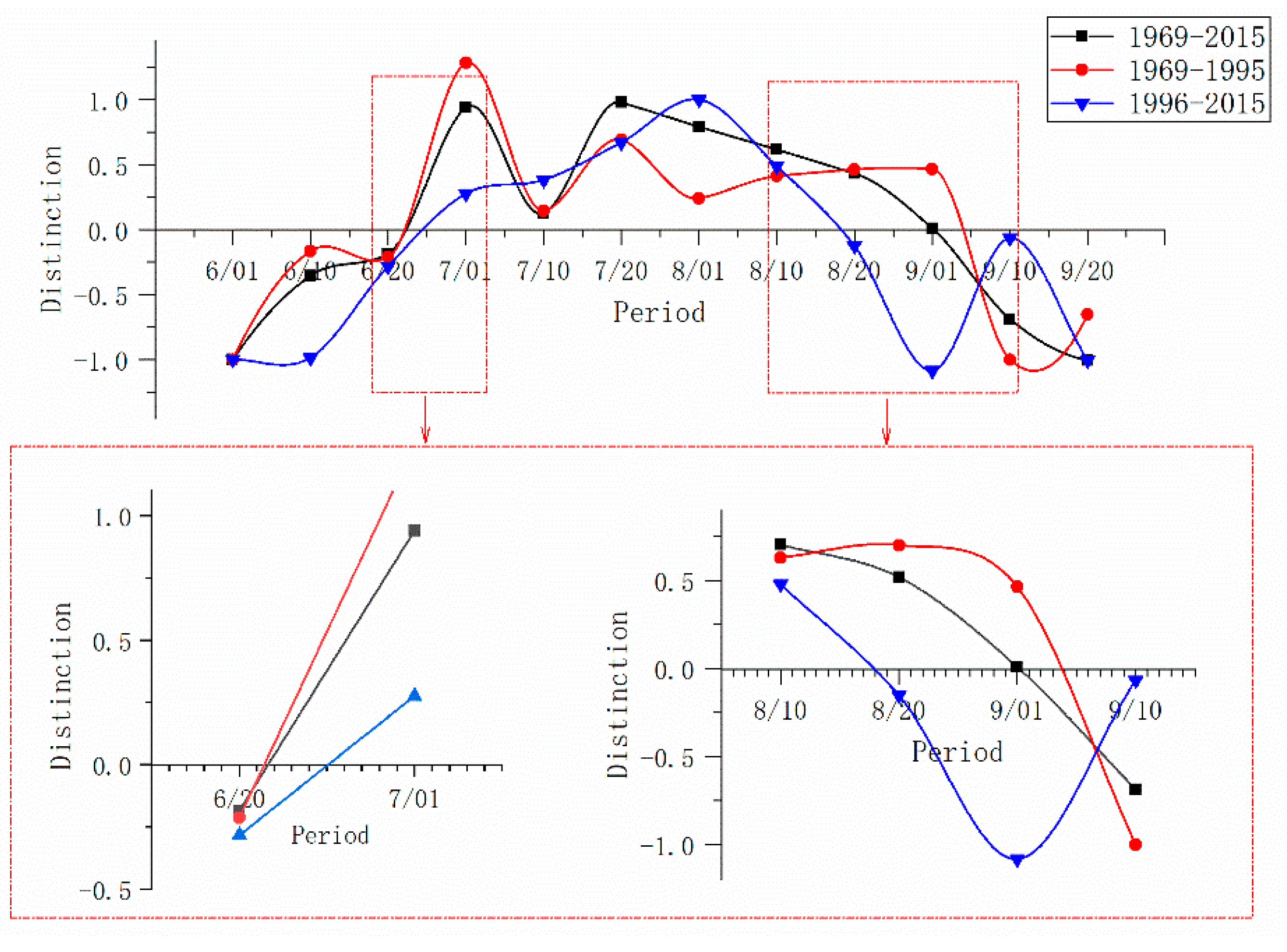
3.2. Abrupt Change over a Year of Rainfall
3.3. Flood Season Division Results
3.3.1. Division by Discriminant Model
3.3.2. Division by Fisher
3.3.3. Evaluation and Comparison of Division Results
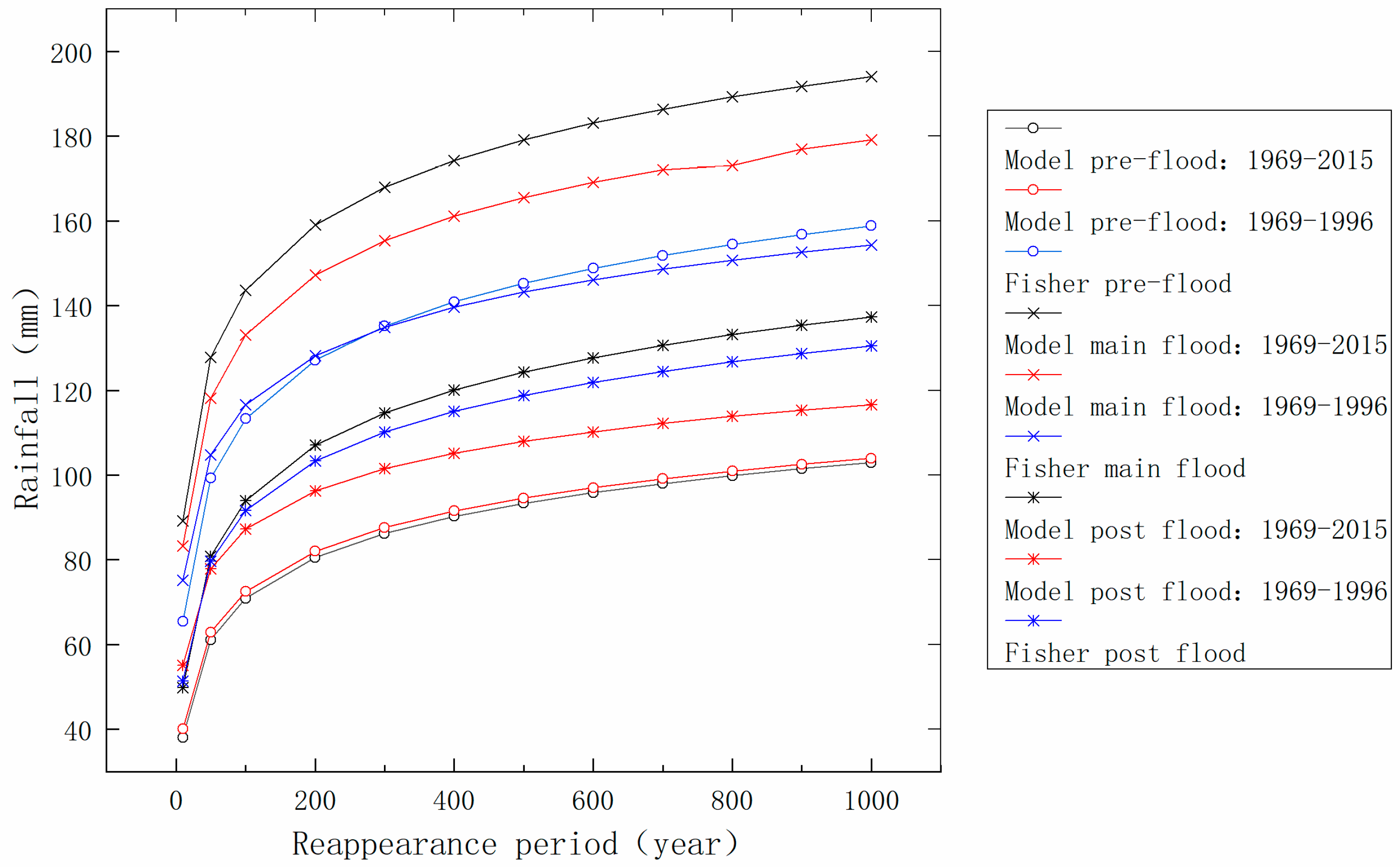
3.4. Reappearance Period Rainfall Design and Reservoir Operation
4. Discussion
5. Conclusions
- (1)
- The discriminant model proposed in this paper has a strong theoretical background, clear mathematical concept, convenient calculation, and direct result. The result of the evaluation index S of the two methods shows that the discriminant model is more reasonable than the Fisher method, and can be applied well for flood season division.
- (2)
- The temporal distribution of rainfall has a significant impact on the results of the flood season. The main flood season in the Zhangjia Zhuang reservoir during 1969–2015 was 16 days longer than that during 1996–2015, but three days shorter than that during 1969–1996. Specifically, the pre-flood season was from 1 June to 22 June during 1969–2015 and 1969–1995, while it ran from 1 June to 25 June during 1996–2015. The main flood season was from 23 June to 1 September during 1969–2015, while it was from 23 June to 4 September during 1969–1995, and from 26 June to 18 August during 1996–2015.
- (3)
- The results of flood season division considering abrupt changes in rainfall will bring great benefits to reservoir operation and water resources protection. However, the risk for reservoirs caused by the shortening of the main flood season needs to be further analyzed, in order to ensure the rationality and feasibility of flood season staging considering abrupt rainfall change.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.X.; Sun, X.D.; Tian, Z.Y.; Ce, L. Applied Research of quantitative analysis methods to division of flood seasonal phases for Tanghe Reservoir. Adv. Civ. Eng. 2011, 90, 2570–2577. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.C.; Malik, S. Assessment of flood hazard in a riverine tract between Damodar and Dwarkeswar River, Hugli District, West Bengal, India. Spat. Inf. Res. 2018, 26, 91–101. [Google Scholar] [CrossRef]
- Wang, H.J.; Xiao, W.H.; Wang, J.H.; Wang, Y.C.; Huang, Y.; Hou, B.D.; Lu, C.Y. The Impact of Climate Change on the Duration and Division of Flood Season in the Fenhe River Basin, China. Water 2017, 8, 105. [Google Scholar] [CrossRef]
- International Panel of Climate Change (IPCC) Working Group I. IPCC Fifth Assessment Report (AR5); IPCC: Stockholm, Sweden, 2013. [Google Scholar]
- Huang, Y.F.; Puah, Y.J.; Chua, K.C.; Lee, T.S. Analysis of monthly and seasonal rainfall trends using the Holt’s test. Int. J. Climatol. 2014, 35, 1500–1509. [Google Scholar] [CrossRef]
- Odekunle, T.O. Determining rainy season onset and retreat over Nigeria from precipitation amount and number of rainy days. Theor. Appl. Climatol. 2006, 83, 193–201. [Google Scholar] [CrossRef]
- Sâmia, R.G.; Alan, J.P.C.; Mary, T.K. Revised method to detect the onset and demise dates of the rainy season in the South American Monsoon areas. Theor. Appl. Climatol. 2015, 126, 481–491. [Google Scholar] [CrossRef]
- Hachigonta, S.; Reason, J.C.; Tadross, M. An analysis of onset date and rainy season duration over Zambia. Theor. Appl. Climatol. 2008, 91, 229–243. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, Y.B.; Zhu, X.P.; Wang, Q.W. Flood Season Division Based on Qualitative Change and Quantitative Change Discriminant Mode and Principal Component Analysis Method. Water Power 2018, 44, 27–31. (In Chinese) [Google Scholar]
- Gu, R.Y.; Zhou, W.C.; Bai, M.L.; Di, R.Q.; Yang, J. Influence of climate change on ice slush period at Inner Mongolia section of Yellow River. J. Desert Res. 2012, 32, 1751–1756. (In Chinese) [Google Scholar]
- Pan, W.; Fei, J.; Man, Z.M.; Zheng, J.Y.; Zhuang, H.Z. The fluctuation of the beginning time of flood season in North China during AD1766-1911. Quat. Int. 2015, 380, 377–381. [Google Scholar] [CrossRef]
- Owusu, K.; Waylen, P.R. The changing rainy season climatology of mid-Ghana. Theor. Appl. Climatol. 2013, 112, 419–430. [Google Scholar] [CrossRef]
- Ding, L.L.; Ge, Q.S.; Zheng, J.Y.; Hao, Z.X. Variation of starting date of pre-summer rainy season in South China from 1736 to 2010. J. Geogr. Sci. 2014, 24, 845–857. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.L.; Li, W.; Xiong, H.K.; Zhang, W.X.; Guo, H.J.; Xu, D.L.; Wang, Z.X. Application of changing-point method for flood season stage in Geheyan Reservoir. J. Yangtze River Sci. Res. Inst. 2007, 24, 8–11. (In Chinese) [Google Scholar]
- Jin, B.M.; Fang, G.H. Application of fuzzy set analysis method on flood stage study of Nanping. Water Power 2010, 36, 20–22. (In Chinese) [Google Scholar]
- Gao, B.; Liu, K.L.; Wang, Y.T.; Hu, S.Y. Application of system clustering method to dividing flood season of reservoir. Water Resour. Hydropower Eng. 2005, 35, 1–5. (In Chinese) [Google Scholar]
- Tian, S.M.; Su, X.H.; Wang, W.H.; Lai, R.X. Application of Fractal Theory in The River Regime in The Lower Yellow River. Appl. Mech. Mater. 2012, 190, 1238–1243. [Google Scholar] [CrossRef]
- Wang, Q.W.; Zhu, X.P.; Wu, P.L.; Tang, L. Analysis on the Influences of Different Domains on Flood Season Division Based on the Theory of Transition. Water Power 2018, 44, 10–14. (In Chinese) [Google Scholar]
- Tang, L.; Zhang, Y.B.; Zhu, X.P.; Wang, Q.W. Study on the Influence for Division of Flood Season Based on PCA-Fisher Optimal Dissection Method. Water Power 2018, 44, 13–16. (In Chinese) [Google Scholar]
- Chen, S.Y. Based on the dialectics three laws mathematical theorems system evaluation theory, model and method: And concerning set pair analysis and evaluation method. J. Eng. Heilongjiang Univ. 2010, 1, 11–16. (In Chinese) [Google Scholar]
- Modarres, R.; Sarhadi, A. Rainfall trends analysis of Iran in the last half of the twentieth century. J. Geophys. Res. 2009, 114, D03101. [Google Scholar] [CrossRef]
- Sneyers, R. On the Statistical Analysis of Series of Observations; Technical Note 143; WMO: Geneva, Sweden, 1990; p. 192. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Zelenakova, M.; Purcz, P.; Blist’an, P.; Vranayova, Z.; Hlavata, H.; Diaconu, D.C.; Portela, M.M. Trends in Precipitation and Temperatures in Eastern Slovakia (1962–2014). Water 2018, 10, 727. [Google Scholar] [CrossRef]
- Zelenakova, M.; Alkhalaf, I.; Purcz, P.; Blistan, P.; Pelikan, P.; Portela, M.M.; Silva, A.T. Trends of rainfall as a support for integrated water resources management in Syria. Desalin. Water Treat. 2017, 86, 285–296. [Google Scholar] [CrossRef]
- Onyutha, C. Identification of sub-trends from hydro-meteorological series. Stoch. Environ. Res. Risk Assess. 2015, 30, 189–205. [Google Scholar] [CrossRef]
- Onyutha, C. Statistical Uncertainty in Hydrometeorological Trend Analyses. Adv. Meteorol. 2016, 2016, 8701617. [Google Scholar] [CrossRef]
- Onyutha, C. On Rigorous Drought Assessment Using Daily Time Scale: Non-Stationary Frequency Analyses, Revisited Concepts, and a New Method to Yield Non-Parametric Indices. Hydrology 2017, 4, 48. [Google Scholar] [CrossRef]
- Onyutha, C. Statistical analyses of potential evapotranspiration changes over the period 1930-2012 in the Nile River riparian countries. Agric. For. Meteorol. 2016, 226, 80–95. [Google Scholar] [CrossRef]
- He, H.W.; Zhang, A.L. The application of Fisher method to dividing seismicity period in Yunnan province. J. Seismol. Res. 1994, 17, 231–239. (In Chinese) [Google Scholar]
- Chang, J.; Wang, Y.G.; Zhao, Y.; Li, F.X. Characteristics of Climate Change of Precipitation and Rain Days in the Yellow River Basin during Recent 50 Years. Plateau Meteorol. 2014, 33, 43–54. [Google Scholar] [CrossRef]
- Zelenakova, M.; Vido, J.; Portela, M.M.; Purcz, P.; Blistan, P.; Hlavata, H.; Hlustik, P. Precipitation Trends over Slovakia in the Period 1981–2013. Water 2017, 9, 922. [Google Scholar] [CrossRef]
- Zelenakova, M.; Purcz, P.; Blist’an, P.; Alkhalaf, I.; Hlavata, H.; Portela, M.M.; Silva, A.T. Precipitation trends detection as a tool for integrated water resources management in Slovakia. Desalin. Water Treat. 2017, 99, 83–90. [Google Scholar] [CrossRef]




| Period | Pre (Days) | Main (Days) | Post (Days) |
|---|---|---|---|
| 1969–2015 | 1 June–22 June (22) | 23 June–1 September (69) | 2 September–30 September (29) |
| 1969–1995 | 1 June–22 June (22) | 23 June–4 September (72) | 5 September–30 September (26) |
| 1996–2015 | 1 June–25 June (25) | 26 June–18 August (53) | 19 August–30 September (42) |
| k | B (n, k) | f (k) | Classification |
|---|---|---|---|
| 2 | 0.899 | 1–4, 5–12 | |
| 3 | 0.379 | 0.52 | 1–4, 5–9, 10–12 |
| 4 | 0.243 | 0.136 | 1–2, 5, 6–9, 10–12 |
| 5 | 0.149 | 0.094 | 1–2, 3–4, 5–6, 7–9, 10–12 |
| 6 | 0.077 | 0.072 | 1–2, 3–4, 5–6, 7–9, 10–12 |
| 7 | 0.04 | 0.037 | 1–2, 3, 4, 5, 6, 7–9, 10–12 |
| 8 | 0.022 | 0.018 | 1–2, 3, 4, 5, 6, 7, 8–9, 10–12 |
| 9 | 0.015 | 0.007 | 1–2, 3, 4, 5, 6, 7, 8–9, 10–11, 12 |
| 10 | 0.022 | −0.007 | 1–2, 3, 4, 5, 6, 7, 8–9, 10, 11, 12 |
| 11 | 0.006 | 0.016 | 1–2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 |
| k | B (n, k) | f (k) | Classification |
|---|---|---|---|
| 2 | 1.490 | 1–4, 5–12 | |
| 3 | 0.761 | 0.729 | 1–4, 5–9, 10–12 |
| 4 | 0.496 | 0.265 | 1–4, 5, 6–9, 10–12 |
| 5 | 0.234 | 0.262 | 1–2, 3–4, 5–6, 7–9, 10–12 |
| 6 | 0.097 | 0.137 | 1–2, 3–4, 5–6, 7–9, 10–11, 12 |
| 7 | 0.043 | 0.054 | 1–2, 3–4, 5, 6, 7–9, 10–11, 12 |
| 8 | 0.024 | 0.019 | 1–2, 3–4, 5, 6, 7–9, 10, 11, 12 |
| 9 | 0.015 | 0.009 | 1–2, 3–4, 5, 6, 7, 8–9, 10, 11, 12 |
| 10 | 0.007 | 0.008 | 1–2, 3, 4, 5, 6, 7, 8–9, 10, 11, 12 |
| 11 | 0.000 | 0.007 | 1, 2, 3, 4, 5, 6, 7, 8–9, 10, 11, 12 |
| k | B (n, k) | f (k) | Classification |
|---|---|---|---|
| 2 | 1.073 | 1–4, 5–12 | |
| 3 | 0.421 | 0.652 | 1–4, 5–9, 10–12 |
| 4 | 0.285 | 0.136 | 1–4, 5–6, 7–9, 10–12 |
| 5 | 0.192 | 0.093 | 1–2, 3–4, 5–6, 7–9, 10–12 |
| 6 | 0.192 | 0.000 | 1–2, 3–4, 5–6, 7–9, 10–12 |
| 7 | 0.149 | 0.043 | 1–2, 3–4, 5, 6, 7–9, 10–11, 12 |
| 8 | 0.070 | 0.079 | 1–2, 3–4, 5, 6, 7–9, 10, 11, 12 |
| 9 | 0.044 | 0.026 | 1–2, 3–4, 5, 6, 7–8, 9, 10, 11, 12 |
| 10 | 0.026 | 0.018 | 1–2, 3–4, 5, 6, 7, 8, 9, 10, 11, 12 |
| 11 | 0.000 | 0.026 | 1–2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 |
| Period | Item | Model | S-Model | Fisher | S-Fisher | ||||
|---|---|---|---|---|---|---|---|---|---|
| Pre | Main | Post | Pre | Main | Post | ||||
| 1969–2015 | S | 4.14 | 8.06 | 5.41 | 6.19 | 7.90 | 5.48 | ||
| weight | 0.30 | 0.40 | 0.30 | 6.09 | 0.30 | 0.40 | 0.30 | 6.66 | |
| 0.25 | 0.50 | 0.25 | 6.42 | 0.25 | 0.50 | 0.25 | 6.87 | ||
| 0.20 | 0.60 | 0.20 | 6.75 | 0.20 | 0.60 | 0.20 | 7.07 | ||
| 1969–1995 | S | 4.72 | 8.76 | 5.34 | 7.22 | 8.36 | 5.89 | ||
| weight | 0.30 | 0.40 | 0.30 | 6.52 | 0.30 | 0.40 | 0.30 | 7.28 | |
| 0.25 | 0.50 | 0.25 | 6.90 | 0.25 | 0.50 | 0.25 | 7.46 | ||
| 0.20 | 0.60 | 0.20 | 7.27 | 0.20 | 0.60 | 0.20 | 7.64 | ||
| 1996–2015 | S | 3.26 | 7.42 | 5.36 | 4.79 | 7.29 | 4.91 | ||
| weight | 0.30 | 0.40 | 0.30 | 5.55 | 0.30 | 0.40 | 0.30 | 5.83 | |
| 0.25 | 0.50 | 0.25 | 5.87 | 0.25 | 0.50 | 0.25 | 6.07 | ||
| 0.20 | 0.60 | 0.20 | 6.18 | 0.20 | 0.60 | 0.20 | 6.31 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Zhang, Y. Considering Abrupt Change in Rainfall for Flood Season Division: A Case Study of the Zhangjia Zhuang Reservoir, Based on a New Model. Water 2018, 10, 1152. https://doi.org/10.3390/w10091152
Tang L, Zhang Y. Considering Abrupt Change in Rainfall for Flood Season Division: A Case Study of the Zhangjia Zhuang Reservoir, Based on a New Model. Water. 2018; 10(9):1152. https://doi.org/10.3390/w10091152
Chicago/Turabian StyleTang, Li, and Yongbo Zhang. 2018. "Considering Abrupt Change in Rainfall for Flood Season Division: A Case Study of the Zhangjia Zhuang Reservoir, Based on a New Model" Water 10, no. 9: 1152. https://doi.org/10.3390/w10091152
APA StyleTang, L., & Zhang, Y. (2018). Considering Abrupt Change in Rainfall for Flood Season Division: A Case Study of the Zhangjia Zhuang Reservoir, Based on a New Model. Water, 10(9), 1152. https://doi.org/10.3390/w10091152