Effect of a Lateral Jet on the Turbulent Flow Characteristics of an Open Channel Flow with Rigid Vegetation
Abstract
1. Introduction
2. Experimental Equipment and Conditions
2.1. Sink Device
2.2. Experimental Equipment
2.3. Experimental Conditions
2.4. Vegetation Materials and Configurations
3. Results and Discussion
3.1. Distribution of the Average Flow Field in Transverse Jets under Vegetation
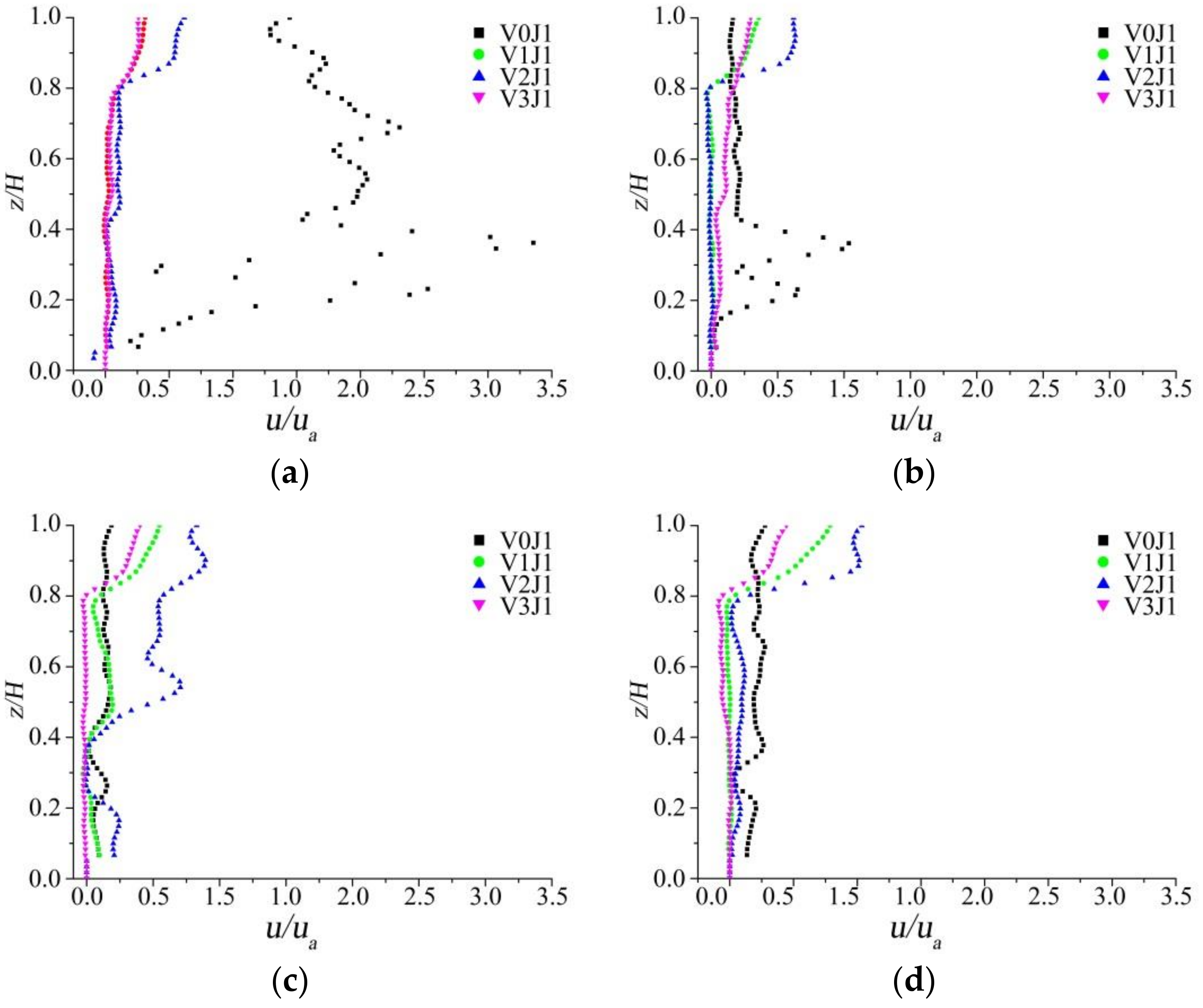
3.2. Vertical Flow Velocity Distribution of a Transverse Jet Along a Vertical Line with Vegetation
3.3. Transverse Jet Motion Trajectory with Vegetation
3.4. Turbulence Intensity
3.5. Reynolds Stress
4. Conclusions
- The study of the time-average flow rates shows that vegetation significantly disturbs the flow field around a lateral jet. Without vegetation, due to turbulent entrainment, the jet flow rate was strongly blended with the main flow rate and the flow velocity in the core region was increased. The flow rate decreased in the downstream direction. Due to the flow around the vegetation, the flow velocity distribution changed significantly, exhibiting horseshoe, spotted, wake and reverse vortices of different sizes in different locations. A comparison of four different vegetation arrangements showed that the vegetation arrangement influences the jet flow field, most obviously for the rhombic arrangement.
- According to the analysis of the vertical flow velocity, the flow velocity in the inner region of the vegetation and near the bottom of the trough was reduced. The flow velocity along the water depth was of S and anti-S types, and the flow velocity of the free layer was approximately logarithmic.
- By comparing the jet trajectories under different conditions, it was found that jet penetration was significantly greater in the cases with vegetation than for the case without vegetation, and the jet trajectory was more curved for the diamond vegetation arrangement.
- The analysis of turbulence intensity and Reynolds stress showed that the flow gradient was very large due to the strong water flow turbulence, and the Reynolds stress peaks at the top of the vegetation (z/H = 0.8) and near the water surface. We found that the relative turbulence intensity varies most along the water depth ratio for the rhombic arrangement of vegetation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hussein, J.; Capp, S.P.; George, W.K. Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 1994, 258, 31–75. [Google Scholar] [CrossRef]
- Fischer, B.H.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Chapter 6—Mixing in reservoirs. In Mixing Inland Coastal Waters; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Sanders, H.J.P.; Sarh, B.; Gökalp, I. Variable density effects in axisymmetric isothermal turbulent jets: A comparison between a first- and a second-order turbulence model. Int. J. Heat Mass Transf. 1997, 40, 823–842. [Google Scholar] [CrossRef]
- Cha, J.; Lim, S.; Kim, T.; Shin, W.G. The effect of the Reynolds number on the velocity and temperature distributions of a turbulent condensing jet. Int. J. Heat Fluid Flow 2017, 67, 125–132. [Google Scholar] [CrossRef]
- Coletti, F.; Benson, M.J.; Ling, J.; Elkins, C.J.; Eaton, J.K. Turbulent transport in an inclined jet in crossflow. Int. J. Heat Fluid Flow 2013, 43, 149–160. [Google Scholar] [CrossRef]
- Fox, J.F.; Smith, M.M.; Nuttall, G.A. Kaplans Essentials of Cardiac Anesthesia; Elsevier: Amsterdam, The Netherlands, 2018; pp. 426–472. [Google Scholar]
- Jirka, H.G.; Bleninger, T.; Burrows, R.; Larsen, T. Environmental Quality Standards in the EC-Water Framework Directive: Consequences for Water Pollution Control for Point Sources; KIT: Karlsruhe, Germany, 2004. [Google Scholar]
- Yang, W.; Choi, S.U. Impact of stem flexibility on mean flow and turbulence structure in depth-limited open channel flows with submerged vegetation. J. Hydraul. Res. 2009, 47, 445–454. [Google Scholar] [CrossRef]
- Freund, J.B. Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 2001, 438, 277–305. [Google Scholar] [CrossRef]
- Yu, C. Introduction to Environmental Fluid Mechanics; Tsinghua University Press: Beijing, China, 1992. [Google Scholar]
- Kamotani, Y.; Greber, I. Experiments on a turbulent jet in a crossflow. AIAA J. 1972, 30, 1425–1429. [Google Scholar] [CrossRef]
- Fischer, H.B.; List, J.E.; Koh, C.R.; Imberger, J.; Brooks, N.H. Chapter 9—Turbulent Jets and Plumes. In Mixing in Inland and Coastal Waters; Elsevier Inc.: New York, NY, USA, 1979; pp. 315–389. [Google Scholar]
- Smith, S.H.; Mungal, M.G. Mixing, structure and scaling of the jet in cross-flow. J. Fluid Mech. 1998, 357, 83–122. [Google Scholar] [CrossRef]
- Rajaratnam, N. Erosion by turbulent jets. J. Hydraul. Res. 1981, 19, 339–358. [Google Scholar] [CrossRef]
- Lee, J.; Kuang, C.; Chen, G. The structure of a turbulent jet in crossflow—Effect of jet-to-crossflow velocity. China Ocean Eng. 2002, 16, 1–20. [Google Scholar]
- Zeng, Y.; Yan, W. Experimental study of three-dimensional circular vertical buoyant jet characteristics in a flowing environment. Exp. Fluid Mech. 2005, 19, 39–46. [Google Scholar]
- Zhang, C.; Jian, M.; Qin, C.; Yang, D. Numerical simulation of vertical circular pure jet in shallow water environment. J. Zhejiang Univ. 2006, 12, 2163–2167. [Google Scholar]
- Li, W.; Gu, J.; Yan, C.; Wang, Y. Experimental study on jet trajectory and diffusion characteristics in crossflow based on PIV. Hydrodyn. Res. Prog. 2018, 33, 207–215. [Google Scholar]
- Gao, M.; Huai, W.; Xiao, Y.; Yang, Z.; Ji, B. Large eddy simulation of a vertical buoyant jet in a vegetated channel. Int. J. Heat Fluid Flow 2018, 70, 114–124. [Google Scholar] [CrossRef]
- Meftah, B.M.; de Serio, F.; Mossa, M. Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 2014, 26, 1624–1635. [Google Scholar] [CrossRef]
- Yang, K.; Liu, X.; Cao, S.; Zhang, Z. The turbulent characteristics of floodplain flow in a complex river channel under the action of vegetation. J. Hydraul. Eng. 2005, 36, 1263–1268. [Google Scholar]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. Oceans 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, G.; Xu, L.; Li, Z. Application of PIV technology in submerged jet of experimental model of plunge pool. In Proceedings of the National Conference on Experimental Fluid Mechanics, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Li, C.; Yan, W.; Yang, H. Study on the characteristics of non-submerged rigid vegetation flow in curved corners. J. Huazhong Univ. Sci. Technol. 2012, 40, 49–53. [Google Scholar]
- Wen, H.; Yu, N.A.; Han, T.; Ai, L.I. Experimental study on vertical turbulent jet discharged from the bottom of shallow water. J. Hydraul. Eng. 2002, 13, 26–30. [Google Scholar]
- Li, R. Effect of tall vegetations on flow and sediment. J. Hydraulic Div. ASCE 1973, 99, 793–814. [Google Scholar]
- Lindner, K.; Saenger, W. Crystal and molecular structure of cyclohepta-amylose dodecahydrate. Carbohydr. Res. 1982, 99, 103–115. [Google Scholar] [CrossRef]
- Murphy, E.; Ghisalberti, M.; Nepf, H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 2007, 43, 687–696. [Google Scholar] [CrossRef]
- De Serio, F.; Meftah, M.B.; Mossa, M.; Termini, D. Experimental investigation on dispersion mechanisms in rigid and flexible vegetated beds. Adv. Water Resour. 2017. [Google Scholar] [CrossRef]
- Meftah, M.B.; Mossa, M. Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 2013, 25, 13–25. [Google Scholar] [CrossRef]
- Meftah, M.B.; De Serio, F.; Malcangio, D.; Mossa, M.; Petrillo, A.F. Experimental study of a vertical jet in a vegetated crossflow. J. Environ. Manag. 2015, 164, 19–31. [Google Scholar] [CrossRef] [PubMed]
- Malcangio, D.; Meftah, M.B.; Chiaia, G.; De Serio, F.; Mossa, M.; Petrillo, A. Experimental Studies on Vertical Dense Jets in a Crossflow; Taylor & Francis Group: Oxford, UK, 2016. [Google Scholar]
- Meftah, M.B.; Mossa, M. Turbulence measurement of vertical dense jets in crossflow. Water 2018, 10, 286. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 2007, 593, 1–32. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, H.; Hua, M.; Wang, Z. Experimental study on the mixing characteristics of co-directional jets. Adv. Water Sci. 2006, 17, 512–517. [Google Scholar]
- Li, Z.; Yan, W.; Qian, Z. Numerical simulation of radial turbulent jet in still water environment. J. Hydraul. Eng. 2009, 40, 1320–1325. [Google Scholar]
- Xiao, Y.; Lei, M.; Li, K.; Liu, G.; Yan, J. Experimental study on flow characteristics of porous jets in cross-flows. Adv. Water Sci. 2012, 23, 390–395. [Google Scholar]
- Sherif, S.A.; Pletcher, R.H. Measurements of the flow and turbulence characteristics of round jets in crossflow. J. Fluids Eng. 1989, 111, 165–171. [Google Scholar] [CrossRef]
- New, T.H.; Lim, T.T.; Luo, S.C. Effects of jet velocity profiles on a round jet in cross-flow. Exp. Fluids 2006, 40, 859–875. [Google Scholar] [CrossRef]
- Wright, S.J. Effects of Ambient Crossflows and Density Stratification on the Characteristic Behavior of Round, Turbulent Bouyant Jets; California Institute of Technology: Pasadena, CA, USA, 1977. [Google Scholar]
- Knudsen, M. Buoyant Horizontal Jets in an Ambient Flow. Ph.D. Thesis, University of Canterbury, Canterbury, UK, 1988. [Google Scholar]
- Margason, R.J. The Path of a Jet Directed at Large Angles to a Subsonic Stream; Langley Research Center: Hampton, VA, USA, 1968. [Google Scholar]
- Pratte, B.D.; Baines, W.D. Profiles of the round turbulent jet in a cross-flow. J. Hydraulic Div. 1967, 92, 53–64. [Google Scholar]












| Run | Condition | Q (m3/h) | H (m) | ua (m/s) | u0 (m/s) | R | Re | X (m) | Y (m) |
|---|---|---|---|---|---|---|---|---|---|
| V0J1 | No | 6 | 0.15 | 0.037 | 0.28 | 7.57 | 2791 | ||
| V1J1 | Single row | 6 | 0.15 | 0.037 | 0.28 | 7.57 | 2791 | 0.03 | 0.02 |
| V2J1 | Double row | 6 | 0.15 | 0.037 | 0.28 | 7.57 | 2791 | 0.02 | 0.035 |
| V3J1 | Diamond | 6 | 0.15 | 0.037 | 0.28 | 7.57 | 2791 | 0.02 | 0.02 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, S.; Feng, M.; Chen, K.; Wang, W.; Zheng, B. Effect of a Lateral Jet on the Turbulent Flow Characteristics of an Open Channel Flow with Rigid Vegetation. Water 2018, 10, 1204. https://doi.org/10.3390/w10091204
Teng S, Feng M, Chen K, Wang W, Zheng B. Effect of a Lateral Jet on the Turbulent Flow Characteristics of an Open Channel Flow with Rigid Vegetation. Water. 2018; 10(9):1204. https://doi.org/10.3390/w10091204
Chicago/Turabian StyleTeng, Sufen, Minquan Feng, Kailin Chen, Weijie Wang, and Bangmin Zheng. 2018. "Effect of a Lateral Jet on the Turbulent Flow Characteristics of an Open Channel Flow with Rigid Vegetation" Water 10, no. 9: 1204. https://doi.org/10.3390/w10091204
APA StyleTeng, S., Feng, M., Chen, K., Wang, W., & Zheng, B. (2018). Effect of a Lateral Jet on the Turbulent Flow Characteristics of an Open Channel Flow with Rigid Vegetation. Water, 10(9), 1204. https://doi.org/10.3390/w10091204





