Optimization of Enhanced Ultrafiltration Conditions for Cd with Mixed Biosurfactants Using the Box-Behnken Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Experimental Methods
2.3. Box-Behnken Response Curve Design
2.4. Sample Measurements and Calculation
3. Results and Analysis
3.1. Analysis of the Cd2+ Rejection Coefficient
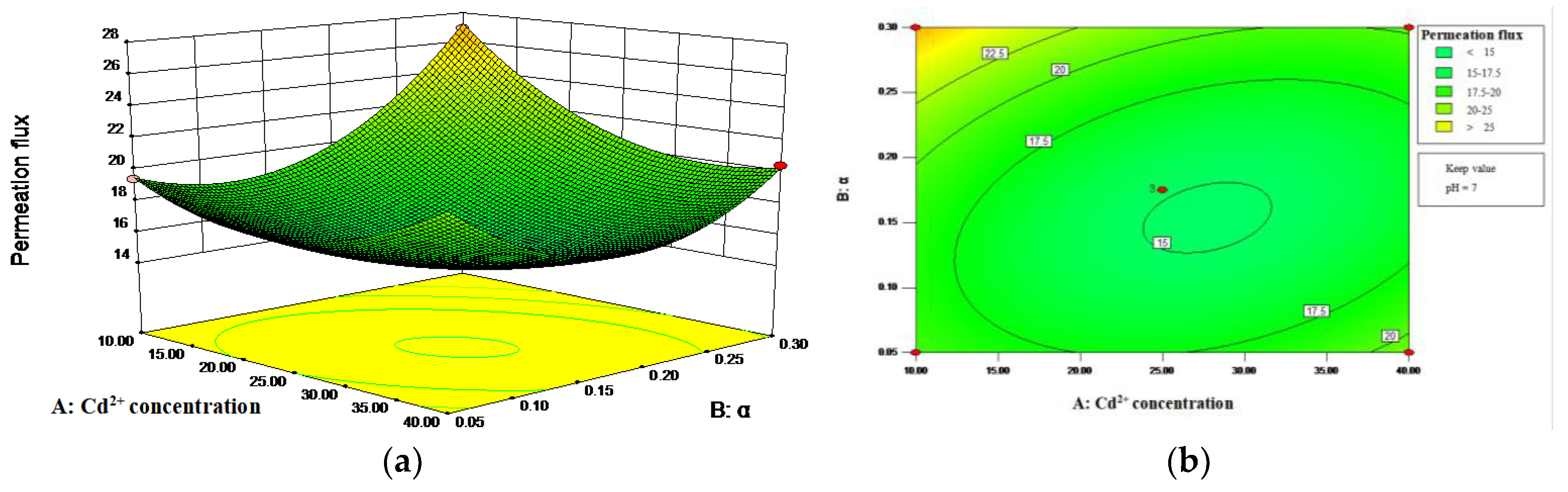
3.2. Analysis of Permeation Flux
3.3. Prediction and Validation of Optimum Filtration Conditions
4. Conclusions
- (1)
- Interactions among the three factors (the initial Cd2+ concentration, the ratio of biosurfactants (α) and the pH) affect the enhanced ultrafiltration of Cd2+, and the significance of their effects on the rejection coefficient follows the order α < Cd2+ concentration < pH. The degree of impact on the permeation flux follows the order Cd2+ concentration < α < pH.
- (2)
- The optimum Cd2+ removal conditions obtained from the experiments are as follows: Cd2+ concentration: 10.0 mg/L; α: 0.30; and pH: 9.58. Under these conditions, the Cd2+ rejection coefficient reaches 99.14 %, and the permeation flux reaches 37.36 L/m2·h. The experimental results confirm that the experimental values agree well with the theoretically predicted values.
Author Contributions
Funding
Conflicts of Interest
References
- Tortora, F.; Innocenzi, V.; Prisciandaro, M.; Vegliò, F.; di Celso, G.M. Heavy Metal Removal from Liquid Wastes by Using Micellar-Enhanced Ultrafiltration. Water Air Soil Pollut. 2016, 227, 1–11. [Google Scholar] [CrossRef]
- Rzętała, M.A. Cadmium contamination of sediments in the water reservoirs in Silesian Upland (southern Poland). J. Soils Sediments 2016, 16, 2458–2470. [Google Scholar] [CrossRef]
- García-Alix, A.; Jimenez-Espejo, F.J.; Lozano, J.A.; Jiménez-Moreno, G.; Martinez-Ruiz, F. Anthropogenic impact and lead pollution throughout the Holocene in Southern Iberia. Sci. Total Environ. 2013, 449, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.; Chen, J.; Ru, X.; Chen, J.; Wu, H.; Wei, C. Heavy metals in river surface sediments affected with multiple pollution sources, South China: Distribution, enrichment and source apportionment. J. Geochem. Explor. 2016, 176, 9–19. [Google Scholar] [CrossRef]
- Sánchez-Chardi, A. Biomonitoring potential of five sympatric tillandsia, species for evaluating urban metal pollution (cd, hg and pb). Atmos. Environ. 2016, 131, 352–359. [Google Scholar] [CrossRef]
- Hua, M.; Zhang, S.; Pan, B.; Zhang, W.; Lv, L.; Zhang, Q. Heavy metal removal from water/wastewater by nanosized metal oxides: A review. J. Hazard. Mater. 2012, 211–212, 317–331. [Google Scholar] [CrossRef] [PubMed]
- Savic, I.M.; Stojiljkovic, S.T.; Gajic, D.G. Modeling and optimization of energy-efficient procedures for removing lead(II) and zinc(II) ions from aqueous solutions using the central composite design. Energy 2014, 77, 66–72. [Google Scholar] [CrossRef]
- Qiu, W.; Zheng, Y. Removal of lead, copper, nickel, cobalt, and zinc from water by a cancrinite-type zeolite synthesized from fly ash. Chem. Eng. J. 2009, 145, 483–488. [Google Scholar] [CrossRef]
- Tao, H.C.; Zhang, H.R.; Li, J.B.; Ding, W.Y. Biomass based activated carbon obtained from sludge and sugarcane bagasse for removing lead ion from wastewater. Bioresour. Technol. 2015, 192, 611–617. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Cao, X.; Zhao, L. Comparison of rice husk- and dairy manure-derived biochars for simultaneously removing heavy metals from aqueous solutions: Role of mineral components in biochars. Chemosphere 2013, 92, 955–961. [Google Scholar] [CrossRef] [PubMed]
- Ronda, A.; Calero, M.; Blázquez, G.; Pérez, A.; Martín-Lara, M.A. Optimization of the use of a biosorbent to remove heavy metals: Regeneration and reuse of exhausted biosorbent. J. Taiwan Inst. Chem. Eng. 2015, 51, 109–118. [Google Scholar] [CrossRef]
- Wang, J.; Chen, C. The current status of heavy metal pollution and treatment technology development in china. Environ. Technol. Rev. 2015, 4, 39–53. [Google Scholar] [CrossRef]
- Burakov, A.E.; Galunin, E.V.; Burakova, I.V.; Kucherova, I.E. Adsorption of heavy metals on conventional and nanostructured materials for wastewater treatment purposes: A review. Ecotoxicol. Environ. Saf. 2017, 148, 702. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.J.; You, S.J.; Wang, X.H.; Zhou, X.; Gan, Y.; Ren, N.Q. Synthesis of carbonaceous nanowire membrane for removing heavy metal ions and high water flux. Chem. Eng. J. 2013, 226, 217–226. [Google Scholar] [CrossRef]
- Wang, R.; Guan, S.; Sato, A.; Wang, X.; Wang, Z.; Yang, R. Nanofibrous microfiltration membranes capable of removing bacteria, viruses and heavy metal ions. J. Membr. Sci. 2013, 446, 376–382. [Google Scholar] [CrossRef]
- Lu, J.; Li, Y.; Yin, M.; Ma, X.; Lin, S. Removing heavy metal ions with continuous aluminum electrocoagulation: A study on back mixing and utilization rate of electro-generated al ions. Chem. Eng. J. 2015, 267, 86–92. [Google Scholar] [CrossRef]
- Al-Shannag, M.; Al-Qodah, Z.; Bani-Melhem, K.; Qtaishat, M.R.; Alkasrawi, M. Heavy metal ions removal from metal plating wastewater using electrocoagulation: Kinetic study and process performance. Chem. Eng. J. 2015, 260, 749–756. [Google Scholar] [CrossRef]
- Mitomo, S.K.; Nakahara, M.; Saeki, R.; Murakami, I. Recovery of heavy metals separated from high concentration wastewater by new sulfide precipitation system. J. Surf. Finish. Soc. Jpn. 2014, 65, 528–530. [Google Scholar] [CrossRef]
- Salehi, R.; Mousavi, S.M.; Taherian, M. Assessment of micellar-enhanced ultrafiltration process performance for removal of pharmaceutical contaminant from wastewater using response surface methodology. Int. J. Environ. Sci. Technol. 2018. [Google Scholar] [CrossRef]
- Fu, H.Y.; Zhang, Z.B.; Chai, T.; Huang, G.H.; Yu, S.J.; Liu, Z. Study of the removal of aniline from wastewater via meuf using mixed surfactants. Water 2017, 9, 365. [Google Scholar] [CrossRef]
- Tanhaei, B.; Chenar, M.P.; Saghatoleslami, N.; Hesampour, M.; Kallioinen, M.; Sillanpää, M. Removal of nickel ions from aqueous solution by micellar-enhanced ultrafiltration, using mixed anionic-non-ionic surfactants. Sep. Purif. Technol. 2014, 138, 169–176. [Google Scholar] [CrossRef]
- Chavan, M. Mathematical modelling for removal of mixture of heavy metal ions from waste-water using micellar enhanced ultrafiltration (meuf) process. Sep. Sci. Technol. 2015, 50, 365–372. [Google Scholar]
- Schwarze, M.; Groß, M.; Moritz, M.; Buchner, G.; Kapitzki, L.; Chiappisi, L.; Gradzielski, M. Micellar enhanced ultrafiltration (meuf) of metal cations with oleylethoxycarboxylate. J. Membr. Sci. 2015, 478, 140–147. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, M.; Zeng, G.; Li, M.; Zhang, J.; Zhong, H.; Liu, Y.; Shao, B.; Li, Z.; Wang, Z.; et al. Investigation on the reaction of phenolic pollutions to mono-rhamnolipid micelles using MEUF. Environ. Sci. Pollut. Res. 2017, 24, 1230–1240. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.D.; Nguyen, N.K. Small Box–Behnken designs with orthogonal blocks. Stat. Probab. Lett. 2014, 85, 84–90. [Google Scholar] [CrossRef]






| Size of Main Engine (cm) | Membrane Area (cm2) | Power (Kw) | Minimum Circulating Volume (mL) | Working Pressure (MPa) | Filtration Capacity (L/h) | Applicable Temperature (°C) |
|---|---|---|---|---|---|---|
| 23 × 27 × 30 | 150 | 0.06 | 80 | ≤0.5 | 0.3–3 | 5–50 |
| Membrane Type | Membrane Material | Molecular Weight Cutoff (Dalton) | Permeation Flux (L/m2·h) | Membrane Area (cm2) | pH |
|---|---|---|---|---|---|
| SMU-420 | PVDF | 10,000 | 24–53 | 150 | 2–12 |
| Variable | Symbol | Variable Levels | ||
|---|---|---|---|---|
| Low (−1) | Middle (0) | High (+1) | ||
| Cd2+ Concentration (mg/L) | A | 10 | 25 | 40 |
| α | B | 0.05 | 0.175 | 0.3 |
| pH | C | 4 | 7 | 10 |
| Std | Run | Factor | Experimental Cd2+ Rejection Coefficient (%) | Predicted Cd2+ Rejection Coefficient (%) | ||
|---|---|---|---|---|---|---|
| A | B | C | ||||
| 1 | 15 | −1 | −1 | 0 | 99.7 | 98.2 |
| 2 | 2 | 1 | −1 | 0 | 76.2 | 80.1 |
| 3 | 5 | −1 | 1 | 0 | 99.3 | 95.4 |
| 4 | 4 | 1 | 1 | 0 | 79.7 | 81.2 |
| 5 | 3 | −1 | 0 | −1 | 50.5 | 54.1 |
| 6 | 7 | 1 | 0 | −1 | 27.2 | 25.4 |
| 7 | 12 | −1 | 0 | 1 | 98.0 | 99.9 |
| 8 | 8 | 1 | 0 | 1 | 99.8 | 96.3 |
| 9 | 9 | 0 | −1 | −1 | 43.3 | 41.3 |
| 10 | 11 | 0 | 1 | −1 | 39.7 | 40.1 |
| 11 | 6 | 0 | −1 | 1 | 99.6 | 99.3 |
| 12 | 1 | 0 | 1 | 1 | 96.7 | 98.8 |
| 13 | 10 | 0 | 0 | 0 | 94.1 | 93.6 |
| 14 | 14 | 0 | 0 | 0 | 94.4 | 93.6 |
| 15 | 13 | 0 | 0 | 0 | 92.2 | 93.6 |
| Source | df | SS | MS | F-Value | P | Significant |
|---|---|---|---|---|---|---|
| Model | 9 | 9253.67 | 1028.19 | 65.52 | <0.001 | ** |
| Linear | 3 | 7332.54 | 768.63 | 48.98 | <0.001 | ** |
| Square | 3 | 1759.71 | 586.57 | 37.38 | 0.001 | ** |
| Interaction | 3 | 161.43 | 53.81 | 3.43 | 0.109 | |
| A | 1 | 521.64 | 41.76 | 2.66 | 0.164 | |
| B | 1 | 1.44 | 2.08 | 0.13 | 0.731 | |
| C | 1 | 6809.45 | 2004.08 | 127.7 | 0.000 | ** |
| A2 | 1 | 5.38 | 30.96 | 1.97 | 0.219 | |
| B2 | 1 | 0.27 | 13.98 | 0.89 | 0.389 | |
| C2 | 1 | 1754.06 | 1754.06 | 111.77 | <0.001 | ** |
| AB | 1 | 3.80 | 3.80 | 0.24 | 0.643 | |
| AC | 1 | 157.50 | 157.50 | 10.04 | 0.025 | * |
| BC | 1 | 0.12 | 0.12 | 0.01 | 0.933 | |
| Residual | 5 | 78.47 | 15.69 | |||
| Lack of fit | 3 | 75.62 | 25.21 | 17.71 | 0.054 | |
| Pure error | 2 | 2.85 | 1.42 | |||
| Cor total | 14 | 9332.14 | ||||
| R2 = 0.992 |
| Std | Run | Factor | Experimental Values of Permeation Flux (L/m2·h) | Predicted Values of Permeation Flux (L/m2·h) | ||
|---|---|---|---|---|---|---|
| A | B | C | ||||
| 1 | 15 | −1 | −1 | 0 | 19.4 | 19.5 |
| 2 | 2 | 1 | −1 | 0 | 21.3 | 21.0 |
| 3 | 5 | −1 | 1 | 0 | 26.9 | 27.2 |
| 4 | 4 | 1 | 1 | 0 | 20.4 | 20.3 |
| 5 | 3 | −1 | 0 | −1 | 4.4 | 3.3 |
| 6 | 7 | 1 | 0 | −1 | 3.5 | 2.9 |
| 7 | 12 | −1 | 0 | 1 | 28.4 | 29.0 |
| 8 | 8 | 1 | 0 | 1 | 22.9 | 24.0 |
| 9 | 9 | 0 | −1 | −1 | 3.3 | 4.3 |
| 10 | 11 | 0 | 1 | −1 | 3.8 | 4.5 |
| 11 | 6 | 0 | −1 | 1 | 25.1 | 24.4 |
| 12 | 1 | 0 | 1 | 1 | 32.1 | 31.2 |
| 13 | 10 | 0 | 0 | 0 | 15.5 | 15.1 |
| 14 | 14 | 0 | 0 | 0 | 14.9 | 15.1 |
| 15 | 13 | 0 | 0 | 0 | 14.9 | 15.1 |
| Source | df | SS | MS | F-Value | P | Significant |
|---|---|---|---|---|---|---|
| Model | 9 | 1299.65 | 144.405 | 113.57 | <0.001 | ** |
| Linear | 3 | 1132.76 | 50.798 | 39.95 | 0.001 | ** |
| Square | 3 | 133.40 | 44.465 | 34.97 | 0.001 | ** |
| Interaction | 3 | 33.49 | 11.164 | 8.78 | 0.019 | * |
| A | 1 | 15.12 | 5.272 | 4.15 | 0.097 | |
| B | 1 | 24.85 | 23.115 | 18.18 | 0.008 | ** |
| C | 1 | 1092.78 | 92.741 | 72.94 | <0.001 | ** |
| A2 | 1 | 28.09 | 29.207 | 22.97 | 0.005 | ** |
| B2 | 1 | 69.54 | 61.690 | 48.52 | 0.001 | ** |
| C2 | 1 | 35.77 | 35.770 | 28.13 | 0.003 | ** |
| AB | 1 | 17.64 | 17.640 | 13.87 | 0.014 | * |
| AC | 1 | 5.29 | 5.290 | 4.16 | 0.097 | |
| BC | 1 | 10.56 | 10.562 | 8.31 | 0.034 | * |
| Residual | 5 | 6.36 | 1.271 | |||
| Lack of fit | 3 | 6.12 | 2.039 | 16.99 | 0.056 | |
| Pure error | 2 | 0.24 | 0.120 | |||
| Cor total | 14 | 1306.00 | ||||
| R2 = 0.995 |
| Optimization Condition | Response Project | Response Result | Desirability | Optimized Composite Desirability |
|---|---|---|---|---|
| Cd2+ concentration = 10.0 mg/L | Cd2+ rejection rate | 99.14% | 1.00 | 1.00 |
| Α = 0.30 | Permeation flux | 37.36 L/m2·h | 1.00 | |
| pH = 9.58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, T.; Yan, H.; Zhang, Z.; Xu, M.; Wu, Y.; Jin, L.; Huang, G.; Fu, H. Optimization of Enhanced Ultrafiltration Conditions for Cd with Mixed Biosurfactants Using the Box-Behnken Response Surface Methodology. Water 2019, 11, 442. https://doi.org/10.3390/w11030442
Chai T, Yan H, Zhang Z, Xu M, Wu Y, Jin L, Huang G, Fu H. Optimization of Enhanced Ultrafiltration Conditions for Cd with Mixed Biosurfactants Using the Box-Behnken Response Surface Methodology. Water. 2019; 11(3):442. https://doi.org/10.3390/w11030442
Chicago/Turabian StyleChai, Tian, Huizhi Yan, Zhibin Zhang, Min Xu, Yicheng Wu, Lei Jin, Guohe Huang, and Haiyan Fu. 2019. "Optimization of Enhanced Ultrafiltration Conditions for Cd with Mixed Biosurfactants Using the Box-Behnken Response Surface Methodology" Water 11, no. 3: 442. https://doi.org/10.3390/w11030442
APA StyleChai, T., Yan, H., Zhang, Z., Xu, M., Wu, Y., Jin, L., Huang, G., & Fu, H. (2019). Optimization of Enhanced Ultrafiltration Conditions for Cd with Mixed Biosurfactants Using the Box-Behnken Response Surface Methodology. Water, 11(3), 442. https://doi.org/10.3390/w11030442





