Hydropower from the Alpine Cryosphere in the Era of Climate Change: The Case of the Sabbione Storage Plant in Italy
Abstract
:1. Introduction
2. Case Study
3. Data Base
3.1. Poly-Hydro Model Setup (2000–2017)
3.2. Glacier’s Cover Dynamics (2000–2017)
3.3. Hydropower Production and Price
3.4. Climate Projections (2018–2100)
4. Methods
4.1. Ice Flow Modelling and Mass Balance
τb = 1.5 if ∆H > 1.6 km
if T > TThresh
Mice,snow = 0 if T < TThresh
4.2. Hydrological Model
4.3. Hydropower Production Model
4.4. Hydrological and Hydropower Projections Until 2100
5. Results
5.1. Modelling of Sabbione Glacier
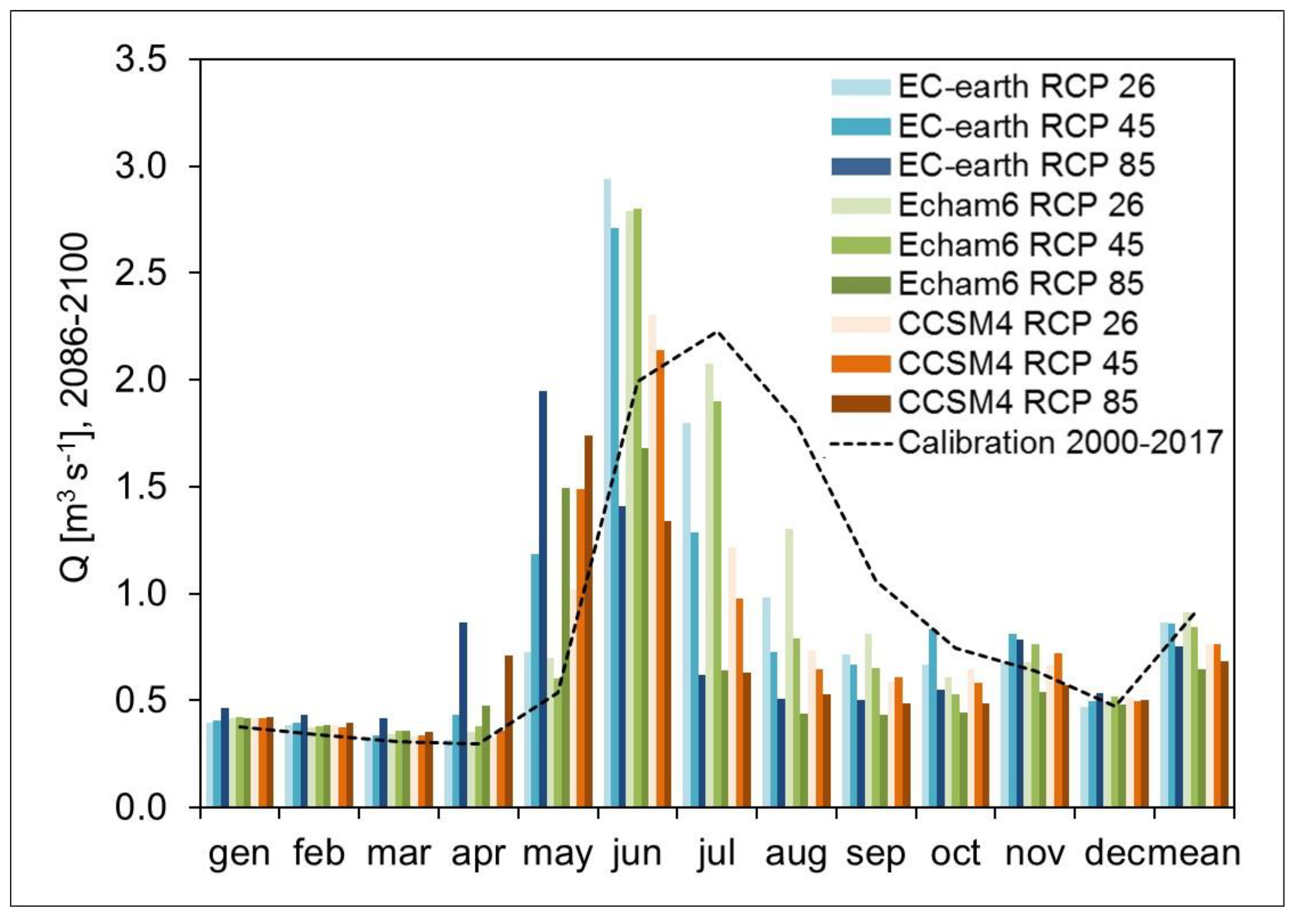
5.2. Stream Flows and Hydropower Production
5.3. Future Hydro-Climatology
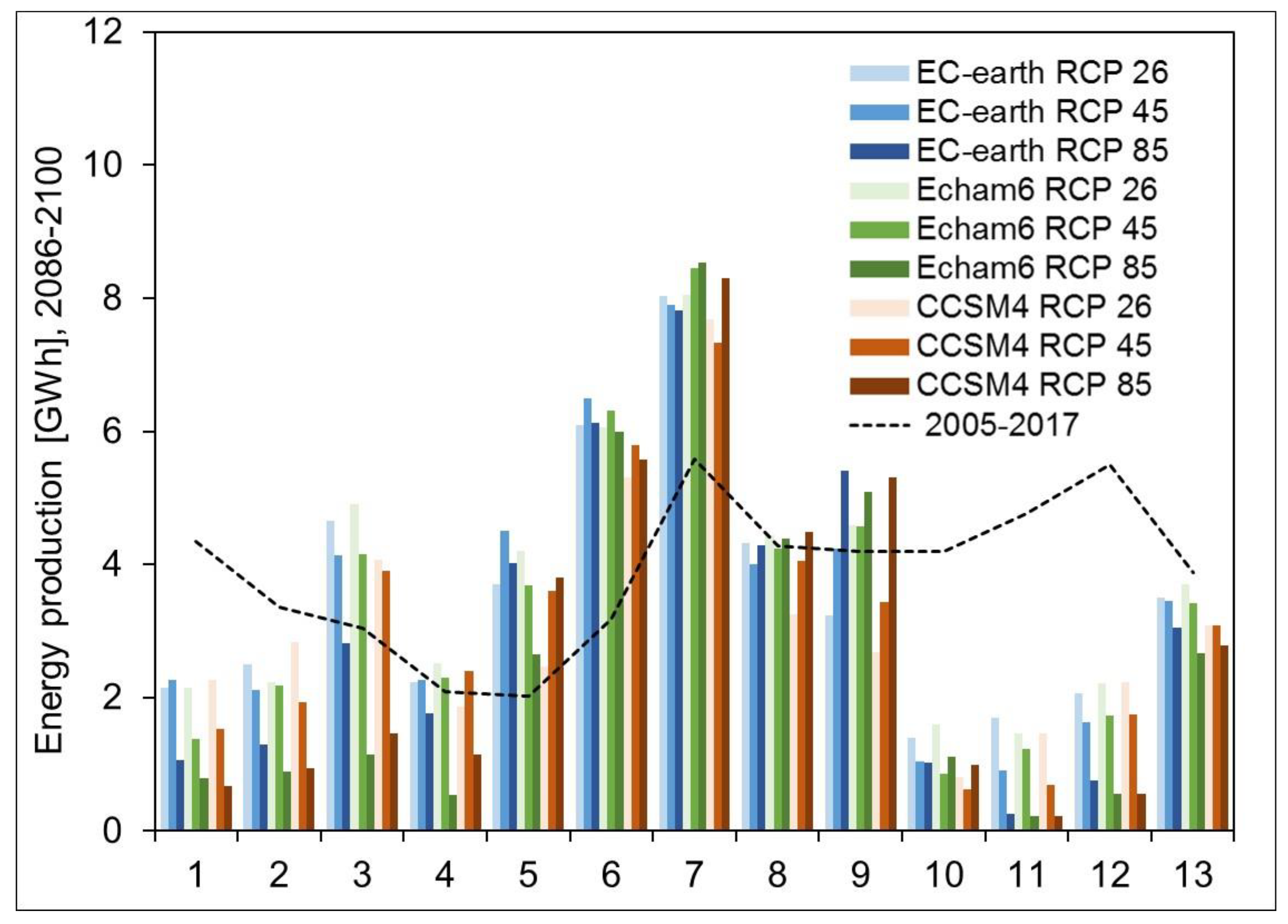
5.4. Future Hydropower Production
6. Discussion
6.1. Recent Cryospheric Dynamics of High Altitude Alpine Catchment
6.2. Cryospheric Water under Future Climate Change
6.3. Hydropower Production under Climate Change
6.4. Limitations and Outlooks
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaygusuz, K. Hydropower and the world’s energy future. Energy Sources 2004, 26, 215–224. [Google Scholar] [CrossRef]
- Ravazzani, G.; Dalla Valle, F.; Gaudard, L.; Mendlik, T.; Gobiet, A.; Mancini, M. Assessing climate impacts on hydropower production: The case of the Toce River Basin. Climate 2016, 4, 16. [Google Scholar] [CrossRef]
- Giuliani, M.; Anghileri, D.; Castelletti, A.; Vu, P.N.; Soncini-Sessa, R. Large storage operations under climate change: Expanding uncertainties and evolving tradeoffs. Environ. Res. Lett. 2016, 11, 035009. [Google Scholar] [CrossRef]
- Akbari-Alashti, H.; Soncini, A.; Dinpashoh, Y.; Fakheri-Fard, A.; Talatahari, S.; Bocchiola, D. Operation of two major reservoirs of Iran under IPCC scenarios during the XXI century. Hydrol. Process. 2018, 32, 3254–3271. [Google Scholar] [CrossRef]
- Gaudard, L.; Romerio, F. The future of hydropower in Europe: Interconnecting climate, markets and policies. Environ. Sci. Policy 2014, 37, 172–181. [Google Scholar] [CrossRef]
- Viganò, G.; Confortola, G.; Fornaroli, R.; Cabrini, R.; Canobbio, S.; Mezzanotte, V.; Bocchiola, D. Effects of future climate change on a river habitat in an Italian alpine catchment. J. Hydrol. Eng. 2015, 21, 04015063. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Azzoni, R.S.; Diolaiuti, G. A methodology for monitoring and modeling of high altitude Alpine catchments. Prog. Phys. Geogr. 2017, 41, 393–420. [Google Scholar] [CrossRef]
- Aili, T.; Soncini, A.; Bianchi, A.; Diolaiuti, G.; D’Agata, C.; Bocchiola, D. Assessing water resources under climate change in high-altitude catchments: A methodology and an application in the Italian Alps. Theor. Appl. Climatol. 2018, 135, 1–22. [Google Scholar] [CrossRef]
- D’Agata, C.; Bocchiola, D.; Soncini, A.; Maragno, D.; Smiraglia, C.; Diolaiuti, G.A. Recent area and volume loss of Alpine glaciers in the Adda River of Italy and their contribution to hydropower production. Cold Reg. Sci. Technol. 2018, 148, 172–184. [Google Scholar] [CrossRef]
- Maran, S.; Volonterio, M.; Gaudard, L. Climate change impacts on hydropower in an alpine catchment. Environ. Sci. Policy 2014, 43, 15–25. [Google Scholar] [CrossRef]
- Barry, R.G. The status of research on glaciers and global glacier recession: A review. Prog. Phys. Geogr. 2006, 30, 285–306. [Google Scholar] [CrossRef]
- Mann, M.E. Little ice age. In Encyclopedia of Global Environmental Change; Wiley: Chichester, UK, 2002; Volume 1, pp. 504–509. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.408.1689&rep=rep1&type=pdf (accessed on 31 July 2019).
- Oerlemans, J. Quantifying global warming from the retreat of glaciers. Science 1994, 264, 243–245. [Google Scholar] [CrossRef] [PubMed]
- Dyurgerov, M.B.; Meier, M.F. Twentieth century climate change: Evidence from small glaciers. Proc. Natl. Acad. Sci. USA 2000, 97, 1406–1411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maragno, D.; Diolaiuti, G.; D’agata, C.; Mihalcea, C.; Bocchiola, D.; Bianchi Janetti, E.; Smiraglia, C. New evidence from Italy (Adamello Group, Lombardy) for analysing the ongoing decline of Alpine glaciers. Geogr. Fis. Din. Quat. 2009, 32, 31–39. [Google Scholar]
- Diolaiuti, G.; Bocchiola, D.; D’agata, C.; Smiraglia, C. Evidence of climate change impact upon glaciers’ recession within the Italian Alps. Theor. Appl. Climatol. 2012, 109, 429–445. [Google Scholar] [CrossRef]
- Diolaiuti, G.A.; Bocchiola, D.; Vagliasindi, M.; D’agata, C.; Smiraglia, C. The 1975–2005 glacier changes in Aosta Valley (Italy) and the relations with climate evolution. Prog. Phys. Geogr. 2012, 36, 764–785. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; Volume 32, Available online: https://wg1.ipcc.ch/SR/documents/SR1.5_LAM3_Room_Assignment.pdf (accessed on 31 July 2019).
- Brunetti, M.; Lentini, G.; Maugeri, M.; Nanni, T.; Auer, I.; Boehm, R.; Schoener, W. Climate variability and change in the Greater Alpine Region over the last two centuries based on multi-variable analysis. Int. J. Climatol. 2009, 29, 2197–2225. [Google Scholar] [CrossRef]
- Zemp, M.; Paul, F.; Hoelze, M.; Haeberli, W. Glacier fluctuations in the European Alps, 1850–2000. In Darkening Peaks: Glacier Retreat, Science, and Society; Orlove, B., Wiegandt, E., Luckman, B.H., Eds.; University of California Press: Berkeley, CA, USA, 2008; pp. 152–167. ISBN 9780520235056. [Google Scholar]
- Smiraglia, C.; Diolaiuti, G.A. Il Nuovo Catasto dei Ghiacciai Italiani. [The New Italian Glacier Inventory]; EVK2CNR, Ed.; EVK2CNR: Bergamo, Italy, 2015; p. 400. ISBN 9788894090802. [Google Scholar]
- Smiraglia, C.; Diolaiuti, G.; Pelfini, M.; Belò, M.; Citterio, M.; Carnielli, T.; D’Agata, C. Glacier changes and their impacts on mountain tourism. In Darkening Peaks: Glacier Retreat, Science, and Society; Orlove, B., Wiegandt, E., Luckman, B.H., Eds.; University of California Press: Berkeley, CA, USA, 2008; pp. 206–215. ISBN 9780520235056. [Google Scholar]
- Meier, M.F. Contribution of small glaciers to global sea level. Science 1984, 226, 1418–1421. [Google Scholar] [CrossRef]
- Minora, U.; Senese, A.; Bocchiola, D.; Soncini, A.; D’agata, C.; Ambrosini, R.; Diolaiuti, G. A simple model to evaluate ice melt over the ablation area of glaciers in the Central Karakoram National Park, Pakistan. Ann. Glaciol. 2015, 56, 202–216. [Google Scholar] [CrossRef] [Green Version]
- Bocchiola, D.; Mihalcea, C.; Diolaiuti, G.; Mosconi, B.; Smiraglia, C.; Rosso, R. Flow prediction in high altitude ungauged catchments: A case study in the Italian Alps (Pantano Basin, Adamello Group). Adv. Water Resour. 2010, 33, 1224–1234. [Google Scholar] [CrossRef]
- Bocchiola, D. Long term (1921–2011) changes of alpine catchments regime in northern Italy. Adv. Water Resour. 2014, 70, 51–64. [Google Scholar] [CrossRef]
- Bombelli, G.M.; Soncini, A.; Bianchi, A.; Bocchiola, D. Potentially modified hydropower production under climate change in the Italian Alps. Hydrol. Process. 2019, 1–18. [Google Scholar] [CrossRef]
- Bocchiola, D.; Soncini, A.; Senese, A.; Diolaiuti, G. Modelling hydrological components of the Rio Maipo of Chile, and their prospective evolution under climate change. Climate 2018, 6, 57. [Google Scholar] [CrossRef]
- Groppelli, B.; Soncini, A.; Bocchiola, D.; Rosso, R. Evaluation of future hydrological cycle under climate change scenarios in a mesoscale alpine watershed of Italy. Nat. Hazards Earth Sys. Sci. 2011, 11, 1769–1785. [Google Scholar] [CrossRef]
- Mazza, A.; Mercalli, L. Il Ghiacciaio Meridionale dell’Hohsand (Alta Val Formazza): Un secolo di evoluzione climatica ei rapporti con la produzione idroelettrica. Oscellana 1992, 22, 30–44. [Google Scholar]
- Paro, L. Permafrost e forme periglaciali alle falde del corno di Ban. In L’ambiente Glaciale e Periglaciale dei Sabbioni (Hohsand). Formazza; Arpa Piemonte: Torino, Italy, 2012; 56p, Published in fulfilment of the Program: Interreg di cooperazione transfrontaliera Italia-Svizzera 2007–2013. In Italian; Available online: http://www.arpa.piemonte.it/pubblicazioni-2/pubblicazioni-anno-2012/sabbioni/at_download/file (accessed on 10 August 2019).
- Belotti, P.; Biagi, L.; Brovelli, M.A.; Campi, A.; Campus, S.; Cannata, M.; Credali, M.; Manzino, A.M.; Sansò, F.; Siletto, G.B. Introduzione al progetto HELI-DEM [An introduction to HELI-DEM project]. Bollettino della Società Italiana di Fotogrammetria e Topografia 2013, 13, 11–22. Available online: http://www.fondazionepolitecnico.it/uploads/test/SIFET_Il%20Progetto%20HELI-DEM.pdf (accessed on 31 July 2019).
- Bocchiola, D.; Rosso, R. The distribution of daily Snow Water Equivalent in the Central Italian Alps. Adv. Water Resour. 2007, 30, 135–147. [Google Scholar] [CrossRef]
- Valt, M.; Chiambretti, I.; Dellavedova, P. Fresh snow density on the Italian Alps. In Geophysical Research Abstracts; Copernicus: Göttingen, Germany, 2014; Volume 16, Available online: https://meetingorganizer.copernicus.org/EGU2014/EGU2014-9715.pdf (accessed on 31 July 2019).
- Soncini, A.; Bocchiola, D.; Confortola, G.; Minora, U.; Vuillermoz, E.; Salerno, F.; Diolaiuti, G. Future hydrological regimes and glacier cover in the Everest region: The case study of the upper Dudh Koshi basin. Sci. Total Environ. 2016, 565, 1084–1101. [Google Scholar] [CrossRef] [Green Version]
- Baldasso, V.; Soncini, A.; Azzoni, R.S.; Diolaiuti, G.; Bocchiola, D. Recent evolution of glaciers in Western Asia in response to global warming: The case study of mount Ararat, Turkey, Theoret. Appl. Climatol. 2018, 1–15. [Google Scholar] [CrossRef]
- Ente Nazionale Energia Elettrica ENEL, 2014. Morasco. Centrale Idroelettrica. Available online: https://web.archive.org/web/20140706072532/http://www.enel.it:80/it-IT/impianti/mappa/dettaglio/morasco-formazza/p/090027d98192f97b (accessed on 31 July 2019).
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Available online: http://www.climatechange2013.org/images/report/WG1AR5_Frontmatter_FINAL.pdf (accessed on 31 July 2019).
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Brokopf, R. Atmospheric component of the MPI-M earth system model: ECHAM6. J. Adv. Model. Earth Syst. 2013, 5, 146–172. [Google Scholar] [CrossRef]
- Hazeleger, W.; Severijns, C.; Semmler, T.; Ştefănescu, S.; Yang, S.; Wang, X.; Bougeault, P. EC-Earth: A seamless earth-system prediction approach in action. Bull. Am. Meteorol. Soc. 2010, 91, 1357–1364. [Google Scholar] [CrossRef]
- Groppelli, B.; Bocchiola, D.; Rosso, R. Spatial downscaling of precipitation from GCMs for climate change projections using random cascades: A case study in Italy. Water Resour. Res. 2011, 47, W03519. [Google Scholar] [CrossRef]
- Soncini, A.; Bocchiola, D.; Confortola, G.; Bianchi, A.; Rosso, R.; Mayer, C.; Lambrecht, A.; Palazzi, E.; Smiraglia, C.; Diolaiuti, G.A. Future hydrological regimes in the upper Indus basin: A case study from a high-altitude glacierized catchment. J. Hydrometeorol. 2015, 16, 306–326. [Google Scholar] [CrossRef]
- Haeberli, W.; Hölzle, M. Application of inventory data for estimating characteristics of and regional climate-change effects on mountain glaciers: A pilot study with the European Alps. Ann. Glaciol. 1995, 21, 206–212. [Google Scholar] [CrossRef]
- Oerlemans, J. Glaciers and Climate Change; August Aimé Balkema Publishers: Brookfield, VT, USA, 2001; p. 148. [Google Scholar]
- Bocchiola, D.; Soncini, A. Water Resources Modeling and Prospective Evaluation in the Indus River Under Present and Prospective Climate Change. In Indus River Basin; Elsevier: Amsterdam, The Netherlands, 2019; pp. 17–56. [Google Scholar] [CrossRef]
- Hargreaves, G.H. The estimation of potential and crop evapotranspiration. Am. Soc. Agric. Eng. Trans. 1974, 17, 701–704. [Google Scholar] [CrossRef]
- Bombelli, G.M.; Soncini, A.; Bianchi, A.; Bocchiola, D. Influence of climate change scenarios on energy price: A case study in Italy. Submitt. Environ. Model. Assess. 2018. submitted. [Google Scholar]
- Apadula, F.; Bassini, A.; Elli, A.; Scapin, S. Relationships between meteorological variables and monthly electricity demand. Appl. Energy 2012, 98, 346–356. [Google Scholar] [CrossRef]
- Grossi, G.; Caronna, P.; Ranzi, R. Hydrologic vulnerability to climate change of the Mandrone glacier (Adamello-Presanella group, Italian Alps). Adv. Water Resour. 2013, 55, 190–203. [Google Scholar] [CrossRef] [Green Version]
- Garavaglia, R.; Marzorati, A.; Confortola, G.; Bocchiola, D.; Cola, G.; Manzata, E.; Senese, A.; Smiraglia, C.; Diolaiuti, G.A. Evoluzione del ghiacciaio dei Forni. Neve Valanghe 2014, 81, 60–67. [Google Scholar]
- Diolaiuti, G.A. The recent reduction of the Lombardy glaciers: Results of the post recent mass balances. Geogr. Fis. Din. Quat. 2001, 5, 65–75. [Google Scholar]
- Cannone, N.; Diolaiuti, G.; Guglielmin, M.; Smiraglia, C. Accelerating climate change impacts on alpine glacier forefield ecosystems in the European Alps. Ecol. Appl. 2008, 18, 637–648. [Google Scholar] [CrossRef]
- D’Agata, C.; Bocchiola, D.; Maragno, D.; Smiraglia, C.; Diolaiuti, G.A. Glacier shrinkage driven by climate change during half a century (1954–2007) in the Ortles-Cevedale group (Stelvio National Park, Lombardy, Italian Alps). Theor. Appl. Climatol. 2014, 116, 169–190. [Google Scholar] [CrossRef]
- Confortola, G.; Soncini, A.; Bocchiola, D. Climate change will affect hydrological regimes in the Alps: A case study in Italy. J. Alpine Res. 2013, 101, 3–19. [Google Scholar] [CrossRef]
- Bavay, M.; Grünewald, T.; Lehning, M. Response of snow cover and runoff to climate change in high Alpine catchments of Eastern Switzerland. Adv. Water Resour. 2013, 55, 4–16. [Google Scholar] [CrossRef]
- Gaudard, L.; Gabbi, J.; Bauder, A.; Romerio, F. Long-term uncertainty of hydropower revenue due to climate change and electricity prices. Water Resour. Manag. 2016, 30, 1325–1343. [Google Scholar] [CrossRef]
- Gaudard, L.; Gilli, M.; Romerio, F. Climate change impacts on hydropower management. Water Resour. Manag. 2013, 27, 5143–5156. [Google Scholar] [CrossRef]
- Konz, M.; Seibert, J. On the value of glacier mass balances for hydrological model calibration. J. Hydrol. 2010, 385, 238–246. [Google Scholar] [CrossRef] [Green Version]
- Mulder, M.; Scholtens, B. The impact of renewable energy on electricity prices in the Netherlands. Renew. Energy 2013, 57, 94–100. [Google Scholar] [CrossRef]
- Faggian, P.; Giorgi, F. An analysis of global model projections over Italy, with particular attention to the Italian Greater Alpine Region (GAR). Clim. Chang. 2009, 96, 239–258. [Google Scholar] [CrossRef]
- Fuss, S.; Canadell, J.G.; Peters, G.P.; Tavoni, M.; Andrew, R.M.; Ciais, P.; Le Quéré, C. Betting on negative emissions. Nat. Clim. Chang. 2014, 4, 850–853. [Google Scholar] [CrossRef]











| Temperature (°C) | Precipitation (mm) | ||||
|---|---|---|---|---|---|
| Month | Mean | Max | Min | Rainfall | SWE |
| Jan | −7.3 | −3.0 | −11.4 | 5 | 104 |
| Feb | −7.3 | −2.1 | −11.6 | 8 | 124 |
| Mar | −4.5 | 1.3 | −9.0 | 15 | 147 |
| Apr | −1.8 | 3.9 | −6.0 | 29 | 171 |
| May | 2.1 | 7.4 | −1.8 | 129 | 243 |
| Jun | 6.2 | 10.6 | 2.3 | 143 | 154 |
| Jul | 8.0 | 11.5 | 4.2 | 142 | 142 |
| Aug | 7.9 | 11.1 | 4.5 | 161 | 164 |
| Sep | 4.5 | 7.8 | 1.2 | 124 | 133 |
| Oct | 1.5 | 5.3 | −1.9 | 87 | 137 |
| Nov | −3.2 | 0.7 | −6.7 | 25 | 217 |
| Dec | −6.2 | −2.2 | −10.1 | 6 | 123 |
| AWS | Latitude (°) | Longitude (°) | Altitude (m asl) |
|---|---|---|---|
| Agnel lake | 45°28′5″ N | 7°8′23″ E | 2304 |
| Monviso | 44°39′37″ N | 7°05′19″ E | 3325 |
| Moro pass | 45°59′49″ N | 7°58′35″ E | 2820 |
| Gastaldi lodge | 45°17′53″ N | 7°08′36″ E | 2659 |
| Vaccarone lodge | 45°09′15″ N | 6°54′59″ E | 2745 |
| Sommeiller | 45°07′54″ N | 6°50′34″ E | 2981 |
| Col Agnel | 44°40′51″ N | 6°58′43″ E | 2685 |
| Sestriere Banchetta | 44°57′54″ N | 6°54′36″ E | 2480 |
| Bocchetta delle Pisse | 45°52′32″ N | 7°54′04″ E | 2410 |
| SLFARO | 46°02′ N | 7°26′ E | 3301 |
| SLFGLA | 47°00′ N | 9°00′ E | 2909 |
| SLFSIM | 46°28′ N | 8°58′ E | 2580 |
| SLFSI2 | 46°28′ N | 8°59′ E | 2450 |
| SLFVAL | 46°31′ N | 8°38′ E | 2448 |
| SLFANV | 46° 9′ N | 7°35′ E | 2896 |
| SLFAN2 | 46°11′ N | 7°32′ E | 2630 |
| SLFAR2 | 46°18′ N | 7°33′ E | 2850 |
| SLFBED | 46°31′ N | 8°38′ E | 2962 |
| SLFBEL | 46°23′ N | 8°10′ E | 2556 |
| SLFBER | 46°26′ N | 10°00′ E | 2959 |
| SLFBE2 | 46°26′ N | 10°00′ E | 2450 |
| SLFBE3 | 46°26′ N | 9°55′ E | 2620 |
| SLFBR2 | 46°33′ N | 9°53′ E | 2510 |
| EGH | 46°30′ N | 8°17′ E | 2893 |
| SLFELA | 46°33′ N | 9°53′ E | 3114 |
| SLFTUM | 46°47′ N | 8°59′ E | 3050 |
| GOR | 45°59′ N | 7°47′ E | 3129 |
| SLFCHA | 46°23′ N | 7°09′ E | 2540 |
| CMA | 46°50′ N | 9°10′ E | 2480 |
| Formazza | 46°25′60″ N | 8°21′30″ E | 2453 |
| Date | Type | Source |
|---|---|---|
| 4 October 1999 | Orthophoto | BLOM-CGR |
| 8 September 2007 | Orthophoto | AGEA |
| 26 July 2012 | Orthophoto | AGEA |
| Summer 2015 | Orthophoto | Cons. TEA |
| 14 October 2017 | Satellite | SENTINEL |
| Parameter | Unit | Description | Value | Method |
| αci,s | (-) | Albedo, clean ice, snow | 0.3, 0.7 | [7] |
| TMFci,s | (mm d−1 °C−1) | Thermal melt factor, clean ice, snow | 5.3, 3.4 | ice stakes, AWS |
| RMFci,s | (mm d−1 W−1 m2) | Radiation melt factor, clean ice, snow | 0, 4 × 10−3 | ice stakes, nivometer |
| Fv | (%) | Vegetation cover, average | 22 | Land cover |
| K | (mm d−1) | Saturated conductivity | 4 | [8] |
| k | (-) | Ground flow exponent | 1.5 | [8] |
| WMax | (mm) | Max soil storage, average | 52 | land cover |
| θw,θs | (-) | Water content, wilting, field capacity | 0.15, 0.35 | [29] |
| Ks | (m−3 y−1) | Ice flow basal sliding coeff. | 1.5 × 10−21 | [8] |
| Kd | (m−1 y−1) | Ice flow internal deformation coeff. | 1.2 × 10−24 | [8] |
| Goodness of fit | ||||
| Variable | Unit | Description | Bias (%) | NSE(R2) (-) |
| Mci | (mm d−1) | Ice ablation | 0.0 | 0.63 |
| Ms | (mm d−1) | Snow ablation Formazza | 4.0 | 0.86 |
| Date | ICA Mod. (km2) | ICA Obs. (km2) | Diff. Mod.–Obs. (%) |
|---|---|---|---|
| 1 January 2000 | 4.2 | 4.2 | 0% (setup) |
| 8 September 2007 | 3.6 | 3.6 | 0% |
| 26 July 2012 | 3.3 | 3.4 | −4% |
| 10 September 2015 | 3.1 | 3.0 | +3% |
| 10 October 2017 | 2.9 | 2.7 | +8% |
| ΔICA (2000–2017) | −1.3 | −1.5 | −13% |
| ΔICA% (2000–2017) | −31 | −36 | +5% |
| Variable | ΔEp% | ΔT% | ΔP% | ΔQ% | ΔICA% |
|---|---|---|---|---|---|
| ΔEp% | - | 0.007 | <10−4 | <10−4 | 0.014 |
| ΔT% | −0.616 | - | 0.063 | 0.005 | 0.043 |
| ΔP% | 0.958 | −0.447 | - | <10−4 | 0.097 |
| ΔQ% | 0.999 | −0.626 | 0.960 | - | 0.015 |
| ΔICA% | 0.569 | −0.482 | 0.404 | 0.563 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stucchi, L.; Bombelli, G.M.; Bianchi, A.; Bocchiola, D. Hydropower from the Alpine Cryosphere in the Era of Climate Change: The Case of the Sabbione Storage Plant in Italy. Water 2019, 11, 1599. https://doi.org/10.3390/w11081599
Stucchi L, Bombelli GM, Bianchi A, Bocchiola D. Hydropower from the Alpine Cryosphere in the Era of Climate Change: The Case of the Sabbione Storage Plant in Italy. Water. 2019; 11(8):1599. https://doi.org/10.3390/w11081599
Chicago/Turabian StyleStucchi, Leonardo, Giovanni Martino Bombelli, Alberto Bianchi, and Daniele Bocchiola. 2019. "Hydropower from the Alpine Cryosphere in the Era of Climate Change: The Case of the Sabbione Storage Plant in Italy" Water 11, no. 8: 1599. https://doi.org/10.3390/w11081599
APA StyleStucchi, L., Bombelli, G. M., Bianchi, A., & Bocchiola, D. (2019). Hydropower from the Alpine Cryosphere in the Era of Climate Change: The Case of the Sabbione Storage Plant in Italy. Water, 11(8), 1599. https://doi.org/10.3390/w11081599







