Impact of Ionic Strength and Charge Density on Donnan Potential in the NaCl-Cation Exchange Membrane System
Abstract
:1. Introduction
2. Theory
2.1. The Donnan Equilibrium Theory
2.2. Effect of Osmotic Pressure on Donnan’s Potential
2.3. The Debye–Huckel Theory
2.4. The Meissner Corresponding State Model
2.5. Numerical Solution Strategy
3. Results and Discussion
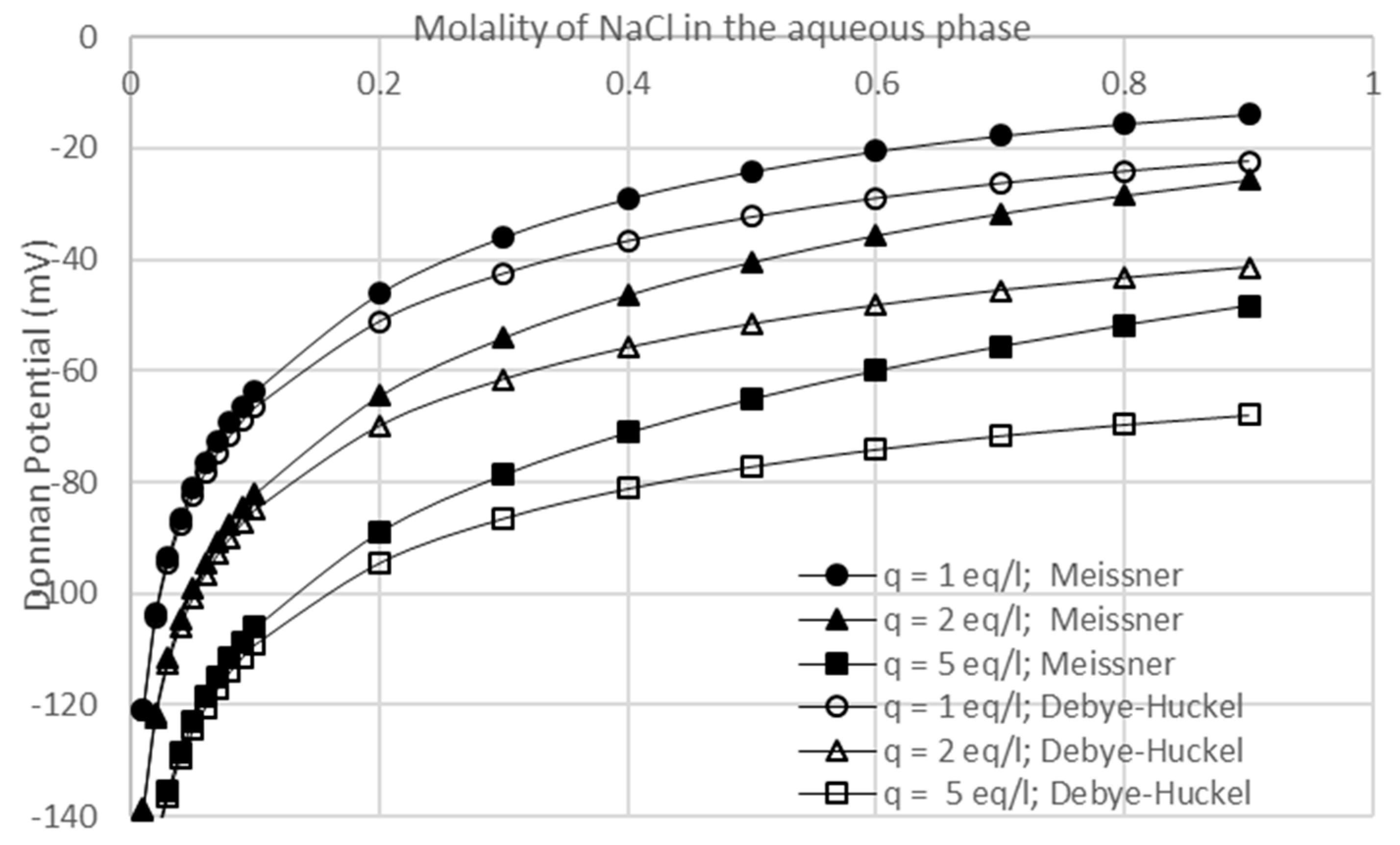
3.1. Model Verification
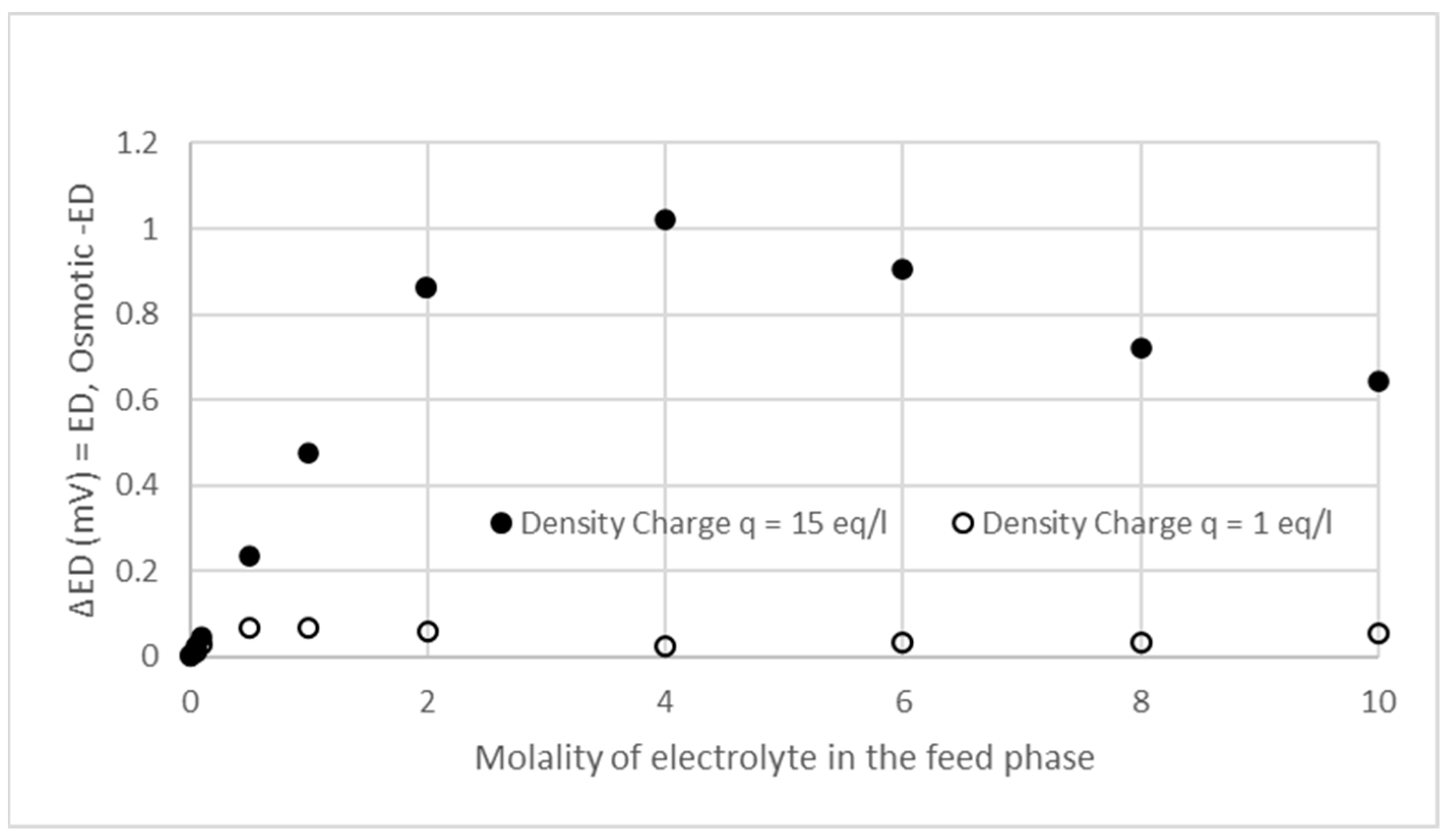
3.2. Effects of Osmotic Pressure, Ionic Adsorption, and Ionic Pairing on Donnan Potential
3.3. Effects of Membrane Fixed Charge Density and Electrolyte Concentration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Disclaimer
References
- Lee, S.B.; Kim, J.H.; Lee, H.B.; Lee, J.W. Advances in microfluidic membrane emulsification for water desalination. J. Membr. Sci. 2020, 610, 118258. [Google Scholar]
- Wang, S.; Zhang, Q.; Chen, T.; Ma, Y. Microfluidic electrochemical desalination: Principles, applications, and perspectives. J. Membr. Sci. 2021, 635, 119512. [Google Scholar]
- Lin, Y.; Cheng, J. Recent advances in microfluidic-based electrodialysis for desalination. J. Mater. Chem. A 2021, 9, 159–180. [Google Scholar]
- Al-Amshawee, S.; Yunus, M.Y.; Azoddein, A.M.; Hassell, D.G.; Dakhil, I.H.; Abu Hasan, H. Electrodialysis desalination for water and wastewater: A review. Chem. Eng. J. 2020, 380, 122231. [Google Scholar] [CrossRef]
- Ma, J.J. Research progress on separation and purification of whey protein based on membrane technology. Chem. Ind. Eng. Prog. 2022, 41, 2826–2838. [Google Scholar]
- Liang, T.; Lu, H.; Ma, J.; Sun, L.; Wang, J. Progress on membrane technology for separating bioactive peptides. J. Food Eng. 2023, 340, 111321. [Google Scholar] [CrossRef]
- Nayak, S.K.; Dutta, K.; Gohil, J.M. (Eds.) Advancements in Polymer-Based Membranes for Water Remediation; Elsevier Inc.: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Liu, Y.; Wu, X.; Dai, L.; Wu, X.; Ding, J.; Chen, R.; Ding, R.; Liu, J.; Van der Bruggen, B. Recovery of nickel in the form of Ni(OH)2 from plating wastewater containing Ni-EDTA using bipolar membrane electrodialysis. Chemosphere 2023, 310, 136822. [Google Scholar] [CrossRef]
- Kumar, P.S.; Varsha, M.; Rathi, B.S.; Rangasamy, G. Electrodeionization: Principle, techniques and factors influencing its performance. Environ. Res. 2023, 216, 114756. [Google Scholar] [CrossRef]
- Ba, X.; Chen, J.; Wang, X.; Wang, J.; Jiang, B. An integrated electrolysis-microfiltration-ion exchange closed-loop system for effective water softening without chemicals input and spent regenerant discharge. Desalination 2023, 553, 116481. [Google Scholar] [CrossRef]
- Chen, W.; Shen, H.; Gong, Y.; Li, P.; Cheng, C. Anion exchange membranes with efficient acid recovery obtained by quaternized poly epichlorohydrin and polyvinyl alcohol during diffusion dialysis. J. Membr. Sci. 2023, 674, 121514. [Google Scholar] [CrossRef]
- Tanaka, Y. Ion Exchange Membranes Fundamentals and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Mulder, M. Basic Principles of Membrane Technology, 2nd ed.; Kluer Academic Publishers: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Gokturk, P.A.; Sujanani, R.; Qian, J.; Wang, Y.; Katz, L.E.; Freeman, B.D.; Crumlin, E.J. The Donnan potential revealed. Nat. Commun. 2022, 13, 5880. [Google Scholar] [CrossRef]
- Higa, M.; Taniokaa, A.; Kirab, A. A novel measurement method of Donnan potential at an interface between a charged membrane and mixed salt solution. J. Membr. Sci. 1998, 140, 213–220. [Google Scholar] [CrossRef]
- Higa, M.; Kira, A.; Tanioka, A.; Miyasaka, K. Ionic partition equilibrium in a charged membrane immersed in a mixed ionic solution. J. Chem. Soc. Faraday Trans. 1993, 89, 3433–3435. [Google Scholar] [CrossRef]
- Higa, M.; Kira, A. Theory and simulation of ion transport in nonstationary states against concentration gradients across ion-exchange membranes. J. Phys. Chem. 1992, 96, 9518–9523. [Google Scholar] [CrossRef]
- Sonin, A.A.; Grossman, G. Ion transport through layered ion exchange membranes. J. Phys. Chem. 1972, 76, 3996–4006. [Google Scholar] [CrossRef]
- Tester, J.W.; Model, M. Thermodynamics and Its Applications, 3rd ed.; Prectice Hall PTR: Hoboken, NJ, USA, 1997. [Google Scholar]
- Scotto, J.; Florit, M.I.; Posadas, D. The effect of membrane equilibrium on the behavior of electrochemically active polymers. J. Electroanal. Chem. 2016, 774, 42–50. [Google Scholar] [CrossRef]
- Chen, G. Donnan Equilibrium Revisited: Coupling between Ion Concentrations, Osmotic Pressure, and Donnan Potential; World Scientific Pub Co Pte Ltd.: Singapore, 2022; Volume 7, Available online: https://hdl.handle.net/1721.1/150833 (accessed on 22 May 2023).
- McQuarrie, D.A. Statistical Mechanics; Harper and Row: New York, NY, USA, 1976. [Google Scholar]
- Meissner, H.P.; Tester, J.W. Activity coefficients of strong electrolytes in aqueous solutions. Ind. Eng. Chem. Proc. Des. Dev. 1972, 11, 128–133. [Google Scholar] [CrossRef]
- Kitto, D.; Kamcev, J. Manning condensation in ion exchange membranes: A review on ion partitioning and diffusion models. J. Polym. Sci. 2022, 60, 2929–2973. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef]
- Kohns, M.; Horsch, M.; Hasse, H. Partial molar volume of NaCl and CsCl in mixtures of water and methanol by experiment and molecular simulation. Fluid Phase Equilibria 2018, 458, 30–39. [Google Scholar] [CrossRef]
- Mafe, S.; Manzanares, J.A.; Reiss, H. Donnan phenomena in membranes with charge due to ion adsorption. Effects of the interaction between adsorbed charged groups. J. Chem. Phys. 1993, 98, 2325–2331. [Google Scholar] [CrossRef]
- Takagi, R.; Nakagaki, M. Theoretical study of the effect of ion adsorption on membrane potential and its application to collodion membranes. J. Membrane Sci. 1990, 53, 19–35. [Google Scholar] [CrossRef]
- Laksminarayanaiah, N. Transport Phenomena in Membranes; Academic Press: New York, NY, USA, 1969. [Google Scholar]
- Manzanares, J.A.; Mafe, S.; Bisquert, J. Electric Double Layer at the Membrane/Solution Interface: Distribution of Electric Potential and Estimation of the Charge Stored. Phys. Chem. 1992, 96, 538–544. [Google Scholar] [CrossRef]
- Dewan, S.; Carnevale, V.; Bankura, A.; Eftekhari-Bafrooei, A.; Fiorin, G.; Klein, M.L.; Borguet, E. Structure of Water at Charged Interfaces: A Molecular Dynamics Study. Langmuir 2014, 30, 8056–8065. [Google Scholar] [CrossRef]
- Gonella, G.; Backus, E.H.G.; Nagata, Y.; Bonthuis, D.J.; Loche, P.; Schlaich, A.; Netz, R.R.; Kühnle, A.; McCrum, I.T.; Koper, M.T.M.; et al. Water at charged interfaces. Nat. Rev. Chem. 2021, 5, 466–485. [Google Scholar] [CrossRef]
- Mafe, S.; Ramirez, P.; Tanioka, A.; Pellicer, J. Model for Counterion-Membrane-Fixed Ion Pairing and Donnan Equilibrium in Charged Membranes. J. Phys. Chem. B 1997, 101, 1851–1856. [Google Scholar] [CrossRef]
- Sawamura, S.; Egoshi, N.; Setoguchi, Y.; Matsuo, H. Solubility of sodium chloride in water under high pressure. Fluid Phase Equilibria 2007, 254, 158–162. [Google Scholar] [CrossRef]
- Jiang, H.; Debenedetti, P.G.; Panagiotopoulos, A.Z. Nucleation in aqueous NaCl solutions shifts from 1-step to 2-step mechanism on crossing the spinodal. J. Chem. Phys. 2019, 150, 124502. [Google Scholar] [CrossRef]
- Soniat, M.; Pool, G.; Franklin, L.; Rick, S.W. Ion association in aqueous solution. Fluid Phase Equilibria 2016, 407, 31–38. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sakaji, B.A.K.; Husseini, G.A.; Darwish, N.A. Impact of Ionic Strength and Charge Density on Donnan Potential in the NaCl-Cation Exchange Membrane System. Water 2023, 15, 3830. https://doi.org/10.3390/w15213830
Al-Sakaji BAK, Husseini GA, Darwish NA. Impact of Ionic Strength and Charge Density on Donnan Potential in the NaCl-Cation Exchange Membrane System. Water. 2023; 15(21):3830. https://doi.org/10.3390/w15213830
Chicago/Turabian StyleAl-Sakaji, Baraa A. K., Ghaleb A. Husseini, and Naif A. Darwish. 2023. "Impact of Ionic Strength and Charge Density on Donnan Potential in the NaCl-Cation Exchange Membrane System" Water 15, no. 21: 3830. https://doi.org/10.3390/w15213830
APA StyleAl-Sakaji, B. A. K., Husseini, G. A., & Darwish, N. A. (2023). Impact of Ionic Strength and Charge Density on Donnan Potential in the NaCl-Cation Exchange Membrane System. Water, 15(21), 3830. https://doi.org/10.3390/w15213830





