Research on the Impact of Using a Combination of Rigid and Flexible Vegetation on Slope Hydrological Properties in Loess Regions
Abstract
:1. Introduction
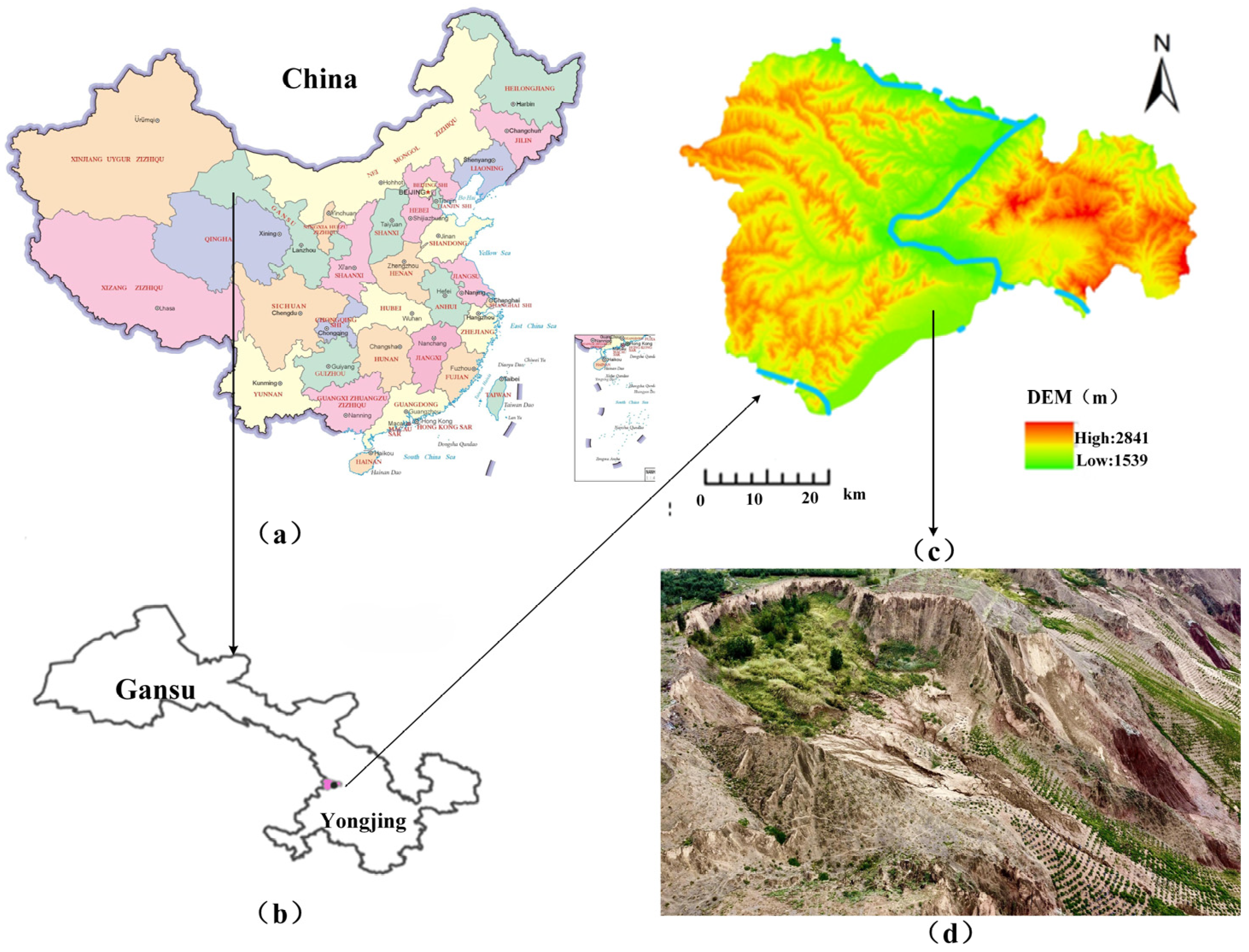
2. Study Area and Materials
3. Methods and Experimental Design
3.1. Methodology
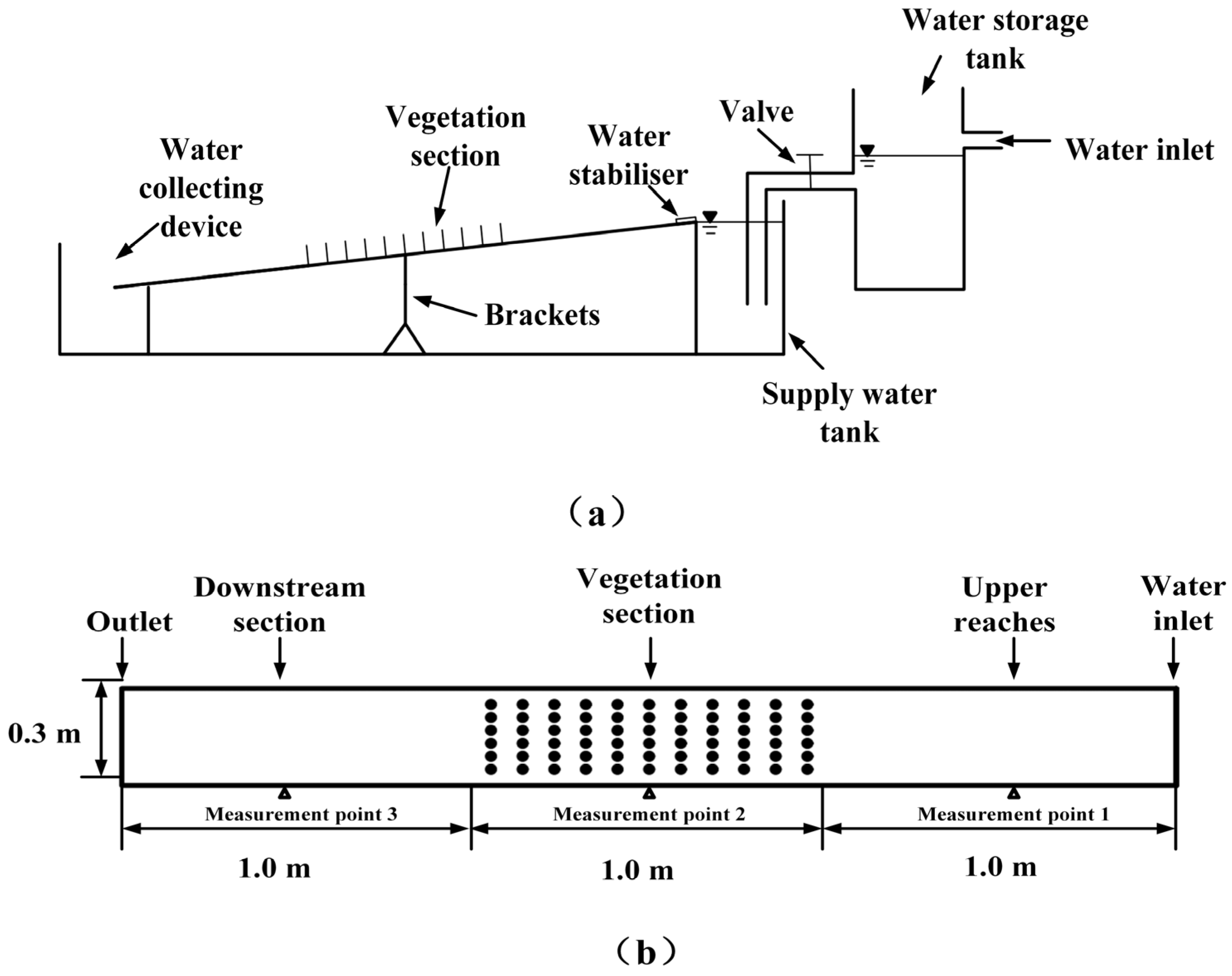
3.2. Scrub Test Design
3.3. Rigid–Flexible Vegetation Design
4. Parameter Determination
5. Results
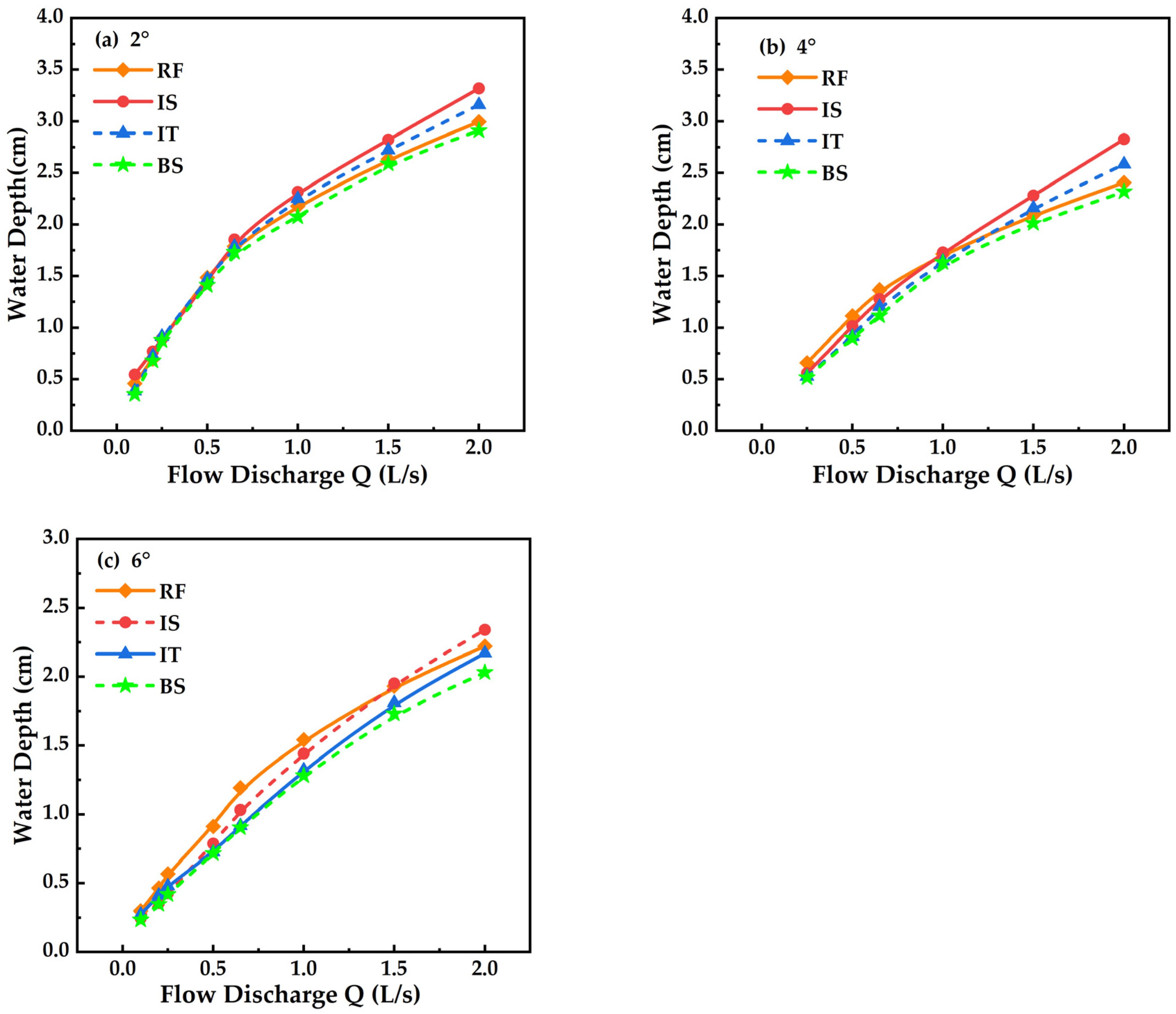
5.1. Changes in Water Depth and Slope Flow Velocity under Different Combinations of Rigid–Flexible Vegetation Cover
5.2. Changes in Slope Flow Patterns Based on Different Combinations of Rigid–Flexible Vegetation Cover
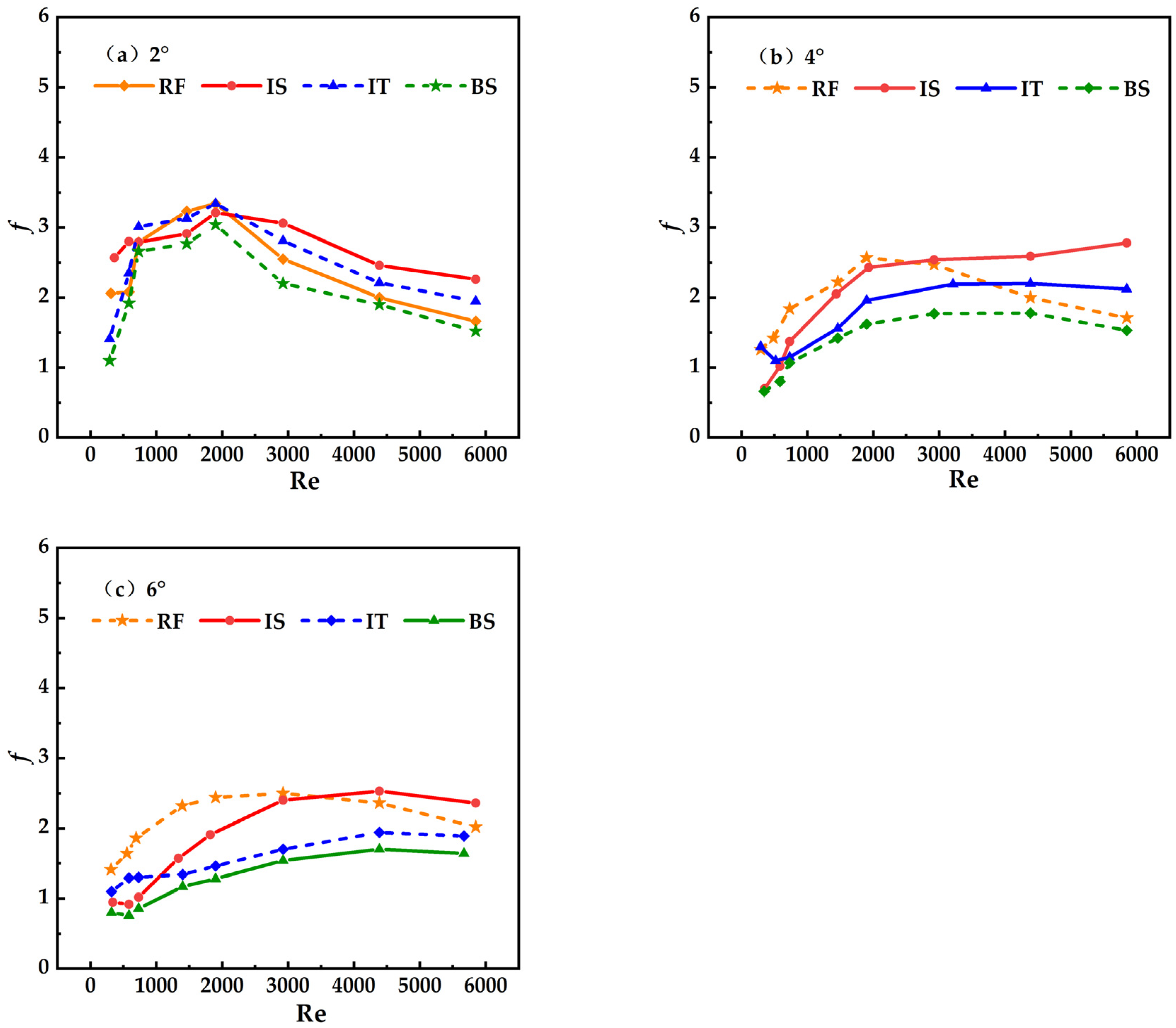
5.3. Variation in Slope Flow Resistance Coefficient Based on Different Vegetation Combinations
5.3.1. Effect of Flow Rate on Drag Coefficient
5.3.2. Influence of Flow Pattern and Flow Regime on the Drag Coefficient
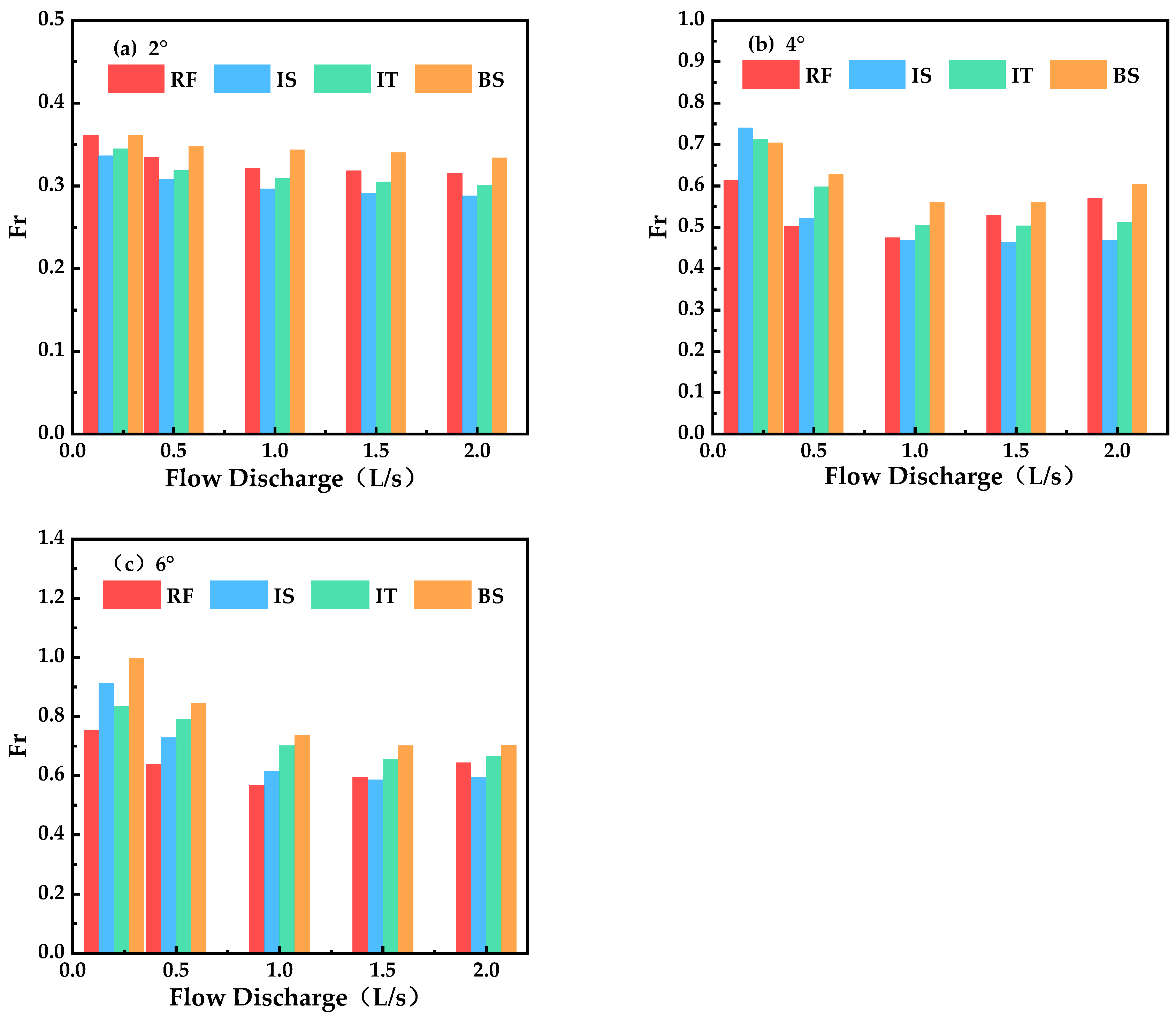
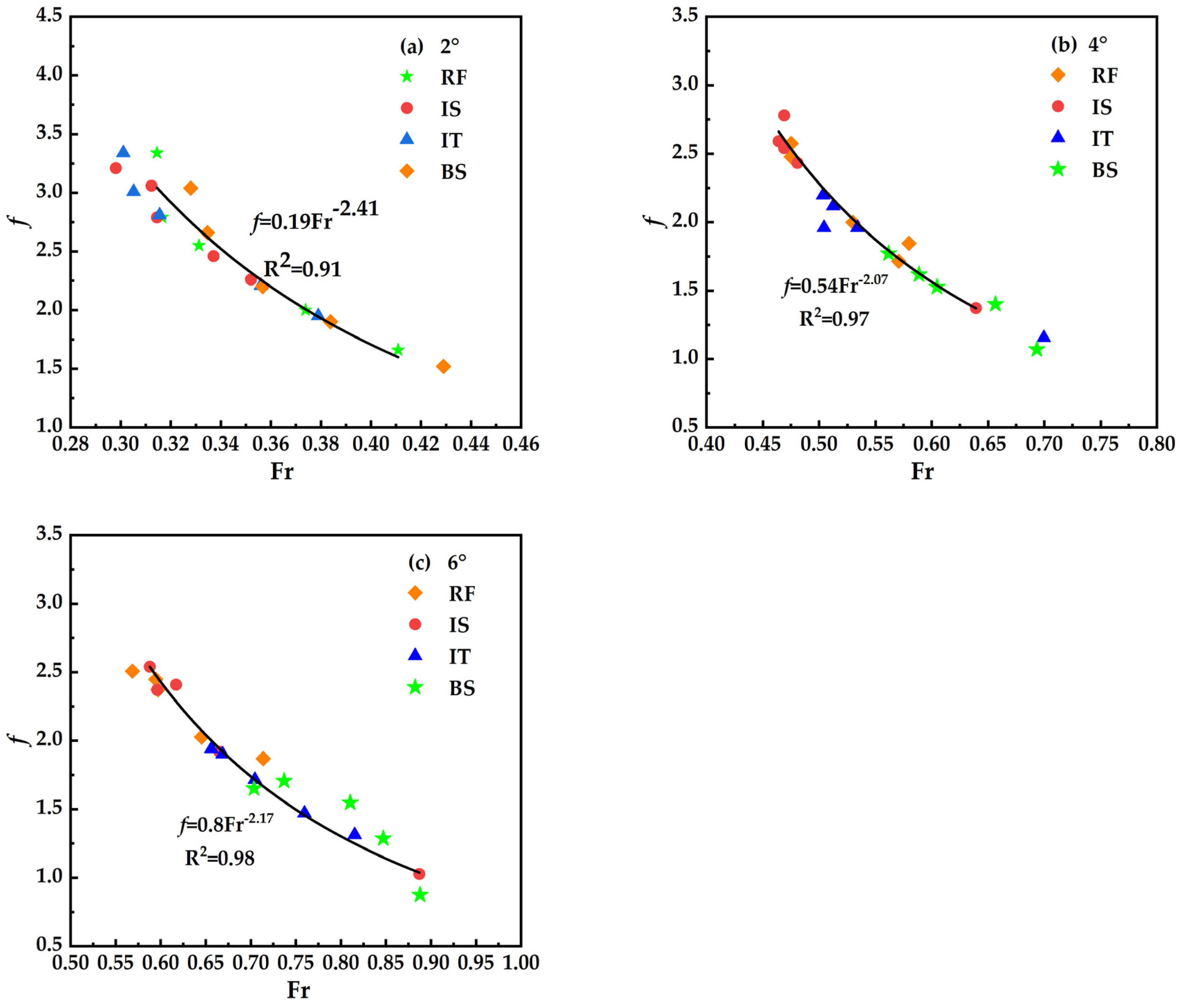
5.3.3. Influence of Froude Number on the Integrated Drag Coefficient
5.4. Model Validation
6. Discussion
6.1. Influence of Vegetation Cover and Slope on the Hydraulic Characteristics of Slope Flow
6.2. Effect of Rigid and Flexible Vegetation on the Hydraulic Characteristics of Slope Flows
6.3. Proposals for the Future
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, X.; Li, P.; Hou, X.; Li, T.; Zhang, G. Microstructure of compacted loess and its influence on the Soil-Water characteristic curve. Adv. Mater. Sci. Eng. 2020, 2020, 3402607. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Liu, H. Scale characters analysis for gully structure in the watersheds of loess landforms based on digital elevation models. Front. Earth Sci. 2018, 12, 431–443. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Z.; Wang, G.; Sun, X.; Cui, N. Overland-Flow resistance characteristics of nonsubmerged vegetation. J. Irrig. Drain. Eng. 2017, 143, 04017021. [Google Scholar] [CrossRef]
- Qin, W.; Cao, W.; Guo, Q.; Yu, Y.; Yin, Z. Review of the effects of vegetation patterns on soil erosion and sediment yield. Acta Ecol. 2017, 37, 4905–4912. [Google Scholar]
- Zhang, J.; Zhang, S.; Chen, S.; Liu, M. Effects of sparse rigid stem vegetation coverage on hydrodynamic characteristics of overland flow in a gentle slope area. Arab. J. Geosci. 2021, 14, 1445. [Google Scholar] [CrossRef]
- Wang, W.; Huai, W.; Zeng, Y.; Zhou, J. Analytical solution of velocity distribution for flow through submerged large deflection flexible vegetation. Appl. Math. Mech. 2015, 36, 107–120. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Liu, Y.; Liu, Y. Effects of farmland vegetation row direction on overland flow hydraulic characteristics. Hydrol. Res. 2018, 49, 1991–2001. [Google Scholar] [CrossRef]
- Ding, W.; Li, M. Effects of grass coverage and distribution patterns on erosion and overland flow hydraulic characteristics. Environ. Earth Sci. 2016, 75, 477. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, X.; Chen, L.; Li, B.; Liu, T.; Ai, B.; Yang, L.; Liu, B.; Chen, Q. Macrobenthic assemblage characteristics under stressed waters and ecological health assessment using AMBI and M-AMBI: A case study at the Xin’an River Estuary, Yantai, China. Acta Oceanol. Sin. 2018, 37, 77–86. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, J.; Huang, Y.; Wang, G.; Zhang, M. Effects of vegetation stems on hydraulics of overland flow under varying water discharges. Land Degrad. Dev. 2016, 27, 748–757. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Zhao, L.; Pan, X.; Lei, X.Z. Experimental study of the effects of different height flexible vegetation on hydraulic characteristics of overland flow. Mech. Eng. 2016, 38, 283–289. [Google Scholar]
- Luo, M.; Pan, C.; Peng, J.; Wang, L. Characteristics of the sediment transport process in vegetation hillslopes under different flow rates. Water 2023, 15, 2922. [Google Scholar] [CrossRef]
- Han, D.; Deng, J.; Gu, C.; Mu, X.; Gao, P.; Gao, J. Effect of shrub-grass vegetation coverage and slope gradient on runoff and sediment yield under simulated rainfall. Int. J. Sediment Res. 2021, 36, 29–37. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Jia, J.; Zhen, Q.; Zhang, X. Effect of vegetation on the flow pathways of steep hillslopes: Overland flow plot-scale experiments and their implications. Catena 2021, 204, 105438. [Google Scholar] [CrossRef]
- Peng, Q.; Liu, X.; Huang, E.; Yang, K. Experimental study on the influence of vegetation on the slope flow concentration time. Nat. Hazards 2019, 98, 751–763. [Google Scholar] [CrossRef]
- Zhang, K.; Jing, H.F.; Song, Y.T.; Li, C.G. Experimental study on flow characteristics in a flume with flexible vegetation. Yangtze River 2018, 49, 97–102. [Google Scholar]
- Tang, H.; Tian, Z.; Yan, J.; Yuan, S. Determining drag coefficients and their application in modelling of turbulent flow with submerged vegetation. Adv. Water Resour. 2014, 69, 134–145. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Ma, L.; Xue, M.H.; Sun, X.; Wang, F.X.; Li, H.Y.; Song, T.Y. Experimental study on hydraulic characteristics of overland flow under different surface roughness. J. Shaanxi Norm. Univ. (Nat. Sci. Ed.) 2023, 51, 1–10. [Google Scholar]
- Zhang, S.; Zhang, J.; Liu, Y.; Liu, Y.; Wang, Z. The effects of vegetation distribution pattern on overland flow. Water Environ. J. 2018, 32, 392–403. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Critical resistance affecting sub- to Super-Critical transition flow by vegetation. J. Earthq. Tsunami 2019, 13, 1950004. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, J.; Zhang, M.; Wang, F.; Zhang, T. Sediment deposition and overland flow hydraulics in simulated vegetative filter strips under varying vegetation covers. Hydrol. Process. 2016, 30, 163–175. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Liu, Y.; Liu, Y.; Li, G. The resistance effect of vegetation stem diameter on overland runoff under different slope gradients. Water Sci. Technol. 2018, 78, 2383–2391. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, S.; Wang, C.; Wang, W.; Ma, L. Influence of combined stem vegetation distribution and discretization on the hydraulic characteristics of overland flow. J. Clean. Prod. 2022, 376, 134188. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Yang, P.; Wang, Y. Experimental study of overland flow through rigid emergent vegetation with different densities and location arrangements. Water 2018, 10, 1638. [Google Scholar] [CrossRef]
- Cantalice, J.R.B.; Melo, R.O.; Silva, Y.J.A.B.; Cunha Filho, M.; Araújo, A.M.; Vieira, L.P.; Bezerra, S.A.; Barros, G.; Singh, V.P. Hydraulic roughness due to submerged, emergent and flexible natural vegetation in a semiarid alluvial channel. J. Arid Environ. 2015, 114, 1–7. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, Y.; Xu, S.; Ji, X.; Wang, S.; Ding, S. Relationships between riparian vegetation pattern and the hydraulic characteristics of upslope runoff. Sustainability 2019, 11, 2966. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, X.Y.; Tian, Y.; Zhang, X.; Fan, X.G.; Cui, Q.L. Experimental Study on the Response Characteristics of Flow-Sediment Transport on Slope to the Vegetation Coverage. J. Basic Sci. Eng. 2020, 28, 632–641. [Google Scholar]
- Huo, Y.P.; Zhu, B.B. Experimental Study on Impacts of Vegetation Patterns on Sediment Yield of Slope. Res. Soil Water Conserv. 2022, 29, 14–20. [Google Scholar]
- Wu, W.J.; Su, X.; Ye, W.L.; Wei, W.H.; Yang, T.; Feng, L.T. Lateral pressure in formation of saturated loess landslide—Case study of Heifangtai, Gansu Province. Chin. J. Geotech. Eng. 2018, 40, 135–140. [Google Scholar]
- Tao, H.; Lei, S.; Gong, L.; Shi, X.; Zhang, M.; Yang, G. Study on erosion and stability of the ecological slope. Front. Earth Sci. 2023, 10, 1071231. [Google Scholar] [CrossRef]
- Li, Y.B. Problems and countermeasures of comprehensive soil and water loss management in Yongjing county, Gansu province. Beijing Agric. 2015, 17, 69–70. [Google Scholar]
- Wu, F.C.; Shen, H.W.; Chou, Y.J. Variation of roughness coefficients for unsubmerged and submerged vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Crompton, O.; Katul, G.G.; Thompson, S. Resistance formulations in shallow overland flow along a hillslope covered with patchy vegetation. Water Resour. Res. 2020, 56, e2020WR027194. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, K.D.; Yang, M.Y.; Gao, Y.L.; Ma, X.L. Dynamics characteristics of rill flow on loess slope. Sci. Soil Water Conserv. 2016, 14, 45–51. [Google Scholar]
- Jiang, B.H.; Yang, K.J.; Cao, S.Y.; Chen, L. Modeling the velocity distribution in compound channels with vegetated floodplains based on the equivalent resistance. Shuili Xuebao 2012, 43, 20–26. [Google Scholar]
- Zeng, H.Y.; Huai, W.X.; Zhang, J.; Li, Q.B. Flow resistance of emerged rigid vegetations in open channels. Shuili Xuebao 2011, 42, 834–838+847. [Google Scholar]
- Zhao, X.; Chen, X.; Huang, J.; Wu, P.; Helmers, M.J. Effects of vegetation cover of natural grassland on runoff and sediment yield in loess hilly region of China. J. Sci. Food Agric. 2014, 94, 497–503. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, G.; Yi, L.; Zhang, P. Effects of patterned Artemisia capillaris on overland flow resistance under varied rainfall intensities in the Loess Plateau of China. J. Hydrol. Hydromech. 2014, 62, 334–342. [Google Scholar] [CrossRef]
- Rehman, O.U.; Rashid, M.; Kausar, R.; Alvi, S.; Hussain, R. Slope gradient and vegetation cover effects on the runoff and sediment yield in hillslope agriculture. Turk. J. Agric. Food Sci. Technol. 2015, 3, 478–483. [Google Scholar] [CrossRef]
- Madi, H.; Mouzai, L.; Bouhadef, M. Plants Cover Effects on Overland Flow and on Soil Erosion under Simulated Rainfall Intensity. Int. J. Environ. Ecol. Eng. 2013, 7, 561–565. [Google Scholar]
- An, J.; Zheng, F.; Lu, J.; Li, G. Investigating the role of raindrop impact on hydrodynamic mechanism of soil erosion under simulated rainfall conditions. Soil Sci. 2012, 177, 517–526. [Google Scholar] [CrossRef]
- Xiao, P.Q.; Yao, W.Y.; Shen, Z.Z. Experimental study on erosion process and hydrodynamics mechanism of alfalfa grassland. Shuili Xuebao 2011, 42, 232–237. [Google Scholar]
- Zhang, G.; Hu, J. Effects of patchy distributed Artemisia capillaris on overland flow hydrodynamic characteristics. Int. Soil Water Conserv. Res. 2019, 7, 81–88. [Google Scholar] [CrossRef]
- Ren, K.M.; Wei, W.; Zhao, X.N.; Feng, T.J.; Chen, D.; Yu, Y. Simulation of the effect of slope vegetation cover and allocation pattern on water erosion in the loess hilly region. Acta Ecol. Sin. 2018, 38, 8031–8039. [Google Scholar]
- Shen, H.; Zheng, F.; Wen, L.; Han, Y.; Hu, W. Impacts of rainfall intensity and slope gradient on rill erosion processes at loessial hillslope. Soil Tillage Res. 2016, 155, 429–436. [Google Scholar] [CrossRef]
- Igwe, P.U.; Ezeukwu, J.C.; Edoka, N.E. A review of vegetation cover as a natural factor to soil erosion. Int. J. Rural. Dev. Environ. Health Res. 2017, 1, 21–28. [Google Scholar]






| Natural Moisture Content (%) | Dry Density (g/cm3) | Relative Particle Density | Plastic Limit (%) | Liquid Limit (%) | Soil Particle Size <0.005 mm (%) | Soil Particle Size 0.005~0.05 mm (%) | Soil Particle Size >0.05 mm (%) |
|---|---|---|---|---|---|---|---|
| 3.2 | 1.29 | 2.63 | 17.8 | 23.7 | 16 | 60 | 24 |
| Slope | Regression Equation | R2 |
|---|---|---|
| 2° | h = 1.466Q0.642 | 0.993 |
| 4° | h = 1.500Q0.672 | 0.986 |
| 6° | h = 1.465Q0.634 | 0.993 |
| Slope | Regression Equation | R2 |
|---|---|---|
| 2° | v = 0.076ln(Q + 0.364) + 0.213 | 0.976 |
| 4° | v = 0.345ln(Q + 3.9) − 0.327 | 0.994 |
| 6° | v = 0.093ln(Q + 0.334) + 0.255 | 0.993 |
| Independent Variable | Implicit Variable | Combination | DF | SS | MS | f |
|---|---|---|---|---|---|---|
| Flow Discharge | Water Depth | RF | 3 | 0.016 | 0.008 | 213.333 |
| IS | 3 | 0.029 | 0.015 | 316.814 | ||
| IT | 3 | 0.032 | 0.016 | 141.833 | ||
| BS | 3 | 0.037 | 0.019 | 277.715 | ||
| Flow Velocity | RF | 5 | 0.068 | 0.010 | 262.050 | |
| IS | 5 | 0.036 | 0.005 | 112.018 | ||
| IT | 5 | 0.051 | 0.007 | 65.565 | ||
| BS | 5 | 0.055 | 0.008 | 115.573 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, H.; Wang, F.; Shi, X.; Bu, S.; Bao, Z.; Zhang, D.; Xiong, L. Research on the Impact of Using a Combination of Rigid and Flexible Vegetation on Slope Hydrological Properties in Loess Regions. Water 2024, 16, 1140. https://doi.org/10.3390/w16081140
Tao H, Wang F, Shi X, Bu S, Bao Z, Zhang D, Xiong L. Research on the Impact of Using a Combination of Rigid and Flexible Vegetation on Slope Hydrological Properties in Loess Regions. Water. 2024; 16(8):1140. https://doi.org/10.3390/w16081140
Chicago/Turabian StyleTao, Hu, Fucui Wang, Xi Shi, Shilong Bu, Ziming Bao, Dezhi Zhang, and Lifeng Xiong. 2024. "Research on the Impact of Using a Combination of Rigid and Flexible Vegetation on Slope Hydrological Properties in Loess Regions" Water 16, no. 8: 1140. https://doi.org/10.3390/w16081140






