Flood Water Depth Prediction with Convolutional Temporal Attention Networks
Abstract
1. Introduction
- We propose a deep learning approach that predicts water depths at high spatial resolution for a two-hour lead time, given elevation data, water depth at starting time, and rainfall intensity values for the forecast duration.
- We introduce the new, large-scale pluvial flood dataset SwissFlood (which is available for download at https://doi.org/10.5281/zenodo.7797844) and make it publicly available. It contains pluvial floods for 100 catchments in Switzerland generated with a hydrodynamic flood model [17]. The rainfall events were extracted from rainfall observation data of the last forty years collected in Switzerland by MeteoSwiss [18].
- In our study, we aim to analyse the ability of our data-driven model to generalise the prediction of future water depth across catchments and rainfall events. All rainfall events used in this study are unique. We provide a quantitative as well as a qualitative analysis of our approach to evaluate its performance.
2. Related Work
3. Datasets
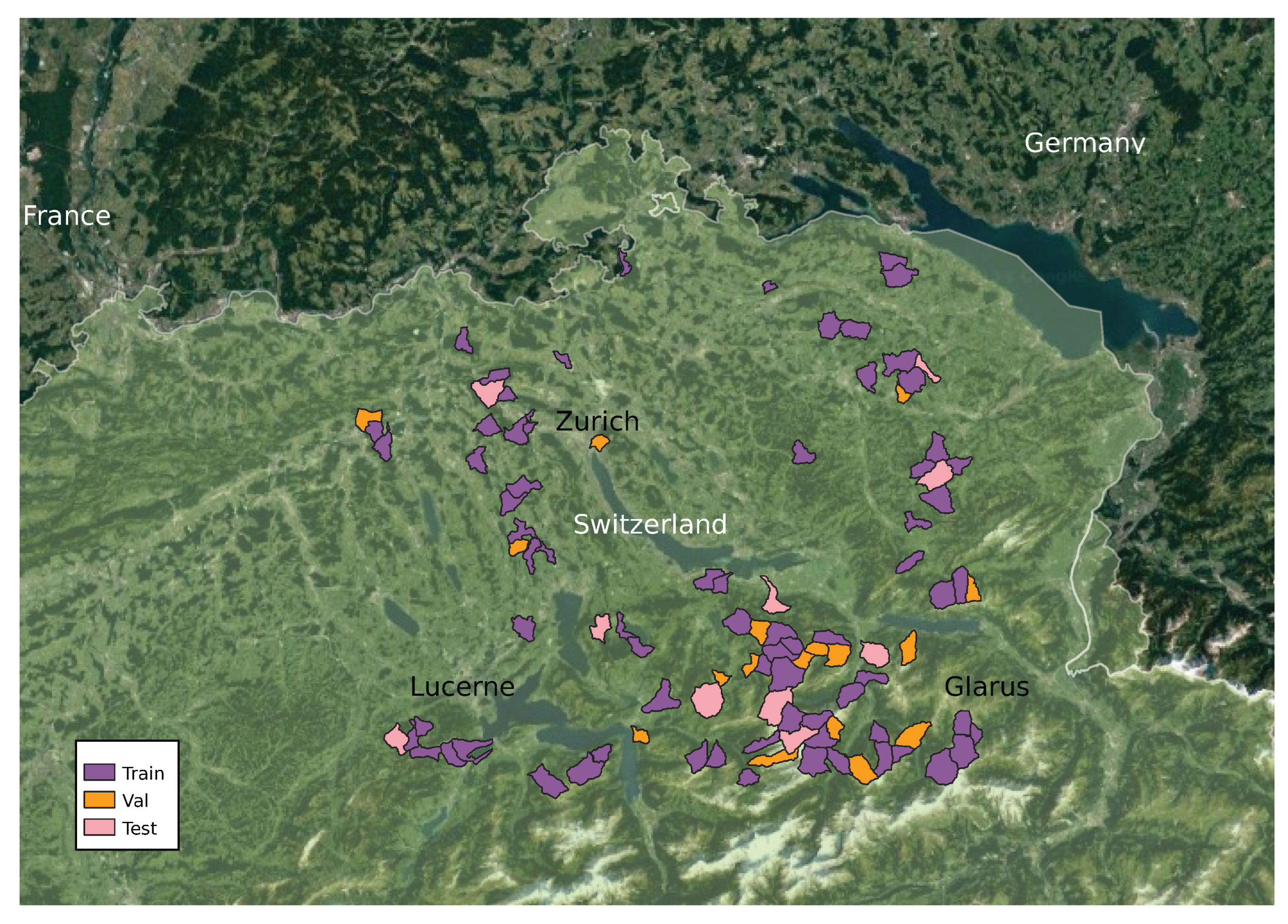
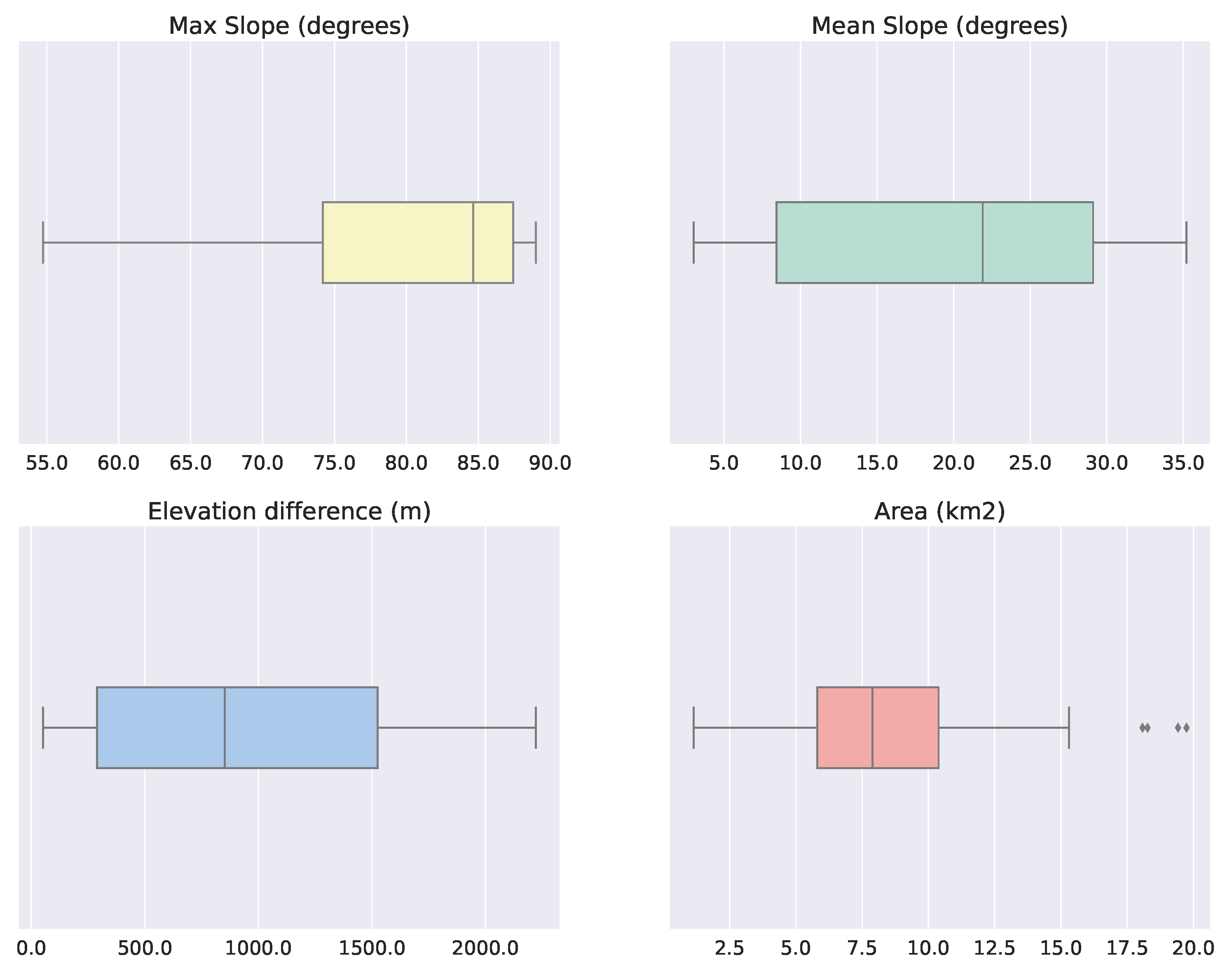
3.1. Catchments
3.2. Rainfall Data
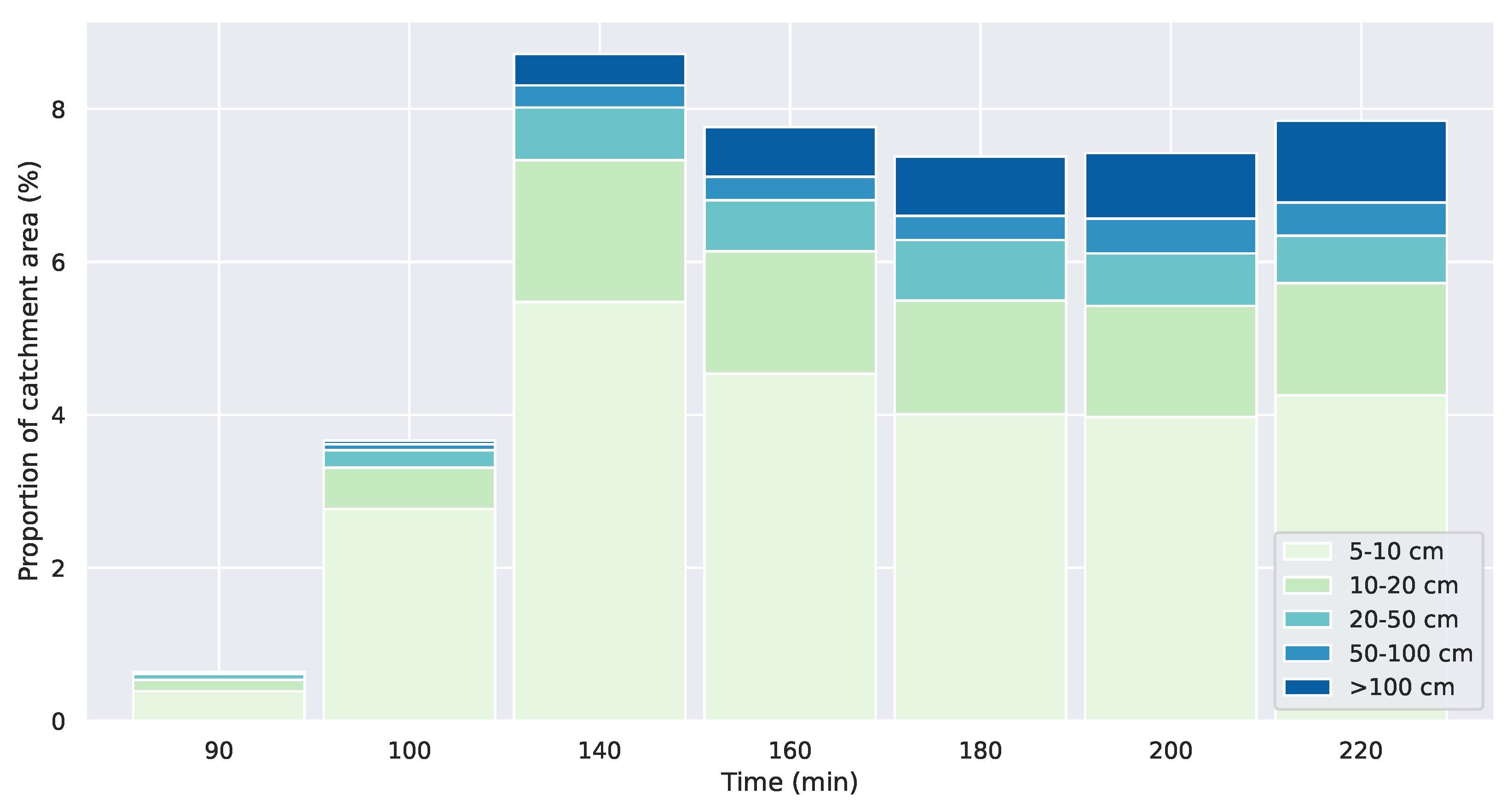
3.3. Water Depth
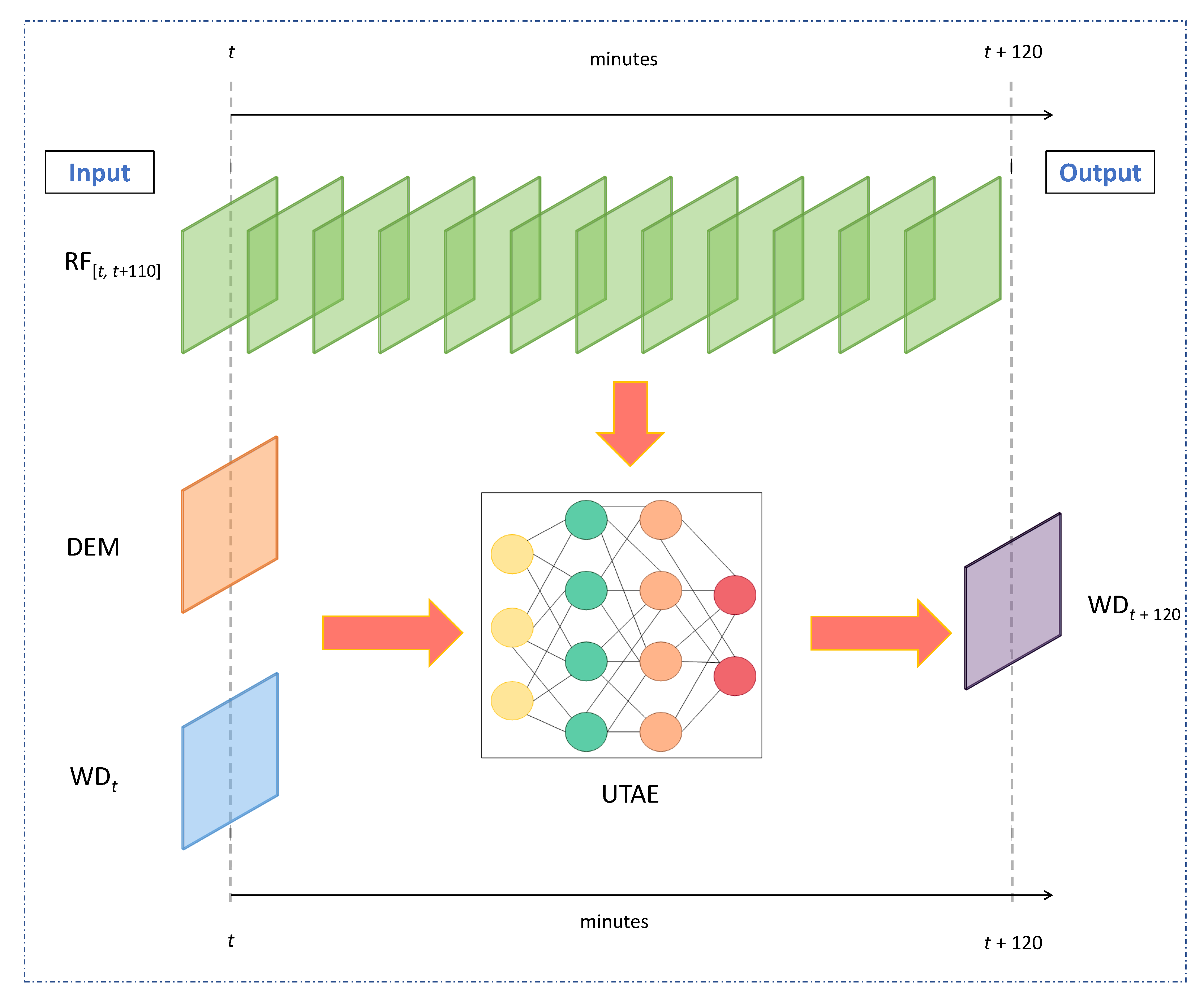
4. Methodology
- A raster map of terrain elevations for catchment c.
- Water depth at time-step for catchment c.
- Rainfall intensity values for the two-hour time window between starting time t and target time . The intensity is discretised to steps of 10 min, i.e., the input consists of 12 rainfall values .
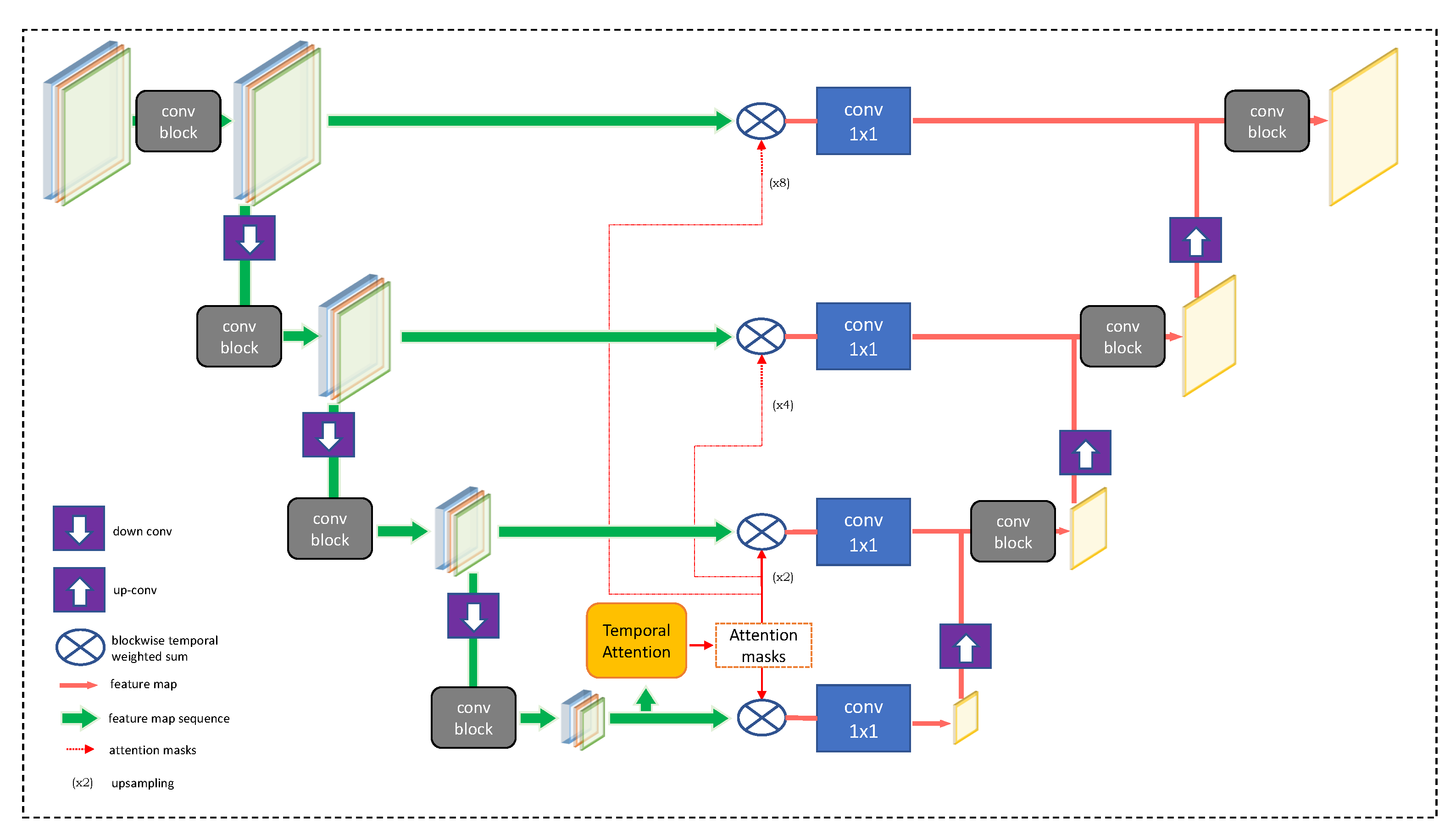
4.1. Deep Learning Model
4.2. Model Training
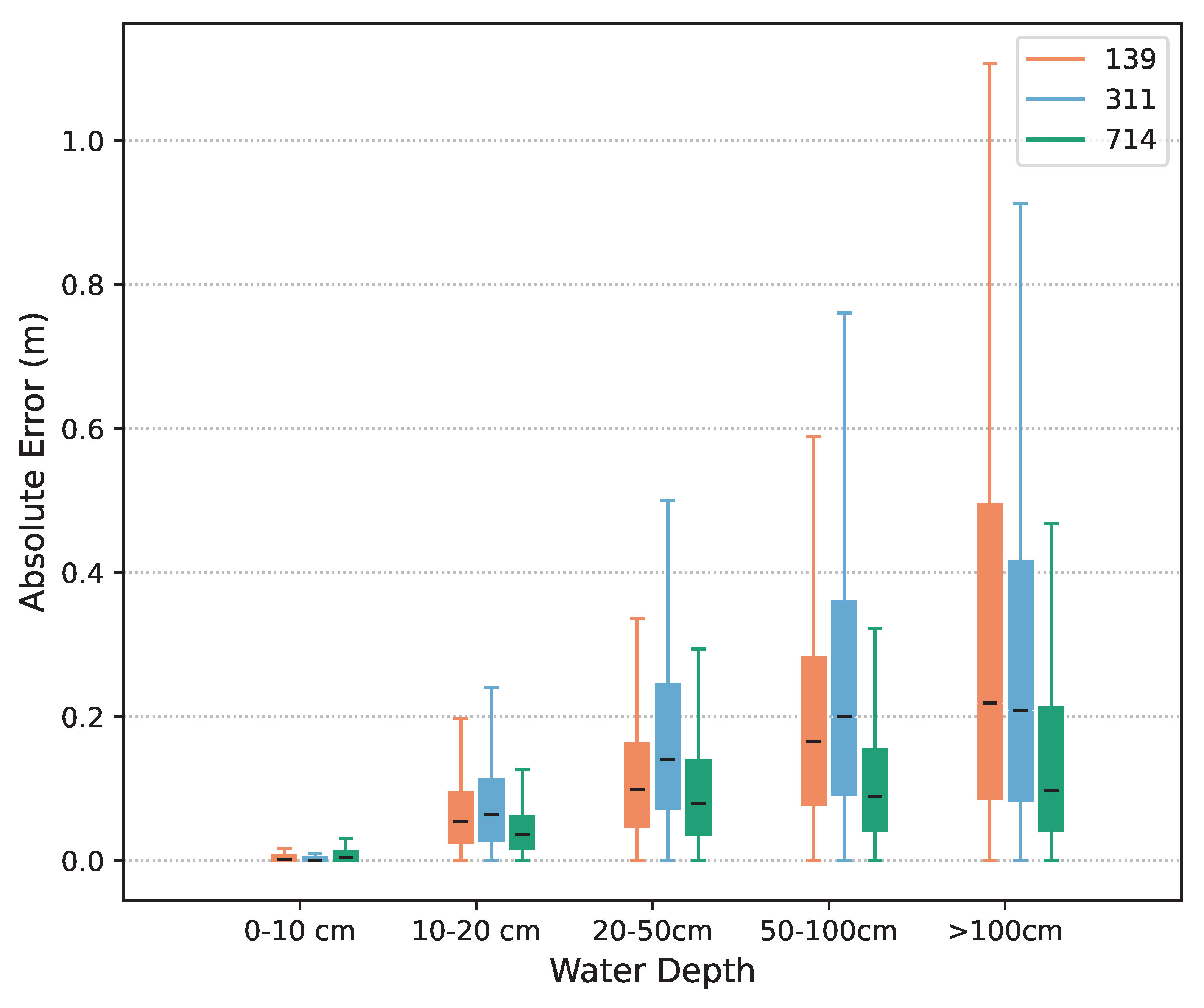
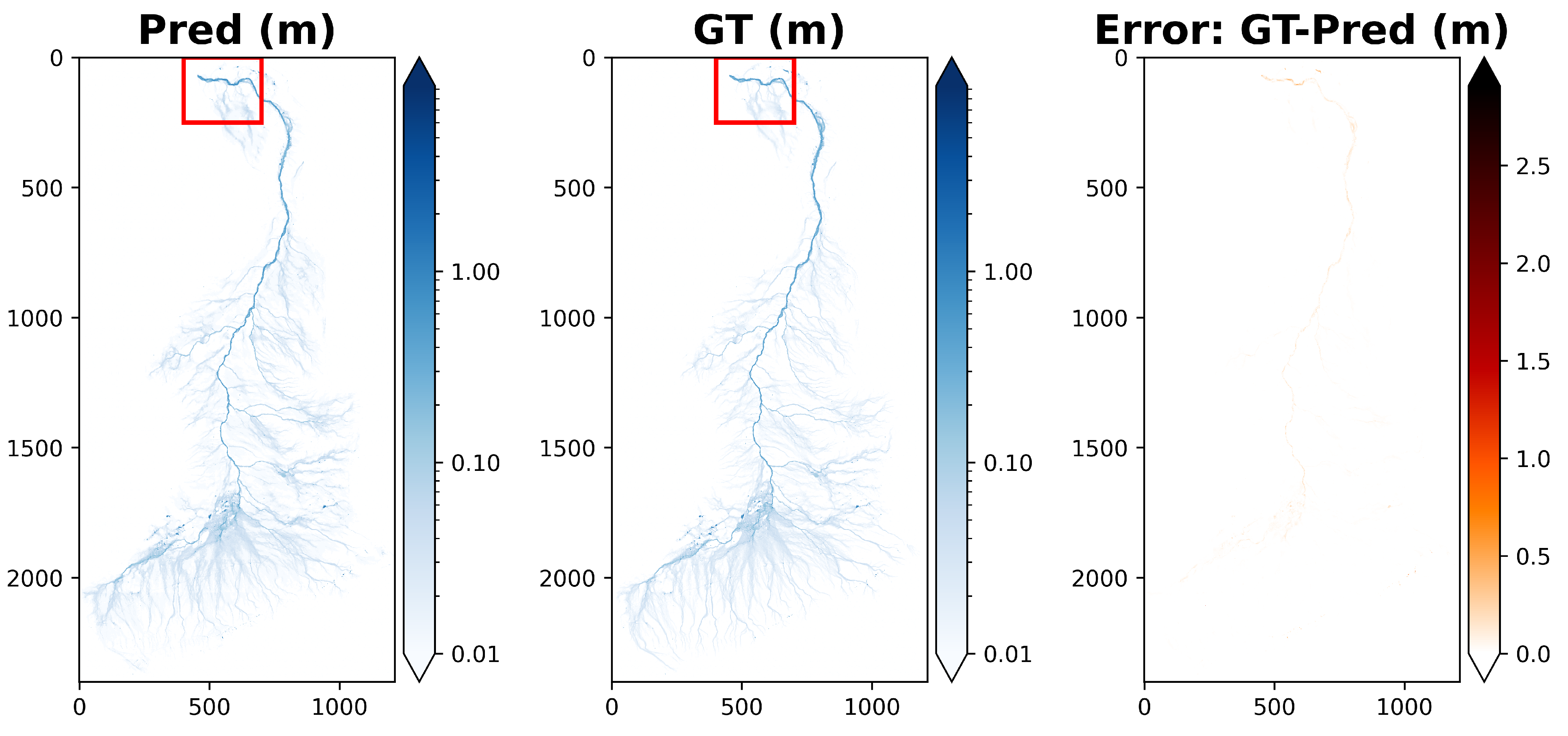
5. Results
Ablation Studies
6. Discussion and Conclusions
6.1. Limitations of the Proposed Approach
6.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- do Lago, C.A.; Giacomoni, M.H.; Bentivoglio, R.; Taormina, R.; Gomes, M.N.; Mendiondo, E.M. Generalizing rapid flood predictions to unseen urban catchments with conditional generative adversarial networks. J. Hydrol. 2023, 618, 129276. [Google Scholar] [CrossRef]
- UNESCO. World Water Assessment Programme. In The United Nations World Water Development Report 2020: Water and Climate Change; UNESCO: Paris, France, 2020. [Google Scholar]
- Bhola, P.K.; Leandro, J.; Disse, M. Framework for Offline Flood Inundation Forecasts for Two-Dimensional Hydrodynamic Models. Geosciences 2018, 8, 346. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A deep convolutional neural network model for rapid prediction of fluvial flood inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD–Topographic deep learning for predicting urban pluvial flood water depth. J. Hydrol. 2021, 603, 126898. [Google Scholar] [CrossRef]
- Hu, R.; Fang, F.; Pain, C.; Navon, I. Rapid spatio-temporal flood prediction and uncertainty quantification using a deep learning method. J. Hydrol. 2019, 575, 911–920. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Guo, Z.; Leitão, J.P.; Simões, N.E.; Moosavi, V. Data-driven flood emulation: Speeding up urban flood predictions by deep convolutional neural networks. J. Flood Risk Manag. 2021, 14, e12684. [Google Scholar] [CrossRef]
- Xie, S.; Wu, W.; Mooser, S.; Wang, Q.; Nathan, R.; Huang, Y. Artificial neural network based hybrid modeling approach for flood inundation modeling. J. Hydrol. 2021, 592, 125605. [Google Scholar] [CrossRef]
- Yokoya, N.; Yamanoi, K.; He, W.; Baier, G.; Adriano, B.; Miura, H.; Oishi, S. Breaking Limits of Remote Sensing by Deep Learning From Simulated Data for Flood and Debris-Flow Mapping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Cui, L.; Wang, J.; Zuo, D.; Peng, D. Improving urban flood susceptibility mapping using transfer learning. J. Hydrol. 2021, 602, 126777. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Moosavi, V.; Leitão, J.P. Data-driven rapid flood prediction mapping with catchment generalizability. J. Hydrol. 2022, 609, 127726. [Google Scholar] [CrossRef]
- Lin, Q.; Leandro, J.; Wu, W.; Bhola, P.; Disse, M. Prediction of Maximum Flood Inundation Extents with Resilient Backpropagation Neural Network: Case Study of Kulmbach. Front. Earth Sci. 2020, 8, 332. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, W.; Nathan, R.; Wang, Q.J. A rapid flood inundation modelling framework using deep learning with spatial reduction and reconstruction. Environ. Model. Softw. 2021, 143, 105112. [Google Scholar] [CrossRef]
- Guidolin, M.; Chen, A.S.; Ghimire, B.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Model. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef]
- MeteoSwiss. Federal Office for Meteorology and Climatology. 2023. Available online: https://www.meteoswiss.admin.ch/ (accessed on 17 January 2024).
- Garnot, V.S.F.; Landrieu, L. Panoptic Segmentation of Satellite Image Time Series With Convolutional Temporal Attention Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 4872–4881. [Google Scholar]
- Jafarzadegan, K.; Abbaszadeh, P.; Moradkhani, H. Sequential data assimilation for real-time probabilistic flood inundation mapping. Hydrol. Earth Syst. Sci. 2021, 25, 4995–5011. [Google Scholar] [CrossRef]
- Bentivoglio, R.; Isufi, E.; Jonkman, S.N.; Taormina, R. Deep learning methods for flood mapping: A review of existing applications and future research directions. Hydrol. Earth Syst. Sci. 2022, 26, 4345–4378. [Google Scholar] [CrossRef]
- Wang, Y.; Karimi, H.A. Impact of spatial distribution information of rainfall in runoff simulation using deep learning method. Hydrol. Earth Syst. Sci. 2022, 26, 2387–2403. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Kröhnert, M.; Eltner, A. Versatile Mobile and Stationary Low-Cost Approaches for Hydrological Measurements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 543–550. [Google Scholar] [CrossRef]
- Ning, H.; Li, Z.; Hodgson, M.E.; Wang, C.S. Prototyping a Social Media Flooding Photo Screening System Based on Deep Learning. ISPRS Int. J. Geo-Inf. 2020, 9, 104. [Google Scholar] [CrossRef]
- Chaudhary, P.; D’Aronco, S.; Moy de Vitry, M.; Leitão, J.P.; Wegner, J.D. Flood-Water Level Estimation from Social Media Images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-2/W5, 5–12. [Google Scholar] [CrossRef]
- Chaudhary, P.; D’Aronco, S.; Leitão, J.; Schindler, K.; Wegner, J. Water level prediction from social media images with a multi-task ranking approach. ISPRS J. Photogramm. Remote Sens. 2020, 167, 252–262. [Google Scholar] [CrossRef]
- Quan, K.A.C.; Nguyen, V.T.; Nguyen, T.C.; Nguyen, T.V.; Tran, M.T. Flood Level Prediction via Human Pose Estimation from Social Media Images. In Proceedings of the 2020 International Conference on Multimedia Retrieval, ICMR ’20, New York, NY, USA, 8–11 June 2020; pp. 479–485. [Google Scholar]
- Moy de Vitry, M.; Kramer, S.; Wegner, J.D.; Leitão, J.P. Scalable flood level trend monitoring with surveillance cameras using a deep convolutional neural network. Hydrol. Earth Syst. Sci. 2019, 23, 4621–4634. [Google Scholar] [CrossRef]
- Lütjens, B.; Leshchinskiy, B.; Requena-Mesa, C.; Chishtie, F.; Rodríguez, N.D.; Boulais, O.; Piña, A.; Newman, D.; Lavin, A.; Gal, Y.; et al. Physics-informed GANs for Coastal Flood Visualization. arXiv 2020, arXiv:2010.08103. [Google Scholar]
- Lütjens, B.; Leshchinskiy, B.; Requena-Mesa, C.; Chishtie, F.; Rodríguez, N.D.; Boulais, O.; Sankaranarayanan, A.; Piña, A.; Gal, Y.; Raïssi, C.; et al. Physically Consistent Generative Adversarial Networks for Coastal Flood Visualization. arXiv 2021, arXiv:2104.04785. [Google Scholar]
- Bowes, B.D.; Tavakoli, A.; Wang, C.; Heydarian, A.; Behl, M.; Beling, P.A.; Goodall, J.L. Flood mitigation in coastal urban catchments using real-time stormwater infrastructure control and reinforcement learning. J. Hydroinform. 2020, 23, 529–547. [Google Scholar] [CrossRef]
- Chaudhary, P.; Leitão, J.P.; Donauer, T.; D’Aronco, S.; Perraudin, N.; Obozinski, G.; Perez-Cruz, F.; Schindler, K.; Wegner, J.D.; Russo, S. Flood Uncertainty Estimation Using Deep Ensembles. Water 2022, 14, 2980. [Google Scholar] [CrossRef]
- Seleem, O.; Ayzel, G.; Bronstert, A.; Heistermann, M. Transferability of data-driven models to predict urban pluvial flood water depth in Berlin, Germany. Nat. Hazards Earth Syst. Sci. 2023, 23, 809–822. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Xu, D.; Dwelle, M.C.; Sargsyan, K.; Wright, D.B.; Katopodes, N.; Kim, J.; Tran, V.N.; Warnock, A.; Fatichi, S.; et al. Breaking Down the Computational Barriers to Real-Time Urban Flood Forecasting. Geophys. Res. Lett. 2021, 48, e2021GL093585. [Google Scholar] [CrossRef]
- Tran, H.; Leonarduzzi, E.; De la Fuente, L.; Hull, R.B.; Bansal, V.; Chennault, C.; Gentine, P.; Melchior, P.; Condon, L.E.; Maxwell, R.M. Development of a Deep Learning Emulator for a Distributed Groundwater-Surface Water Model: ParFlow-ML. Water 2021, 13, 3393. [Google Scholar] [CrossRef]
- Muñoz, D.F.; Muñoz, P.; Moftakhari, H.; Moradkhani, H. From local to regional compound flood mapping with deep learning and data fusion techniques. Sci. Total. Environ. 2021, 782, 146927. [Google Scholar] [CrossRef]
- Kao, I.F.; Liou, J.Y.; Lee, M.H.; Chang, F.J. Fusing stacked autoencoder and long short-term memory for regional multistep-ahead flood inundation forecasts. J. Hydrol. 2021, 598, 126371. [Google Scholar] [CrossRef]
- Chang, D.L.; Yang, S.H.; Hsieh, S.L.; Wang, H.J.; Yeh, K.C. Artificial Intelligence Methodologies Applied to Prompt Pluvial Flood Estimation and Prediction. Water 2020, 12, 3552. [Google Scholar] [CrossRef]
- Lin, Q.; Leandro, J.; Gerber, S.; Disse, M. Multistep Flood Inundation Forecasts with Resilient Backpropagation Neural Networks: Kulmbach Case Study. Water 2020, 12, 3568. [Google Scholar] [CrossRef]
- Zahura, F.T.; Goodall, J.L.; Sadler, J.M.; Shen, Y.; Morsy, M.M.; Behl, M. Training Machine Learning Surrogate Models from a High-Fidelity Physics-Based Model: Application for Real-Time Street-Scale Flood Prediction in an Urban Coastal Community. Water Resour. Res. 2020, 56, e2019WR027038. [Google Scholar] [CrossRef]
- Ghimire, B.; Chen, A.S.; Guidolin, M.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. Formulation of a fast 2D urban pluvial flood model using a cellular automata approach. J. Hydroinform. 2012, 15, 676–686. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Yang, X. An Overview of the Attention Mechanisms in Computer Vision. J. Physics Conf. Ser. 2020, 1693, 012173. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Garnot, V.S.F.; Landrieu, L. Lightweight Temporal Self-Attention for Classifying Satellite Image Time Series. In Proceedings of the Advanced Analytics and Learning on Temporal Data: 5th ECML PKDD Workshop, AALTD 2020, Ghent, Belgium, 18 September 2020. [Google Scholar]
- Agarap, A.F. Deep Learning using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 1 June 2015; Volume 37, pp. 448–456. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Shalev, G.; El-Yaniv, R.; Klotz, D.; Kratzert, F.; Metzger, A.; Nevo, S. Accurate Hydrologic Modeling Using Less Information. arXiv 2019, arXiv:1911.09427. [Google Scholar]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ciampiconi, L.; Elwood, A.; Leonardi, M.; Mohamed, A.; Rozza, A. A survey and taxonomy of loss functions in machine learning. arXiv 2023, arXiv:2301.05579. [Google Scholar]
- Pugliese, R.; Regondi, S.; Marini, R. Machine learning-based approach: Global trends, research directions, and regulatory standpoints. Data Sci. Manag. 2021, 4, 19–29. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Cortés-Andrés, J.; Camps-Valls, G.; Sippel, S.; Székely, E.; Sejdinovic, D.; Diaz, E.; Pérez-Suay, A.; Li, Z.; Mahecha, M.; Reichstein, M. Physics-aware nonparametric regression models for Earth data analysis. Environ. Res. Lett. 2022, 17, 054034. [Google Scholar] [CrossRef]
- Marcus, G.F. Deep Learning: A Critical Appraisal. arXiv 2018, arXiv:1801.00631. [Google Scholar]


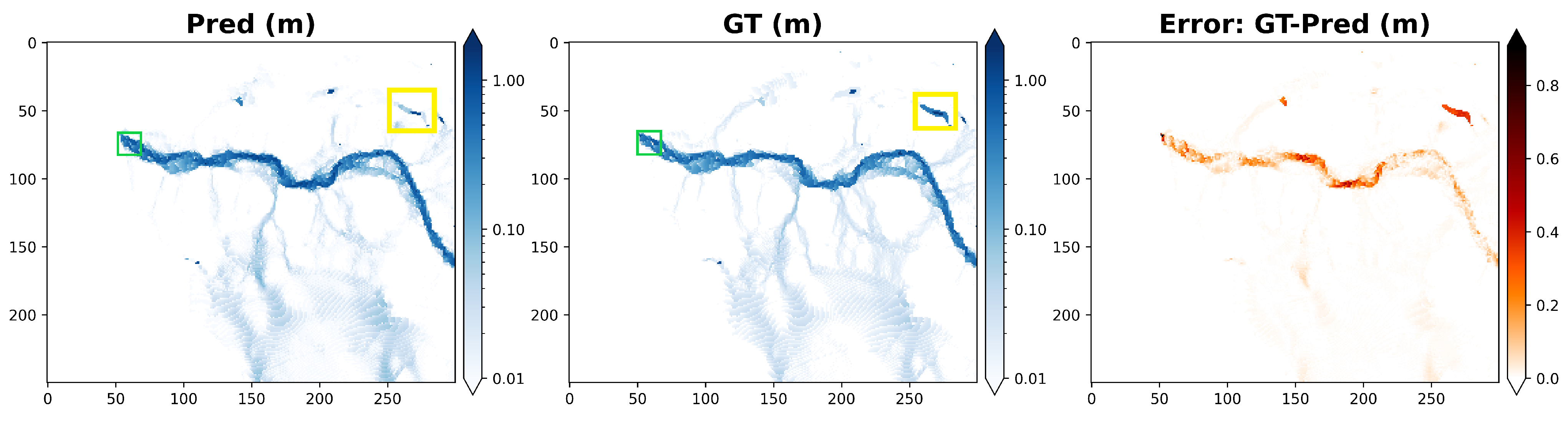

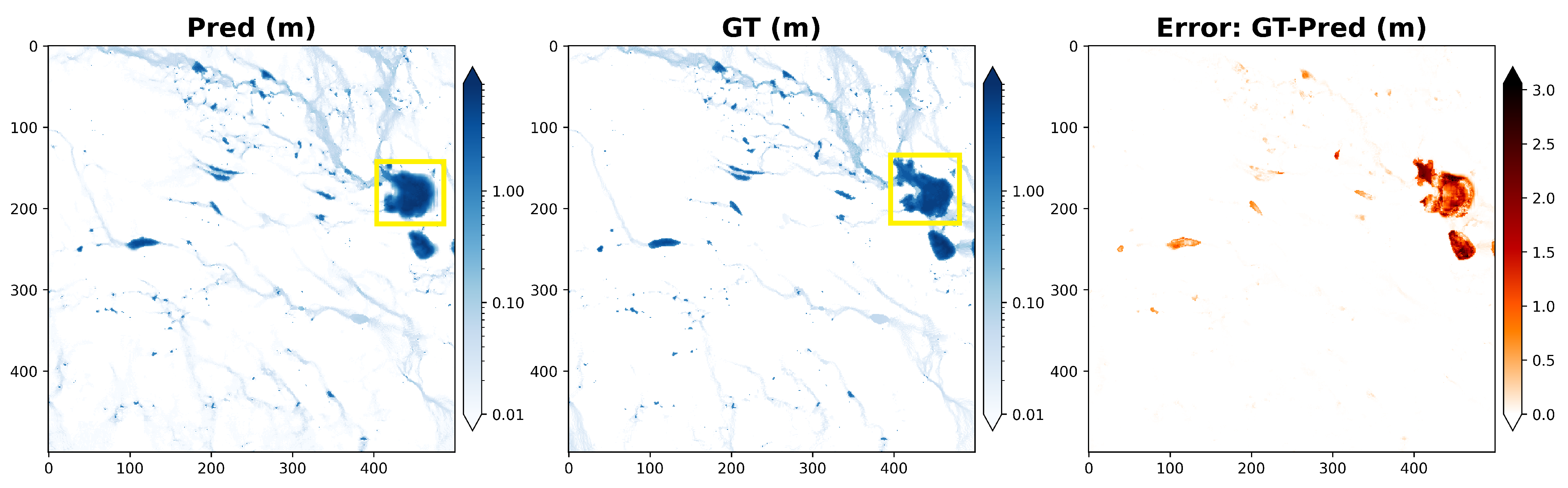
| Mean Absolute Errors (cm) | |||||||
|---|---|---|---|---|---|---|---|
| all | ≥5 | ≥10 | ≥20 | ≥50 | ≥100 | ||
| Baseline-1 | unseen | 1.61 | 28.29 | 46.75 | 67.54 | 97.37 | 117.82 |
| seen | 1.45 | 21.15 | 35.51 | 54.87 | 86.60 | 105.35 | |
| Baseline-2 | unseen | 2.40 | 27.33 | 44.41 | 63.51 | 91.65 | 112.05 |
| seen | 2.07 | 20.28 | 33.53 | 51.34 | 81.55 | 100.25 | |
| Baseline-3 | unseen | 2.35 | 27.91 | 46.09 | 66.65 | 96.78 | 117.85 |
| seen | 2.05 | 20.70 | 34.90 | 54.05 | 86.18 | 105.74 | |
| Ours | unseen | 1.18 | 17.99 | 28.99 | 40.79 | 57.06 | 67.76 |
| seen | 0.75 | 7.50 | 11.81 | 16.72 | 23.59 | 26.86 | |
| Mean Absolute Errors (cm) | |||||||
|---|---|---|---|---|---|---|---|
| All | ≥5 | ≥10 | ≥20 | ≥50 | ≥100 | ||
| NSE | unseen | 1.56 | 23.16 | 37.49 | 53.61 | 78.09 | 97.58 |
| L1 | unseen | 1.47 | 24.7 | 40.53 | 58.46 | 85.02 | 106.03 |
| L2 | unseen | 1.70 | 24.6 | 39.47 | 56.74 | 83.93 | 105.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhary, P.; Leitão, J.P.; Schindler, K.; Wegner, J.D. Flood Water Depth Prediction with Convolutional Temporal Attention Networks. Water 2024, 16, 1286. https://doi.org/10.3390/w16091286
Chaudhary P, Leitão JP, Schindler K, Wegner JD. Flood Water Depth Prediction with Convolutional Temporal Attention Networks. Water. 2024; 16(9):1286. https://doi.org/10.3390/w16091286
Chicago/Turabian StyleChaudhary, Priyanka, João P. Leitão, Konrad Schindler, and Jan Dirk Wegner. 2024. "Flood Water Depth Prediction with Convolutional Temporal Attention Networks" Water 16, no. 9: 1286. https://doi.org/10.3390/w16091286
APA StyleChaudhary, P., Leitão, J. P., Schindler, K., & Wegner, J. D. (2024). Flood Water Depth Prediction with Convolutional Temporal Attention Networks. Water, 16(9), 1286. https://doi.org/10.3390/w16091286







