CO2 is Dominant Greenhouse Gas Emitted from Six Hydropower Reservoirs in Southeastern United States during Peak Summer Emissions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
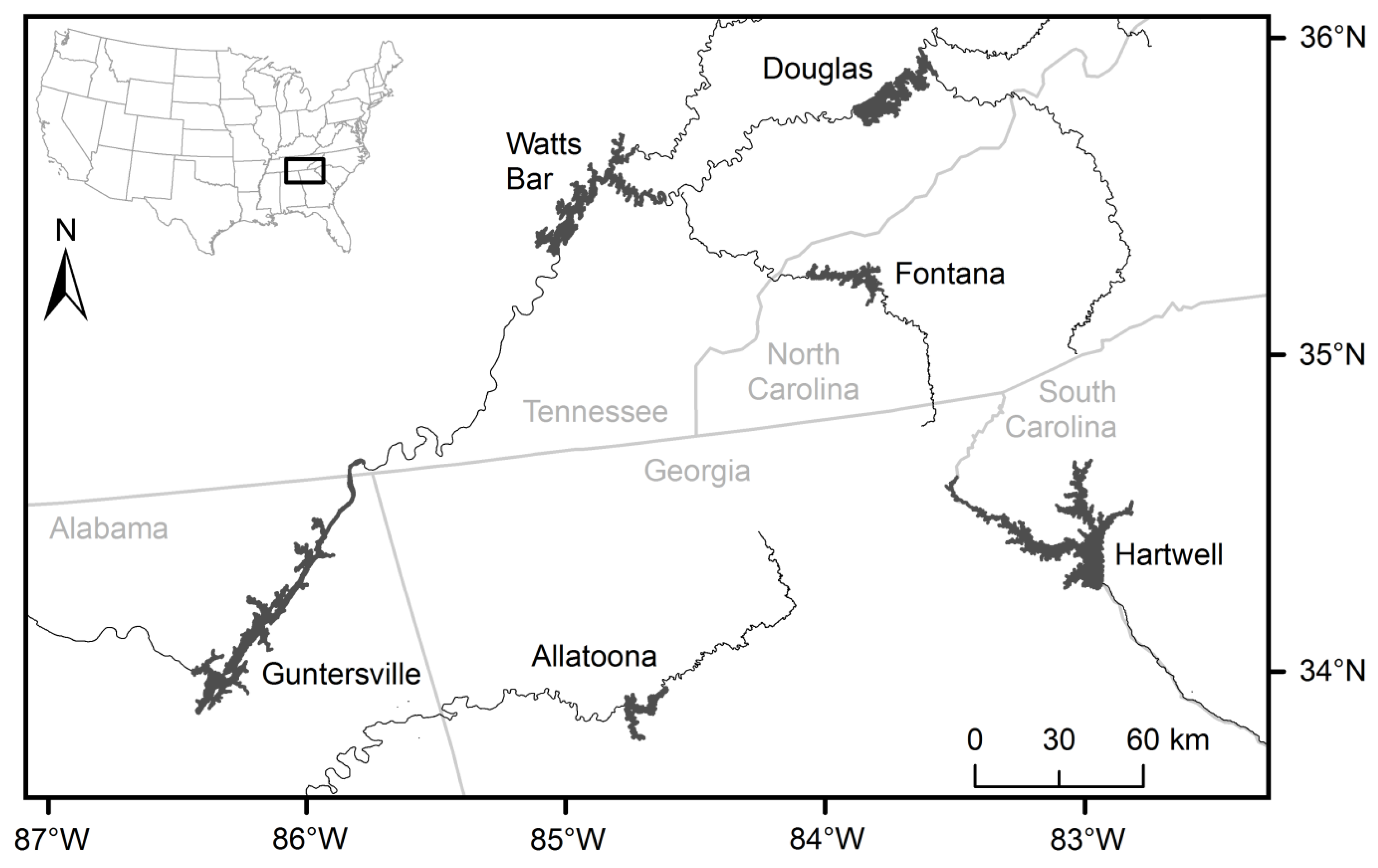
| Reservoir | Year Constructed | Surface Area (km2) | Percent Area in Coves | Volume (106 m3) | Mean Depth (m) | Shoreline Development Index 1 | Mean Annual Flow (m3 s−1) | Residence Time (day) |
|---|---|---|---|---|---|---|---|---|
| Allatoona | 1949 | 49 | 63 | 453 | 9.2 | 17.6 | 58 | 36 |
| Douglas | 1943 | 115 | 41 | 1334 | 11.6 | 22.6 | 254 | 91 |
| Fontana | 1944 | 43 | 44 | 1780 | 41.4 | 16.1 | 123 | 180 |
| Guntersville | 1939 | 279 | 49 | 1256 | 4.5 | 24.2 | 1397 | 14 |
| Hartwell | 1962 | 226 | 48 | 3145 | 13.9 | 29.0 | 161 | 56 |
| Watts Bar | 1942 | 176 | 46 | 1396 | 7.9 | 26.1 | 964 | 21 |
2.2. Diffusive Emissions Measurements
2.3. Measurements of Dissolved Gases in Water
2.4. Ebullition Measurements
2.5. Other Water Quality Factors
2.6. Pathway Emissions Calculations
3. Results
3.1. Water Quality and Wind Speed
| Reservoir | Profile Temperature Range (°C) | Profile DO Range (mg·L−1) | Mean Secchi Depth (m) | Mixed Layer Depth (m) | Mean Chlorophyll a (µg·L−1) | Mean Wind Speed (m·s−1) |
|---|---|---|---|---|---|---|
| Allatoona | 17.9–26.6 | 0.2–6.6 | 1.92 | 15 | 4.4 | 2.0 |
| Douglas | 18.1–28.8 | 0.1–9.4 | 2.14 | 9 | 3.7 | 1.4 |
| Fontana | 12.5–26.3 | 2.4–8.6 | 3.95 | 13 | 5.9 | 1.0 |
| Guntersville | 20.8–26.5 | 6.0–8.7 | 1.37 | all | 1.8 | 1.5 |
| Hartwell | 11.4–28.5 | 0.2–8.2 | 3.43 | 13 | 9.5 | 1.9 |
| Watts Bar | 24.1–27.7 | 0.6–10.0 | 1.45 | all | 2.3 | 3.0 |

3.2. Gas Concentrations and Emission Rates


| Reservoir | Diffusion (kg·day−1) | Ebullition (kg·day−1) | Tailwater (kg·day−1) | Total (kg·day−1) | Total (mg·m−2·day−1) |
|---|---|---|---|---|---|
| CO2 | |||||
| Allatoona | 80,200 | 13 | 38,064 | 118,277 | 2414 |
| Douglas | 78,235 | 3 | 87,844 | 166,082 | 1444 |
| Fontana | 28,192 | 2 | 14,546 | 42,740 | 994 |
| Guntersville | 315,943 | 114 | 185,094 | 501,151 | 1796 |
| Hartwell | 213,013 | 6 | 50,844 | 263,863 | 1168 |
| Watts Bar | 172,422 | 8 | 313,372 | 485,802 | 2760 |
| CH4 | |||||
| Allatoona | 678 | 767 | 7708 | 9153 | 187 |
| Douglas | 874 | 0 | 3704 | 4578 | 40 |
| Fontana | 251 | 0 | 0 | 251 | 6 |
| Guntersville | 1495 | 3834 | 446 | 5775 | 21 |
| Hartwell | 5151 | 47 | 0 | 5198 | 23 |
| Watts Bar | 1156 | 170 | 0 | 1326 | 8 |
3.3. Reservoir-Wide Emissions
3.4. Contributing Factors
| Parameter | CO2 Diffusion | CO2 Ebullition | CO2 Tailwater | CO2 Total | CH4 Diffusion | CH4 Ebullition | CH4 Tailwater | CH4 Total |
|---|---|---|---|---|---|---|---|---|
| Minimum temperature | 0.28 | 0.36 | 0.89 | 0.84 | -0.57 | 0.32 | 0.06 | 0.03 |
| Maximum temperature | −0.39 | −0.63 | 0.09 | −0.13 | 0.41 | −0.60 | −0.24 | −0.24 |
| Minimum DO | 0.00 | 0.72 | −0.17 | −0.13 | −0.50 | 0.43 | −0.35 | −0.32 |
| Maximum DO | −0.73 | −0.43 | 0.50 | 0.02 | −0.50 | −0.65 | −0.78 | −0.83 |
| Secchi depth | −0.48 | −0.55 | −0.71 | −0.80 | 0.37 | −0.54 | −0.24 | −0.24 |
| Mean chlorophyll a | −0.18 | −0.50 | −0.68 | −0.62 | 0.83 | −0.41 | −0.07 | −0.03 |
| Surface area | −0.02 | 0.32 | 0.06 | 0.04 | 0.13 | 0.08 | −0.55 | −0.47 |
| Percent main channel by area | −0.97 | −0.61 | 0.01 | −0.49 | −0.33 | −0.84 | −0.83 | −0.88 |
| Volume | −0.52 | −0.53 | −0.45 | −0.62 | 0.58 | −0.64 | −0.65 | −0.60 |
| Mean depth | −0.53 | −0.44 | −0.46 | −0.63 | −0.14 | −0.47 | −0.23 | −0.28 |
| Shoreline development index | −0.10 | 0.10 | 0.05 | −0.01 | 0.31 | −0.10 | −0.57 | −0.49 |
| Mean annual flow | −0.13 | −0.16 | 0.19 | 0.08 | 0.41 | −0.28 | −0.50 | −0.44 |
| Residence time | 0.06 | 0.54 | 0.47 | 0.40 | −0.51 | 0.29 | −0.43 | −0.41 |
3.5. Global Warming Potential
4. Discussion
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Campeau, A.; del Giorgio, P.A. Patterns in CH4 and CO2 concentrations across boreal rivers: Major drivers and implications for fluvial greenhouse emissions under climate change scenarios. Glob. Chang. Biol. 2014, 20. [Google Scholar] [CrossRef]
- Tadonléké, R.D.; Marty, J.; Planas, D. Assessing factors underlying variation of CO2 emissions in boreal lakes vs. reservoirs. FEMS Microbiol. Ecol. 2012, 79. [Google Scholar] [CrossRef] [PubMed]
- Kosten, S.; Roland, F.; da Motta Marques, D.M.L.; van Nes, E.H.; Mazzeo, N.; Sternberg, L.; Scheffer, M.; Cole, J.J. Climate-dependent CO2 emissions from lakes. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Tranvik, L.J.; Downing, J.A.; Cotner, J.B.; Loiselle, S.A.; Striegl, R.G.; Ballatore, T.J.; Dillon, P.; Finlay, K.; Fortino, K.; Knoll, L.B.; et al. Lakes and reservoirs as regulators of carbon cycling and climate. Limnol. Oceanogr. 2009, 54. [Google Scholar] [CrossRef]
- Bergström, A.K.; Algesten, G.; Sobek, S.; Tranvik, L.; Jansson, M. Emission of CO2 from hydroelectric reservoirs in northern Sweden. Arch. Hydrobiol. 2004, 159. [Google Scholar] [CrossRef]
- Duarte, C.M.; Prairie, Y.T. Prevalence of heterotrophy and atmospheric CO2 emissions from aquatic ecosystems. Ecosystems 2005, 8. [Google Scholar] [CrossRef]
- Failer, E.; El-Hadari, M.H.; Mutaz, M.A.S. The Merowe Dam and its hydropower plant in Sudan. Wasserwirtschaft 2011, 101, 10–16. [Google Scholar] [CrossRef]
- Barros, N.; Cole, J.J.; Tranvik, L.J.; Prairie, Y.T.; Bastviken, D.; Huszar, V.L.M.; del Giorgio, P.; Roland, F. Carbon emission from hydroelectric reservoirs linked to reservoir age and latitude. Nat. Geosci. 2011, 4. [Google Scholar] [CrossRef]
- Tremblay, A.; Lambert, M.; Gagnon, L. Do hydroelectric reservoirs emit greenhouse gases? Environ. Manag. 2004, 33. [Google Scholar] [CrossRef]
- Galy-Lacaux, C.; Delmas, R.; Kouadio, G.; Richard, S.; Gosse, P. Long-term greenhouse gas emissions from hydroelectric reservoirs in tropical forest regions. Glob. Biogeochem. Cycles 1999, 13. [Google Scholar] [CrossRef]
- Teodoru, C.R.; Prairie, Y.T.; del Giorgio, P.A. Spatial heterogeneity of surface CO2 fluxes in a newly created Eastmain-1 Reservoir in Northern Quebec, Canada. Ecosystems 2011, 14. [Google Scholar] [CrossRef]
- Sobek, S.; Algesten, G.; Bergström, A.; Jansson, M.; Tranvik, L.J. The catchment and climate regulation of pCO2 in boreal lakes. Glob. Chang. Biol. 2003, 9. [Google Scholar] [CrossRef]
- Sobek, S.; Tranvik, L.J.; Cole, J.J. Temperature independence of carbon dioxide supersaturation in global lakes. Glob. Biogeochem. Cycles 2005, 19. [Google Scholar] [CrossRef]
- Trolle, D.; Staehr, P.A.; Davidson, T.A.; Bjerring, R.; Lauridsen, T.L.; Sondergaard, M.; Jeppesen, E. Seasonal dynamics of CO2 flux across the surface of shallow temperate lakes. Ecosystems 2012, 15, 336–347. [Google Scholar] [CrossRef]
- Soumis, N.; Duchemin, E.; Canuel, R.; Lucotte, M. Greenhouse gas emissions from reservoirs of the western United States. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Borrel, G.; Jezequel, D.; Biderre-Petit, C.; Morel-Desrosiers, N.; Morel, J.; Peyret, P.; Fonty, G.; Lehours, A. Production and consumption of methane in freshwater lake ecosystems. Res. Microbiol. 2011, 162. [Google Scholar] [CrossRef] [PubMed]
- Bastviken, D.; Cole, J.J.; Pace, M.; Tranvik, L. Methane emissions from lakes: Dependence of lake characteristics, two regional assessments, and a global estimate. Glob. Biogeochem. Cycles 2004, 18. [Google Scholar] [CrossRef]
- Rich, P.H.; Wetzel, R.G. Detritus in the lake ecosystem. Am. Nat. 1978, 112, 57–71. [Google Scholar] [CrossRef]
- DelSontro, T.; McGinnis, D.F.; Sobek, S.; Ostrovsky, I.; Wehrli, B. Extreme methane emissions from a Swiss hydropower reservoir: Contribution from bubbling sediments. Environ. Sci. Technol. 2010, 44, 2419–2425. [Google Scholar] [CrossRef] [PubMed]
- Ostrovsky, I.; Tegowski, J. Hydroacoustic analysis of spatial and temporal variability of bottom sediment characteristics in Lake Kinneret in relation to water level fluctuation. Geo-Mar. Lett. 2003, 30, 261–269. [Google Scholar] [CrossRef]
- Murase, J.; Sakai, Y.; Sugimoto, A.; Okubo, K.; Sakamoto, M. Sources of dissolved methane in Lake Biwa. Limnology 2003, 4. [Google Scholar] [CrossRef]
- Kelly, C.A.; Rudd, J.W.M.; Bodaly, R.A.; Roulet, N.P.; St. Louis, V.L.; Heyes, A.; Moore, T.R.; Schiff, S.; Aravena, R.; Scott, K.J.; et al. Increases in fluxes of greenhouse gases and methyl mercury following flooding of an experimental reservoir. Environ. Sci. Technol. 1997, 31. [Google Scholar] [CrossRef]
- Matthews, D.A.; Effler, S.W.; Matthews, C.M. Long-term trends in methane flux from the sediments of Onondaga Lake, NY: Sediment diagenesis and impacts on dissolved oxygen resources. Arch. Hydrobiol. 2005, 163. [Google Scholar] [CrossRef]
- Huttunen, J.T.; Alm, J.; Liikanen, A.; Juutinen, S.; Larmola, T.; Hammar, T.; Silvola, J.; Martikainen, P.J. Fluxes of methane, carbon dioxide and nitrous oxide in boreal lakes and potential anthropogenic effects on the aquatic greenhouse gas emissions. Chemosphere 2003, 52. [Google Scholar] [CrossRef]
- Casper, P.; Maberly, S.C.; Hall, G.H.; Finlay, B.J. Fluxes of methane and carbon dioxide from a small productive lake to the atmosphere. Biogeochemistry 2000, 49. [Google Scholar] [CrossRef]
- Goldenfum, J.A. Challenges and solutions for assessing the impact of freshwater reservoirs on natural GHG emissions. Ecohydrol. Hydrobiol. 2012, 12. [Google Scholar] [CrossRef]
- Tremblay, A.; Varfalvy, L.; Roehm, G.; Garneau, M. Greenhouse Gas Emissions—Fluxes and Processes: Hydroelectric Reservoirs and Natural Environments; Springer: Berlin, Germany, 2005. [Google Scholar]
- Beaulieu, J.J.; Smolenski, R.L.; Nietch, C.T.; Townsend-Small, A.; Elovitz, M.S. High methane emissions from a midlatitude reservoir draining an agricultural watershed. Environ. Sci. Technol. 2014, 48. [Google Scholar] [CrossRef] [PubMed]
- Stewart, A.J.; Mosher, J.J.; Mulholland, P.J.; Fortner, A.M.; Phillips, J.R.; Bevelhimer, M.S. Greenhouse Gas Emissions from U.S. Hydropower Reservoirs: FY2011 Annual Progress Report; ORNL/TM-2012/90; Department of Energy: Washington, DC, USA, 2011.
- Mosher, J.J.; Fortner, A.M.; Phillips, J.R.; Bevelhimer, M.S.; Stewart, A.J.; Troia, M.J. Spatial and temporal correlates of greenhouse gas diffusion from a hydropower reservoir in the southern United States. Water 2015, 7, 5910–5927. [Google Scholar] [CrossRef]
- The Southeast Regional Climate Center. Monthly and Seasonal Climate Information. Available online: http://www.sercc.com/climateinfo/monthly_seasonal (accessed on 4 January 2016).
- Goldenfum, J.A. GHG Measurement Guidelines for Freshwater Reservoirs; The International Hydropower Association: London, UK, 2010; Available online: http://www.hydropower.org/sites/default/files/publications-docs/GHG%20Measurement%20Guidelines%20for%20Freshwater%20Reservoirs.pdf (accessed on 4 January 2016).
- Wetzel, R.G. Limnology: Lake and River Ecosystems, 3rd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Zar, J.H. Biostatistical Analysis, 2nd ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Lelieveld, J.; Crutzen, P.J.; Dentener, F.J. Changing concentration, lifetime and climate forcing of atmospheric methane. Tellus B 1998, 50. [Google Scholar] [CrossRef]
- St. Louis, V.L.; Kelly, C.A.; Duchemin, E.; Rudd, J.W.M.; Rosenberg, D.M. Reservoir surfaces as sources of greenhouse gases to the atmosphere: A global estimate. BioScience 2000, 50, 766–775. [Google Scholar] [CrossRef]
- Kemenes, A.; Forsberg, B.R.; Melack, J.M. CO2 emissions from a tropical hydroelectric reservoir (Balbina, Brazil). J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Duchemin, E.; Lucotte, M.; Canuel, R.; Chamberland, A. Production of greenhouse gases CH4 and CO2 by hydroelectric reservoirs of the boreal region. Glob. Biogeochem. Cycles 1995, 9. [Google Scholar] [CrossRef]
- DelSontro, T.; Kunz, M.J.; Kempter, T.; Wüest, A.; Wehrli, B.; Senn, D.B. Spatial heterogeneity of methane ebullition in a large tropical reservoir. Environ. Sci. Technol. 2011, 45. [Google Scholar] [CrossRef] [PubMed]
- Webb, D.H.; Mangum, L.N.; Bates, A.L.; Murphy, H.D. Aquatic vegetation in Guntersville reservoir following grass carp stocking. In Proceedings of the Grass Carp Symposium, Gainesville, FL, USA, 7–9 March 1994.
- Dacey, J.W.H. Pressurized ventilation in the yellow waterlily. Ecology 1981, 62, 1137–1147. [Google Scholar] [CrossRef]
- Lindberg, S.E.; Dong, W.; Chanton, J.; Qualls, R.G.; Meyers, T. A mechanism for bimodal emission of gaseous mercury from aquatic macrophytes. Atmos. Environ. 2005, 39, 1289–1301. [Google Scholar] [CrossRef]
- Ribaudo, C.; Bartoli, M.; Longhi, D.; Castaldi, S.; Neubauer, S.C.; Viaroli, P. CO2 and CH4 fluxes across a Nuphar lutea (L.) Sm. stand. J. Limnol. 2012, 71, 200–210. [Google Scholar] [CrossRef] [Green Version]
- DelSontro, T.; McGinnis, D.F.; Wehrli, B.; Ostrovsky, I. Size does matter: Importance of large bubbles and small-scale hot spots for methane transport. Environ. Sci. Technol. 2015, 49. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bevelhimer, M.S.; Stewart, A.J.; Fortner, A.M.; Phillips, J.R.; Mosher, J.J. CO2 is Dominant Greenhouse Gas Emitted from Six Hydropower Reservoirs in Southeastern United States during Peak Summer Emissions. Water 2016, 8, 15. https://doi.org/10.3390/w8010015
Bevelhimer MS, Stewart AJ, Fortner AM, Phillips JR, Mosher JJ. CO2 is Dominant Greenhouse Gas Emitted from Six Hydropower Reservoirs in Southeastern United States during Peak Summer Emissions. Water. 2016; 8(1):15. https://doi.org/10.3390/w8010015
Chicago/Turabian StyleBevelhimer, Mark S., Arthur J. Stewart, Allison M. Fortner, Jana R. Phillips, and Jennifer J. Mosher. 2016. "CO2 is Dominant Greenhouse Gas Emitted from Six Hydropower Reservoirs in Southeastern United States during Peak Summer Emissions" Water 8, no. 1: 15. https://doi.org/10.3390/w8010015
APA StyleBevelhimer, M. S., Stewart, A. J., Fortner, A. M., Phillips, J. R., & Mosher, J. J. (2016). CO2 is Dominant Greenhouse Gas Emitted from Six Hydropower Reservoirs in Southeastern United States during Peak Summer Emissions. Water, 8(1), 15. https://doi.org/10.3390/w8010015






