Hydrologic Response of Climate Change in the Source Region of the Yangtze River, Based on Water Balance Analysis
Abstract
:1. Introduction
2. Study Area and Methods
2.1. Study Area and Data
2.2. Methods
2.2.1. Trend Analysis
2.2.2. Water Balance and Uncertainty Analysis
2.2.3. Correlation Analysis
3. Results
3.1. Basic State of Climatic Variables
3.2. Temporal Trends
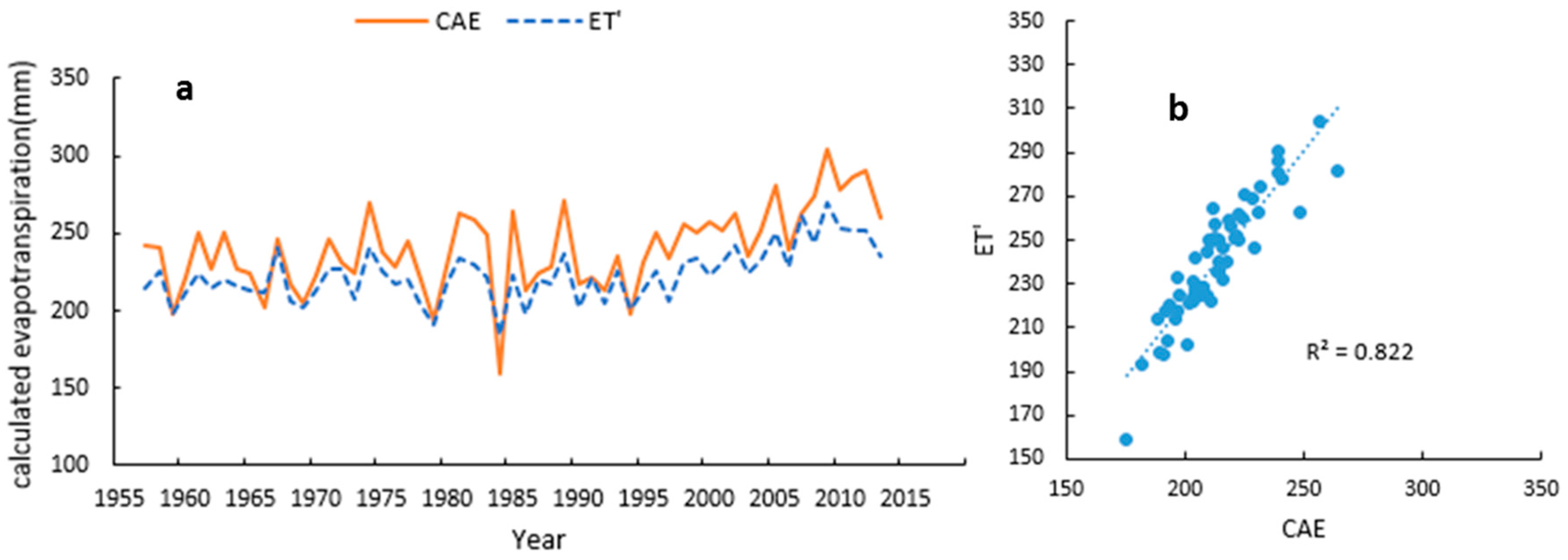
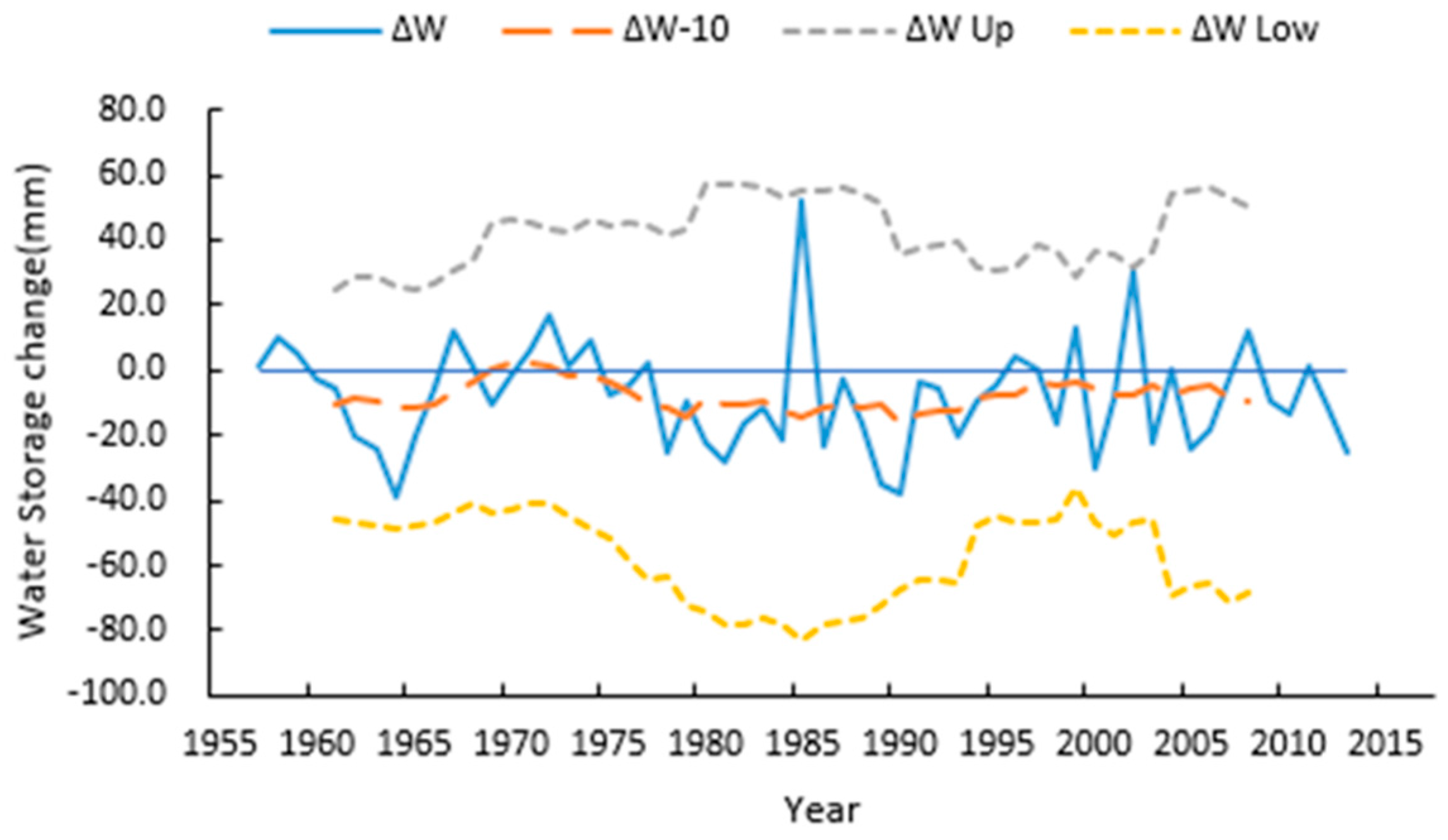
3.3. Water Balance and Uncertainty Analysis
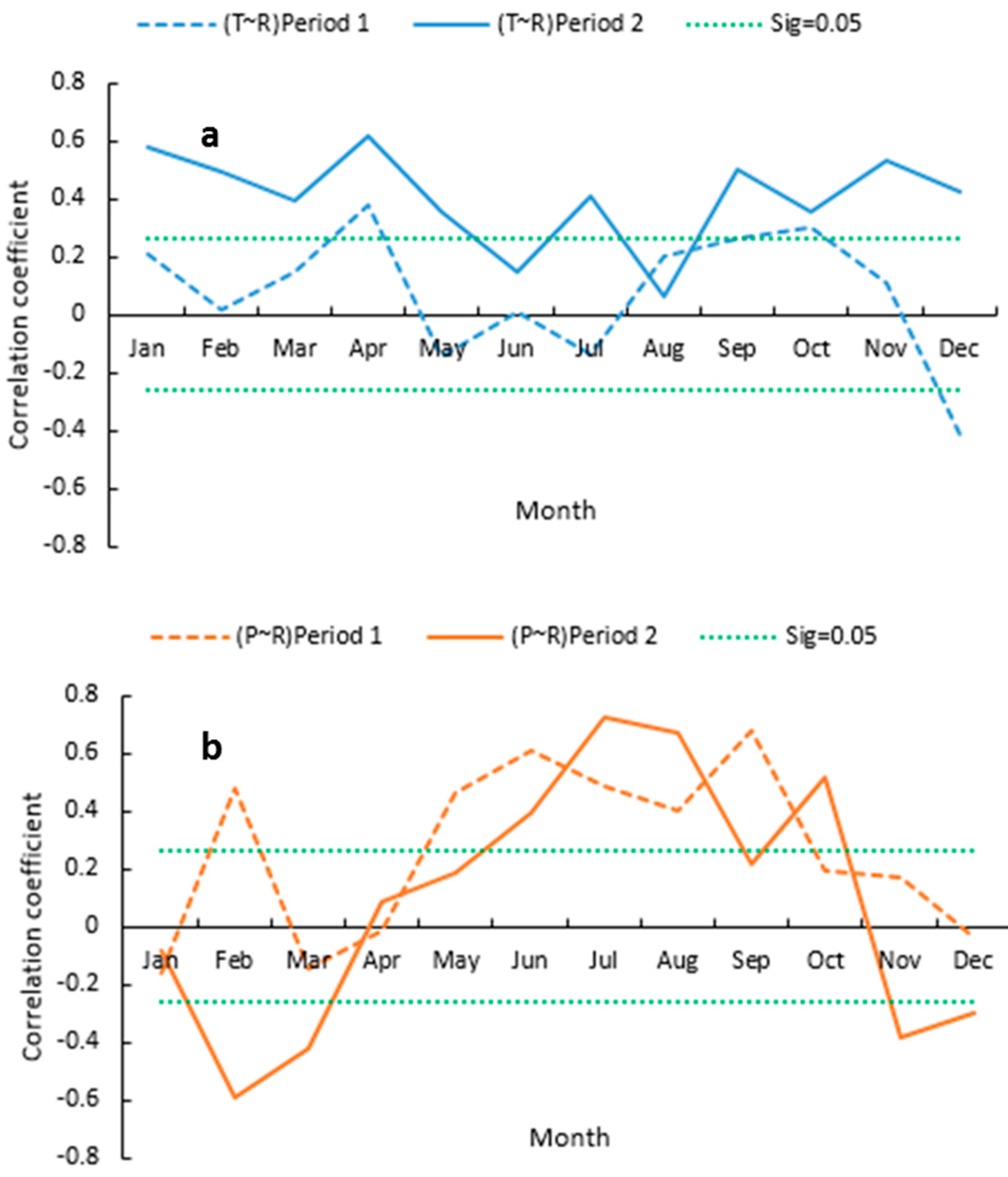
3.4. Correlation between Hydro-Climatic Variables
4. Conclusions
- (1)
- The temperature in the SRYR increased at a rate of 0.34 °C/decade, and the precipitation and evaporation also increased by 11.4 and 7.6 mm/decade, respectively. The runoff depth increased by 3.3 mm/decade;
- (2)
- The annual water storage change appears stable. However, it displays a continuous small negative trend. Based on water balance equation, the increase in calculated evapotranspiration derived from significantly increasing temperature and precipitation lead to relatively stable water storage during the study period;
- (3)
- Temperature is the dominating factor for runoff during the cold season (November to April) and precipitation for the runoff during the warm season (May to October). Temperature appears to have increased as a dominating factor during the recent 1991–2013 period as compared to the period 1957–1990. Decreasing correlation between precipitation and runoff also indicates the enhancing influence of temperature on runoff in winter.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.M.B.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Hu, Y.G.; Jiang, L.L.; Wang, S.P.; Zhang, Z.H.; Luo, C.Y.; Bao, X.Y.; Niu, H.S.; Xu, G.P.; Duan, J.C.; Zhu, X.X.; et al. The temperature sensitivity of ecosystem respiration to climate change in an alpine meadow on the Tibet plateau: A reciprocal translocation experiment. Agric. For. Meteorol. 2016, 216, 93–104. [Google Scholar] [CrossRef]
- Wu, Q.; Dong, X.; Liu, Y.; Jin, H. Responses of permafrost the qinghai-tibet plateau, China, to climate change and engineering construction. Arct. Antarct. Alp. Res. 2007, 39, 682–687. [Google Scholar] [CrossRef]
- Liu, Z.F.; Yao, Z.J.; Wang, R. Contribution of glacial melt to river runoff as determined by stable isotopes at the source region of the Yangtze River, China. Hydrol. Res. 2016, 47, 442–453. [Google Scholar] [CrossRef]
- Yao, T.D.; Liu, X.D.; Wang, N.L.; Shi, Y.F. Amplitude of climatic changes in Qinghai-Tibetan Plateau. Chin. Sci. Bull. 2000, 45, 1236–1243. [Google Scholar] [CrossRef]
- Liu, S.Y.; Zhang, Y.; Zhang, Y.S.; Ding, Y.J. Estimation of glacier runoff and future trends in the Yangtze River source region, China. J. Glaciol. 2009, 55, 353–362. [Google Scholar]
- Yang, J.P.; Ding, Y.J.; Chen, R.S. Climatic causes of ecological and environmental variations in the source regions of the Yangtze and Yellow Rivers of China. Environ. Geol. 2007, 53, 113–121. [Google Scholar] [CrossRef]
- Zhang, S.; Hua, D.; Meng, X.; Zhang, Y. Climate change and its driving effect on the runoff in the “Three-River Headwaters” region. J. Geogr. Sci. 2011, 21, 963–978. [Google Scholar] [CrossRef]
- Bing, L.F.; Shao, Q.Q.; Liu, J.Y. Runoff characteristics in flood and dry seasons based on wavelet analysis in the source regions of the Yangtze and Yellow rivers. J. Geogr. Sci. 2012, 22, 261–272. [Google Scholar] [CrossRef]
- Chongyi, E.; Hu, H.; Xie, H.; Sun, Y. Temperature change and its elevation dependency in the source region of the Yangtze River and Yellow River. J. Geogr. Geol. 2014, 6, 124–131. [Google Scholar]
- Kang, S.; Zhang, Y.; Qin, D.; Ren, J.; Zhang, Q.; Grigholm, B.; Mayewski, P.A. Recent temperature increase recorded in an ice core in the source region of Yangtze River. Chin. Sci. Bull. 2007, 52, 825–831. [Google Scholar] [CrossRef]
- Yao, Z.J.; Liu, Z.F.; Huang, H.Q.; Liu, G.H.; Wu, S.S. Statistical estimation of the impacts of glaciers and climate change on river runoff in the headwaters of the Yangtze River. Quat. Int. 2014, 336, 89–97. [Google Scholar] [CrossRef]
- Wu, S.S.; Yao, Z.J.; Huang, H.Q.; Liu, Z.F.; Chen, Y.S. Glacier retreat and its effect on stream flow in the source region of the Yangtze River. J. Geogr. Sci. 2013, 23, 849–859. [Google Scholar] [CrossRef]
- Fang, Y.P.; Qin, D.H.; Ding, Y.J. Frozen soil change and adaptation of animal husbandry: A case of the source regions of Yangtze and Yellow Rivers. Environ. Sci. Policy 2011, 14, 555–568. [Google Scholar] [CrossRef]
- Duo, B.; Bianbaciren; Li, L.; Wang, W.; Zhaxiyangzong. The response of lake change to climate fluctuation in north Qinghai-Tibet Plateau in last 30 years. J. Geogr. Sci. 2009, 19, 131–142. [Google Scholar]
- Huang, L.; Liu, J.Y.; Shao, Q.Q.; Liu, R.G. Changing inland lakes responding to climate warming in Northeastern Tibetan Plateau. Clim. Chang. 2011, 109, 479–502. [Google Scholar] [CrossRef]
- Xiang, L.W.; Wang, H.S.; Steffen, H.; Wu, P.; Jia, L.L.; Jiang, L.M.; Shen, Q. Groundwater storage changes in the Tibetan Plateau and adjacent areas revealed from GRACE satellite gravity data. Earth Planet. Sci. Lett. 2016, 449, 228–239. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.Y.; Sun, W.X.; Shen, Y.P.; Li, G. Glacier changes since the Little Ice Age maximum in the western Qilian Shan, northwest China, and consequences of glacier runoff for water supply. J. Glaciol. 2003, 49, 117–124. [Google Scholar]
- Zhang, M.F.; Ren, Q.S.; Wei, X.H.; Wang, J.S.; Yang, X.L.; Jiang, Z.S. Climate change, glacier melting and streamflow in the Niyang River Basin, Southeast Tibet, China. Ecohydrology 2011, 4, 288–298. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Qian, K.; Wang, X.-S.; Lv, J.; Wan, L. The wavelet correlative analysis of climatic impacts on runoff in the source region of Yangtze River, in China. Int. J. Climatol. 2014, 34, 2019–2032. [Google Scholar] [CrossRef]
- Kenney, J.F.; Keeping, E.S. Linear Regression and Correlation. Math. Stat. 1951, 8, 199–237. [Google Scholar]
- Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Yuan, F.F.; Berndtsson, R.; Zhang, L.; Uvo, C.B.; Hao, Z.C.; Wang, X.P.; Yasuda, H. Hydro Climatic Trend and Periodicity for the Source Region of the Yellow River. J. Hydrol. Eng. 2015, 20, 05015003. [Google Scholar] [CrossRef]
- Takahashi, K.; Wang, C.G. The projection formula for evapotranspiration from the monthly mean temperatureand monthly precipitation. Meteorol. Sci. Technol. 1979, 26, 29–32. (In Chinese) [Google Scholar]
- Zhang, G.S.; Shi, X.H.; Li, D.L.; Wang, Q.C.; Dai, S. Climate change in Tuotuohe Area at the headwaters of Yangtze River. J. Glaciol. Geocryol. 2006, 28, 678–685. (In Chinese) [Google Scholar]
- Karlsson, J.M.; Lyon, S.W.; Destouni, G. Thermokarst lake, hydrological flow and water balance indicators of permafrost change in Western Siberia. J. Hydrol. 2012, 464, 459–466. [Google Scholar] [CrossRef]
- Langbein, W.B. Annual Runoff in the United States; US Geological Survey Circular: Reston, VA, USA, 1949; p. 54.
- Turc, L. Estimation of irrigation water requirements, potential evapotranspiration: A simple climatic formula evolved up to date. Ann. Agron. 1961, 12, 13–49. [Google Scholar]
- Tabari, H. Evaluation of Reference Crop Evapotranspiration Equations in Various Climates. Water Resour. Manag. 2010, 24, 2311–2337. [Google Scholar] [CrossRef]
- Federer, C.A.; Vorosmarty, C.; Fekete, B. Intercomparison of methods for calculating potential evaporation in regional and global water balance models. Water Resour. Res. 1996, 32, 2315–2321. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical Contributions to the Theory of Evolution. III. Regression, Heredity, and Panmixia. Philos. Trans. R. Soc. Lond. 1896, 187, 253–318. [Google Scholar] [CrossRef]
- Taylor, W.A. Change-Point Analysis: A Powerful New Tool for Detecting Changes. Available online: http://www.variation.com/cpa/tech/changepoint.html (accessed on 10 February 2017).
- Yuan, F.; Hao, Z.; Berndtsson, R.; Jiang, P.; Yasuda, H. The Mass Balance of Glacier No. 1 at the Headwaters of the Urumqi River in Relation to Northern Hemisphere Teleconnection Patterns. Water 2016, 8, 100. [Google Scholar] [CrossRef]
- Gao, J.B.; Huang, J.; Li, S.C.; Cai, Y.L. The New Progresses and Development Trends in the Research of Physio-Geographical Regionalization in China. Prog. Geogr. 2010, 29, 1400–1407. (In Chinese) [Google Scholar]
- Xie, C.W.; Ding, Y.J.; Liu, S.Y.; Wang, G.X. Comparison Analysis of Runoff Change in the Source Regions of the Yangtze and Yellow Rivers. J. Glaciol. Geocryol. 2003, 25, 414–422. (In Chinese) [Google Scholar]
- Liang, C.; Hou, X.B.; Pan, N. Spatial and temporal variations of precipitation and runoff in the source region of the Yangtze River. South-to-North Water Divers. Sci. Technol. 2011, 9, 35–39. (In Chinese) [Google Scholar] [CrossRef]
- Li, L.; Shen, H.Y.; Dai, S.; Li, H.M.; Xiao, J.S. Response of water resources to climate change and its future trend in the source region of the Yangtze River. J. Geogr. Sci. 2013, 23, 208–218. [Google Scholar] [CrossRef]
- Wang, K.L.; Cheng, G.D.; Ding, Y.J.; Shen, Y.P.; Jiang, H. Characteristics of water vapor transport and atmospheric circulation of precipitation over the source regions of the Yellow and Yangtze Rivers. J. Glaciol. Geocryol. 2006, 28, 8–14. (In Chinese) [Google Scholar]
- Li, S.S.; Zhang, M.J.; Wang, B.L.; Li, X.F.; Luo, S.F. Spatial difference of precipitation variation in Three-River headwaters region of China in recent 51 years. Chin. J. Ecol. 2012, 31, 2635–2643. (In Chinese) [Google Scholar]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef]
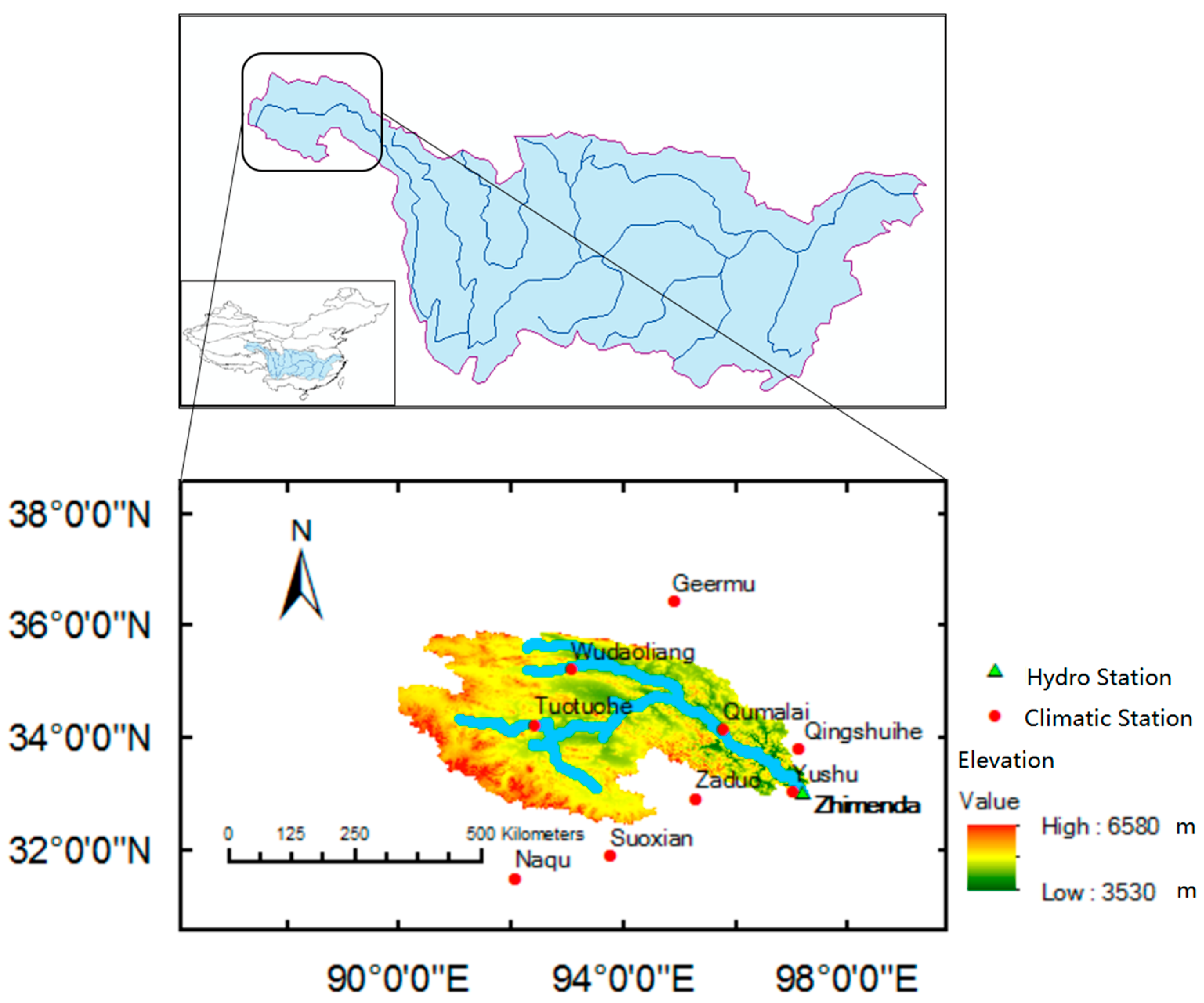
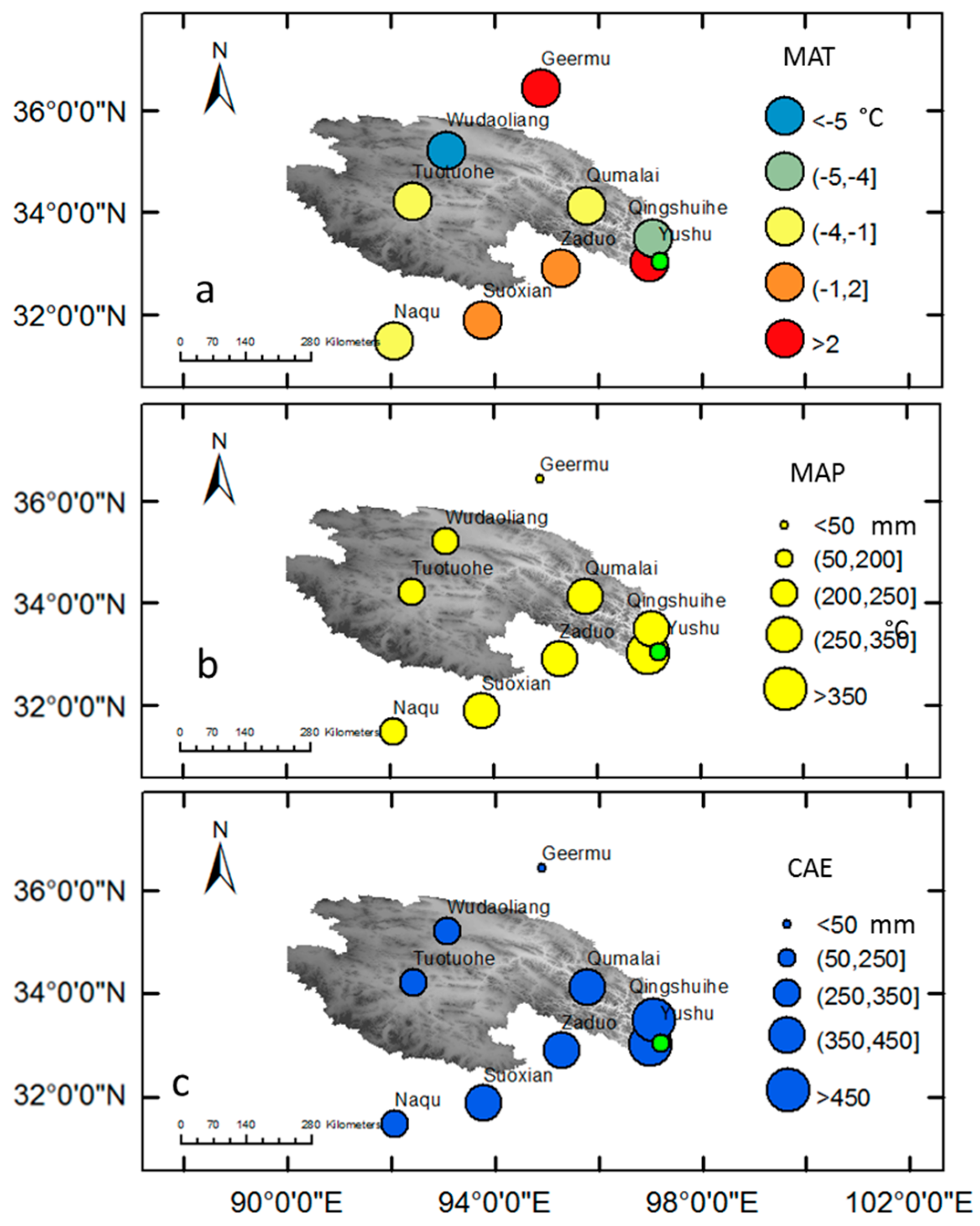


| Station | Longitude | Latitude | Elevation (m) | Mean Annual Temp. (°C) | Mean Annual Precip. (mm) | Thiessen Weight |
|---|---|---|---|---|---|---|
| Temperature and Precipitation | ||||||
| Wudaoliang | 93.08 | 35.22 | 4612 | −5.3 | 288.7 | 0.217 |
| Tuotuohe | 92.43 | 34.22 | 4533 | −3.9 | 289.4 | 0.416 |
| Qumalai | 95.78 | 34.13 | 4175 | −2.0 | 414.2 | 0.188 |
| Yushu | 97.02 | 33.02 | 3717 | 3.4 | 486.2 | 0.028 |
| Qingshuihe | 97.08 | 33.48 | 4415 | −4.5 | 516.7 | 0.028 |
| Geermu | 94.90 | 36.42 | 2808 | 5.2 | 42.2 | 0.025 |
| Zaduo | 95.30 | 32.90 | 4066 | 0.7 | 358.8 | 0.040 |
| Naqu | 92.07 | 31.48 | 4507 | −1.1 | 292.0 | 0.003 |
| Suoxian | 93.78 | 31.89 | 4023 | 1.9 | 380.6 | 0.056 |
| Runoff | Basin Average | |||||
| Zhimenda | 97.22 | 33.03 | −2.9 | 327.4 | ||
| Trend Analysis Indices | Temperature | Precipitation | Run-Off | Evapotranspiration | Change in Water Storage |
|---|---|---|---|---|---|
| Gradient | 0.34 | 11.4 | 3.3 | 7.6 | −1.1 |
| (°C/decade) | (mm/decade) | (mm/decade) | (mm/decade) | (mm/decade) | |
| MK Sig. | 0.000 * | 0.004 * | 0.077 | 0.000 * | 0.156 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Y.; Berndtsson, R.; An, D.; Zhang, L.; Hao, Z.; Yuan, F. Hydrologic Response of Climate Change in the Source Region of the Yangtze River, Based on Water Balance Analysis. Water 2017, 9, 115. https://doi.org/10.3390/w9020115
Du Y, Berndtsson R, An D, Zhang L, Hao Z, Yuan F. Hydrologic Response of Climate Change in the Source Region of the Yangtze River, Based on Water Balance Analysis. Water. 2017; 9(2):115. https://doi.org/10.3390/w9020115
Chicago/Turabian StyleDu, Yiheng, Ronny Berndtsson, Dong An, Linus Zhang, Zhenchun Hao, and Feifei Yuan. 2017. "Hydrologic Response of Climate Change in the Source Region of the Yangtze River, Based on Water Balance Analysis" Water 9, no. 2: 115. https://doi.org/10.3390/w9020115
APA StyleDu, Y., Berndtsson, R., An, D., Zhang, L., Hao, Z., & Yuan, F. (2017). Hydrologic Response of Climate Change in the Source Region of the Yangtze River, Based on Water Balance Analysis. Water, 9(2), 115. https://doi.org/10.3390/w9020115







