On the Multiplicative Degree-Based Topological Indices of Silicon-Carbon Si₂C₃-I[p,q] and Si₂C₃-II[p,q]

Abstract

The application of graph theory in chemical and molecular structure research has far exceeded people’s expectations, and it has recently grown exponentially. In the molecular graph, atoms are represented by vertices and bonds by edges. Topological indices help us to predict many physico-chemical properties of the concerned molecular compound. In this article, we compute Generalized first and multiplicative Zagreb indices, the multiplicative version of the atomic bond connectivity index, and the Generalized multiplicative Geometric Arithmetic index for silicon-carbon $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ and $S{i}_2{C}_{3^{-}}\mathrm{II}\left[p,q\right]$ second.

1. Introduction

For quite a few years, Chemical Graph theory has been assuming an imperative part in mathematical chemistry, quantitative structure-activity relationships (QSAR) and structure-property relationships (QSPR), and closeness/assorted variety investigation of sub-atomic libraries [1]. Essentially, molecular descriptors utilized as a part of these research fields are obtained from the graph of molecule, which speak to use some method to calculate numbers associated with molecular graph then using these number to describe molecule [1,2].

In chemical graph theory, a graph of molecule is a simple connected graph, in which atoms and chemical bonds are represented by vertices and edges respectively. A graph is connected if there is a connection between any pair of vertices. A network is a connected graph that has no multiple edge and loop. The number of vertices that are connected to a fixed vertex v is called the degree of v. The distance between two vertices is the length of the shortest path between them. The concept of valence in chemistry and the concept of degree in a graph is somehow closely related. For details on bases of graph theory, we refer to the book [3]. Throughout this paper, G denotes connected graph, V and E denote the vertex set and the edge set, respectively, and $d_v$ denotes the degree of a vertex.

The topological index of the graph of a chemical compound is the number associated with it. In 1947 Weiner laid the foundation of the topological index when he was approximating the boiling point of alkanes and introduced the Weiner index [4]. Till now, more than 140 topological indices are defined, but none of them is enough to determine all physico-chemical properties of understudy molecule. However, these indices together can do this to some extent. Later, in 1975, Milan Randić introduced Randić index [5]. In 1998, Bollobas and Erdos [6] and Amic et al. [7] defined the generalized Randić index, which got attention from both chemists and mathematicians [8]. The Randić index is one of the most popular, studied, and applied topological indices. Many reviews, papers, and books [9,10,11,12,13] are written on this simple graph invariant.

In 1972, Gutman introduced the first and the second Zagreb indices in [14].

$$M_1\left(G\right)={\displaystyle \sum _{u\in V\left(G\right)}{\left(d_u\right)}^2}={\displaystyle \sum _{uv\in E(G)}\left(d_u+d_v\right)},$$

$$M_2\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}{d}_u\times d_v}.$$

These indices have applied to study molecular chirality, complexity, hetero-systems, and ZE-isomerism [15].

Some indices are The first and second multiplicative Zagreb indices [16] are related to Wiener’s work and defined as:

$$I{I}_1\left(G\right)={{\displaystyle \prod _{u\in V\left(G\right)}\left(d_u\right)}}^2,$$

$$I{I}_2\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}{d}_u\times d_v}.$$

and the Narumi-Katayama index [17]:

$$NK\left(G\right)={\displaystyle \prod _{u\in V\left(G\right)}{d}_u}.$$

In computational chemistry, these types of indices are the focus of considerable research, like the Wiener index [18,19,20]. For example, in 2011. Gutman [18] studied and characterized the multiplicative first and second Zagreb indices for trees and determined the unique trees that give maximum and minimum values for M1(G) and M2(G), respectively. In [20], authors extended Gutman’s result and defined the following index for k-trees:

$$W_1^s\left(G\right)={\displaystyle \prod _{u\in V\left(G\right)}{\left(d_u\right)}^s}.$$

Notice that for s = 1, 2 the above defined index is the Narumi-Katayama and Zagreb index, respectively. Based on the successful consideration of multiplicative Zagreb indices, M. Eliasi et al. [21] defined a new version of the multiplicative first Zagreb index as:

$$I{I}_1^{\ast }\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}\left(d_u+d_v\right)}.$$

Furthering the study of topological indices, the first and second hyper-Zagreb indices of a graph [22] are defined as:

$$HI{I}_1\left(G\right)={{\displaystyle \prod _{uv\in E\left(G\right)}\left(d_u+d_v\right)}}^2,$$

$$HI{I}_2\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}{\left(d_u\times d_v\right)}^2}.$$

In [23], Kulli et al. defined the first and second generalized multiplicative Zagreb indices:

$$M{Z}_1^a\left(G\right)={{\displaystyle \prod _{uv\in E\left(G\right)}\left(d_u+d_v\right)}}^a,$$

$$M{Z}_2^a\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}{\left(d_u\times d_v\right)}^a}.$$

Multiplicative sum connectivity and multiplicative product connectivity indices [24] are defined as:

$$SCII\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_u+d_v}}},$$

$$PCII\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}\frac{1}{\sqrt{d_u\times d_v}}}.$$

Note that for $\alpha =1$, first and second generalized multiplicative Zagreb indices are first and second multiplicative Zagreb indices, respectively, and for $\alpha =2$, first and second generalized multiplicative Zagreb indices are first and second hyper multiplicative Zagreb indices, respectively. For $\alpha =-\frac{1}{2}$ first and second generalized multiplicative Zagreb indices are multiplicative sum connectivity and multiplicative product connectivity indices.

Multiplicative atomic bond connectivity index, multiplicative Geometric arithmetic index, and generalized multiplicative Geometric arithmetic index are defined as

$$ABCII\left(G\right)={\displaystyle \prod _{uv\in E\left( G\right)}\sqrt{\frac{d_u+d_v-2}{d_u\times d_v}}},$$

$$GAII\left(G\right)={\displaystyle \prod _{uv\in E\left(G\right)}\frac{2\sqrt{d_u\times d_v}}{d_u+d_v}},$$

$$G{A}^{a}II\left(G\right)={{\displaystyle \prod _{uv\in E\left(G\right)}\left(\frac{2\sqrt{d_u\times d_v}}{d_u+d_v}\right)}}^a.$$

In this paper, we compute Generalized first and second multiplicative Zagreb indices, multiplicative version of Atomic bond connectivity index and Generalized multiplicative Geometric Arithmetic index for silicon-carbon $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ and $S{i}_2{C}_{3^{-}}II\left[p,q\right]$. Now we discuss the graph of $S{i}_2{C}_{3^{-}}I$ and $S{i}_2{C}_{3^{-}}II.$

In Figure 1, one unit of $S{i}_2{C}_{3^{-}}I$ is shown. Molecular graph of $S{i}_2{C}_{3^{-}}I$ is shown in Figure 2, in which p denotes the number of cells attached in a single row and q denotes the number of total rows where each row contains p cells. In Figure 3 and Figure 4, we demonstrate how cells are connected in one row (chain) and how one row is connected to another row.

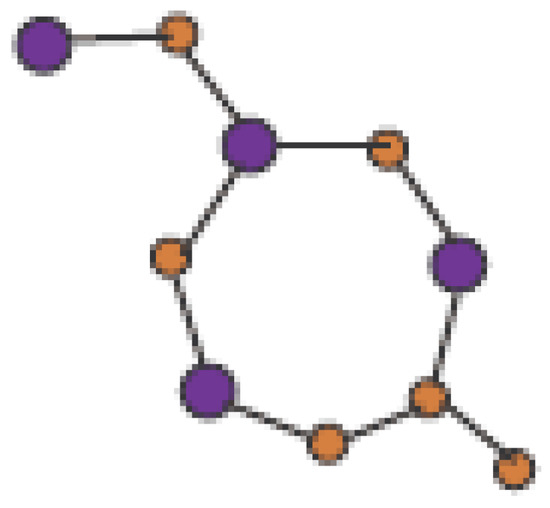
Figure 1. Unit Cell of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$.

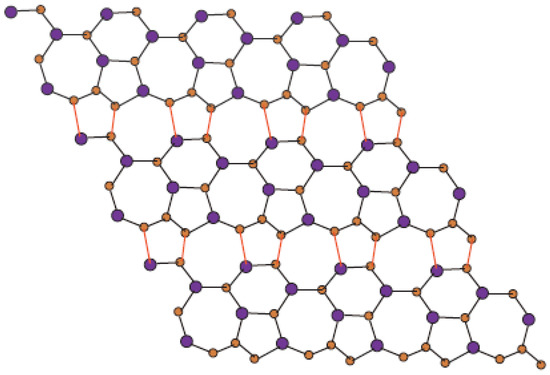
Figure 2. Sheet of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ for p = 4 and q = 3.

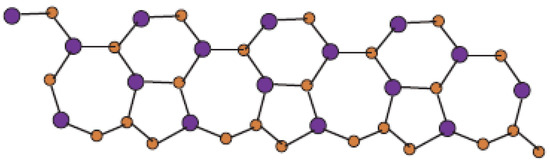
Figure 3. Sheet of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ for p = 4 and q = 1.

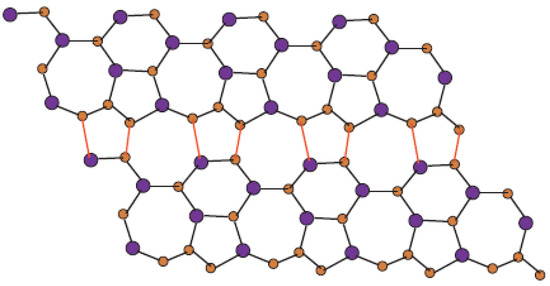
Figure 4. Sheet of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ for p = 4 and q = 2.

In Figure 1, Figure 2, Figure 3 and Figure 4, carbon atoms are shown as brown, and silicon atoms Si are shown as blue.

In Figure 5, one unit of $S{i}_2{C}_{3^{-}}II$ is given. By connecting p cells in a row and then connecting q rows where each row contains p cells, we get molecular graph of $S{i}_2{C}_{3^{-}}II$. The molecular graph of $S{i}_2{C}_{3^{-}}II$ is shown in Figure 6 for p = 3 and q = 4. Figure 7 and Figure 8 demonstrate how cells are connected in a row (chain) and how a row is connected to another row. We will use $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ to represent this molecular graph.

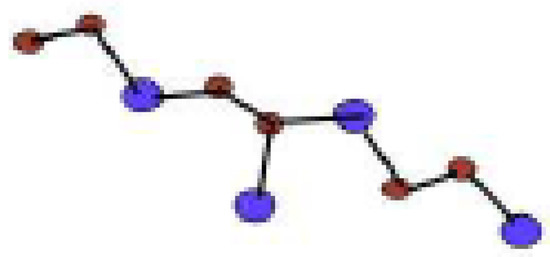
Figure 5. One Unit of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$.

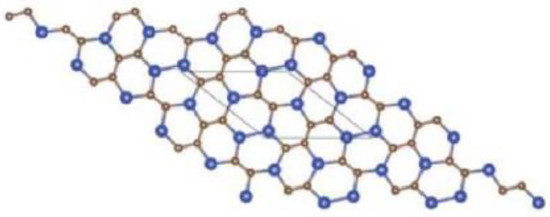
Figure 6. Sheet of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ for p = 3 and q = 3.

Figure 7. Sheet of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ for p = 5 and q = 1.

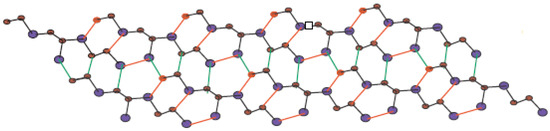
Figure 8. Sheet of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ for p = 5 and q = 2.

2. Computational Results

In this section we give our main results.

Theorem 1.

Let $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ be the Silicon Carbide. Then

$$M{Z}_1^a\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{\alpha \left(15pq-7p-9q+9\right)}\times {\left(3\right)}^{\alpha \left(15pq-9p-13q+8\right)}\times {\left(5\right)}^{\alpha \left(6p+8q-9\right)}.$$

$$M{Z}_2^a\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{4\alpha \left(2p+3q-2\right)}\times {\left(3\right)}^{6\alpha \left(5pq+2p-3q+1\right)}.$$

$$G{A}^{\alpha }II\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{\alpha \left(9p+12q-13\right)}\times {\left(3\right)}^{\alpha \left(3p+4q-5\right)}\times {\left(5\right)}^{\alpha \left(9-6p-8q\right)}.$$

Proof. 

Let G be the graph of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$. From the graph of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ (Figure 1, Figure 2, Figure 3 and Figure 4), we can see that the total number of vertices are $10pq$, and total number of edges are $15pq-2p-3q$.

The edge set of $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ with $p,q\ge 1$ has following five partitions:

$$E_{\left\{1,2\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)|d_u=1,d_v=2\right\},$$

$$E_{\left\{1,3\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)|d_u=1,d_v=3\right\},$$

$$E_{\left\{2,2\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)|d_u=2,d_v=2\right\},$$

$$E_{\left\{2,3\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)|d_u=2,d_v=3\right\}.$$

Additionally, it has

$$E_{\left\{3,3\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)|d_u=3,d_v=3\right\}.$$

Now,

$$\left|E_{\left\{1,2\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)\right|=1,$$

$$\left|E_{\left\{1,3\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)\right|=1,$$

$$\left|E_{\left\{2,2\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)\right|=p+2q,$$

$$\left|E_{\left\{2,3\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)\right|=6p-1+8\left(q-1\right),$$

and

$$\left|E_{\left\{3,3\right\}}\left(S{i}_2{C}_{3^{-}}I\left[p,q\right]\right)\right|=15pq-9p-13q+7.$$

$$\begin{array}{l}M{Z}_1^a\left(S{i}_2{C}_{3^{-}}I\right)={{\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}I\right)}\left(d_u+d_v\right)}}^{\alpha }\\ ={\left(1+2\right)}^{\alpha }\times {\left(1+3\right)}^{\alpha }\times {\left(2+2\right)}^{\alpha \left(p+2q\right)}\times {\left(2+3\right)}^{\alpha \left(6p+8q-9\right)}\times {\left(3+3\right)}^{\alpha \left(15pq-9p-13q+7\right)}\\ ={\left(2\right)}^{\alpha \left(15pq-7p-9q+9\right)}\times {\left(3\right)}^{\alpha \left(15pq-9p-13q+8\right)}\times {\left(5\right)}^{\alpha \left(6p+8q-9\right)}.\end{array}$$

$$\begin{array}{l}M{Z}_2^a\left(S{i}_2{C}_{3^{-}}I\right)={\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}I\right)}{\left(d_u\times d_v\right)}^{\alpha }}\\ ={\left(1\times 2\right)}^{\alpha }\times {\left(1\times 3\right)}^{\alpha }\times {\left(2\times 2\right)}^{\alpha \left(p+2q\right)}\times {\left(2\times 3\right)}^{\alpha \left(6p+8q-9\right)}\times {\left(3\times 3\right)}^{\alpha \left(15pq-9p-13q+7\right)}\\ ={\left(2\right)}^{4\alpha \left(2p+3q-2\right)}\times {\left(3\right)}^{6\alpha \left(5pq+2p-3q+1\right)}.\end{array}$$

$$\begin{array}{l}G{A}^{\alpha }II\left(S{i}_2{C}_3-I\right)={{\displaystyle \prod _{uv\in E\left(S{i}_2{C}_3-I\right)}\left(\frac{2\sqrt{d_u\times d_v}}{d_u+d_v}\right)}}^{\alpha }\\ ={\left(\frac{2\sqrt{1\times 2}}{1+2}\right)}^{\alpha }\times {\left(\frac{2\sqrt{1\times 3}}{1+3}\right)}^{\alpha }\times {\left(\frac{2\sqrt{2\times 2}}{2+2}\right)}^{\alpha (p+2q)}\times {\left(\frac{2\sqrt{2\times 3}}{2+3}\right)}^{\alpha (6p+8q-9)}\times {\left(\frac{2\sqrt{3\times 3}}{3+3}\right)}^{\alpha (15pq-9p-13q+7)}\\ ={\left(2\right)}^{\alpha (9p+12q-13)}\times {\left(3\right)}^{\alpha (3p+4q-5)}\times {\left(5\right)}^{\alpha (9-6p-8q)}.\end{array}$$

☐

Theorem 2.

Let $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ be the Silicon Carbide. Then,

$$M{Z}_1\left(S{i}_2{C}_{3^{-}}I\right)=I{I}_1^{\ast }\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{15pq-7p-9q+9}\times {\left(3\right)}^{15pq-9p-13q+8}\times {\left(5\right)}^{6p+8q-9}.$$

$$M{Z}_2\left(S{i}_2{C}_{3^{-}}I\right)=I{I}_2\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{4\left(2p+3q-2\right)}\times {\left(3\right)}^{6\left(5pq+2p-3q+1\right)}.$$

$$GAII\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{9p+12q-13}\times {\left(3\right)}^{3p+4q-5}\times {\left(5\right)}^{9-6p-8q}.$$

Proof. 

Taking $\alpha =1$, in Theorem 1, we get our desired results. ☐

Theorem 3.

Let $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ be the Silicon Carbide. Then,

$$HI{I}_1\left(S{i}_2{C}_{3^{-}}I\right)={\left(3\right)}^{30pq-18p-26q+16}\times {\left(2\right)}^{30pq-14p-18q+18}\times {\left(5\right)}^{12p+16q-18}.$$

$$HI{I}_2\left(S{i}_2{C}_{3^{-}}I\right)={\left(2\right)}^{8\left(2p+3q-2\right)}\times {\left(3\right)}^{12\left(5pq-2p-3q+6\right)}.$$

Proof. 

Taking $\alpha =2$, in Theorem 1, we get our desired results. ☐

Theorem 4.

Let $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ be the Silicon Carbide. Then,

$$SCII\left(S{i}_2{C}_{3^{-}}I\right)={\left(\frac{1}{2}\right)}^{1+p+2q}\times \left(\frac{1}{\sqrt{3}}\right)\times {\left(\frac{1}{\sqrt{5}}\right)}^{6p+8q-9}\times {\left(\frac{1}{\sqrt{6}}\right)}^{15pq-9p-13q+7}.$$

$$PCII\left(S{i}_2{C}_{3^{-}}I\right)={\left(\frac{1}{2}\right)}^{2\left(2p+3q-2\right)}\times {\left(\frac{1}{3}\right)}^{3\left(5pq-2p-3q+1\right)}.$$

Proof. 

Taking $\alpha =-\frac{1}{2}$, in Theorem 1, we get our desired results. ☐

Theorem 5.

Let $S{i}_2{C}_{3^{-}}I\left[p,q\right]$ be the Silicon Carbide. Then,

$$ABCII\left(S{i}_2{C}_{3^{-}}I\right)={\left[{\left(\frac{1}{2}\right)}^{\frac{1}{2}}\right]}^{16p+23q-15pq-16}\times {\left[{\left(\frac{1}{3}\right)}^{\frac{1}{2}}\right]}^{15pq-9p-13q+8}.$$

Proof. 

$$\begin{array}{l}ABCII\left(S{i}_2{C}_{3^{-}}I\right)={\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}I\right)}\sqrt{\frac{d_u+d_v-2}{d_u\times d_v}}}\\ =\left(\sqrt{\frac{1+2-2}{1\times 2}}\right)\times \left(\sqrt{\frac{1+3-2}{1\times 3}}\right)\times {\left(\sqrt{\frac{2+2-2}{2\times 2}}\right)}^{p+2q}\times {\left(\sqrt{\frac{2+3-2}{2\times 3}}\right)}^{6p+8q-9}\times {\left(\sqrt{\frac{3+3-2}{2\times 3}}\right)}^{15pq-9p-13q+7}\\ ={\left[{\left(\frac{1}{2}\right)}^{\frac{1}{2}}\right]}^{16p+23q-15pq-16}\times {\left[{\left(\frac{1}{3}\right)}^{\frac{1}{2}}\right]}^{15pq-9p-13q+8}.\end{array}$$

☐

Theorem 6.

Let $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ be the Silicon Carbide. Then,

$$M{Z}_1^a\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{\alpha \left(15pq-9p-9q+13\right)}\times {\left(3\right)}^{\alpha \left(15pq-13p-13q+13\right)}\times {\left(5\right)}^{\alpha \left(8p+8q-14\right)}.$$

$$M{Z}_2^a\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{12\alpha \left(p+q-1\right)}\times {\left(3\right)}^{3\alpha \left(10pq+6p-6q+3\right)}.$$

$$G{A}^{\alpha }II\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{\alpha \left(12p+12q-19\right)}\times {\left(3\right)}^{\alpha \left(4p+4q-\frac{17}{2}\right)}\times {\left(5\right)}^{\alpha \left(14-8p-8q\right)}.$$

Proof. 

Let G be the graph of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$. From the graph of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ (Figure 5, Figure 6, Figure 7 and Figure 8), we can see that the total number of vertices are $10pq$ and total number of edges are $15pq-3p-3q$.

The edge set of $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ with $p,q\ge 1$ has following five partitions:

$$E_{\left\{1,2\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)|d_u=1,d_v=2\right\},$$

$$E_{\left\{1,3\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)|d_u=1,d_v=3\right\},$$

$$E_{\left\{2,2\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)|d_u=2,d_v=2\right\},$$

$$E_{\left\{2,2\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)|d_u=2,d_v=2\right\}.$$

Additionally, it has

$$E_{\left\{3,3\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)=\left\{e=uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)|d_u=3,d_v=3\right\}.$$

Now,

$$\left|E_{\left\{1,2\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)\right|=2,$$

$$\left|E_{\left\{1,3\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)\right|=1,$$

$$\left|E_{\left\{2,2\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)\right|=2p+2q,$$

$$\left|E_{\left\{2,3\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)\right|=8p+8q-14,$$

and

$$\left|E_{\left\{3,3\right\}}\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)\right|=15pq-13p-13q+11.$$

$$\begin{array}{l}M{Z}_1^a\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)={{\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)}\left(d_u+d_v\right)}}^{\alpha }\\ ={\left(1+2\right)}^{2\alpha }\times {\left(1+3\right)}^{\alpha }\times {\left(2+2\right)}^{\alpha \left(2p+2q\right)}\times {\left(2+3\right)}^{\alpha \left(8p+8q-14\right)}\times {\left(3+3\right)}^{\alpha \left(15pq-13p-13q+11\right)}\\ ={\left(2\right)}^{\alpha \left(15pq-9p-9q+13\right)}\times {\left(3\right)}^{\alpha \left(15pq-13p-13q+13\right)}\times {\left(5\right)}^{\alpha \left(8p+8q-14\right)}.\end{array}$$

$$\begin{array}{l}M{Z}_2^a\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)={\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)}{(d_u\times d_v)}^{\alpha }}\\ ={\left(1\times 2\right)}^{2\alpha }\times {\left(1\times 3\right)}^{\alpha }\times {\left(2\times 2\right)}^{\alpha \left(2p+2q\right)}\times {\left(2\times 3\right)}^{\alpha \left(8p+8q-14\right)}\times {\left(3\times 3\right)}^{\alpha \left(15pq-13p-13q+11\right)}\\ ={\left(2\right)}^{12\alpha \left(p+q-1\right)}\times {\left(3\right)}^{3\alpha \left(10pq+6p-6q+3\right)}.\end{array}$$

$$\begin{array}{l}G{A}^{\alpha }II\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)={{\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)}\left(\frac{2\sqrt{d_u\times d_v}}{d_u+d_v}\right)}}^{\alpha }\\ ={\left(\frac{2\sqrt{1\times 2}}{1+2}\right)}^{2\alpha }\times {\left(\frac{2\sqrt{1\times 3}}{1+3}\right)}^{\alpha }\times {\left(\frac{2\sqrt{2\times 2}}{2+2}\right)}^{\alpha \left(2p+2q\right)}\times {\left(\frac{2\sqrt{2\times 3}}{2+3}\right)}^{\alpha \left(8p+8q-14\right)}\times {\left(\frac{2\sqrt{3\times 3}}{3+3}\right)}^{\alpha \left(15pq-13p-13q+11\right)}\\ ={\left(2\right)}^{\alpha \left(12p+12q-19\right)}\times {\left(3\right)}^{\alpha \left(4p+4q-\frac{17}{2}\right)}\times {\left(5\right)}^{\alpha \left(14-8p-8q\right)}.\end{array}$$

☐

Theorem 7.

Let $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ be the Silicon Carbide. Then,

$$M{Z}_1\left(S{i}_2{C}_{3^{-}}II\right)=I{I}_1^{\ast }\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{15pq-9p-9q+13}\times {\left(3\right)}^{15pq-13p-13q+13}\times {\left(5\right)}^{8p+8q-14}.$$

$$M{Z}_2\left(S{i}_2{C}_{3^{-}}II\right)=I{I}_2\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{12\left(p+q-1\right)}\times {\left(3\right)}^{3\left(10pq+6p-6q+3\right)}.$$

$$G{A}^{\alpha }II\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{\alpha \left(12p+12q-19\right)}\times {\left(3\right)}^{\alpha \left(4p+4q-\frac{17}{2}\right)}\times {\left(5\right)}^{\alpha \left(14-8p-8q\right)}.$$

Proof. 

Taking $\alpha =1$, in Theorem 6, we get our desired results. ☐

Theorem 8.

Let $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ be the Silicon Carbide. Then,

$$HI{I}_1\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{30pq-18p-18q+26}\times {\left(3\right)}^{30pq-26p-26q+26}\times {\left(5\right)}^{16p+16q-28}.$$

$$HI{I}_2\left(S{i}_2{C}_{3^{-}}II\right)={\left(2\right)}^{24\left(p+q-1\right)}\times {\left(3\right)}^{6\left(10pq-6p-6q+3\right)}.$$

Proof. 

Taking $\alpha =2$, in Theorem 6, we get our desired results. ☐

Theorem 9.

Let $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ be the Silicon Carbide. Then,

$$SCII\left(S{i}_2{C}_{3^{-}}II\right)={\left(\frac{1}{2}\right)}^{1+2p+2q}\times \left(\frac{1}{3}\right)\times {\left(\frac{1}{5}\right)}^{4p+4q-7}\times {\left(\frac{1}{\sqrt{6}}\right)}^{15pq-13p-13q+11}.$$

$$PCII\left(S{i}_2{C}_{3^{-}}II\right)={\left(\frac{1}{2}\right)}^{6\left(p+q-1\right)}\times {\left(\frac{1}{3}\right)}^{3\left(5pq-3p-3q+\frac{1}{2}\right)}.$$

Proof. 

Taking $\alpha =-\frac{1}{2}$, in Theorem 6, we get our desired results. ☐

Theorem 10.

Let $S{i}_2{C}_{3^{-}}II\left[p,q\right]$ be the Silicon Carbide. Then,

$$ABCII\left(S{i}_2{C}_{3^{-}}II\right)={\left[\left(\frac{1}{2}\right)\right]}^{\frac{23}{2}p+\frac{23}{2}q-\frac{15}{2}pq-12}\times {\left[{\left(\frac{1}{3}\right)}^{\frac{1}{2}}\right]}^{15pq-13p-13q+11}.$$

Proof. 

$$\begin{array}{l}ABCII\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)={\displaystyle \prod _{uv\in E\left(S{i}_2{C}_{3^{-}}II\left[p,q\right]\right)}\sqrt{\frac{d_u+d_v-2}{d_u\times d_v}}}\\ =\left(\sqrt{\frac{1+2-2}{1\times 2}}\right)\times \left(\sqrt{\frac{1+3-2}{1\cdot 3}}\right)\times {\left(\sqrt{\frac{2+2-2}{2\times 2}}\right)}^{p+2q}\times {\left(\sqrt{\frac{2+3-2}{2\times 3}}\right)}^{6p+8q-9}\times {\left(\sqrt{\frac{3+3-2}{2\times 3}}\right)}^{15pq-9p-13q+7}\\ ={\left[\left(\frac{1}{2}\right)\right]}^{\frac{23}{2}p+\frac{23}{2}q-\frac{15}{2}pq-12}\times {\left[{\left(\frac{1}{3}\right)}^{\frac{1}{2}}\right]}^{15pq-13p-13q+11}.\end{array}$$

☐

3. Remarks

Multiplicative, degree-based topological indices for silicon-carbon have been investigated here. Our results can help us to understand the physical features, chemical reactivity, and biological activities of silicon-carbon. For example, the atom-bond connectivity (ABC) index provides a very good correlation for computing the strain energy of molecules [25]. ABC is used to describe the heats of formation of alkanes, resulting in a good quantitative structure-property relationship (QSPR) model (r = 0.9970) [26]. The GA index has as much predictive power as that of the Randic index, so the GA index is more useful than the Randic index [25]. The first and second Zagreb indices were found to occur for the computation of the total π-electron energy of molecules and have a strong relationship with Weiner index [27]. The computation of distance-based and counting-related topological indices for these symmetrical graphs is an open challenge and is yet to be investigated. Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 are taken from [28].