Imaginary Chemical Potential, NJL-Type Model and Confinement–Deconfinement Transition
Abstract
:1. Introduction
- Sign problem free,
- Possible analytic continuation process to the real chemical potential,
- Relationship with the real chemical potential region via the canonical ensemble.
2. Roberge–Weiss Periodicity and Transition
- Roberge–Weiss (RW) periodicity:Special periodicity of the grand-canonical partition function () along the -axis where and ; . See Section 2.1 for details.
- Roberge–Weiss (RW) transition:Special first-order transition which is characterized by the phase of the Polyakov loop and the quark number density appearing at above the Roberge–Weiss endpoint temperature. See Section 2.2 for details.
- Trivial and nontrivial images:Origin of the RW periodicity at high temperature. These are corresponding to minima of the thermodynamic potential characterized by the phase of the Polyakov loop. See Section 2.2.2 for details.
- Spontaneous shift symmetry breaking:Symmetry which characterizes the RW transition line. This symmetry is associated from the time reversal or the charge conjugation and transformations via the semidirect product (It is first discussed by using the combination of the charge conjugation and symmetries in Ref. [41].). In other words, the system symmetry at is enhanced. The modified Polyakov-loop then becomes the order-parameter of the spontaneous breaking of this symmetry. See Section 2.4 for details.
- Roberge–Weiss (RW) endpoint:Endpoint of the first-order RW transition line. There are possibilities that the endpoint becomes the second-order (trivial scenario) or the first-order (nontrivial scenario) near the physical quark mass. The RW endpoint temperature is denoted by . See Section 2.3 for details.
2.1. Roberge–Weiss Periodicity
2.2. Roberge–Weiss Transition
2.2.1. RW Periodicity in the Confined Phase
2.2.2. RW Periodicity in the Deconfined Phase
- Trivial-image: for ,
- Nontrivial-images: for , for ,
2.3. Roberge–Weiss Endpoint
2.4. Shift Symmetry Breaking
3. Interplay of Imaginary Chemical Potential
- Prepare lattice QCD data for several observables at finite .
- Prepare a suitable effective model which reproduces the RW periodicity and the transition.
- Set initial model parameters.
- Calculate observables by using the model and compare them.
- Reset model parameters.
3.1. Analytic Continuation
3.2. Boundary Condition of Fermion for the Temporal Direction
3.3. Aharonov–Bohm Phase
- flux insertion to holes of spatial closed loops.
- Exchanging of i-th and -th quarks.
- Moving of the quark along loops.
4. NJL-Type Model at Finite Imaginary Chemical Potential
4.1. Nambu–Jona–Lasinio Model
4.2. Polyakov-Loop Extended Nambu–Jona–Lasinio Model
5. Application of Imaginary Chemical Potential to Explore the QCD Phase Diagram
5.1. Analytic Continuation Method
5.2. Canonical Ensemble Method
5.2.1. Approach 1: Modified Polyakov-Loop Representation
5.2.2. Approach 2: Trivial -Image Restriction
5.3. Lee–Yang Zero Analysis
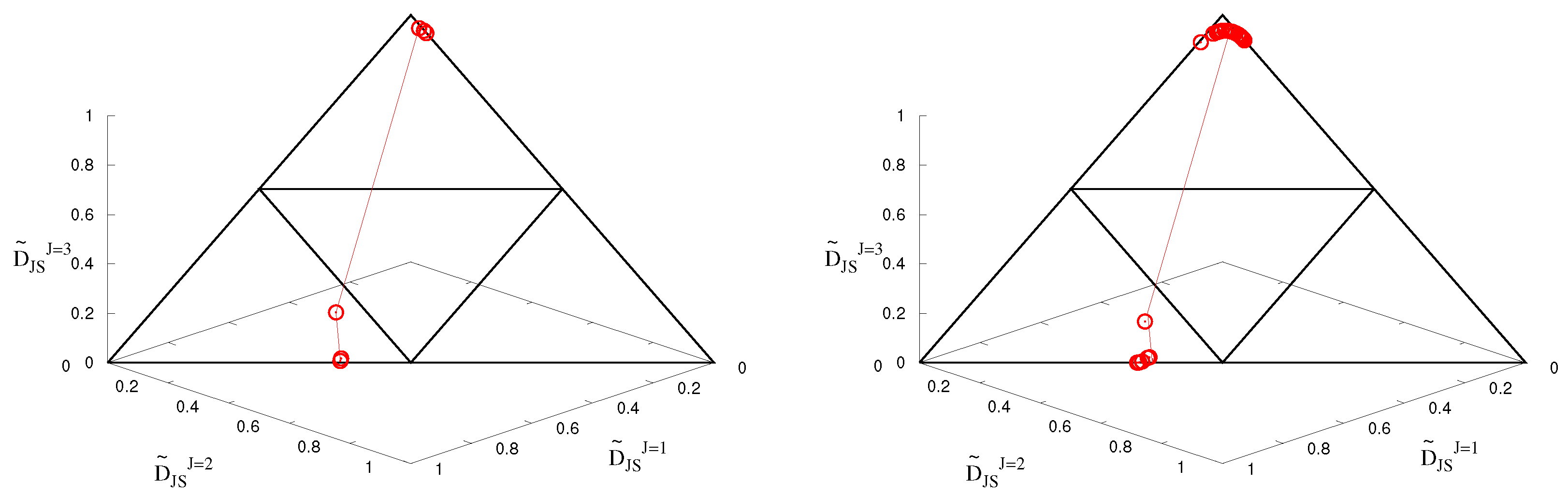
6. Similarities Measurement
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- De Forcrand, P. Simulating QCD at finite density. PoS 2009, LAT2009, 010. [Google Scholar]
- Parisi, G.; Wu, Y.S. Perturbation Theory Without Gauge Fixing. Sci. Sin. 1981, 24, 483. [Google Scholar]
- Parisi, G. On complex probabilities. Phys. Lett. 1983, B131, 393–395. [Google Scholar] [CrossRef]
- Witten, E. Analytic Continuation Of Chern-Simons Theory. AMS/IP Stud. Adv. Math. 2011, 50, 347–446. [Google Scholar]
- Cristoforetti, M.; Di Renzo, F.; Scorzato, L. New approach to the sign problem in quantum field theories: High density QCD on a Lefschetz thimble. Phys. Rev. 2012, D86, 074506. [Google Scholar] [CrossRef]
- Fujii, H.; Honda, D.; Kato, M.; Kikukawa, Y.; Komatsu, S.; Sano, T. Hybrid Monte Carlo on Lefschetz thimbles—A study of the residual sign problem. JHEP 2013, 1310, 147. [Google Scholar] [CrossRef]
- Mori, Y.; Kashiwa, K.; Ohnishi, A. Toward solving the sign problem with path optimization method. Phys. Rev. 2017, D96, 111501. [Google Scholar] [CrossRef]
- Mori, Y.; Kashiwa, K.; Ohnishi, A. Application of a neural network to the sign problem via the path optimization method. PTEP 2018, 2018, 023B04. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. 2004, B591, 277–284. [Google Scholar] [CrossRef]
- Haas, L.M.; Braun, J.; Pawlowski, J.M. On the QCD phase diagram at finite chemical potential. AIP Conf. Proc. 2011, 1343, 459–461. [Google Scholar] [CrossRef]
- Biernat, E.P.; Gross, F.; Peña, T.; Stadler, A. Confinement, quark mass functions, and spontaneous chiral symmetry breaking in Minkowski space. Phys. Rev. 2014, D89, 016005. [Google Scholar] [CrossRef]
- Fischer, C.S. QCD at finite temperature and chemical potential from Dyson–Schwinger equations. Prog. Part. Nucl. Phys. 2019, 105, 1–60. [Google Scholar] [CrossRef]
- Biernat, E.P.; Gross, F.; Peña, M.T.; Stadler, A.; Leitão, S. Quark mass function from a one-gluon-exchange-type interaction in Minkowski space. Phys. Rev. 2018, D98, 114033. [Google Scholar] [CrossRef]
- Miyahara, A.; Torigoe, Y.; Kouno, H.; Yahiro, M. Equation of state and transition temperatures in the quark-hadron hybrid model. Phys. Rev. 2016, D94, 016003. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Light Quarks at Low Temperatures. Phys. Lett. 1987, B184, 83–88. [Google Scholar] [CrossRef]
- Allton, C.; Doring, M.; Ejiri, S.; Hands, S.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Redlich, K. Thermodynamics of two flavor QCD to sixth order in quark chemical potential. Phys. Rev. 2005, D71, 054508. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. Is there still any Tc mystery in lattice QCD? Results with physical masses in the continuum limit III. JHEP 2010, 9, 073. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K. Fluctuations of conserved charges at finite temperature from lattice QCD. JHEP 2012, 01, 138. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. QCD equation of state at nonzero chemical potential: Continuum results with physical quark masses at order mu2. JHEP 2012, 8, 053. [Google Scholar] [CrossRef]
- Hasenfratz, A.; Toussaint, D. Canonical ensembles and nonzero density quantum chromodynamics. Nucl. Phys. 1992, B371, 539–549. [Google Scholar] [CrossRef]
- Alexandru, A.; Faber, M.; Horvath, I.; Liu, K.F. Lattice QCD at finite density via a new canonical approach. Phys. Rev. 2005, D72, 114513. [Google Scholar] [CrossRef]
- Kratochvila, S.; de Forcrand, P. QCD at zero baryon density and the Polyakov loop paradox. Phys. Rev. 2006, D73, 114512. [Google Scholar] [CrossRef]
- De Forcrand, P.; Kratochvila, S. Finite density QCD with a canonical approach. Nucl. Phys. Proc. Suppl. 2006, 153, 62–67. [Google Scholar] [CrossRef] [Green Version]
- Li, A.; Alexandru, A.; Liu, K.F.; Meng, X. Finite density phase transition of QCD with Nf = 4 and Nf = 2 using canonical ensemble method. Phys. Rev. 2010, D82, 054502. [Google Scholar] [CrossRef]
- Roberge, A.; Weiss, N. Gauge Theories With Imaginary Chemical Potential and the Phases of QCD. Nucl. Phys. 1986, B275, 734. [Google Scholar] [CrossRef]
- Sato, M. Topological discrete algebra, ground state degeneracy, and quark confinement in QCD. Phys. Rev. 2008, D77, 045013. [Google Scholar] [CrossRef]
- Wen, X.G. Topological Order in Rigid States. Int. J. Mod. Phys. 1990, B4, 239. [Google Scholar] [CrossRef]
- Kashiwa, K.; Ohnishi, A. Topological feature and phase structure of QCD at complex chemical potential. Phys. Lett. 2015, B750, 282–286. [Google Scholar] [CrossRef]
- Kashiwa, K.; Ohnishi, A. Quark number holonomy and confinement-deconfinement transition. Phys. Rev. 2016, D93, 116002. [Google Scholar] [CrossRef]
- Kashiwa, K.; Ohnishi, A. Topological deconfinement transition in QCD at finite isospin density. Phys. Lett. 2017, B772, 669–674. [Google Scholar] [CrossRef]
- D’Elia, M.; Lombardo, M.P. Finite density QCD via imaginary chemical potential. Phys. Rev. 2003, D67, 014505. [Google Scholar] [CrossRef]
- De Forcrand, P.; Philipsen, O. The QCD phase diagram for small densities from imaginary chemical potential. Nucl. Phys. 2002, B642, 290–306. [Google Scholar] [CrossRef]
- De Forcrand, P.; Philipsen, O. The QCD phase diagram for three degenerate flavors and small baryon density. Nucl. Phys. 2003, B673, 170–186. [Google Scholar] [CrossRef]
- D’Elia, M.; Lombardo, M.P. QCD thermodynamics from an imaginary mu(B): Results on the four flavor lattice model. Phys. Rev. 2004, D70, 074509. [Google Scholar] [CrossRef]
- Chen, H.S.; Luo, X.Q. Phase diagram of QCD at finite temperature and chemical potential from lattice simulations with dynamical Wilson quarks. Phys. Rev. 2005, D72, 034504. [Google Scholar] [CrossRef]
- Bonati, C.; Cossu, G.; D’Elia, M.; Sanfilippo, F. The Roberge-Weiss endpoint in Nf = 2 QCD. Phys. Rev. 2011, D83, 054505. [Google Scholar] [CrossRef]
- Nagata, K.; Nakamura, A. Imaginary Chemical Potential Approach for the Pseudo-Critical Line in the QCD Phase Diagram with Clover-Improved Wilson Fermions. Phys. Rev. 2011, D83, 114507. [Google Scholar] [CrossRef]
- Bonati, C.; de Forcrand, P.; D’Elia, M.; Philipsen, O.; Sanfilippo, F. Chiral phase transition in two-flavor QCD from an imaginary chemical potential. Phys. Rev. 2014, D90, 074030. [Google Scholar] [CrossRef]
- Takahashi, J.; Kouno, H.; Yahiro, M. Quark number densities at imaginary chemical potential in Nf = 2 lattice QCD with Wilson fermions and its model analyses. Phys. Rev. 2015, D91, 014501. [Google Scholar] [CrossRef]
- Doi, T.M.; Kashiwa, K. Dirac-mode expansion of quark number density and its implications of the confinement-deconfinement transition. arXiv 2017, arXiv:1706.00614. [Google Scholar]
- Kashiwa, K.; Sasaki, T.; Kouno, H.; Yahiro, M. Two-color QCD at imaginary chemical potential and its impact on real chemical potential. Phys. Rev. 2013, D87, 016015. [Google Scholar] [CrossRef]
- Sakai, Y.; Kashiwa, K.; Kouno, H.; Yahiro, M. Polyakov loop extended NJL model with imaginary chemical potential. Phys. Rev. 2008, D77, 051901. [Google Scholar] [CrossRef]
- Nishida, Y. Phase structures of strong coupling lattice QCD with finite baryon and isospin density. Phys. Rev. 2004, D69, 094501. [Google Scholar] [CrossRef]
- Kawamoto, N.; Miura, K.; Ohnishi, A.; Ohnuma, T. Phase diagram at finite temperature and quark density in the strong coupling limit of lattice QCD for color SU(3). Phys. Rev. 2007, D75, 014502. [Google Scholar] [CrossRef]
- Garcia Martin, R.; Pelaez, J. Chiral condensate thermal evolution at finite baryon chemical potential within Chiral Perturbation Theory. Phys. Rev. 2006, D74, 096003. [Google Scholar] [CrossRef]
- Ayala, A.; Bashir, A.; Dominguez, C.; Gutierrez, E.; Loewe, M.; Raya, A. QCD phase diagram from finite energy sum rules. Phys. Rev. 2011, D84, 056004. [Google Scholar] [CrossRef]
- Gross, D.J.; Pisarski, R.D.; Yaffe, L.G. QCD and Instantons at Finite Temperature. Rev. Mod. Phys. 1981, 53, 43. [Google Scholar] [CrossRef]
- Weiss, N. The Effective Potential for the Order Parameter of Gauge Theories at Finite Temperature. Phys. Rev. 1981, D24, 475. [Google Scholar] [CrossRef]
- Sakamoto, M.; Takenaga, K. On Gauge Symmetry Breaking via Euclidean Time Component of Gauge Fields. Phys. Rev. 2007, D76, 085016. [Google Scholar] [CrossRef]
- Kouno, H.; Sakai, Y.; Kashiwa, K.; Yahiro, M. Roberge-Weiss phase transition and its endpoint. J. Phys. 2009, G36, 115010. [Google Scholar] [CrossRef]
- Kashiwa, K.; Yahiro, M.; Kouno, H.; Matsuzaki, M.; Sakai, Y. Correlations among discontinuities in the QCD phase diagram. J. Phys. 2009, G36, 105001. [Google Scholar] [CrossRef]
- De Forcrand, P.; Philipsen, O. Constraining the QCD phase diagram by tricritical lines at imaginary chemical potential. Phys. Rev. Lett. 2010, 105, 152001. [Google Scholar] [CrossRef] [PubMed]
- D’Elia, M.; Sanfilippo, F. The Order of the Roberge-Weiss endpoint (finite size transition) in QCD. Phys. Rev. 2009, D80, 111501. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Mariti, M.; Mesiti, M.; Negro, F.; Sanfilippo, F. Roberge-Weiss endpoint at the physical point of Nf = 2 + 1 QCD. Phys. Rev. 2016, D93, 074504. [Google Scholar] [CrossRef]
- Bonati, C.; Calore, E.; D’Elia, M.; Mesiti, M.; Negro, F.; Sanfilippo, F.; Schifano, S.F.; Silvi, G.; Tripiccione, R. Roberge-Weiss endpoint and chiral symmetry restoration in Nf = 2 + 1 QCD. Phys. Rev. 2019, D99, 014502. [Google Scholar] [CrossRef]
- Goswami, J.; Karsch, F.; Lahiri, A.; Schmidt, C. QCD phase diagram for finite imaginary chemical potential with HISQ fermions. arXiv 2018, arXiv:1811.02494. [Google Scholar]
- Shimizu, H.; Yonekura, K. Anomaly constraints on deconfinement and chiral phase transition. Phys. Rev. 2018, D97, 105011. [Google Scholar] [CrossRef]
- Kikuchi, Y. ’t Hooft Anomaly, Global Inconsistency, and Some of Their Applications. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 2018. [Google Scholar]
- Nishimura, H.; Tanizaki, Y. High-temperature domain walls of QCD with imaginary chemical potentials. arXiv 2019, arXiv:1903.04014. [Google Scholar]
- Kashiwa, K.; Matsuzaki, M.; Kouno, H.; Sakai, Y.; Yahiro, M. Meson mass at real and imaginary chemical potentials. Phys. Rev. 2009, D79, 076008. [Google Scholar] [CrossRef]
- Bilgici, E.; Bruckmann, F.; Gattringer, C.; Hagen, C. Dual quark condensate and dressed Polyakov loops. Phys. Rev. 2008, D77, 094007. [Google Scholar] [CrossRef]
- Bilgici, E.; Bruckmann, F.; Danzer, J.; Gattringer, C.; Hagen, C.; Ilgenfritz, E.M.; Maas, A. Fermionic boundary conditions and the finite temperature transition of QCD. Few Body Syst. 2010, 47, 125–135. [Google Scholar] [CrossRef]
- Bilgici, E. Signatures of Confinement and Chiral Symmetry Breaking In Spectral Quantities of Lattice Dirac Operators. Ph.D. Thesis, University of Graz, Graz, Austria, 2009. [Google Scholar]
- Bruckmann, F.; Endrodi, G. Dressed Wilson loops as dual condensates in response to magnetic and electric fields. Phys. Rev. 2011, D84, 074506. [Google Scholar] [CrossRef]
- Fischer, C.S. Deconfinement phase transition and the quark condensate. Phys. Rev. Lett. 2009, 103, 052003. [Google Scholar] [CrossRef]
- Fischer, C.S.; Mueller, J.A. Chiral and deconfinement transition from Dyson-Schwinger equations. Phys. Rev. 2009, D80, 074029. [Google Scholar] [CrossRef]
- Kashiwa, K.; Kouno, H.; Yahiro, M. Dual quark condensate in the Polyakov-loop extended NJL model. Phys. Rev. 2009, D80, 117901. [Google Scholar] [CrossRef]
- Gatto, R.; Ruggieri, M. Dressed Polyakov loop and phase diagram of hot quark matter under magnetic field. Phys. Rev. 2010, D82, 054027. [Google Scholar] [CrossRef]
- Zhang, Z.; Miao, Q. Dual condensates at finite isospin chemical potential. Phys. Lett. B 2015, 753, 670–676. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, H. Dual meson condensates in the Polyakov-loop extended linear sigma model. arXiv 2017, arXiv:1705.09953. [Google Scholar]
- Xu, F.; Mao, H.; Mukherjee, T.K.; Huang, M. Dressed Polyakov loop and flavor dependent phase transitions. Phys. Rev. 2011, D84, 074009. [Google Scholar] [CrossRef]
- Sasagawa, S.; Tanaka, H. The separation of the chiral and deconfinement phase transitions in the curved space-time. Prog. Theor. Phys. 2012, 128, 925–939. [Google Scholar] [CrossRef]
- Flachi, A. Deconfinement transition and Black Holes. Phys. Rev. 2013, D88, 041501. [Google Scholar] [CrossRef]
- Benič, S. Physical interpretation of the dressed Polyakov loop in the Nambu-Jona-Lasinio model. Phys. Rev. 2013, D88, 077501. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Huang, S.; Schreiber, B. Statistical mechanics of relativistic anyon-like systems. Nucl. Phys. B 1994, 426, 644–660. [Google Scholar] [CrossRef]
- Kondo, K.I. Toward a first-principle derivation of confinement and chiral-symmetry-breaking crossover transitions in QCD. Phys. Rev. 2010, D82, 065024. [Google Scholar] [CrossRef]
- Kashiwa, K.; Hell, T.; Weise, W. Nonlocal Polyakov-Nambu-Jona-Lasinio model and imaginary chemical potential. Phys. Rev. 2011, D84, 056010. [Google Scholar] [CrossRef]
- Kitazawa, M.; Koide, T.; Kunihiro, T.; Nemoto, Y. Chiral and color superconducting phase transitions with vector interaction in a simple model. Prog. Theor. Phys. 2002, 108, 929–951. [Google Scholar] [CrossRef]
- Kashiwa, K.; Kouno, H.; Sakaguchi, T.; Matsuzaki, M.; Yahiro, M. Chiral phase transition in an extended NJL model with higher-order multi-quark interactions. Phys. Lett. 2007, B647, 446–451. [Google Scholar] [CrossRef]
- Kashiwa, K.; Kouno, H.; Matsuzaki, M.; Yahiro, M. Critical endpoint in the Polyakov-loop extended NJL model. Phys. Lett. 2008, B662, 26–32. [Google Scholar] [CrossRef]
- Sugano, J.; Takahashi, J.; Ishii, M.; Kouno, H.; Yahiro, M. Determination of the strength of the vector-type four-quark interaction in the entanglement Polyakov-loop extended Nambu-Jona-Lasinio model. Phys. Rev. 2014, D90, 037901. [Google Scholar] [CrossRef]
- Braun, J.; Gies, H.; Pawlowski, J.M. Quark Confinement from Color Confinement. Phys. Lett. 2010, B684, 262–267. [Google Scholar] [CrossRef]
- Roessner, S.; Ratti, C.; Weise, W. Polyakov loop, diquarks and the two-flavour phase diagram. Phys. Rev. 2007, D75, 034007. [Google Scholar] [CrossRef]
- Schaefer, B.J.; Pawlowski, J.M.; Wambach, J. The Phase Structure of the Polyakov—Quark-Meson Model. Phys. Rev. 2007, D76, 074023. [Google Scholar] [CrossRef]
- Haas, L.M.; Stiele, R.; Braun, J.; Pawlowski, J.M.; Schaffner-Bielich, J. Improved Polyakov-loop potential for effective models from functional calculations. Phys. Rev. 2013, D87, 076004. [Google Scholar] [CrossRef]
- Meisinger, P.N.; Miller, T.R.; Ogilvie, M.C. Phenomenological equations of state for the quark gluon plasma. Phys. Rev. 2002, D65, 034009. [Google Scholar] [CrossRef]
- Pisarski, R.D. Why the quark gluon plasma isn’t a plasma. In Proceedings of the Strong and Electroweak Matter Meeting (SEWM), Marseille, France, 13–17 June 2000; pp. 107–117. [Google Scholar] [CrossRef]
- Dumitru, A.; Pisarski, R.D. Degrees of freedom and the deconfining phase transition. Phys. Lett. 2002, B525, 95–100. [Google Scholar] [CrossRef]
- Scavenius, O.; Dumitru, A.; Lenaghan, J.T. The K/pi ratio from condensed Polyakov loops. Phys. Rev. 2002, C66, 034903. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. 2006, D73, 014019. [Google Scholar] [CrossRef]
- Dumitru, A.; Guo, Y.; Hidaka, Y.; Altes, C.P.K.; Pisarski, R.D. How Wide is the Transition to Deconfinement? Phys. Rev. 2011, D83, 034022. [Google Scholar] [CrossRef]
- Fukushima, K.; Kashiwa, K. Polyakov loop and QCD thermodynamics from the gluon and ghost propagators. Phys. Lett. 2013, B723, 360–364. [Google Scholar] [CrossRef]
- Kashiwa, K.; Pisarski, R.D.; Skokov, V.V. Critical endpoint for deconfinement in matrix and other effective models. Phys. Rev. 2012, D85, 114029. [Google Scholar] [CrossRef]
- Kashiwa, K.; Pisarski, R.D. Roberge-Weiss transition and ’t Hooft loops. Phys. Rev. 2013, D87, 096009. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Boyda, D.L.; Goy, V.A.; Molochkov, A.V.; Nakamura, A.; Nikolaev, A.A.; Zakharov, V.I. New approach to canonical partition functions computation in Nf = 2 lattice QCD at finite baryon density. Phys. Rev. 2017, D95, 094506. [Google Scholar] [CrossRef]
- Karbstein, F.; Thies, M. How to get from imaginary to real chemical potential. Phys. Rev. D 2007, 75, 025003. [Google Scholar] [CrossRef]
- Kouji, K.; Hiroaki, K. Roberge-Weiss periodicity, canonical sector and modified Polyakov-loop. arXiv 2019, arXiv:1903.11737. [Google Scholar]
- Yang, C.N.; Lee, T.D. Statistical theory of equations of state and phase transitions. 1. Theory of condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] [CrossRef]
- Nakamura, A.; Nagata, K. Probing QCD phase structure using baryon multiplicity distribution. PTEP 2016, 2016, 033D01. [Google Scholar] [CrossRef]
- Nagata, K.; Kashiwa, K.; Nakamura, A.; Nishigaki, S.M. Lee-Yang zero distribution of high temperature QCD and the Roberge-Weiss phase transition. Phys. Rev. 2015, D91, 094507. [Google Scholar] [CrossRef]
- Wakayama, M.; Borynakov, V.G.; Boyda, D.L.; Goy, V.A.; Iida, H.; Molochkov, A.V.; Nakamura, A.; Zakharov, V.I. Lee-Yang zeros in lattice QCD for searching phase transition points. arXiv 2018, arXiv:1802.02014. [Google Scholar]
- Kashiwa, K.; Ohnishi, A. Investigation of confinement-deconfinement transition via probability distributions. arXiv 2017, arXiv:1712.06220. [Google Scholar]
- Almasi, G.A.; Friman, B.; Morita, K.; Lo, P.M.; Redlich, K. Fourier coefficients of the net-baryon number density and chiral criticality. arXiv 2018, arXiv:1805.04441. [Google Scholar]
- Ejiri, S.; Karsch, F.; Redlich, K. Hadronic fluctuations at the QCD phase transition. Phys. Lett. 2006, B633, 275–282. [Google Scholar] [CrossRef]
- Karsch, F.; Redlich, K. Probing freeze-out conditions in heavy ion collisions with moments of charge fluctuations. Phys. Lett. 2011, B695, 136–142. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef] [Green Version]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashiwa, K. Imaginary Chemical Potential, NJL-Type Model and Confinement–Deconfinement Transition. Symmetry 2019, 11, 562. https://doi.org/10.3390/sym11040562
Kashiwa K. Imaginary Chemical Potential, NJL-Type Model and Confinement–Deconfinement Transition. Symmetry. 2019; 11(4):562. https://doi.org/10.3390/sym11040562
Chicago/Turabian StyleKashiwa, Kouji. 2019. "Imaginary Chemical Potential, NJL-Type Model and Confinement–Deconfinement Transition" Symmetry 11, no. 4: 562. https://doi.org/10.3390/sym11040562




