Abstract
Temperature dependence of the magnetic field penetration depth was calculated for water intercalated sodium cobaltate superconductor NaCoOHO. Assuming that the system is in the chiral d+id–wave superconducting state, it was shown that the shifting of the excitation spectrum nodal points off the normal phase Fermi surface due to variation of the sodium content x changes the functional form of the temperature dependence of from exponential to linear in the low temperatures region. It is argued that this change in the functional form of T–dependence of the can serve as a proof for the chiral symmetry of the superconducting order parameter in the sodium cobaltate.
1. Introduction
Unusual properties of the superconducting state of the electron subsystem in sodium cobaltate NaCoO are due to the quasi-two-dimensional nature of the current carrier dynamics, as well as the triangular symmetry of the conducting layers of the crystal lattice formed by cobalt ions [1,2]. Cooper instability in these compounds occurs in the sodium content region under water intercallation [3,4,5], and the maximum critical temperature does not exceed 5 K.
According to the experimental data on spin-lattice relaxation [6,7,8,9,10] and specific heat [11,12,13], there must be nodal points in the excitation spectrum of Bogolyubov quasiparticles. Besides, the drop of the spin contribution to the knight shift with decreasing temperature below [14,15,16,17] points to the spin-singlet superconductivity.
In the paper [18] it was shown that the mentioned experimental features can be described on the basis of a microscopic approach, assuming that the system is in the chiral d+id-wave superconducting state, but the pairing occurs between the holes which are not on the nearest, but on the next nearest cobalt ions. Otherwise, the nodal (or rather Dirac) points are located only at the edges and in the center of the Brillouin zone and thus could not appear on the Fermi surface of the normal phase.
Complete suppression of Cooper pairing on the nearest sites (as it was supposed in [18]) is possible due to strong Coulomb repulsion of holes from the first coordination sphere. Since, however, in sodium cobaltates is not large, the study of superconductivity in these systems cannot be limited by taking into account the pairing between holes only from the second coordination sphere, it is also necessary to include pairings of the holes located on the nearest ions. In this case, as it was shown in [19], it is also possible for nodal points, at a certain value x, to be on the Fermi surface of normal phase, but for this it is necessary that the pairing amplitude for holes on the next nearest cobalt ions exceeded the pairing amplitude for holes on the nearest ions .
Vanishing only at certain points in the Brillouin zone is an important feature of the complex order parameter with d+id–type of symmetry. For example, for d– and d–pairings (separately forbidden by the triangular lattice symmetry) the whole lines of zeros are formed in the Brillouin zone and, therefore, the nodal points in the excitation spectrum of Bogolyubov quasiparticles exist on the Fermi surface at any current carriers concentration. For d+id pairing, nodal points on the Fermi surface can appear only at certain values of .
Given the above, we can assume that if the chiral order parameter is actually realized in sodium cobaltates, and the nodal points of this order parameter are on the Fermi surface at some value of x (from the interval ), as stated in [18], then changing x should obviously shift these nodal points off the Fermi surface. This should necessarily lead for the gap to appear in the Bogolyubov quasi-particles excitation spectrum on the entire Fermi surface and, therefore, to the changes in the temperature dependence of various thermodynamic quantities in the superconducting state.
To verify the possibility of experimental observation of this effect in the sodium cobaltate NaCoOHO, and, therefore, to prove that the order parameter in these materials has a d+id-wave symmetry, we study theoretically modifications of the temperature dependence of the magnetic field penetration depth when x changes in the range in which Cooper instability occurs.
The paper is organized as follows. In the second section, a microscopic model of sodium cobaltates is formulated. The third section discusses in detail the formula for calculating the temperature dependence of the London penetration depth. The fourth section presents the results of numerical calculations of as a function of temperature. The final fifth section presents the main conclusion of the study. For convenience, cumbersome calculations were moved in Appendix A and Appendix B.
2. Model
Microscopic three-band model for sodium cobaltates, accounting for all orbitals of cobalt ions and 2p orbitals of oxygen ions, was elaborated in [20] (LDA), [21] (DMFT), [22] (FRG). It was found that only one band, formed predominantly by 3d-orbitals (), intersects Fermi level, so that Fermi surface is represented by only one hole pocket around -point in the Brillouin zone. At the same time, another LDA-calculations at [23,24] besides the large Fermi surface around -point of the Brillouin zone give also six small -pockets in the vicinity of K-points. However, according to ARPES data [25,26,27] in the wide doping range x, there is only one wide Fermi surface in the vicinity of -point. Thus we assume that electronic structure of the sodium cobaltates in the doping range of interest can be well described within the effective one-band or -band model [28]. The dispersion law of the hole-like quasiparticles of this band in the tight-binding approximation can be written as
where t – is the tunneling integral between nearest-neighbor cabalt ions, and the wavenumbers and are given in the units of triangular lattice parameter a. The tunneling integral between next-nearest-neighbors was considered to be small here and hence was discarded. Though the energy spectrum (1) resembles the spectrum of non-interacting quasiparticles [29], the value of t is assumed to take into account renormalizations due to all interactions in the system. We chose t to be equal to 0.123 eV [28]. Dispersion of in the direction perpendicular to the triangular planes is not taken into account because spacing between the planes in water intercalated sodium cobaltates is fairly large, about 20 Angstroms [3].
Since, in the absence of sodium, the cobaltates are paramagnetic metal, and the compound NaCoO is a band dielectric [1], it is reasonable to assume that the value of corresponds to exactly one hole per cobalt ion in the – band (), and at the number of holes is zero. Therefore, there is a relationship between x and : . Since the interval for x variation we are interested in does not include the vicinity of the point , where the unusual dielectric phase arises, we can assume that the model of -band (1) describes correctly the spectral properties of the sodium cobaltate in the region of the phase diagram where superconductivity is observed.
Without going into the detail of the nature of Cooper instability, we just postulate the existence in the ensemble of holes of a superconducting pairing in the d+id–channel, which gives rise to one superconducting gap in the quasiparticle spectrum. According to this the amplitudes of the superconducting order parameter (), at , will be considered below as parameters of the model. The amplitude will be defined by the critical temperature using the well-known, in the BCS theory [30], relation: (see also [31,32]). The ratio of amplitudes will be determined so that the nodal points of the chiral order parameter were right on the Fermi surface at the optimal value of x (i.e. a value of x corresponding to the maximum critical temperature ). Since the Cooper instability in the sodium cobaltite occurs in the interval , and the maximum equal to 5 K corresponds to the middle of this interval, it seems natural to approximate the concentration dependence of the critical temperature in the given interval by parabola: . The change in the amplitude of the order parameter with temperature will be modelled by the formula
also following from BCS theory.
When calculating the value of , we will also need the distance d between the CoO-layers. According to experimental data [3].
3. Equation for the London Penetration Depth
Evaluation of the magnetic field penetration depth is based on the London equation [33]
describing in the local approximation the linear relationship of the superconducting current density with a magnetic field vector-potential A. A comprehensive description of the methods for calculating the London penetration depth can be found in the textbooks [31,32] and original papers [34,35,36,37]. We shall follow the paper [37] where a simple and physically clear derivation of the formula for is given for arbitrary dispersion laws and gap functions of any symmetry. The formula reads as follows
where
When writing Expressions (4) and (5), the following notations were used: e—electron charge, c—speed of light, ℏ—Planck’s constant, T—temperature in energy units. The Bogoliubov quasiparticle spectrum is expressed in the usual way via the dispersion of holes and the gap function
where , – chemical potential.
Note that summation in Formula (4) runs over three components of the wave vector k: , and . Since the integrand function does not depend on , the triple summation can be reduced to a double one:
where S is the area of the CoO-layer, and d is the, defined above, distance between layers. Derivation of Formulas (4) and (5) could be found in Appendix A.
The right part of Expression (4) can be conveniently written as the sum of two terms
The first term
gives the value of at , and the second term
describes temperature variation of . In Formula (9): —Fermi-Dirac distribution function.
In the case of spin-singlet pairing two types of symmetry of the superconducting order parameter are usually considered: s—and d+id—type. For triangular lattice we write down the order parameter of interest, with d+id–wave symmetry, in the complex form [18,38]:
where are the above-introduced pairing amplitudes between n-th neighbors, and the functions and are defined by expressions
Functions are related to -symmetry of the order parameter, and functions – -symmetry. It should be remembered here that the second harmonics () in (10) are necessary to be accounted for to shift the nodal points of the gap function inside the Brillouin zone on the Fermi contour. In this regard, it is worth clarifying the seemingly contradicting conclusion of the paper [22] on the absence of higher harmonic contributions to the d+id-wave pairing. The fact is that the paper [22] does not take into account both the implied by us intersite interactions, leading to the d+id-pairing, and the intersite Coulomb repulsion, which leads to the suppression of the first harmonic amplitude as compared to the second harmonic amplitude (see formula (10)). As a consequence, the authors of [22] did not obtain the nodal points of the gap function on the Fermi contour for d+id-pairing.
In the paper [37], Formula (4) was used to analyze the temperature dependence of the magnetic field penetration depth in cuprate HTSCs. The current carriers spectrum was constructed as a superposition of square lattice invariants and the tunneling integrals were chosen so as to fit the dispersion curves to the result of –experiments. The order parameter for the cuprates was written as a difference of cosines: . In our case, related to the triangular lattice, quasimomentum dependence of the function is defined by Formula (1) and the order-parameter—by Equation (10).
4. Temperature Dependence of the London Penetration Depth for the Chiral Order Parameter
Given the results of the paper [19] we will choose the ratio between the amplitudes of the and so that the Dirac points of the spectrum were strictly on the Fermi contour at the value , corresponding to the middle of the interval and, respectively, to the maximum value of . For the quasiparticle spectrum (1) and the gap function (10), this condition is satisfied at (see Figure 1). It can be shown (see Appendix B) that in this case the low-temperature corrections to the function are linear in T, i.e., at .
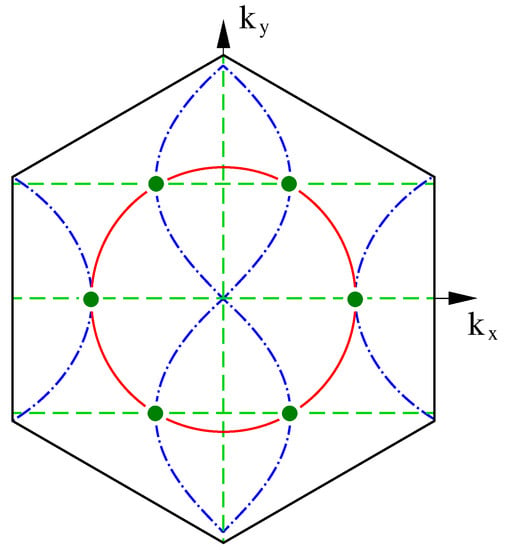
Figure 1.
The Brillouin zone of triangular lattice of cobalt ions. The red solid line represents the Fermi contour at . The blue dash-dotted and green dashed lines show zeros position for respectively real and imaginary parts of the chiral order parameter . The points of the Brillouin zone where all three lines intersect (marked by green circles) indicate the position of the Dirac points of the Bogolyubov spectrum . The model parameters are: eV, , , = 5 K.
When the value of x changes, the nodal points shift and, as a result, the superconducting gap becomes different from zero on the entire Fermi contour. In this case the low-temperature part of the function should become exponential.
This means that if the order parameter in the sodium cobaltates has a chiral symmetry of d+id-type, as it was assumed in the paper [18], then with x variation we should also expect changes in the functional form of temperature dependence of at : for the function should be linear, but for values x other than – exponential.
Note that for pure d (or d) pairing, as well as for s-pairing, the function should not change its analytical form in the low-temperature limit. In the first case, the nodal points of the gap function on the Fermi surface exist at any value of x, which means the for all x is linear in T, and in the second case, there is always a gap on the entire Fermi surface and, therefore, for any x the T-dependence of must be exponential.
An important practical question that arises in this regard is the possibility to observe the modification of the functional form of with changing the value of x in the narrow range , in which sodium cobaltate manifests Cooper instability.
Figure 2 shows the temperature dependence of , calculated at the concentration using the formula (4). The value of at zero temperature turns out to be cm.
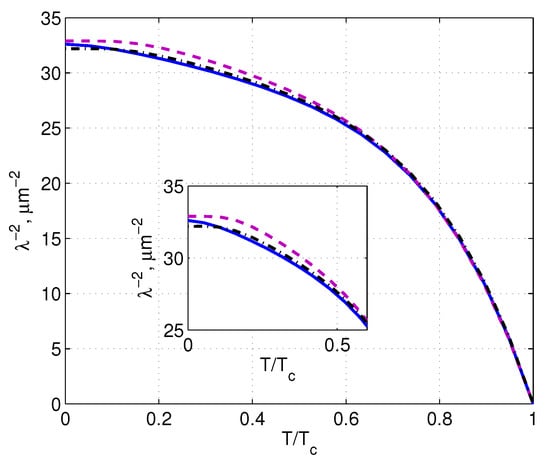
Figure 2.
Temperature dependencies of in NaCoOHO with the chiral (d+id) order parameter for different values of x: the solid curve is for ; dashed — ; dash-dotted — . Parameters of the model are: eV, , , = 5 K. The insert shows the same curves on the enlarged scale.
The other two curves in Figure 2, dashed and dash-dotted, are calculated for x values corresponding to the boundaries of the superconducting region at and respectively.
The analysis of the presented curves (see also the insert in Figure 2) clearly indicates the change in the analytical form of the temperature dependence of in the low-temperature region. It is seen that the solid line has a finite slope relative to the horizontal axis at , which indicates a linear dependence of the function at low temperatures and thus reveal the nodal points in the excitation spectrum on the Fermi surface. The dashed and dash-dotted lines corresponding to the x values lying on the boundaries of the superconducting region on the phase diagram are almost parallel to the horizontal axis in the limit. This means that for these values of x in the Bogolyubov excitation spectrum, there is a gap on the entire Fermi surface.
5. Conclusions
In conclusion, we note that demonstrated possibility to observe the change in the analytical form of the temperature dependence of the inversed square of the London penetration depth in sodium cobaltate NaCoOHO with sodium doping x change may provide an evidence for the chiral order parameter with d+id – wave symmetry to be realized in this compound. For comparison we remind that in cuprate HTSC the Cooper instability occurs in the d–channel. In this case, there are always nodal points in the spectrum of Bogolyubov excitations on the Fermi surface, and therefore the linear dependence of in the low temperature region is preserved at any doping. In paper [39], the linearity of the function was proposed to be considered as a proof of d–wave pairing in cuprates. Similarly, in s-wave superconductors the temperature dependence of is always described by an exponential function.
The insufficient amount of experimental data on the London penetration depth in sodium cobaltates is due to weak motivation of such experiments, we believe. We are aware of just a few of the experiments [40,41] with not good enough accuracy of measurements. The goal of the paper is to suggest to experimentalists a practical way to identify the order parameter symmetry in sodium cobaltate superconductors by analysing the changes in temperature dependence of the inverse square of the London penetration depth with doping.
Author Contributions
Conceptualization, D.D.; Formal analysis, D.D. and A.K.; Investigation, D.D. and A.K.; Methodology, D.D.; Software, A.K.; Supervision, D.D.; Validation, D.D.; Visualization, A.K.; Writing—original draft, D.D.
Funding
The work was financially supported by the Russian Foundation for Basic Research (RFBR) (project no. 18-02-00837) and by the program of the Presidium of the Russian Academy of Sciences No. 12 “Fundamental problems of high-temperature superconductivity”.
Acknowledgments
The authors would like to acknowledge V.V. Val’kov for useful discussions and valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| HTSC | High Temperature Super Conductor |
| ARPES | Angle-Resolved Photo Emission Spectroscopy |
| LDA | Local Density Approximation |
| DMFT | Dynamical Mean-Field Theory |
| FRG | Functional Renormalization Group |
Appendix A
Derivation of the formula for the magnetic field penetration depth in superconductors on the triangular lattice is carried out following the paper [37]. As is known [42], the account for the magnetic field in the conduction electron Hamiltonian in the tight binding approximation leads to the renormalization of the tunneling amplitude :
where and are the radius-vectors of the sites f and m between which the electron tunnels, is the magnetic field vector-potential. In this case the kinetic energy operator for electrons is
where the operator creates (annihilates) an electron on the site f with spin projection .
In the regime of weak magnetic fields (for which only the Peierls substitution (A1) is valid), the vector-potential changes little on the scale of interatomic distances. This fact allows us to expand the phase factor in Expression (A1) in powers of
where , and the value of the vector is taken at the point . In accordance with the expansion (A3), we represent the Hamiltonian (A2) as
Corrections of the first order in to the kinetic energy Hamiltonian in the quasimomentum representation can be written in the form [37]
In this formula, N is the number of crystal lattice sites, and Fourier transforms of the vector-potential and the second quantization operators are determined by expressions: and respectively. The quasiparticle spectrum for the triangular lattice under consideration is given by Formula (1).
Comparing Expression (A5) for with the formula for the energy of charged particles in the vector-potential field:
we find an expression for the paramagnetic part of the electric current density operator
where V is the crystal volume.
For obtaining the average value of the superconducting current density using the Equation (A7), the thermodynamic average should be calculated at least in the linear approximation in , since in the zero approximation . To calculate the average in the superconducting phase with the required accuracy, we add to the Hamiltonian of a superconductor the operator [31,37]:
where is the Bogoliubov quasiparticle spectrum, , are the creation (annihilation) operators of Bogoliubov quasiparticles with quasimomentum k and quantum number .
Next, we express the operator via –operators, and notice that to find the penetration depth , it is sufficient to consider the long-wavelength limit for the vector-potential Fourier transform . Assuming we find
Taking into account Expression (A9), the formula for the Hamiltonian of a superconductor (A8) can be represented in the form
where is the quasiparticle spectrum subject to a weak magnetic field.
If now in Formula (A7) for we also transform to the Bogolyubov quasi-particle operators, then for the average value of the paramagnetic part of the current density in the long-wavelength limit we obtain
Since the thermodynamic averaging in (A11) involves a density matrix with the Hamiltonian (A10), then , where f is the Fermi-Dirac distribution function. Finally given the smallness of , we obtain the expression for the paramagnetic part of the current density:
To calculate the diamagnetic part of the current density , we write down the expression for in the long-wavelength limit using Formulas (A2) and (A3):
Let us rewrite Expression (A13) in terms of –operators and average it over thermodynamic ensemble. Comparing the result with the current density definition (A6), after a few simple transformations, we find:
where and are coefficients of the Bogolyubov – transformation: , .
Combining Expressions (A12) and (A14), we obtain the formula for the net superconducting current density
It is seen that in the normal phase (at ), the superconducting current density , as it should be, turns into zero.
Formally, from Expression (A15) it follows that the superconducting current density is proportional not to the vector-potential , but to the superposition of the dispersion gradient and the gap function gradient . This fact gives reason to suspect the nondiagonality of the tensor connecting the current density with the vector-potential . However, if we consider each projection () of the supercurrent density in Expression (A15) separately and take into account the symmetry of the integrand, then each of these projections turns out to be proportional only to the corresponding projection of the vector-potential :
Numerical calculations show that, for both s – and – wave order parameter symmetry, the coefficient between and in Formula (A16) is actually independent of the value of . Choosing, for definiteness, the direction of the vector along x-axis, and comparing the expression for the superconducting current density (A16) to the London Equation (3) we obtain Formula (4) for the magnetic field penetration depth .
Appendix B
The general idea of calculating the low-temperature corrections to the thermodynamic properties of superconductors is explained in the book [43]. To analyze the low-temperature behavior of the inverse London penetration depth squared in quasi-two-dimensional superconductors on a triangular lattice, consider the situation when the nodal points of the Bogolyubov quasiparticle spectrum are located right on the Fermi surface (see Figure 1). It is obvious that in the limit , the main contribution to the integral in Expression (9) for the function arises from a small neighborhoods of six nodal points, marked in Figure 1 with bold circles. To be definite, consider the contribution to the integral (9) from a small neighborhood of the nodal point C located in the positive domain of the -axis and having coordinates . It is seen that in this point the gradients of the spectrum and the real part of the gap function are directed along the -axis, and the gradient of the imaginary part of — along the -axis. This allows one to expand these functions in the neighborhood of the point C as: , , , where , and are the values of the spectrum, real and imaginary parts of the gap function in the point C respectively. Substituting these expansions in the formula (9) and introducing new variables: , , we get:
where , and the letters next to the symbol of integral mean that the integration is over small neighborhood around the point C.
Further we note that, in the limit , the main contribution to the integral over in Expression (A17) originates on the interval . Therefore, for the integral in formula (A17) we can write approximately
where . Since in the integral over x, the main contribution is due to the neighborhood of zero, the limits of integration over x can be extended to infinity. Given that in this case , we finally find:
Obviously integration over neighborhoods of other nodal points in formula (9) will also lead to linear low-temperature corrections to the value of .
References
- Ivanova, N.N.; Ovchinnikov, S.G.; Korshunov, M.M.; Eremin, I.M.; Kazak, N.V. Specific features of spin, charge, and orbital ordering in cobaltites. Phys. Usp. 2009, 52, 789–810. [Google Scholar] [CrossRef]
- Sakurai, H.; Ihara, Y.; Takada, K. Superconductivity of cobalt oxide hydrate Nax(H3O)zCoO2·yH2O. Phys. C Supercoductivity Appl. 2015, 514, 378–387. [Google Scholar] [CrossRef]
- Takada, K.; Sakurai, H.; Takayama-Muromachi, E.; Izumi, F.; Dilanian, R.; Sasaki, N. Superconductivity in two-dimensional CoO2 layers. Nature 2003, 422, 53–55. [Google Scholar] [CrossRef]
- Schaak, R.E.; Klimczuk, T.; Foo, M.L.; Cava, R.J. Superconductivity phase diagram of NaxCoO2·1.3H2O. Nature 2003, 42, 527–529. [Google Scholar] [CrossRef] [PubMed]
- Jin, R.; Sales, B.C.; Khalifah, P.; Mandrus, D. Observation of bulk superconductivity in NaxCoO2·yH2O and NaxCoO2·yD2O powder and single crystals. Phys. Rev. Lett. 2003, 91, 217001. [Google Scholar] [CrossRef]
- Ishida, K.; Ihara, Y.; Kitagawa, K.; Murakawa, H.; Maeno, Y.; Michioka, C.; Kato, M.; Yoshimura, K.; Takada, K.; Sasaki, T.; et al. Unconventional Superconductivity and Nearly Ferromagnetic Spin Fluctuations in NaxCoO2·yH2O. J. Phys. Soc. Jpn. 2003, 72, 3041. [Google Scholar] [CrossRef]
- Fujimoto, T.; Zheng, G.; Kitaoka, Y.; Meng, R.L.; Cmaidalka, J.; Chu, C.W. Unconventional Superconductivity and Electron Correlations in the Cobalt Oxyhydrate Na0.35CoO2·yH2O. Phys. Rev. Lett. 2004, 92, 047004. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.-Q.; Matano, K.; Meng, R.L.; Cmaidalka, J.; Chu, C.W. Na content dependence of superconductivity and the spin correlations in NaxCoO2·1.3H2O. J. Phys. Condens. Matter 2006, 18, L63. [Google Scholar] [CrossRef]
- Ihara, Y.; Takeya, H.; Ishida, K.; Ikeda, H.; Michioka, C.; Yoshimura, K.; Takada, K.; Sasaki, T.; Sakurai, H.; Takayama-Muromachi, E. Unconventional Superconductivity Induced by Quantum Critical Fluctuations in Hydrate Cobaltate Nax(H3O)zCoO2·yH2O—Relationship between Magnetic Fluctuations and Superconductivity Revealed by Co Nuclear Quadrupole Resonance. J. Phys. Soc. Jpn. 2006, 75, 124714. [Google Scholar] [CrossRef]
- Michioka, C.; Ohta, H.; Itoh, Y.; Yoshimura, K. 59Co Nuclear Quadrupole Resonance Studies of Superconducting and Nonsuperconducting Bilayer Water Intercalated Sodium Cobalt Oxides NaxCoO2·yH2O. J. Phys. Soc. Jpn. 2006, 75, 063701. [Google Scholar] [CrossRef]
- Lorenz, B.; Cmaidalka, J.; Meng, R.L.; Chu, C.W. Thermodynamic properties in the normal and superconducting states of NaxCoO2·yH2O powder measured by heat capacity experiments. Physica C 2004, 402, 106–113. [Google Scholar] [CrossRef][Green Version]
- Yang, H.D.; Lin, J.-Y.; Sun, C.P.; Kang, Y.C.; Huang, C.L.; Takada, K.; Sasaki, T.; Sakurai, H.; Takayama-Muromachi, E. Evidence of nodal superconductivity in Na0.35CoO2·1.3H2O: A specific-heat study. Phys. Rev. B 2005, 71, 020504. [Google Scholar] [CrossRef]
- Jin, R.; Sales, B.C.; Li, S.; Mandrus, D. Dependence of the specific heat of NaxCoO2·yH2O/D2O on sodium and water concentrations. Phys. Rev. B 2005, 72, 060512R. [Google Scholar] [CrossRef]
- Zheng, G.-Q.; Matano, K.; Chen, D.P.; Lin, C.T. Spin singlet pairing in the superconducting state of NaxCoO2·1.3H2O: Evidence from a 59Co Knight shift in a single crystal. Phys. Rev. B 2006, 73, 180503. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Moyoshi, T.; Watanabe, H.; Yokoi, M.; Sato, M. Magnetic Properties of Superconducting Cobalt Oxides NaxCoO2·yH2O. J. Phys. Soc. Jpn. 2006, 75, 074717. [Google Scholar] [CrossRef]
- Ihara, Y.; Ishida, K.; Ohta, H.; Yoshimura, K. Co-NMR Measurements on Crystalline Sample of the Bilayere Hydrate Nax(H3O)zCoO2·yH2O. J. Phys. Soc. Jpn. 2008, 77, 073702. [Google Scholar] [CrossRef]
- Onoda, M.; Takao, K.; Ikeda, T. Spin-singlet superconductivity and antiferromagnetic correlations for the field-aligned powder of the triangular lattice NaxCoO2·yH2O. Physica C 2009, 469, 162–167. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Z. Nodal d + id pairing and topological phases on the triangular lattice of NaxCoO2·yH2O: evidence for an unconventional superconducting state. Phys. Rev. Lett. 2008, 100, 217002. [Google Scholar] [CrossRef] [PubMed]
- Valkov, V.V.; Valkova, T.A.; Mitskan, V.A. Superconducting Phase with the (d + id) Order Parameter in an Ensemble of Hubbard Fermions on the Triangular Lattice. JETP Lett. 2015, 102, 399. [Google Scholar] [CrossRef]
- Korshunov, M.M.; Eremin, I.; Shorikov, A.; Anisimov, V.I.; Renner, M.; Brenig, W. Itinerant in-plane magnetic fluctuations and many-body correlations in NaxCoO2. Phys. Rev. B 2007, 75, 094511. [Google Scholar] [CrossRef]
- Bourgeois, A.; Aligia, A.A.; Rozenberg, M.J. Dynamical Mean Field Theory of an Effective Three-Band Model for NaxCoO2. Phys. Rev. Lett. 2009, 102, 066402. [Google Scholar] [CrossRef]
- Kiesel, M.L.; Platt, C.; Hanke, W.; Thomale, R. Model Evidence of an Anisotropic Chiral d+id-Wave Pairing State for the Water-Intercalated NaxCoO2·yH2O Superconductor. Phys. Rev. Lett. 2013, 111, 097001. [Google Scholar] [CrossRef]
- Lee, K.; Kunes, J.; Pickett, W.E. Charge disproportionation and spin ordering tendencies in NaxCoO2. Phys. Rev. B 2004, 70, 045104. [Google Scholar] [CrossRef]
- Johannes, M.D.; Mazin, I.I.; Singh, D.J.; Papaconstantopoulos, D.A. Erratum: Nesting, Spin Fluctuations, and Odd-Gap Superconductivity in NaxCoO2·yH2O. Phys. Rev. Lett. 2005, 94, 169901. [Google Scholar] [CrossRef]
- Qian, D.; Wray, L.; Hsieh, D.; Viciu, L.; Cava, R.J.; Luo, J.L.; Wu, D.; Wang, N.L.; Hasan, M.Z. Complete d-Band Dispersion Relation in Sodium Cobaltates. Phys. Rev. Lett. 2006, 97, 186405. [Google Scholar] [CrossRef]
- Shimojima, T.; Ishizaka, K.; Tsuda, S.; Kiss, T.; Yokoya, T.; Chainani, A.; Shin, S.; Badica, P.; Yamada, K.; Togano, K. Angle-resolved photoemission study of the cobalt oxide superconductor NaxCoO2·yH2O: observation of the Fermi surface. Phys. Rev. Lett. 2006, 97, 267003. [Google Scholar] [CrossRef]
- Geck, J.; Borisenko, S.V.; Berger, H.; Eschrig, H.; Fink, J.; Knupfer, M.; Koepernik, K.; Koitzsch, A.; Kordyuk, A.A.; Zabolotnyy, V.B.; et al. Anomalous Quasiparticle Renormalization in Na0.73CoO2: Role of Interorbital Interactions and Magnetic Correlations. Phys. Rev. Lett. 2007, 99, 046403. [Google Scholar] [CrossRef]
- Korshunov, M.M.; Eremin, I. Dynamical magnetic susceptibility in the lamellar cobaltate superconductor NaxCoO2·yH2O. Phys. Rev. B 2008, 77, 064510. [Google Scholar] [CrossRef]
- Hanisch, T.; Uhrig, G.S.; Muller-Hartmann, E. Lattice dependence of saturated ferromagnetism in the Hubbard model. Phys. Rev. B 1997, 56, 13960. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Schrieffer, J.R. Theory of Superconductivity; Benjamin: New York, NY, USA, 1964. [Google Scholar]
- Tinkham, M. Introduction to Superconductivity; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- London, F. Superfluids; Dover Publications: New York, NY, USA, 1961. [Google Scholar]
- Misawa, S. London penetration depth in a tight-binding model of layered narrow-band anisotropic superconductors. Phys. Rev. B 1995, 51, 11791. [Google Scholar] [CrossRef]
- Benfatto, L.; Caprara, S.; Castro, C.D. Gap and pseudogap evolution within the charge-ordering scenario for superconducting cuprates. Eur. Phys. J. B 2000, 17, 95. [Google Scholar] [CrossRef]
- Sheehy, D.E.; Davis, T.P.; Franz, M. Unified theory of the ab-plane and c-axis penetration depths of underdoped cuprates. Phys. Rev. B 2004, 70, 054510. [Google Scholar] [CrossRef]
- Eremin, M.V.; Larionov, I.A.; Lyubin, I.E. London penetration depth in the tight binding approximation: Orthorhombic distortion and oxygen isotope effects in cuprates. J. Phys. Condens. Matter 2010, 22, 185704. [Google Scholar] [CrossRef][Green Version]
- Sigrist, M.; Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 1991, 63, 239. [Google Scholar] [CrossRef]
- Hardy, W.N.; Bonn, D.A.; Morgan, D.C.; Liang, R.; Zhang, K. Precision measurements of the temperature dependence of λ in YBa2Cu3O6.95: Strong evidence for nodes in the gap function. Phys. Rev. Lett. 1993, 70, 3999. [Google Scholar] [CrossRef]
- Kanegel, A.; Keren, A.; Patlagan, L.; Chashka, K.B.; King, P.; Amato, A. Muon Spin Relaxation Measurements of NaxCoO2·yH2O. Phys. Rev. Lett. 2004, 92, 257007. [Google Scholar] [CrossRef]
- Higemoto, W.; Oshishi, K.; Koda, A.; Kadono, R.; Ishida, K.; Takada, K.; Sakurai, H.; Takayama-Muromachi, E.; Sasaki, T. Possible unconventional superconductivity in NaxCoO2·yH2O probed by muon spin rotation and relaxation. Phys. Rev. B 2004, 70, 134508. [Google Scholar] [CrossRef]
- Feynman, R.; Leighton, R.; Sands, M. The Feynman Lectures on Physics; Addison-Wesley: London, UK, 1964. [Google Scholar]
- Mineev, V.P.; Samohin, K.V. Introduction to Unconventional Superconductivity; MIPT publishing: Moscow, Russia, 1998. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).