Impact of Nonlinear Thermal Radiation on the Time-Dependent Flow of Non-Newtonian Nanoliquid over a Permeable Shrinking Surface
Abstract
:1. Introduction
2. Formulation of the Problem
3. Numerical Procedure
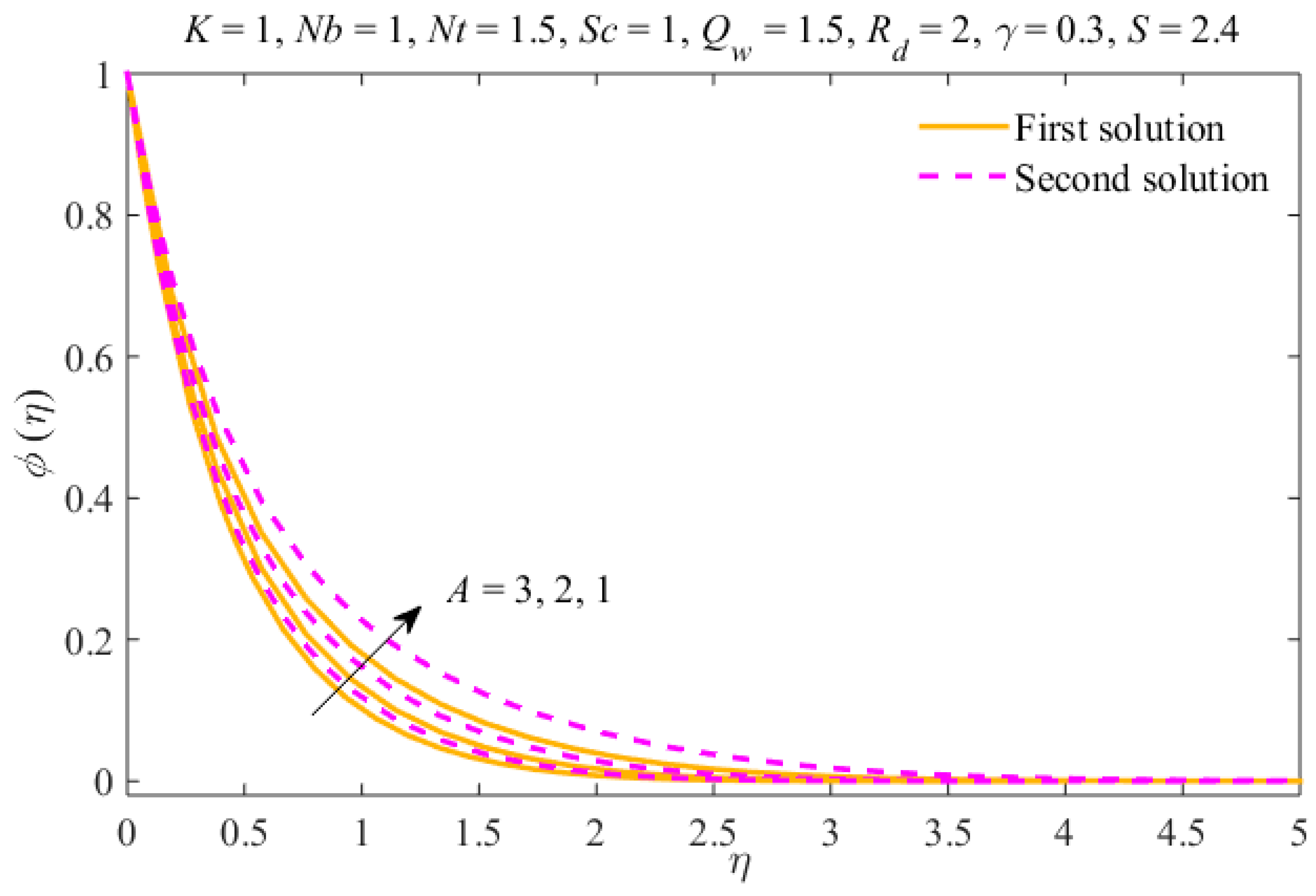
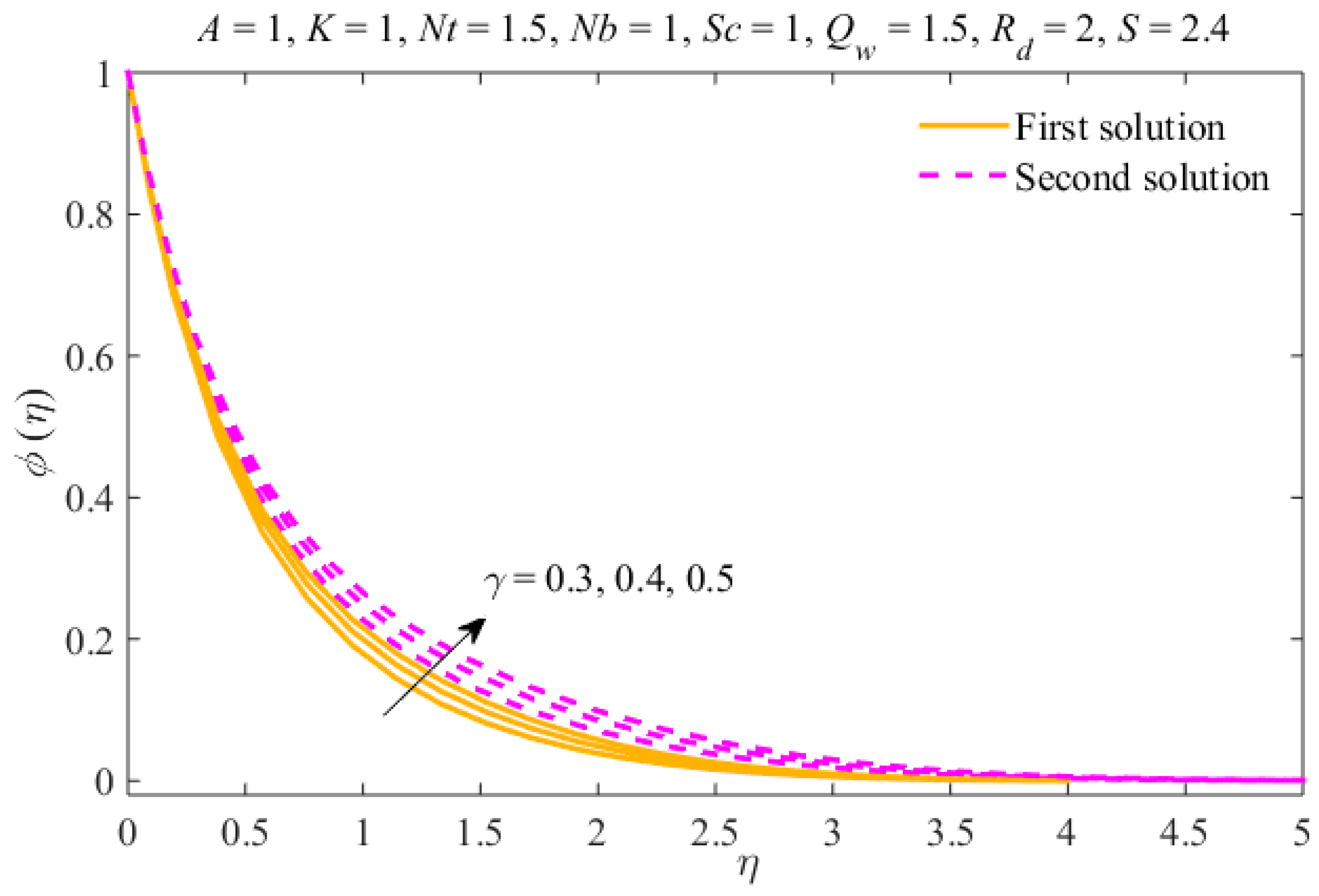
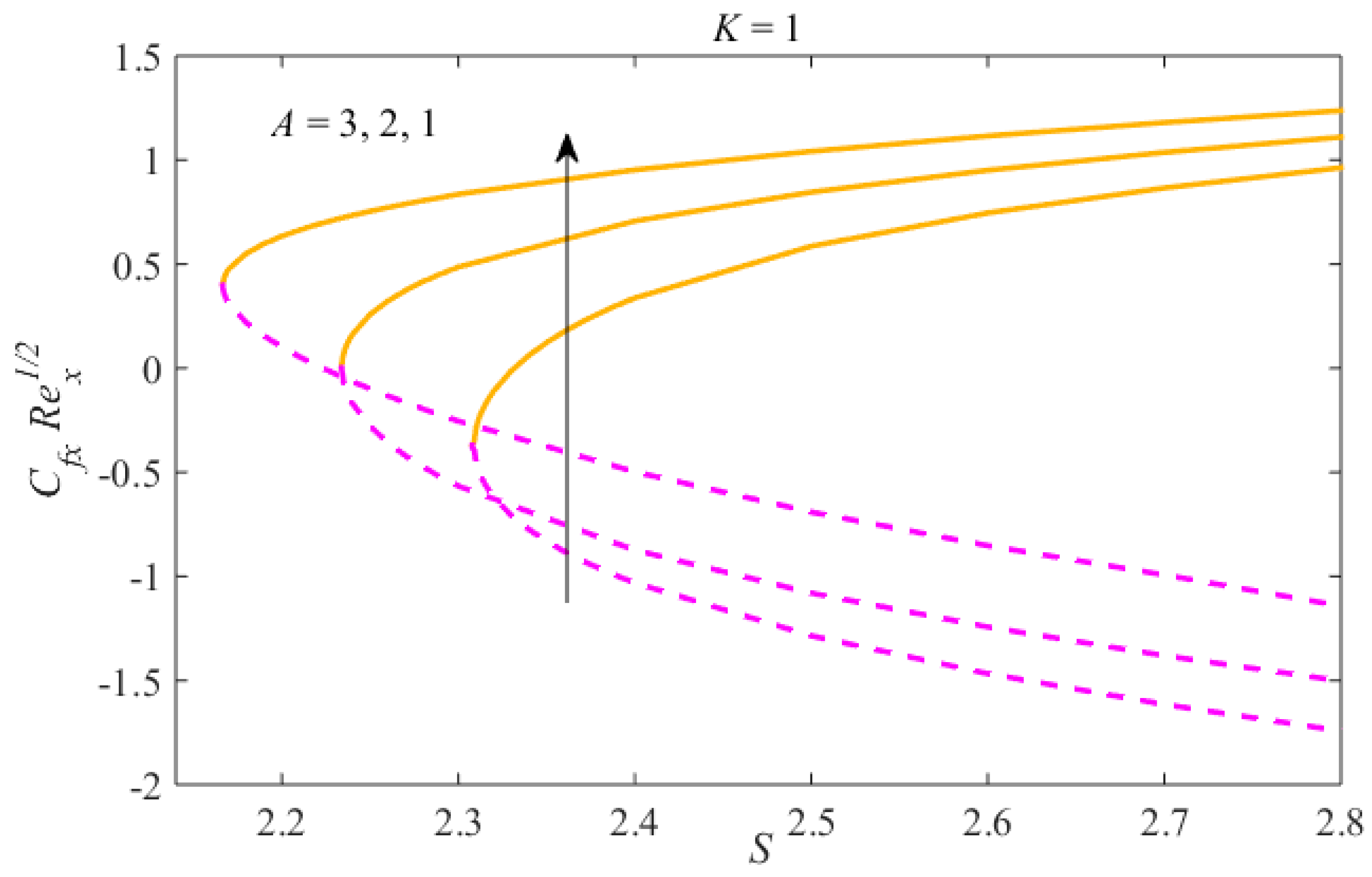
4. Results and Discussion
5. Conclusions
- Multiple results have been obtained for decelerating flow only, and for precise values of .
- The liquid velocity declines in the first result and increases in the second due to . The concentration and temperature fields rise in the first result and diminish in the second result.
- The thicknesses of the concentration and thermal boundary layers increase due to in both results.
- The liquid temperature and nanomaterial concentration decrease due to thermal radiation in both results.
- The nanoparticles distribution can be controlled through the mechanism of Brownian motion and the thermophoresis effect.
- The time-dependent and non-Newtonian parameters delay the separation of the boundary.
Author Contributions
Funding
Conflicts of Interest
References
- Keçebaş, A.; Yürüsoy, M. Similarity solutions of unsteady boundary layer equations of a special third grade fluid. Int. J. Eng. Sci. 2006, 44, 721–729. [Google Scholar] [CrossRef]
- Ellahi, R.; Riaz, A. Analytical solutions for MHD flow in a third-grade fluid with variable viscosity. Math. Comput. Model. 2010, 52, 1783–1793. [Google Scholar] [CrossRef]
- Sahoo, B.; Do, Y. Effects of slip on sheet-driven flow and heat transfer of a third grade fluid past a stretching sheet. Int. Comm. Heat Mass Transf. 2010, 37, 1064–1071. [Google Scholar] [CrossRef]
- Sahoo, B.; Poncet, S. Flow and heat transfer of a third grade fluid past an exponentially stretching sheet with partial slip boundary condition. Int. J. Heat Mass Transf. 2011, 54, 5010–5019. [Google Scholar] [CrossRef] [Green Version]
- Abbasbandy, S.; Hayat, T. On series solution for unsteady boundary layer equations in a special third grade fluid. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3140–3146. [Google Scholar] [CrossRef]
- Rehman, A.; Nadeem, S.; Malik, M.Y. Boundary layer stagnation-point flow of a third grade fluid over an exponentially stretching sheet. Braz. J. Chem. Eng. 2013, 30, 611–618. [Google Scholar] [CrossRef] [Green Version]
- Hussain, T.; Hayat, T.; Shehzad, S.A.; Alsaedi, A.; Chen, B. A model of solar radiation and Joule heating in flow of third grade nanofluid. Z. Nat. A 2015, 70, 177–184. [Google Scholar] [CrossRef]
- Naganthran, K.; Nazar, R.; Pop, I. Unsteady stagnation-point flow and heat transfer of a special third grade fluid past a permeable stretching/shrinking sheet. Sci. Rep. 2016, 6, 24632. [Google Scholar] [CrossRef] [Green Version]
- Reddy, G.J.; Hiremath, A.; Kumar, M. Computational modeling of unsteady third-grade fluid flow over a vertical cylinder: A study of heat transfer visualization. Results Phys. 2018, 8, 671–682. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Rana, P.; Bhargava, R. Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet: A numerical study. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 212–226. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M.; Khan, W.A.; Ayaz, M. Modern development on the features of magnetic field and heat sink/source in Maxwell nanofluid subject to convective heat transport. Phys. Lett. A 2018, 382, 1992–2002. [Google Scholar] [CrossRef]
- Khan, M.; Irfan, M.; Khan, W.A. Impact of heat source/sink on radiative heat transfer to Maxwell nanofluid subject to revised mass flux condition. Results Phys. 2018, 9, 851–857. [Google Scholar] [CrossRef]
- Zaib, A.; Abelman, S.; Chamkha, A.J.; Rashidi, M.M. Entropy generation in a Williamson nanofluid near a stagnation point over a moving plate with binary chemical reaction and activation energy. Heat Transf. Res. 2018, 49, 1131–1149. [Google Scholar] [CrossRef]
- Bibi, M.; Rehman, K.-U.; Malik, M.Y.; Tahir, M. Numerical study of unsteady Williamson fluid flow and heat transfer in the presence of MHD through a permeable stretching surface. Eur. Phys. J. Plus 2018, 133, 154. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Khan, M.I.; Alsaedi, A. Theoretical investigation of Ree-Eyring nanofluid flow with entropy optimization and Arrhenius activation energy between two rotating disks. Comp. Methods Prog. Biomed. 2019, 177, 57–68. [Google Scholar] [CrossRef]
- Aziz, A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1064–1068. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. MHD mixed convection from a vertical plate embedded in a porous medium with a convective boundary condition. Int. J. Therm. Sci. 2010, 49, 1813–1820. [Google Scholar] [CrossRef]
- Ishak, A. Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Appl. Math. Comput. 2014, 217, 837–842. [Google Scholar] [CrossRef]
- Yao, S.; Fang, T.; Zhong, Y. Heat transfer of a generalized stretching/shrinking wall problem with convective boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 752–760. [Google Scholar] [CrossRef]
- Rahman, M.M.; Merkin, J.H.; Pop, I. Mixed convection boundary-layer flow past a vertical flat plate with a convective boundary condition. Acta Mech. 2015, 226, 2441–2460. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Simulations for Maxwell fluid flow past a convectively heated exponentially stretching sheet with nanoparticles. AIP Adv. 2015, 5. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, W.; Haq, R.U. Magnetohydrodynamic (MHD) stagnation point flow of nanofluid past a stretching sheet with convective boundary condition. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1155–1164. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Stagnation point flow of MHD chemically reacting nanofluid over a stretching convective surface with slip and radiative heat. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 695–703. [Google Scholar] [CrossRef]
- Khan, M.; Hashim; Hussain, M.; Azam, M. Magnetohydrodynamic flow of Carreau fluid over a convectively heated surface in the presence of non-linear radiation. J. Magn. Magn. Mater. 2016, 412, 63–68. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A. Analytical study for unsteady nanofluid MHD flow impinging on heated stretching sheet. J. Mol. Liq. 2016, 219, 216–223. [Google Scholar] [CrossRef]
- Fosdick, R.L.; Rajagopal, K.R. Thermodynamics and stability of fluids of third grade. Proc. R. Sot. Lond. A 1980, 339, 351. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Nandy, S.K. Slip effects on unsteady stagnation-point flow and heat transfer over a shrinking sheet. Meccanica 2013, 48, 1599–1606. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Unsteady flow and heat transfer past an axisymmetric permeable shrinking sheet with radiation effect. Int. J. Numer. Meth. Fluids 2011, 67, 1310–1320. [Google Scholar] [CrossRef]
- Rohni, A.M. Flow over an unsteady shrinking sheet with suction in a nanofluid. Int. Conf. Math. Comput. Biol. 2012, 9, 511–519. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Roşca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
- Roşca, N.C.; Pop, I. Mixed convection stagnation point flow past a vertical flat plate with a second order slip: Heat flux case. Int. J. Heat Mass Transf. 2013, 65, 102–109. [Google Scholar] [CrossRef]
- Ridha, A. Aiding flows non-unique similarity solutions of mixed-convection boundary-layer equations. Z. Angew. Math. Phys. 1996, 47, 341–352. [Google Scholar] [CrossRef]

















| S | A | ||||||
|---|---|---|---|---|---|---|---|
| First Solution | Second Solution | First Solution | Second Solution | First Solution | Second Solution | ||
| 2.8 | −3 | 0.9627 | −1.7424 | 1.0894 | 1.0855 | 2.7589 | 2.5893 |
| −2 | 1.1099 | −1.5024 | 1.0863 | 1.0804 | 2.6085 | 2.4075 | |
| −1 | 1.2370 | −1.1420 | 1.0816 | 1.0713 | 2.1800 | 2.0495 | |
| 2.6 | −3 | 0.7457 | −1.4673 | 1.0867 | 1.0831 | 2.5777 | 2.4429 |
| −2 | 0.9505 | −1.2430 | 1.0828 | 1.0770 | 2.4220 | 2.2570 | |
| −1 | 1.1154 | −0.8527 | 1.0766 | 1.0659 | 2.2332 | 2.0209 | |
| 2.4 | −3 | 0.3372 | −1.0314 | 1.0831 | 1.0807 | 2.3910 | 2.3136 |
| −2 | 0.7068 | −0.8738 | 1.0782 | 1.0735 | 2.2324 | 2.1203 | |
| −1 | 0.9524 | −0.4982 | 1.0699 | 1.0602 | 2.0347 | 1.8766 | |
| A | Sc |
|---|---|
| −3 | 2.3079 |
| −2 | 2.2338 |
| −1 | 2.1665 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaib, A.; Khan, U.; Khan, I.; M. Sherif, E.-S.; Nisar, K.S.; Seikh, A.H. Impact of Nonlinear Thermal Radiation on the Time-Dependent Flow of Non-Newtonian Nanoliquid over a Permeable Shrinking Surface. Symmetry 2020, 12, 195. https://doi.org/10.3390/sym12020195
Zaib A, Khan U, Khan I, M. Sherif E-S, Nisar KS, Seikh AH. Impact of Nonlinear Thermal Radiation on the Time-Dependent Flow of Non-Newtonian Nanoliquid over a Permeable Shrinking Surface. Symmetry. 2020; 12(2):195. https://doi.org/10.3390/sym12020195
Chicago/Turabian StyleZaib, A., Umair Khan, Ilyas Khan, El-Sayed M. Sherif, Kottakkaran Sooppy Nisar, and Asiful H. Seikh. 2020. "Impact of Nonlinear Thermal Radiation on the Time-Dependent Flow of Non-Newtonian Nanoliquid over a Permeable Shrinking Surface" Symmetry 12, no. 2: 195. https://doi.org/10.3390/sym12020195







