A Multistable Chaotic Jerk System with Coexisting and Hidden Attractors: Dynamical and Complexity Analysis, FPGA-Based Realization, and Chaos Stabilization Using a Robust Controller
Abstract
:1. Introduction
2. System Description
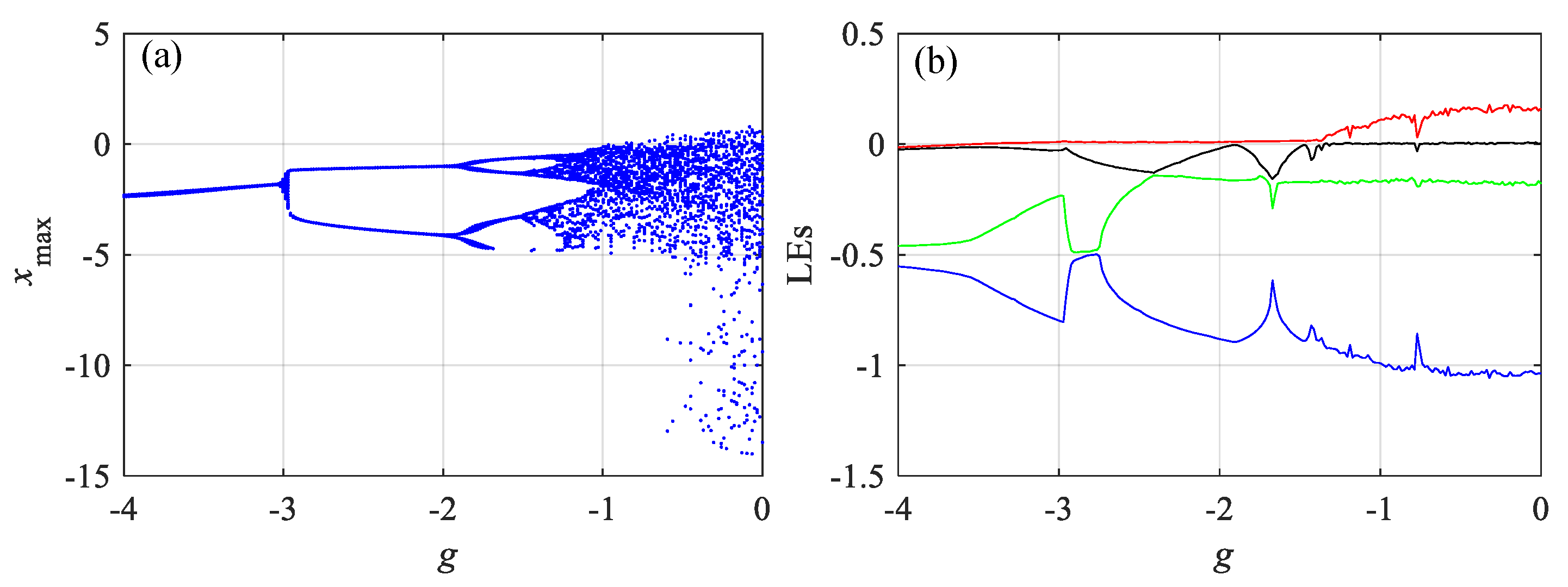
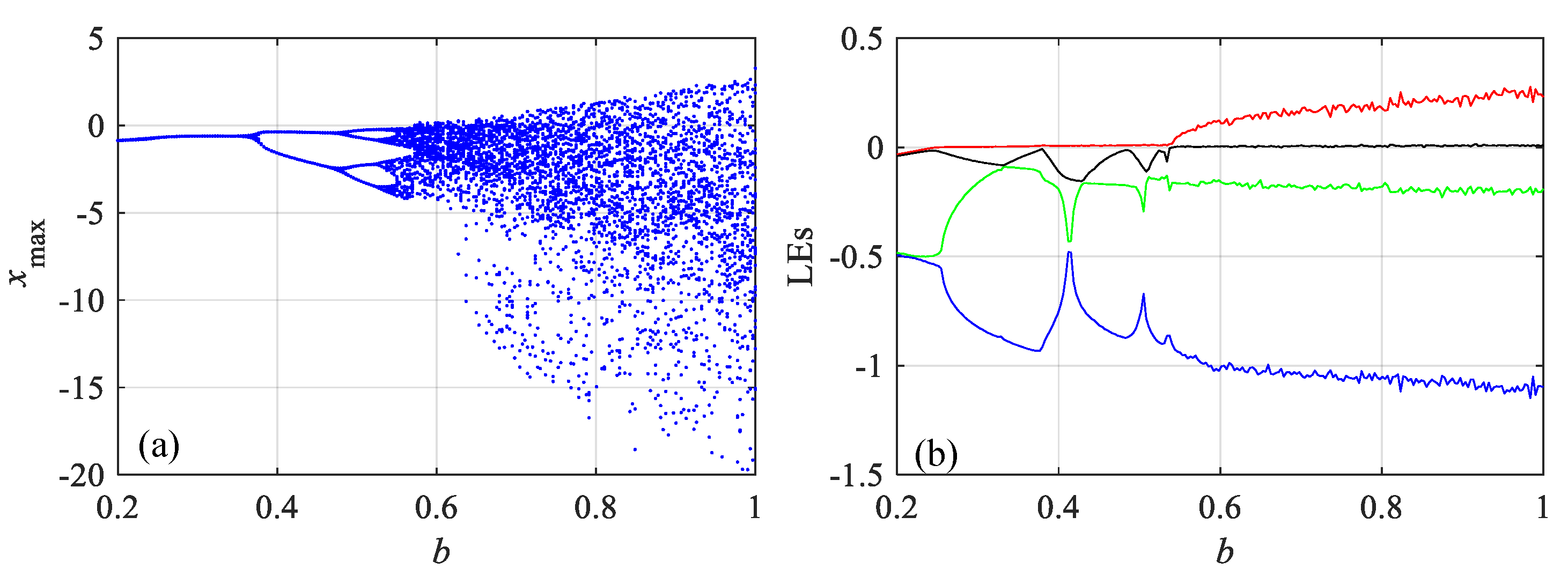
2.1. Dynamical Analysis
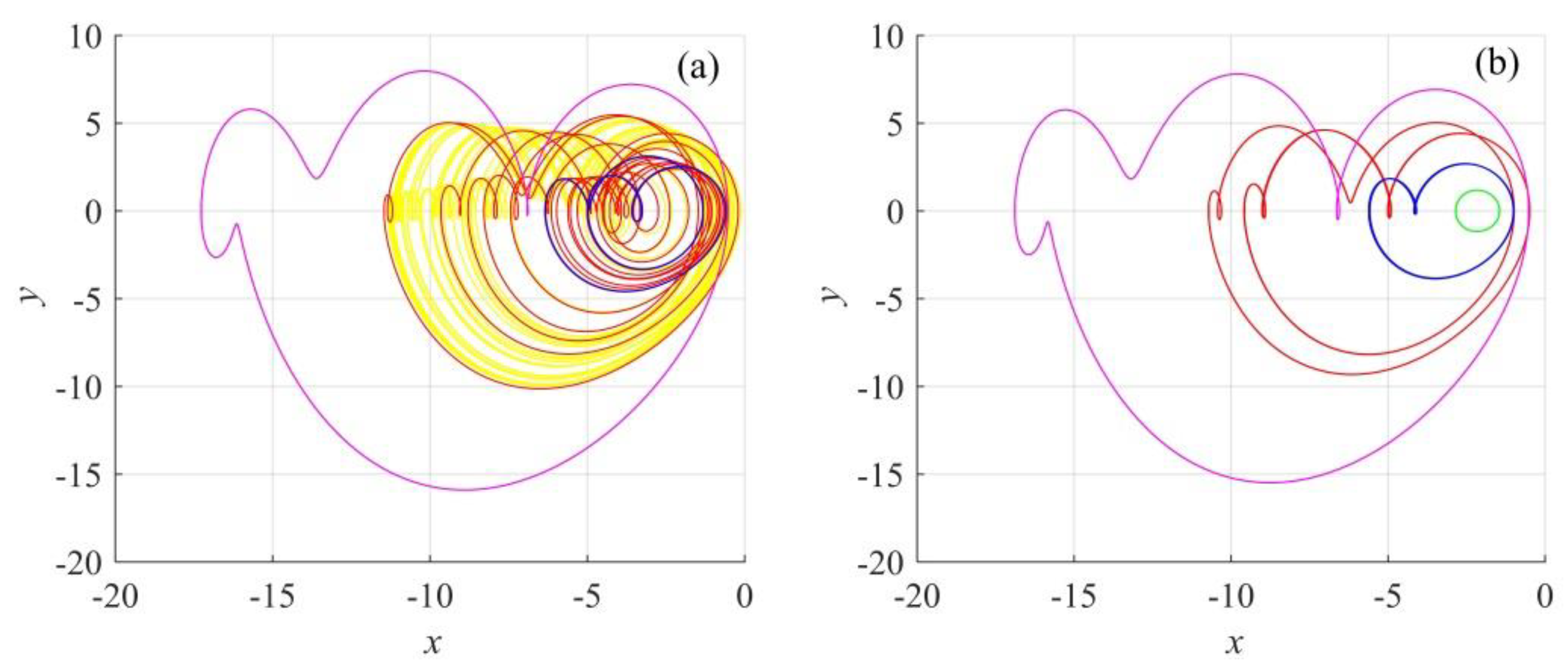
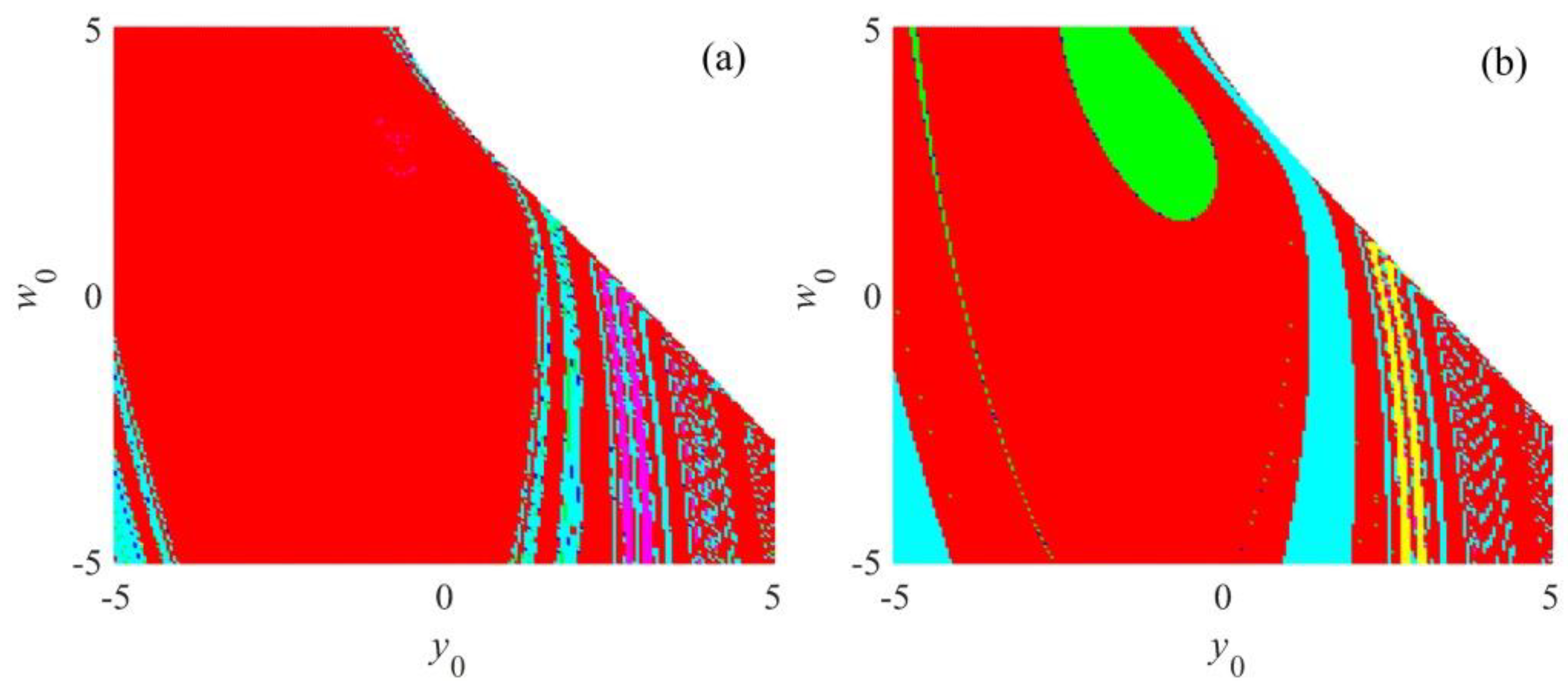
2.2. Coexisting Attractors
2.3. Hidden Chaotic Attractor
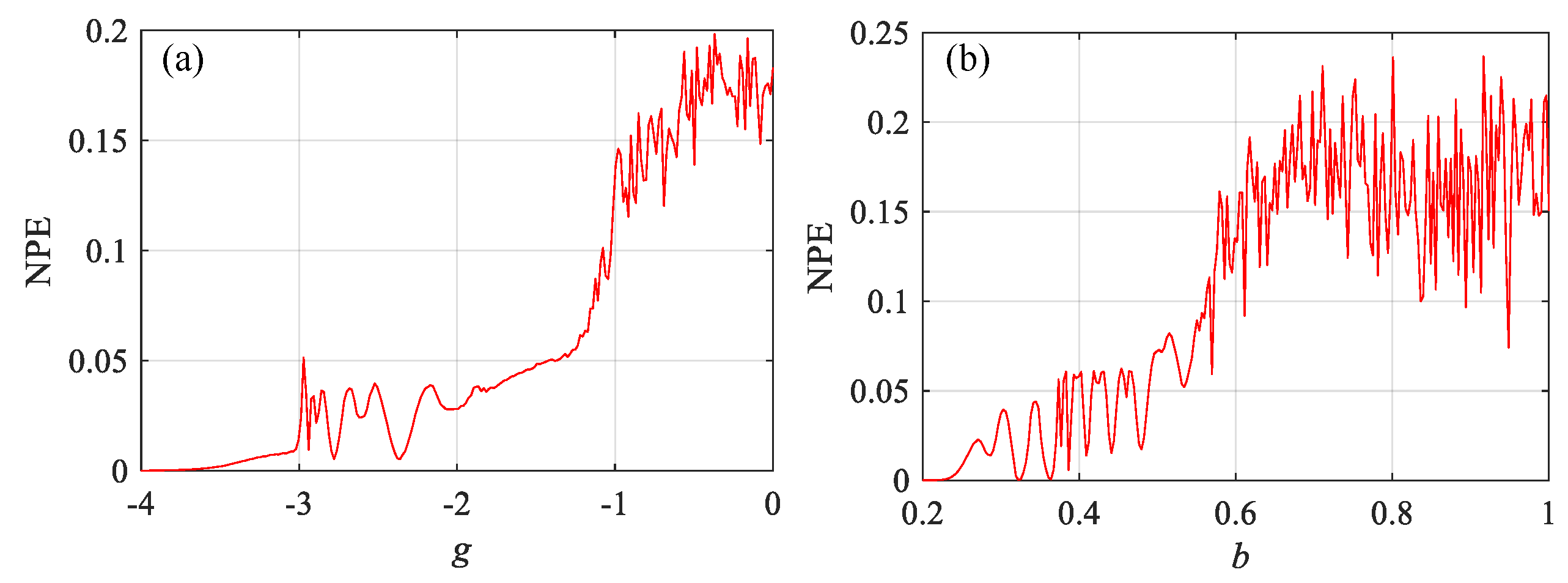
3. Complexity Analysis
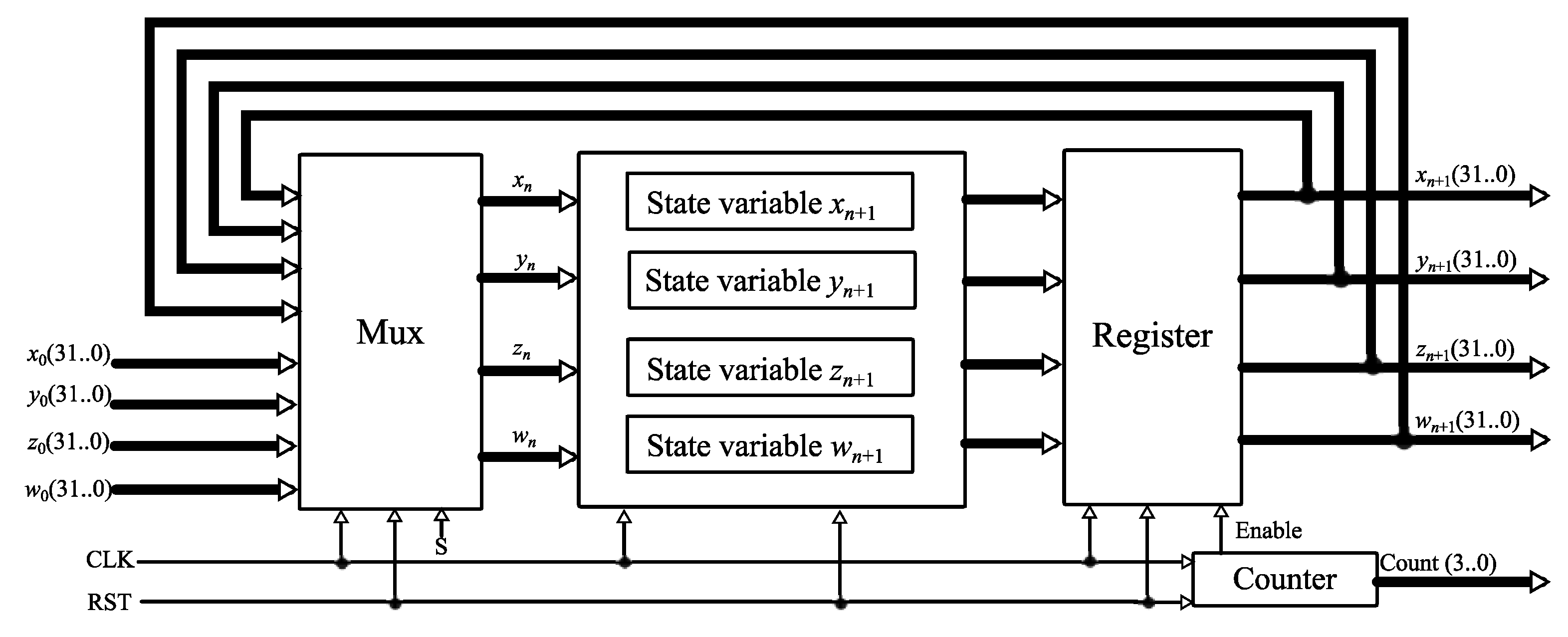
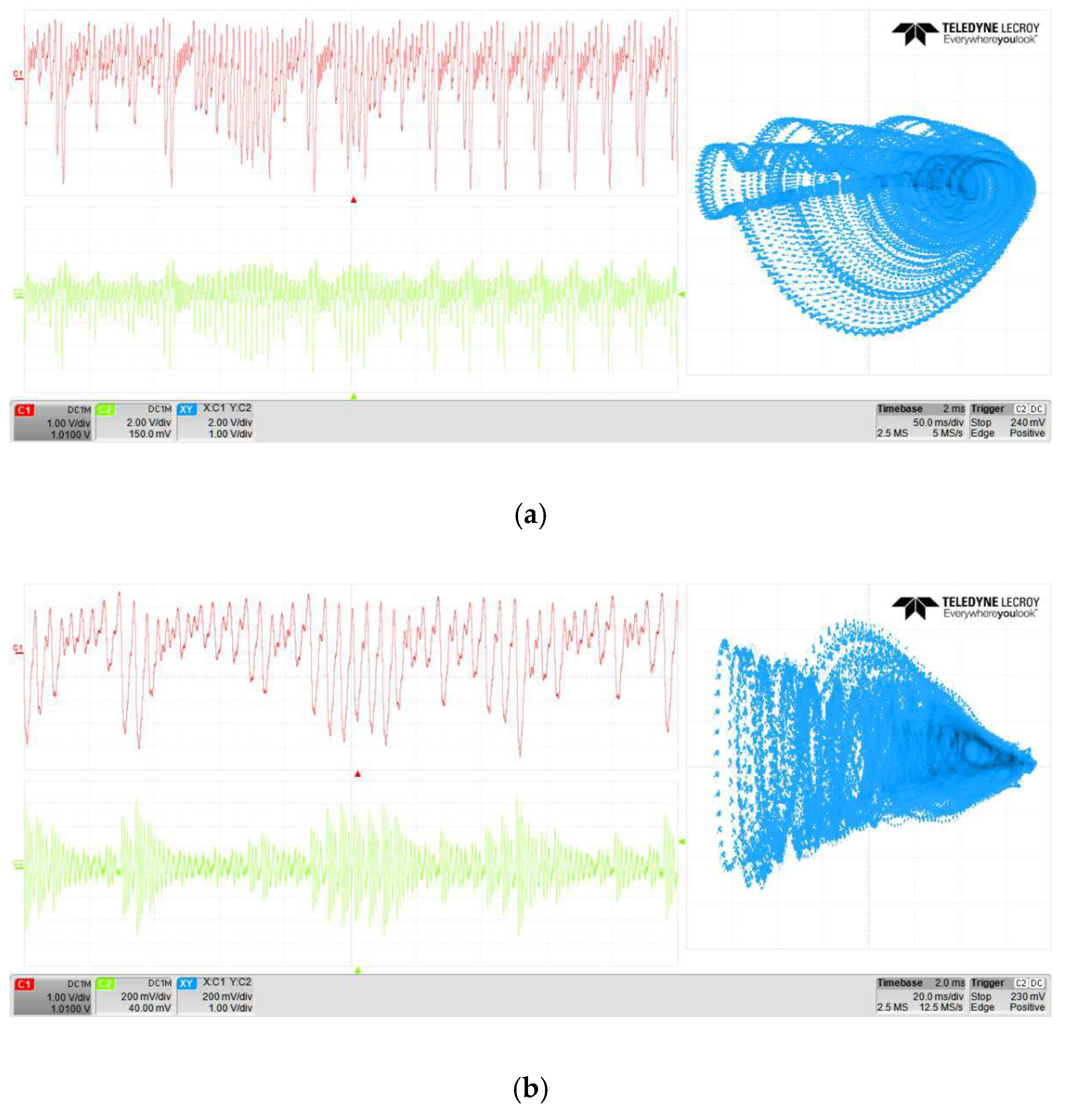
4. FPGA Implementation
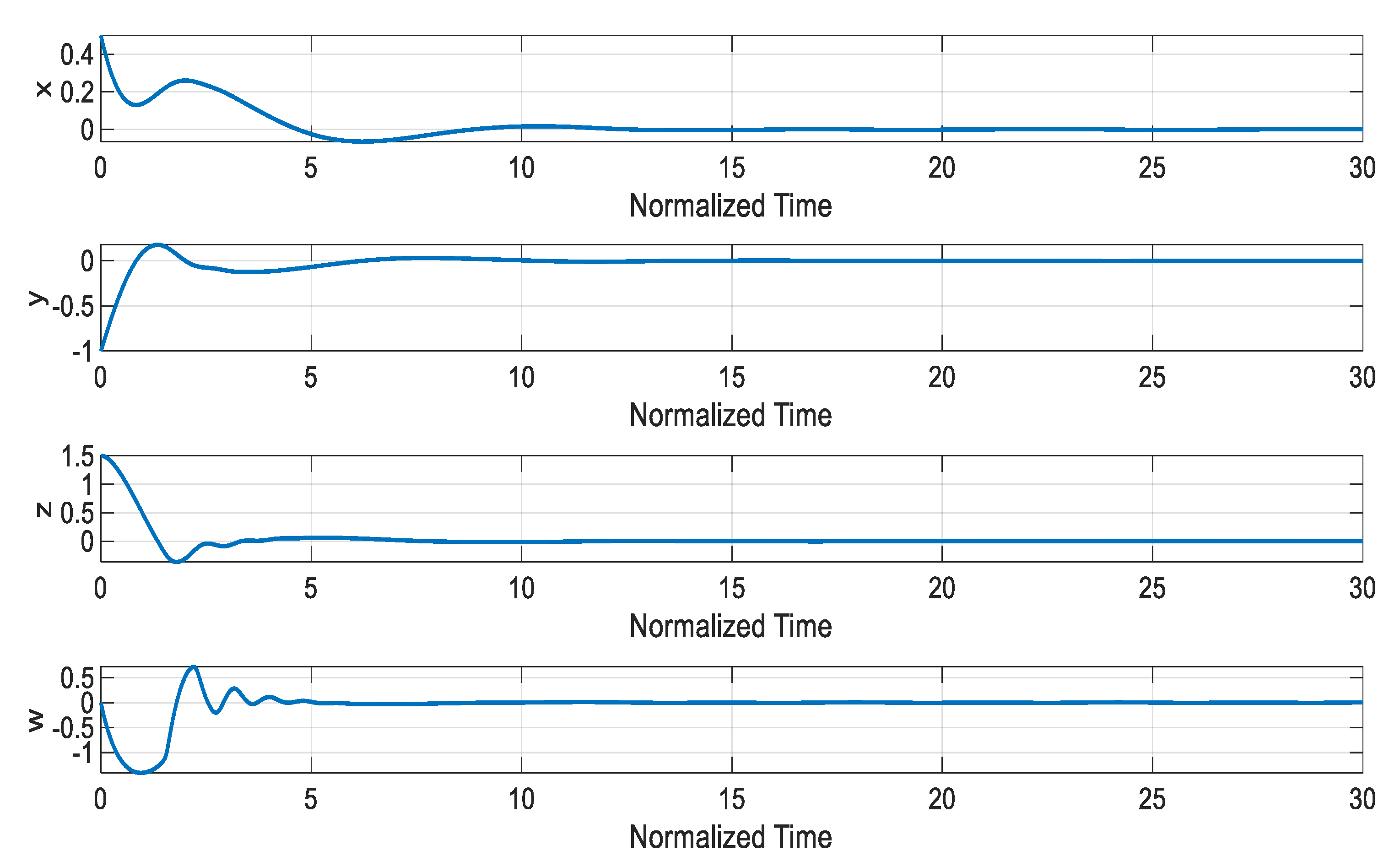
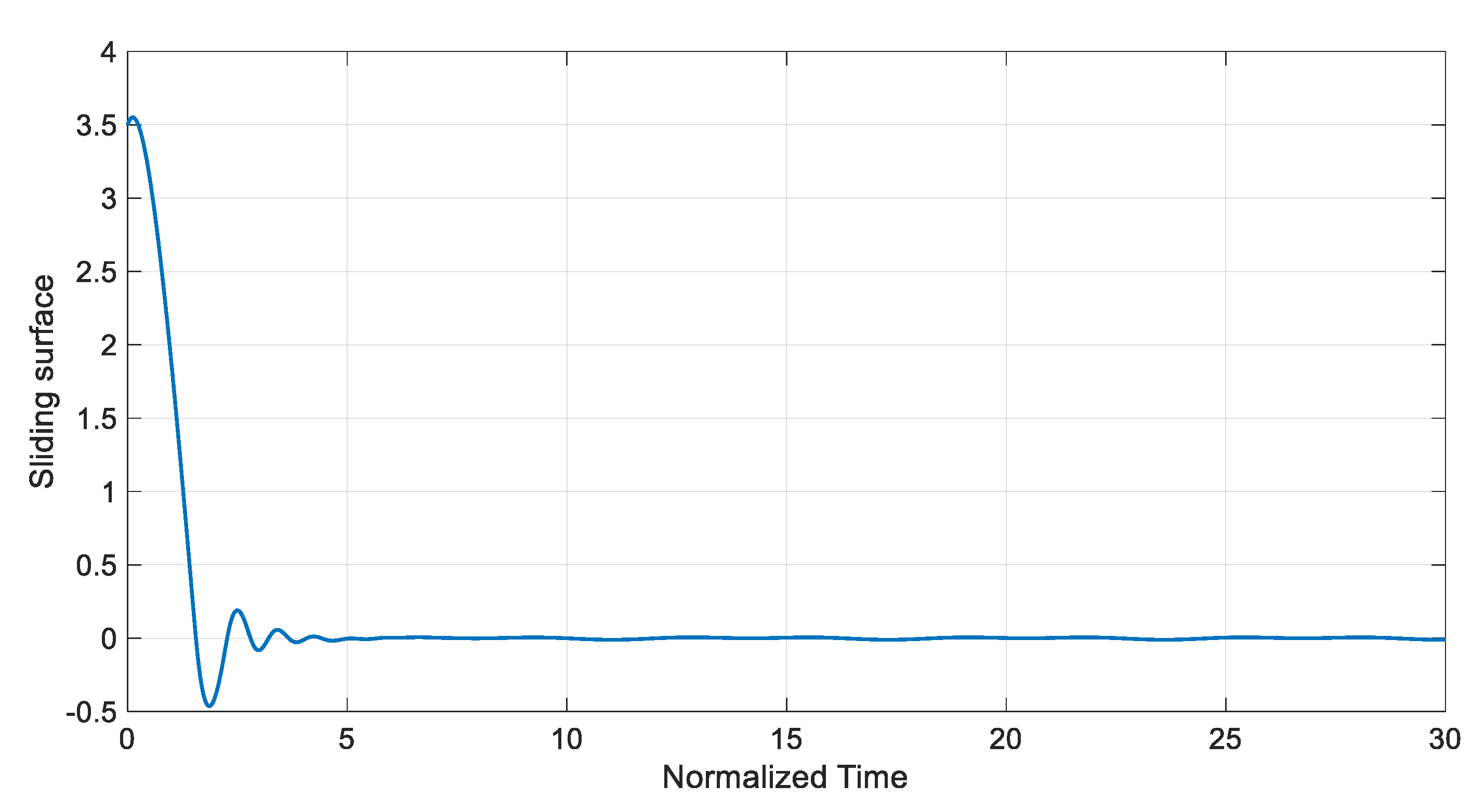
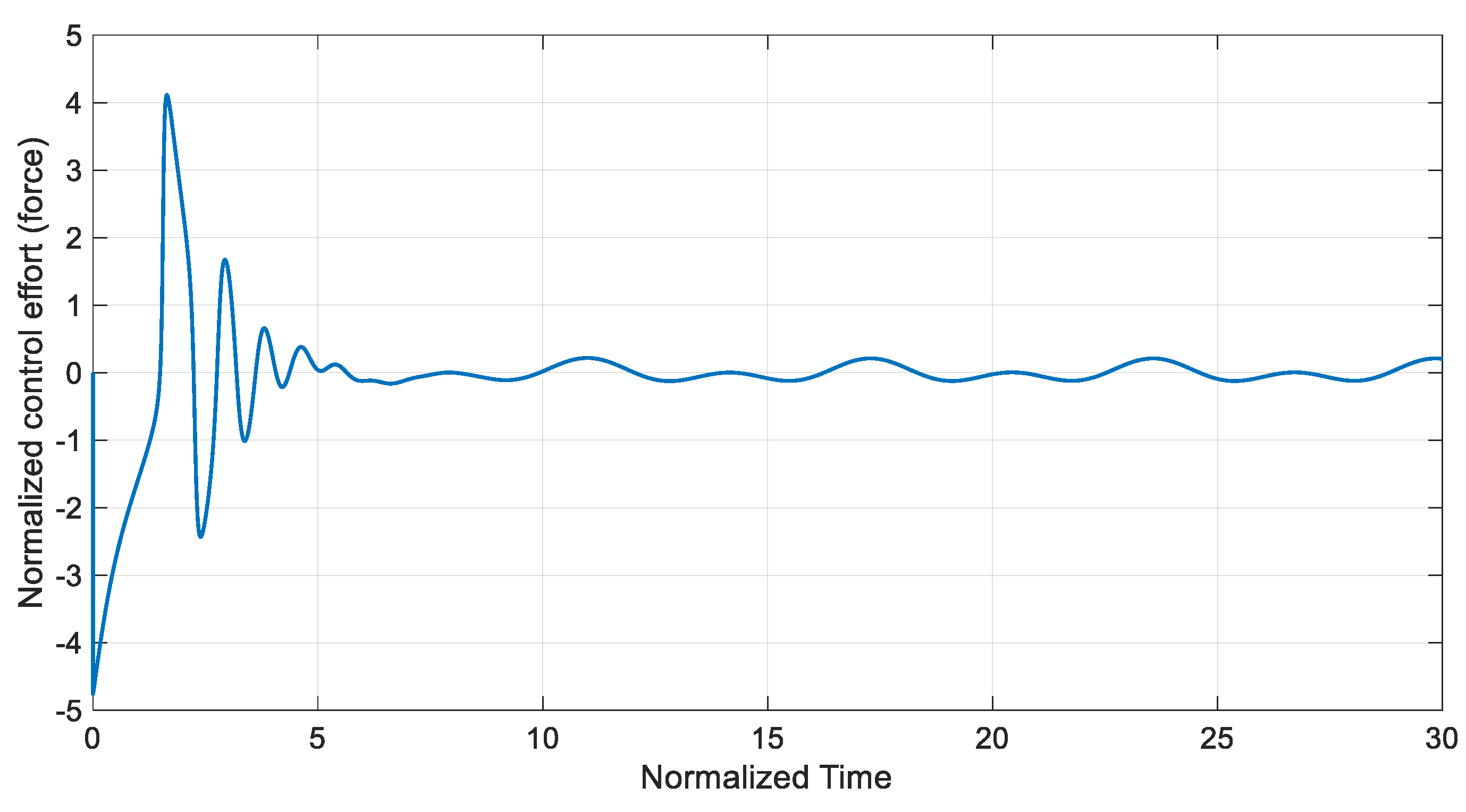
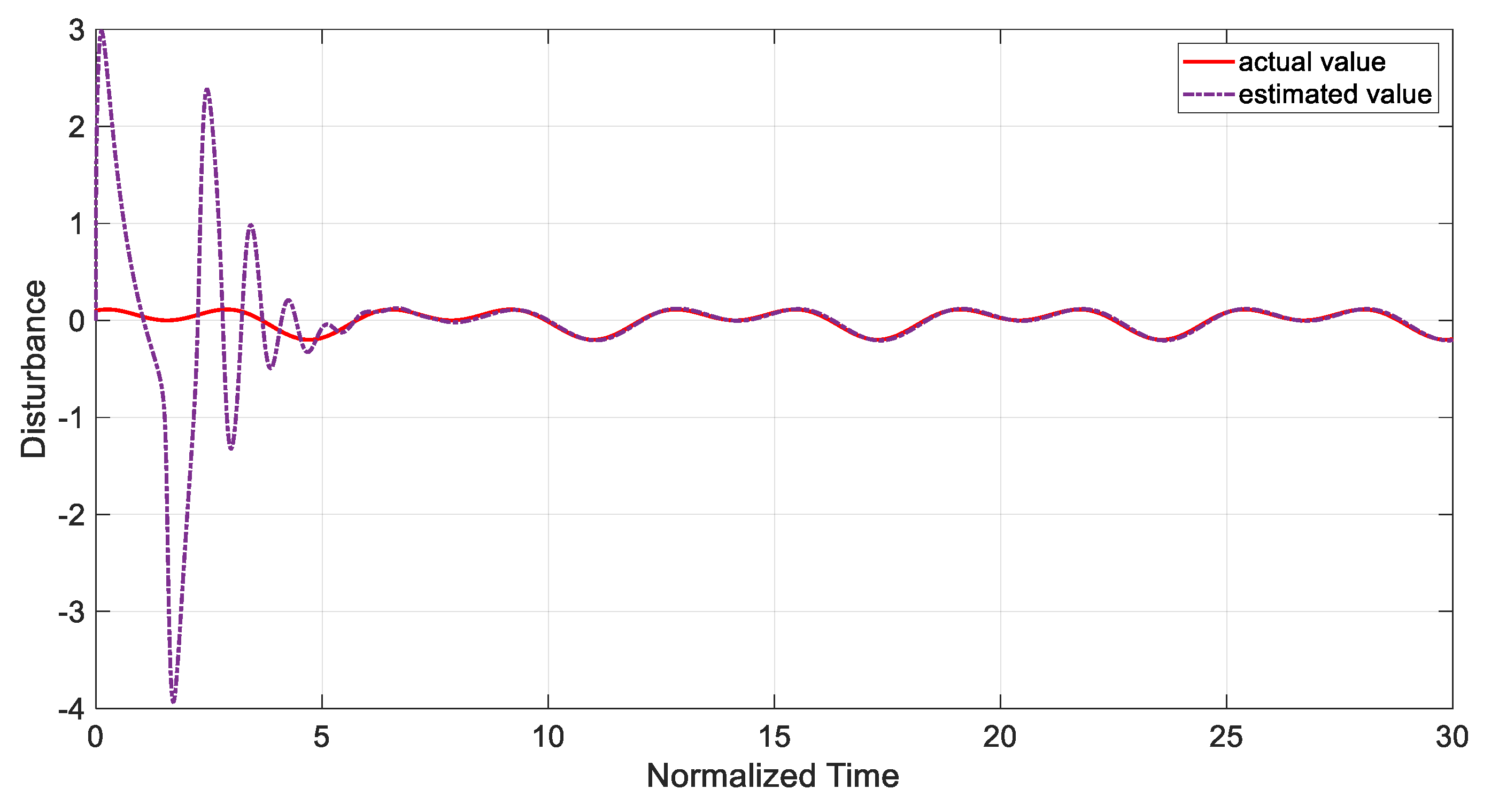
5. Controller Design
Disturbance Observer-Based SMC
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vaidyanathan, S.; Volos, C. Advances and Applications in Chaotic Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Kapitaniak, T.; Jafari, S.; Wang, X. Dynamics and circuit of a chaotic system with a curve of equilibrium points. Int. J. Electron. 2017, 105, 385–397. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jahanshahi, H.; Varan, M.; Bayır, I.; Pham, V.-T.; Jafari, S.; Karthikeyan, A. A hyperchaotic memristor oscillator with fuzzy based chaos control and LQR based chaos synchronization. AEU Int. J. Electron. Commun. 2018, 94, 55–68. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.; Zambrano-Serrano, E.; Volos, C.; Jafari, S.; Kengne, J.; Rajagopal, K. A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy 2018, 20, 564. [Google Scholar] [CrossRef] [Green Version]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Eisencraft, M.; Attux, R.; Suyama, R. Chaotic Signals in Digital Communications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jahanshahi, H.; Rajagopal, K.; Akgul, A.; Sari, N.N.; Namazi, H.; Jafari, S. Complete analysis and engineering applications of a megastable nonlinear oscillator. Int. J. Non-Linear Mech. 2018, 107, 126–136. [Google Scholar] [CrossRef]
- Jahanshahi, H. Smooth control of HIV/AIDS infection using a robust adaptive scheme with decoupled sliding mode supervision. Eur. Phys. J. Spéc. Top. 2018, 227, 707–718. [Google Scholar] [CrossRef]
- Yousefpour, A.; Bahrami, A.; Haeri Yazdi, M.R. Multi-frequency piezomagnetoelastic energy harvesting in the monostable mode. J. Theor. Appl. Vib. Acoust. 2018, 4, 1–18. [Google Scholar]
- Yousefpour, A.; Vahidi-Moghaddam, A.; Rajaei, A.; Ayati, M. Stabilization of nonlinear vibrations of carbon nanotubes using observer-based terminal sliding mode control. Trans. Inst. Meas. Control 2019, 42, 1047–1058. [Google Scholar] [CrossRef]
- Lai, Q.; Wang, L. Chaos, bifurcation, coexisting attractors and circuit design of a three-dimensional continuous autonomous system. Optik 2016, 127, 5400–5406. [Google Scholar] [CrossRef]
- Wang, X.; Pham, V.-T.; Volos, C. Dynamics, circuit design, and synchronization of a new chaotic system with closed curve equilibrium. Complexity 2017, 2017, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, T.; Biswas, D. Theory and experiment of a first-order chaotic delay dynamical system. Int. J. Bifurc. Chaos 2013, 23, 1330020. [Google Scholar] [CrossRef]
- Bouali, S.; Buscarino, A.; Fortuna, L.; Frasca, M.; Gambuzza, L.V. Emulating complex business cycles by using an electronic analogue. Nonlinear Anal. Real World Appl. 2012, 13, 2459–2465. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Shahriari-Kahkeshi, M.; Alcaraz, R.; Wang, X.; Singh, V.P.; Pham, V.-T. Entropy Analysis and Neural Network-based Adaptive Control of a Non-Equilibrium Four-Dimensional Chaotic System with Hidden Attractors. Entropy 2019, 21, 156. [Google Scholar] [CrossRef] [Green Version]
- Yousefpour, A.; Jahanshahi, H. Fast disturbance-observer-based robust integral terminal sliding mode control of a hyperchaotic memristor oscillator. Eur. Phys. J. Spéc. Top. 2019, 228, 2247–2268. [Google Scholar] [CrossRef]
- Devaney, R. An Introduction to Chaotic Dynamical Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Larrondo, H.; González, C.; Martin, M.; Plastino, A.; Rosso, O.A. Intensive statistical complexity measure of pseudorandom number generators. Phys. A Stat. Mech. Appl. 2005, 356, 133–138. [Google Scholar] [CrossRef]
- Staniczenko, P.P.A.; Lee, C.F.; Jones, N.S. Rapidly detecting disorder in rhythmic biological signals: A spectral entropy measure to identify cardiac arrhythmias. Phys. Rev. E 2009, 79, 011915. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, Q.; Fan, S.-Z.; Lu, C.-W.; Lin, T.Y.; Abbod, M.; Shieh, J.-S. Analysis of EEG via Multivariate Empirical Mode Decomposition for Depth of Anesthesia Based on Sample Entropy. Entropy 2013, 15, 3458–3470. [Google Scholar] [CrossRef] [Green Version]
- En-Hua, S.; Zhi-Jie, C.; Fan-Ji, G. Mathematical foundation of a new complexity measure. Appl. Math. Mech. 2005, 26, 1188–1196. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Zhu, C.-X. Complexity analyses of multi-wing chaotic systems. Chin. Phys. B 2013, 22, 050506. [Google Scholar] [CrossRef]
- Sun, K.-H.; He, S.-B.; He, Y.; Yin, L.-Z. Complexity Analysis of Chaotic Pseudo-Random Sequences Based on Spectral Entropy Algorithm. Acta Phys. Sin. 2013, 62, 010501. [Google Scholar]
- Sharma, P.R.; Shrimali, M.D.; Prasad, A.; Kuznetsov, N.V.; Leonov, G. Control of multistability in hidden attractors. Eur. Phys. J. Spéc. Top. 2015, 224, 1485–1491. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, S. Generating Multiple Chaotic Attractors from Sprott B System. Int. J. Bifurc. Chaos 2016, 26, 1650177. [Google Scholar] [CrossRef]
- Sprott, J.C.; Jafari, S.; Khalaf, A.J.M.; Kapitaniak, T. Megastability: Coexistence of a countable infinity of nested attractors in a periodically-forced oscillator with spatially-periodic damping. Eur. Phys. J. Spéc. Top. 2017, 226, 1979–1985. [Google Scholar] [CrossRef] [Green Version]
- Bao, B.; Chen, M.; Bao, H.; Xu, Q. Extreme multistability in a memristive circuit. Electron. Lett. 2016, 52, 1008–1010. [Google Scholar] [CrossRef]
- Bao, B.; Jiang, T.; Xu, Q.; Chen, M.; Wu, H.; Hu, Y. Coexisting infinitely many attractors in active band-pass filter-based memristive circuit. Nonlinear Dyn. 2016, 86, 1711–1723. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.; Pano-Azucena, A.; Obeso-Rodelo, P.; Nuñez-Perez, J.-C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simul. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Muñoz-Pacheco, J.M.; Tlelo-Cuautle, E.; Toxqui-Toxqui, I.; Sánchez-López, C.; Trejo-Guerra, R. Frequency limitations in generating multi-scroll chaotic attractors using CFOAs. Int. J. Electron. 2014, 101, 1559–1569. [Google Scholar] [CrossRef]
- Pham, V.-T.; Volos, C.; Jafari, S.; Kapitaniak, T. Coexistence of hidden chaotic attractors in a novel no-equilibrium system. Nonlinear Dyn. 2016, 87, 2001–2010. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Volos, C.; Gotthans, T.; Wang, X.; Vo, D.H. A chaotic system with rounded square equilibrium and with no-equilibrium. Optik 2017, 130, 365–371. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.; Golpayegani, S.M.R.H. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Pham, V.-T.; Akgul, A.; Volos, C.; Jafari, S.; Kapitaniak, T. Dynamics and circuit realization of a no-equilibrium chaotic system with a boostable variable. AEU-Int. J. Electron. Commun. 2017, 78, 134–140. [Google Scholar] [CrossRef]
- Ren, S.; Panahi, S.; Rajagopal, K.; Akgul, A.; Pham, V.-T.; Jafari, S. A New Chaotic Flow with Hidden Attractor: The First Hyperjerk System with No Equilibrium. Z. Nat. A 2018, 73, 239–249. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, C.-Y.; Zhao, X.-W.; Kengne, J.; Volos, C. Constructing Chaotic System With Multiple Coexisting Attractors. IEEE Access 2019, 7, 24051–24056. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.; Hu, W.; Xu, Y. Infinite Multistability in a Self-Reproducing Chaotic System. Int. J. Bifurc. Chaos 2017, 27, 1750160. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef] [Green Version]
- Leonov, G.; Kuznetsov, N.V.; Vagaitsev, V. Hidden attractor in smooth Chua systems. Phys. D Nonlinear Phenom. 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Leonov, G.A.; Vagaitsev, V.I. Analytical-numerical method for attractor localization of generalized Chua’s system. IFAC Proc. Vol. 2010, 43, 29–33. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.V.; Vagaitsev, V. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wu, X. Fractional symbolic network entropy analysis for the fractional-order chaotic systems. Phys. Scr. 2020, 95, 035220. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y. A simple Jerk-like system without equilibrium: Asymmetric coexisting hidden attractors, bursting oscillation and double full Feigenbaum remerging trees. Chaos Solitons Fractals 2019, 120, 25–40. [Google Scholar] [CrossRef]
- Kengne, J.; Signing, V.R.F.; Chedjou, J.C.; Leutcho, G.D. Nonlinear behavior of a novel chaotic jerk system: Antimonotonicity, crises, and multiple coexisting attractors. Int. J. Dyn. Control 2017, 6, 468–485. [Google Scholar] [CrossRef]
- Elwakil, A.S.; Kennedy, M.P. Improved implementation of Chua’s chaotic oscillator using current feedback op amp. IEEE Trans. Circuits Syst. I 2000, 47, 76–79. [Google Scholar] [CrossRef] [Green Version]
- Chiu, R.; Mora-Gonzalez, M.; Lopez-Mancilla, D. Implementation of a chaotic oscillator into a simple microcontroller. IERI Procedia 2013, 4, 247–252. [Google Scholar] [CrossRef] [Green Version]
- De La Hoz, M.Z.; Acho, L.; Vidal, Y. An Experimental Realization of a Chaos-Based Secure Communication Using Arduino Microcontrollers. Sci. World J. 2015, 2015, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Yau, H.-T.; Wu, C.-H.; Liang, Q.-C.; Li, S.C. Implementation of optimal PID control for chaos synchronization by FPGA chip. In Proceedings of the 2011 International Conference on Fluid Power and Mechatronics, Beijing, China, 17–20 August 2011; pp. 56–61. [Google Scholar]
- Shah, D.K.; Chaurasiya, R.B.; Vyawahare, V.A.; Pichhode, K.; Patil, M. FPGA implementation of fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 245–257. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; De La Fraga, L.G.; Pham, V.-T.; Volos, C.; Jafari, S.; Quintas-Valles, A.D.J. Dynamics, FPGA realization and application of a chaotic system with an infinite number of equilibrium points. Nonlinear Dyn. 2017, 89, 1129–1139. [Google Scholar] [CrossRef]
- Ya-Ming, X.; Li-Dan, W.; Shu-Kai, D. A memristor-based chaotic system and its field programmable gate array implementation. Acta Phys Sin. 2016, 65, 120503. [Google Scholar]
- Wang, Q.; Yu, S.; Li, C.; Lu, J.; Fang, X.; Guyeux, C.; Bahi, J. Theoretical Design and FPGA-Based Implementation of Higher-Dimensional Digital Chaotic Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 401–412. [Google Scholar] [CrossRef] [Green Version]
- Tuncer, T. The implementation of chaos-based PUF designs in field programmable gate array. Nonlinear Dyn. 2016, 86, 975–986. [Google Scholar] [CrossRef]
- Dong, E.; Liang, Z.; Du, S.; Chen, Z. Topological horseshoe analysis on a four-wing chaotic attractor and its FPGA implement. Nonlinear Dyn. 2015, 83, 623–630. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Rangel-Magdaleno, J.; Carbajal-Gómez, V.H.; Rodriguez-Gomez, G. Generating a 50-scroll chaotic attractor at 66 MHz by using FPGAs. Nonlinear Dyn. 2016, 85, 2143–2157. [Google Scholar] [CrossRef]
- Wang, Q.-X.; Yu, S.; Guyeux, C.; Bahi, J.; Fang, X.-L. Study on a new chaotic bitwise dynamical system and its FPGA implementation. Chin. Phys. B 2015, 24, 060503. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, B.; Zhou, Y. Sine-Transform-Based Chaotic System With FPGA Implementation. IEEE Trans. Ind. Electron. 2018, 65, 2557–2566. [Google Scholar] [CrossRef]
- Muñoz-Pacheco, J.M.; Tlelo-Cuautle, E.; Flores-Tiro, I.; Trejo-Guerra, R. Experimental Synchronization of two Integrated Multi-scroll Chaotic Oscillators. J. Appl. Res. Technol. 2014, 12, 459–470. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Muñoz-Pacheco, J.M.; Gómez-Pavón, L.D.C.; Luis-Ramos, A.; Chen, G. Synchronization in a fractional-order model of pancreatic β-cells. Eur. Phys. J. Spéc. Top. 2018, 227, 907–919. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S. An optimal fuzzy PID control approach for docking maneuver of two spacecraft: Orientational motion. Eng. Sci. Technol. Int. J. 2017, 20, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. Optimal FPID Control Approach for a Docking Maneuver of Two Spacecraft: Translational Motion. J. Aerosp. Eng. 2017, 30, 04017011. [Google Scholar] [CrossRef]
- Ma, Q.; Luo, W.; Jahanshahi, H.; Cavusoglu, U.; Akgul, A.; Lin, X. A novel s-box design algorithm and fuzzy-pid controller design for a 5-d burke–shaw system with hidden hyperchaos. System 2019, 2, 3. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Jafarzadeh, M.; Sari, N.N.; Pham, V.-T.; Huynh, V.; Nguyen, X.Q. Robot Motion Planning in an Unknown Environment with Danger Space. Electronics 2019, 8, 201. [Google Scholar] [CrossRef] [Green Version]
- Sari, N.N.; Jahanshahi, H.; Fakoor, M. Adaptive Fuzzy PID Control Strategy for Spacecraft Attitude Control. Int. J. Fuzzy Syst. 2019, 21, 769–781. [Google Scholar] [CrossRef]
- Mahmoodabadi, M.; Jahanshahi, H. Multi-objective optimized fuzzy-PID controllers for fourth order nonlinear systems. Eng. Sci. Technol. Int. J. 2016, 19, 1084–1098. [Google Scholar] [CrossRef] [Green Version]
- Soradi-Zeid, S.; Jahanshahi, H.; Yousefpour, A.; Bekiros, S. King algorithm: A novel optimization approach based on variable-order fractional calculus with application in chaotic financial systems. Chaos Solitons Fractals 2020, 132, 109569. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jahanshahi, H.; Jafari, S.; Weldegiorgis, R.; Karthikeyan, A.; Duraisamy, P. Coexisting attractors in a fractional order hydro turbine governing system and fuzzy PID based chaos control. Asian J. Control 2020. [Google Scholar] [CrossRef]
- Rajaei, A.; Moghaddam, A.V.; Chizfahm, A.; Sharifi, M. Control of malaria outbreak using a non-linear robust strategy with adaptive gains. IET Control Theory Appl. 2019, 13, 2308–2317. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic jerk functions. Am. J. Phys. 1997, 65, 537. [Google Scholar] [CrossRef]
- Harris, D.; Harris, S. Digital Design and Computer Architecture; Morgan Kaufmann: Burlington, MA, USA, 2010. [Google Scholar]
- Chen, M.; Chen, W.-H. Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. Int. J. Adapt. Control Signal Process. 2009, 24, 51–64. [Google Scholar] [CrossRef]







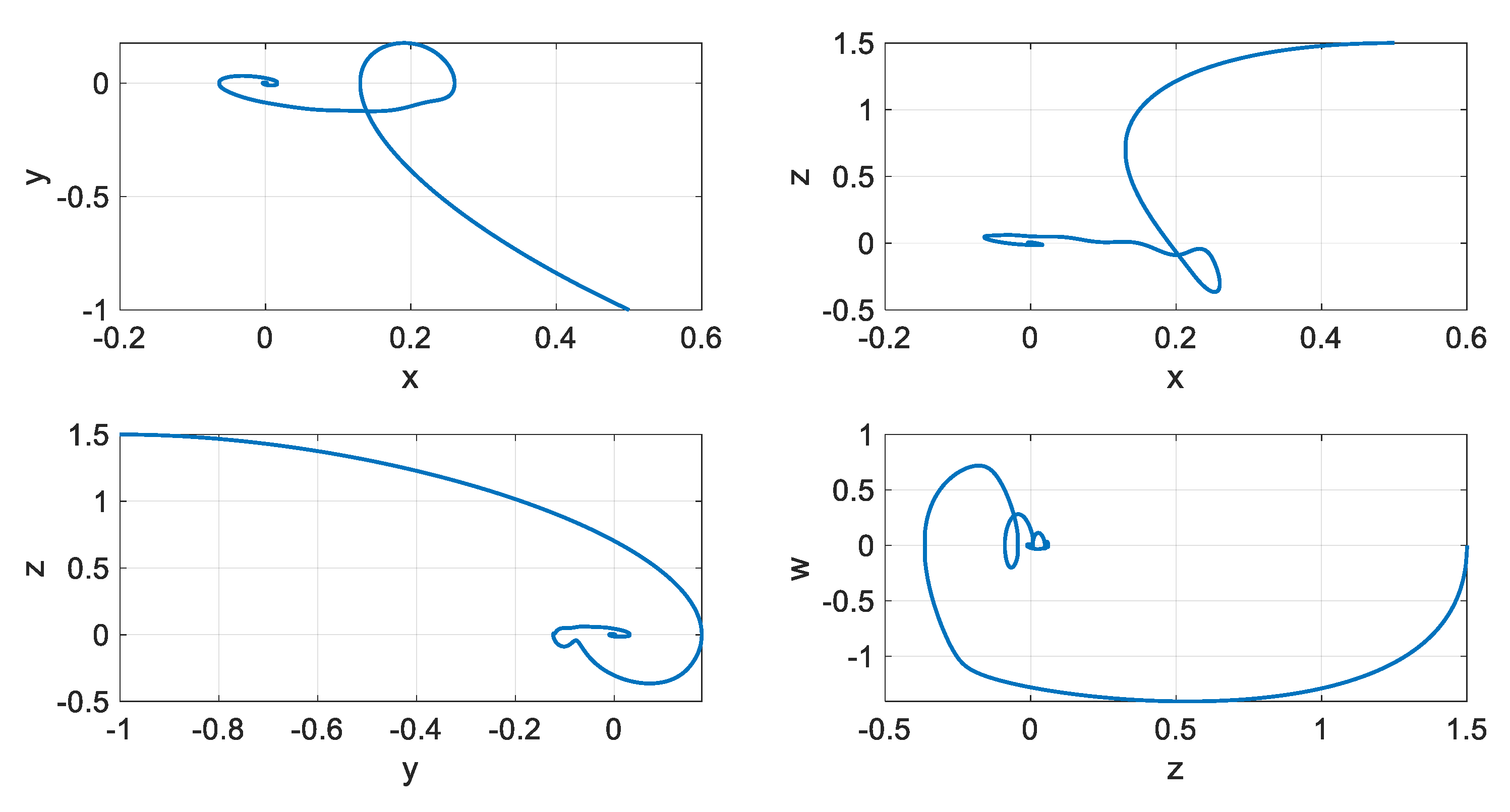
| Resources | Used |
|---|---|
| Total logic elements | 1652/149,760 (1%) |
| Total registers | 946 |
| Total pins | 25/508 (5%) |
| Total virtual pins | 0 |
| Total memory bits | 192/6, 635, 520 (<1%) |
| Embedded multiplier 9-bit elements | 92/720 (13%) |
| Latency | 105.9 ns |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; He, S.; Pano Azucena, A.D.; Yousefpour, A.; Jahanshahi, H.; López, M.A.; Alcaraz, R. A Multistable Chaotic Jerk System with Coexisting and Hidden Attractors: Dynamical and Complexity Analysis, FPGA-Based Realization, and Chaos Stabilization Using a Robust Controller. Symmetry 2020, 12, 569. https://doi.org/10.3390/sym12040569
Chen H, He S, Pano Azucena AD, Yousefpour A, Jahanshahi H, López MA, Alcaraz R. A Multistable Chaotic Jerk System with Coexisting and Hidden Attractors: Dynamical and Complexity Analysis, FPGA-Based Realization, and Chaos Stabilization Using a Robust Controller. Symmetry. 2020; 12(4):569. https://doi.org/10.3390/sym12040569
Chicago/Turabian StyleChen, Heng, Shaobo He, Ana Dalia Pano Azucena, Amin Yousefpour, Hadi Jahanshahi, Miguel A. López, and Raúl Alcaraz. 2020. "A Multistable Chaotic Jerk System with Coexisting and Hidden Attractors: Dynamical and Complexity Analysis, FPGA-Based Realization, and Chaos Stabilization Using a Robust Controller" Symmetry 12, no. 4: 569. https://doi.org/10.3390/sym12040569







