A Gamma-Type Distribution with Applications
Abstract
:1. Introduction
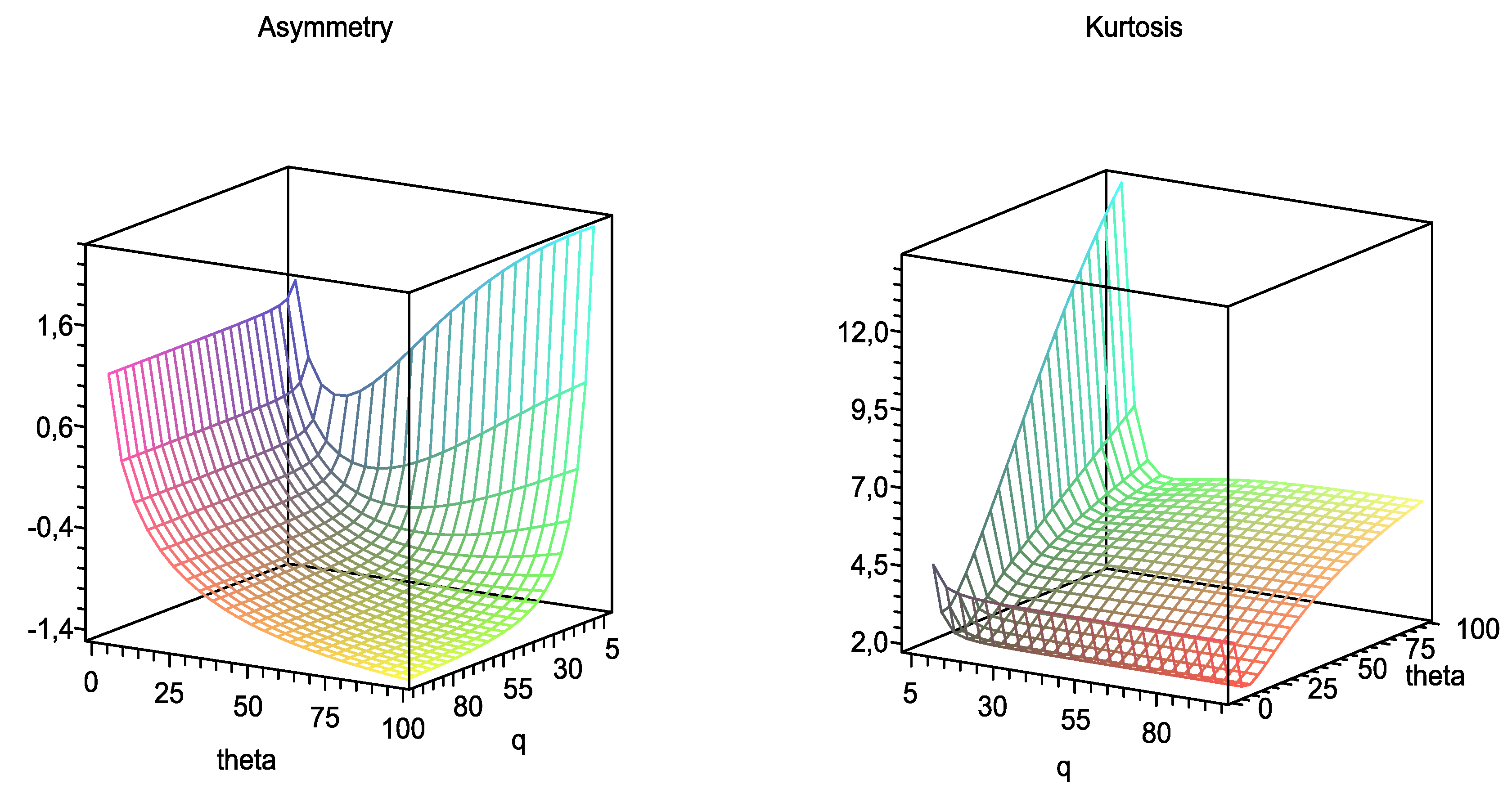
2. Slashed Quasi-Gamma Distribution
- ,
3. Inference
3.1. Moment Estimators
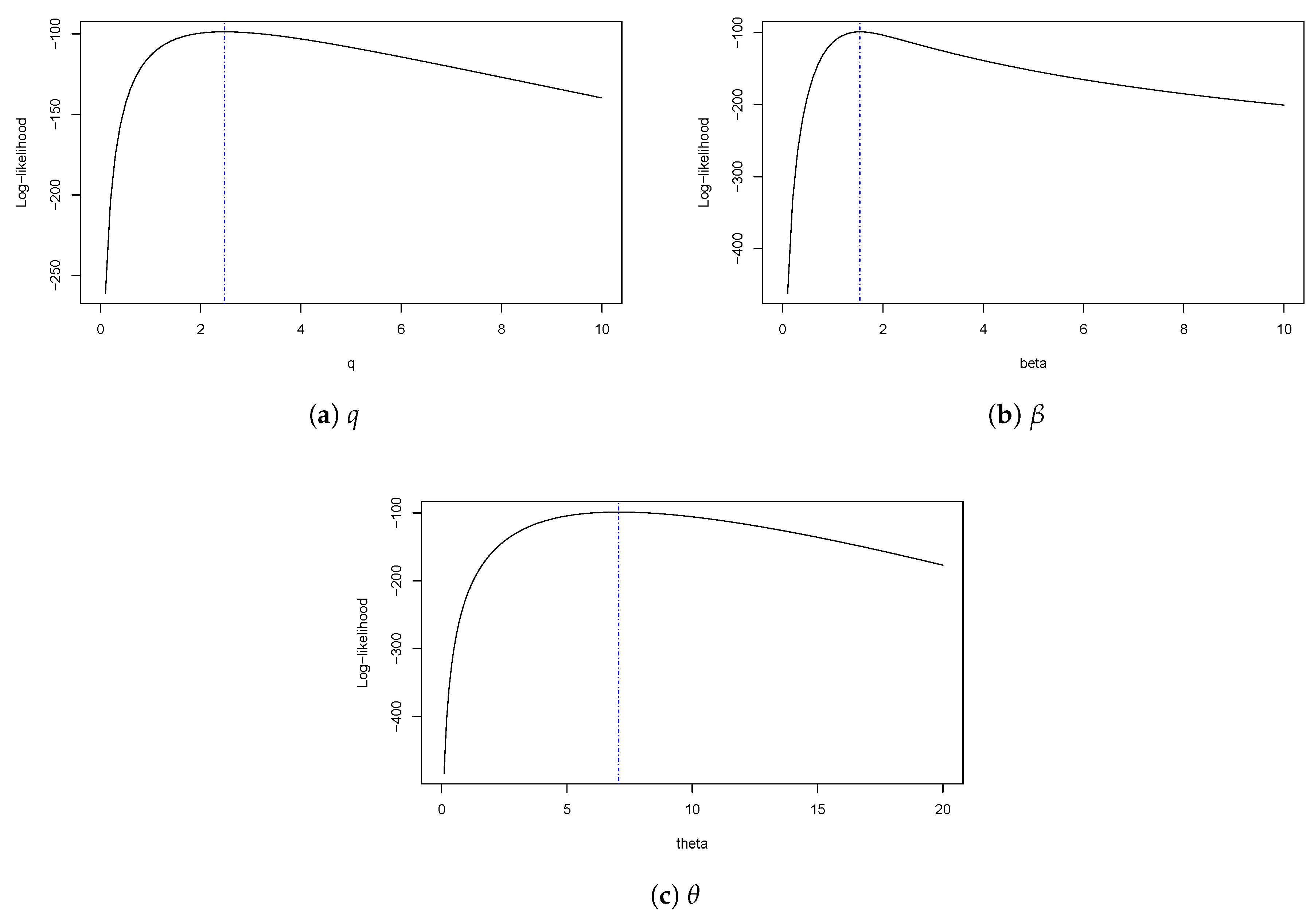
3.2. Maximum Likelihood Estimators
3.3. Observed Information Matrix
4. Simulation
5. Applications
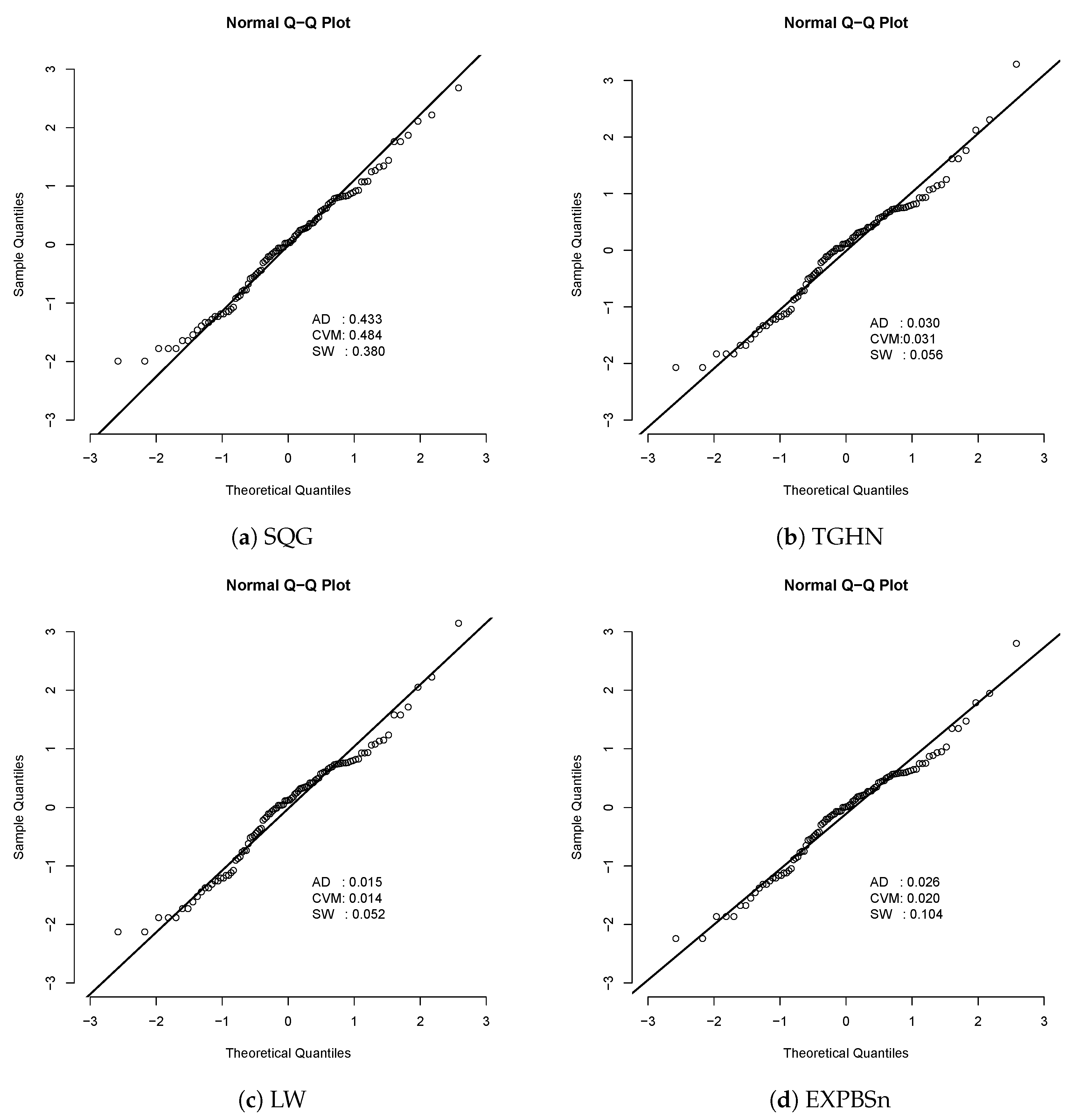
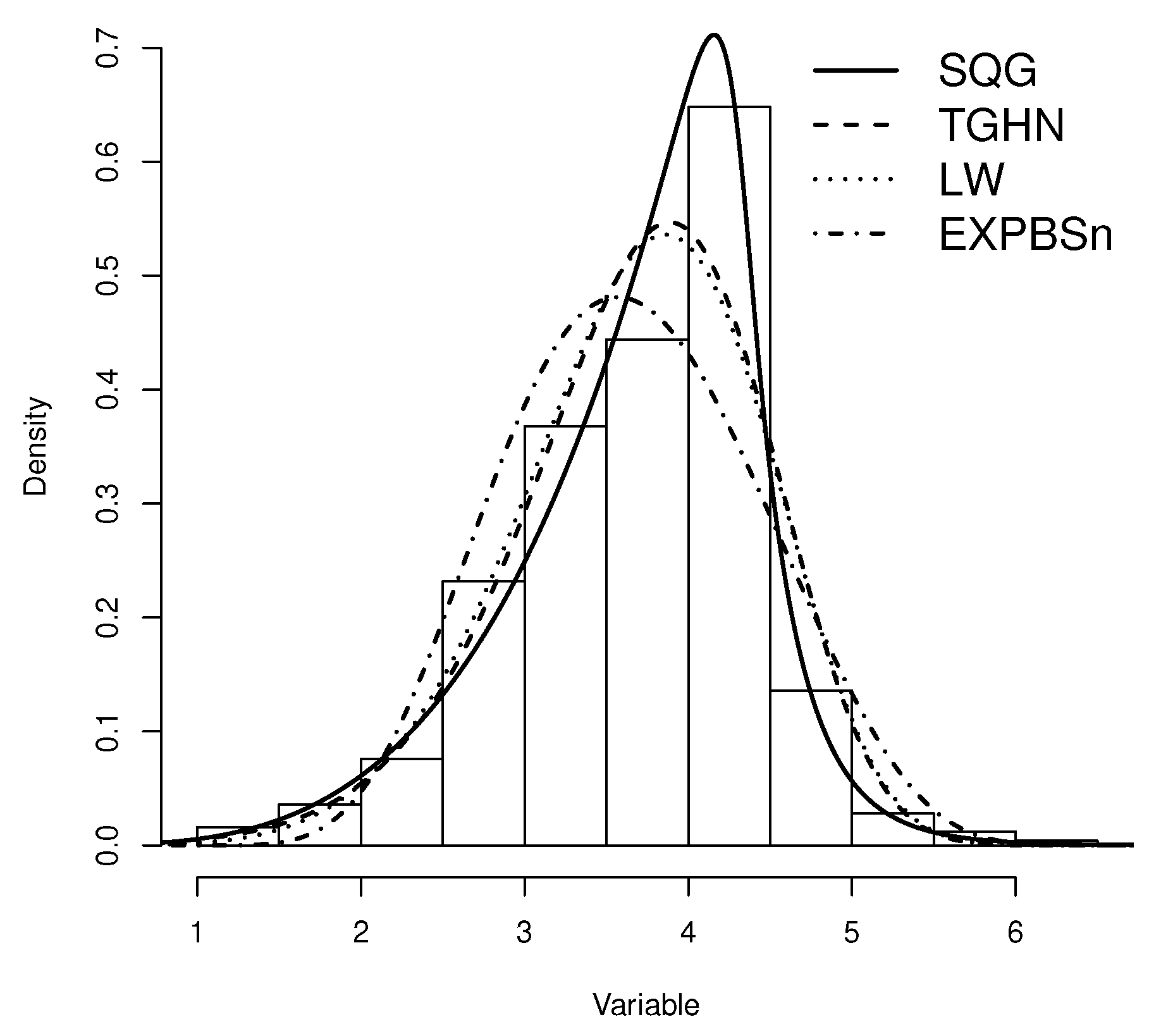
5.1. Application 1
5.2. Application 2
6. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Meeker, W.; Escobar, L. Statistical Methods for Reliability Data; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Kleiber, C.; Kotz, S. Statistical Size Distributions in Economics and Actuarial Sciences; Wiley-Interscience: Hoboken, NJ, USA, 2003; ISBN 0-471-15064-9. [Google Scholar]
- Gómez, H.W.; Quintana, F.A.; Torres, F.J. A new family of slash-distribution with elliptical contours. Stat. Probab. Lett. 2008, 77, 717–725. [Google Scholar] [CrossRef]
- Arslan, O. An alternative multivariate skew-slash distribution. Stat. Probab. Lett. 2008, 78, 2756–2761. [Google Scholar] [CrossRef]
- Gómez, H.W.; Olivares-Pacheco, J.F.; Venegas, O. An extension of the generalized Birnbaum–Saunders distribution. Stat. Probab. Lett. 2009, 79, 331–338. [Google Scholar] [CrossRef]
- Olivares-Pacheco, J.F.; Cornide, H.; Monasterio, M. An extension of the two-parameter weibull distribution. Colomb. J. Stat. 2010, 33, 219–231. [Google Scholar]
- Olmos, N.M.; Varela, H.; Gómez, H.W.; Bolfarine, H. An extension of the half-normal distribution. Stat. Pap. 2012, 53, 875–886. [Google Scholar] [CrossRef]
- Olmos, N.M.; Varela, H.; Bolfarine, H.; Gómez, H.W. An extension of the generalized half-normal distribution. Stat. Pap. 2014, 55, 967–981. [Google Scholar] [CrossRef]
- Iriarte, Y.A.; Gómez, H.W.; Varela, H.; Bolfarine, H. Slashed Rayleigh distribution. Colomb. J. Stat. 2015, 38, 31–44. [Google Scholar] [CrossRef]
- Iriarte, Y.A.; Vilca, F.; Varela, H.; Gómez, H.W. Slashed Generalized Rayleigh distribution. Commun. Stat. Theory Methods 2017, 46, 4686–4699. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Generalized Modified Slash Birnbaum–Saunders Distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef] [Green Version]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury: Pacific Grove, CA, USA, 2002. [Google Scholar]
- R Core Team, R. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: http://www.R-project.org/ (accessed on 4 March 2020).
- Andrews, D.F.; Herzberg, A.M. Data: A Collection of Problems from Many Fields for the Student and Research Worker; Springer Series in Statistics; Springer: New York, NY, USA, 1985. [Google Scholar]
- Barlow, R.E.; Toland, R.H.; Freeman, T. A Bayesian Analysis of Stress-Rupture Life of Kevlar 49/Epoxy Spherical Pressure Vessels. In Proceedings of the Canadian Conference in Application of Statistics; Marcel Dekker: New York, NY, USA, 1984. [Google Scholar]
- Salinas, H.; Iriarte, Y.; Astorga, J. A transmuted version of the generalized half-normal distribution. Proyecciones (Antofagasta) 2019, 38, 567–583. [Google Scholar] [CrossRef] [Green Version]
- Reyes, J.; Iriarte, Y.; Jodrá, P.; Gómez, H.W. The Slash Lindley-Weibull Distribution. Methodol. Comput. Appl. Probab. 2019, 21, 235–251. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. An alpha-power extension for the Birnbaum–Saunders distribution. Statistics 2014, 48, 896–912. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Dunn, P.; Smyth, G. Randomized Quantile Residual. J. Comput. Graph. Stat. 1996, 5, 236–244. [Google Scholar]



| True Value | |||||
|---|---|---|---|---|---|
| 3 | 5 | 1 | 3.346(1.427) | 5.201(0.939) | 1.191(0.513) |
| 2 | 3.105(0.898) | 5.263(0.904) | 2.356(1.126) | ||
| 3 | 2.909(0.712) | 5.248(0.867) | 3.303(1.212) | ||
| 5 | 7 | 1 | 5.363(1.842) | 7.380(1.572) | 1.136(0.477) |
| 2 | 5.140(1.204) | 7.246(1.115) | 2.356(1.006) | ||
| 3 | 4.976(1.026) | 7.271(1.060) | 3.368(1.477) | ||
| 10 | 10 | 1 | 10.475(2.780) | 10.593(2.430) | 1.083(0.293) |
| 2 | 10.190(1.965) | 10.626(2.052) | 2.318(0.949) | ||
| 3 | 10.016(1.637) | 10.539(1.997) | 3.418(1.307) | ||
| True Value | |||||
| 3 | 5 | 1 | 3.050(0.829) | 5.141(0.660) | 1.053(0.238) |
| 2 | 3.087(0.654) | 5.087(0.581) | 2.262(0.773) | ||
| 3 | 3.062(0.573) | 5.110(0.599) | 3.223(1.058) | ||
| 5 | 7 | 1 | 5.099(1.100) | 7.238(1.038) | 1.034(0.195) |
| 2 | 5.080(0.837) | 7.169(0.907) | 2.167(0.587) | ||
| 3 | 5.088(0.761) | 7.166(0.844) | 3.210(1.122) | ||
| 10 | 10 | 1 | 10.173(1.859) | 10.376(1.697) | 1.041(0.169) |
| 2 | 10.187(1.422) | 10.165(1.355) | 2.153(0.530) | ||
| 3 | 10.141(1.201) | 10.200(1.231) | 3.369(1.007) | ||
| True Value | |||||
| 3 | 5 | 1 | 3.017(0.588) | 5.069(0.469) | 1.038(0.156) |
| 2 | 3.061(0.449) | 5.038(0.409) | 2.143(0.482) | ||
| 3 | 3.050(0.401) | 5.035(0.395) | 3.017(1.019) | ||
| 5 | 7 | 1 | 5.078(0.786) | 7.039(0.677) | 1.024(0.132) |
| 2 | 5.032(0.557) | 7.065(0.582) | 2.073(0.349) | ||
| 3 | 5.075(0.516) | 7.014(0.537) | 3.178(0.891) | ||
| 10 | 10 | 1 | 10.050(1.215) | 10.207(1.081) | 1.017(0.108) |
| 2 | 10.077(0.928) | 10.057(0.897) | 2.053(0.298) | ||
| 3 | 10.064(0.794) | 10.124(0.884) | 3.148(0.569) | ||
| Dataset | n | ||||
|---|---|---|---|---|---|
| Rupture stress times | 101 |
| Estimated | TGHN | LW | EXPBSn | SQG |
|---|---|---|---|---|
| - | 0.622 (1.021) | 3.420 (0.666) | 1.541 (0.170) | |
| - | 0.837 (0.109) | - | 7.063 (0.771) | |
| q | - | - | - | 2.471 (0.535) |
| 2.094 (0.330) | - | - | - | |
| 0.811 (0.064) | 1.046 (1.168) | 0.055 (0.025) | - | |
| 0.854 (0.168) | - | 3.661 (0.697) | - | |
| LLF | −102.277 | −102.597 | −100.692 | −98.669 |
| AIC | 210.554 | 211.195 | 207.385 | 203.338 |
| BIC | 218.399 | 219.040 | 215.230 | 211.183 |
| Dataset | n | ||||
|---|---|---|---|---|---|
| Logarithm of the | 500 |
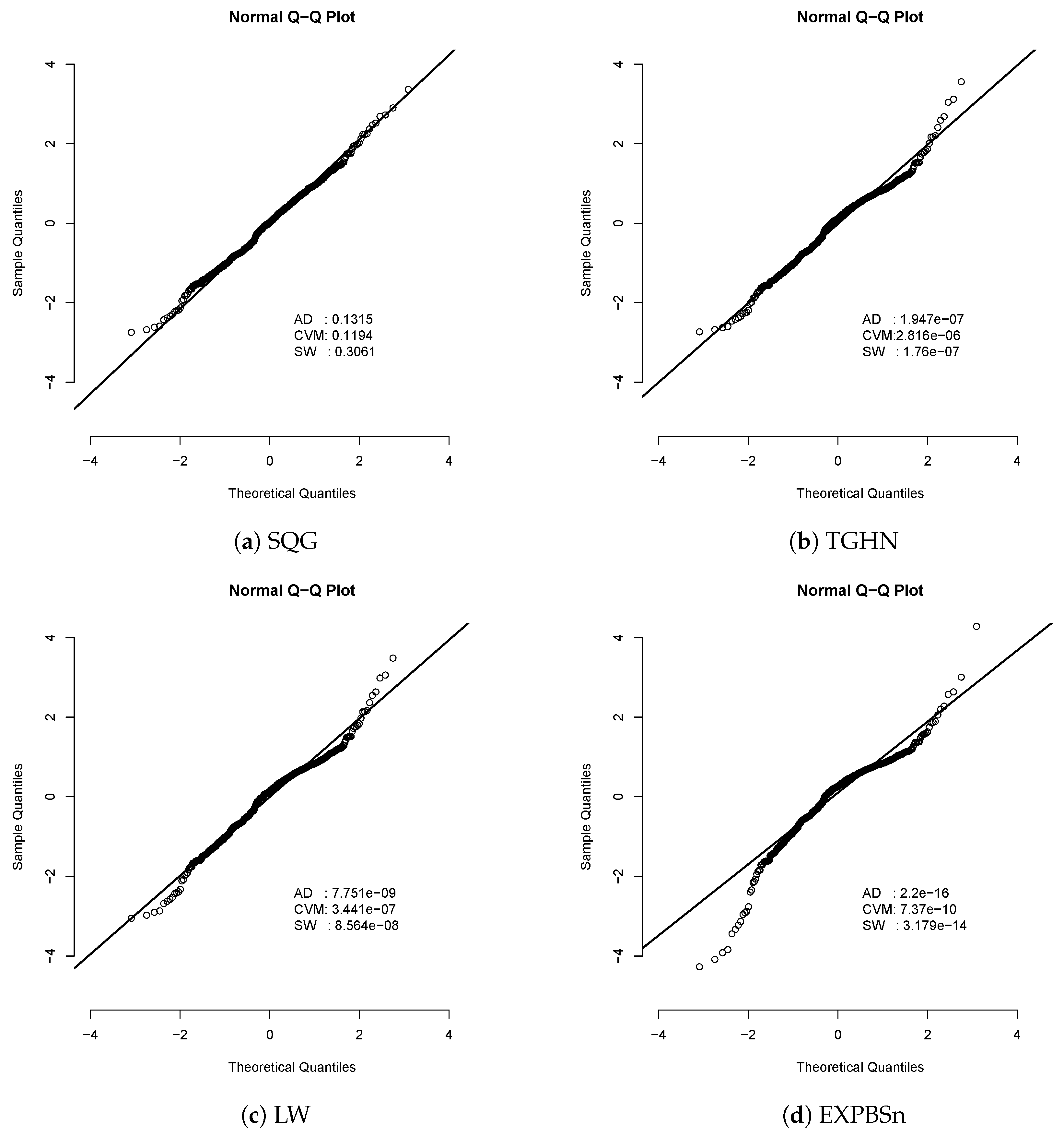
| Estimated | TGHN | LW | EXPBSn | SQG |
|---|---|---|---|---|
| - | 9.646 (3.752) | 0.060 (0.010) | 4.281 (0.036) | |
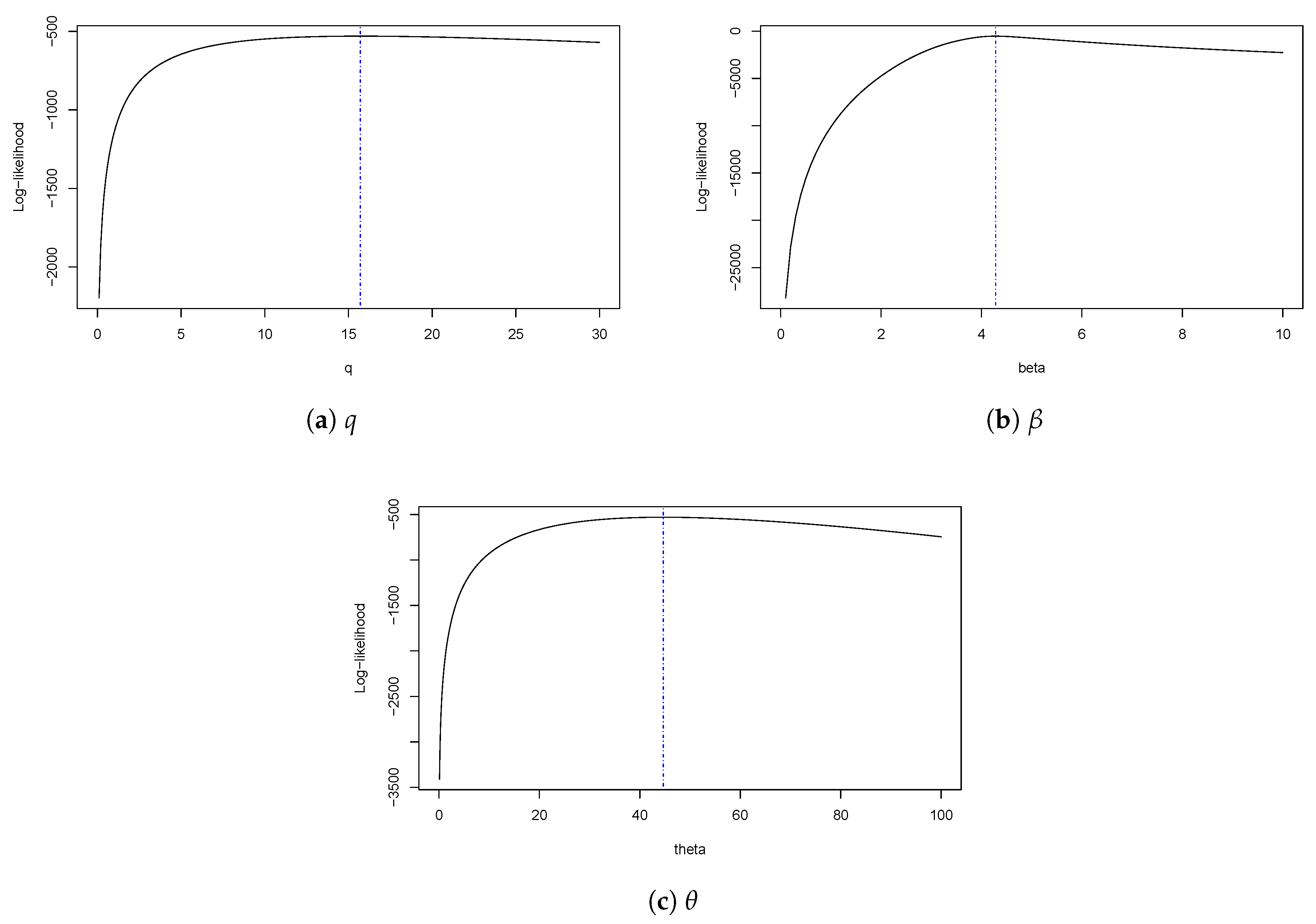
| - | 5.723 (0.195) | - | 44.664 (2.214) | |
| q | - | - | - | 15.710 (1.586) |
| 3.738 (0.053) | - | - | - | |
| 3.120 (0.163) | 157.002 (345.840) | 5.199 (0.110) | - | |
| −0.892 (0.082) | - | 0.033 (0.012) | - | |
| LLF | −555.785 | −557.436 | −591.954 | −530.462 |
| AIC | 1117.571 | 1120.872 | 1189.908 | 1066.924 |
| BIC | 1130.215 | 1133.516 | 1202.552 | 1079.568 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iriarte, Y.A.; Varela, H.; Gómez, H.J.; Gómez, H.W. A Gamma-Type Distribution with Applications. Symmetry 2020, 12, 870. https://doi.org/10.3390/sym12050870
Iriarte YA, Varela H, Gómez HJ, Gómez HW. A Gamma-Type Distribution with Applications. Symmetry. 2020; 12(5):870. https://doi.org/10.3390/sym12050870
Chicago/Turabian StyleIriarte, Yuri A., Héctor Varela, Héctor J. Gómez, and Héctor W. Gómez. 2020. "A Gamma-Type Distribution with Applications" Symmetry 12, no. 5: 870. https://doi.org/10.3390/sym12050870





