Geodesics of a Static Charged Black Hole Spacetime in f(R) Gravity
Abstract
:1. Introduction
2. Null Geodesics for Static Solution in Non-Linear MAXWELL Gravity
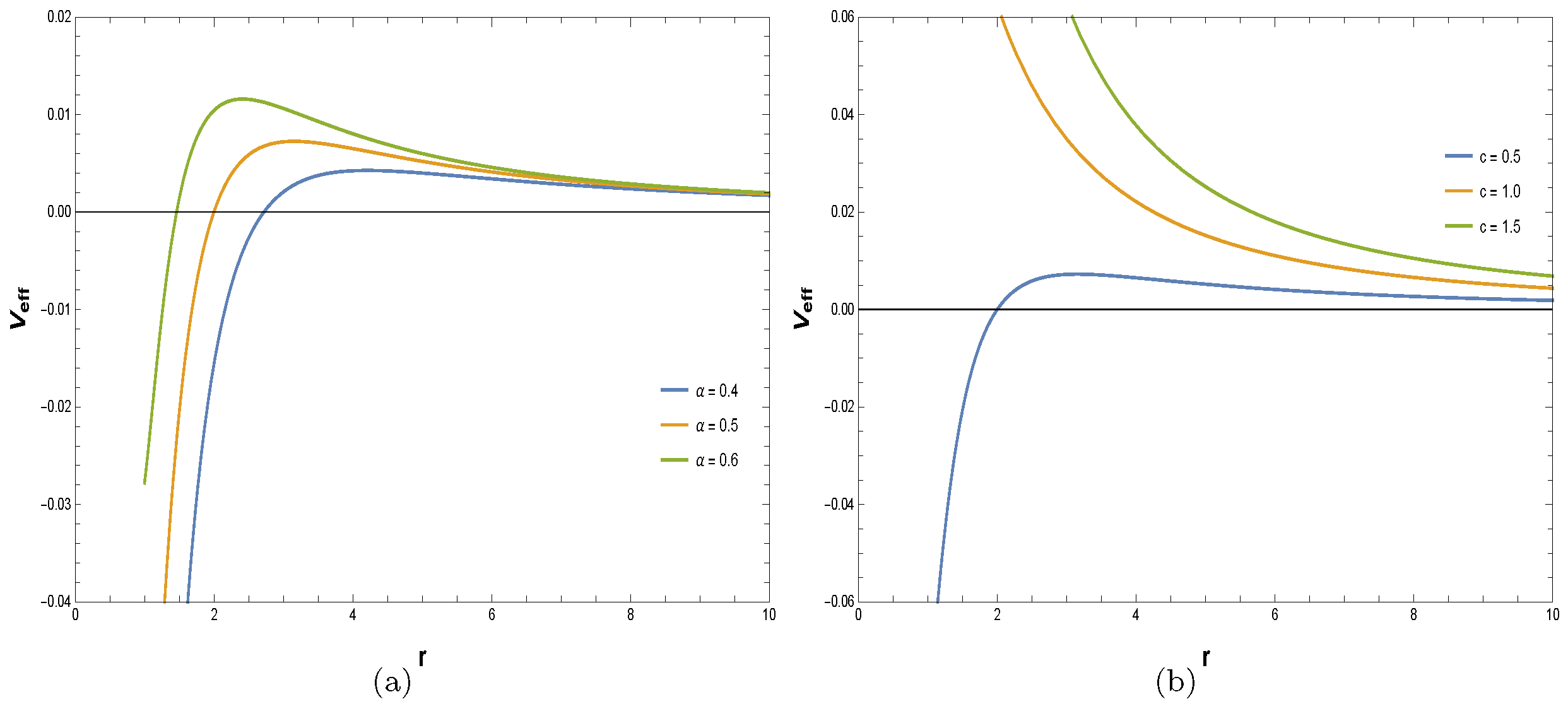
3. Photon Orbit
4. The Frequency Shift of Photon Emitted by Timelike Particles
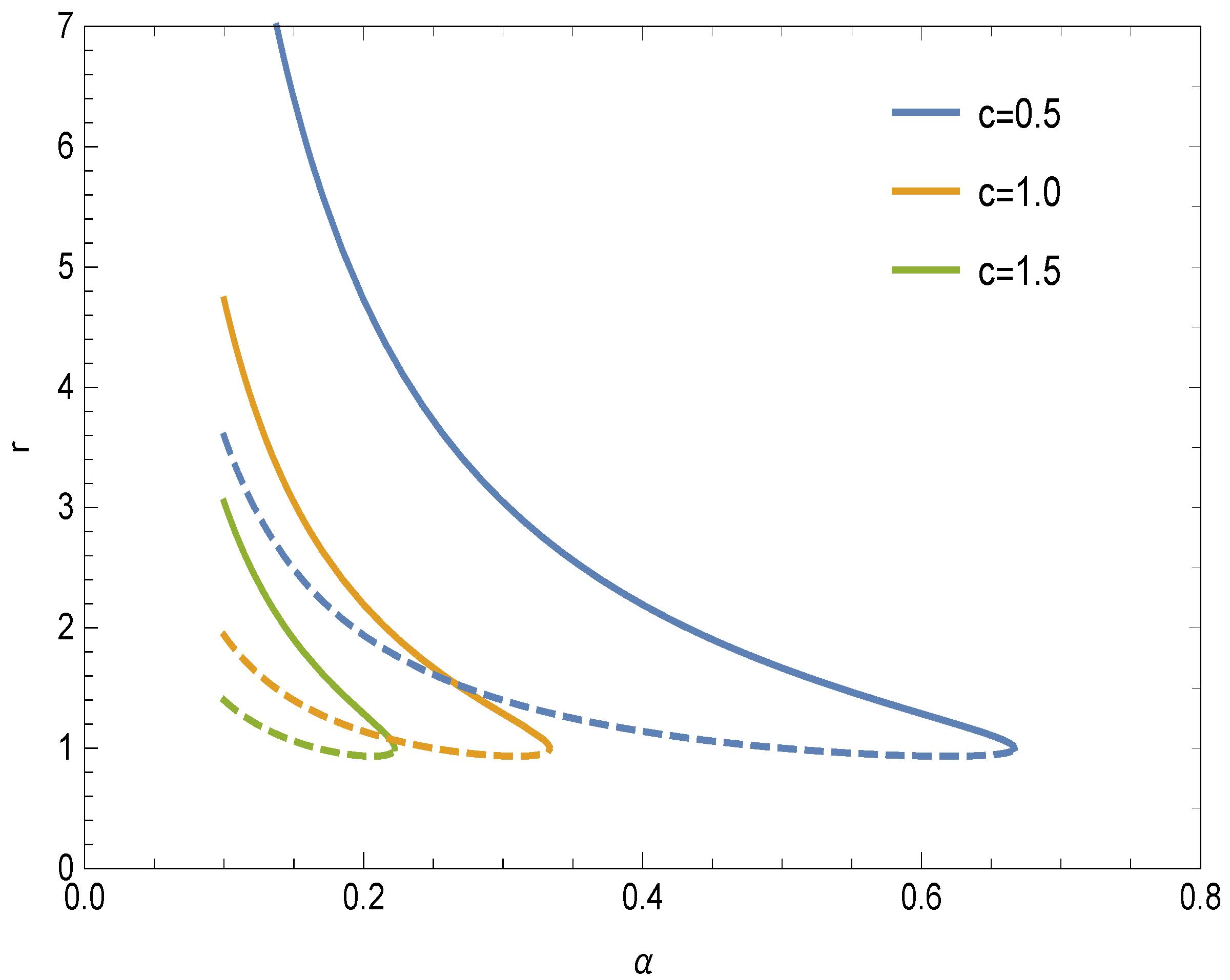
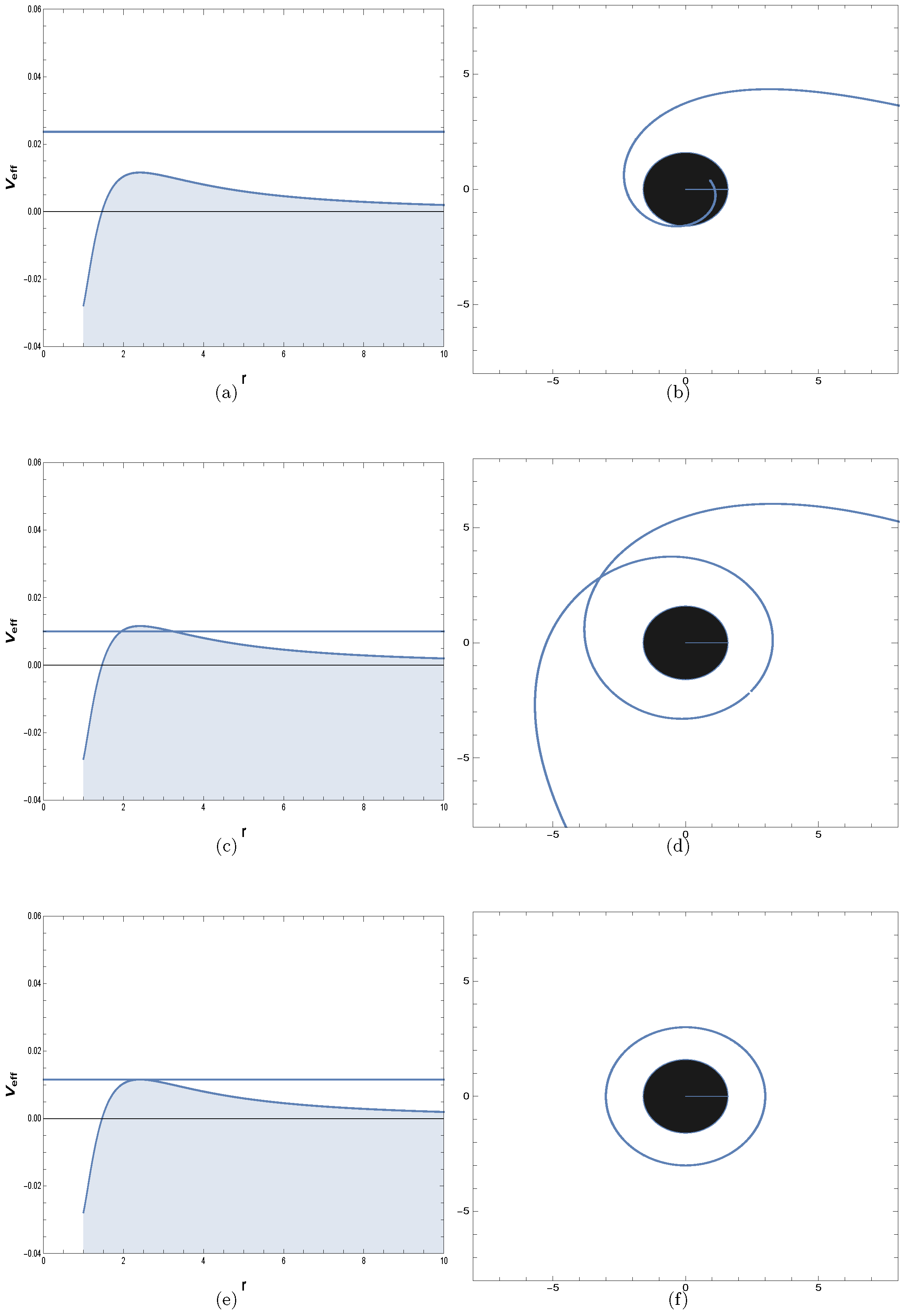
5. Stability Analysis of Geodesics via Lyapunov Exponents
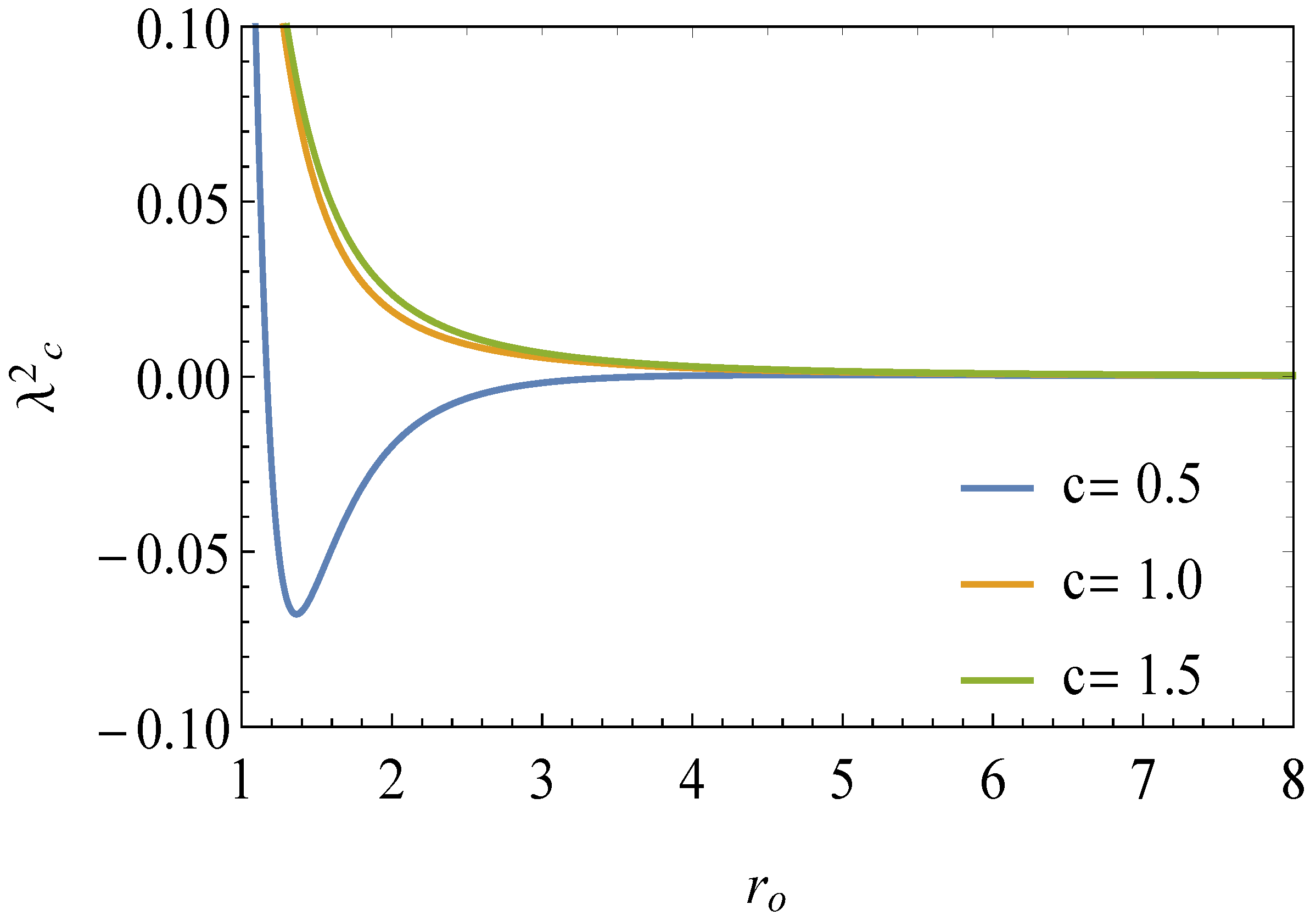
5.1. Stability of Timelike Geodesics
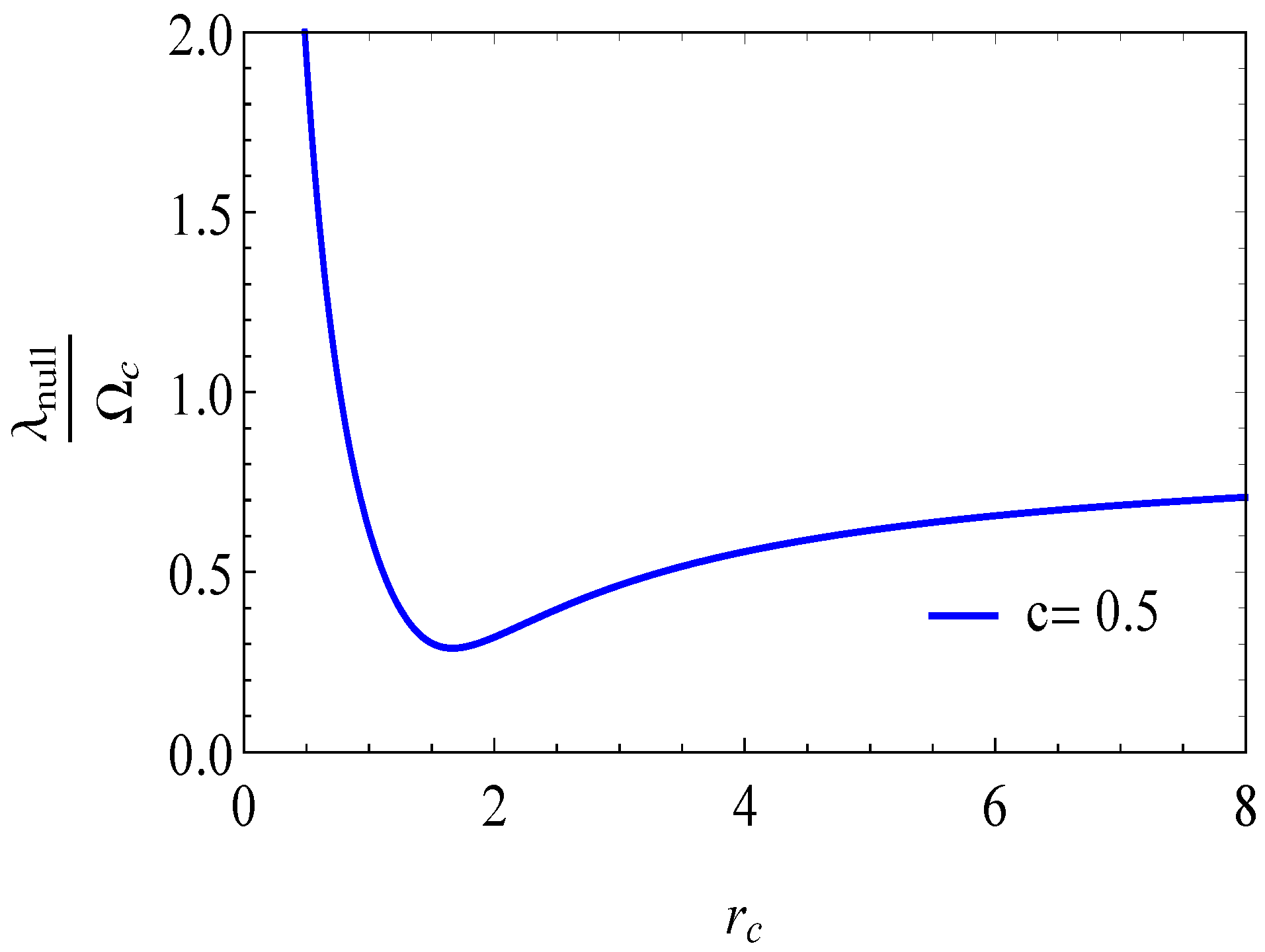
5.2. Stability of Null Geodesics
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Utiyama, R.; DeWitt, B.S. Renormalization of a Classical Gravitational Field Interacting with Quantized Matter Fields. J. Math. Phys. 1962, 3, 608. [Google Scholar] [CrossRef]
- Schmidt, H.-J. Fourth Order Gravity: Equations, History, And Applications to Cosmology. Int. J. Geom. Methods Mod. Phys. 2007, 4, 209. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. F(R) Theories of Gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef] [Green Version]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of Dark Energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef] [Green Version]
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Rev. Relativ. 2010, 13, 1. [Google Scholar] [CrossRef] [Green Version]
- Kunz, M. The phenomenological approach to modeling the dark energy. C. R. Phys. 2012, 13, 539. [Google Scholar] [CrossRef] [Green Version]
- Nashed, G.G.L. Kerr–Newman Solution and Energy in Teleparallel Equivalent of Einstein Theory. Mod. Phys. Lett. A 2007, 22, 1047. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wang, Y.; Li, M. Holographic dark energy. Phys. Rep. 2017, 696, 1. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Dark energy and gravity. Gen. Relativ. Gravit. 2008, 40, 529. [Google Scholar] [CrossRef] [Green Version]
- Sami, M. Models of Dark Energy. In The Invisible Universe: Dark Matter and Dark Energy; Springer: Berlin/Heidelberg, Germany, 2007; pp. 219–256. [Google Scholar]
- Nashed, G.G.L. Brane world black holes in teleparallel theory equivalent to general relativity and their Killing vectors, energy, momentum and angular momentum. Chin. Phys. B 2010, 19, 020401. [Google Scholar] [CrossRef] [Green Version]
- Sahni, V.; Starobinsky, A. Reconstructing Dark Energy. Int. J. Mod. Phys. D 2006, 15, 2105. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Vacuum Nonsingular Black Hole in Tetrad Theory of Gravitation. Nuovo Cim. B 2002, 117, 521. [Google Scholar]
- Nashed, G.G.L. Reissner Nordstrom Solutions and Energy in Teleparallel Theory. Mod. Phys. Lett. 2006, 21, 2241. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified Cosmic History in Modified Gravity: From F(R) Theory To Lorentz Non-Invariant Models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.T. Symmetric Solutions to the Gauss-Bonnet Extended Einstein Equations. Nucl. Phys. B 1986, 268, 737. [Google Scholar] [CrossRef]
- Nashed, G.; Nojiri, S. Nontrivial Black Hole Solutions in f(R) Gravitational Theory. Phys. Rev. D 2020, 102, 124022. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Rotating Charged Black Hole Spacetimes in Quadratic f(R) Gravitational Theories. Int. J. Mod. Phys. D 2018, 27, 1850074. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Nojiri, S. Analytic Charged BHs in f(R) Gravity. Phys. Lett. B 2021, 820, 136475. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Spherically symmetric charged black holes in f(R) gravitational theories. Eur. Phys. J. Plus 2018, 133, 18. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Bamba, K. Charged Spherically Symmetric Taub–NUT Black Hole Solutions in f(R) Gravity. Prog. Theor. Exp. Phys. 2020, 2020, 043E05. [Google Scholar] [CrossRef]
- Antoniadis, I.; Rizos, J.; Tamvakis, K. Singularity-free cosmological solutions of the superstring effective action. Nucl. Phys. B 1994, 415, 497. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.; Alcaniz, J.; Reboucas, M.; Carvalho, F. Energy Conditions in F(R) Gravity. Phys. Rev. D 2007, 76, 083513. [Google Scholar] [CrossRef] [Green Version]
- Nashed, G.G.L. Higher Dimensional Charged Black Hole Solutions in f(R) Gravitational Theories. Adv. High Energy Phys. 2018, 2018, 7323574. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Anti-Evaporation of Schwarzschild–De Sitter Black Holes in f(R) Gravity. Class. Quantum Gravity 2013, 30, 125003. [Google Scholar] [CrossRef] [Green Version]
- Shah, P.; Samanta, G.C. Stability Analysis for Cosmological Models in f(R) Gravity Using Dynamical System Analysis. Eur. Phys. J. C 2019, 79, 1. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the New Field Theory. Proc. Roy. Soc. Lond. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Kruglov, S.I. Born-Infeld-Type Electrodynamics and Magnetic Black Holes. Ann. Phys. 2017, 383, 550–559. [Google Scholar] [CrossRef] [Green Version]
- Soleng, H.H. Charged Black Points in General Relativity Coupled to the Logarithmic U(1) Gauge Theory. Phys. Rev. D 1995, 52, 6178–6181. [Google Scholar] [CrossRef] [Green Version]
- Panah, B.E. Can the power Maxwell nonlinear electrodynamics theory remove the singularity of electric field of point-like charges at their locations? Europhys. Lett. 2021, 134, 20005. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Pearson: Boston, MA, USA, 2013. [Google Scholar]
- Newton, I. Philosophia Naturalis Principia Mathematica; Nabu Press: Charleston, SC, USA, 1687. [Google Scholar]
- Thirring, H. Über die Wirkung rotierender ferner Massen in der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 1–32. [Google Scholar]
- Lense, J.; Thirring, H. Über den Einfluß der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 1–14. [Google Scholar]
- Lense, J.; Thirring, H. On the influence of the proper rotation of a central body on the motion of the planets and the moon, according to einstein’s theory of gravitation. Z. Phys. 1918, 19, 156–163. [Google Scholar]
- Ciufolini, I.; Wheeler, J.A. Gravitation and Inertia; Princeton University Press: Princeton, NJ, USA, 1995. [Google Scholar]
- Mashhoon, B.; Hehl, F.W.; Theiss, D.S. On the gravitational effects of rotating masses: The thirring-lense papers. Gen. Relativ. Gravit. 1984, 16, 711–750. [Google Scholar] [CrossRef]
- de Sitter, W. On Einstein’s theory of gravitation and its astronomical consequences. Second paper. Mnras 1916, 77, 155–184. [Google Scholar] [CrossRef] [Green Version]
- Dass, A.; Liberati, S. Gravitoelectromagnetism in metric f(R) and Brans–Dicke theories with a potential. Gen. Rel. Grav. 2019, 51, 84. [Google Scholar] [CrossRef] [Green Version]
- Elizalde, E.; Nashed, G.G.L.; Nojiri, S.; Odintsov, S.D. Spherically Symmetric Black Holes with Electric and Magnetic Charge in Extended Gravity: Physical Properties, Causal Structure, and Stability Analysis in Einstein’s and Jordan’s Frames. Eur. Phys. J. C 2020, 80, 109. [Google Scholar] [CrossRef] [Green Version]
- Uniyal, R.; Nandan, H.; Purohit, K. Null Geodesics and Observables Around the Kerr–Sen Black Hole. Class. Quantum Gravity 2017, 35, 025003. [Google Scholar] [CrossRef] [Green Version]
- Kuniyal, R.S.; Uniyal, R.; Nandan, H.; Purohit, K. Null Geodesics in a Magnetically Charged Stringy Black Hole Spacetime. Gen. Relativ. Gravit. 2016, 48, 46. [Google Scholar] [CrossRef] [Green Version]
- Kuniyal, R.S.; Uniyal, R.; Biswas, A.; Nandan, H.; Purohit, K. Null Geodesics and Red–Blue Shifts of Photons Emitted from Geodesic Particles Around a Noncommutative Black Hole Space–Time. Int. J. Mod. Phys. A 2018, 33, 1850098. [Google Scholar] [CrossRef] [Green Version]
- Nashed, G.; Saridakis, E.N. New Rotating Black Holes in Nonlinear Maxwell F(R) Gravity. Phys. Rev. D 2020, 102, 124072. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. One-loop f(R) gravity in de Sitter Universe. J. Cosmol. Astropart. Phys. 2005, 2, 010. [Google Scholar] [CrossRef] [Green Version]
- Ayon-Beato, E.; Garcia, A. New Regular Black Hole Solution from Nonlinear Electrodynamics. Phys. Lett. B 1999, 464, 25. [Google Scholar] [CrossRef] [Green Version]
- Koivisto, T.; Kurki-Suonio, H. Cosmological Perturbations in the Palatini Formulation of Modified Gravity. Class. Quant. Grav. 2006, 23, 2355. [Google Scholar] [CrossRef]
- Hod, S. Spherical Null Geodesics of Rotating Kerr Black Holes. Phys. Lett. B 2013, 718, 1552. [Google Scholar] [CrossRef] [Green Version]
- Uniyal, R.; Nandan, H.; Jetzer, P. Bending Angle of Light in Equatorial Plane of Kerr–Sen Black Hole. Phys. Lett. B 2018, 782, 185. [Google Scholar] [CrossRef]
- Sharma, P.; Nandan, H.; Gannouji, R.; Uniyal, R.; Abebe, A. Deflection of Light by a Rotating Black Hole Surrounded by “Quintessence”. Int. J. Mod. Phys. A 2020, 35, 2050155. [Google Scholar] [CrossRef]
- Kala, S.; Nandan, H.; Sharma, P. Deflection of Light around a Rotating BTZ Black Hole. Mod. Phys. Lett. A 2020, 35, 2050323. [Google Scholar] [CrossRef]
- Nashed, G. Uniqueness of Non-Trivial Spherically Symmetric Black Hole Solution in Special Classes of F(R) Gravitational Theory. Phys. Lett. B 2021, 812, 136012. [Google Scholar] [CrossRef]
- Becerril, R.; Valdez-Alvarado, S.; Nucamendi, U. Obtaining Mass Parameters of Compact Objects from Redshifts and Blueshifts Emitted by Geodesic Particles around Them. Phys. Rev. D 2016, 94, 124024. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Miranda, A.S.; Berti, E.; Witek, H.; Zanchin, V.T. Geodesic stability, Lyapunov exponents, and quasinormal modes. Phys. Rev. D 2009, 79, 064016. [Google Scholar] [CrossRef] [Green Version]
- Giri, S.; Nandan, H. Stability Analysis of Geodesics and Quasinormal Modes of a Dual Stringy Black Hole via Lyapunov Exponents. Gen. Relativ. Gravit. 2021, 53, 1. [Google Scholar] [CrossRef]
- Sano, M.; Sawada, Y. Measurement of the Lyapunov Spectrum from a Chaotic Time Series. Phys. Rev. Lett. 1985, 55, 1082. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, P. Stability Analysis and Quasinormal Modes of Reissner–Nordstrom Space-Time via Lyapunov Exponent. Pramana 2016, 87, 5. [Google Scholar] [CrossRef] [Green Version]
- Mondal, M.; Pradhan, P.; Rahaman, F.; Karar, I. Geodesic Stability and Quasi Normal Modes Via Lyapunov Exponent for Hayward Black Hole. Mod. Phys. Lett. A 2020, 35, 2050249. [Google Scholar] [CrossRef]
- Pradhan, P. The Thirteenth Marcel Grossmann Meeting: On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories; World Scientific: Stockholm, Sweden, 2015; pp. 1892–1894. [Google Scholar]
- Cornish, N.J.; Levin, J. Lyapunov timescales and black hole binaries. Class. Quantum Gravity 2003, 20, 1649. [Google Scholar] [CrossRef] [Green Version]
- Cornish, N.J. Chaos and gravitational waves. Phys. Rev. D 2001, 64, 084011. [Google Scholar] [CrossRef] [Green Version]
- Hilborn, R.C. Chaos and Nonlinear Dynamics: An Introduction for Scientists and Engineers; Oxford University Press on Demand: Oxford, UK, 2000. [Google Scholar]
- Suzuki, S.; Maeda, K.-I. Chaos In Schwarzschild Spacetime: The Motion of a Spinning Particle. Phys. Rev. D 1997, 55, 4848. [Google Scholar] [CrossRef] [Green Version]
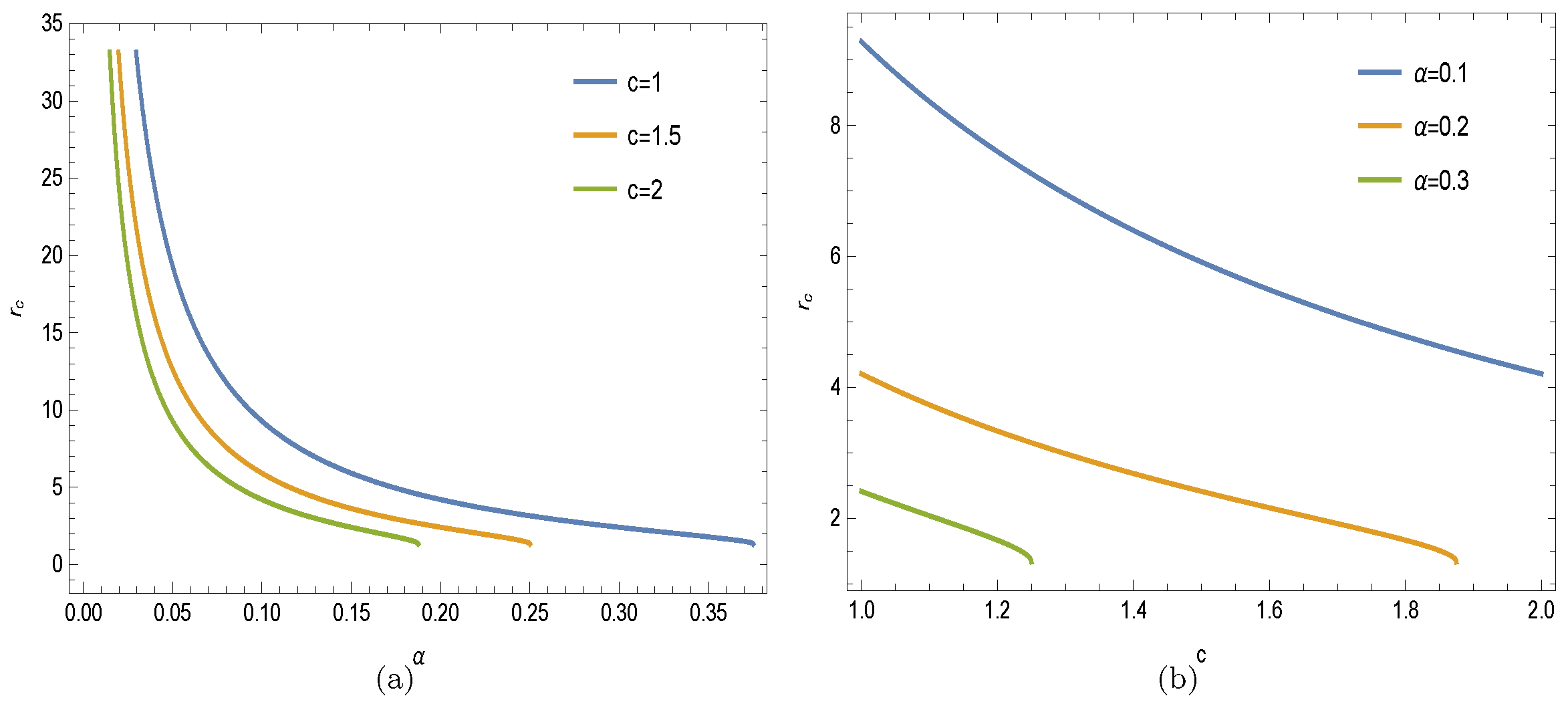


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, P.; Nandan, H.; Nashed, G.G.L.; Giri, S.; Abebe, A. Geodesics of a Static Charged Black Hole Spacetime in f(R) Gravity. Symmetry 2022, 14, 309. https://doi.org/10.3390/sym14020309
Sharma P, Nandan H, Nashed GGL, Giri S, Abebe A. Geodesics of a Static Charged Black Hole Spacetime in f(R) Gravity. Symmetry. 2022; 14(2):309. https://doi.org/10.3390/sym14020309
Chicago/Turabian StyleSharma, Prateek, Hemwati Nandan, Gamal G. L. Nashed, Shobhit Giri, and Amare Abebe. 2022. "Geodesics of a Static Charged Black Hole Spacetime in f(R) Gravity" Symmetry 14, no. 2: 309. https://doi.org/10.3390/sym14020309





