Effects of Large-Diameter Shield Tunneling on the Pile Foundations of High-Speed Railway Bridge and Soil Reinforcement Schemes
Abstract
:1. Introduction
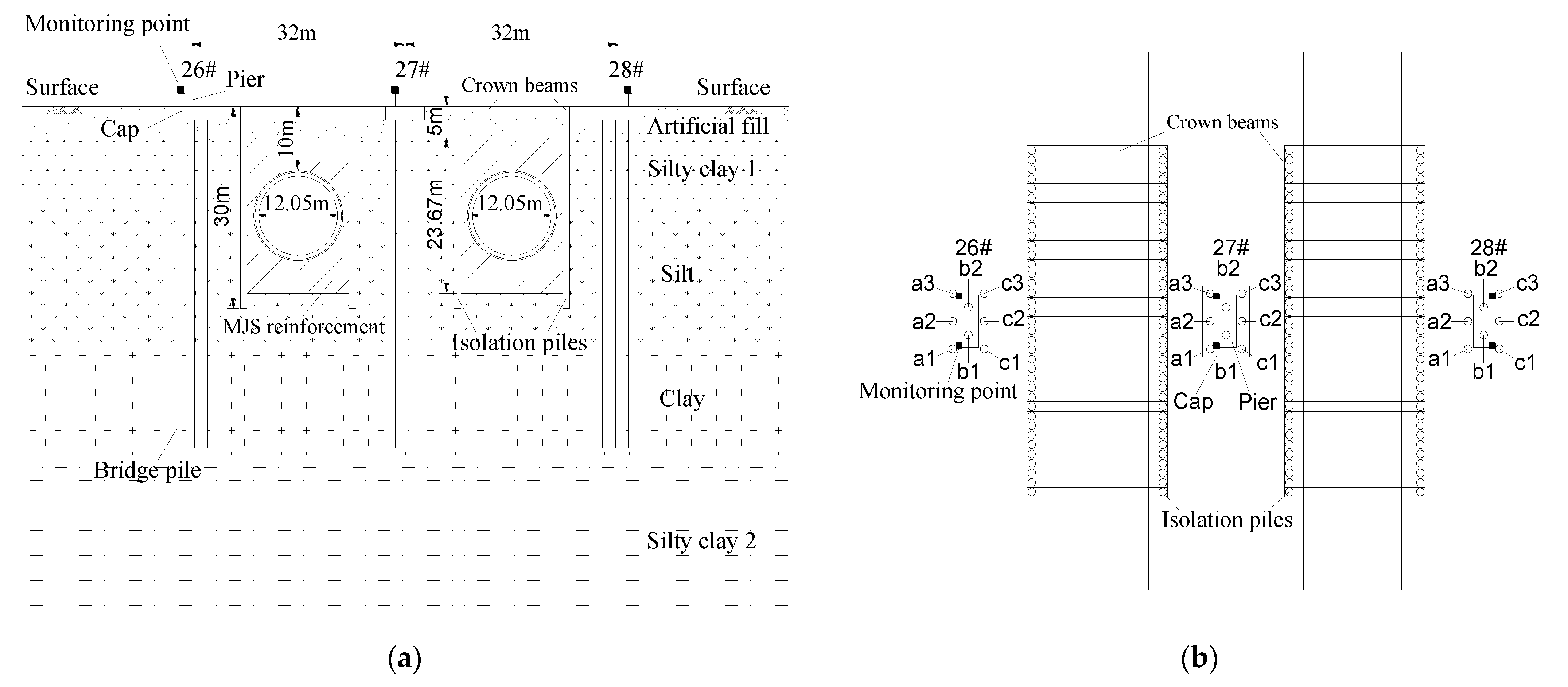
2. Overview of the Engineering
3. Symmetrical Finite Element Models
4. Effects of Shield Tunneling on Adjacent Pile Foundations
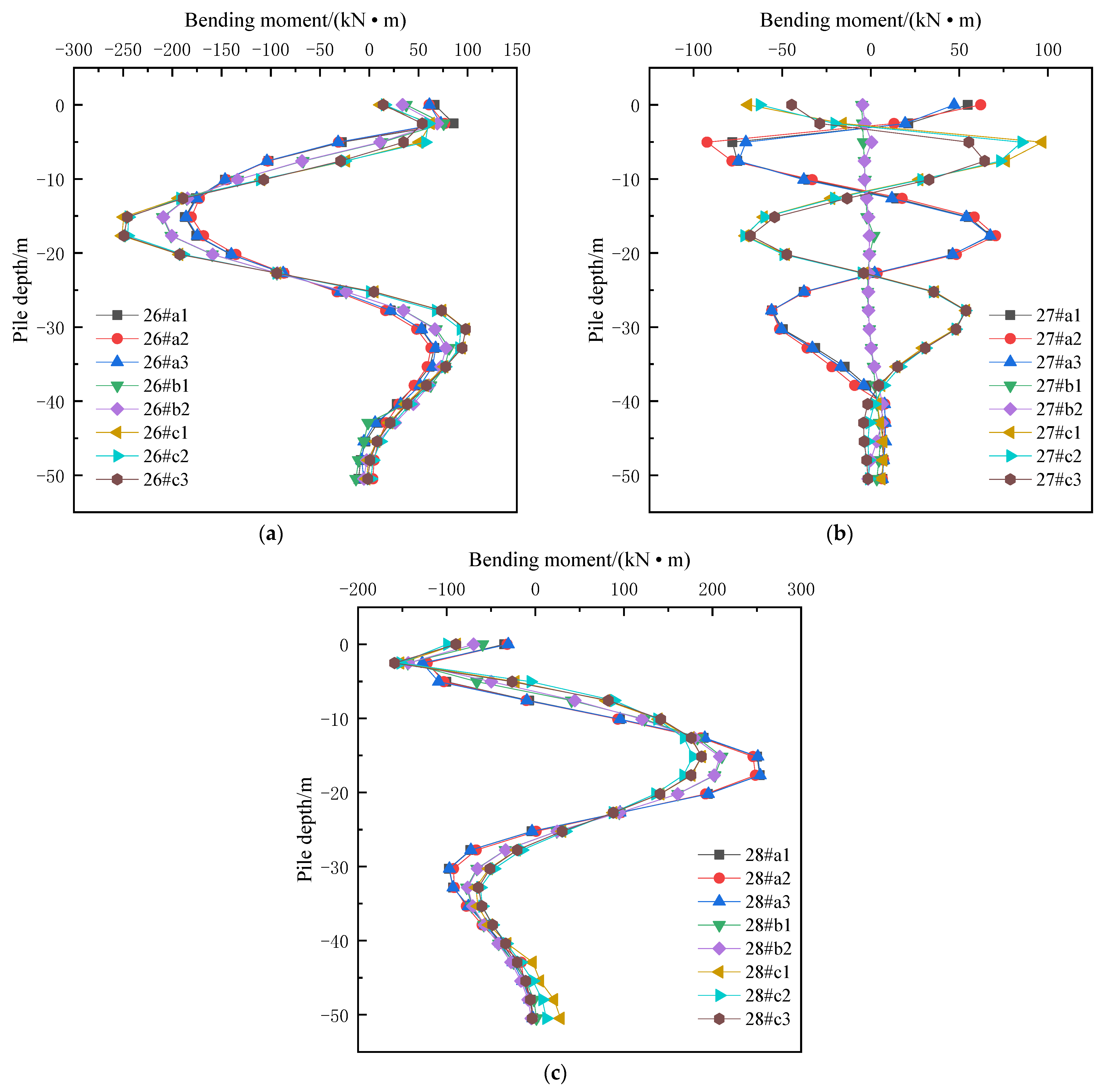
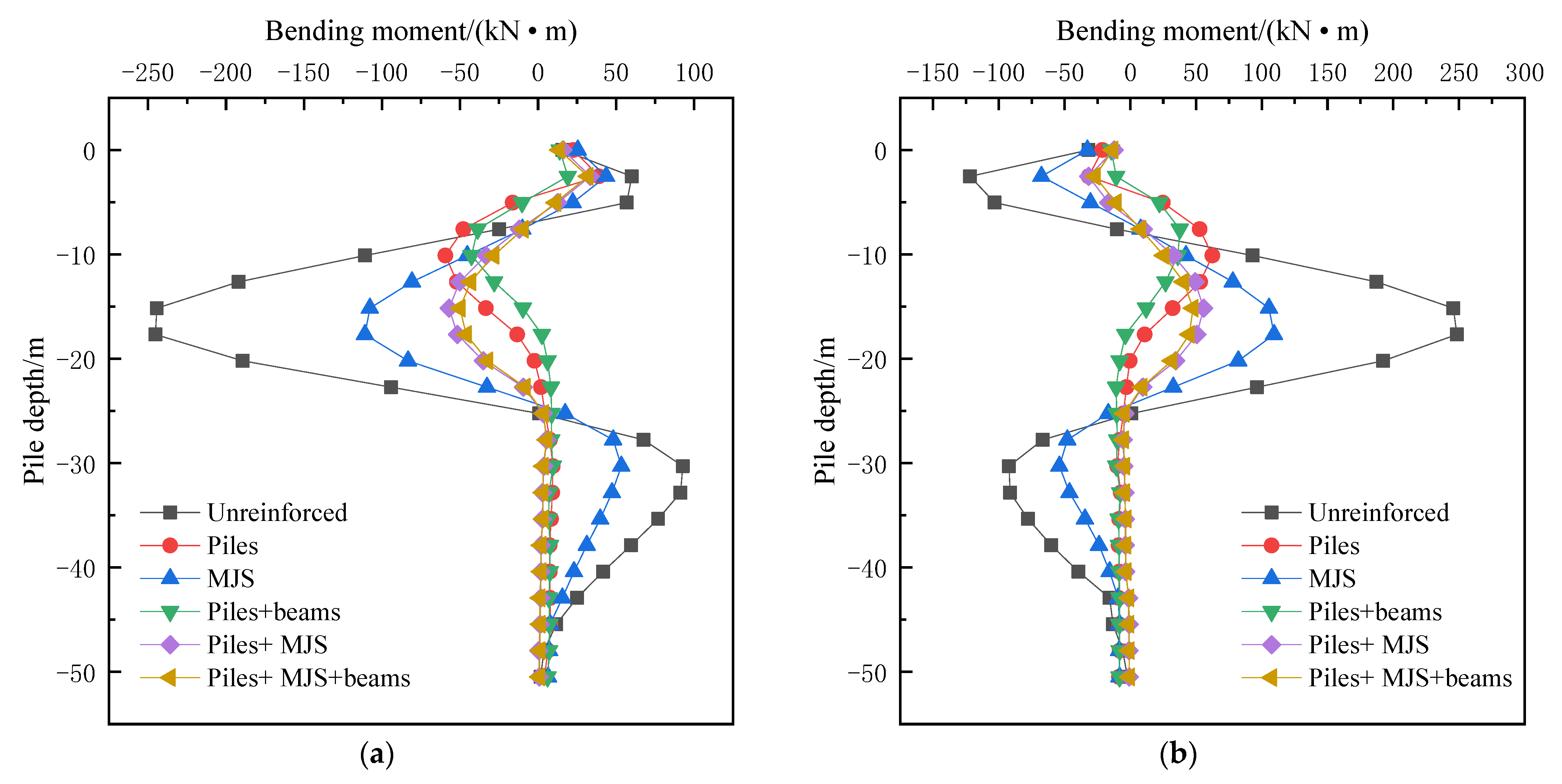
4.1. Effects of Shield Tunneling on Bending Moment of Adjacent Bridge Piles
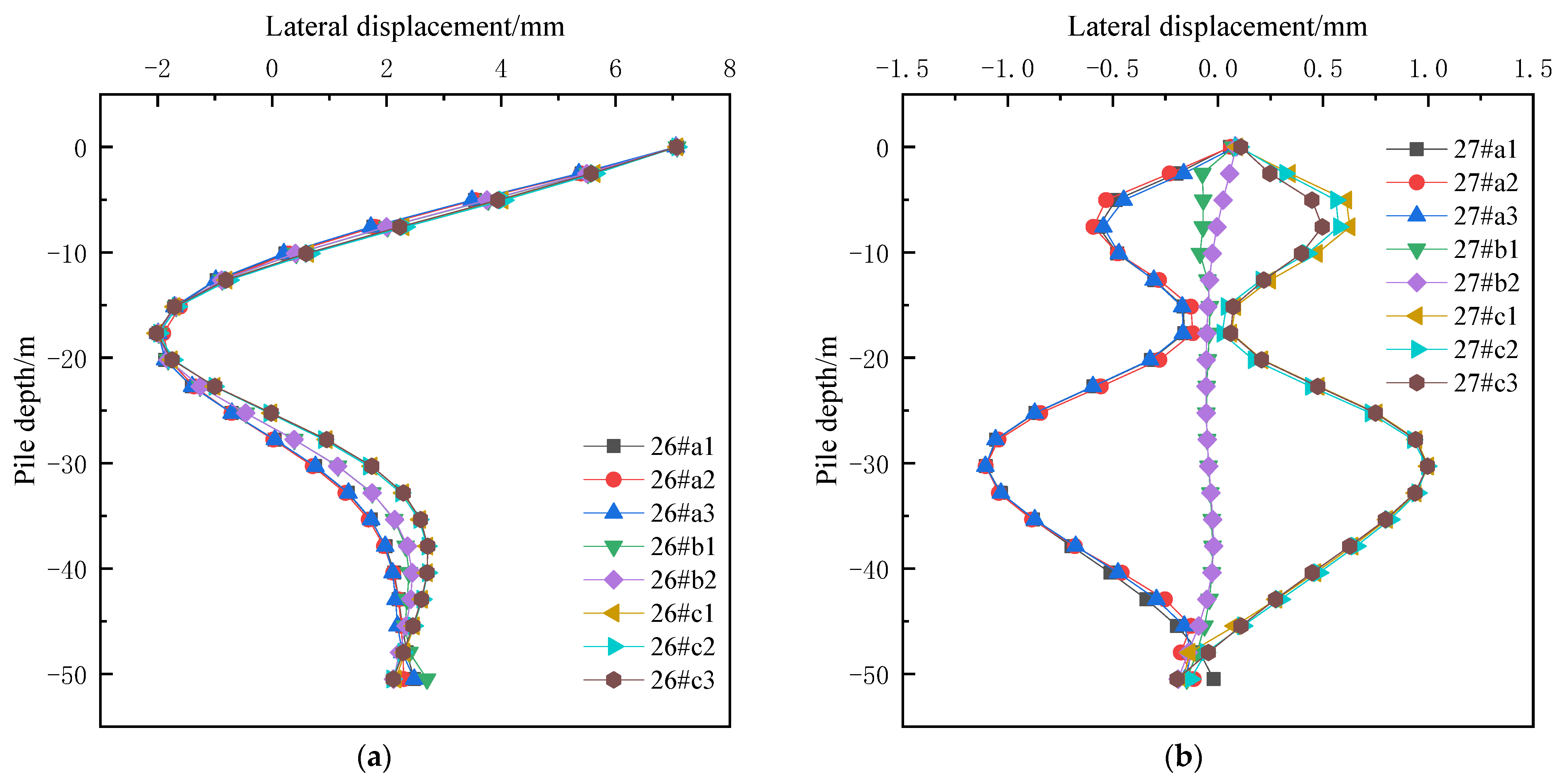
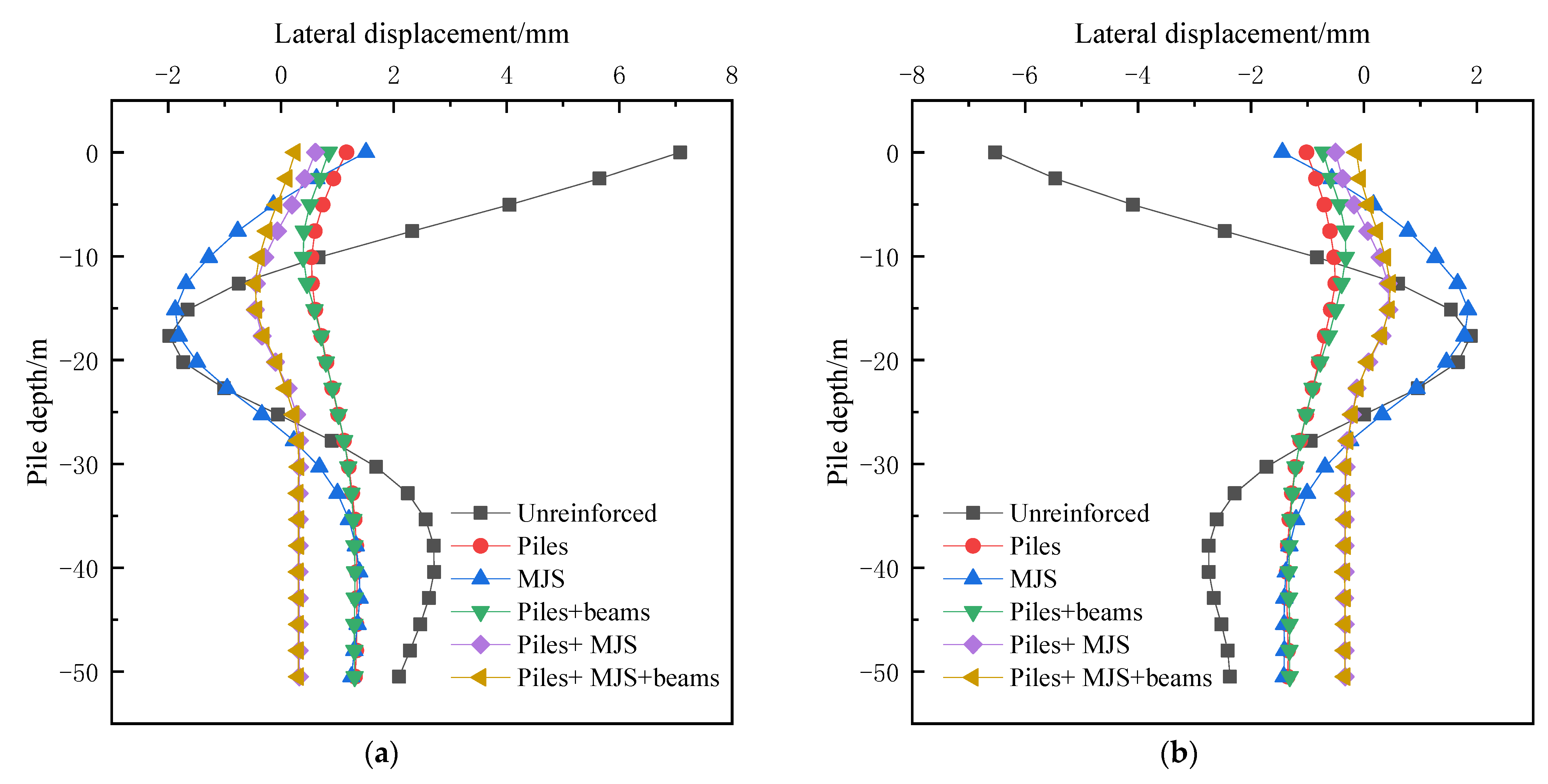
4.2. Effects of Shield Tunneling on the Displacement of Adjacent Pile Foundations
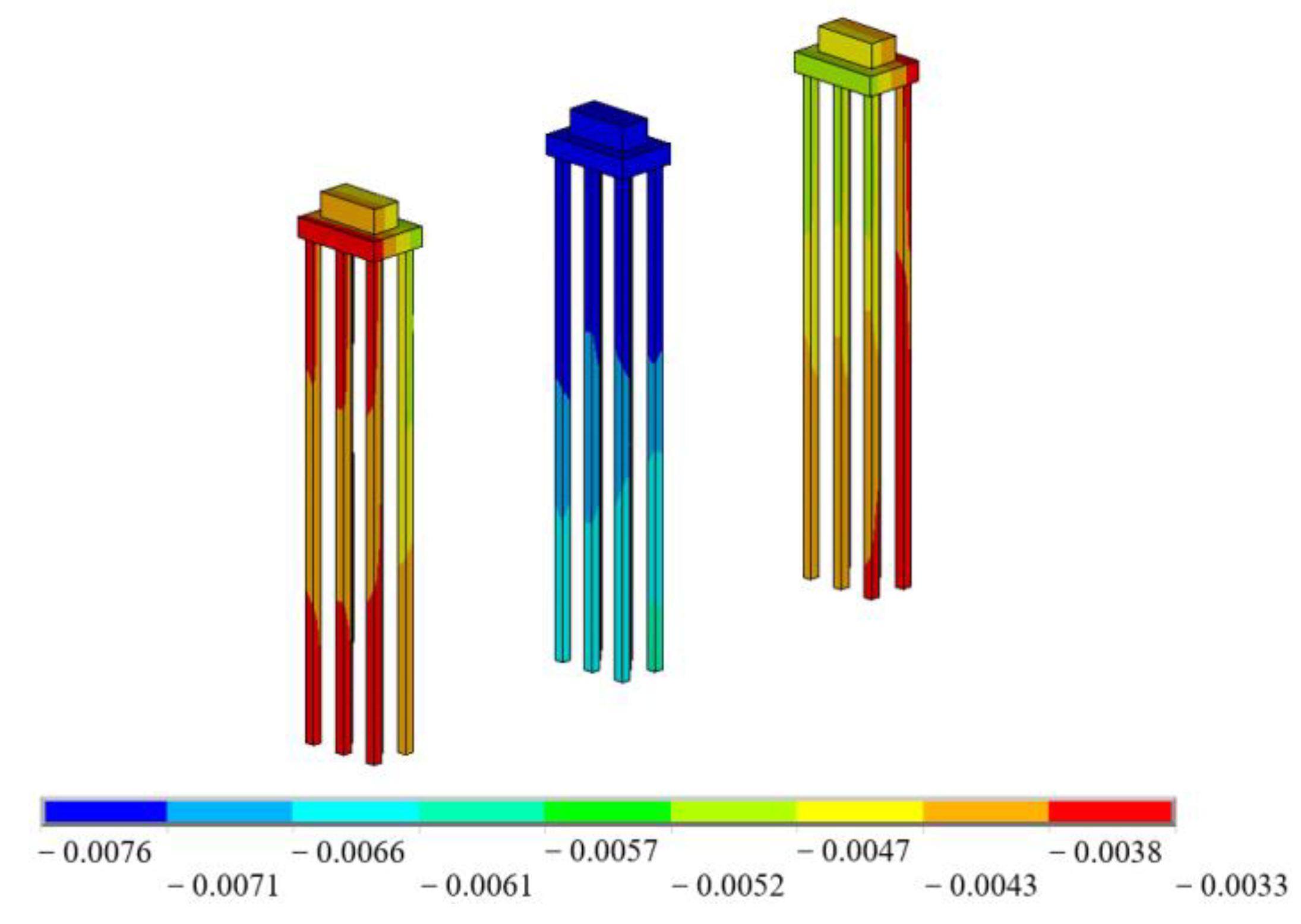
5. Analysis of the Effects of Soil Reinforcement Schemes
- (1)
- Without any soil reinforcement measures, the maximum bending moment of the bridge piles was 248 kN · m, the bending deformation of the bridge piles was large, the maximum lateral displacement of the top of the piers was 7.1 mm, and the maximum settlement of the middle pier top was −7.2 mm. Since they cannot meet the displacement control requirements of ±2 mm for the piers of the existing high-speed railway under the condition of unlimited train speed, reinforcement measures must be taken for the soil layers in the affected section in advance before the construction of large-diameter shield tunneling through the high-speed railway bridge.
- (2)
- After five soil reinforcement schemes including isolation piles’ protection, MJS reinforcement, isolation piles + crown beams, isolation piles + MJS reinforcement, and isolation piles + MJS reinforcement + crown beams were adopted respectively, the maximum bending moment of the bridge piles was −111 kN · m, the bending deformation of the bridge piles was greatly reduced, the maximum lateral displacement of piers top was 1.5 mm, and the maximum settlement of middle pier top was −1.8 mm. Therefore, these five soil reinforcement schemes had obvious protective effects on adjacent pile foundations, and could significantly reduce the maximum bending moment, lateral displacement, and settlement of pile foundations.
- (3)
- When isolated piles were adopted for protection alone, the maximum bending moment of bridge piles was 62 kN · m, the maximum lateral displacement of the top of the piers was 1.2 mm, and the maximum settlement of the middle pier top was −1.2 mm. The control effect was better than that of MJS reinforcement alone, so isolation pile protection should be preferred.
- (4)
- Compared with isolated piles’ protection alone, the bending moment and lateral displacement of bridge piles could be further reduced by using isolated pile + crown beams protection at the same time, but the effect on the maximum bending moment of the bridge piles was relatively small.
- (5)
- After five soil layer reinforcement schemes were adopted respectively, the lateral displacement and settlement of the top of the piers could be controlled within ± 2 mm, which could meet the structural deformation control requirements specified during the construction of shield tunneling through high-speed railway bridges. Considering the economy of the construction cost and the effects of soil reinforcement, isolation pile protection should be preferred. In order to ensure the absolute safety of high-speed train operation during shield tunneling, it is recommended to adopt the reinforcement scheme of isolation piles + MJS reinforcement + crown beams, which can further control the lateral displacement and settlement of piers top within ±1 mm.
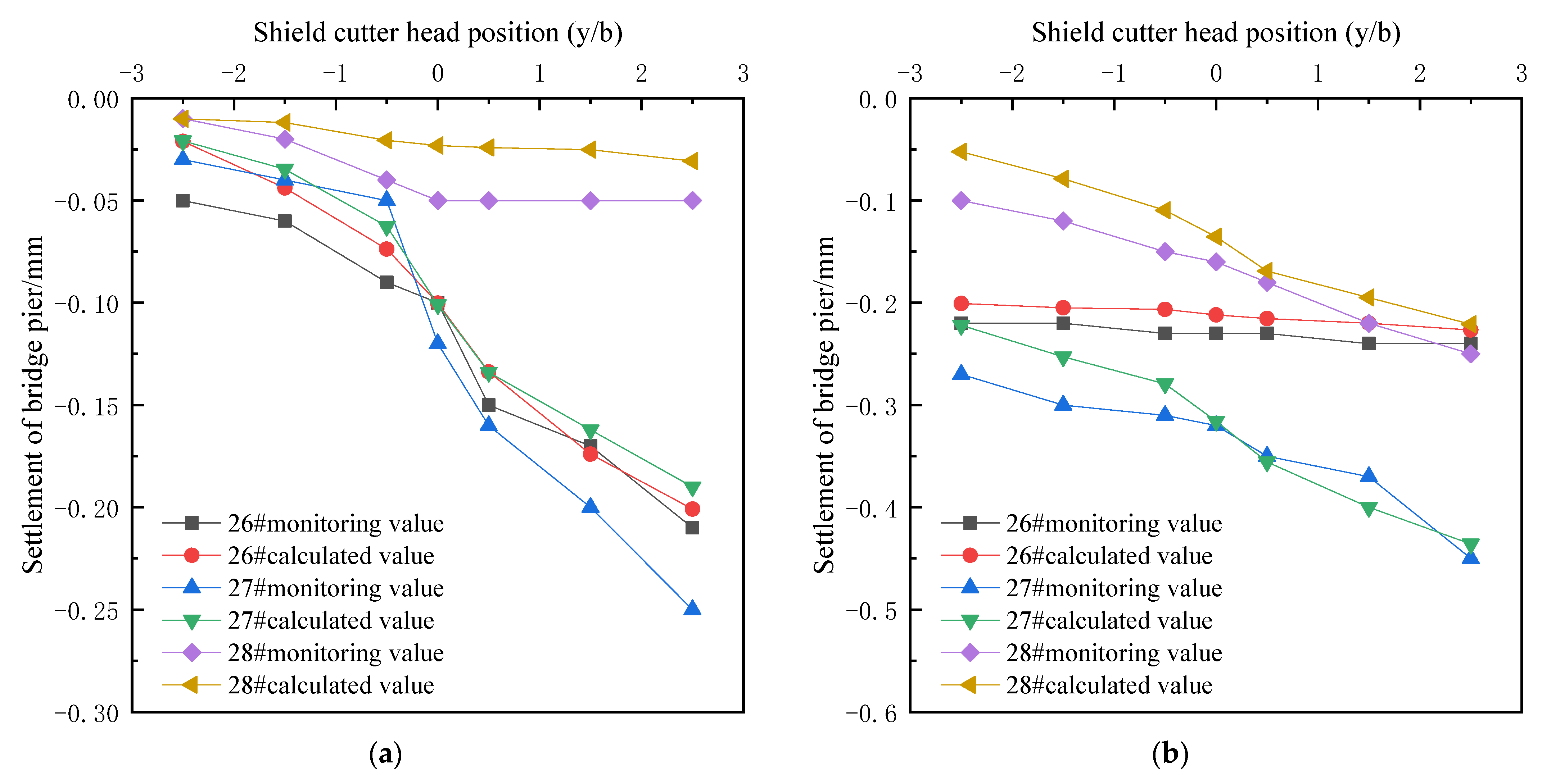
6. Verification of Numerical Simulation Results
7. Conclusions
- The completion of shield tunneling will cause additional bending moments of adjacent bridge piles. The bending moments’ distribution law of bridge piles in a symmetrical position is basically symmetrical. At the elevation above the tunnel crown or below the tunnel bottom, the bridge piles outside the twin tunnels mainly produce the bending moment which makes the side of the bridge piles away from the tunnel bear tension, and the maximum bending moment appears at the piles’ body at the same height as the center of the tunnels; the bending moment of bridge piles located between the twin tunnels is relatively small, which generally does not play a controlling role.
- The completion of shield tunneling will cause additional lateral displacement of adjacent bridge piles. The lateral displacement distribution law of bridge piles in a symmetrical position is basically symmetrical. At the elevation above the tunnel crown or below the tunnel bottom, the bridge piles outside the twin tunnels mainly produce lateral displacement with direction pointing to the tunnel. At the elevation from the tunnel crown to the tunnel bottom, the bridge piles outside the twin tunnel mainly produce lateral displacement with direction away from the tunnel; the lateral displacement of bridge piles located between the twin tunnels is also relatively small, which generally does not play a control role.
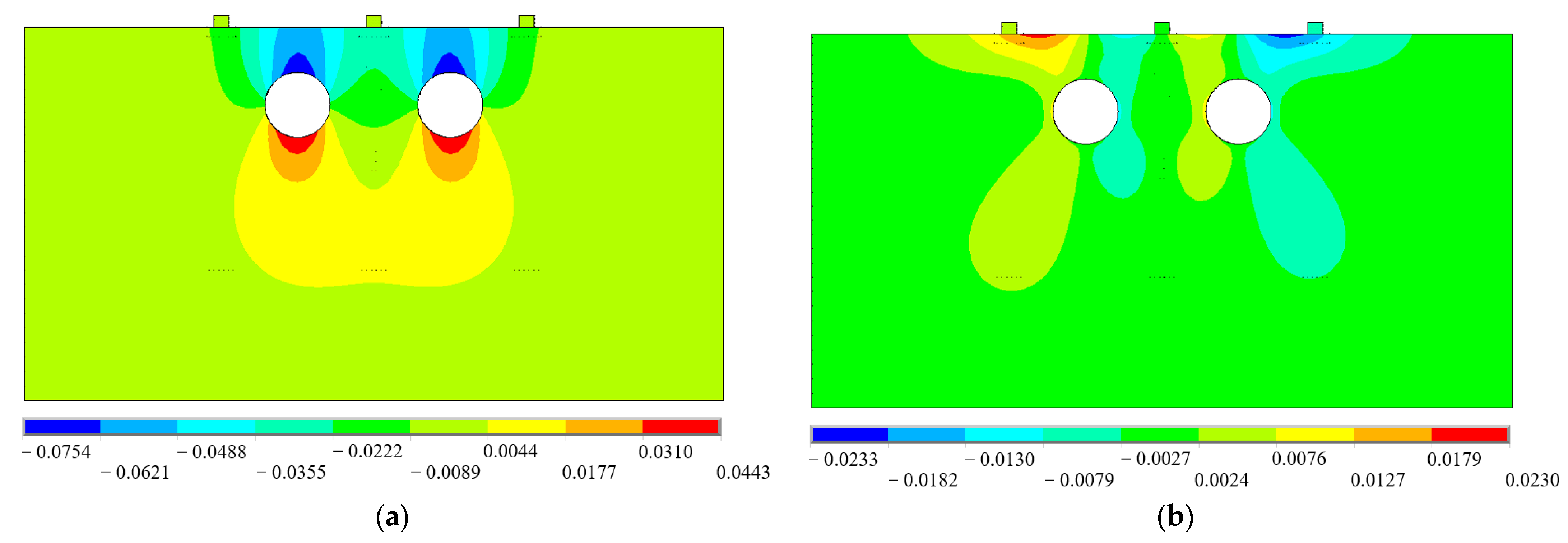
- The completion of shield tunneling will cause the settlement of adjacent pile foundations and piers. The settlement value of pile foundations and piers in symmetrical positions are almost the same. The settlement of the pier located between the twin tunnels is significantly higher than that of the piers outside the twin tunnels. Without any soil reinforcement measures, the final settlement of the pier located between the twin tunnels is −7.2 mm. Reinforcement measures must be adopted for the soil layer in the affected section in advance to meet the operation safety of high-speed railway trains during the construction of shield tunneling through the high-speed railway bridge.
- The five soil layer reinforcement schemes can significantly reduce the bending moment and displacement of adjacent bridge pile foundations, and have better protection effects. The protection effect of isolated piles’ protection alone is better than that of MJS reinforcement alone, so isolated piles’ protection should be preferred. More than two kinds of soil reinforcement measures can be adopted at the same time to further control the lateral displacement and settlement of piers within ±1 mm, to ensure the absolute safety of high-speed rail trains’ operation during shield tunneling.
- Under the condition of isolation piles + MJS reinforcement + crown beams reinforcement, the field monitoring of the displacements of adjacent piers during the construction of shield tunneling through the high-speed railway bridge was carried out. The numerical simulation results are basically consistent with the field monitoring data. Therefore, the numerical simulation can better reflect the actual effects of large-diameter shield tunneling on the pile foundation of adjacent high-speed railway bridges.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Poulos, H.G.; Loganathan, N.J.J.O.G. Pile responses caused by tunneling. J. Geotech. Geoenviron. Eng. 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Jacobsz, S.W.; Standing, J.R.; Mair, R.J.; Hagiwara, T.; Sugiyama, T. Centrifuge modelling of tunnelling near driven piles. Soils Found. 2004, 44, 49–56. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Lu, H.; Peng, S.Y. Three-dimensional centrifuge modelling of the effects of twin tunnelling on an existing pile. Tunn. Undergr. Space Technol. 2013, 35, 189–199. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Soomro, M.A.; Hong, Y. Three-dimensional centrifuge modelling of pile group responses to side-by-side twin tunneling. Tunn. Undergr. Space Technol. 2014, 43, 350–361. [Google Scholar] [CrossRef]
- Basile, F. Effects of tunnelling on pile foundations. Soils Found. 2014, 54, 280–295. [Google Scholar] [CrossRef]
- Yoo, C. Interaction between tunneling and bridge foundation–A 3D numerical investigation. Comput. Geotech. 2013, 49, 70–78. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Wang, L.; Zeng, Z.; Gu, D. Numerical simulation and analysis of the pile underpinning technology used in shield tunnel crossings on bridge pile foundations. Undergr. Space. 2021, 6, 396–408. [Google Scholar] [CrossRef]
- Yang, M.; Sun, Q.; Li, W.C.; Ma, K. Three-dimensional finite element analysis on effects of tunnel construction on nearby pile foundation. J. Cent. South Univ. 2011, 18, 909–916. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Lu, H. Effects of the construction sequence of twin tunnels at different depths on an existing pile. Can. Geotech. J. 2014, 51, 173–183. [Google Scholar] [CrossRef]
- Soomro, M.A.; Ng, C.W.W.; Memon, N.A.; Bhanbhro, R. Lateral behaviour of a pile group due to side-by-side twin tunnelling in dry sand: 3D centrifuge tests and numerical modelling. Comput. Geotech. 2018, 101, 48–64. [Google Scholar] [CrossRef]
- He, S.; Lai, J.; Li, Y.; Wang, K.; Wang, L.; Zhang, W. Pile group response induced by adjacent shield tunnelling in clay: Scale model test and numerical simulation. Tunn. Undergr. Space Technol. 2022, 120, 104039. [Google Scholar] [CrossRef]
- Pang, C.H.; Yong, K.Y.; Chow, Y.K. Three-dimensional numerical simulation of tunnel advancement on adjacent pile foundation. Undergr. Space Use Anal. Past Lessons Future. 2005, 2, 1141–1148. [Google Scholar]
- Liu, C.; Zhang, Z.; Regueiro, R.A. Pile and pile group response to tunnelling using a large diameter slurry shield—Case study in Shanghai. Comput. Geotech. 2014, 59, 21–43. [Google Scholar] [CrossRef]
- Shen, J.W.; Liu, L. Numerical analysis and field monitoring for studying effects of shield tunnelling on nearby piles. Rock Soil Mech 2015, 36, 709–714. (In Chinese) [Google Scholar]
- Li, C.; Zhong, Z.; He, G.; Liu, X. Response of the ground and adjacent end-bearing piles due to side-by-side twin tunnelling in compound rock strata. Tunn. Undergr. Space Technol. 2019, 89, 91–108. [Google Scholar] [CrossRef]
- Wang, J.; Wen, Z. Analysis of Construction Impact of a Large Diameter Shield Tunneling Side-Crossing Viaduct Pile Foundations in Short Distance. Geotech. Geol. Eng. 2021, 39, 5587–5598. [Google Scholar] [CrossRef]
- Liu, Z.; He, P.; Zhang, A.Q. Analysis of Effects of Shield Tunnel Construction Process and Supporting Ways on Pile Groups of High-speed Railway Viaduct. Eng. Mech. 2016, 33, 219–226. (In Chinese) [Google Scholar]
- Tang, J.; Yan Liu, J.; Liu, Y. Study on the measures of tunnels side-crossing bridge based on sheltering effects of isolation piles. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Zhuhai, China, 28’30 April 2017; Volume 81, p. 012156. [Google Scholar]
- Ma, W.; Liu, J.; Zhang, L. Analysis of the impact of large-diameter shield construction adjacent to the side of the pile foundation. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Changsha, China, 18’20 September 2020; Volume 634, p. 012109. [Google Scholar]
- Wu, B.; Zhang, Z.; Huang, W. Comparison and selection of reinforcement schemes for shield tunnelling close crossing high-speed railway viaduct group. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Guangzhou, China, 08’10 March 2019; Volume 267, p. 042119. [Google Scholar]
- Wang, K.; Li, Z.P.; Jiang, H.T. The Deformation Laws and Control Measures of the Bridge Affected by the Construction of Long-Distance Overlapping Tunnels. Chin. Civil. Eng. J. 2020, 53, 180–185. (In Chinese) [Google Scholar]
- Qiu, H.; Wang, Z.; Ayasrah, M.M.; Fu, C.; Gang, L. Numerical Study on the Reinforcement Measures of Tunneling on Adjacent Piles. Symmetry 2022, 14, 288. [Google Scholar] [CrossRef]
- Li, X.X.; Yang, Z.H. Influences of Construction of Side-crossing Shield Tunnel on Adjacent Pile Foundation and Reinforcement Effect of Protection Measures. Rock Soil Mech. 2015, 36, 537–541. (In Chinese) [Google Scholar]
- Li, Z.; Lv, J.; Xie, X.; Fu, H.; Huang, J.; Li, Z. Mechanical Characteristics of Structures and Ground Deformation Caused by Shield Tunneling Under-Passing Highways in Complex Geological Conditions Based on the MJS Method. Appl. Sci. 2021, 11, 9323. [Google Scholar] [CrossRef]
- Li, C.; Gong, B.; Tao, H.; Chen, Y. Numerical Investigation of Deformation Influence of Existing Viaduct Piles under MJS Construction Method. J. Eng. Sci. Tech. Rev. 2022, 15, 32–39. [Google Scholar] [CrossRef]
- Li, X.; Zhang, D.; Hou, Y.; Cao, L.; Li, Q. Analysis of Ground and Structure Deformation Characteristics During Shield Tunneling in Tianjin Subway. China Railw. Sci 2018, 39, 71–80. (In Chinese) [Google Scholar]
- Lou, P.; Li, Y.; Lu, S.; Xiao, H.; Zhang, Z. Deformation and Mechanical Characteristics of Existing Foundation Pit and Tunnel Itself Caused by Shield Tunnel Undercrossing. Symmetry 2022, 14, 263. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics, and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Alejano, L.R.; Bobet, A. Drucker—prager criterion. In The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007-2014. Springer: Cham, Switzerland, 2012; pp. 247–252. [Google Scholar]
- Zhou, S.; Wang, B.; Dong, X.; Sun, Y. Computational and Analytical Methods in Urban Rail Transit Underground Engineering, 1st ed.; China Communications Press: Beijing, China, 2014; pp. 109–110. [Google Scholar]
- Zhu, F.; Yang, P.; Ong, C.W. Numerical Analysis on Influence of Shield Tunnel Excavation to Neighboring Piles. Chin. J. Geotech. Eng. 2008, 2, 298–302. (In Chinese) [Google Scholar]
- TB 10182-2017; National Railway Administration of the People’s Republic of China. Technical Specification for Highway and Municipal Engineering under Crossing High Speed Railway. China Railway Publishing House: Beijing, China, 2017.



| Soil Layers | Thick (m) | Density (kN·m−3) | Cohesion Force (kPa) | Frictional Angle (°) | Compression Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Artificial fill | 5 | 18.2 | 10 | 15 | 4.5 | 0.3 |
| Silty clay 1 | 10 | 19 | 18 | 12 | 5 | 0.3 |
| Silt | 22 | 18.9 | 22 | 22 | 7 | 0.27 |
| Clay | 16 | 19.2 | 35 | 14 | 8 | 0.3 |
| Silty clay 2 | 27 | 19.4 | 30 | 14 | 6.5 | 0.25 |
| MJS reinforcement | — | 21 | 40 | 23 | 400 | 0.23 |
| Structures | Density (kN·m−3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Shield shell | 142 | 210,000 | 0.3 |
| Segment | 26 | 34,500 | 0.2 |
| Isochronous layer | 22.5 | 50 (early stage) | 0.25 |
| 500 (later stage) | |||
| Bridge piers | 25 | 31,500 | 0.2 |
| Pile foundations | 25 | 31,500 | 0.2 |
| Isolation piles | 25 | 30,000 | 0.2 |
| Crown beams | 25 | 30,000 | 0.2 |
| Condition | Maximum Bending Moment of Bridge Piles (kN•m) | Lateral Displacement of Piers Top (mm) | Settlement of Piers Top (mm) | ||||
|---|---|---|---|---|---|---|---|
| 26#c2 | 28#a2 | 26#c2 | 28#a2 | 26# | 27# | 28# | |
| Unreinforced | −245 | 248 | 7.1 | −6.5 | −4.7 | −7.2 | −4.6 |
| Piles | −59 | 62 | 1.2 | −1.1 | −0.4 | −1.2 | −0.3 |
| MJS | −111 | 109 | 1.5 | −1.4 | −1.2 | −1.8 | −1.2 |
| Piles + beams | −43 | 38 | 0.9 | −0.8 | −0.2 | −1.0 | −0.2 |
| Piles + MJS | −57 | 56 | 0.6 | −0.6 | −0.4 | −0.6 | −0.4 |
| Piles + MJS + beams | −50 | 48 | 0.3 | −0.2 | −0.2 | −0.4 | −0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Wang, B.; Guo, W. Effects of Large-Diameter Shield Tunneling on the Pile Foundations of High-Speed Railway Bridge and Soil Reinforcement Schemes. Symmetry 2022, 14, 1913. https://doi.org/10.3390/sym14091913
Yang Q, Wang B, Guo W. Effects of Large-Diameter Shield Tunneling on the Pile Foundations of High-Speed Railway Bridge and Soil Reinforcement Schemes. Symmetry. 2022; 14(9):1913. https://doi.org/10.3390/sym14091913
Chicago/Turabian StyleYang, Qiaohong, Bing Wang, and Wenhua Guo. 2022. "Effects of Large-Diameter Shield Tunneling on the Pile Foundations of High-Speed Railway Bridge and Soil Reinforcement Schemes" Symmetry 14, no. 9: 1913. https://doi.org/10.3390/sym14091913
APA StyleYang, Q., Wang, B., & Guo, W. (2022). Effects of Large-Diameter Shield Tunneling on the Pile Foundations of High-Speed Railway Bridge and Soil Reinforcement Schemes. Symmetry, 14(9), 1913. https://doi.org/10.3390/sym14091913






