Characterization of Quantum and Classical Critical Points for an Integrable Two-Qubit Spin–Boson Model
Abstract
:1. Introduction
2. Model
3. Dynamics
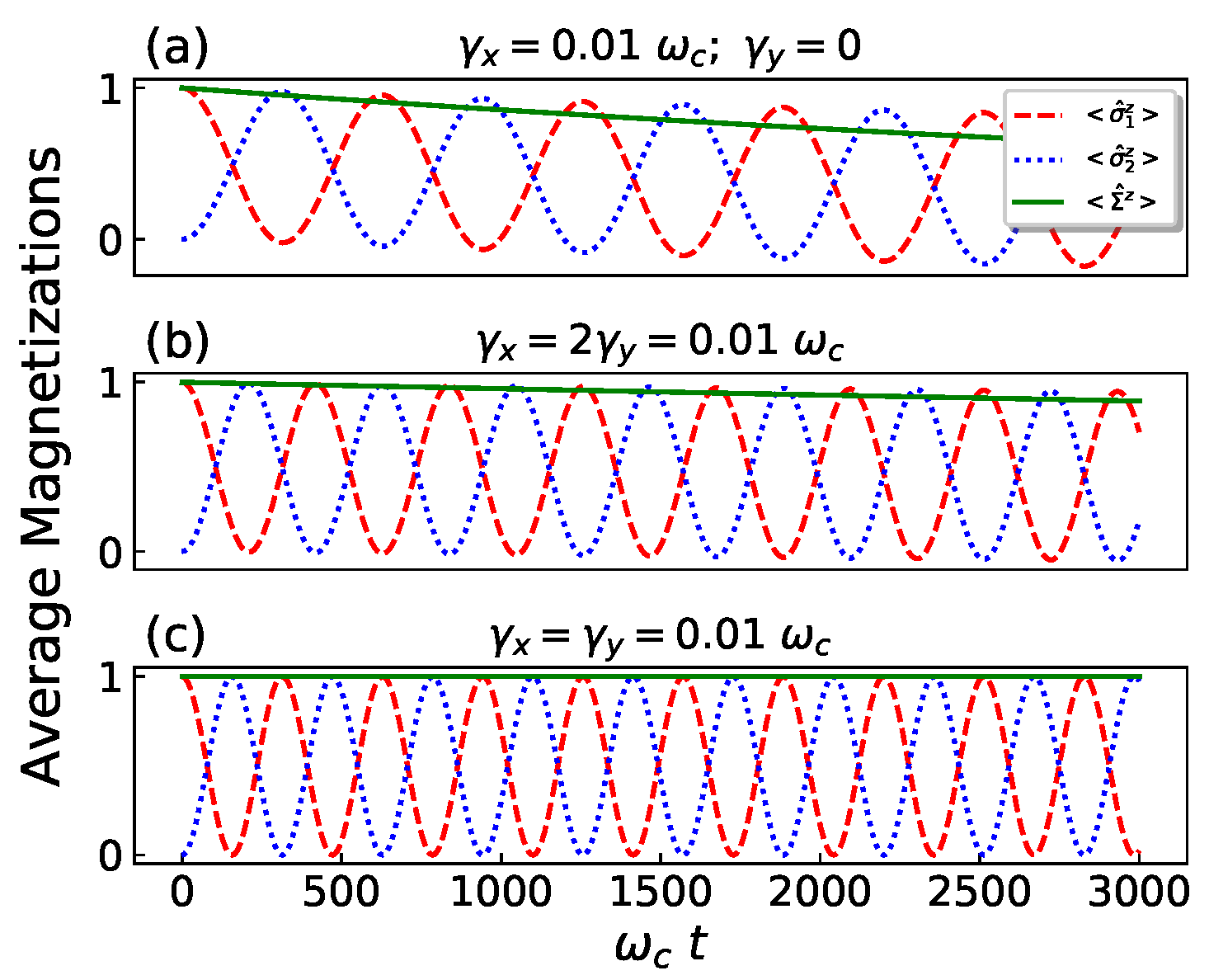
3.1. Conditions
 (
( ), , and .
), , and .3.2. Decoherence-Free Subspace
3.3. Ohmic Regime
Mixing Subspaces
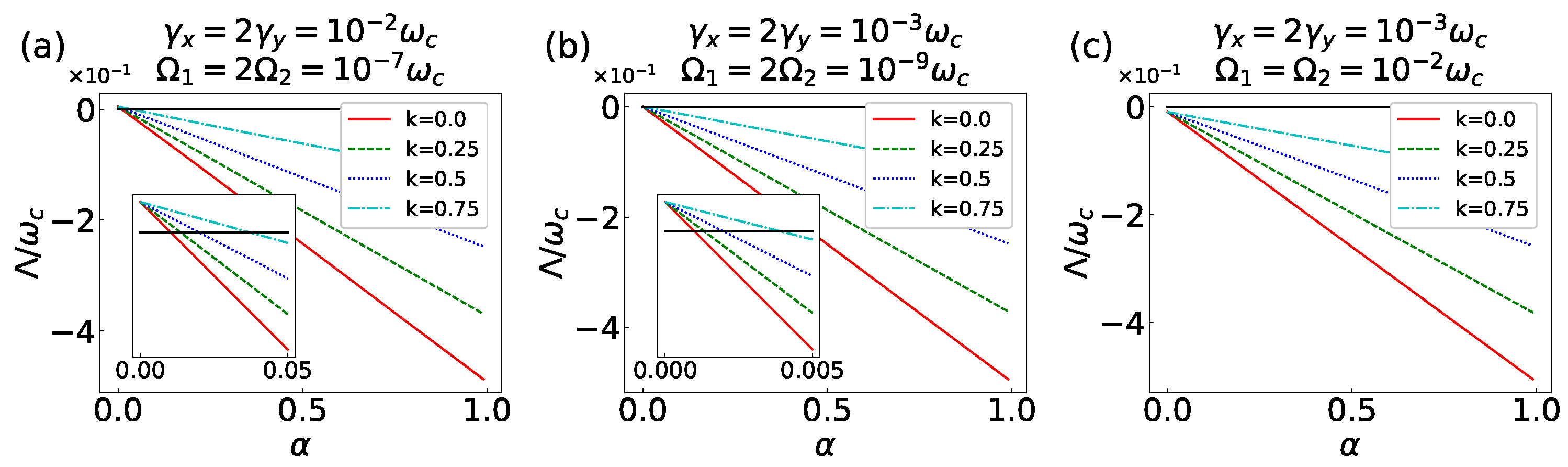
4. Quantum Phase Transitions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. The Model and Its Symmetries
Appendix B. Observables’ Mapping
Appendix C. Ground State of the Single-Impurity Spin–Boson Model
References
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press on Demand: Oxford, UK, 2002. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1–85. [Google Scholar] [CrossRef]
- Le Hur, K.; Doucet-Beaupré, P.; Hofstetter, W. Entanglement and Criticality in Quantum Impurity Systems. Phys. Rev. Lett. 2007, 99, 126801. [Google Scholar] [CrossRef] [PubMed]
- Vojta, M.; Tong, N.H.; Bulla, R. Quantum Phase Transitions in the Sub-Ohmic Spin-Boson Model: Failure of the Quantum-Classical Mapping. Phys. Rev. Lett. 2005, 94, 070604. [Google Scholar] [CrossRef] [PubMed]
- Bulla, R.; Tong, N.H.; Vojta, M. Numerical Renormalization Group for Bosonic Systems and Application to the Sub-Ohmic Spin-Boson Model. Phys. Rev. Lett. 2003, 91, 170601. [Google Scholar] [CrossRef] [PubMed]
- Hur, K.L. Entanglement entropy, decoherence, and quantum phase transitions of a dissipative two-level system. Ann. Phys. 2008, 323, 2208–2240. [Google Scholar] [CrossRef]
- Nazir, A.; McCutcheon, D.P.S.; Chin, A.W. Ground state and dynamics of the biased dissipative two-state system: Beyond variational polaron theory. Phys. Rev. B 2012, 85, 224301. [Google Scholar] [CrossRef]
- Winter, A.; Rieger, H.; Vojta, M.; Bulla, R. Quantum Phase Transition in the Sub-Ohmic Spin-Boson Model: Quantum Monte Carlo Study with a Continuous Imaginary Time Cluster Algorithm. Phys. Rev. Lett. 2009, 102, 030601. [Google Scholar] [CrossRef] [PubMed]
- Deng, T.; Yan, Y.; Chen, L.; Zhao, Y. Dynamics of the two-spin spin-boson model with a common bath. J. Chem. Phys. 2016, 144, 144102. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Fujihashi, Y.; Chen, L.; Zhao, Y. Finite-temperature time-dependent variation with multiple Davydov states. J. Chem. Phys. 2017, 146, 124127. [Google Scholar] [CrossRef] [PubMed]
- Vojta, M. Quantum phase transitions. Rep. Prog. Phys. 2003, 66, 2069–2110. [Google Scholar] [CrossRef]
- Rossini, D.; Vicari, E. Coherent and dissipative dynamics at quantum phase transitions. Phys. Rep. 2021, 936, 1–110. [Google Scholar] [CrossRef]
- Carollo, A.; Valenti, D.; Spagnolo, B. Geometry of quantum phase transitions. Phys. Rep. 2020, 838, 1–72. [Google Scholar] [CrossRef]
- Carollo, A.; Spagnolo, B.; Dubkov, A.A.; Valenti, D. On quantumness in multi-parameter quantum estimation. J. Stat. Mech. Theory Exp. 2019, 2019, 094010. [Google Scholar] [CrossRef]
- Kundu, S.; Makri, N. Time evolution of bath properties in spin-boson dynamics. J. Phys. Chem. B 2021, 125, 8137–8151. [Google Scholar] [CrossRef] [PubMed]
- Dunnett, A.J.; Chin, A.W. Matrix Product State Simulations of Non-Equilibrium Steady States and Transient Heat Flows in the Two-Bath Spin-Boson Model at Finite Temperatures. Entropy 2021, 23, 77. [Google Scholar] [CrossRef] [PubMed]
- Lemmer, A.; Cormick, C.; Tamascelli, D.; Schaetz, T.; Huelga, S.F.; Plenio, M.B. A trapped-ion simulator for spin-boson models with structured environments. New J. Phys. 2018, 20, 073002. [Google Scholar] [CrossRef]
- Lerma-Hernández, S.; Villaseñor, D.; Bastarrachea-Magnani, M.A.; Torres-Herrera, E.J.; Santos, L.F.; Hirsch, J.G. Dynamical signatures of quantum chaos and relaxation time scales in a spin-boson system. Phys. Rev. E 2019, 100, 012218. [Google Scholar] [CrossRef] [PubMed]
- Leppäkangas, J.; Braumüller, J.; Hauck, M.; Reiner, J.M.; Schwenk, I.; Zanker, S.; Fritz, L.; Ustinov, A.V.; Weides, M.; Marthaler, M. Quantum simulation of the spin-boson model with a microwave circuit. Phys. Rev. A 2018, 97, 052321. [Google Scholar] [CrossRef]
- Puebla, R.; Casanova, J.; Houhou, O.; Solano, E.; Paternostro, M. Quantum simulation of multiphoton and nonlinear dissipative spin-boson models. Phys. Rev. A 2019, 99, 032303. [Google Scholar] [CrossRef]
- Wenderoth, S.; Breuer, H.P.; Thoss, M. Non-Markovian effects in the spin-boson model at zero temperature. Phys. Rev. A 2021, 104, 012213. [Google Scholar] [CrossRef]
- Magazzù, L.; Denisov, S.; Hänggi, P. Asymptotic Floquet states of a periodically driven spin-boson system in the nonperturbative coupling regime. Phys. Rev. E 2018, 98, 022111. [Google Scholar] [CrossRef] [PubMed]
- De Filippis, G.; de Candia, A.; Cangemi, L.M.; Sassetti, M.; Fazio, R.; Cataudella, V. Quantum phase transitions in the spin-boson model: Monte Carlo method versus variational approach à la Feynman. Phys. Rev. B 2020, 101, 180408. [Google Scholar] [CrossRef]
- Wang, Y.Z.; He, S.; Duan, L.; Chen, Q.H. Quantum phase transitions in the spin-boson model without the counterrotating terms. Phys. Rev. B 2019, 100, 115106. [Google Scholar] [CrossRef]
- Wang, Y.Z.; He, S.; Duan, L.; Chen, Q.H. Rich phase diagram of quantum phases in the anisotropic subohmic spin-boson model. Phys. Rev. B 2020, 101, 155147. [Google Scholar] [CrossRef]
- Shen, L.T.; Yang, J.W.; Zhong, Z.R.; Yang, Z.B.; Zheng, S.B. Quantum phase transition and quench dynamics in the two-mode Rabi model. Phys. Rev. A 2021, 104, 063703. [Google Scholar] [CrossRef]
- Aurell, E.; Donvil, B.; Mallick, K. Large deviations and fluctuation theorem for the quantum heat current in the spin-boson model. Phys. Rev. E 2020, 101, 052116. [Google Scholar] [CrossRef]
- Miessen, A.; Ollitrault, P.J.; Tavernelli, I. Quantum algorithms for quantum dynamics: A performance study on the spin-boson model. Phys. Rev. Res. 2021, 3, 043212. [Google Scholar] [CrossRef]
- Villaseñor, D.; Pilatowsky-Cameo, S.; Bastarrachea-Magnani, M.A.; Lerma-Hernández, S.; Santos, L.F.; Hirsch, J.G. Quantum vs classical dynamics in a spin-boson system: Manifestations of spectral correlations and scarring. New J. Phys. 2020, 22, 063036. [Google Scholar] [CrossRef]
- Pino, M.; García-Ripoll, J.J. Quantum annealing in spin-boson model: From a perturbative to an ultrastrong mediated coupling. New J. Phys. 2018, 20, 113027. [Google Scholar] [CrossRef]
- Magazzù, L.; Forn-Díaz, P.; Belyansky, R.; Orgiazzi, J.L.; Yurtalan, M.; Otto, M.R.; Lupascu, A.; Wilson, C.; Grifoni, M. Probing the strongly driven spin-boson model in a superconducting quantum circuit. Nat. Commun. 2018, 9, 1403. [Google Scholar] [CrossRef]
- Lambert, N.; Ahmed, S.; Cirio, M.; Nori, F. Modelling the ultra-strongly coupled spin-boson model with unphysical modes. Nat. Commun. 2019, 10, 3721. [Google Scholar] [CrossRef]
- Casanova, J.; Puebla, R.; Moya-Cessa, H.; Plenio, M.B. Connecting n th order generalised quantum Rabi models: Emergence of nonlinear spin-boson coupling via spin rotations. npj Quantum Inf. 2018, 4, 47. [Google Scholar] [CrossRef]
- Zhou, N.; Chen, L.; Zhao, Y.; Mozyrsky, D.; Chernyak, V.; Zhao, Y. Ground-state properties of sub-Ohmic spin-boson model with simultaneous diagonal and off-diagonal coupling. Phys. Rev. B 2014, 90, 155135. [Google Scholar] [CrossRef]
- Bera, S.; Florens, S.; Baranger, H.U.; Roch, N.; Nazir, A.; Chin, A.W. Stabilizing spin coherence through environmental entanglement in strongly dissipative quantum systems. Phys. Rev. B 2014, 89, 121108. [Google Scholar] [CrossRef]
- Dolgitzer, D.; Zeng, D.; Chen, Y. Dynamical quantum phase transitions in the spin-boson model. Opt. Express 2021, 29, 23988–23996. [Google Scholar] [CrossRef]
- Wang, Y.Z.; He, S.; Duan, L.; Chen, Q.H. Quantum tricritical point emerging in the spin-boson model with two dissipative spins in staggered biases. Phys. Rev. B 2021, 103, 205106. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, Y.; Lü, Z.; Zhao, Y. Variational Study of the Two-Impurity Spin–Boson Model with a Common Ohmic Bath: Ground-State Phase Transitions. Ann. Der Phys. 2018, 530, 1800120. [Google Scholar] [CrossRef]
- Nägele, P.; Weiss, U. Dynamics of coupled spins in the white- and quantum-noise regime. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 622–628. [Google Scholar] [CrossRef]
- Storcz, M.J.; Hellmann, F.; Hrelescu, C.; Wilhelm, F.K. Decoherence of a two-qubit system away from perfect symmetry. Phys. Rev. A 2005, 72, 052314. [Google Scholar] [CrossRef]
- Garst, M.; Kehrein, S.; Pruschke, T.; Rosch, A.; Vojta, M. Quantum phase transition of Ising-coupled Kondo impurities. Phys. Rev. B 2004, 69, 214413. [Google Scholar] [CrossRef]
- McCutcheon, D.P.S.; Nazir, A.; Bose, S.; Fisher, A.J. Separation-dependent localization in a two-impurity spin-boson model. Phys. Rev. B 2010, 81, 235321. [Google Scholar] [CrossRef]
- Bonart, J. Dissipative phase transition in a pair of coupled noisy two-level systems. Phys. Rev. B 2013, 88, 125139. [Google Scholar] [CrossRef]
- Orth, P.P.; Roosen, D.; Hofstetter, W.; Le Hur, K. Dynamics, synchronization, and quantum phase transitions of two dissipative spins. Phys. Rev. B 2010, 82, 144423. [Google Scholar] [CrossRef]
- Zheng, H.; Lü, Z.; Zhao, Y. Ansatz for the quantum phase transition in a dissipative two-qubit system. Phys. Rev. E 2015, 91, 062115. [Google Scholar] [CrossRef] [PubMed]
- Winter, A.; Rieger, H. Quantum phase transition and correlations in the multi-spin-boson model. Phys. Rev. B 2014, 90, 224401. [Google Scholar] [CrossRef]
- Nägele, P.; Campagnano, G.; Weiss, U. Dynamics of dissipative coupled spins: Decoherence, relaxation and effects of a spin-boson bath. New J. Phys. 2008, 10, 115010. [Google Scholar] [CrossRef]
- Thorwart, M.; Hänggi, P. Decoherence and dissipation during a quantum XOR gate operation. Phys. Rev. A 2001, 65, 012309. [Google Scholar] [CrossRef]
- Storcz, M.J.; Wilhelm, F.K. Decoherence and gate performance of coupled solid-state qubits. Phys. Rev. A 2003, 67, 042319. [Google Scholar] [CrossRef]
- Grimaudo, R.; de Castro, A.S.M.a.; Messina, A.; Solano, E.; Valenti, D. Quantum Phase Transitions for an Integrable Quantum Rabi-like Model with Two Interacting Qubits. Phys. Rev. Lett. 2023, 130, 043602. [Google Scholar] [CrossRef]
- Grimaudo, R.; Valenti, D.; Sergi, A.; Messina, A. Superradiant Quantum Phase Transition for an Exactly Solvable Two-Qubit Spin-Boson Model. Entropy 2023, 25, 187. [Google Scholar] [CrossRef]
- Calvo, R.; Abud, J.E.; Sartoris, R.P.; Santana, R.C. Collapse of the EPR fine structure of a one-dimensional array of weakly interacting binuclear units: A dimensional quantum phase transition. Phys. Rev. B 2011, 84, 104433. [Google Scholar] [CrossRef]
- Napolitano, L.M.B.; Nascimento, O.R.; Cabaleiro, S.; Castro, J.; Calvo, R. Isotropic and anisotropic spin-spin interactions and a quantum phase transition in a dinuclear Cu(II) compound. Phys. Rev. B 2008, 77, 214423. [Google Scholar] [CrossRef]
- Kang, Y.H.; Chen, Y.H.; Wu, Q.C.; Huang, B.H.; Song, J.; Xia, Y. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. Sci. Rep. 2016, 6, 36737. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Xia, Y.; Song, J.; An, N.B. Generation of N-atom W-class states in spatially separated cavities. J. Opt. Soc. Am. B 2013, 30, 2142–2147. [Google Scholar] [CrossRef]
- Li, J.; Paraoanu, G.S. Generation and propagation of entanglement in driven coupled-qubit systems. New J. Phys. 2009, 11, 113020. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef] [PubMed]
- Hua, M.; Tao, M.J.; Deng, F.G. Universal quantum gates on microwave photons assisted by circuit quantum electrodynamics. Phys. Rev. A 2014, 90, 012328. [Google Scholar] [CrossRef]
- Romero, G.; Ballester, D.; Wang, Y.M.; Scarani, V.; Solano, E. Ultrafast Quantum Gates in Circuit QED. Phys. Rev. Lett. 2012, 108, 120501. [Google Scholar] [CrossRef]
- Barends, R.; Quintana, C.M.; Chen, Y.; Kafri, D.; Collins, R.; Naaman, O.; Boixo, S.; Arute, F.; Atya, K.; Buell, D.; et al. Diabatic Gates Frequency-Tunable Supercond Qubits. Phys. Rev. Lett. 2019, 123, 210501. [Google Scholar] [CrossRef] [PubMed]
- Nataf, P.; Ciuti, C. Protected Quantum Computation with Multiple Resonators in Ultrastrong Coupling Circuit QED. Phys. Rev. Lett. 2011, 107, 190402. [Google Scholar] [CrossRef]
- Lizuain, I.; Casanova, J.; García-Ripoll, J.J.; Muga, J.G.; Solano, E. Zeno physics in ultrastrong-coupling circuit QED. Phys. Rev. A 2010, 81, 062131. [Google Scholar] [CrossRef]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299–366. [Google Scholar] [CrossRef]
- Anappara, A.A.; De Liberato, S.; Tredicucci, A.; Ciuti, C.; Biasiol, G.; Sorba, L.; Beltram, F. Signatures of the ultrastrong light-matter coupling regime. Phys. Rev. B 2009, 79, 201303. [Google Scholar] [CrossRef]
- Todorov, Y.; Andrews, A.M.; Colombelli, R.; De Liberato, S.; Ciuti, C.; Klang, P.; Strasser, G.; Sirtori, C. Ultrastrong Light-Matter Coupling Regime with Polariton Dots. Phys. Rev. Lett. 2010, 105, 196402. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G. Maintaining coherence in quantum computers. Phys. Rev. A 1995, 51, 992–997. [Google Scholar] [CrossRef] [PubMed]
- Palma, G.M.; Suominen, K.A.; Ekert, A. Quantum computers and dissipation. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1996, 452, 567–584. [Google Scholar]
- Morozov, V.G.; Roepke, G. Two-time correlation functions in an exactly solvable spin-boson model. Theor. Math. Phys. 2011, 168, 1271–1277. [Google Scholar] [CrossRef]
- Nesterov, A.I.; Rodríguez Fernández, M.A.; Berman, G.P.; Wang, X. Decoherence as a detector of the Unruh effect. Phys. Rev. Res. 2020, 2, 043230. [Google Scholar] [CrossRef]
- Grimaudo, R.; Nakazato, H.; Messina, A.; Vitanov, N.V. Dzyaloshinskii-Moriya and dipole-dipole interactions affect coupling-based Landau-Majorana-Stückelberg-Zener transitions. Phys. Rev. Res. 2020, 2, 033092. [Google Scholar] [CrossRef]
- Yoshinaga, A.; Tatsuta, M.; Matsuzaki, Y. Entanglement-enhanced sensing using a chain of qubits with always-on nearest-neighbor interactions. Phys. Rev. A 2021, 103, 062602. [Google Scholar] [CrossRef]
- Hatomura, T.; Yoshinaga, A.; Matsuzaki, Y.; Tatsuta, M. Quantum metrology based on symmetry-protected adiabatic transformation: Imperfection, finite time duration, and dephasing. New J. Phys. 2022, 24, 033005. [Google Scholar] [CrossRef]
- Ghiu, I.; Grimaudo, R.; Mihaescu, T.; Isar, A.; Messina, A. Quantum Correlation Dynamics in Controlled Two-Coupled-Qubit Systems. Entropy 2020, 22, 785. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Chuang, I.L. NMR techniques for quantum control and computation. Rev. Mod. Phys. 2005, 76, 1037–1069. [Google Scholar] [CrossRef]
- Weidt, S.; Randall, J.; Webster, S.C.; Lake, K.; Webb, A.E.; Cohen, I.; Navickas, T.; Lekitsch, B.; Retzker, A.; Hensinger, W.K. Trapped-Ion Quantum Logic with Global Radiation Fields. Phys. Rev. Lett. 2016, 117, 220501. [Google Scholar] [CrossRef] [PubMed]
- Gaetan, A.; Miroshnychenko, Y.; Wilk, T.; Chotia, A.; Viteau, M.; Comparat, D.; Pillet, P.; Browaeys, A.; Grangier, P. Observation of collective excitation of two individual atoms in the Rydberg blockade regime. Nat. Phys. 2009, 5, 115–118. [Google Scholar] [CrossRef]
- Urban, E.; Johnson, T.A.; Henage, T.; Isenhower, L.; Yavuz, D.; Walker, T.; Saffman, M. Observation of Rydberg blockade between two atoms. Nat. Phys. 2009, 5, 110–114. [Google Scholar] [CrossRef]
- Ying, Z.J.; Cong, L.; Sun, X.M. Quantum phase transition and spontaneous symmetry breaking in a nonlinear quantum Rabi model. J. Phys. A Math. Theor. 2020, 53, 345301. [Google Scholar] [CrossRef]
- Ying, Z.J. Symmetry-breaking patterns, tricriticalities, and quadruple points in the quantum Rabi model with bias and nonlinear interaction. Phys. Rev. A 2021, 103, 063701. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Ying, Z.J.; Luo, H.G. Fundamental Models in the Light–Matter Interaction: Quantum Phase Transitions and the Polaron Picture. Adv. Quantum Technol. 2021, 4, 2000139. [Google Scholar] [CrossRef]
- Ying, Z.J. From Quantum Rabi Model To Jaynes–Cummings Model: Symmetry-Breaking Quantum Phase Transitions, Symmetry-Protected Topological Transitions and Multicriticality. Adv. Quantum Technol. 2022, 5, 2100088. [Google Scholar] [CrossRef]
- Ying, Z.J. Hidden Single-Qubit Topological Phase Transition without Gap Closing in Anisotropic Light-Matter Interactions. Adv. Quantum Technol. 2022, 5, 2100165. [Google Scholar] [CrossRef]
- Grimaudo, R.; Man’ko, V.I.; Man’ko, M.A.; Messina, A. Dynamics of a harmonic oscillator coupled with a Glauber amplifier. Phys. Scr. 2019, 95, 024004. [Google Scholar] [CrossRef]
- Grimaudo, R.; Vitanov, N.V.; Magalhães de Castro, A.S.; Valenti, D.; Messina, A. Greenberger-Horne-Zeilinger-state Generation in Qubit-Chains via a Single Landau-Majorana-Stückelberg-Zener π/2-pulse. Fortschritte Phys. 2022, 70, 2200010. [Google Scholar] [CrossRef]
- Grimaudo, R.; Magalhães de Castro, A.S.; Messina, A.; Valenti, D. Spin-Chain-Star Systems: Entangling Multiple Chains of Spin Qubits. Fortschritte Phys. 2022, 70, 2200042. [Google Scholar] [CrossRef]
- Qian, X.; Zeng, C.; Zhou, N. Quantum criticality of the Ohmic spin-boson model in a high dense spectrum: Symmetries, quantum fluctuations and correlations. Phys. A Stat. Mech. Its Appl. 2021, 580, 126157. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 1976, 9, 1387. [Google Scholar] [CrossRef]
- Zurek, W.H. Cosmological experiments in superfluid helium? Nature 1985, 317, 505–508. [Google Scholar] [CrossRef]
- Feshbach, H. Unified theory of nuclear reactions. Ann. Phys. 1958, 5, 357–390. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Conceptual aspects of -symmetry and pseudo-Hermiticity: A status report. Phys. Scr. 2010, 82, 038110. [Google Scholar] [CrossRef]
- Rotter, I.; Bird, J.P. A review of progress in the physics of open quantum systems: Theory and experiment. Rep. Prog. Phys. 2015, 78, 114001. [Google Scholar] [CrossRef] [PubMed]
- Sergi, A.; Zloshchastiev, K.G. Non-Hermitian quantum dynamics of a two-level system and model of dissipative environment. Int. J. Mod. Phys. B 2013, 27, 1350163. [Google Scholar] [CrossRef]
- Sergi, A.; Zloshchastiev, K.G. Time correlation functions for non-Hermitian quantum systems. Phys. Rev. A 2015, 91, 062108. [Google Scholar] [CrossRef]
- Brody, D.C.; Graefe, E.M. Mixed-State Evolution in the Presence of Gain and Loss. Phys. Rev. Lett. 2012, 109, 230405. [Google Scholar] [CrossRef] [PubMed]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Kapral, R.; Ciccotti, G. Mixed quantum-classical dynamics. J. Chem. Phys. 1999, 110, 8919–8929. [Google Scholar] [CrossRef]
- Kapral, R. Quantum-classical dynamics in a classical bath. J. Phys. Chem. A 2001, 105, 2885–2889. [Google Scholar] [CrossRef]
- Sergi, A. Deterministic constant-temperature dynamics for dissipative quantum systems. J. Phys. A Math. Theor. 2007, 40, F347. [Google Scholar] [CrossRef]
- Sergi, A.; Grimaudo, R.; Hanna, G.; Messina, A. Proposal of a Computational Approach for Simulating Thermal Bosonic Fields in Phase Space. Physics 2019, 1, 402–411. [Google Scholar] [CrossRef]
- Longhi, S. Quantum-optical analogies using photonic structures. Laser Photonics Rev. 2009, 3, 243–261. [Google Scholar] [CrossRef]
- Grimaudo, R.; de Castro, A.S.M.; Kuś, M.; Messina, A. Exactly solvable time-dependent pseudo-Hermitian su(1,1) Hamiltonian models. Phys. Rev. A 2018, 98, 033835. [Google Scholar] [CrossRef]
- Grimaudo, R.; de Castro, A.S.M.; Nakazato, H.; Messina, A. Analytically solvable 2×2PT-symmetry dynamics from su(1,1)-symmetry problems. Phys. Rev. A 2019, 99, 052103. [Google Scholar] [CrossRef]
- Grimaudo, R.; Messina, A.; Sergi, A.; Vitanov, N.V.; Filippov, S.N. Two-Qubit Entanglement Generation through Non-Hermitian Hamiltonians Induced by Repeated Measurements on an Ancilla. Entropy 2020, 22, 1184. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grimaudo, R.; Messina, A.; Nakazato, H.; Sergi, A.; Valenti, D. Characterization of Quantum and Classical Critical Points for an Integrable Two-Qubit Spin–Boson Model. Symmetry 2023, 15, 2174. https://doi.org/10.3390/sym15122174
Grimaudo R, Messina A, Nakazato H, Sergi A, Valenti D. Characterization of Quantum and Classical Critical Points for an Integrable Two-Qubit Spin–Boson Model. Symmetry. 2023; 15(12):2174. https://doi.org/10.3390/sym15122174
Chicago/Turabian StyleGrimaudo, Roberto, Antonino Messina, Hiromichi Nakazato, Alessandro Sergi, and Davide Valenti. 2023. "Characterization of Quantum and Classical Critical Points for an Integrable Two-Qubit Spin–Boson Model" Symmetry 15, no. 12: 2174. https://doi.org/10.3390/sym15122174







