Nonlinear Dynamics of a Piecewise Modified ABC Fractional-Order Leukemia Model with Symmetric Numerical Simulations
Abstract
1. Introduction
2. Preliminaries
3. Qualitative Analysis
- (C1) ∃; ∀, we arrive at:
- (C2) ∃ & ;
4. Stability Analysis
- Case 1: for , we haveOn further simplification:
- Case 2: for , we havefor . Since, we have assume solutions of the piecewise TB model (1), this implies, these are the fixed points of the operator , or mathematically, , and . Thus, from (23), we proceed to the following relationAlso, we haveBy the help of (23), (24), and (25), we haveFor . Thus, the presumed model is Hyers–Ulam stable. Furthermore, replacing α by the system (20) impliesNow , this implies the solution of the piecewise TB model (1) is generalized HU stable. □
5. Numerical Scheme
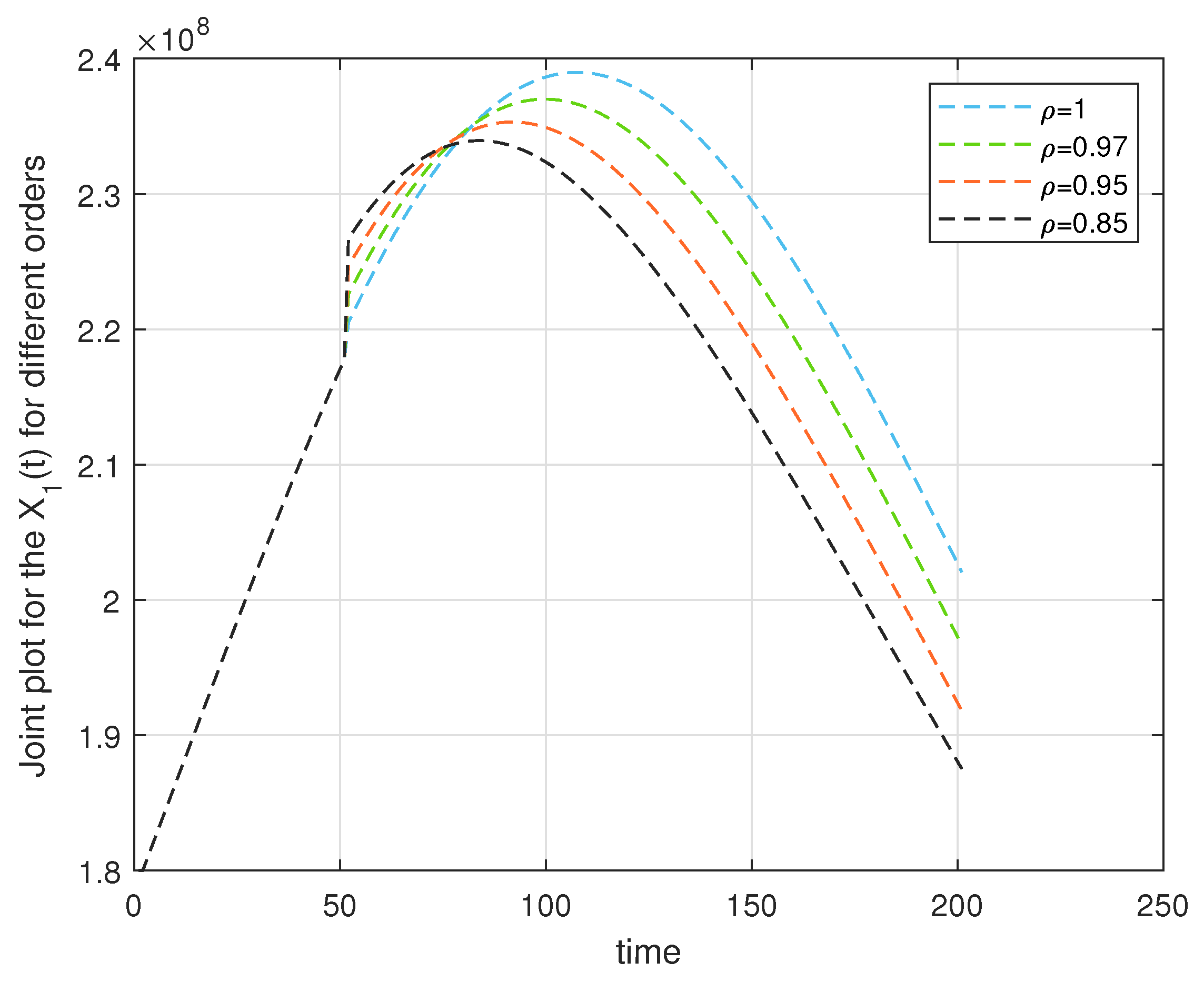
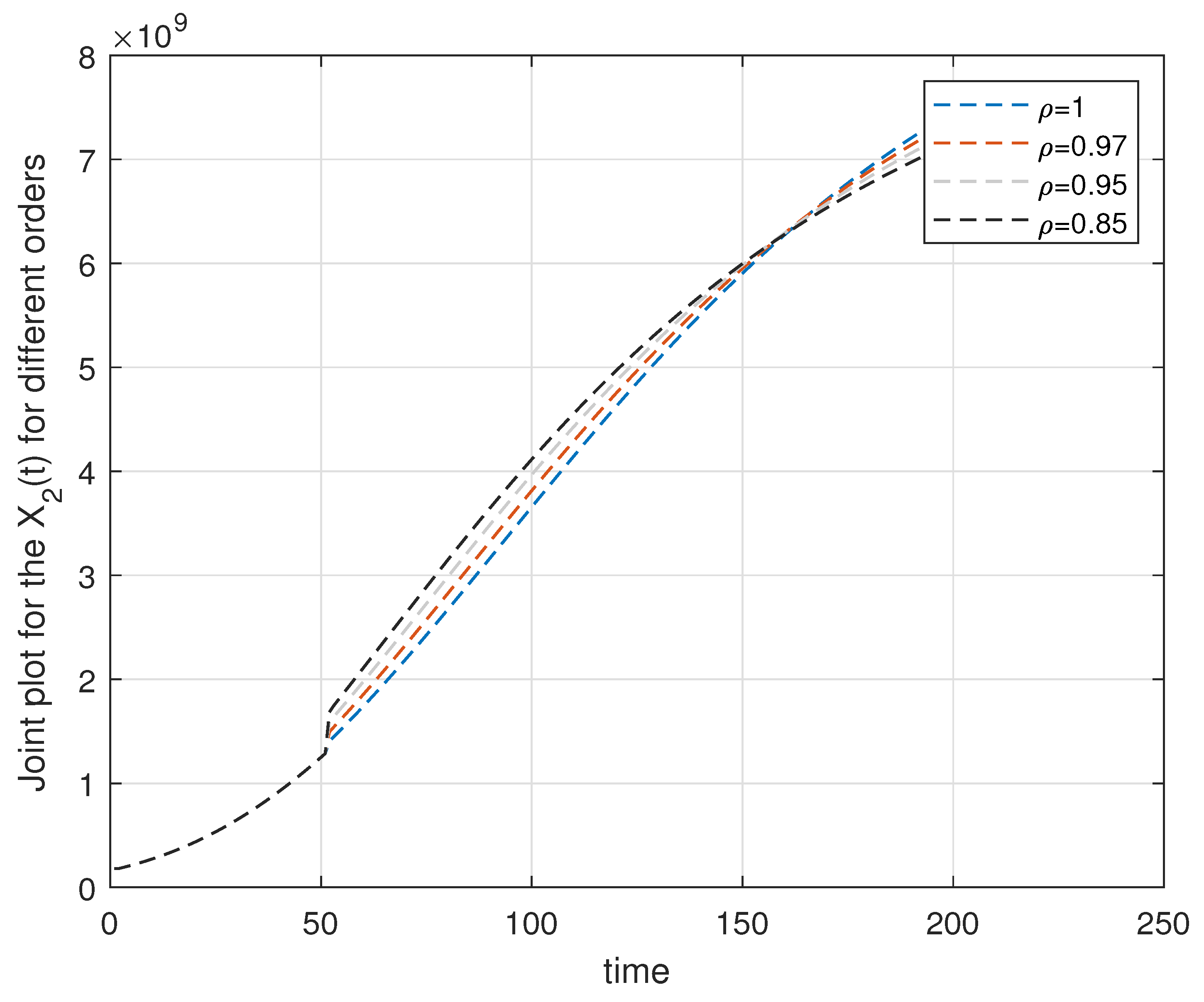
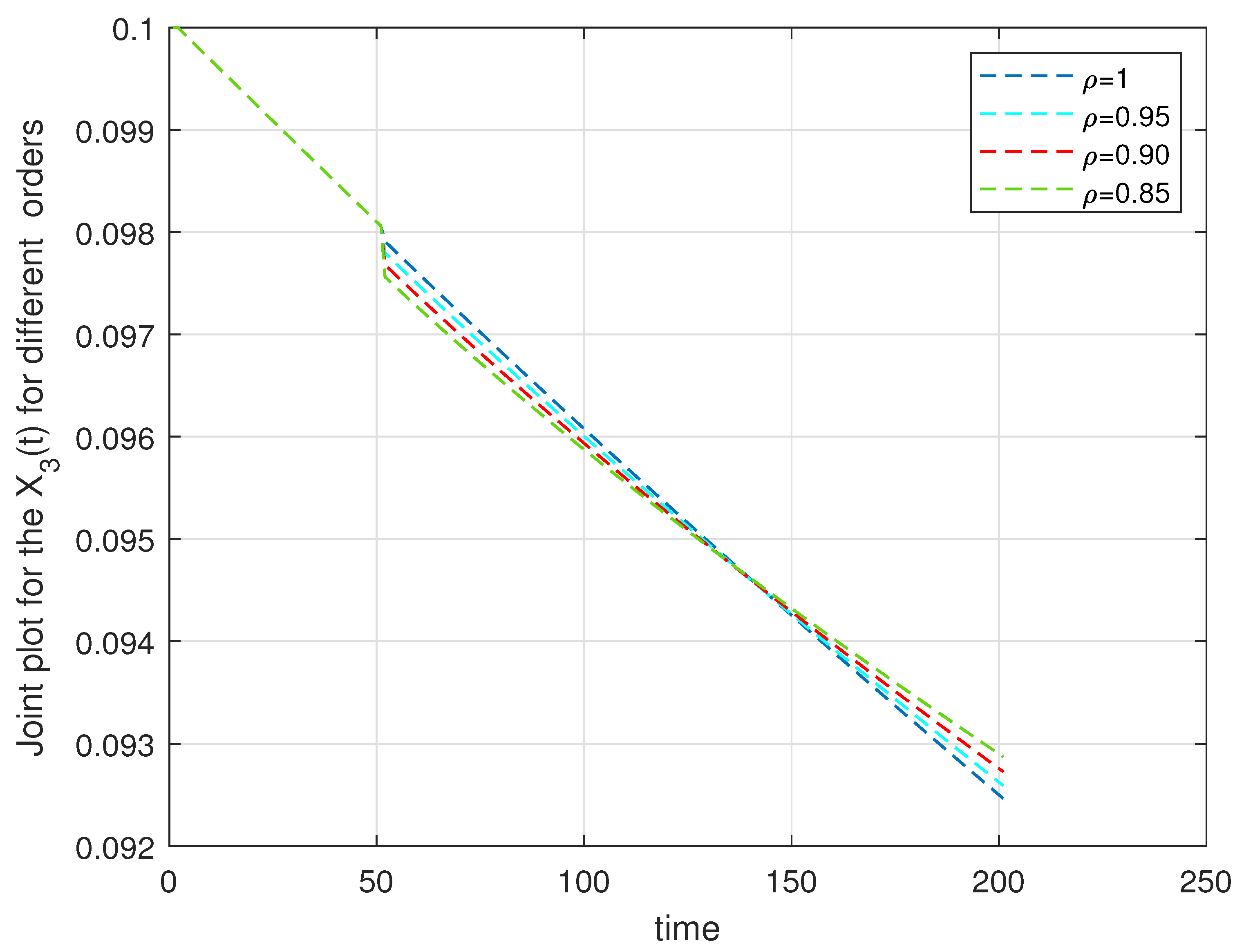
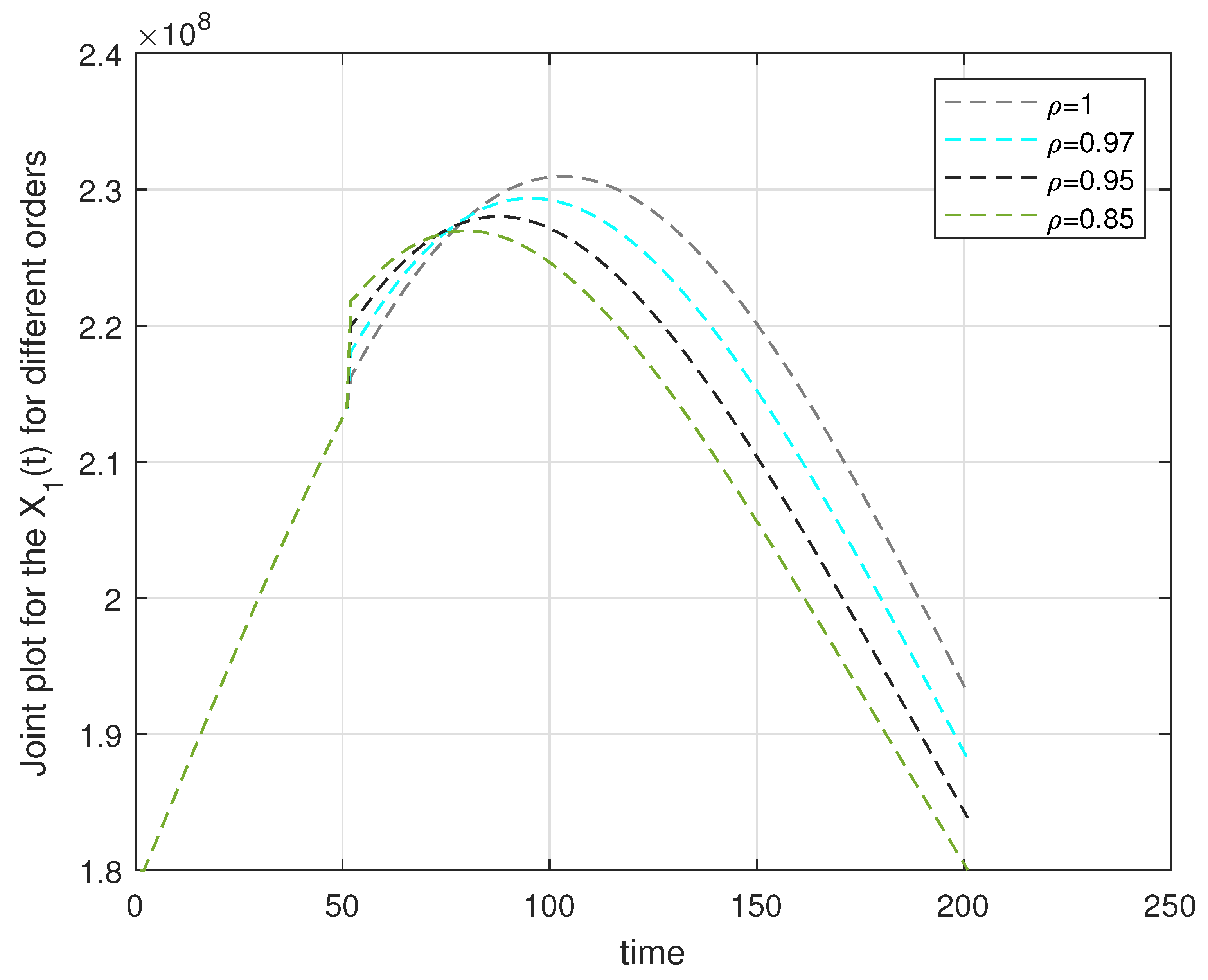
6. Computational Discussion for the Leukemia Model
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Atangana–Baleanu in Caputo’s sense |
| FDEs | fractional differential equations |
| FPT | fixed-point theorems |
References
- Doebelin, E. System Dynamics: Modeling, Analysis, Simulation, Design; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef]
- Velten, K. Mathematical Modeling and Simulation: Introduction for Scientists and Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Formaggia, L.; Quarteroni, A.; Veneziani, A. Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bunimovich-Mendrazitsky, S.; Kronik, N.; Vainstein, V. Optimization of Interferon–Alpha and Imatinib Combination Therapy for Chronic Myeloid Leukemia: A Modeling Approach. Adv. Theory Simul. 2019, 2, 1800081. [Google Scholar] [CrossRef]
- Khatun, M.S.; Biswas, M.H. Modeling the effect of adoptive T cell therapy for the treatment of leukemia. Comput. Math. Methods 2020, 2, e1069. [Google Scholar] [CrossRef]
- Piller, G. The history of leukemia: A personal perspective. Blood Cells 1993, 19, 521–529. [Google Scholar] [PubMed]
- Drexler, H.G.; Minowada, J. History and classification of human leukemia-lymphoma cell lines. Leuk. Lymphoma 1998, 31, 305–316. [Google Scholar] [CrossRef] [PubMed]
- Thomas, X. First contributors in the history of leukemia. World J. Hematol. 2013, 2, 62–70. [Google Scholar] [CrossRef]
- Mehranfar, S.; Zeinali, S.; Hosseini, R.; Mohammadian, M.; Akbarzadeh, A.; Feizi, A.H. History of leukemia: Diagnosis and treatment from beginning to now. Galen Med. J. 2017, 6, 12–22. [Google Scholar] [CrossRef]
- Afenya, E. Acute leukemia and chemotherapy: A modeling viewpoint. Math. Biosci. 1996, 138, 79–100. [Google Scholar] [CrossRef] [PubMed]
- Khatun, M.S.; Biswas, M.H. Mathematical analysis and optimal control applied to the treatment of leukemia. J. Appl. Math. Comput. 2020, 64, 331–353. [Google Scholar] [CrossRef]
- Nobile, M.S.; Vlachou, T.; Spolaor, S.; Bossi, D.; Cazzaniga, P.; Lanfrancone, L.; Mauri, G.; Pelicci, P.G.; Besozzi, D. Modeling cell proliferation in human acute myeloid leukemia xenografts. Bioinformatics 2019, 35, 3378–3386. [Google Scholar] [CrossRef]
- Li, Y.F.; Combes, F.P.; Hoch, M.; Lorenzo, S.; Sy, S.K.; Ho, Y.Y. Population pharmacokinetics of asciminib in tyrosine kinase inhibitor-treated patients with Philadelphia chromosome-positive chronic myeloid leukemia in chronic and acute phases. Clin. Pharmacokinet. 2022, 61, 1393–1403. [Google Scholar] [CrossRef] [PubMed]
- Islam, Y.; Ahmad, I.; Zubair, M.; Shahzad, K. Double integral sliding mode control of leukemia therapy. Biomed. Signal Process. Control 2020, 61, 102046. [Google Scholar] [CrossRef]
- Islam, Y.; Ahmad, I.; Zubair, M.; Islam, A. Adaptive terminal and supertwisting sliding mode controllers for acute Leukemia therapy. Biomed. Signal Process. Control 2022, 71, 103121. [Google Scholar] [CrossRef]
- Awadalla, M.; Subramanian, M.; Abuasbeh, K. Existence and Ulam–Hyers Stability Results for a System of Coupled Generalized Liouville–Caputo Fractional Langevin Equations with Multipoint Boundary Conditions. Symmetry 2023, 15, 198. [Google Scholar] [CrossRef]
- Alesemi, M.; Shahrani, J.S.; Iqbal, N.; Shah, R.; Nonlaopon, K. Analysis and Numerical Simulation of System of Fractional Partial Differential Equations with Non-Singular Kernel Operators. Symmetry 2023, 15, 233. [Google Scholar] [CrossRef]
- Baitiche, Z.; Benchohra, C.D.C.M.; Zhou, Y. A New Class of Coupled Systems of Nonlinear Hyperbolic Partial Fractional Differential Equations in Generalized Banach Spaces Involving the ψ–Caputo Fractional Derivative. Symmetry 2021, 13, 2412. [Google Scholar] [CrossRef]
- Srinivasa, K.; Baskonus, H.M.; Sanchez, Y.G. Numerical solutions of the mathematical models on the digestive system and COVID-19 pandemic by hermite wavelet technique. Symmetry 2021, 13, 2428. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New concept in calculus:Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Ahmad, S.; Yassen, M.F.; Alam, M.M.; Alkhati, S.; Jarad, F.; Riaz, M.B. A numerical study of dengue internal transmission model with fractional piecewise derivative. Results Phys. 2022, 39, 105798. [Google Scholar] [CrossRef]
- Heydari, M.H.; Razzaghi, M.; Baleanu, D. A numerical method based on the piecewise Jacobi functions for distributed-order fractional Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106873. [Google Scholar] [CrossRef]
- Kafle, R.C.; Kim, D.Y.; Holt, M.M. Gender-specific trends in cigarette smoking and lung cancer incidence: A two-stage age-stratified Bayesian joinpoint model. Cancer Epidemiol. 2023, 84, 102364. [Google Scholar] [CrossRef]
- Abdelmohsen, S.A.M.; Yassen, M.F.; Ahmad, S.; Abdelbacki, A.M.M.; Khan, J. Theoretical and numerical study of the rumours spreading model in the framework of piecewise derivative. Eur. Phys. J. Plus 2022, 137, 738. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Z.; Pang, Y.; Akgul, A.; Baleanu, D. Dynamics of HIV-TB coinfection model using classical and Caputo piecewise operator: A dynamic approach with real data from South-East Asia, European and American regions. Chaos Solitons Fractals 2022, 165, 112879. [Google Scholar] [CrossRef]
- Hasan, A.; Akgul, A.; Farman, M.; Chaudhry, F.; Sultan, M.; De la Sen, M. Epidemiological Analysis of Symmetry in Transmission of the Ebola Virus with Power Law Kernel. Symmetry 2023, 15, 665. [Google Scholar] [CrossRef]
- Shah, A.; Khan, H.; De la Sen, M.; Alzabut, J.; Etemad, S.; Deressa, C.T.; Rezapour, S. On Non-Symmetric Fractal-Fractional Modeling for Ice Smoking: Mathematical Analysis of Solutions. Symmetry 2022, 15, 87. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, J. Lie symmetry analysis of fractional ordinary differential equation with neutral delay. AIMS Math. 2021, 6, 3592–3605. [Google Scholar] [CrossRef]
- Liu, Y. On piecewise continuous solutions of higher order impulsive fractional differential equations and applications. Appl. Math. Comput. 2016, 287, 38–49. [Google Scholar] [CrossRef]
- Ansari, K.J.; Asma; Ilyas, F.; Shah, K.; Khan, A.; Abdeljawad, T. On new updated concept for delay differential equations with piecewise Caputo fractional-order derivative. Waves Random Complex Media 2023, 1–20. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.I.; Jacobs, B.A.; McGann, A.V. Discretization of fractional differential equations by a piecewise constant approximation. Math. Model. Nat. Phenom. 2017, 12, 23–36. [Google Scholar] [CrossRef]
- Al-Refai, M.; Baleanu, D. On an Extension of the Operator with Mittag-Leffler Kernel. Fractals 2022, 30, 1–7. [Google Scholar] [CrossRef]
- Al-Refai, M. Proper inverse operators of fractional derivatives with nonsingular kernels. Rend. Del Circ. Mat. Palermo Ser. 2022, 71, 525–535. [Google Scholar] [CrossRef]
- Khan, A.; Abdeljawad, T.; Gomez-Aguilar, J.F.; Khan, H. Dynamical study of fractional order mutualism parasitism food web module. Chaos Solitons Fractals 2020, 134, 109685. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Gulzar, H. Existence of solutions for hybrid modified ABC-fractional differential equations with p-Laplacian operator and an application to a waterborne disease model. Alex. Eng. J. 2023, 70, 665–672. [Google Scholar] [CrossRef]
- Boutiara, A.; Matar, M.M.; Alzabut, J.; Samei, M.E.; Khan, H. On ABC coupled Langevin fractional differential equations constrained by Perov’s fixed point in generalized Banach spaces. AIMS Math. 2023, 8, 12109–12132. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Baleanu, D.; Alobaidi, G.; Rehman, M.U. Existence of solutions and a numerical scheme for a generalized hybrid class of n-coupled modified ABC-fractional differential equations with an application. AIMS Math. 2023, 8, 6609–6625. [Google Scholar] [CrossRef]
- Khan, A.; Ain, Q.T.; Abdeljawad, T.; Nisar, K.S. Exact Controllability of Hilfer Fractional Differential System with Non-instantaneous Impluleses and State Dependent Delay. Qual. Theory Dyn. Syst. 2023, 22, 62. [Google Scholar] [CrossRef]
- Djaout, A.; Benbachir, M.; Lakrib, M.; Matar, M.M.; Khan, A.; Abdeljawad, T. Solvability and stability analysis of a coupled system involving generalized fractional derivatives. AIMS Math. 2023, 8, 7817–7839. [Google Scholar] [CrossRef]
- Thirthar, A.A.; Abboubakar, H.; Khan, A.; Abdeljawad, T. Mathematical modeling of the COVID-19 epidemic with fear impact. AIMS Math. 2023, 8, 6447–6465. [Google Scholar] [CrossRef]
- Houas, M.; Kaushik, K.; Kumar, A.; Khan, A.; Abdeljawad, T. Existence and stability results of pantograph equation with three sequential fractional derivatives. AIMS Math. 2023, 8, 5216–5232. [Google Scholar] [CrossRef]
- Khan, A.; Shah, K.; Abdeljawad, T.; Alqudah, M.A. Existence of results and computational analysis of a fractional order two strain epidemic model. Results Phys. 2022, 39, 105649. [Google Scholar] [CrossRef]
- Scholtes, S. Introduction to Piecewise Differentiable Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Tanvi, A.; Aggarwal, R.; Raj, Y.A. A fractional order TB co-infection model in the presence of exogenous reinfection and recurrent TB. Nonlinear Dyn. 2021, 104, 4701–4725. [Google Scholar]
- Zeb, A.; Alzahrani, A. Non-standard finite difference scheme and analysis of smoking model with reversion class. Res. Phys. 2021, 21, 103785. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Gusu, D.M.; Mohammed, P.O.; Wedajo, G.; Nonlaopon, K.; Hamed, Y.S. Solutions of general fractional-order differential equations by using the spectral Tau method. Fractal Fract. 2022, 6, 7. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Abd-Elhameed, W.M.; Ahmed, H.M. New fractional derivative expression of the shifted third-kind Chebyshev polynomials: Application to a type of nonlinear fractional pantograph differential equations. J. Funct. Spaces 2022, 2022, 3966135. [Google Scholar] [CrossRef]
- Doha, E.; Abd-Elhameed, W.M.; Ahmed, H. The coefficients of differentiated expansions of double and triple Jacobi polynomials. Bull. Iran. Math. Soc. 2012, 38, 739–765. [Google Scholar]
- Ain, Q.T.; Nadeem, M.; Akgul, A.; De la Sen, M. Controllability of Impulsive Neutral Fractional Stochastic Systems. Symmetry 2022, 14, 2612. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Alzabut, J.; Alfwzan, W.F.; Gulzar, H. Nonlinear Dynamics of a Piecewise Modified ABC Fractional-Order Leukemia Model with Symmetric Numerical Simulations. Symmetry 2023, 15, 1338. https://doi.org/10.3390/sym15071338
Khan H, Alzabut J, Alfwzan WF, Gulzar H. Nonlinear Dynamics of a Piecewise Modified ABC Fractional-Order Leukemia Model with Symmetric Numerical Simulations. Symmetry. 2023; 15(7):1338. https://doi.org/10.3390/sym15071338
Chicago/Turabian StyleKhan, Hasib, Jehad Alzabut, Wafa F. Alfwzan, and Haseena Gulzar. 2023. "Nonlinear Dynamics of a Piecewise Modified ABC Fractional-Order Leukemia Model with Symmetric Numerical Simulations" Symmetry 15, no. 7: 1338. https://doi.org/10.3390/sym15071338
APA StyleKhan, H., Alzabut, J., Alfwzan, W. F., & Gulzar, H. (2023). Nonlinear Dynamics of a Piecewise Modified ABC Fractional-Order Leukemia Model with Symmetric Numerical Simulations. Symmetry, 15(7), 1338. https://doi.org/10.3390/sym15071338





