Construction of Ruled Surfaces from the W-Curves and Their Characterizations in ${\mathbb{E}}^3$

Abstract

Ruled surfaces are considered one of the significant aspects of differential geometry. These surfaces are formed by the motion of a straight line called a generator, and every curve that intersects all the generators is called a directrix. In the present research paper, we explore a family of ruled surfaces constructed from circular helices (W-curve) using the Frenet frame in the Euclidean space ${\mathbb{E}}^3$. We derive the explicit formulas for the second mean curvature and second Gaussian curvature. We present some ruled surfaces, and we describe their properties. In addition, we determine the sufficient conditions for these surfaces to be minimal, flat, II-minimal, and II-flat. Also, we obtain sufficient conditions for the base curve for these ruled surfaces to be a geodesic curve, an asymptotic line, and a principal line. Furthermore, we present an application for a ruled surface whose base curve is a circular helix, we compute some quantities for this surface such as the mean curvature and Gaussian curvatures and we plot the ruled surface with its base curve, and at symmetric points and along a symmetry axis.

1. Introduction

The primary objective of classical differential geometry is to comprehend the characteristics of specific types of surfaces in ${\mathbb{E}}^3$, including developable surfaces, ruled surfaces, minimal surfaces, and other related surfaces. Ruled surfaces (R-S) in Euclidean 3-space are geometric entities formed by straight lines, called rulings, that move through space while remaining tangent to a fixed line, known as the directrix. These surfaces have practical applications in fields such as architecture and computer graphics. Understanding their characteristics contributes to a deeper comprehension of geometry and its real-world implications.

Many researchers studied the (R-S) and their diverse characteristics. Gürsoy [1] analyzed the dual integral invariant of a closed ruled surface and presented some new results of the geometric interpretations for the real angle of pitch and the real pitch of a closed ruled surface. Köse [2] expressed the pitch and the angle of pitch of a closed ruled surface in terms of the integral invariants for the dual spherical closed curve that corresponds to the closed ruled surface. Turgut, et al. [3,4] investigated the properties of timelike (R-S) in Minkowski 3-space, along with the structure of developable timelike (R-S). The curve of striction, the central point, and the distribution parameter of these surfaces were also discussed. The angles between normal vectors at various sites on a ruling, the behavior of tangent planes along a ruling, and the unique value of the distribution parameter along a ruling were covered.

Ali et al. [5,6,7] investigated the mathematical description of helical structures in Euclidean 3-space, specifically, general helices and their position vectors concerning the Frenet frame for both general helices and slant helices. In addition, examples such as circular general helices, spherical general helices, Salkowski curves, and circular slant helices were presented.

Barros [8] proposed Lancret’s theorem for general helices in a three-dimensional real-space form. This theorem distinguishes the relationship between hyperbolic and spherical geometries, furthermore studying the problems related to general helices in the 3-sphere, including the closed curve problem and solving natural equations.

Ilarslan, et al. [9] focused on studying the position vectors of timelike and null helices in Minkowski space ${\mathbb{E}}^{3,1}$. These curves have constant curvatures, and their position vectors are utilized to characterize timelike and null helices with images on the Lorentzian sphere ${\mathbb{S}}_1^2$ or pseudo-hyperbolical space ${\mathbb{H}}_0^2$.

Monterde [10] described a family of curves with constant curvature and non-constant torsion. These curves are characterized as space curves, and their normal vectors form a constant angle with a fixed line. The relationship between these curves and rational curves using a double Pythagorean hodograph was explored. In addition, a method for constructing closed curves with constant curvature and continuous torsion using pieces of Salkowski curves was presented.

Classical differential geometry employs intrinsic equations to determine the position vectors of curves, such as $\kappa =\kappa \left(s\right)$ and $\tau =\tau \left(s\right)$, where $\kappa$ and $\tau$ represent the curvature and torsion of the curve, respectively. To understand the behavior of curves, a comprehensive examination of position vectors is necessary. Slant helices encompass various types of helices, including general helices, Salkowski, anti-Salkowski, and constant precession curves. A helix is a geometric curve characterized by constant non-zero curvature and torsion. The circular helix, also known as the W-curve, is a special type of general helix [11,12,13].

Recently, in [14], the (R-S) in a three-dimensional sphere with finite-type and pointwise 1-type spherical Gauss map were investigated. Some new characterizations of the Clifford torus and the great sphere of the 3-sphere were described. Some new applications of spherical (R-S) in a three-dimensional sphere were provided. In [15], the first-order infinitesimal bending of a curve in three-dimensional Euclidean space is considered to obtain an (R-S). The properties of this kind of (R-S) were described and the conditions for (R-S) by bending to be developable were obtained.

In [16], the dual expression of Valeontis’ concept for the parallel p-equidistant (R-S) in Euclidean space was investigated, utilizing the Study mapping. In addition, the dual part of the dual angle on the unit dual sphere corresponded to the p-distance and was defined by (R-S). Furthermore, the dual parallel equidistant (R-S) was obtained. In [17], the parallel q-equidistant (R-S) was defined such that the binormal vectors of two given differentiable curves are parallel along the striction curves of their corresponding binormal (R-S). In addition, the distance between the asymptotic planes is constant at certain points. Some properties were specified and plotted for these surfaces. In the case of closed surfaces, the integral invariants such as the pitch, the angle of the pitch, and the drall of them were given. It is known, see, e.g., [18], that surfaces of revolutions characterize inner conditions, i.e., there exists an equidistant vector field. For (R-S), the similar inner conditions do not exist. Therefore, it is relevant to examine the characteristics of (R-S) in our work.

In [19,20,21,22], the features and applications of generated surfaces across various mathematical fields have been specified. The investigation of equiform Bishop spherical image governed surfaces in Minkowski 3-space yields important minimality and developability requirements, with consequences for computer-aided geometric design and physics. Simultaneously, research on inextensible (R-S), which are especially important in computer vision and animation, provides insights into tangential, normal, and binormal (R-S). These surfaces are formed by a curve with constant torsion. Furthermore, the study of circular surfaces in the Euclidean 3-space provides geometric analysis, minimality criteria, and systematic parametrization, all of which are valuable applications in computer-aided design and architecture.

Our study focuses on (R-S) constructed from the W-curve in ${\mathbb{E}}^3$. We determine some quantities of the constructed (R-S) such as mean, Gaussian, second mean, and second Gaussian curvatures. We provide some special (R-S) with their properties. Also, the sufficient conditions for the constructed (R-S) to be minimal, flat, II-minimal, and II-flat surfaces are determined. In addition, the sufficient conditions for the base curve for constructed (R-S) to be a geodesic, an asymptotic line, and a principal line are determined.

The outline of the present research is organized as follows: In Section 2, we present some geometric concepts about (R-S) in the Euclidean 3-space. In Section 3, we construct (R-S) from the W-curves. In Section 4, we investigate some special (R-S) and describe their properties. In Section 5, we provide an application of (R-S). Finally, we present our conclusions.

2. Geometric Concepts

Consider a rectangular coordinate system in three-dimensional Euclidean space denoted by $u=(u_1,u_2,u_3)$ with metric defined as $\langle u,u\rangle =d{u}_1^2+d{u}_2^2+d{u}_3^2$.

For any curve $\gamma =\gamma \left(s\right):I\subset \mathrm{R}\to {\mathbb{E}}^3$, where s represents the arc-length parameter, we define the moving Frenet frame along $\gamma$ as $\mathcal{F}=\left\{T\left(s\right),N\left(s\right),B\left(s\right)\right\}$. The Frenet equations for the curve $\gamma$ can be expressed as

$$\left[\begin{array}{c}{T}^{\prime }\left(s\right)\\ N^{\prime }\left(s\right)\\ B^{\prime }\left(s\right)\end{array}\right]=\left[\begin{array}{ccc}0& \kappa \left(s\right)& 0\\ -\kappa \left(s\right)& 0& \tau \left(s\right)\\ 0& -\tau \left(s\right)& \tau \left(s\right)\end{array}\right]\left[\begin{array}{c}T\left(s\right)\\ N\left(s\right)\\ B\left(s\right)\end{array}\right].$$

(1)

Here, $\kappa \left(s\right)$ and $\tau \left(s\right)$ represent the curvature and torsion of the curve $\gamma$, respectively. The vectors $T,N$, and B are mutually orthonormal vectors that satisfy the following conditions:

$$\left\{\begin{array}{c}\langle T,T\rangle =\langle N,N\rangle =\langle B,B\rangle =1,\hfill \\ \langle T,N\rangle =\langle N,B\rangle =\langle B,T\rangle =0,\hfill \\ \det (T,N,B)=1.\hfill \end{array}\right.$$

(2)

Definition 1 

([23,24]). A ruled surface (R-S) is a surface constructed from straight lines parametrized by $\gamma \left(s\right)$ and $X\left(s\right)$. It can be represented parametrically as

$$Q\left(s,v\right)=\gamma \left(s\right)+vX\left(s\right),$$

(3)

where $\gamma =\gamma \left(s\right):I\subset \mathrm{R}\to {\mathbb{E}}^3$ is the directrix or base curve and $X\left(s\right)$ represents a unit vector in the direction of the ruling of the (R-S). If there exists a common perpendicular line for two constructive rulings on the (R-S), the point where this perpendicular intersects the main rulings is called a central point. The locus of these central points is known as the striction curve, and its parametrization on the (R-S) (3) is given by [4]

$${\gamma }^{*}\left(s\right)=\gamma \left(s\right)-\frac{\langle {\gamma }^{\prime }\left(s\right),X^{\prime }\left(s\right)\rangle }{\parallel X^{\prime }\left(s\right){\parallel }^2}X\left(s\right).$$

(4)

If $\parallel X^{\prime }\left(s\right)\parallel =0$, then the (R-S) does not have any striction curve, and it is identified as cylindrical. In such a case, the base curve can serve as a striction curve.

Definition 2 

([25]). The unit normal vector field $U_n$ on the surface Q is defined by

$$U_n=\frac{Q_s\wedge Q_v}{\parallel Q_s\wedge Q_v\parallel },$$

(5)

where $Q_s=\frac{\partial Q(s,v)}{\partial s}$ and $Q_v=\frac{\partial Q(s,v)}{\partial v}$.

Definition 3 

([25]). Let ${\kappa }_g$, ${\kappa }_n$, ${\tau }_g$ be the geodesic curvature, normal curvature, and geodesic torsion, respectively, associated with the curve $\gamma \left(s\right)$ on the surface Q. They can be defined by the following formula:

$${\kappa }_g=\langle U_n\wedge T,T^{\prime }\rangle ,{\kappa }_n=\langle {\gamma }^{″},U_n\rangle ,{\tau }_g=\langle U_n\wedge U_n^{\prime },T^{\prime }\rangle .$$

Definition 4 

([25]). The curve $\gamma \left(s\right)$ lying on a surface Q is a geodesic curve, an asymptotic line, and a principal line if and only if ${\kappa }_g=0$, ${\kappa }_n=0$, and ${\tau }_g=0$, respectively.

Definition 5 

([25]). Let K, H, and λ denote the Gaussian curvature (GC), mean curvature (MC), and distribution parameter, respectively. They can be defined by the following formulas:

$$\begin{array}{cc}\hfill K& =\frac{h_{11}{h}_{22}-h_{12}^2}{g_{11}{g}_{22}-g_{12}^2},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill H& =\frac{g_{11}{h}_{22}+g_{22}{h}_{11}-2g_{12}{h}_{12}}{2\left(g_{11}{g}_{22}-g_{12}^2\right)},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \lambda & =\frac{\det \left({\gamma }^{\prime },X,X^{\prime }\right)}{\parallel X^{\prime }{\parallel }^2}.\hfill \end{array}$$

(8)

where $g_{ij}$ and $h_{ij}$, $i,j=1,2$ represent the first fundamental quantities and second fundamental quantities, respectively and they can be expressed as

$$g_{11}=\langle Q_s,Q_s\rangle ,g_{12}=\langle Q_s,Q_v\rangle ,g_{22}=\langle Q_v,Q_v\rangle .$$

(9)

$$h_{11}=\langle Q_{ss},U_n\rangle ,h_{12}=\langle Q_{sv},U_n\rangle ,h_{22}=\langle Q_{vv},U_n\rangle .$$

(10)

Definition 6 

([26]). Let $H_{II}$ denote the second mean curvature (S-MC) for the (R-S) in ${\mathbb{E}}^3$ and define it by

$$H_{II}=H+\frac{1}{4}{\Delta }_{II}\log \left(\right|K\left|\right),$$

(11)

where H and K denote the (MC) and (GC) for the (R-S). Also, let ${\Delta }_{II}$ denote the Laplacian for functions. Explicitly, we have

$$H_{II}=H+\frac{1}{2\sqrt{\left|\det \right(II\left)\right|}}\sum _{i,j}\frac{\partial }{\partial x^i}\left(\sqrt{\left|\det \right(II\left)\right|}{h}^{ij}\frac{\partial }{\partial x^j}\left(\ln \sqrt{\left|K\right|}\right)\right),$$

(12)

where $\left(h^{ij}\right)$ denotes the inverse of the matrix $\left(h_{ij}\right)$, the indices $i,j$ belong to $\{1,2\}$ and the parameters $x^1,x^2$ represent the coordinates s and v, respectively.

Definition 7 

([27]). Let $K_{II}$ denote the second Gaussian curvature (S-GC) for the (R-S) in ${\mathbb{E}}^3$, which is defined from Brioschi’s formula in the Euclidean 3-space by replacing the components of the metric tensors $g_{11},g_{12}$, and $g_{22}$ by the components of the curvature tensors $h_{11},h_{12}$, and $h_{22}$, respectively:

$$\begin{array}{cc}{K}_{II}& =\frac{1}{{\left(\det \left(II\right)\right)}^2}(\left|\begin{array}{ccc}-\frac{1}{2}{h}_{11,vv}+h_{12,sv}-\frac{1}{2}{h}_{22,ss}\hfill & \frac{1}{2}{h}_{11,s}\hfill & h_{12,s}-\frac{1}{2}{h}_{11,v}\hfill \\ h_{12,v}-\frac{1}{2}{h}_{22,s}\hfill & h_{11}\hfill & h_{12}\hfill \\ \frac{1}{2}{h}_{22,v}\hfill & h_{12}\hfill & h_{22}\hfill \end{array}\right|\\ & -\left|\begin{array}{ccc}0\hfill & \frac{1}{2}{h}_{11,v}\hfill & \frac{1}{2}{h}_{22,s}\hfill \\ \frac{1}{2}{h}_{11,v}\hfill & h_{11}\hfill & h_{12}\hfill \\ \frac{1}{2}{h}_{22,s}\hfill & h_{12}\hfill & h_{22}\hfill \end{array}\right|).\end{array}$$

(13)

It is widely acknowledged that a minimal surface exhibits the (S-GC) $K_{II}=0$. However, it is crucial to note that a surface with a vanishing (S-GC) does not necessarily qualify as minimal [27]. In the context of our investigation, the following definitions are essential:

Definition 8 

([25]). A flat or developable surface in ${\mathbb{E}}^3$ is characterized by having zero (GC), while a minimal surface is defined by having zero (MC).

Definition 9 

([28]). A non-developable surface in ${\mathbb{E}}^3$ is called II-flat surface if its (S-GC) $K_{II}=0$ and it is called a II-minimal surface if its (S-MC) $H_{II}=0$.

3. Construction of Ruled Surfaces in ${\mathbb{E}}^{\mathbf{3}}$

We consider the (R-S) with circular helix curve $\gamma \left(s\right)$ (a family of curves with constant curvature $\kappa \left(s\right)=\kappa$ and constant torsion $\tau \left(s\right)=\tau$) as a base curve. Therefore, the (R-S) can be constructed by

$$Q(s,v)=\gamma \left(s\right)+vX\left(s\right),v\in \mathbb{R},X^{\prime }\left(s\right)\ne 0.$$

(14)

$$X\left(s\right)=\sum _{i=1}^3{u}_i{e}_i\left(s\right)=u_{1}T+u_{2}N+u_{3}B,u_1^2+u_2^2+u_3^2=1,$$

(15)

where $X\left(s\right)$ is a unit vector with fixed components. From (4), it easy to see that the parametrization of the striction curve on the (R-S) that is described by (14) is defined by the following form

$$\begin{array}{c}{\gamma }^{*}\left(s\right)=\gamma \left(s\right)+\frac{u_2\kappa }{\parallel X^{\prime }{\left(s\right)\parallel }^2}X\left(s\right)\hfill \\ \\ =\gamma \left(s\right)+\frac{u_2\kappa }{u_2^2({\kappa }^2+{\tau }^2)+{(u_1\kappa -u_3\tau )}^2}(u_{1}T+u_{2}N+u_{3}B).\hfill \end{array}$$

(16)

Theorem 1. 

Consider the (R-S) given by (14), then, the first fundamental quantities $g_{ij}$ are given by

$$\begin{array}{c}{g}_{11}=1-2u_2\kappa v+\widehat{c}{v}^2,\hfill \\ g_{12}=u_1,\hfill \\ g_{22}=1,\hfill \\ \widehat{a}=\kappa u_3+\tau u_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.\hfill \end{array}$$

(17)

Also, the unit normal vector field $U_n$ to the (R-S) is obtained by

$$\begin{array}{c}{U}_n=\frac{1}{\delta }\left(-\widehat{b}vT+(\widehat{a}{u}_{2}v-u_3)N+(u_2-\widehat{d}v)B\right),\hfill \end{array}$$

(18)

where ${\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2$, $\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{d}=\kappa -\widehat{a}{u}_3.$

Proof. 

The natural frame $\{Q_s,Q_v\}$ is given by

$$\begin{array}{c}{Q}_s=(1-\kappa u_{2}v)T+(\kappa u_1-\tau u_3)vN+\left(\tau u_{2}v\right)B,\hfill \\ Q_v=u_{1}T+u_{2}N+u_{3}B.\hfill \end{array}$$

(19)

Since the metric tensors $\left(g_{ij}\right)$ are defined by (9), then by using Equation (19), we obtain:

$$g_{11}=1-2u_2\kappa v+\left((u_1^2+u_2^2){\kappa }^2-2u_1{u}_3\kappa \tau +(u_2^2+u_3^2){\tau }^2\right)v^2,g_{12}=u_1,g_{22}=1.$$

Choose

$$\begin{array}{c}\widehat{a}=\kappa u_3+\tau u_1,\hfill \\ \widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2,\hfill \end{array}$$

(20)

then

$$g_{11}=1-2u_2\kappa v+\widehat{c}{v}^2,g_{12}=u_1,g_{22}=1.$$

(21)

The vector product of the vectors $Q_s$ and $Q_v$ is given as:

$$\begin{array}{c}{Q}_s\wedge Q_v=(\widehat{a}{u}_1-\tau )vT+(\widehat{a}{u}_{2}v-u_3)N+(u_2-(\kappa -\widehat{a}{u}_3)v)B.\hfill \end{array}$$

(22)

For simplicity, we choose

$$\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{d}=\kappa -\widehat{a}{u}_3.$$

(23)

Then

$$\begin{array}{c}{Q}_s\wedge Q_v=-\widehat{b}vT+(\widehat{a}{u}_{2}v-u_3)N+(u_2-\widehat{d}v)B.\hfill \end{array}$$

(24)

Also, we have

$$\begin{array}{c}\parallel Q_s\wedge Q_v{\parallel }^2={\left(\widehat{b}v\right)}^2+{(\widehat{a}{u}_{2}v-u_3)}^2+{(u_2-\widehat{d}v)}^2.\hfill \end{array}$$

(25)

By straightforward computation, we obtain

$$\begin{array}{c}\parallel Q_s\wedge Q_v{\parallel }^2={\delta }^2,\hfill \\ {\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2.\hfill \end{array}$$

(26)

Since the unit normal vector field $U_n$ to the (R-S) is defined by (5), then by using (24) and (26), we obtain

$$\begin{array}{c}{U}_n=\frac{1}{\delta }\left(-\widehat{b}vT+(\widehat{a}{u}_{2}v-u_3)N+(u_2-\widehat{d}v)B\right).\hfill \end{array}$$

By using (20) and (23), we obtain the unit normal vector as the following explicit formula:

$$\begin{array}{c}{U}_n=\frac{1}{\delta }((u_1{u}_3\kappa -(u_2^2+u_3^2)\tau )vT+(u_1{u}_2\tau v-(1-u_2\kappa v)u_3)N\hfill \\ +(u_2+u_1{u}_3\tau v-\kappa (u_1^2+u_2^2)v)B),\hfill \\ \delta ={\left(1-u_1^2-2u_2\kappa v+({\kappa }^2+{\tau }^2-{(\kappa u_3+\tau u_1)}^2)v^2\right)}^{\frac{1}{2}}\hfill \end{array}$$

(27)

□

Theorem 2. 

Consider the (R-S) given by (14). Then,

$$h_{11}=\frac{1}{\delta }(-\widehat{a}{\delta }^2+\widehat{b}{u}_1),h_{12}=\frac{\widehat{b}}{\delta },h_{22}=0,$$

(28)

where

$$\begin{array}{c}{\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\hfill \\ \widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.\hfill \end{array}$$

Proof. 

Taking the second partial derivatives of (19) with respect to s and v, then we obtain

$$\begin{array}{c}{Q}_{ss}=-\kappa (\kappa u_1-\tau u_3)vT+(\kappa -u_2({\kappa }^2+{\tau }^2)v)N+\tau (\kappa u_1-\tau u_3)vB,\hfill \\ Q_{sv}=(-\kappa u_2)T+(\kappa u_1-\tau u_3)N+\left(\tau u_2\right)B,\hfill \\ Q_{vv}=0.\hfill \end{array}$$

(29)

Since the curvature tensors $h_{ij}$ are defined by (10), then by using (18) and the first equation of (29), we have

$$\begin{array}{cc}\hfill h_{11}& =\frac{1}{\delta }((\kappa \widehat{b}(\kappa u_1-\tau u_3)-\widehat{a}{u}_2^2({\kappa }^2+{\tau }^2)-\tau \widehat{d}(\kappa u_1-\tau u_3))v^2\hfill \\ \hfill & +(({\kappa }^2+{\tau }^2)u_2{u}_3+\kappa \widehat{a}{u}_2+\tau u_2(\kappa u_1-\tau u_3))v-\kappa u_3).\hfill \end{array}$$

After some complicated computations, we obtain:

$$\begin{array}{cc}\hfill h_{11}& =\frac{1}{\delta }\left(-\kappa u_3+(\kappa u_3+\tau u_1)\left(2u_2\kappa v-({\kappa }^2+{\tau }^2-{(\kappa u_3+\tau u_1)}^2)v^2\right)\right).\hfill \end{array}$$

We can rewrite $h_{11}$ in the following simple form:

$$h_{11}=\frac{1}{\delta }(-\widehat{a}{\delta }^2+\widehat{b}{u}_1).$$

(30)

Also, by using (18) and the second equation of (29), we have

$$h_{12}=\frac{1}{\delta }\left(\kappa \widehat{b}{u}_{2}v+(\kappa u_1-\tau u_3)(-u_3+\widehat{a}{u}_{2}v)+\tau u_2(u_2-\stackrel{\widehat{^}}{d}v)\right).$$

Explicitly, we obtain

$$h_{12}=\frac{1}{\delta }\left(-u_1{u}_3\kappa +(u_2^2+u_3^2)\tau \right).$$

Or we can obtain the following simple form for $h_{12}$ as

$$\begin{array}{c}{h}_{12}=\frac{\widehat{b}}{\delta },\hfill \end{array}$$

(31)

In addition, the metric tensor $h_{22}$ can be given by using (18) and the third equation of (29) as

$$h_{22}=0.$$

(32)

□

Lemma 1. 

Consider the (R-S) given by (14); then, $h^{ij}$ are given by

$$h^{11}=0,h^{12}=\frac{\delta }{\widehat{b}},h^{22}=-\frac{\delta }{{\widehat{b}}^2}(-\widehat{a}{\delta }^2+\widehat{b}{u}_1),$$

(33)

where

$$\begin{array}{c}{\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\hfill \\ \widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.\hfill \end{array}$$

Lemma 2. 

The (GC) and (MC) for the (R-S), are given in explicit form by

$$\begin{array}{cc}\hfill K& =-{\left(\frac{(u_2^2+u_3^2)\tau -u_1{u}_3\kappa }{{\delta }^2}\right)}^2,\hfill \\ \hfill H& =\frac{1}{2{\delta }^3}((\kappa u_3+\tau u_1)(2u_1{u}_3\kappa \tau -(u_1^2+u_2^2){\kappa }^2-(u_2^2+u_3^2){\tau }^2)v^2\hfill \\ \hfill & +2u_2(\kappa u_3+\tau u_1)\kappa v-2u_1(u_2^2+u_3^2)\tau +u_3\kappa (2u_1^2-1)).\hfill \end{array}$$

(34)

Proof. 

Substituting from (17) and (28) into (6) and (7), then

$$K=-\frac{{\widehat{b}}^2}{{\delta }^4},H=-\frac{1}{2{\delta }^3}\left(\widehat{a}{\delta }^2+\widehat{b}{u}_1\right).$$

(35)

where

$${\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.$$

Hence, the lemma holds.   □

Lemma 3. 

The (R-S) described by (14) in ${\mathbb{E}}^3$ is a flat surface ($K=0$) at any point $(s,v)$ on the surface $(u_i\ne 0,i=1,2,3)$ if and only if the following condition holds:

$$\begin{array}{c}\hfill \frac{\tau }{\kappa }=\frac{u_1{u}_3}{u_2^2+u_3^2}.\end{array}$$

Lemma 4. 

The distribution parameter λ is obtained as the explicit form:

$$\lambda =\frac{\tau -(\kappa u_3+\tau u_1)u_1}{{\kappa }^2+{\tau }^2-{(\kappa u_3+\tau u_1)}^2}.$$

(36)

Proof. 

Since

$$X\left(s\right)=u_{1}T+u_{2}N+u_{3}B.$$

(37)

Taking the derivative of (37) with respect to the parameter s, then

$$X^{\prime }\left(s\right)=(-\kappa u_2)T+(\kappa u_1-\tau u_3)N+\tau u_{2}B.$$

Also, we have

$$\det ({\gamma }^{\prime },X\left(s\right),X^{\prime }\left(s\right))=\tau -(\kappa u_3+\tau u_1)u_1=\widehat{b}.$$

(38)

The norm $\parallel X^{\prime }\left(s\right)\parallel$ is given as

$$\parallel X^{\prime }{\left(s\right)\parallel }^2={(-\kappa u_2)}^2+{(\kappa u_1-\tau u_3)}^2+{\left(\tau u_2\right)}^2.$$

Hence, we obtain

$$\parallel X^{\prime }{\left(s\right)\parallel }^2={\kappa }^2+{\tau }^2-{(\kappa u_3+\tau u_1)}^2=\widehat{c}.$$

(39)

Since the distribution parameter $\lambda$ is defined by

$$\lambda =\frac{\det ({\gamma }^{\prime },X\left(s\right),X^{\prime }\left(s\right))}{\parallel X^{\prime }{\left(s\right)\parallel }^2}.$$

(40)

Substituting from (38) and (39) into (40),

$$\lambda =\frac{\widehat{b}}{\widehat{c}},$$

where $\widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.$ □

Theorem 3. 

The (S-MC) of the (R-S) that is constructed by (14) is given as follows:

$$\begin{array}{cc}\hfill H_{II}& =\frac{-1}{2{\widehat{b}}^2{\delta }^3}\sum _{i=0}^4{A}_i{v}^i,\widehat{b}\ne 0,\delta \ne 0,\hfill \\ \hfill A_0& =2\widehat{a}\widehat{c}{(1-u_1^2)}^2+\widehat{b}\left((\widehat{a}\widehat{b}-2\widehat{c}{u}_1)(1-u_1^2)+u_1({\widehat{b}}^2+4{\kappa }^2{u}_2^2)\right),\hfill \\ \hfill A_1& =-2u_2\kappa \left(4(1-u_1^2)\widehat{a}\widehat{c}+\widehat{b}(\widehat{a}\widehat{b}+2\widehat{c}{u}_1)\right),\hfill \\ \hfill A_2& =\widehat{c}\left(8\widehat{a}{u}_2^2{\kappa }^2+\widehat{a}{\widehat{b}}^2+2\widehat{c}(\widehat{b}{u}_1+2\widehat{a}(1-u_1^2))\right),\hfill \\ \hfill A_3& =-8\widehat{a}{\widehat{c}}^2{u}_2\kappa ,\hfill \\ \hfill A_4& =2\widehat{a}{\widehat{c}}^3,\hfill \end{array}$$

(41)

where

$$\begin{array}{cc}\hfill {\delta }^2& =1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\hfill \\ \hfill \widehat{a}& =\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.\hfill \end{array}$$

Proof. 

The (S-MC) is defined by (12), and it can be expressed explicitly in the following form:

$$\begin{array}{cc}\hfill H_{II}& =H+\frac{1}{2\sqrt{\left|\det \right(II\left)\right|}}(\frac{\partial }{\partial s}\left(\sqrt{\left|\det \right(II\left)\right|}\left(h^{11}\frac{\partial }{\partial s}\left(\ln \sqrt{\left|K\right|}\right)+h^{12}\frac{\partial }{\partial v}\left(\ln \sqrt{\left|K\right|}\right)\right)\right)\hfill \\ \hfill & +\frac{\partial }{\partial v}\left(\sqrt{\left|\det \right(II\left)\right|}\left(h^{21}\frac{\partial }{\partial s}\left(\ln \sqrt{\left|K\right|}\right)+h^{22}\frac{\partial }{\partial v}\left(\ln \sqrt{\left|K\right|}\right)\right)\right)),\hfill \end{array}$$

(42)

From (28), we have:

$$h=\det \left(II\right)=-\frac{\widehat{b}}{{\delta }^2}.$$

(43)

Since the first equation of (34) defines the (GC) of the (R-S), then by taking the first partial derivatives of $\left(\ln \sqrt{\left|K\right|}\right)$ with respect to the parameters s and v, we obtain

$$\begin{array}{cc}\hfill \frac{\partial }{\partial s}\left(\ln \sqrt{\left|K\right|}\right)& =0,\hfill \\ \hfill \frac{\partial }{\partial v}\left(\ln \sqrt{\left|K\right|}\right)& =-\frac{2(-\kappa u_2+\widehat{c}v)}{{\delta }^2}.\hfill \end{array}$$

(44)

Substituting from (33), the second equation of (34), (43) and (44) into (42), then we obtain:

$$H_{II}=\frac{-1}{2{\widehat{b}}^2{\delta }^3}\left(2\widehat{a}\widehat{c}{\delta }^4+\widehat{b}(\widehat{a}\widehat{b}-2\widehat{c}{u}_1){\delta }^2+{\widehat{b}}^3{u}_1+4\widehat{b}{u}_1{(-\kappa u_2+\widehat{c}v)}^2\right).$$

(45)

Since ${\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2$, then we have

$$\begin{array}{cc}\hfill H_{II}& =\frac{-1}{2{\widehat{b}}^2{\delta }^3}(2\widehat{a}\widehat{c}{(1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2)}^2+\widehat{b}(\widehat{a}\widehat{b}-2\widehat{c}{u}_1)(1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2)\hfill \\ \hfill & +{\widehat{b}}^3{u}_1+4\widehat{b}{u}_1{(-\kappa u_2+\widehat{c}v)}^2).\hfill \end{array}$$

(46)

By substituting $\widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2,$ into (46) and by taking the coefficients of $v^i,i=0,1,2,3,4$, hence the lemma holds.   □

Lemma 5. 

Consider the (R-S) defined by (14), and whose (S-MC) is given by (41), then there are no II-minimal (R-S) whose base curve is a circular helix at any point $(s,v)$ in ${\mathbb{E}}^3$ for $(u_i\ne 0,i=1,2,3)$.

Proof. 

The (R-S) is II-minimal surface, if the (S-MC) vanishes ($H_{II}=0$). Then all coefficients $A_i$ will equal zero. Thus, we have:

• For $A_1=0$, $\widehat{b}\ne 0$, then $\kappa =0$.
• Also, for $A_2=A_3=A_4=0$, $\widehat{b}\ne 0$, then $\widehat{c}=0$.
• Since $\widehat{c}={\kappa }^2+{\tau }^2-{(\kappa u_3+\tau u_1)}^2$, then $\tau =0$, which implies a contradiction.   □

Theorem 4. 

The (S-GC) $K_{II}$ of the (R-S) described by (14) is given as follows:

$$\begin{array}{cc}\hfill K_{II}& =\frac{-1}{2{\widehat{b}}^2{\delta }^3}\sum _{i=0}^4{B}_i{v}^i,\widehat{b}\ne 0,\delta \ne 0,\hfill \\ \hfill B_0& =\widehat{c}(1-u_1^2)\left(\widehat{a}(1-u_1^2)+\widehat{b}{u}_1\right)-2u_1{u}_2^2\widehat{b}{\kappa }^2,\hfill \\ \hfill B_1& =2u_2\widehat{c}\kappa \left(-2(1-u_1^2)\widehat{a}+\widehat{b}{u}_1\right),\hfill \\ \hfill B_2& =\widehat{c}\left(4\widehat{a}{u}_2^2{\kappa }^2+2(1-u_1^2)\widehat{a}\widehat{c}-\widehat{b}\widehat{c}{u}_1\right),\hfill \\ \hfill B_3& =-4\widehat{a}{\widehat{c}}^2{u}_2\kappa ,\hfill \\ \hfill B_4& =\widehat{a}{\widehat{c}}^3,\hfill \end{array}$$

(47)

where

$$\begin{array}{cc}\hfill {\delta }^2& =1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\hfill \\ \hfill \widehat{a}& =\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.\hfill \end{array}$$

Proof. 

Taking the partial derivatives of the curvatures tensors (28) with respect to the parameters $s,v$, then

$$h_{11,s}=0,h_{12,s}=0,h_{22,s}=0.$$

(48)

Also,

$$\begin{array}{cc}\hfill h_{11,v}& =-\frac{1}{{\delta }^3}(\widehat{a}{\delta }^2+\widehat{b}{u}_1)(-\kappa u_2+\widehat{c}v),\hfill \\ \hfill h_{12,v}& =-\frac{\widehat{b}}{{\delta }^3}(-\kappa u_2+\widehat{c}v).\hfill \end{array}$$

(49)

In addition, the second partial derivatives of $h_{ij}$ with respect to the parameters $s,v$ are given as follows:

$$\begin{array}{cc}\hfill h_{11,vv}& =\frac{1}{{\delta }^5}((\widehat{a}{\delta }^2+\widehat{b}{u}_1)\left({(-\kappa u_2+\widehat{c}v)}^2-\widehat{c}{\delta }^2\right)\hfill \\ \hfill & +2\widehat{b}{u}_1{(-\kappa u_2+\widehat{c}v)}^2),\hfill \\ \hfill h_{11,sv}& =0,h_{12,sv}=0.\hfill \end{array}$$

(50)

Since the (S-GC) $K_{II}$ of the (R-S) is defined by (13), then by substituting (43) and (48)–(50) into (13), we obtain

$$K_{II}=-\frac{1}{2{\widehat{b}}^2{\delta }^3}\left(\widehat{a}\widehat{c}{\delta }^4+\widehat{b}\widehat{c}{u}_1{\delta }^2-2\widehat{b}{u}_1{(-\kappa u_2+\widehat{c}v)}^2\right).$$

(51)

By substituting ${\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2$ into (51) and by taking the coefficients of $v^i,i=0,1,2,3,4$, hence the lemma holds.   □

Lemma 6. 

Consider the (R-S) defined by (14), and whose (S-GC) is given by (47), then there are no II-flat (R-S) at any point $(s,v)$ in ${\mathbb{E}}^3$ for $(u_i\ne 0,i=1,2,3)$.

Proof. 

The (R-S) is II-flat surface, if the (S-GC) $K_{II}=0$. Then all coefficients $B_i$ will equal zero for $\widehat{b}\ne 0$ and $\delta \ne 0$. So, for $B_1=B_2=B_3=B_4=0$, $\widehat{b}\ne 0$, then $\widehat{c}=0$.

• Also, $B_0=0$ implies that $\kappa =0$.
• Since $\widehat{c}={\kappa }^2+{\tau }^2-{(\kappa u_3+\tau u_1)}^2$, hence, $\tau =0$, which implies a contradiction.   □

Lemma 7. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the curve $\gamma \left(s\right)$ on the surface Q are obtained by the following formula:

$$\begin{array}{cc}\hfill {\kappa }_g& =\frac{\kappa }{\delta }\left(u_2-(\kappa -\widehat{a}{u}_3)v\right),\hfill \\ \hfill {\kappa }_n& =\frac{\kappa }{\delta }\left(-u_3+\widehat{a}{u}_{2}v\right),\hfill \\ \hfill {\tau }_g& =\frac{\kappa }{{\delta }^2}\left(\left(\widehat{a}\widehat{c}{u}_2\right)v^2-(\widehat{a}\kappa u_2^2+\widehat{c}{u}_3)v+\kappa u_2{u}_3\right),\hfill \end{array}$$

(52)

where ${\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.$

Proof. 

The vector product of the normal vector $U_n$ Equation (18) with the unit tangent vector T is

$$U_n\wedge T=\frac{1}{\delta }\left((u_2-\widehat{d}v)N-(-u_3+\widehat{a}{u}_{2}v)B\right).$$

(53)

Since the geodesic curvature ${\kappa }_g$ is defined by

$${\kappa }_g=\langle U_n\wedge T,T^{\prime }\rangle =\kappa \langle U_n\wedge T,N\rangle ,$$

(54)

taking the inner product (53) with the unit normal vector N, then we obtain

$${\kappa }_g=\frac{\kappa }{\delta }\left(u_2-\widehat{d}v\right).$$

(55)

Since, $\widehat{d}=-(\widehat{a}{u}_3-\kappa )$, then

$${\kappa }_g=\frac{\kappa }{\delta }\left(u_2+(\widehat{a}{u}_3-\kappa )v\right).$$

Since the normal curvature ${\kappa }_n$ is defined by

$${\kappa }_n=\langle {\gamma }^{″},U_n\rangle =\kappa \langle N,U_n\rangle .$$

(56)

Taking the inner product of the normal vector $U_n$ (18) and N, then we have

$${\kappa }_n=\frac{\kappa }{\delta }\left(-u_3+\widehat{a}{u}_{2}v\right)=\frac{\kappa }{\delta }\left(-u_3+u_2(\kappa u_3+\tau u_1)v\right).$$

Since the geodesic torsion ${\tau }_g$ is defined by

$${\tau }_g=\langle U_n\wedge U_n^{\prime },T^{\prime }\rangle =\kappa \langle U_n\wedge U_n^{\prime },N\rangle .$$

(57)

Taking the s-derivative of the (18), then

$$U_n^{\prime }=\frac{1}{\delta }\left(-\kappa \left(-u_3+\widehat{a}{u}_{2}v\right)T-(\widehat{b}\kappa v+\tau (u_2-\widehat{d}v))N+\tau (-u_3+\widehat{a}{u}_{2}v)B\right).$$

(58)

The vector product of the vectors $U_n$ and $U_n^{\prime }$ are given, respectively, from (18) and (58) as

$$\begin{array}{cc}\hfill U_n\wedge U_n^{\prime }& =\frac{1}{{\delta }^2}((\tau {(-u_3+\widehat{a}{u}_{2}v)}^2+(u_2-\widehat{d}v)(\widehat{b}\kappa v+\tau (u_2-\widehat{d}v)))T\hfill \\ \hfill & +(\widehat{b}v\tau (-u_3+\widehat{a}{u}_{2}v)-\kappa (-u_3+\widehat{a}{u}_{2}v)(u_2-\widehat{d}v))N\hfill \\ \hfill & +(\widehat{b}v(\widehat{b}\kappa v+\tau (u_2-\widehat{d}v))+\kappa {(-u_3+\widehat{a}{u}_{2}v)}^2)B).\hfill \end{array}$$

(59)

Substituting from (59) into (57), then we have

$${\tau }_g=\frac{\kappa }{{\delta }^2}\left(\widehat{b}v\tau (-u_3+\widehat{a}{u}_{2}v)-\kappa (-u_3+\widehat{a}{u}_{2}v)(u_2-\widehat{d}v)\right).$$

By straightforward computation, we obtain

$${\tau }_g=\frac{\kappa }{{\delta }^2}\left(\widehat{a}{u}_2(\kappa \widehat{d}+\tau \widehat{b})v^2-(u_3(\kappa \widehat{d}+\tau \widehat{b})+\widehat{a}\kappa u_2^2)v+\kappa u_2{u}_3\right).$$

Hence,

$${\tau }_g=\frac{\kappa }{{\delta }^2}\left(\left(\widehat{a}\widehat{c}{u}_2\right)v^2-(\widehat{c}{u}_3+\widehat{a}\kappa u_2^2)v+\kappa u_2{u}_3\right),$$

where ${\delta }^2=1-u_1^2-2u_2\kappa v+\widehat{c}{v}^2,\widehat{a}=\kappa u_3+\tau u_1,\widehat{b}=\tau -\widehat{a}{u}_1,\widehat{c}={\kappa }^2+{\tau }^2-{\widehat{a}}^2.$ □

Lemma 8. 

The base curve of the (R-S) (14) at any point $(s,v)$ on the surface in ${\mathbb{E}}^3$ for $(u_i\ne 0,i=1,2,3)$ is neither a geodesic curve nor an asymptotic line nor a principal line.

Lemma 9. 

The curvatures $K,H$, and the distribution parameter λ at the point $\left(s,0\right)$ are given by

$$\begin{array}{cc}\hfill K=& -{\left(\frac{(u_2^2+u_3^2)\tau -u_1{u}_3\kappa }{u_2^2+u_3^2}\right)}^2,\hfill \\ \hfill H=& -\frac{2(u_2^2+u_3^2)u_1\tau +(1-2u_1^2)u_3\kappa }{2{\left(u_2^2+u_3^2\right)}^{\frac{3}{2}}},\hfill \\ \hfill \lambda & =\frac{(u_2^2+u_3^2)\tau -u_1{u}_3\kappa }{u_2^2({\kappa }^2+{\tau }^2)+{(u_1\kappa -u_3\tau )}^2}.\hfill \end{array}$$

Also, the second curvatures $H_{II}$ and $K_{II}$ are given by

$$\begin{array}{cc}\hfill H_{II}=& \frac{-1}{2{(u_2^2+u_3^2)}^{\frac{3}{2}}{((u_2^2+u_3^2)\tau -u_1{u}_3\kappa )}^2}.((2u_1(u_2^2+u_3^2)\tau +u_3(1-2u_1^2)\kappa )\hfill \\ \hfill & ((u_2^2+u_3^2)\tau -u_1{u}_3\kappa )+2(u_3{(u_2^2+u_3^2)}^2{\tau }^2\hfill \\ \hfill +& u_3(u_2^4-u_1^2{u}_2^2+u_3^2(u_1^2+u_2^2)){\kappa }^2+2u_1(u_2^4-u_3^4)\kappa \tau \left)\kappa \right).\hfill \end{array}$$

$$\begin{array}{cc}\hfill K_{II}=& \frac{1}{2{\left(u_2^2+u_3^2\right)}^{\frac{3}{2}}{((u_2^2+u_3^2)\tau -u_1{u}_3\kappa )}^2}(2u_1{u}_3^2(1-3u_1^2)(u_2^2+u_3^2){\kappa }^2\tau \hfill \\ \hfill & -2u_1{(u_2^2+u_3^2)}^3{\tau }^3-u_3(1-6u_1^2){(u_2^2+u_3^2)}^2\kappa {\tau }^2\hfill \\ \hfill & -u_3\left(u_1^4(u_2^2-u_3^2)+u_2^2{(u_2^2+u_3^2)}^2+u_1^2(u_2^2+u_3^2)(2u_2^2+u_3^2)\right){\kappa }^3)\hfill \end{array}$$

Lemma 10. 

The (R-S) constructed by (14) is a flat surface at any point $(s,0)$ on the surface in ${\mathbb{E}}^3$ for $(u_i\ne 0,i=1,2,3)$ if and only if the following condition holds:

$$\frac{\tau }{\kappa }=\frac{u_1{u}_3}{u_2^2+u_3^2}.$$

Lemma 11. 

The (R-S) constructed by (14) is a minimal surface at the point $\left(s,0\right)$ if and only if the following condition is satisfied:

$$\frac{\tau }{\kappa }=-\frac{\left(1-2u_1^2\right)u_3}{2(u_2^2+u_3^2)u_1}.$$

Lemma 12. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$ and the geodesic torsion ${\tau }_g$ that are associated with the base curve $\gamma \left(s\right)$ at the point $\left(s,0\right)$ are given as follows:

$${\kappa }_g=\frac{u_2\kappa }{\sqrt{u_2^2+u_3^2}},{\kappa }_n=\frac{-u_3\kappa }{\sqrt{u_2^2+u_3^2}},{\tau }_g=\frac{u_2{u}_3{\kappa }^2}{u_2^2+u_3^2}.$$

At the point $\left(s,0\right)$, the relationship between ${\kappa }_g$, ${\kappa }_n$, and ${\tau }_g$ of the base curve $\gamma \left(s\right)$ is given by

$${\kappa }_g^2+{\kappa }_n^2={\kappa }^2,{\kappa }_g{\kappa }_n=-{\tau }_g.$$

4. Special Ruled Surfaces and Their Characterizations

In this section, we discuss some special (R-S), and we describe some of their characterizations.

4.1. The Ruled Surfaces with $u_1=0$

Consider the (R-S) constructed by (14). At $u_1=0$, $u_2^2+u_3^2=1,$ then the (R-S) takes the formula

$$Q(s,v)=\gamma \left(s\right)+v(u_{2}N+u_{3}B).$$

(60)

In this case, we have

$$\begin{array}{cc}\hfill {\delta }^2& =1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2,\hfill \\ \hfill \widehat{a}& =\kappa u_3,\widehat{b}=\tau ,\widehat{c}=u_2^2{\kappa }^2+{\tau }^2.\hfill \end{array}$$

Lemma 13. 

The (GC), (MC), and the distribution parameter λ for the (R-S) at $u_1=0$ are given by

$$\begin{array}{cc}\hfill K& =-\frac{{\tau }^2}{{(1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2)}^2},\hfill \\ \hfill H& =-\frac{\kappa u_3}{2\sqrt{1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2}},\hfill \\ \hfill \lambda & =\frac{\tau }{u_2^2{\kappa }^2+{\tau }^2}.\hfill \end{array}$$

Also, the (S-MC) and (S-GC) for the (R-S) at $u_1=0$ are given by

$$\begin{array}{cc}\hfill H_{II}& =-\frac{{\sum }_{i=0}^4{A}_i{v}^i}{2{\tau }^2{(1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2)}^{\frac{3}{2}}},\hfill \\ \hfill A_0& =\kappa u_3\left(2u_2^2{\kappa }^2+3{\tau }^2\right),\hfill \\ \hfill A_1& =-2{\kappa }^2{u}_2{u}_3\left(4u_2^2{\kappa }^2+5{\tau }^2\right),\hfill \\ \hfill A_2& =\kappa u_3(u_2^2{\kappa }^2+{\tau }^2)\left(12u_2^2{\kappa }^2+5{\tau }^2\right),\hfill \\ \hfill A_3& =-8{\kappa }^2{u}_2{u}_3{(u_2^2{\kappa }^2+{\tau }^2)}^2,\hfill \\ \hfill A_4& =2\kappa u_3{(u_2^2{\kappa }^2+{\tau }^2)}^3.\hfill \end{array}$$

And

$$\begin{array}{cc}\hfill K_{II}& =-\frac{{\sum }_{i=0}^4{B}_i{v}^i}{2{\tau }^2{(1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2)}^{\frac{3}{2}}},\hfill \\ \hfill B_0& =\kappa u_3(u_2^2{\kappa }^2+{\tau }^2),\hfill \\ \hfill B_1& =-4{\kappa }^2{u}_2{u}_3(u_2^2{\kappa }^2+{\tau }^2),\hfill \\ \hfill B_2& =2\kappa u_3(u_2^2{\kappa }^2+{\tau }^2)\left(3u_2^2{\kappa }^2+{\tau }^2\right),\hfill \\ \hfill B_3& =-4u_2{u}_3{\kappa }^2{(u_2^2{\kappa }^2+{\tau }^2)}^2,\hfill \\ \hfill B_4& =\kappa u_3{(u_2^2{\kappa }^2+{\tau }^2)}^3.\hfill \end{array}$$

Lemma 14. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the base curve $\gamma \left(s\right)$ at $u_1=0$, take the following formula:

$$\begin{array}{cc}\hfill {\kappa }_g& =\frac{\kappa u_2(1-\kappa u_{2}v)}{\sqrt{1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2}},\hfill \\ \hfill {\kappa }_n& =\frac{-\kappa u_3(1-\kappa u_{2}v)}{\sqrt{1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2}},\hfill \\ \hfill {\tau }_g& =\frac{\kappa u_3}{(1-2u_2\kappa v+(u_2^2{\kappa }^2+{\tau }^2)v^2)}\left(\kappa u_2(u_2^2{\kappa }^2+{\tau }^2)v^2-(2u_2^2{\kappa }^2+{\tau }^2)v+\kappa u_2\right).\hfill \end{array}$$

Lemma 15. 

There is no flat, minimal, II-minimal, and II-flat (R-S) with $u_1=0$ at every point $\left(s,v\right)$ in ${\mathbb{E}}^3$.

Lemma 16. 

The base curve for the (R-S) constructed by (60) with $u_1=0,u_2\ne 0,u_3\ne 0$ is neither a geodesic curve nor an asymptotic line nor a principal line at every point $\left(s,v\right)$ in ${\mathbb{E}}^3$.

Lemma 17. 

The base curve of the (R-S) constructed by (60) with $u_1=0$ in ${\mathbb{E}}^3$ has the following properties at the point $(s,0)$:

$${\kappa }_g^2+{\kappa }_n^2={\kappa }^2,{\kappa }_g{\kappa }_n=-{\tau }_g.$$

4.2. The Ruled Surfaces with $u_2=0$

Consider the (R-S) constructed by (14). For $u_2=0$, $u_1^2+u_3^2=1,$ then, the equation for the (R-S) (14) takes the following form:

$$Q(s,v)=\gamma \left(s\right)+v(u_{1}T+u_{3}B).$$

(61)

In this case, we have,

$$\begin{array}{cc}\hfill {\delta }^2& =u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2,\hfill \\ \hfill \widehat{a}& =\kappa u_3+\tau u_1,\widehat{b}=-u_3(\kappa u_1-\tau u_3),\widehat{c}={(\kappa u_1-\tau u_3)}^2.\hfill \end{array}$$

Lemma 18. 

The (GC), (MC), and the distribution parameter λ for the (R-S) at $u_2=0$ are given by

$$\begin{array}{cc}\hfill K& =-\frac{u_3^2{(\kappa u_1-\tau u_3)}^2}{{(u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2)}^2},\hfill \\ \hfill H& =-\frac{1}{2{(u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2)}^{3/2}}((\kappa u_3+\tau u_1){(\kappa u_1-\tau u_3)}^2{v}^2\hfill \\ \hfill & +u_3(\kappa (u_3^2-u_1^2)+2u_1{u}_3\tau )),\hfill \\ \hfill \lambda & =\frac{-u_3}{(\kappa u_1-\tau u_3)}.\hfill \end{array}$$

Also, the (S-MC) and (S-GC) for the (R-S) at $u_2=0$ are given by

$$\begin{array}{cc}\hfill H_{II}& =-\frac{{\sum }_{i=0}^4{A}_i{v}^i}{2\left(u_3^2{(\kappa u_1-\tau u_3)}^2\right){(u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2)}^{\frac{3}{2}}},\hfill \\ \hfill A_0& =u_3^3{(\kappa u_1-\tau u_3)}^2\left(\kappa (1+2u_3^2)+2u_1{u}_3\tau \right),\hfill \\ \hfill A_1& =0,\hfill \\ \hfill A_2& =-u_3{(\kappa u_1-\tau u_3)}^4\left(\kappa (7u_1^2-5)-7\tau u_1{u}_3\right),\hfill \\ \hfill A_3& =0,\hfill \\ \hfill A_4& =2(\kappa u_3+\tau u_1){(\kappa u_1-\tau u_3)}^6.\hfill \end{array}$$

And

$$\begin{array}{cc}\hfill K_{II}& =-\frac{{\sum }_{i=0}^4{B}_i{v}^i}{2\left(u_3^2{(\kappa u_1-\tau u_3)}^2\right){(u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2)}^{\frac{3}{2}}},\hfill \\ \hfill B_0& =u_3^3{(\kappa u_1-\tau u_3)}^2\left(-\kappa (u_1^2-u_3^2)+2u_1{u}_3\tau )\right),\hfill \\ \hfill B_1& =0,\hfill \\ \hfill B_2& =u_3{(\kappa u_1-\tau u_3)}^4\left(\kappa (1+u_3^2)+u_1{u}_3\tau \right),\hfill \\ \hfill B_3& =0,\hfill \\ \hfill B_4& =(\kappa u_3+\tau u_1){(\kappa u_1-\tau u_3)}^6.\hfill \end{array}$$

Lemma 19. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the base curve $\gamma \left(s\right)$ at $u_2=0$, take the following formula:

$${\kappa }_g=\frac{-\kappa u_1(\kappa u_1-\tau u_3)v}{\sqrt{u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2}},{\kappa }_n=\frac{-u_3\kappa }{\sqrt{u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2}}{\tau }_g=\frac{-u_3\kappa {(\kappa u_1-\tau u_3)}^{2}v}{u_3^2+{(\kappa u_1-\tau u_3)}^2{v}^2}.$$

Lemma 20. 

The (R-S) given by (61) that constructed with $u_2=0$ in ${\mathbb{E}}^3$ is a flat, II-minimal, and II-flat surface at any point $\left(s,v\right)$ (also at the point $\left(s,0\right)$) if and only if the following condition holds:

$$\begin{array}{c}\hfill \frac{\tau }{\kappa }=\frac{u_1}{u_3}.\end{array}$$

Lemma 21. 

There are no minimal (R-S) with $u_2=0$ at a point $\left(s,v\right)$ in ${\mathbb{E}}^3$.

Lemma 22. 

The base curve for the (R-S) given by (61) is a geodesic curve and a principal line if and only if

$$\begin{array}{c}\hfill \frac{\tau }{\kappa }=\frac{u_1}{u_3}.\end{array}$$

Lemma 23. 

The (R-S) given by (61) that constructed with $u_2=0$ in ${\mathbb{E}}^3$ is characterized by the following conditions at the point $\left(s,0\right)$:

• It is minimal and II-flat if and only if the ratio of the torsion to curvature is equal to

  $$\frac{\tau }{\kappa }=\frac{u_1^2-u_3^2}{2u_1{u}_3}.$$
• It is II-minimal if and only if the ratio of the torsion to curvature is equal to

  $$\frac{\tau }{\kappa }=-\frac{1+2u_3^2}{2u_1{u}_3},\mathrm{or}\frac{\tau }{\kappa }=\frac{u_1}{u_3}.$$
• The base curve for the (R-S) is a geodesic curve and a principal line.

4.3. Ruled Surfaces with $u_3=0$

Consider the (R-S) that is given by (14). For $u_3=0$, then $u_1^2+u_2^2=1,$ thus, the equation for the (R-S) takes the form

$$Q(s,v)=\gamma \left(s\right)+v(u_{1}T+u_{2}N).$$

(62)

In this case, we have

$$\begin{array}{cc}\hfill {\delta }^2& =u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2,\hfill \\ \hfill \widehat{a}& =\tau u_1,\widehat{b}=u_2^2\tau ,\widehat{c}={\kappa }^2+u_2^2{\tau }^2.\hfill \end{array}$$

Lemma 24. 

The (GC), (MC), and the distribution parameter λ at $u_3=0$ are given by

$$\begin{array}{cc}\hfill K& =-\frac{u_2^4{\tau }^2}{{(u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2)}^2},\hfill \\ \hfill H& =-\frac{-u_1\tau }{2{(u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2)}^{\frac{3}{2}}}\left(2u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2\right),\hfill \\ \hfill \lambda & =\frac{u_2^2\tau }{{\kappa }^2+u_2^2{\tau }^2}.\hfill \end{array}$$

Also, the (S-MC) and (S-GC) for the (R-S) at $u_3=0$ are given by

$$\begin{array}{cc}\hfill H_{II}& =-\frac{{\sum }_{i=0}^4{A}_i{v}^i}{2u_2^4{\tau }^2{(u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2)}^{\frac{3}{2}}},\hfill \\ \hfill A_0& =2u_1{u}_2^4\tau (2{\kappa }^2+u_2^2{\tau }^2),\hfill \\ \hfill A_1& =-2u_1{u}_2^3\kappa \tau (6{\kappa }^2+7u_2^2{\tau }^2),\hfill \\ \hfill A_2& =7u_1{u}_2^2\tau ({\kappa }^2+u_2^2{\tau }^2)(2{\kappa }^2+u_2^2{\tau }^2),\hfill \\ \hfill A_3& =-8u_1{u}_2\kappa \tau {({\kappa }^2+u_2^2{\tau }^2)}^2,\hfill \\ \hfill A_4& =2u_1\tau {({\kappa }^2+u_2^2{\tau }^2)}^3.\hfill \end{array}$$

And

$$\begin{array}{cc}\hfill K_{II}& =-\frac{{\sum }_{i=0}^4{B}_i{v}^i}{2u_2^4{\tau }^2{(u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2)}^{\frac{3}{2}}},\hfill \\ \hfill B_0& =2u_1{u}_2^6{\tau }^3,\hfill \\ \hfill B_1& =-2u_1{u}_2^3\kappa \tau ({\kappa }^2+u_2^2{\tau }^2),\hfill \\ \hfill B_2& =u_1{u}_2^2\tau ({\kappa }^2+u_2^2{\tau }^2)(5{\kappa }^2+u_2^2{\tau }^2),\hfill \\ \hfill B_3& =-4u_1{u}_2\kappa \tau {({\kappa }^2+u_2^2{\tau }^2)}^2,\hfill \\ \hfill B_4& =u_1\tau {({\kappa }^2+u_2^2{\tau }^2)}^3.\hfill \end{array}$$

Lemma 25. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the base curve $\gamma \left(s\right)$ at $u_3=0$, take the following formula:

$$\begin{array}{cc}\hfill {\kappa }_g& =\frac{\kappa \left(u_2-\kappa v\right)}{\sqrt{u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2}},\hfill \\ \hfill {\kappa }_n& =\frac{u_1{u}_2\kappa \tau v}{\sqrt{u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2}},\hfill \\ \hfill {\tau }_g& =\frac{u_1{u}_2\kappa \tau \left(({\kappa }^2+u_2^2{\tau }^2)v^2-\kappa u_{2}v\right)}{u_2^2-2u_2\kappa v+({\kappa }^2+u_2^2{\tau }^2)v^2}.\hfill \end{array}$$

Lemma 26. 

Consider the (R-S) given by (62) that constructed with $u_3=0$ in ${\mathbb{E}}^3$, then there is no flat, minimal, II-minimal, and II-flat at every point $\left(s,v\right)$.

Lemma 27. 

The base curve for the (R-S) that is described by (62) with $u_3=0$ is neither a geodesic curve nor an asymptotic line nor a principal line at any point $(s,v)$ where $v\ne 0$ and $u_1\ne 0,u_2\ne 0$.

Lemma 28. 

At the point $\left(s,0\right)$, the base curve of the (R-S) given by (62) is both an asymptotic line and a principal line for $u_1\ne 0,u_2\ne 0$.

4.4. Ruled Surfaces with $u_1=u_2=0$

Consider the (R-S) given by (14). For $u_1=u_2=0,u_3=1$, then

$$Q(s,v)=\gamma \left(s\right)+vB.$$

(63)

$${\delta }^2=1+{\tau }^2{v}^2,\widehat{a}=\kappa ,\widehat{b}=\tau ,\widehat{c}={\tau }^2.$$

Lemma 29. 

The (GC), (MC), and the distribution parameter λ at $u_1=u_2=0,u_3=1$ are given by

$$K=-\frac{{\tau }^2}{{(1+{\tau }^2{v}^2)}^2},H=-\frac{\kappa }{2\sqrt{1+{\tau }^2{v}^2}},\lambda =\frac{1}{\tau }.$$

Also, the (S-MC) and (S-GC) at $u_1=u_2=0,u_3=1$ are given by

$$\begin{array}{cc}\hfill H_{II}& =-\frac{{\sum }_{i=0}^4{A}_i{v}^i}{2{\tau }^2{(1+{\tau }^2{v}^2)}^{3/2}},\hfill \\ \hfill A_0& =3\kappa {\tau }^2,A_1=0,A_2=5\kappa {\tau }^4,A_3=0,A_4=2\kappa {\tau }^6.\hfill \end{array}$$

And

$$\begin{array}{cc}\hfill K_{II}& =-\frac{{\sum }_{i=0}^4{B}_i{v}^i}{2{\tau }^2{(1+{\tau }^2{v}^2)}^{3/2}},\hfill \\ \hfill B_0& =\kappa {\tau }^2,B_1=0,B_2=2\kappa {\tau }^4,B_3=0,B_4=\kappa {\tau }^6.\hfill \end{array}$$

Lemma 30. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the base curve $\gamma \left(s\right)$ at $u_1=u_2=0,u_3=1$, take the following formula:

$${\kappa }_g=0,{\kappa }_n=\frac{-\kappa }{\sqrt{1+{\tau }^2{v}^2}},{\tau }_g=\frac{-\kappa {\tau }^{2}v}{1+{\tau }^2{v}^2}.$$

Lemma 31. 

At any point $(s,v)$ on the surface Q with $u_1=u_2=0,u_3=1$, there are no flat, minimal, II-minimal, and II-flat (R-S) in ${\mathbb{E}}^3$.

Lemma 32. 

The base curve of the (R-S) described by (63) with $u_1=u_2=0,u_3=1$ in ${\mathbb{E}}^3$ is a geodesic curve at any point $(s,v)$, and it is a principal line at a point $(s,0)$.

4.5. Ruled Surfaces with $u_1=u_3=0$ and $u_2=1$

At $u_1=u_3=0$ and $u_2=1$, then Equation (14) takes the form

$$Q(s,v)=\gamma \left(s\right)+vN.$$

(64)

In this case, we have

$$\begin{array}{cc}\hfill {\delta }^2& =1-2\kappa v+({\kappa }^2+{\tau }^2)v^2,\hfill \\ \hfill \widehat{a}& =0,\widehat{b}=\tau ,\widehat{c}={\kappa }^2+{\tau }^2.\hfill \end{array}$$

Lemma 33. 

The (GC), (MC), and distribution parameter λ at $u_1=u_3=0$ are given by

$$\begin{array}{c}\hfill K=-\frac{{\tau }^2}{{(1-2\kappa v+({\kappa }^2+{\tau }^2)v^2)}^2},H=0,\lambda =\frac{\tau }{{\kappa }^2+{\tau }^2}\end{array}$$

Also, the (S-MC) and (S-GC) at $u_1=u_3=0,u_2=1$ are given by

$$H_{II}=0,K_{II}=0.$$

Lemma 34. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the base curve $\gamma \left(s\right)$ at $u_1=u_3=0,u_2=1$, take the following formula:

$${\kappa }_g=\frac{\kappa (1-\kappa v)}{\sqrt{1-2\kappa v+({\kappa }^2+{\tau }^2)v^2}},{\kappa }_n=0,{\tau }_g=0.$$

(65)

Lemma 35. 

At every point $(s,v)$ on the (R-S) for $u_1=u_3=0,u_2=1$, we find that:

• The (R-S) are minimal, II-minimal, and II-flat surfaces but not flat in ${\mathbb{E}}^3$.
• The base curve of the (R-S) (64) in ${\mathbb{E}}^3$ is both an asymptotic line and a principal line.

4.6. Ruled Surfaces with $u_2=u_3=0$

At $u_2=u_3=0,u_1=1$, then the (R-S) (14) takes the form

$$Q(s,v)=\gamma \left(s\right)+vT.$$

(66)

In this case, we have

$$\delta =\kappa v,\widehat{a}=\tau ,\widehat{b}=0,\widehat{c}={\kappa }^2.$$

Lemma 36. 

The (GC), (MC), and the distribution parameter λ for the (R-S) at $u_2=u_3=0,u_1=1$ are given by

$$K=0,H=-\frac{\tau }{2\kappa v},\lambda =0.$$

Also, the (S-MC) and (S-GC) at $u_2=u_3=0,u_1=1$ are undefined $(\widehat{b}=0)$ due to the fact that $\det \left(II\right)=0.$

Lemma 37. 

The geodesic curvature ${\kappa }_g$, the normal curvature ${\kappa }_n$, and the geodesic torsion ${\tau }_g$ associated with the base curve $\gamma \left(s\right)$ at $u_2=u_3=0,u_1=1$, take the following formula:

$${\kappa }_g=-\kappa ,{\kappa }_n=0,{\tau }_g=0.$$

The base curve of the (R-S) (66) in ${\mathbb{E}}^3$ is both an asymptotic line and a principal line at any point $(s,v)$ on the surface.

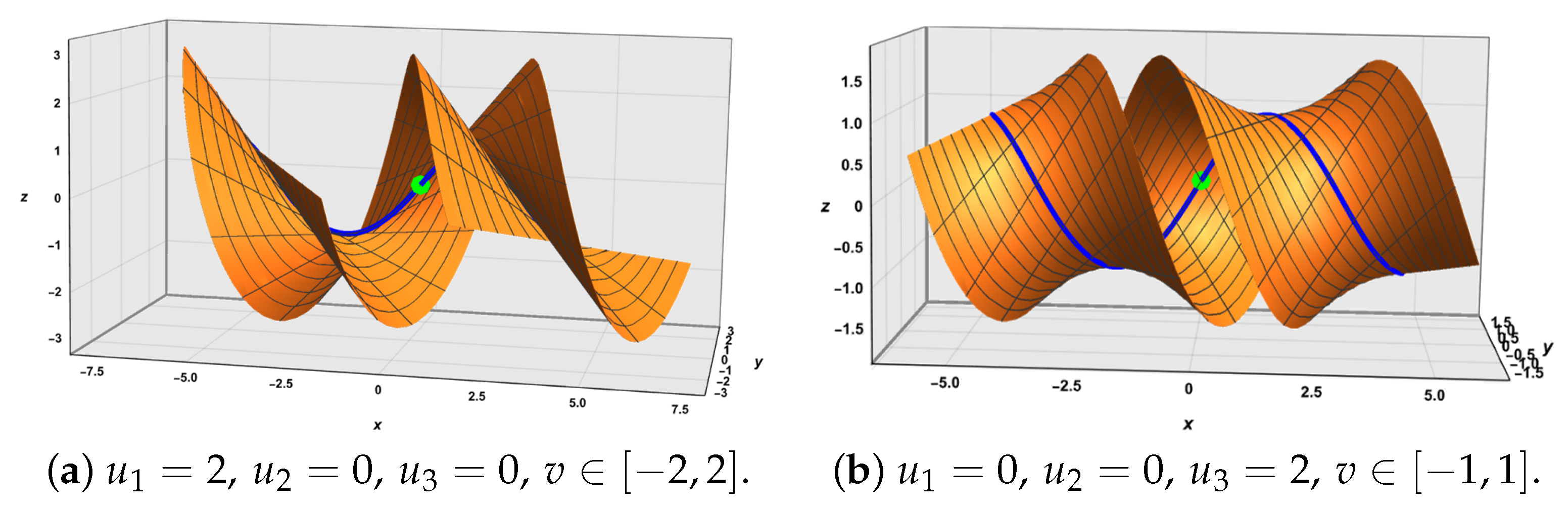
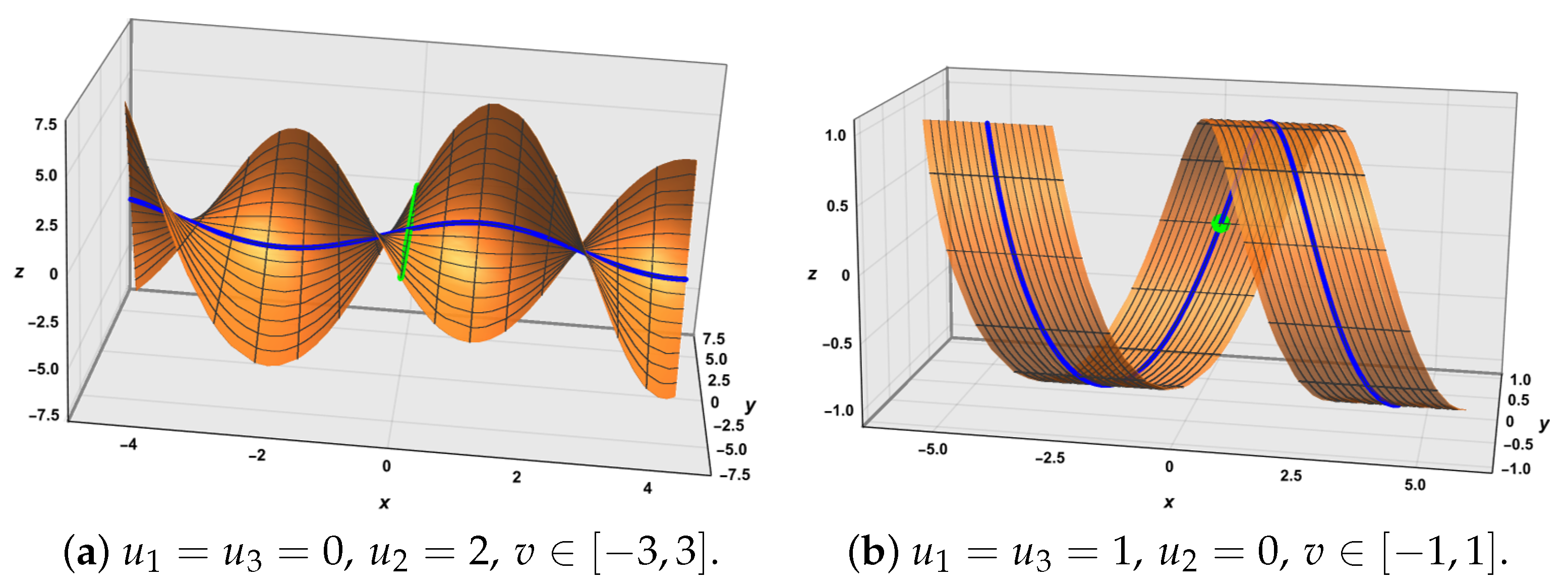
5. Application

Consider the following (R-S):

$$Q(s,v)=\gamma \left(s\right)+v(u_{1}T+u_{2}N+u_{3}B),$$

where $\gamma \left(s\right)$ is a circular helix given by

$$\gamma \left(s\right)=\left(\frac{s}{\sqrt{2}},\cos \frac{s}{\sqrt{2}},\sin \frac{s}{\sqrt{2}}\right).$$

Explicitly, we have

$$\begin{array}{cc}\hfill Q(s,v)& =(\frac{1}{\sqrt{2}}(s+(u_1+u_3)v),(\frac{u_3-u_1}{\sqrt{2}}\sin \frac{s}{\sqrt{2}}-u_2\cos \frac{s}{\sqrt{2}})v+\cos \frac{s}{\sqrt{2}}\hfill \\ \hfill & ,(\frac{u_1-u_3}{\sqrt{2}}\cos \frac{s}{\sqrt{2}}-u_2\sin \frac{s}{\sqrt{2}})v+\sin \frac{s}{\sqrt{2}}).\hfill \end{array}$$

The Frenet frame vectors are

$$\begin{array}{c}T\left(s\right)=\frac{1}{\sqrt{2}}\left(1,-\sin \frac{s}{\sqrt{2}},\cos \frac{s}{\sqrt{\sqrt{2}}}\right),\\ N\left(s\right)=\left(0,-\cos \frac{s}{\sqrt{2}},-\sin \frac{s}{\sqrt{2}}\right),\\ B\left(s\right)=\frac{1}{\sqrt{2}}\left(1,\sin \frac{s}{\sqrt{2}},-\cos \frac{s}{\sqrt{2}}\right),\end{array}$$

with constant curvature and torsion $\kappa =\tau =\frac{1}{2}$.

The (GC), (MC), and distribution $\lambda$, respectively, are given by

$$\begin{array}{cc}\hfill K& =-\frac{{(1-u_1^2-u_1{u}_3)}^2}{4{(1-u_1^2-u_{2}v+\frac{1}{4}(2-{(u_1+u_3)}^2)v^2)}^2},\hfill \\ \hfill H& =-\frac{(u_1+(u_1+u_3)(1-2u_1^2-u_{2}v+\frac{1}{4}(2-{(u_1+u_3)}^2)v^2))}{4{(1-u_1^2-u_{2}v+\frac{1}{4}(2-{(u_1+u_3)}^2)v^2)}^{\frac{3}{2}}},\hfill \\ \hfill \lambda & =\frac{2(1-u_1^2-u_1{u}_3)}{(2-{(u_1+u_3)}^2)}.\hfill \end{array}$$

The visual representation of this application is illustrated in Figure 1 and Figure 2.

6. Conclusions

In the current study, we have focused on the (R-S) that is generated from the W-curve in ${\mathbb{E}}^3$. We have analyzed various properties of the generated (R-S), such as its mean curvature, Gaussian curvature, second mean curvature, and second Gaussian curvature. Additionally, we have presented specific ruled surfaces and discussed their characteristics. Furthermore, we have established the necessary conditions for the generated (R-S) to be minimal, flat, II-minimal, and II-flat surfaces. Moreover, we have identified the conditions for the base curve associated with the generated (R-S) to be a geodesic curve, an asymptotic line, and a principal line. Some of the important results of this work are listed as follows:

• If the unit director vector $X\left(s\right)=u_{2}N+u_{3}B$, then there are no minimal, flat, II-minimal, and II-flat ruled surfaces at every point on the surface. In addition, the base curve (circular helix) for the ruled surface is neither a geodesic curve nor an asymptotic line nor a principal line.
• If the unit director vector $X\left(s\right)=u_{1}T+u_{3}B$, then there are no minimal ruled surfaces at every point on the surface, and there are flat, II-minimal, and II-flat ruled surfaces at any point $(s,v)$ on the surface if and only if the ratio of the torsion and curvature of the base curve is $\frac{\tau }{\kappa }=\frac{u_1}{u_3}$.
  Also, the base curve (circular helix) of the ruled surface is a geodesic curve and a principal line if $\frac{\tau }{\kappa }=\frac{u_1}{u_3}.$
• If the unit director vector $X\left(s\right)=u_{1}T+u_{2}N$, then there are no minimal, flat, II-minimal, and II-flat ruled surfaces at every point $(s,v)$ on the surface. In addition, the base curve (circular helix) for the ruled surface is neither a geodesic curve nor an asymptotic line nor a principal line.
• If the unit director vector $X\left(s\right)=u_{3}B$, then there are no minimal, flat, II-minimal, and II-flat ruled surfaces at every point on the surface. In addition, the base curve (circular helix) of the ruled surface is a geodesic curve at any point $(s,v)$ on the surface and a principal line at the point $(s,0)$.
• If the unit director vector $X\left(s\right)=u_{2}N$, then there are minimal, II-minimal, and II-flat ruled surfaces at every point on the surface, and there is no flat ruled surface. In addition, the base curve (circular helix) for the ruled surface is both an asymptotic line and a principal line at any point $(s,v)$ on the surface.
• If the unit director vector $X\left(s\right)=u_{1}T$, then there are no minimal, II-minimal, and II-flat ruled surfaces at every point on the surface (the unit normal vector to the ruled surface is undefined). In addition, the base curve (circular helix) for the ruled surface is an asymptotic line and a principal line at any point $(s,v)$ on the surface.