Duffin–Kemmer–Petiau and Dirac Equations—A Supersymmetric Connection
Abstract
:1. Introduction
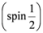 degrees of freedom. In the present paper we extend our results to the case of interacting fields.
degrees of freedom. In the present paper we extend our results to the case of interacting fields.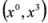 subspace and 2D Pauli equations in
subspace and 2D Pauli equations in 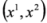 subspace. In Section 5 the Duffin–Kemmer–Petiau equation for spin 0 in crossed fields is split into two 3 × 3 subequations—these equations have the same structure as subequations arising in the Dirac theory. It follows that the free 3 × 3 equations provide a supersymmetric link between the Dirac and DKP theories—this is described in Section 6. In the last Section we discuss our results in a broader context of supersymmetry and Lorentz covariance.
subspace. In Section 5 the Duffin–Kemmer–Petiau equation for spin 0 in crossed fields is split into two 3 × 3 subequations—these equations have the same structure as subequations arising in the Dirac theory. It follows that the free 3 × 3 equations provide a supersymmetric link between the Dirac and DKP theories—this is described in Section 6. In the last Section we discuss our results in a broader context of supersymmetry and Lorentz covariance.2. Relativistic Wave Equations
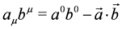 . Four-momentum operators are defined as
. Four-momentum operators are defined as 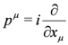 where natural units have been used: c = 1,
where natural units have been used: c = 1,  . The interaction will be introduced via minimal coupling,
. The interaction will be introduced via minimal coupling,
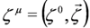 and spinors
and spinors 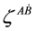 are related by the formula
are related by the formula 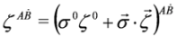 :
: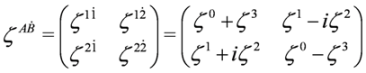
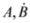 number rows and columns, respectively,
number rows and columns, respectively, 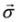 denotes vector built of the Pauli matrices and σ0 is the 2 × 2 unit matrix. Spinor with lowered indices
denotes vector built of the Pauli matrices and σ0 is the 2 × 2 unit matrix. Spinor with lowered indices 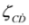 reads:
reads:
2.1. The Dirac Equation
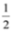 particles, such as electrons and quarks, consistent with both the principles of quantum mechanics and the theory of special relativity [14,15]. The Dirac Equation is [11,16,17]:
particles, such as electrons and quarks, consistent with both the principles of quantum mechanics and the theory of special relativity [14,15]. The Dirac Equation is [11,16,17]: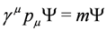
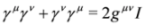 where I is the 4 × 4 unit matrix. In the spinor representation of the Dirac matrices we have:
where I is the 4 × 4 unit matrix. In the spinor representation of the Dirac matrices we have: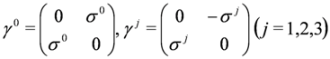
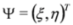 where T denotes transposition of a matrix. Sometimes it is more convenient to use the standard representation:
where T denotes transposition of a matrix. Sometimes it is more convenient to use the standard representation: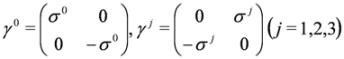
2.2. Subsolutions of the Dirac Equation and Supersymmetry
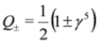 to Equation (4) since γ5 = −iγ0γ1γ2γ3 anticommutes with γμpμ:
to Equation (4) since γ5 = −iγ0γ1γ2γ3 anticommutes with γμpμ:
 ,
, 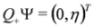 and separate equations for ξ, η follow:
and separate equations for ξ, η follow: 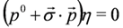
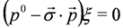
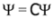 where C is the charge conjugation operator,
where C is the charge conjugation operator, 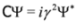 , we obtain in the spinor representation
, we obtain in the spinor representation 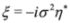 ,
, 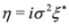 and the Dirac Equation (4) reduces to two separate Majorana equations for two-component spinors:
and the Dirac Equation (4) reduces to two separate Majorana equations for two-component spinors: 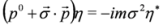
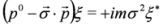
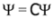 that Majorana particle has zero charge built-in condition. The problem whether neutrinos are described by the Dirac equation or the Majorana equations is still open [18,19,20,21].
that Majorana particle has zero charge built-in condition. The problem whether neutrinos are described by the Dirac equation or the Majorana equations is still open [18,19,20,21].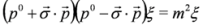
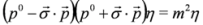
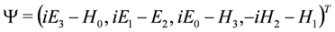
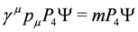
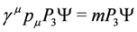
2.3. The Duffin–Kemmer–Petiau Equations
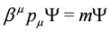
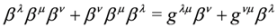
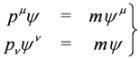
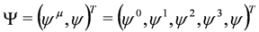
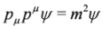 .
.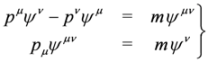
 :
: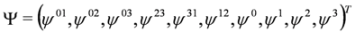
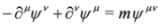 ,
, 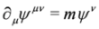 , where Ψλ, Ψμν are real). Because of antisymmetry of Ψμν we have pνΨν = 0what implies spin 1 condition. The set of Equation (21) was first written by Proca [30,31] and in a different context by Lanczos, see [32] and references therein. More on the history of the formalism of Duffin, Kemmer and Petiau can be found in [33].
, where Ψλ, Ψμν are real). Because of antisymmetry of Ψμν we have pνΨν = 0what implies spin 1 condition. The set of Equation (21) was first written by Proca [30,31] and in a different context by Lanczos, see [32] and references therein. More on the history of the formalism of Duffin, Kemmer and Petiau can be found in [33].3. Splitting the Dirac Equation in Longitudinal External Fields
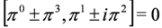
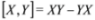 is a commutator. The condition Equation (23) is fulfilled in the Abelian case for
is a commutator. The condition Equation (23) is fulfilled in the Abelian case for
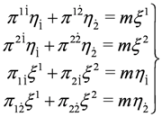
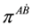 ,
, 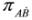 are given by Equations (2) and (3) (note that
are given by Equations (2) and (3) (note that 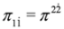 ,
,  ,
, 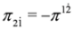 ,
,  ). Obviously, due to relations between components of
). Obviously, due to relations between components of 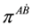 and
and 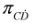 the Equation (25) can be rewritten in terms of components of
the Equation (25) can be rewritten in terms of components of 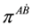 only. Equation (25) corresponds to Equation (4) in the spinor representation of γ matrices and
only. Equation (25) corresponds to Equation (4) in the spinor representation of γ matrices and 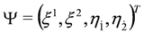 . We assume here that we deal with four-potentials fulfilling condition Equation (23).
. We assume here that we deal with four-potentials fulfilling condition Equation (23).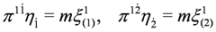
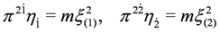
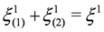

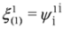 ,
,  ,
, 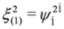 ,
,  .
.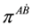 throughout):
throughout):
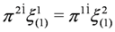

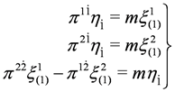
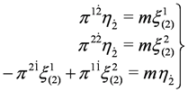
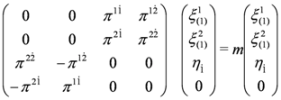
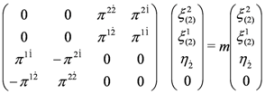
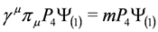
 . There are also other projection operators which lead to analogous three component equations, P1= diag (0,1,1,1), P2= diag (1,0,1,1), P3= diag (1,1,0,1). Acting from the left on Equation (37) with P4 and (1−P4)we obtain two Equations:
. There are also other projection operators which lead to analogous three component equations, P1= diag (0,1,1,1), P2= diag (1,0,1,1), P3= diag (1,1,0,1). Acting from the left on Equation (37) with P4 and (1−P4)we obtain two Equations: 
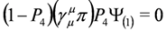
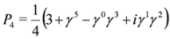 where γ5 = iγ0γ1γ2γ3 (similar formulae can be given for other projection operators P1, P2, P3, see [13] where another convention for γμ matrices was however used). It thus follows that Equation (37) is given representation independent form and is Lorentz covariant (in [9] subsolutions of form Equation (37) were obtained for the free Dirac equation).
where γ5 = iγ0γ1γ2γ3 (similar formulae can be given for other projection operators P1, P2, P3, see [13] where another convention for γμ matrices was however used). It thus follows that Equation (37) is given representation independent form and is Lorentz covariant (in [9] subsolutions of form Equation (37) were obtained for the free Dirac equation).
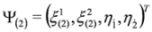 ,
, 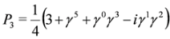 , note that
, note that 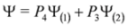 .
.4. Separation of Variables in Subequations
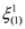 and
and 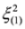 from the first two equations into the third in Equation (33) we get:
from the first two equations into the third in Equation (33) we get: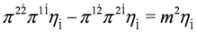
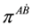 and property Equation (24) we obtain:
and property Equation (24) we obtain: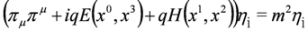
 ,
, 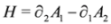 .
.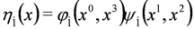
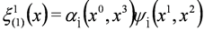
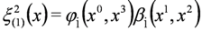
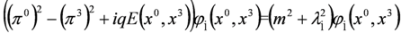
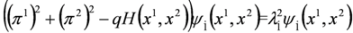
 is the separation constant and we note that Equations (46a) and (46b) are analogous to Equations (12.15) and (12.19) in [10].
is the separation constant and we note that Equations (46a) and (46b) are analogous to Equations (12.15) and (12.19) in [10].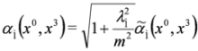 , we obtain 2D Dirac Equation:
, we obtain 2D Dirac Equation:

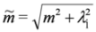 .
.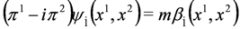
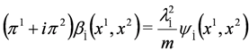

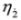 :
: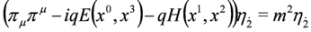
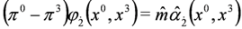
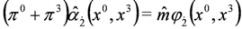
 and
and  and equation:
and equation:

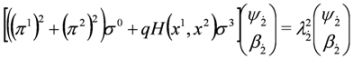
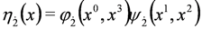
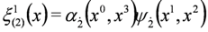
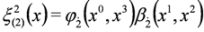
5. Splitting the Spin 0 Duffin–Kemmer–Petiau Equations in Crossed Fields
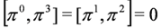
 and is fulfilled by crossed fields [10]:
and is fulfilled by crossed fields [10]: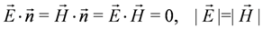
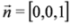 .
.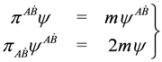
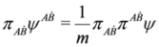 and
and 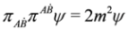 . We have
. We have  and the Klein–Gordon Equation
and the Klein–Gordon Equation 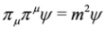 follows.
follows.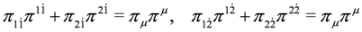

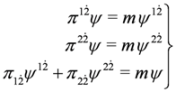
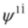 ,
,  or
or 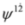 ,
, 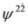 into the third equations). Equation (59) and the set of two Equations (61) and (62) are equivalent. We described Equations (61) and (62) in non-interacting case in [34,35]. Equations (61) and (62) and Equations (33) and (34) have the same structure (recall that
into the third equations). Equation (59) and the set of two Equations (61) and (62) are equivalent. We described Equations (61) and (62) in non-interacting case in [34,35]. Equations (61) and (62) and Equations (33) and (34) have the same structure (recall that 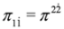 ,
,  ,
, 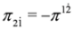 ,
,  ). However these equations cannot be written in the form of the Dirac Equations (35) and (36) because identities analogous to Equations (31) and (32) do not hold, i.e.,
). However these equations cannot be written in the form of the Dirac Equations (35) and (36) because identities analogous to Equations (31) and (32) do not hold, i.e., 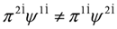 ,
, 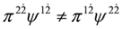 .
.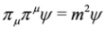 , which can be solved via separation of variables for the case of crossed fields, see Chapter 3 in [10] (the same can be done in Equation (62)).
, which can be solved via separation of variables for the case of crossed fields, see Chapter 3 in [10] (the same can be done in Equation (62)).6. A Supersymmetric Link between Dirac and DKP Theories
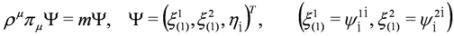
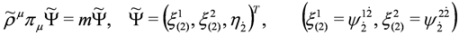
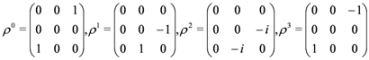



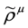 , cf. Equations (65) and (66), and πμ = pμ − qAμ, Aμ obeying condition Equation (57)—fulfilled by crossed fields.
, cf. Equations (65) and (66), and πμ = pμ − qAμ, Aμ obeying condition Equation (57)—fulfilled by crossed fields.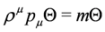
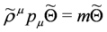
7. Discussion
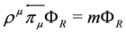
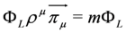
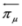 ,
,  mean action of
mean action of 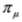 to the right or to the left, respectively (left solutions are actually used in the Dirac theory, where they are denoted as
to the right or to the left, respectively (left solutions are actually used in the Dirac theory, where they are denoted as 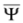 , they are however related to the right solutions by the formula
, they are however related to the right solutions by the formula 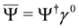 (symbol † denotes Hermitian conjugation) [11]).
(symbol † denotes Hermitian conjugation) [11]).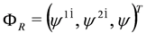 and
and  , are equivalent to Equations (61) and (62) respectively
, are equivalent to Equations (61) and (62) respectively 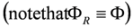 and involve components of the whole spinor
and involve components of the whole spinor 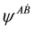 since
since 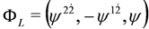 . The same analysis applies to Equation (68), i.e.,
. The same analysis applies to Equation (68), i.e., 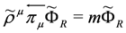 ,
, 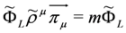 and
and 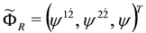 ,
, 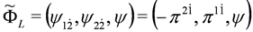 (note that
(note that  and
and 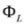 , as well as
, as well as 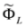 and
and 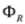 are algebraically related).
are algebraically related).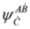 . We might consider left eigensolutions of the operator
. We might consider left eigensolutions of the operator 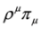 again but this does not change the picture—Equations (63) and (64) involve components
again but this does not change the picture—Equations (63) and (64) involve components  ,
, 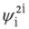 ,
, 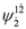 ,
,  only as well as the whole spinor
only as well as the whole spinor 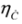 . It follows that in Equations (63) and (64) we deal with Lorentz symmetry breaking—a hypothetical phenomenon considered in some extensions of the Standard Model [37,38,39].
. It follows that in Equations (63) and (64) we deal with Lorentz symmetry breaking—a hypothetical phenomenon considered in some extensions of the Standard Model [37,38,39].References
- Jackiw, R.; Nair, V.P. Relativistic wave equation for anyons. Phys. Rev. D 1991, 43, 1933–1942. [Google Scholar] [CrossRef]
- Plyushchay, M. Fractional spin: Majorana-Dirac field. Phys. Lett. B 1991, 273, 250–254. [Google Scholar] [CrossRef]
- Horváthy, P.; Plyushchay, M.; Valenzuela, M. Bosons, fermions and anyons in the plane, and supersymmetry. Ann. Phys. 2010, 325, 1931–1975. [Google Scholar] [CrossRef]
- Horváthy, P.A.; Plyushchay, M.S.; Valenzuela, M. Supersymmetry between Jackiw–Nair and Dirac–Majorana anyons. Phys. Rev. D 2010, 81. [Google Scholar] [CrossRef]
- Horváthy, P.; Plyushchay, M.; Valenzuela, M. Supersymmetry of the planar Dirac–Deser–Jackiw–Templeton system and of its nonrelativistic limit. J. Math. Phys. 2010, 51. [Google Scholar] [CrossRef]
- Horváthy, P.; Plyushchay, M.; Valenzuela, M. Bosonized supersymmetry from the Majorana–Dirac–Staunton theory and massive higher-spin fields. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Simulik, V.; Krivsky, I. Bosonic symmetries of the massless Dirac equation. Adv. Appl. Clifford Algebr. 1998, 8, 69–82. [Google Scholar] [CrossRef]
- Simulik, V.; Krivsky, I. Bosonic symmetries of the Dirac equation. Phys. Lett. A 2011, 375, 2479–2483. [Google Scholar] [CrossRef]
- Okninski, A. Supersymmetric content of the Dirac and Duffin–Kemmer–Petiau equations. Int. J. Theor. Phys. 2011, 50, 729–736. [Google Scholar] [CrossRef]
- Bagrov, V.; Gitman, D. Exact Solutions of Relativistic Wave Equations; Springer: Berlin, Germany, 1990; Volume 39. [Google Scholar]
- Berestetskii, V.; Lifshitz, E.; Pitaevskii, V. Relativistic Quanturn Theory, Part 1; McGraw-Hill Science: New York, NY, USA, 1971. [Google Scholar]
- Misner, C.; Thorne, K.; Wheeler, J. Gravitation; WH Freeman Co.: New York, NY, USA, 1973. [Google Scholar]
- Corson, E. Theory of Tensors, Spinors, and Wave Equations; Blackie: London, UK, 1953. [Google Scholar]
- Dirac, P. The quantum theory of the electron. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Dirac, P. The quantum theory of the electron. Part II. Proc. R. Soc. Lond. Ser. A 1928, 118, 351–361. [Google Scholar] [CrossRef]
- Bjorken, J.; Drell, S. Relativistic Quantum Mechanics; McGraw-Hill: New York, NY, USA, 1964; Volume 3. [Google Scholar]
- Thaller, B. The Dirac Equation; Springer-Verlag: New York, NY, USA, 1992. [Google Scholar]
- Zralek, M. On the possibilities of distinguishing dirac from majorana neutrinos. Acta Phys. Pol. B 1997, 28, 2225–2257. [Google Scholar]
- Perkins, D. Introduction to High Energy Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Fukugita, M.; Yanagida, T. Physics of Neutrinos and Applications to Astrophysics; Springer Verlag: Berlin, Germany, 2003. [Google Scholar]
- Szafron, R.; Zralek, M. Can we distinguish dirac and majorana neutrinos produced in muon decay? Acta Phys. Pol. B 2009, 40, 3041–3047. [Google Scholar]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo Cimento (1924–1942) 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Feynman, R.; Gell-Mann, M. Theory of the Fermi interaction. Phys. Rev. 1958, 109, 193–198. [Google Scholar] [CrossRef]
- Horvathy, P.; Feher, L.; O’Raifeartaigh, L. Applications of chiral supersymmetry for spin fields in selfdual backgrounds. Int. J. Mod. Phys. 1989, A4, 5277–5285. [Google Scholar]
- Comtet, A.; Horvathy, P. The Dirac equation in Taub-NUT space. Phys. Lett. B 1995, 349, 49–56. [Google Scholar] [CrossRef]
- Duffin, R. On the characteristic matrices of covariant systems. Phys. Rev. 1938, 54. [Google Scholar] [CrossRef]
- Kemmer, N. The particle aspect of meson theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 173, 91–116. [Google Scholar] [CrossRef]
- Kemmer, N. The Algebra of Meson Matrices. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1943; 39, pp. 189–196. [Google Scholar]
- Petiau, G. Contribution a la théorie des équations d’ondes corpusculaires. Acad. R. Belg. Classe Sci. Mem. 1936, 16, 1–136. [Google Scholar]
- Proca, A. Wave theory of positive and negative electrons. J. Phys. Radium 1936, 7, 347–353. [Google Scholar] [CrossRef]
- Proca, A. Sur les equations fondamentales des particules elementaires. Comp. Ren. Acad. Sci. Paris 1936, 202, 1366–1368. [Google Scholar]
- Lanczos, C. Die erhaltungssätze in der feldmäßigen darstellung der diracschen theorie. Zeitschrift Phys. Hadron. Nuclei 1929, 57, 484–493. [Google Scholar]
- Bogush, A.; Kisel, V.; Tokarevskaya, N.; Red’kov, V. Duffin–Kemmer–Petiau formalism reexamined: Non-relativistic approximation for spin 0 and spin 1 particles in a Riemannian space-time. Ann. Fond. Louis Broglie 2007, 32, 355–381. [Google Scholar]
- Okninski, A. Effective quark equations. Acta Phys. Pol. B 1981, 12, 87–94. [Google Scholar]
- Okninski, A. Dynamic theory of quark and meson fields. Phys. Rev. D 1982, 25, 3402–3407. [Google Scholar] [CrossRef]
- Okninski, A. Splitting the Kemmer–Duffin–Petiau equations. Available online: http://arxiv.org/pdf/math-ph/0309013v1.pdf (accessed on 30 July 2012).
- Colladay, D.; Kostelecký, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760–6774. [Google Scholar]
- Visser, M. Lorentz symmetry breaking as a quantum field theory regulator. Phys. Rev. D 2009, 80. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Russell, N. Data tables for Lorentz and CPT violation. Rev. Mod. Phys. 2011, 83, 11–31. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Okniński, A. Duffin–Kemmer–Petiau and Dirac Equations—A Supersymmetric Connection. Symmetry 2012, 4, 427-440. https://doi.org/10.3390/sym4030427
Okniński A. Duffin–Kemmer–Petiau and Dirac Equations—A Supersymmetric Connection. Symmetry. 2012; 4(3):427-440. https://doi.org/10.3390/sym4030427
Chicago/Turabian StyleOkniński, Andrzej. 2012. "Duffin–Kemmer–Petiau and Dirac Equations—A Supersymmetric Connection" Symmetry 4, no. 3: 427-440. https://doi.org/10.3390/sym4030427



