Barrel Pseudotilings
Abstract
:1. Introduction
 . The subject of abstract polytopes and their realizations has developed greatly since and is still evolving (see, e.g., [7,8]).
. The subject of abstract polytopes and their realizations has developed greatly since and is still evolving (see, e.g., [7,8]). have received the most attention (e.g. [6,7], Section 7F of [8]), it still seems worthwhile to investigate other, less symmetrical, classes as well. The construction process connects the barrel pseudotilings to (partially) directed infinite graphs stemming from triangulations, many of which are visually appealing. It may be worth exploring these connections in the future.
have received the most attention (e.g. [6,7], Section 7F of [8]), it still seems worthwhile to investigate other, less symmetrical, classes as well. The construction process connects the barrel pseudotilings to (partially) directed infinite graphs stemming from triangulations, many of which are visually appealing. It may be worth exploring these connections in the future.2. A First Example
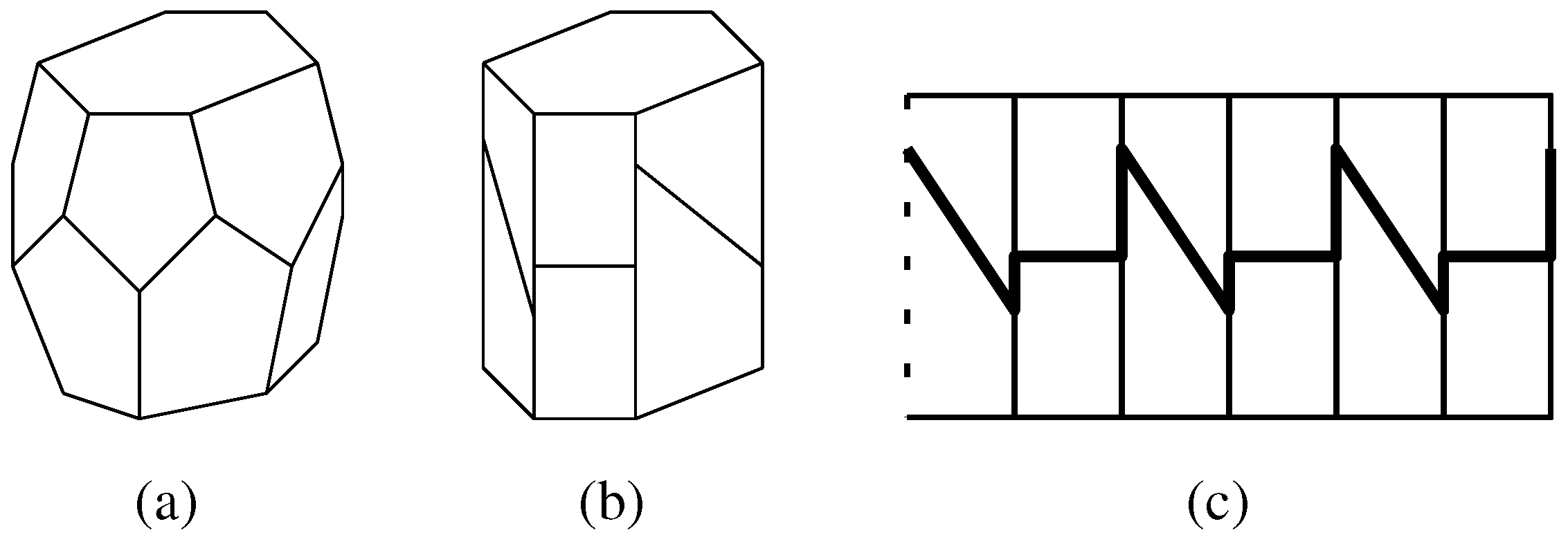
3. Basic Notions
3.1. Tilings and Barrel Polyhedra
 is a locally finite, countable collection of closed topological cells (tiles), which satisfy the following three conditions. First, each tile is a topological d-polytope, a homeomorphic image of a convex d-polytope. Second, the union of all tiles is
is a locally finite, countable collection of closed topological cells (tiles), which satisfy the following three conditions. First, each tile is a topological d-polytope, a homeomorphic image of a convex d-polytope. Second, the union of all tiles is  . Third, the intersection of any two distinct tiles is either empty or a proper face of each; in particular, if this intersection is a k-face of each tile, then it is a k-face of the tiling. In other places in the literature, such a tiling may be called face-to-face (compare [10,11]). A normal tiling is a tiling in which the tiles are uniformly bounded in size (i.e., each tile contains a d-ball of some small radius, and is contained in a d-ball of some larger radius). A tiling of
. Third, the intersection of any two distinct tiles is either empty or a proper face of each; in particular, if this intersection is a k-face of each tile, then it is a k-face of the tiling. In other places in the literature, such a tiling may be called face-to-face (compare [10,11]). A normal tiling is a tiling in which the tiles are uniformly bounded in size (i.e., each tile contains a d-ball of some small radius, and is contained in a d-ball of some larger radius). A tiling of  is simple if all vertices are (d + 1)-valent. However, this latter notion is only applicable when “vertices” and “edges” are well-defined, such as in the context of plane tilings or face-to-face tilings (for any d). The face poset of a (face-to-face) tiling, when amended by a unique largest and a unique smallest (empty) face, can be interpreted as an abstract polytope, see Section 3.4.
is simple if all vertices are (d + 1)-valent. However, this latter notion is only applicable when “vertices” and “edges” are well-defined, such as in the context of plane tilings or face-to-face tilings (for any d). The face poset of a (face-to-face) tiling, when amended by a unique largest and a unique smallest (empty) face, can be interpreted as an abstract polytope, see Section 3.4.3.2. Plane Graphs
3.3. Simplicial Complexes
3.4. Abstract Polytopes
 is a certain kind of graded poset of faces (including a unique smallest face of rank −1, and a unique largest face of rank n), with the partial order being incidence. The rank of a face corresponds to the notion of dimension for traditional polytopes (such as the convex polytopes), and so the traditional terms vertex and edge are used for the rank 0 and rank 1 faces, respectively. The poset
is a certain kind of graded poset of faces (including a unique smallest face of rank −1, and a unique largest face of rank n), with the partial order being incidence. The rank of a face corresponds to the notion of dimension for traditional polytopes (such as the convex polytopes), and so the traditional terms vertex and edge are used for the rank 0 and rank 1 faces, respectively. The poset  needs to satisfy the following two additional combinatorial properties taken from standard polytopes. First,
needs to satisfy the following two additional combinatorial properties taken from standard polytopes. First,  is strongly flag-connected, and second, if two incident faces F < G are exactly two ranks apart, then there exist precisely two faces H such that F < H < G (compare the definitions in [8], pp. 22–25).
is strongly flag-connected, and second, if two incident faces F < G are exactly two ranks apart, then there exist precisely two faces H such that F < H < G (compare the definitions in [8], pp. 22–25). is a graded poset defined for any two incident faces F ≤ G as {H ∈ P|F ≤ H ≤ G}, again with incidence as partial order. A flag is a maximal chain in a poset, and for graded posets of finite rank all flags have the same length (for example, all flags in
is a graded poset defined for any two incident faces F ≤ G as {H ∈ P|F ≤ H ≤ G}, again with incidence as partial order. A flag is a maximal chain in a poset, and for graded posets of finite rank all flags have the same length (for example, all flags in  have length n + 2).
have length n + 2).  is said to be strongly flag-connected if each section of
is said to be strongly flag-connected if each section of  (including
(including  itself) is flag-connected, that is, if each flag can be joined to any other flag (within the same section) via a sequence of flags, changing only one element (face) in the flag at a time.
itself) is flag-connected, that is, if each flag can be joined to any other flag (within the same section) via a sequence of flags, changing only one element (face) in the flag at a time. . For example, in an abstract 4-polytope (which is the kind of polytope that we will encounter in this article), the diamond condition stipulates the following:
. For example, in an abstract 4-polytope (which is the kind of polytope that we will encounter in this article), the diamond condition stipulates the following:- (1) Each edge is incident to precisely two vertices;
- (2) For each 2-face and each of its incident vertices, there are precisely two edges which are incident with both the 2-face and the vertex;
- (3) For each 3-face (facet) and each of its incident edges, there are precisely two 2-faces incident with both;
- (4) There are precisely two facets incident with each 2-face.
 is an injective mapping of its vertices into a suitable Euclidean space, along with a suitable interpretation of its combinatorial structure in the geometric setting. When considering realizations of abstract regular polytopes (see [6,7,8], Section 7F), one usually requires that the symmetry is retained, i.e., that the flag-transitive automorphism group of the abstract polytope carries over to a group of isometries which acts transitively on the flags of the realization. In this paper, however, we drop this requirement in order to obtain more realizations. To give an example of a realization of a 4-polytope that is not necessarily regular, any face-to-face, normal tiling of
is an injective mapping of its vertices into a suitable Euclidean space, along with a suitable interpretation of its combinatorial structure in the geometric setting. When considering realizations of abstract regular polytopes (see [6,7,8], Section 7F), one usually requires that the symmetry is retained, i.e., that the flag-transitive automorphism group of the abstract polytope carries over to a group of isometries which acts transitively on the flags of the realization. In this paper, however, we drop this requirement in order to obtain more realizations. To give an example of a realization of a 4-polytope that is not necessarily regular, any face-to-face, normal tiling of  is a realization of a so-called abstract 4-apeirotope (polytope containing either infinitely many finite faces, or infinite faces, or both).
is a realization of a so-called abstract 4-apeirotope (polytope containing either infinitely many finite faces, or infinite faces, or both).4. Definition of Barrel Pseudotilings
 with unit normal vector u = (0, 0, 1). A STACK OF APEIROPRISMS, or an ∞-PRISM STACK, Φ associated with D, is a doubly infinite right prism, or cylinder, Z = D +
with unit normal vector u = (0, 0, 1). A STACK OF APEIROPRISMS, or an ∞-PRISM STACK, Φ associated with D, is a doubly infinite right prism, or cylinder, Z = D +  together with a family
together with a family  = {A0,...,Ak−1} of k > 1 mutually non-intersecting apeirogons in ∂Z = ∂D +
= {A0,...,Ak−1} of k > 1 mutually non-intersecting apeirogons in ∂Z = ∂D +  (the mantle of the cylinder) with the following properties:
(the mantle of the cylinder) with the following properties: - (1)
is strictly monotone in the direction of u, meaning that every section of Z by a plane parallel to aff(D) meets every apeirogon in
in exactly one point;
- (2) Any two adjacent edges of an apeirogon in
lie in adjacent bounding walls of Z. Thus, each apeirogon A in
spirals around Z, in both directions, such that its vertices lie above the vertices of D;
- (3) For each i = 0,...,k − 1 and each x in Ai, we have x + ru ∈ Al for some l if and only if r ∈
; and in particular, x + ju ∈ Ai+j for each j ∈
, with subscripts taken modulo k. (Thus, more informally, the points directly above x on apeirogons occur at integer distances from x, with the apeirogons repeating periodically modulo ku.)
 are retained as edges of pentagons; each vertical edge (parallel to u) of the mantle is split into three edges by two new vertices, called PARTITION VERTICES, in its relative interior; and each parallelogram on the mantle Ai + [0, 1]u of an apeiroprism (for i = 0, 1,...,k − 1) is subdivided into two coplanar pentagon faces by a new edge that connects a pair of new vertices on opposite vertical edges of the parallelogram. These new edges are called PARTITION EDGES.
are retained as edges of pentagons; each vertical edge (parallel to u) of the mantle is split into three edges by two new vertices, called PARTITION VERTICES, in its relative interior; and each parallelogram on the mantle Ai + [0, 1]u of an apeiroprism (for i = 0, 1,...,k − 1) is subdivided into two coplanar pentagon faces by a new edge that connects a pair of new vertices on opposite vertical edges of the parallelogram. These new edges are called PARTITION EDGES. }, whose union fills the doubly infinite right prism (cylinder) Z = D +
}, whose union fills the doubly infinite right prism (cylinder) Z = D +  . A FINITE STACK is an n-stack for some finite n.
. A FINITE STACK is an n-stack for some finite n.  is a countable collection of vertical ∞-stacks and vertical finite stacks with the following two properties. First, the underlying family of doubly infinite prisms (cyclinders) gives a locally finite tiling of
is a countable collection of vertical ∞-stacks and vertical finite stacks with the following two properties. First, the underlying family of doubly infinite prisms (cyclinders) gives a locally finite tiling of  which, when cut by a horizontal plane, determines a locally finite, simple, face-to-face tiling in this plane. Second, any two barrels associated to distinct stacks in
which, when cut by a horizontal plane, determines a locally finite, simple, face-to-face tiling in this plane. Second, any two barrels associated to distinct stacks in  intersect, if at all, in a common finite face (vertex, edge, or pentagon). Note that the construction of the stacks implies that distinct barrels in the same finite stack also intersect either in a common face (finite polygon), or not at all.
intersect, if at all, in a common finite face (vertex, edge, or pentagon). Note that the construction of the stacks implies that distinct barrels in the same finite stack also intersect either in a common face (finite polygon), or not at all. . The finite barrels by themselves form a tessellation of a noncompact 3-manifold with infinitely many boundary components. In a way, the boundary components get sewn together by the stacks of apeirobarrels.
. The finite barrels by themselves form a tessellation of a noncompact 3-manifold with infinitely many boundary components. In a way, the boundary components get sewn together by the stacks of apeirobarrels. is a (non-regular) 4-apeirotope.
is a (non-regular) 4-apeirotope. is FACE-TO-FACE, in the sense that any two distinct barrels (finite or infinite) intersect, if at all, in a common face, precisely when each ∞-stack consists of at least three apeirobarrels.
is FACE-TO-FACE, in the sense that any two distinct barrels (finite or infinite) intersect, if at all, in a common face, precisely when each ∞-stack consists of at least three apeirobarrels.5. Outline of the Construction
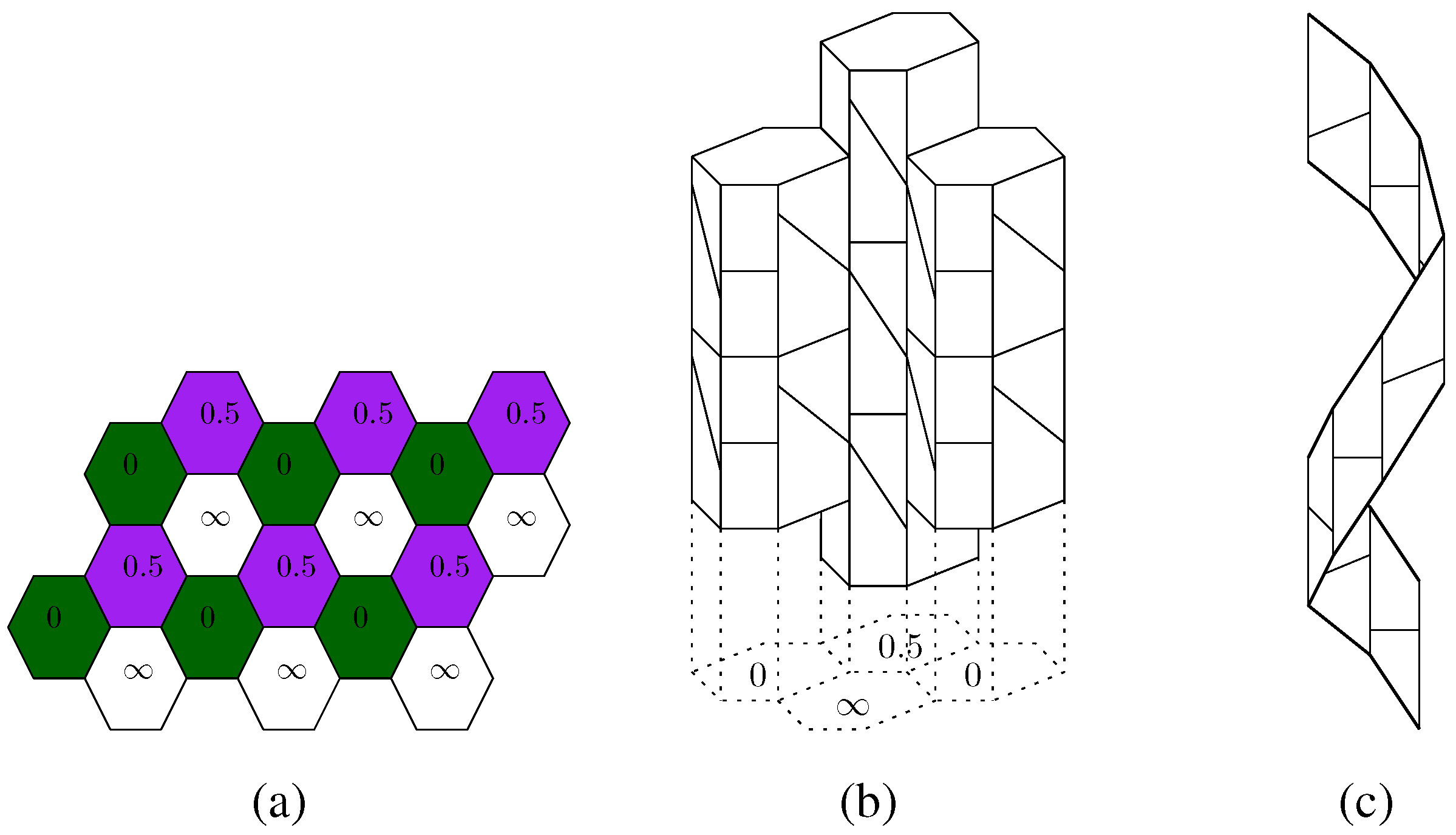
 by (convex, simple) polygons, situated in the horizontal plane through the origin of
by (convex, simple) polygons, situated in the horizontal plane through the origin of  , where the unit normal vector u = (0, 0, 1) denotes the direction “up”. All plane tilings mentioned in this paper are assumed to be of this type (recall that our definition of tiling includes the face-to-face property). We call
, where the unit normal vector u = (0, 0, 1) denotes the direction “up”. All plane tilings mentioned in this paper are assumed to be of this type (recall that our definition of tiling includes the face-to-face property). We call  a base tiling. The faces of
a base tiling. The faces of  will not (or not necessarily) be used in the completed barrel pseudotiling; rather, its tiles serve as guides for the infinite columns in
will not (or not necessarily) be used in the completed barrel pseudotiling; rather, its tiles serve as guides for the infinite columns in  which will extend in the directions ±u. Second, for each n-gonal tile (n ≥ 3) of
which will extend in the directions ±u. Second, for each n-gonal tile (n ≥ 3) of  assign either a color in [0, 1), or ∞, according as the associated column is to be used for a stack of finite barrels, or apeirobarrels. We obtain a coloring or shift function f : T (
assign either a color in [0, 1), or ∞, according as the associated column is to be used for a stack of finite barrels, or apeirobarrels. We obtain a coloring or shift function f : T (  ) → [0, 1) ∪ {∞}, where T (
) → [0, 1) ∪ {∞}, where T (  ) denotes the set of tiles of
) denotes the set of tiles of  . Third, for each finite-colored polygon P, let P +
. Third, for each finite-colored polygon P, let P +  be the underlying cylinder for a stack of right prisms, with the (disjoint) union of prism bases being P +
be the underlying cylinder for a stack of right prisms, with the (disjoint) union of prism bases being P +  .
.  by the amount α = f(P) in [0, 1) in the direction of u, as prescribed by the function f (i.e., shifting by (0,0,α)). The disjoint union of prism bases is now at P + (
by the amount α = f(P) in [0, 1) in the direction of u, as prescribed by the function f (i.e., shifting by (0,0,α)). The disjoint union of prism bases is now at P + (  + α)u. The aim of our construction is to obtain a new face structure on each prism, turning each n-prism into an n-barrel. This is done by respecting topological adjacencies, in fact, by taking the final facial structure of the constructed object (up to rank 2) to be completely determined by the topology.
+ α)u. The aim of our construction is to obtain a new face structure on each prism, turning each n-prism into an n-barrel. This is done by respecting topological adjacencies, in fact, by taking the final facial structure of the constructed object (up to rank 2) to be completely determined by the topology. ) by different amounts. Since
) by different amounts. Since  is locally finite and consists of countably many tiles, it is clearly possible to find a shift function with this property. However, we need to be more restrictive in order to assure that the partition edges and vertices produce only pentagons. Therefore, consider any tile in
is locally finite and consists of countably many tiles, it is clearly possible to find a shift function with this property. However, we need to be more restrictive in order to assure that the partition edges and vertices produce only pentagons. Therefore, consider any tile in  . When cyclically traversing the adjacent tiles in counterclockwise order, and listing the corresponding function values of f (which will be the shift lengths applied to the stacks of finite prisms), using asterisks ∗ as placeholders for tiles colored ∞, we will obtain a symbol like (∗,α0,α1,..., ∗,...). Let us call such a symbol a neighborhood symbol for the respective tile. A neighborhood symbol for a tile is not unique, since the neighbors can be traversed from different starting points, although we do adopt the convention to list the values of f in counterclockwise order around the tile. All neighborhood symbols for the same tile (using the same coloring function f) differ only by a cyclic permutation, so we need to keep in mind that the neighborhood symbol is a cyclic symbol.
. When cyclically traversing the adjacent tiles in counterclockwise order, and listing the corresponding function values of f (which will be the shift lengths applied to the stacks of finite prisms), using asterisks ∗ as placeholders for tiles colored ∞, we will obtain a symbol like (∗,α0,α1,..., ∗,...). Let us call such a symbol a neighborhood symbol for the respective tile. A neighborhood symbol for a tile is not unique, since the neighbors can be traversed from different starting points, although we do adopt the convention to list the values of f in counterclockwise order around the tile. All neighborhood symbols for the same tile (using the same coloring function f) differ only by a cyclic permutation, so we need to keep in mind that the neighborhood symbol is a cyclic symbol. perpendicular to an ∞-colored tile P of the plane tiling. Again, depending on earlier decisions, this may or may not be possible (recall that the condition in step four was only a necessary one). The next section investigates the conditions on f which must be satisfied so that the last two steps of the outline can be carried out.
perpendicular to an ∞-colored tile P of the plane tiling. Again, depending on earlier decisions, this may or may not be possible (recall that the condition in step four was only a necessary one). The next section investigates the conditions on f which must be satisfied so that the last two steps of the outline can be carried out.6. Barrel Pseudotilings with Isolated Apeirostacks
 as situated in the horizontal plane π through the origin of
as situated in the horizontal plane π through the origin of  , always looking at the plane tiling from “above”, where u = (0, 0, 1) denotes the direction “up”. Recall further that
, always looking at the plane tiling from “above”, where u = (0, 0, 1) denotes the direction “up”. Recall further that  functions as an aid in the construction of a barrel pseudotiling
functions as an aid in the construction of a barrel pseudotiling  , and that its faces (vertices, edges, tiles) need not be present in
, and that its faces (vertices, edges, tiles) need not be present in  .
.
 based on
based on  there is an associated upstairs orientation (clockwise or counterclockwise): This is the orientation in which the staircase in the mantle leads “upstairs”, if one were to step on the partition edges (treads), so this is either counterclockwise (up) or clockwise (up). For example, in Figure 1c we go upstairs from left to right, so if what is depicted corresponds to the unwrapped view of the mantle when walking around the outside of the barrel, then the upstairs orientation is counterclockwise. By contrast, remember that the winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards. Note here that, for apeirobarrels, the upstairs orientation does not generally correspond to the winding orientation, compare the examples of unwrapped apeirobarrels in Figure 3. However, in pseudotilings with only isolated ∞-stacks there is indeed such a correspondence, see Lemma 6.3. Before concentrating on pseudotilings with only isolated ∞-stacks, let us establish two general facts.
there is an associated upstairs orientation (clockwise or counterclockwise): This is the orientation in which the staircase in the mantle leads “upstairs”, if one were to step on the partition edges (treads), so this is either counterclockwise (up) or clockwise (up). For example, in Figure 1c we go upstairs from left to right, so if what is depicted corresponds to the unwrapped view of the mantle when walking around the outside of the barrel, then the upstairs orientation is counterclockwise. By contrast, remember that the winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards. Note here that, for apeirobarrels, the upstairs orientation does not generally correspond to the winding orientation, compare the examples of unwrapped apeirobarrels in Figure 3. However, in pseudotilings with only isolated ∞-stacks there is indeed such a correspondence, see Lemma 6.3. Before concentrating on pseudotilings with only isolated ∞-stacks, let us establish two general facts. have the same upstairs orientation. This is the GLOBAL UPSTAIRS ORIENTATION of
have the same upstairs orientation. This is the GLOBAL UPSTAIRS ORIENTATION of  .
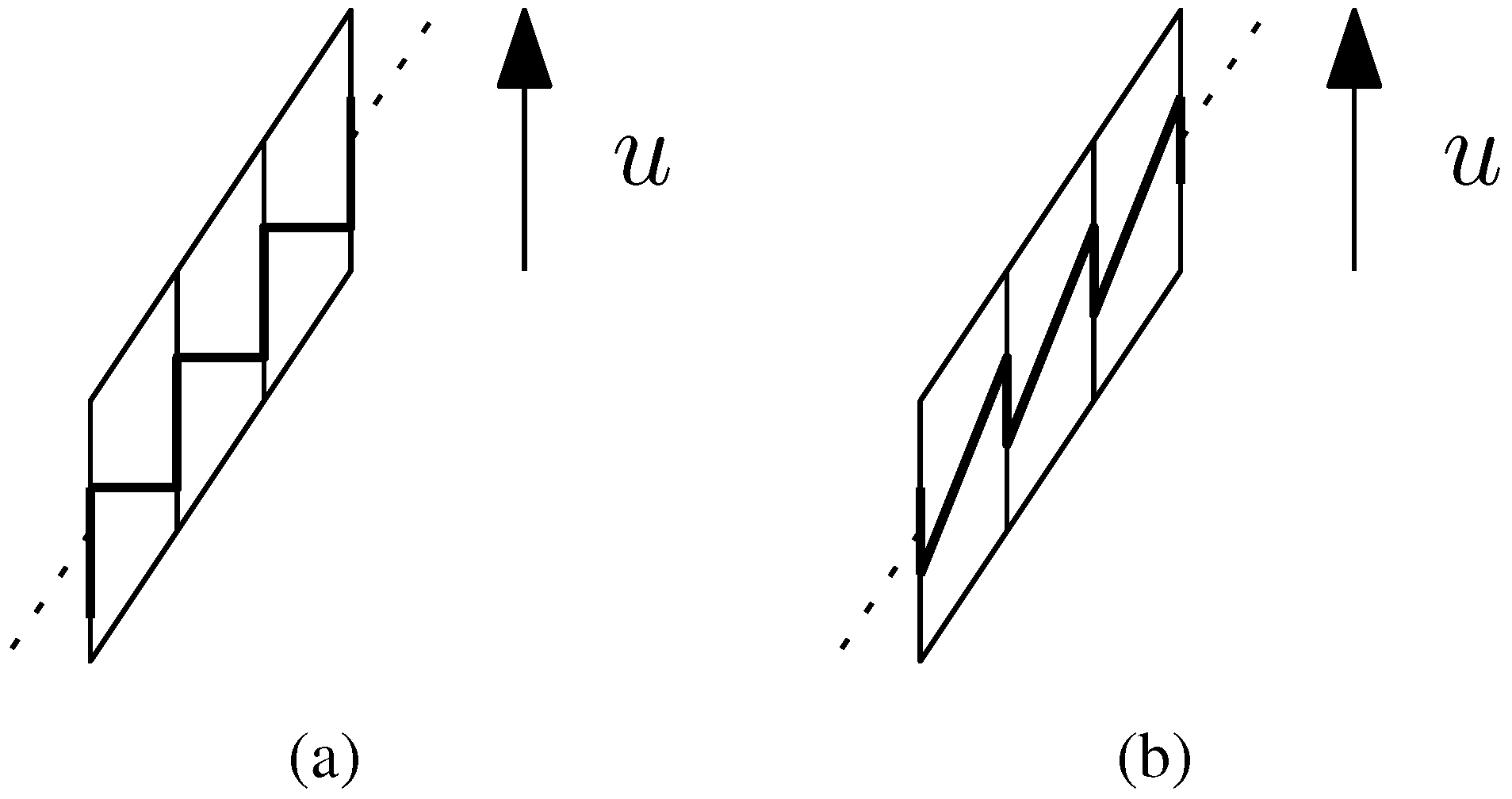
. in the plane π, and assume that tiles P1, P2, and P3 meet there as pictured in Figure 4 (in particular, (P1,P2,P3) is the listing of tiles in counterclockwise order around v). In the pseudotiling, v corresponds to a line v +
in the plane π, and assume that tiles P1, P2, and P3 meet there as pictured in Figure 4 (in particular, (P1,P2,P3) is the listing of tiles in counterclockwise order around v). In the pseudotiling, v corresponds to a line v +  perpendicular to the plane. We move upwards on this line (in direction u = (0, 0, 1)) starting at v, and we mark all vertices of the pseudotiling (note that v may not be one of them). In addition, we label a vertex on this line 1, 2, or 3, depending on whether the vertex in question is incident to a base of a (finite or infinite) barrel of the stack associated to P1, P2, or P3. We obtain a repeating pattern since translation by the vertical unit vector u is a built-in symmetry of the pseudotiling. If the repeating pattern is (1, 2, 3) (i.e., coherent with the right-hand rule), then the upstairs orientation of each barrel meeting a point on this line is counterclockwise, as can easily be seen. Otherwise, if the repeating pattern is (1, 3, 2), then the upstairs orientation of each barrel meeting a point of the line is clockwise. Moreover, if the upstairs orientation for barrels in one stack is set (e.g., in a construction process), then this determines the orientations for all barrels in adjacent stacks. These stacks, in turn, determine the orientations for all stacks adjacent to them, and so forth. Thus, the upstairs orientations of barrels must be globally compatible, i.e., the same.
perpendicular to the plane. We move upwards on this line (in direction u = (0, 0, 1)) starting at v, and we mark all vertices of the pseudotiling (note that v may not be one of them). In addition, we label a vertex on this line 1, 2, or 3, depending on whether the vertex in question is incident to a base of a (finite or infinite) barrel of the stack associated to P1, P2, or P3. We obtain a repeating pattern since translation by the vertical unit vector u is a built-in symmetry of the pseudotiling. If the repeating pattern is (1, 2, 3) (i.e., coherent with the right-hand rule), then the upstairs orientation of each barrel meeting a point on this line is counterclockwise, as can easily be seen. Otherwise, if the repeating pattern is (1, 3, 2), then the upstairs orientation of each barrel meeting a point of the line is clockwise. Moreover, if the upstairs orientation for barrels in one stack is set (e.g., in a construction process), then this determines the orientations for all barrels in adjacent stacks. These stacks, in turn, determine the orientations for all stacks adjacent to them, and so forth. Thus, the upstairs orientations of barrels must be globally compatible, i.e., the same.
 coherently with a particular global upstairs orientation automatically satisfies the necessary condition on the augmented neighborhood symbols for finite-colored tiles (see step four in Section 5). Thus, we have a new and more practical necessary condition on f.
coherently with a particular global upstairs orientation automatically satisfies the necessary condition on the augmented neighborhood symbols for finite-colored tiles (see step four in Section 5). Thus, we have a new and more practical necessary condition on f. , f) gives rise to a barrel pseudotiling in one upstairs orientation, then the same base tiling—with altered coloring—also gives rise to a barrel pseudotiling in the reverse upstairs orientation.
, f) gives rise to a barrel pseudotiling in one upstairs orientation, then the same base tiling—with altered coloring—also gives rise to a barrel pseudotiling in the reverse upstairs orientation. is given by:
is given by:

 with f(T) = ∞ and a neighborhood symbol (α0,α1,...,αn−1) with finite entries. Assume the global upstairs orientation is counterclockwise. An isolated ∞-stack Ω with k ≥ 2 distinct apeirogonal faces (spirals), which consequently consists of k distinct apeirogonal barrels, can be constructed over T if and only if we have αi > αi+1 for precisely k mutually distinct indices i (indices modulo n).
with f(T) = ∞ and a neighborhood symbol (α0,α1,...,αn−1) with finite entries. Assume the global upstairs orientation is counterclockwise. An isolated ∞-stack Ω with k ≥ 2 distinct apeirogonal faces (spirals), which consequently consists of k distinct apeirogonal barrels, can be constructed over T if and only if we have αi > αi+1 for precisely k mutually distinct indices i (indices modulo n). + 1. Only when the staircase reaches a step at a height of
+ 1. Only when the staircase reaches a step at a height of  + 1 or greater will there be a jump from a larger to a smaller entry in the neighborhood symbol. Subsequently, the next jump will occur when a height of
+ 1 or greater will there be a jump from a larger to a smaller entry in the neighborhood symbol. Subsequently, the next jump will occur when a height of  + 2 or greater is reached and so forth. Thus, if the staircase climbs k units when following the global upstairs orientation once around the stack, we obtain k jumps from an αi to a strictly smaller αi+1 in the neighborhood symbol.
+ 2 or greater is reached and so forth. Thus, if the staircase climbs k units when following the global upstairs orientation once around the stack, we obtain k jumps from an αi to a strictly smaller αi+1 in the neighborhood symbol. , f) of a base tiling and coloring (shift) function gives rise to a barrel pseudotiling with only isolated ∞-stacks.
, f) of a base tiling and coloring (shift) function gives rise to a barrel pseudotiling with only isolated ∞-stacks. , f) of a normal, simple, plane base tiling
, f) of a normal, simple, plane base tiling  and a coloring (shift) function
and a coloring (shift) function  ) → [0, 1) ∪ {∞} gives rise to a barrel pseudotiling with only isolated ∞-stacks and counterclockwise global upstairs orientation if and only if the following two conditions hold.
) → [0, 1) ∪ {∞} gives rise to a barrel pseudotiling with only isolated ∞-stacks and counterclockwise global upstairs orientation if and only if the following two conditions hold. - (1) For each vertex v of
where tiles P1, P2, P3 meet in counterclockwise order around v, such that their colors α1 = f(P1), α2 = f(P2), α3 = f(P3) are finite, and of which w.l.o.g. α1 is the smallest, the inequality α1 < α2 < α3 holds;
- (2) For each n-gonal tile P of
with f(P ) = ∞, all entries in a neighborhood symbol (α0,α1,...,αn−1) are finite, and there are at least two distinct indices i such that αi > αi+1 (indices taken modulo n).
7. Barrel Pseudotilings and Decorated Plane Triangulations
 with associated coloring of tiles, which gives rise to a barrel pseudotiling with isolated ∞-stacks, in terms of a (normal) dual triangulation
with associated coloring of tiles, which gives rise to a barrel pseudotiling with isolated ∞-stacks, in terms of a (normal) dual triangulation  . We do this not only for the sake of having dual statements, but also to draw connections to plane graphs (specifically, edge graphs of triangulations of the plane). Note that we do not make the assumption of convexity in the dual, since it is not generally known whether any tiling by convex polygons has a dual which also consists of convex polygons (cf. [10], p. 174).
. We do this not only for the sake of having dual statements, but also to draw connections to plane graphs (specifically, edge graphs of triangulations of the plane). Note that we do not make the assumption of convexity in the dual, since it is not generally known whether any tiling by convex polygons has a dual which also consists of convex polygons (cf. [10], p. 174). is a normal, simple, plane tiling by convex polygons with an appropriate coloring f on the tiles, which gives rise to a barrel pseudotiling with only isolated ∞-stacks in counterclockwise global upstairs orientation (as usual). Then let
is a normal, simple, plane tiling by convex polygons with an appropriate coloring f on the tiles, which gives rise to a barrel pseudotiling with only isolated ∞-stacks in counterclockwise global upstairs orientation (as usual). Then let  be a dual to
be a dual to  , which is a (normal, topological) triangulation of the plane with vertex set V (
, which is a (normal, topological) triangulation of the plane with vertex set V (  ). By slight abuse of notation we also denote the associated infinite geometric simplicial complex with
). By slight abuse of notation we also denote the associated infinite geometric simplicial complex with  . The vertices of
. The vertices of  inherit the coloring or shift function
inherit the coloring or shift function  : V = V (
: V = V (  ) → [0, 1) ∪ {∞} from the function f on the tiles of
) → [0, 1) ∪ {∞} from the function f on the tiles of  . This adds decoration to the triangulation, but we will also add further decoration by directing some of the edges. Let V0 = (
. This adds decoration to the triangulation, but we will also add further decoration by directing some of the edges. Let V0 = (  )−1 ([0, 1)) denote the set of vertices of
)−1 ([0, 1)) denote the set of vertices of  with finite value under
with finite value under  , and let
, and let  0 denote the simplicial subcomplex of
0 denote the simplicial subcomplex of  induced by V0 (it contains all simplices which have only vertices in V0, and the empty simplex).
induced by V0 (it contains all simplices which have only vertices in V0, and the empty simplex). (see [12] or Section 3 of this article for terminology).
(see [12] or Section 3 of this article for terminology).  0 contains no complete simplicial neighborhood of a vertex in
0 contains no complete simplicial neighborhood of a vertex in  , i.e., there are no vertices of
, i.e., there are no vertices of  0 which lie in its interior (we do not use the term relative interior here because
0 which lie in its interior (we do not use the term relative interior here because  0 may be a one-dimensional subcomplex of
0 may be a one-dimensional subcomplex of  ). We have:
). We have: 0| of
0| of  0 is (path-)connected. In fact, |
0 is (path-)connected. In fact, |  0| is obtained from
0| is obtained from  by deleting the mutually disjoint open discs given by the open stars of the vertices in V∞ .
by deleting the mutually disjoint open discs given by the open stars of the vertices in V∞ . naturally induces directions on the edges in
naturally induces directions on the edges in  0, where {x, y} turns into the directed edge, or arc, (x, y) with tail x and head y if
0, where {x, y} turns into the directed edge, or arc, (x, y) with tail x and head y if  (x) <
(x) <  (y) (these values are finite, by definition of
(y) (these values are finite, by definition of  0). Furthermore, every arc is oriented in mathematically positive or negative direction with respect to an incident triangle, depending on whether it runs counterclockwise or clockwise around a point in the triangle’s interior. Since the global upstairs orientation is assumed as mathematically positive (for the pseudotiling based on
0). Furthermore, every arc is oriented in mathematically positive or negative direction with respect to an incident triangle, depending on whether it runs counterclockwise or clockwise around a point in the triangle’s interior. Since the global upstairs orientation is assumed as mathematically positive (for the pseudotiling based on  ), Remark 6.1 implies that every triangle in
), Remark 6.1 implies that every triangle in  0 has two mathematically positive and one mathematically negative oriented arcs. Note that the resulting directed edge graph of
0 has two mathematically positive and one mathematically negative oriented arcs. Note that the resulting directed edge graph of  0, which we denote by
0, which we denote by  , must not have directed cycles, as the value of
, must not have directed cycles, as the value of  increases for successive vertices along directed paths.
increases for successive vertices along directed paths. 0.
0.
 0 such that the underlying topological space
0 such that the underlying topological space  of its link in
of its link in  0 is disconnected. A vertex of
0 is disconnected. A vertex of  0 which is not a cut-vertex is called a regular vertex. Note that the simplicial neighborhood
0 which is not a cut-vertex is called a regular vertex. Note that the simplicial neighborhood  of any regular vertex x in
of any regular vertex x in  0 has as underlying topological space a closed disc whose boundary is a simple cycle containing x (as x cannot be an interior vertex). With directed arcs, there are three types of neighborhoods for regular vertices x, see Figure 6, as classified by the digraph of edges in that neighborhood (closed star), denoted
0 has as underlying topological space a closed disc whose boundary is a simple cycle containing x (as x cannot be an interior vertex). With directed arcs, there are three types of neighborhoods for regular vertices x, see Figure 6, as classified by the digraph of edges in that neighborhood (closed star), denoted  :
: - • x is the tail of all incident arcs, i.e., a source in
. In this case, x is the only source in
. The boundary cycle has a single edge, (x, z), which is oriented negatively (with respect to (wrt) an interior point of the neighborhood), and z is the only sink in
;
- • x is the head of all incident arcs, i.e., a sink in
. In this case, x is the only sink in
, the boundary cycle of
has a single edge, (y, x), which is oriented negatively, and y is the only source in
;
- • x is neither a source nor a sink in
. In this case, x is incident to a unique triangle yxz (labelled counterclockwise) for which it is a transition vertex, that is x is the head of (y, x) and the tail of (x, z) . The only source and sink in
are y and z, respectively. The boundary cycle of
has a single negatively oriented edge, (y, z).
 0 triangle-connected if there is a finite sequence s = t0,t1,...,tn = t of triangles in
0 triangle-connected if there is a finite sequence s = t0,t1,...,tn = t of triangles in  0, such that for i =1,...,n the triangles ti−1 and ti are adjacent (i.e., they share an edge). We call a simplicial subcomplex of
0, such that for i =1,...,n the triangles ti−1 and ti are adjacent (i.e., they share an edge). We call a simplicial subcomplex of  0 induced by a set of mutually triangle-connected triangles of
0 induced by a set of mutually triangle-connected triangles of  0 a triangle component. By definition, the underlying topological space of any triangle component is connected. However, we can also prove the following:
0 a triangle component. By definition, the underlying topological space of any triangle component is connected. However, we can also prove the following: 0, then its underlying topological space |S| is simply connected. In particular, for finite triangle components S, the space |S| is a closed disc.
0, then its underlying topological space |S| is simply connected. In particular, for finite triangle components S, the space |S| is a closed disc.- • The new triangle is glued on at a single positive boundary arc only. In this case this positive boundary arc (which now is no longer on the boundary) is replaced by two positive boundary arcs in Sk+1, and Sk+1 retains exactly one negative arc on its boundary;
- • The new triangle is glued on at a single negative boundary arc only. In this case this negative boundary arc is replaced by a positive and a negative boundary arc in Sk+1, and Sk+1 still has exactly one negative arc on its boundary;
- • The new triangle is glued to two boundary arcs. Since by the induction hypothesis there is only one negative arc in the boundary of Sk, and the new triangle cannot be glued to two previously positive arcs (because they would have to match up with two negative arcs in the triangle), exactly one of those arcs must be positive, and one must be negative. These boundary arcs are replaced by a single positive boundary arc, leading to Sk+1 having only positive arcs in its boundary. This is impossible because it would lead to an oriented cycle in the boundary, i.e., to cyclically ever increasing values of
on the traversed vertices;
- • The new triangle is glued to three boundary arcs. This is also impossible, because as in the previous case, two positive and one negative arc would be removed from the boundary, leading to an oriented cycle in the boundary;
- • The new triangle is glued on at a single positive (negative) boundary arc, and its third vertex is also glued. However, then the new boundary would (topologically) not be a simple closed curve, as four boundary arcs meet at that (glued) vertex, creating more than one cycle (regardless of edge direction) in the boundary. As there is still only one negatively oriented arc, this would lead to an oriented cycle in the boundary, which is forbidden.
 , but in terms of directed and undirected edges. This seems easier to handle in any kind of construction attempt, as the images in the next section show.
, but in terms of directed and undirected edges. This seems easier to handle in any kind of construction attempt, as the images in the next section show. of
of  by convex polygons gives rise to a barrel pseudotiling with isolated ∞-stacks and counterclockwise upstairs orientation if and only if some edges of the (any) dual triangulation
by convex polygons gives rise to a barrel pseudotiling with isolated ∞-stacks and counterclockwise upstairs orientation if and only if some edges of the (any) dual triangulation  can be directed such that the following conditions are all satisfied:
can be directed such that the following conditions are all satisfied:- (1) The set of vertices which are only incident to UNDIRECTED edges, denoted V∞, is a dominating independent set in the edge graph G(
);
- (2) For each x in V∞, the boundary of
has at least two directed arcs going in CLOCKWISE ORIENTATION around an interior point;
- (3) Each triangle in
which has all its boundary edges oriented contains precisely one clockwise arc and two counterclockwise arcs.
 0 has, when edges are directed, exactly one arc on its boundary which is negatively oriented with respect to an interior point. It is not entirely obvious, and therefore remarkable, that conditions (1), (2), (3) prevent directed cycles in the partially directed edge graph of
0 has, when edges are directed, exactly one arc on its boundary which is negatively oriented with respect to an interior point. It is not entirely obvious, and therefore remarkable, that conditions (1), (2), (3) prevent directed cycles in the partially directed edge graph of  (note that a directed cycle should not contain undirected edges).
(note that a directed cycle should not contain undirected edges). 8. A Small Zoo of Examples
 indicate ∞-colored vertices, and arrows indicate an increase in the function
indicate ∞-colored vertices, and arrows indicate an increase in the function  . Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
. Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
 indicate ∞-colored vertices, and arrows indicate an increase in the function
indicate ∞-colored vertices, and arrows indicate an increase in the function  . Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
. Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.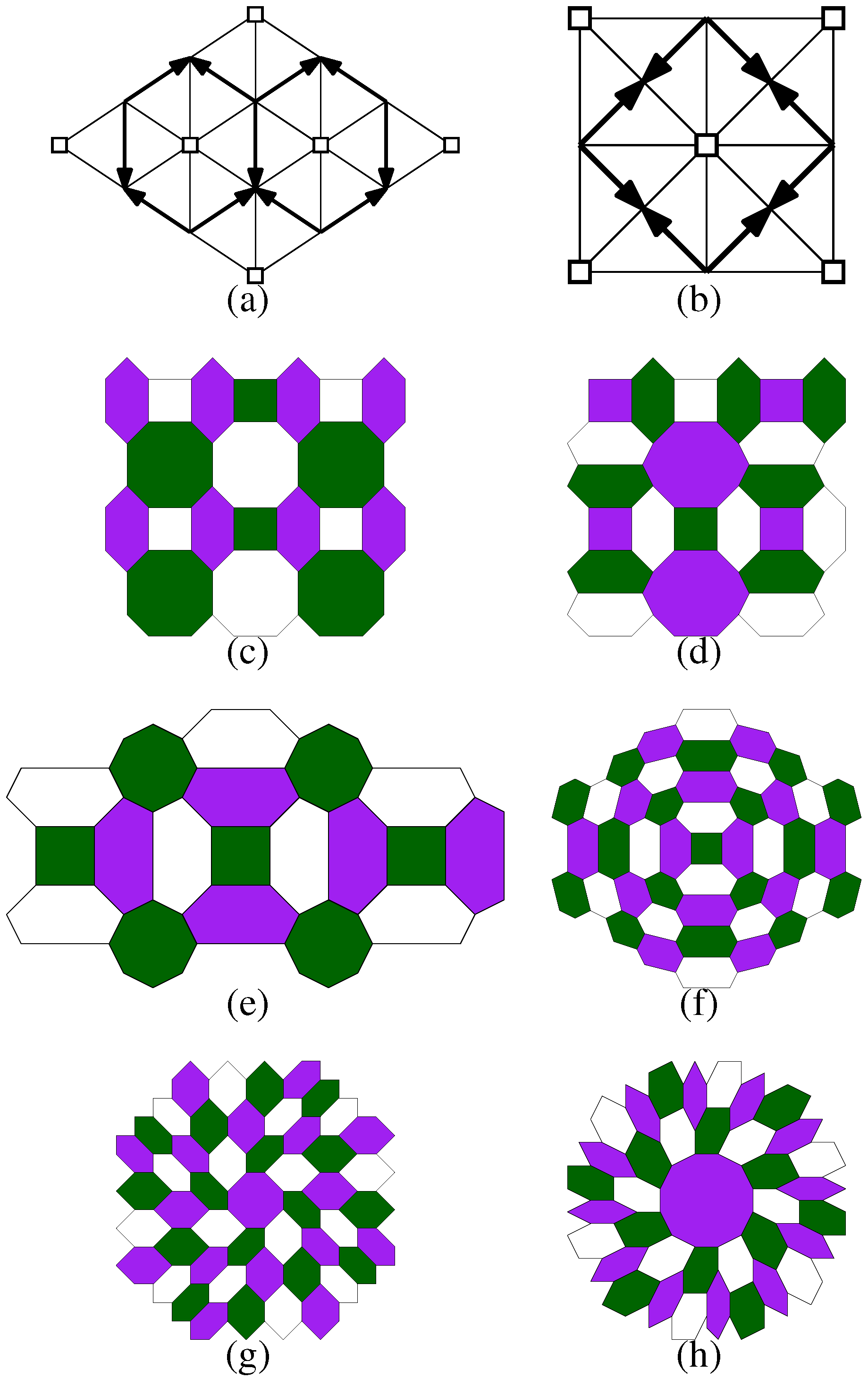
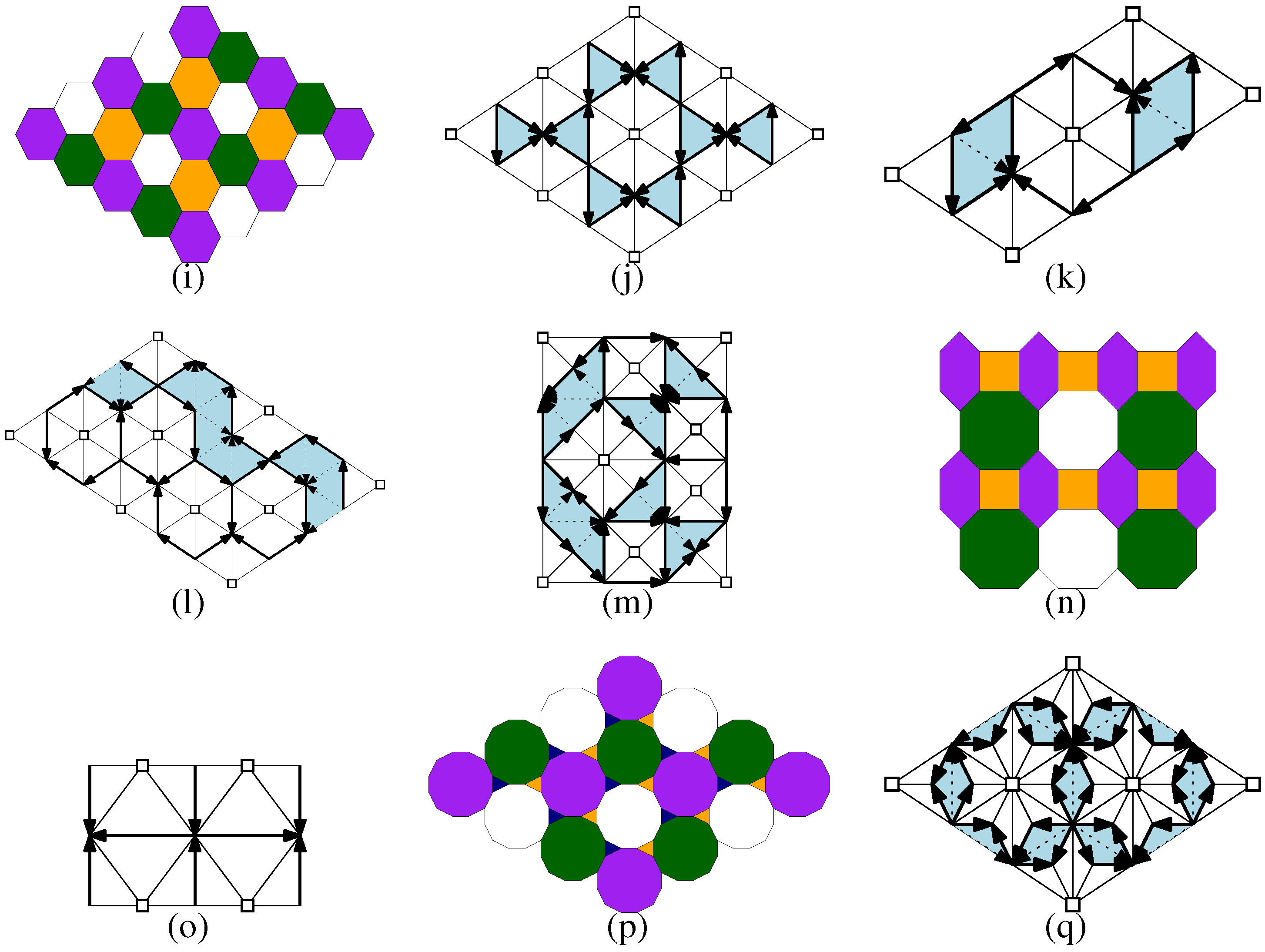
9. Remarks
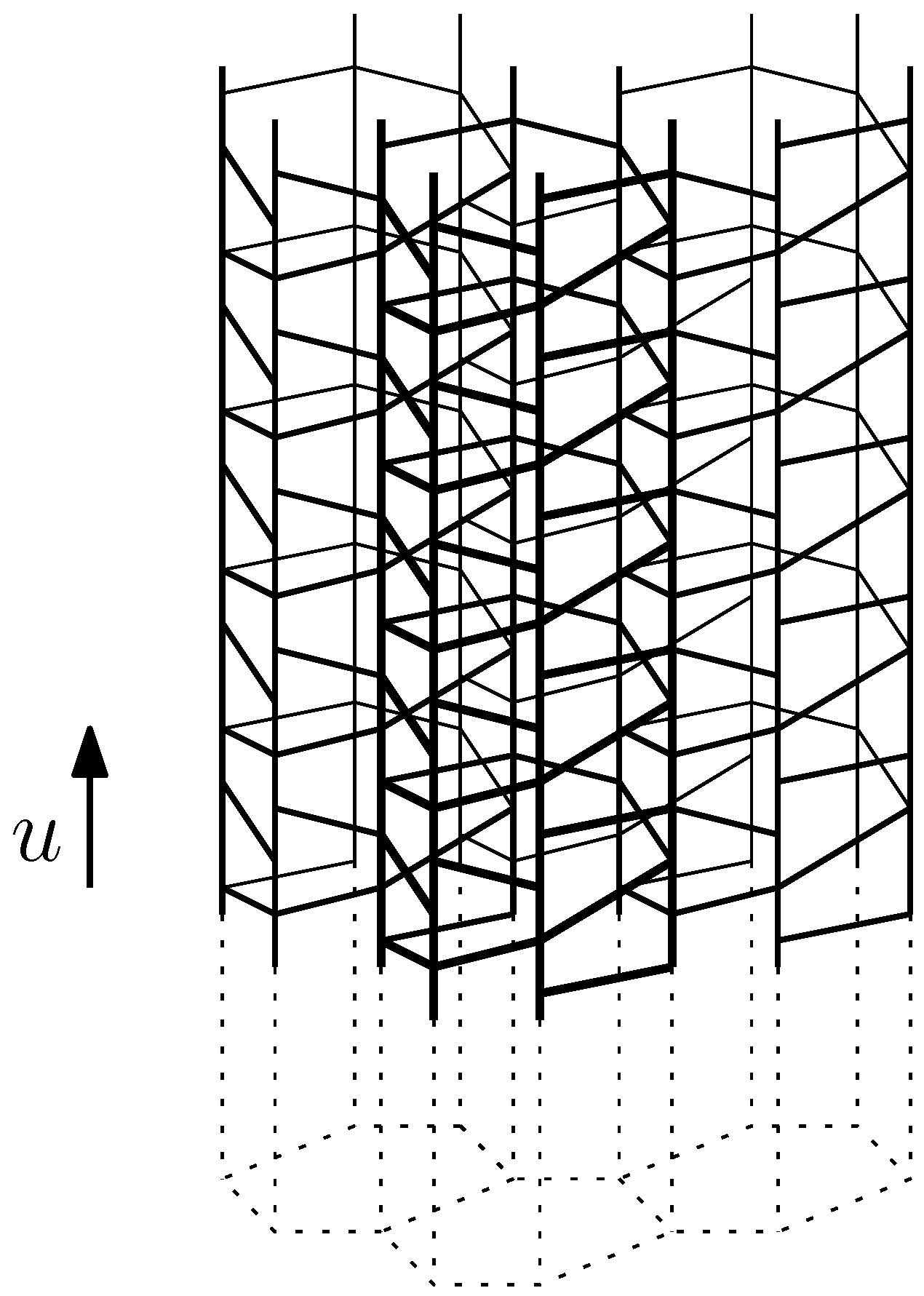
 , but perhaps it would still produce interesting results. Finally, it should be possible to quotient by a multiple of u in order to produce and study finite objects.
, but perhaps it would still produce interesting results. Finally, it should be possible to quotient by a multiple of u in order to produce and study finite objects.Acknowledgments
References and Notes
- Grünbaum, B. Regular polyhedra—old and new. Aequ. Math. 1977, 16, 1–20. [Google Scholar] [CrossRef]
- Schulte, E. Symmetry of polytopes and polyhedra. In Handbook of Discrete and Computational Geometry, 2nd; Goodman, J.E., O’Rourke, J., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; pp. 431–454. [Google Scholar]
- Dress, A.W.M. A combinatorial theory of Grünbaum’s new regular polyhedra, Part I: Günbaums’s new regular polyhedra and their automorphism group. Aequ. Math. 1981, 23, 252–265. [Google Scholar] [CrossRef]
- Dress, A.W.M. A combinatorial theory of Grünbaums’s new regular polyhedra, Part II: Complete enumeration. Aequ. Math. 1985, 29, 222–243. [Google Scholar] [CrossRef]
- Leytem, C. Pseudo-Petrie operators on Grünbaumpolyhedra. Math. Slovaca 1997, 47, 175–188. [Google Scholar]
- McMullen, P.; Schulte, E. Regular polytopes in ordinary space. Discrete Comput. Geom. 1997, 17, 449–478. [Google Scholar] [CrossRef]
- McMullen, P.; Schulte, E. Regular and chiralpolytopes in low dimensions. In The Coxeter Legacy: Reflections and Projections; Davis, C., Ellers, E.W., Eds.; AMS: Providence, RI, USA, 2005; pp. 87–106. [Google Scholar]
- McMullen, P.; Schulte, E. Abstract Regular Polytopes (Encyclopedia of Mathematics and its Applications); Cambridge University Press: Cambridge, UK, 2002; Volume 92. [Google Scholar]
- Grünbaum, B.; Shephard, G.C.; Miller, J.C.P. Uniform tilings with hollow tiles. In The Geometric Vein: The Coxeter Festschrift; Davis, C., Grünbaum, B., Sherk, F.A., Eds.; Springer: New York, NY, USA, 1981; pp. 17–64. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilingsand Patterns; W.H. Freeman and Company: New York, NY, USA, 1987. [Google Scholar]
- Schattschneider, D.; Senechal, D. Tilings. In Handbook of Discrete and Computational Geometry, 2nd; Goodman, J.E., O’Rourke, J., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; pp. 53–72. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Maunder, C.R.F. Algebraic Topology; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Locher, J.L. The Magic of M.C. Escher; Harry N. Abrams: New York, NY, USA, 2000. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Leopold, U. Barrel Pseudotilings. Symmetry 2012, 4, 545-565. https://doi.org/10.3390/sym4030545
Leopold U. Barrel Pseudotilings. Symmetry. 2012; 4(3):545-565. https://doi.org/10.3390/sym4030545
Chicago/Turabian StyleLeopold, Undine. 2012. "Barrel Pseudotilings" Symmetry 4, no. 3: 545-565. https://doi.org/10.3390/sym4030545




