1. Introduction
In this paper, we introduce the concept of pair-wise domination for hypergraphs endowed with a choice function on edges. A hypergraph is a pair
, where
is a set of
n vertices (or nodes) and
is a set of
m non-empty subsets of
V called hyperedges or edges (see for instance [
1]). A
k-hypertournament is a complete
k-hypergraph
(i.e.,
E consists of all the
possible
k-subsets), with each
k-edge endowed with an orientation. Here we are interested in hypergraphs where each edge,
e, has a chosen element
(in place of a complete orientation). We will refer to the pair
as a (complete)
k-hypergraph with choice (or an
choice-hypergraph). For various considerations of choice functions, see for instance [
2,
3]. For some recent work related to choice in the context of Cayley graphs, see [
4].
In the case
, both
k-hypertournaments and hypergraphs with choice reduce to standard tournaments. For discussion of tournaments, see for instance [
5,
6,
7]. The following is an example of a standard tournament with
vertices.
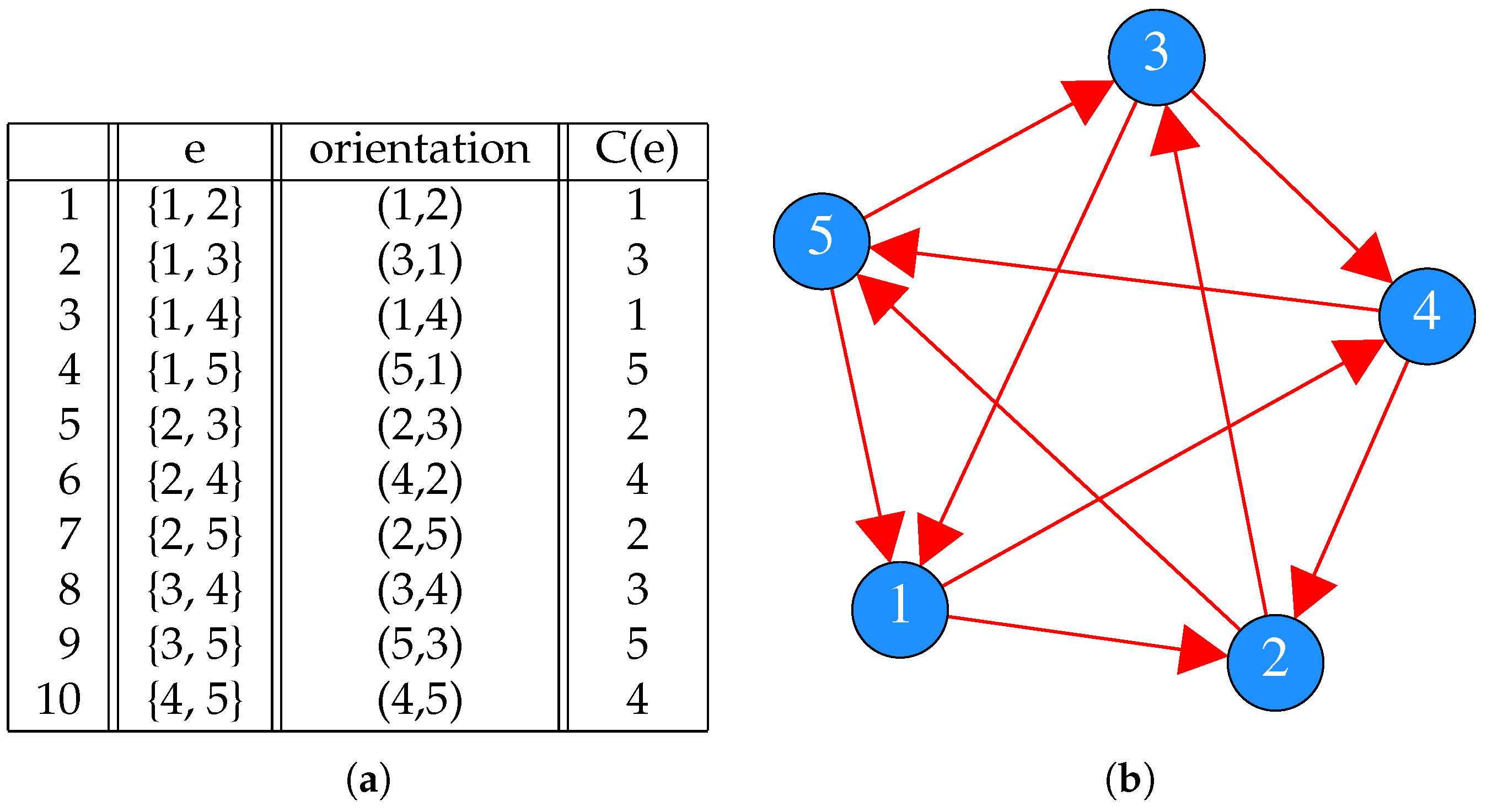
Example 1. Consider the complete 2-hypertournament with five nodes and ten edges, depicted via the table in Figure 1a. Here, for instance, vertex 1 is chosen in the presence of vertices 2 and 4 (the first and third lines in the table). In fact, in this particular instance, each vertex is chosen for exactly two of the edges. Figure 1b gives a graphical display with a directed edge from vertex v to vertex w whenever vertex v is chosen in the presence of w. In the next example, we consider a complete 3-hypergraph with choice.
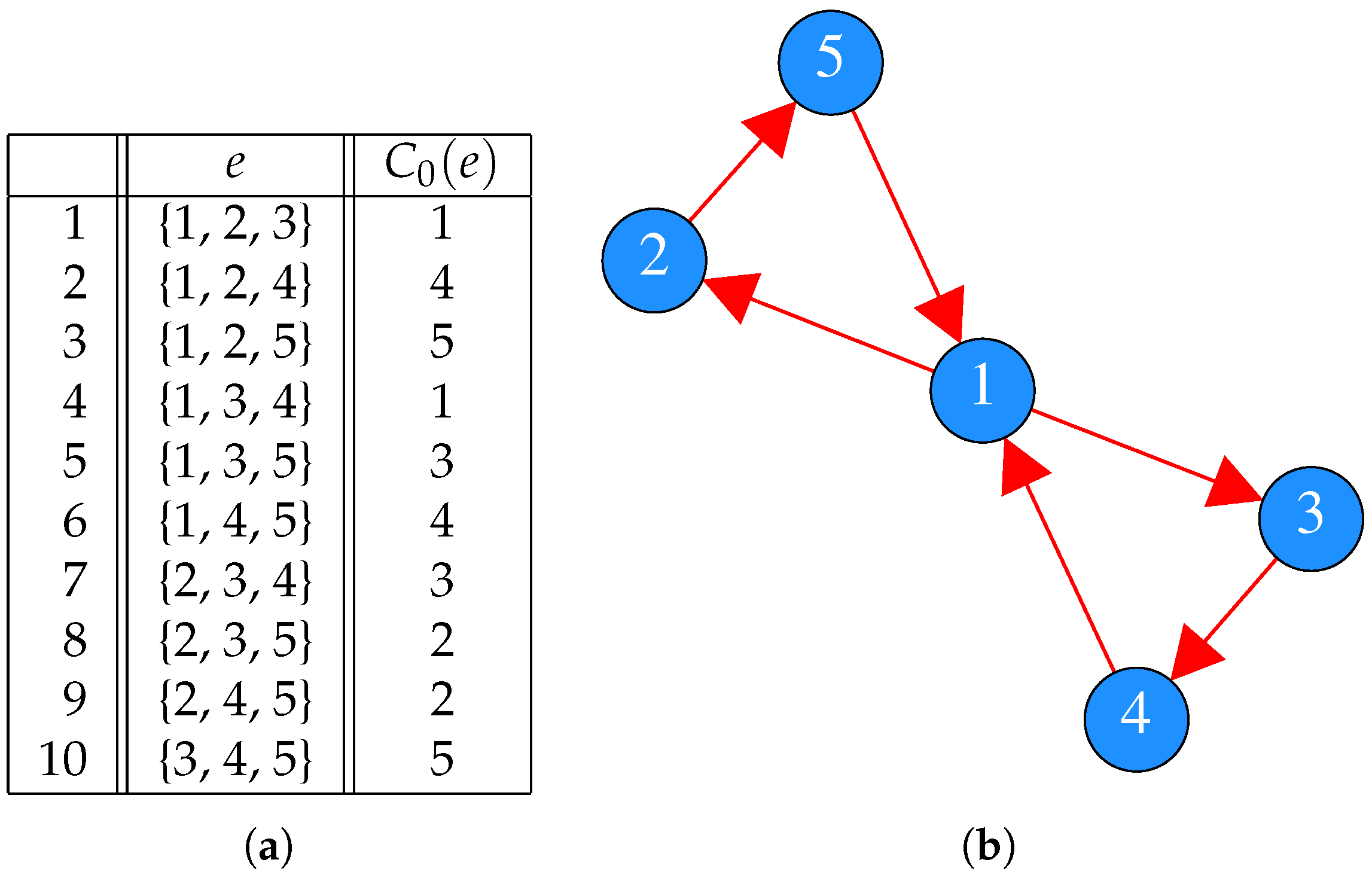
Example 2. Consider the complete 3-hypergraph with choice with five vertices and 10 edges, depicted in the table in Figure 2a. Here, vertex 1 is chosen once in the presence of vertices 2 and 4 (for edges and , respectively), twice in the presence of vertex 3 (again edges and ) and never in the presence of vertex 5. Note that again, as in Example 1, each node is chosen in the case of exactly two edges. In considering possible analogues to Figure 1b, summarizing domination, one might include a directed edge from vertex v to vertex w, if and only if, for edges that include both v and w, the tally of wins for v exceeds that of w. The resulting graph is depicted in Figure 2b. Note that there is a directed edge from vertex 1 to vertex 2, since vertex 1 is chosen for edge , while there is no edge, e, where vertex 2 is chosen when . It may be noted that in this case the associated graph is path connected. Now, define the function
via:
i.e.,
is the number of edges for which
v is chosen in the presence of
w.
Example 2 leads to consideration of potential appropriate graphs on n vertices reflecting domination properties among vertices. Here, we mention three possibilities.
- (i)
There is a directed edge from vertex
v to vertex
w if:
i.e., if vertex
w is never chosen in the presence of vertex
v.
- (ii)
There is a directed edge from vertex
v to vertex
w if:
i.e., among the edges containing both
v and
w,
v is chosen with greater frequency.
- (iii)
There is a directed edge from vertex
v to vertex
w if:
i.e.,
v is chosen for a majority of the edges containing both
v and
w.
We will restrict attention henceforth to Option (ii), above, unless stated otherwise. It should be noted that for a standard tournament graph (i.e.,
) all three formulations are equivalent; furthermore, Option (iii) is a stricter requirement than Option (ii). For discussion of ranking for vertices in hypertournaments, see for instance [
8].
We refer to graphs as in
Figure 2b and
Figure 3 (below) as
-
choice-domination graphs or simply
-domination graphs. When
n and
k are clear from context, we will at times simply refer to these as domination graphs. As with tournaments, domination graphs could be valuable in considerations of individual dominance in competitive settings, as may arise for instance in biology, game theory or decision analysis. Note that hypergraphs with choice allow for analysis of scenarios wherein selection (but not full orientation) information is available.
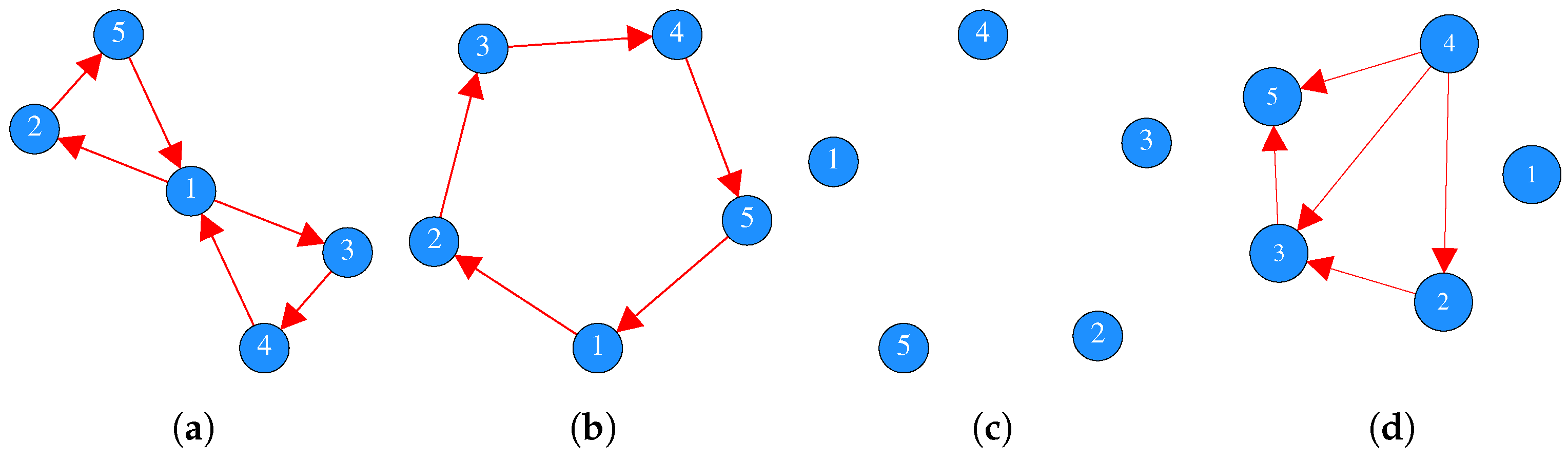
Example 3. Table 1 gives a 3-hypergraph with vertices and edges, along with four possible choice functions, (from Example 2), , and on E, while Figure 3 includes the associated domination graphs, for comparison. For fixed
n and
k, many natural questions arise as to the properties of the resulting domination graphs; for instance:
What are the maximal and minimal number of edges possible for an -domination graph?
What proportion of
-domination graphs are strongly path connected (for example,
Figure 3a,b?
What is the distribution of the number of edges in the domination graph for a uniformly selected choice function on the edges of a k-hypergraph on n vertices?
What is the number of non-isomorphic -domination graphs?
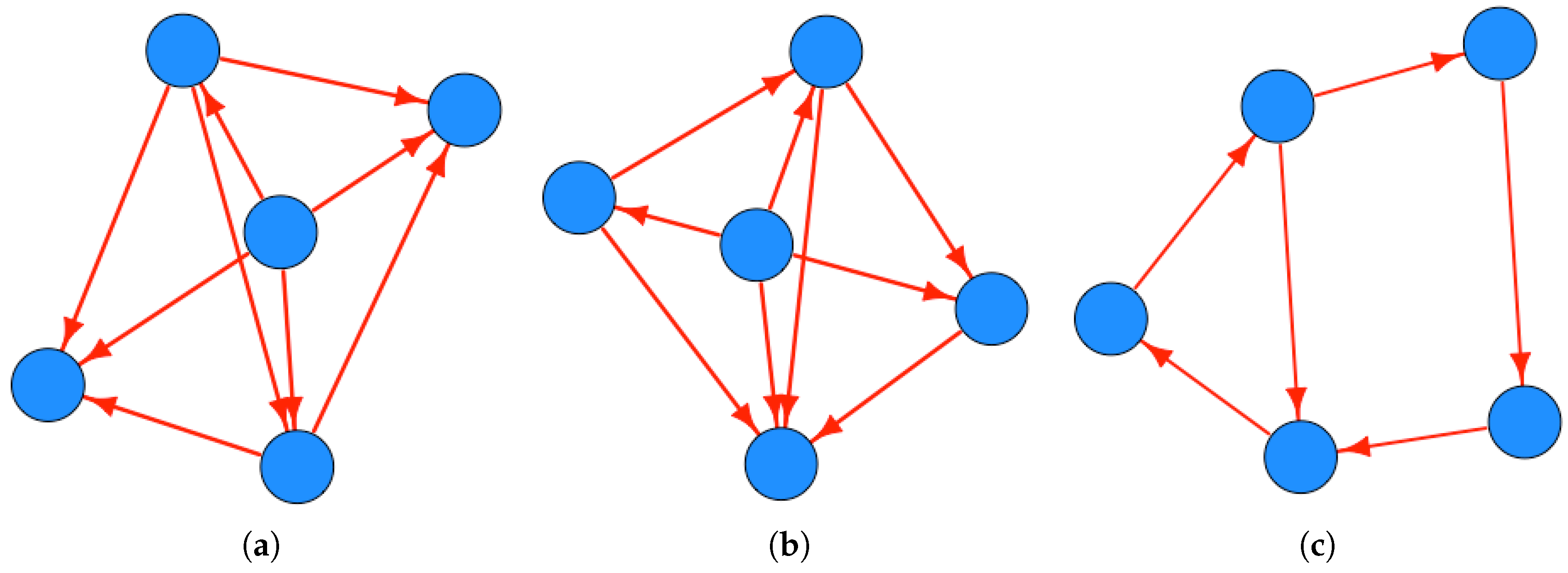
Example 4. ( domination graphs.) For , we have that and the number of distinct choice functions on E is . Table 2 and Table 3 give frequency tables for the number of choice functions leading to domination graphs with a given number of edges, and a given number of strongly connected components, respectively. Note that 3348 choice functions result in strongly connected domination graphs. There are 225 non-isomorphic -domination graphs (of which 21 are strongly connected); plots of these are provided in the Supplementary Materials; Table 4 gives the frequencies for these graphs. The two most frequent domination graphs (each occurring for 1560 distinct choice functions, C), are given in Figure 4a,b respectively; the most frequently occurring strongly connected domination graph is given in Figure 4c. In reference to Question 1 above, in
Section 2 below, we will prove the following two results.
Theorem 1. Suppose and is a complete k-hypergraph on n vertices. If k is odd and , then there exists a choice function, C, on E resulting in a zero-edge domination graph.
Theorem 2. If is a choice-hypergraph with a zero-edge domination graph, then for all :that is, each vertex is chosen for an equal number of edges, in E. The question of minimal edges in associated domination graphs may be of interest in instances where notions of “fairness” and equitable distribution are of importance, such as in resource allocation, decision theory, data and network processing, and clinical trials. Fairness and choice have been considered in the past, notably in the context of social welfare and information processing. The interested reader might like to consult, for instance [
2,
3,
4,
9,
10,
11,
12,
13].
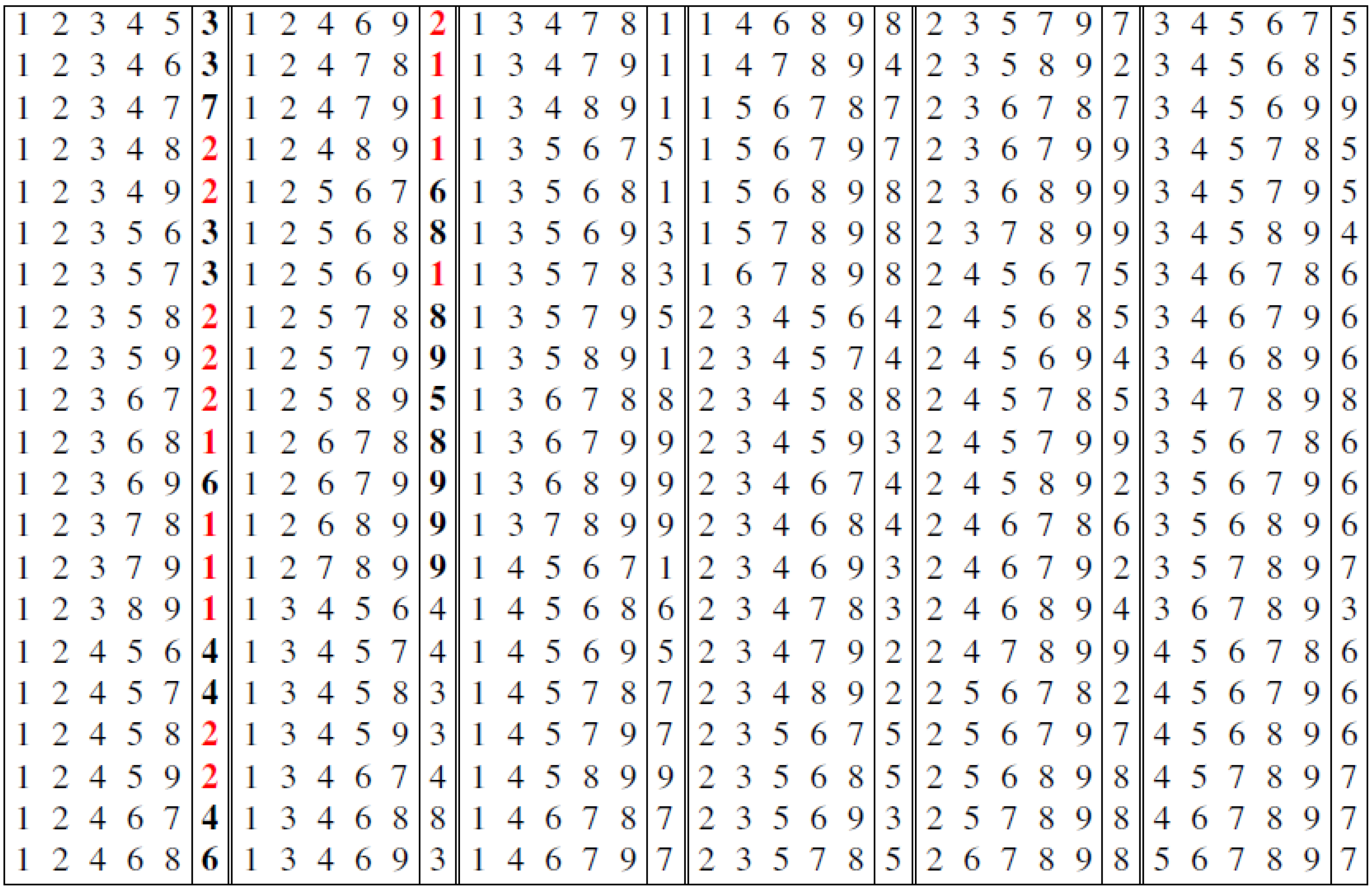
Figure 5 provides an example of a
choice-hypergraph with vertex set
, possessing a zero edge domination graph (employing the construction in the proof of Theorem 1). Note that
, and
(as highlighted in red;
for
satisfying
are indicated in bold). It may also be verified that
, as required by Theorem 2.
Before turning to the proofs of Theorems 1 and 2, we will briefly mention some recent related work on hypertournaments, which carry over to choice-hypergraphs. Recall that a k-hypertournament is a complete k-hypergraph , with each edge endowed with an orientation. We will refer to the oriented edges as arcs.
One concept considered extensively in the literature is score sequences (see for instance [
6,
7,
14,
15,
16,
17,
18]). In particular, for a given
define the
score,
of a vertex
of a
k-hypertournament on
as the number of arcs containing
in which
is not the last element (this is with a complete orientation on the edges, rather than a choice function solely selecting a single element). Similarly, define the
losing score,
as the number of arcs containing
in which
is the last element. The
total score,
, is then given by
. Finally, we obtain the
score sequences ,
and
. Guofei et al. proved the following results regarding the existence of score sequences (see also [
16,
19]).
Theorem 3. (Guofei et al. [14]) Given two non-negative integers n and k with , a non-decreasing sequence of non-negative integers is a losing score sequence of some k-hypertournament if and only if for each j ():with equality when . Theorem 4. (Guofei et al. [14]) Given two non-negative integers n and k with , a non-decreasing sequence of non-negative integers is a score-sequence of some k-hypertournament if and only if for each j ():with equality when . A
k-hypertournament is said to be
regular if for each vertex,
v, the tally of arcs containing
v as the last element is
. Koh and Ree [
16] proved the following.
Theorem 5. (Koh and Ree, [16]) A regular hypertournament exists if and only if . For alternative considerations of regularity, see [
8,
20].
Compare Theorem 5 with Theorems 1 and 2, above. Note that symmetry in domination (i.e., the existence of choice functions resulting in zero-edge domination graphs) is a stronger requirement than regularity. To see this, simply note that all standard tournaments have -edge domination graphs.
For further work on hypertournaments or score sequences, see for instance Pirizda et al. [
15], Landau [
18], Marshall [
8], Khan et al. [
6], Guofei et al. [
14], Gunderson et al. [
21], Li et al. [
22], Guo and Surmacs [
23], and Chou and Guofei [
24].
In the next section, we prove Theorems 1 and 2.
2. Proof of Theorems 1 and 2
Before moving on to the proofs of Theorems 1 and 2, we introduce some preliminary notation. First, suppose
are fixed and
is an
-hypergraph with choice, where
is a complete
k-hypergraph on
n vertices. Without loss of generality, we assume that
. Similar to in [
16], define the rotation operator
, via
, i.e.,
P acts on
k-subsets of
V by shifting the elements (cyclically) to the right by one. Here,
indicates
.g For
and
, define
as the
j-fold iteration of
P and the
order of
e,
, via:
We will denote the set of equivalence classes under successive application of P by . Note that for , is the order of each . We will refer to elements of as rotation classes of H.
In general, addition of the form for and , will be modulo n, unless stated otherwise.
The set is said to be symmetric if , and more generally is symmetric if, for all , . Note that if for some , , then for , , and hence if is symmetric, then R is symmetric. If R is not symmetric, then there exists an such that implies .
Let be the set of all -choice hypergraphs for fixed and be the set of all directed graphs on n vertices. Suppose a domination scheme, D is fixed (see (i)–(iii), above, for examples) and define , where is the domination graph for choice-hypergraph under domination scheme D.
We have the following elementary lemma:
Lemma 1. Suppose H is a k-hypertournament on n vertices with . Then, for any , .
Proof. Suppose
, and
for some
. For any
and any
, set
and represent
e as a binary vector
. We then have, with
and
:
Now, suppose
, with
and
. Then:
Since α is minimal, we have and hence . Thus, since , (9) gives that , and finally . ☐
For convenience of notation, as in (1), define the function
via:
i.e.,
is the number of edges in the rotation class
for which
v is chosen in the presence of
w. Note that
Lemma 2. Suppose with k odd, is a complete k-hypergraph on n vertices, and . If R is symmetric and , then there exists a and , such that , and implies .
Proof. Suppose that
R is symmetric and
. Then, there exists an
i such that
, and hence a permutation
of
such that:
Since
k is odd, there exists a
Q such that:
and taking differences, (13) and (14) imply:
The result follows upon setting , and . □
We will now prove Theorem 1 regarding the existence of choice functions with symmetry in domination.
Proof of Theorem 1. Suppose , k is odd, and is an -choice hypergraph. Consider E, the set of all edges in H, and let be the set of all rotation classes of H, where, by Lemma 1, for , , and . Fix , with , and choose some .
Suppose
R is symmetric and fix an
. Then, by Lemma 2,
, where
and
is closed under additive inverses. For
, set
. Suppose
and
for
. For
,
implies
and
implies
. Note that
if and only if
. Similarly,
if and only if
. Since
is closed under inverses, we have:
Suppose
R is not symmetric, and consider
, and note that
. Fix an
and
, and write
(note that
is not closed under inverses). For
, set:
Now, suppose
and
. For
,
implies
or
, and
implies
or
. Note that
if and only if
, and
if and only if
(i.e.,
). Similarly,
if and only if
, and
if and only if
(i.e.,
). Thus:
Employing (16), (18) and (12), the result follows. □
We will now prove Theorem 2.
Proof of Theorem 2. Suppose
is a choice-hypergraph with a zero-edge domination graph, where
is a complete
k-hypergraph on
n vertices. For a fixed vertex
, define
and
, i.e.,
is the set of edges to which
v belongs and
is the set of edges for which
v is selected. Note that:
Assume
. Since
has a zero-edge domination graph,
for all
and hence:
Thus,
for all
. The result follows upon noting that:
☐