Resource and Reserve Calculation in Seam-Shaped Mineral Deposits; A New Approach: “The Pentahedral Method”
Abstract
:1. Introduction
2. Research Objectives
- Three-dimensional (3D) modeling is mandatory;
- It must allow different interpolation algorithms, including geostatistics;
- The calculation detail has to be user-defined;
- Dilution (material below the cutoff) should be considered, if necessary;
- It must allow estimates with a categorization using distances, number of intercepts, or a combination of both parameters;
- It must allow interpolation, taking into account boreholes filtered by distance: neighborhood influence;
- The results will be stored in a Structured Query Language (SQL) database.
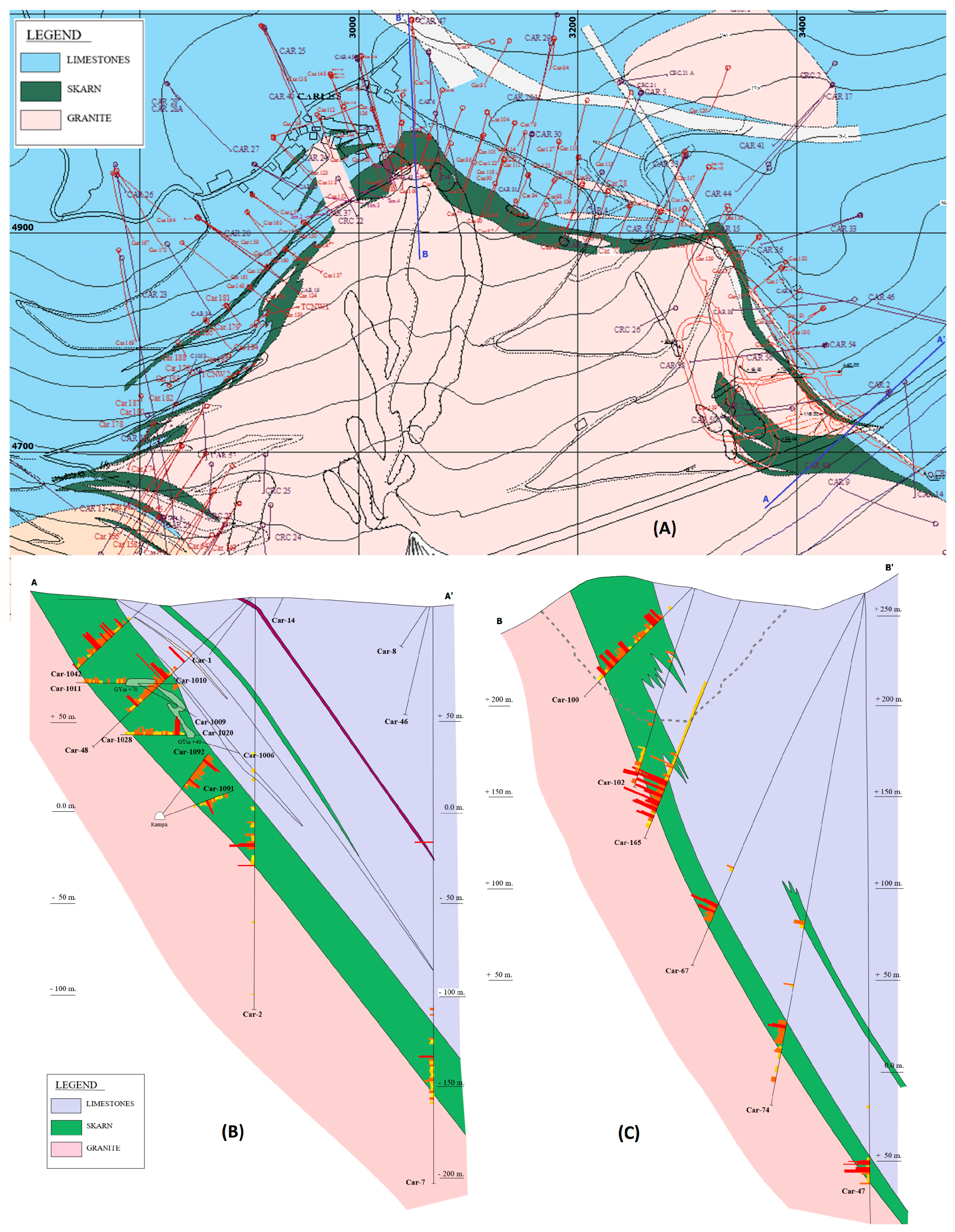
3. Geological Characteristics and Constraints
4. Methodology
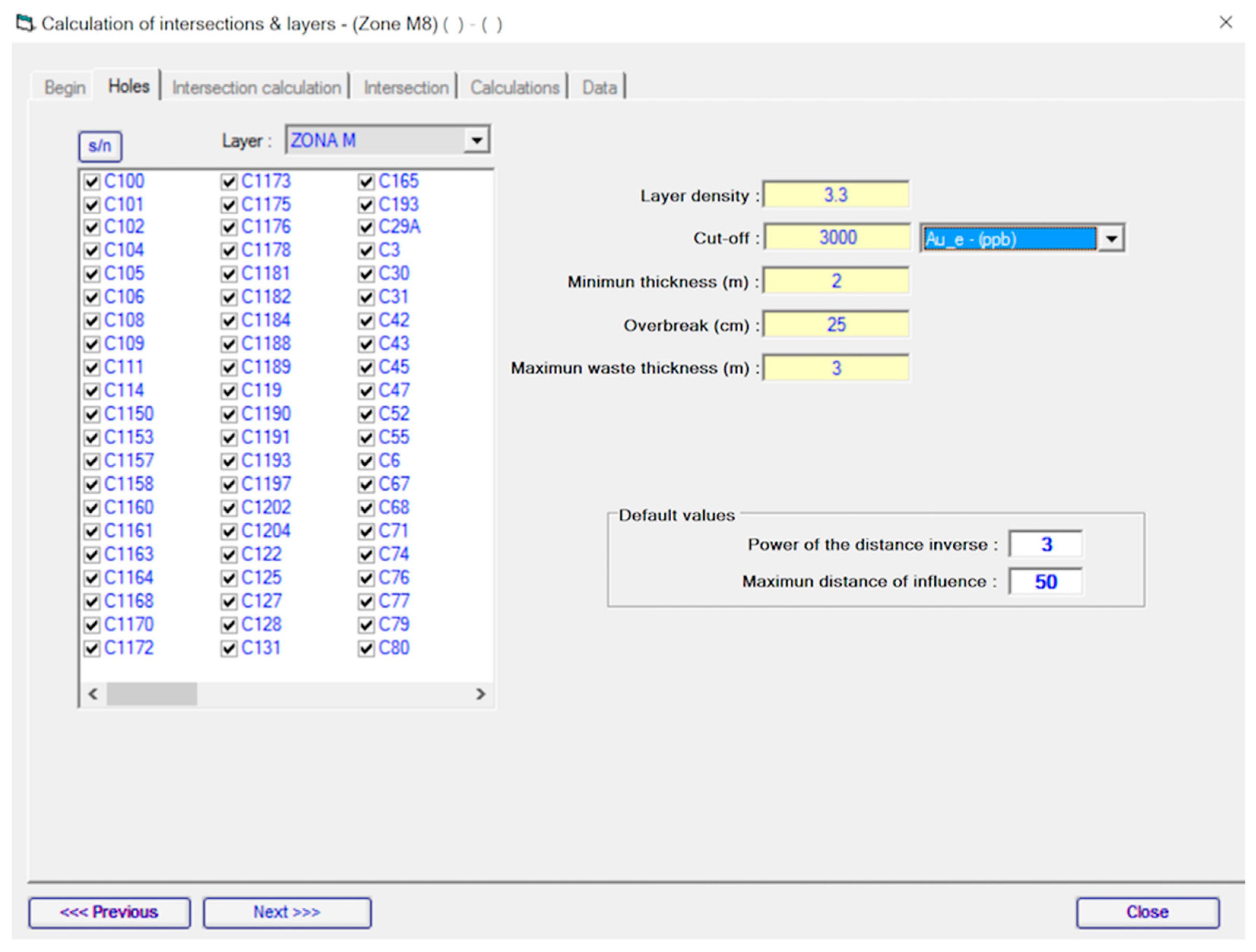
- Determination of the seam localization from the geological information and survey data.
- Construction of a 3D-modeled surface at the center of the seam.
- Generation of an equally-spaced cloud of points in the seam centered surface.
- Calculation of the intercept values of the surveys crossing the seam.
- Execution of a geostatistical study of the intercept values.
- Interpolation of the grade and the thickness of each point of the cloud of points, using the intercept information.
- Definition of the estimation categories and generation of the calculation units.
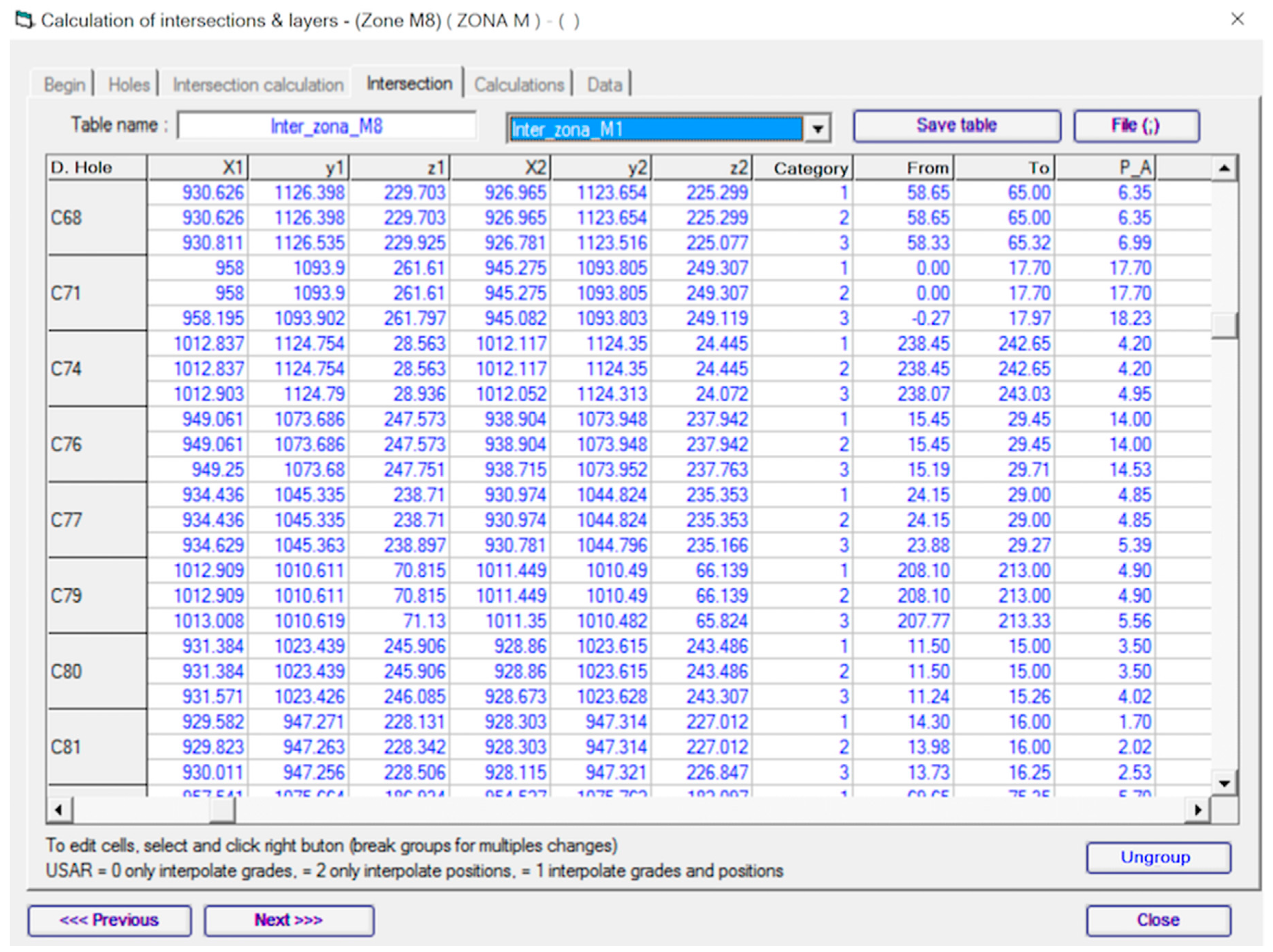
- Database generation and representation.
4.1. Determination of the Seam Localization from the Geological Information and Surveys
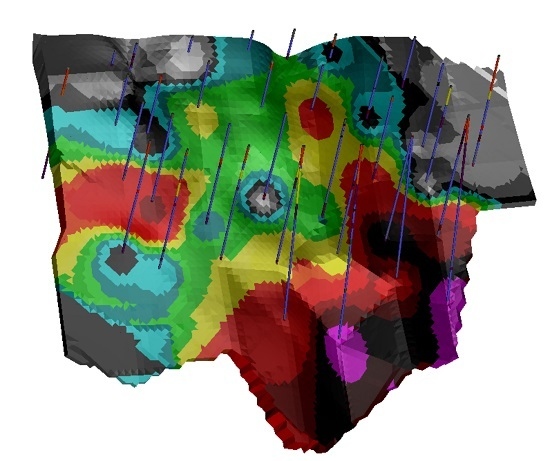
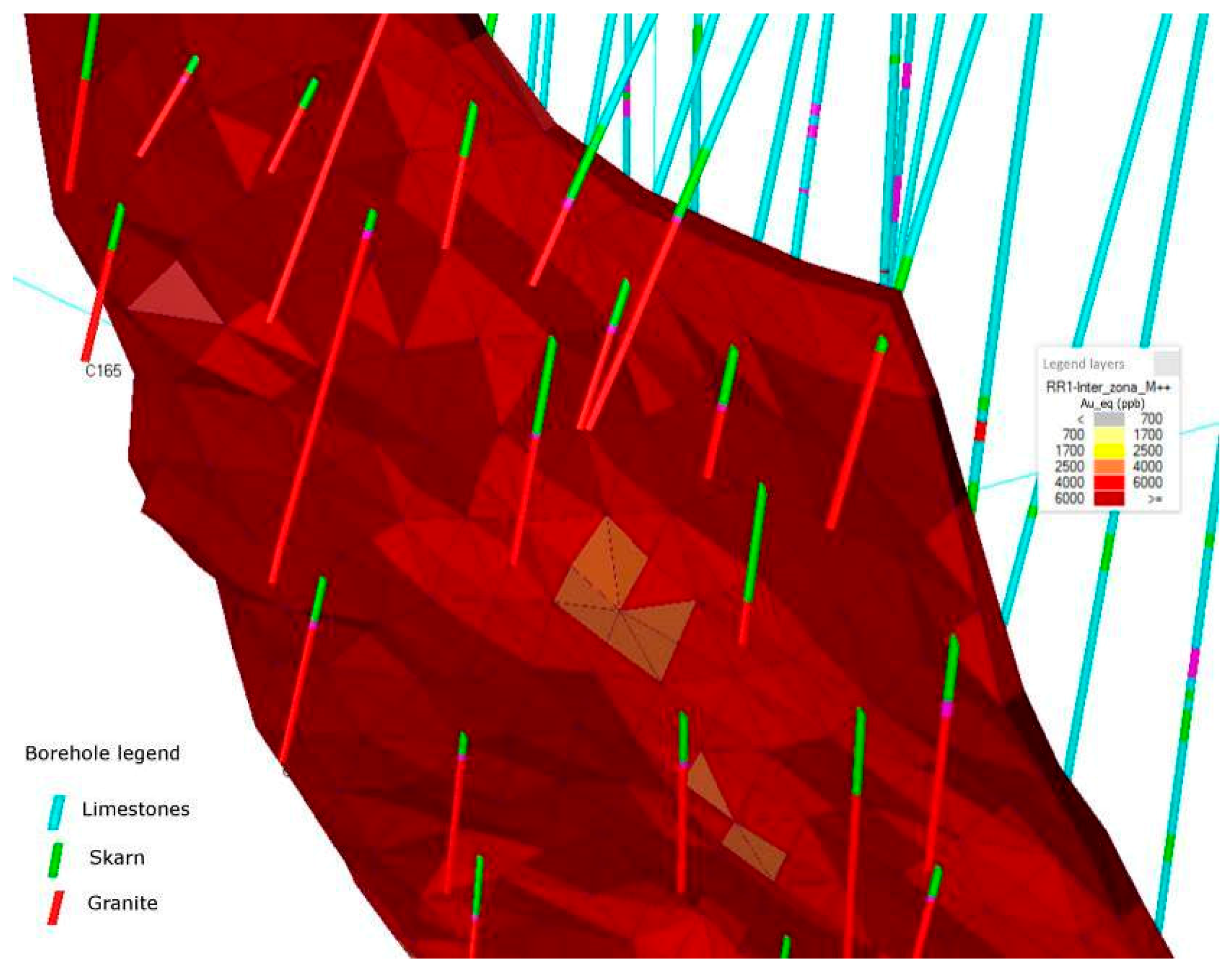
4.2. Construction of a 3D Modeled Surface at the Center of the Seam
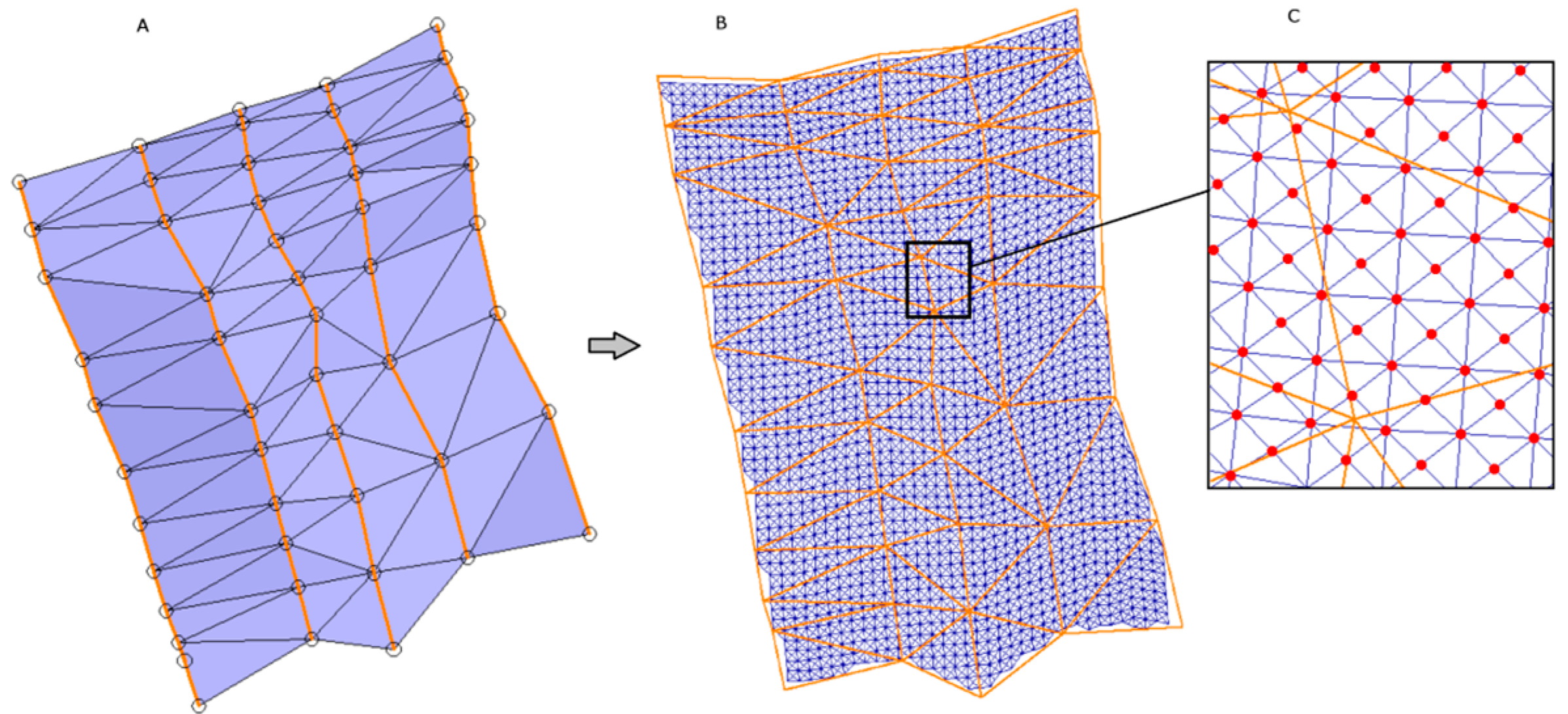
4.3. Generation of an Equally Spaced Cloud of Points in the Seam Centered Surface
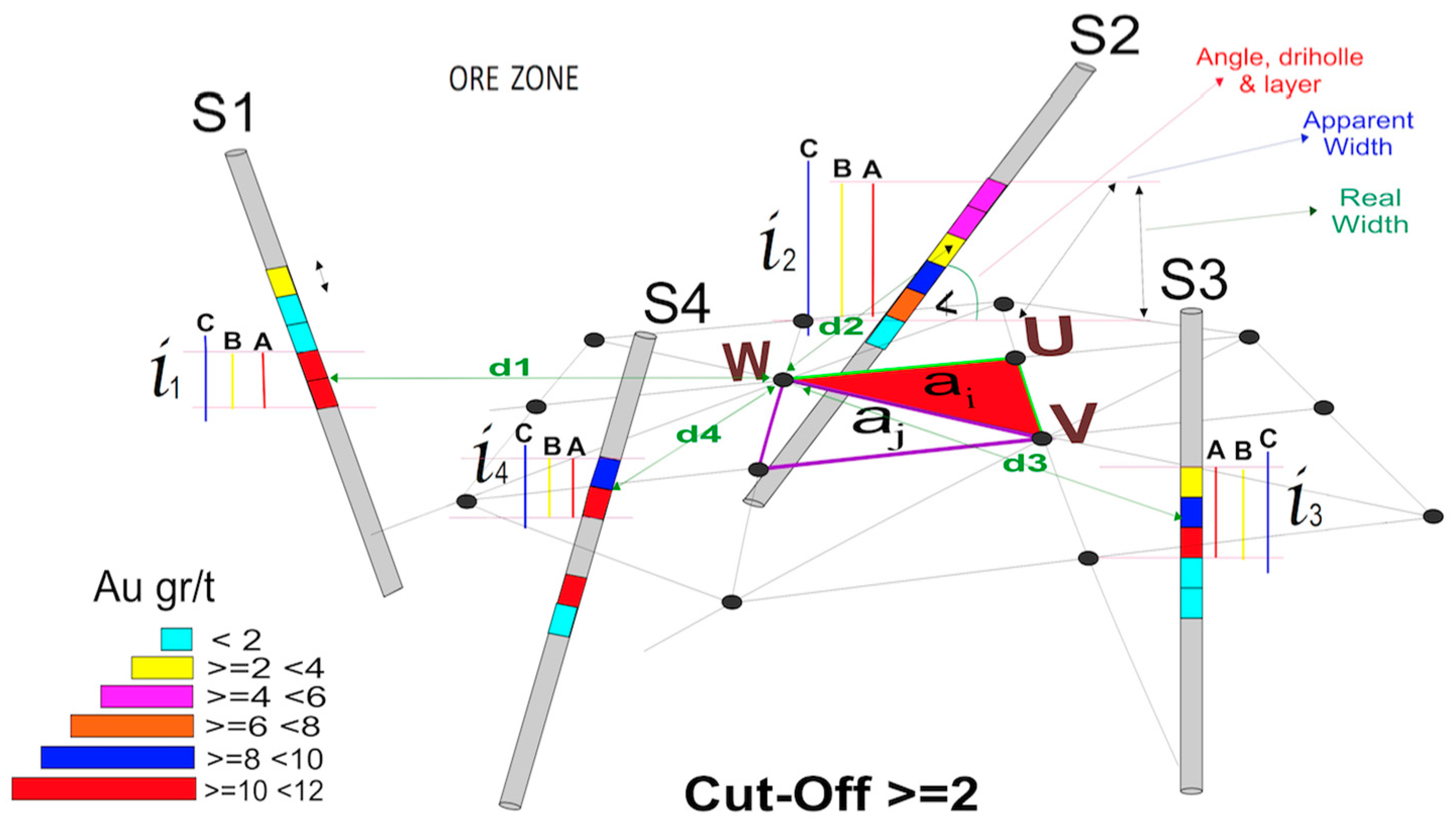
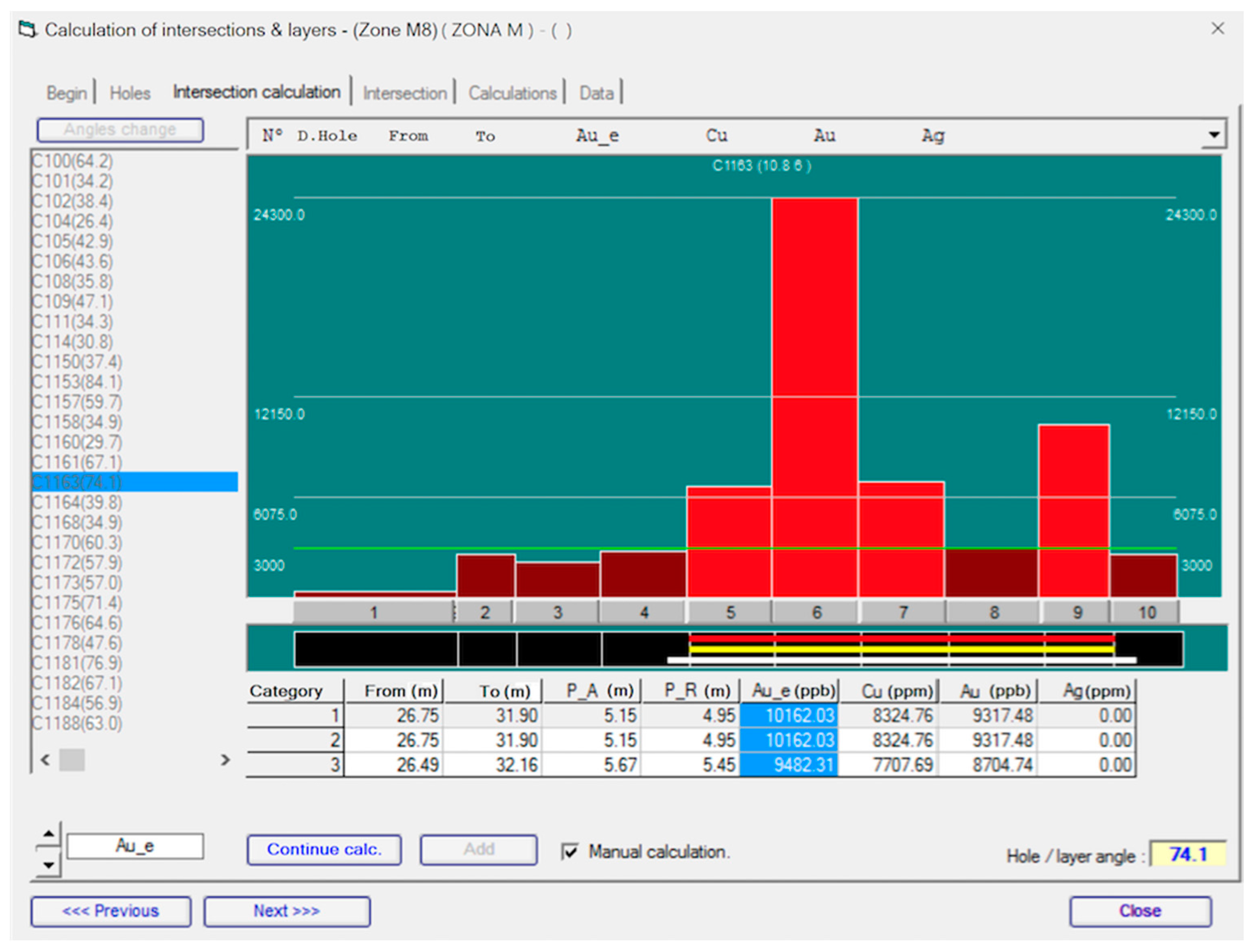
4.4. Calculation of the Intercept Values of the Surveys Crossing the Seam
4.5. Geostatistical Study of the Intercept Values
4.6. Interpolation of the Grade and the Thickness at Each Point of the Cloud of Points (NPS)
- L: Metal grade, in this case: Au_eq.
- P: Real thickness of the intercept.
- d: Distance between the NPS point to be interpolated and the center of the intercept.
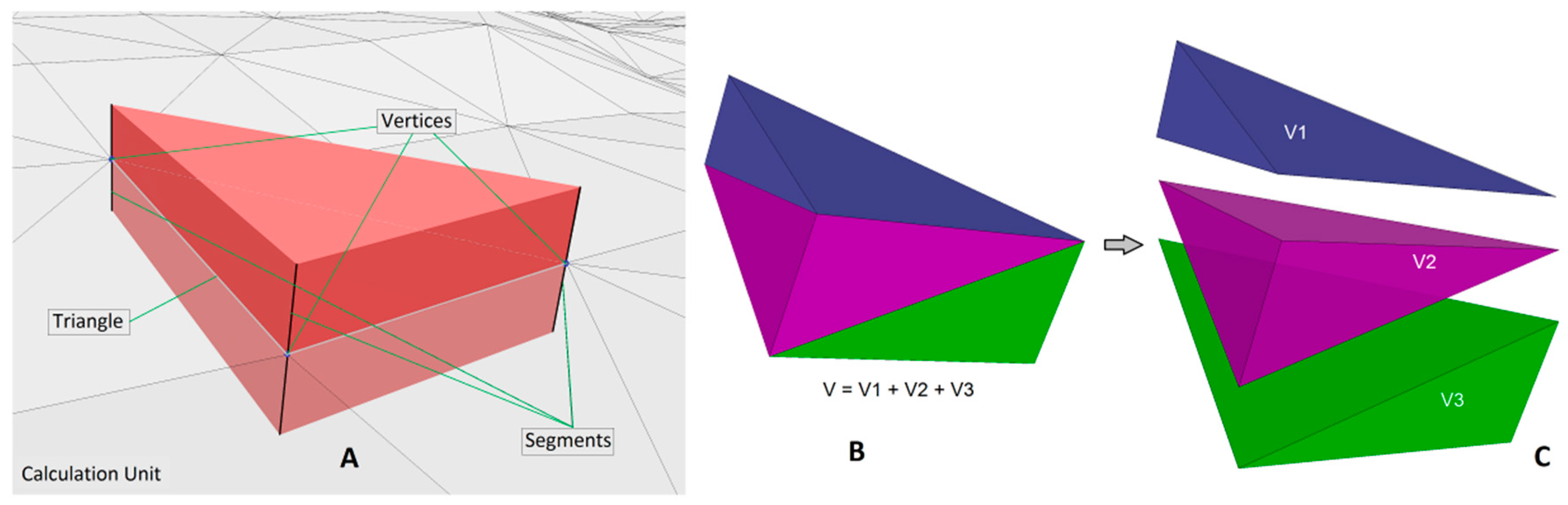
- x: Inverse distance exponent (in the example, x = 3).
- V: Pentahedron volume.
- n: Borehole identification number.
- a: Seam triangle surface.
4.7. Interpolation of the Positions of the Seam Surface Center
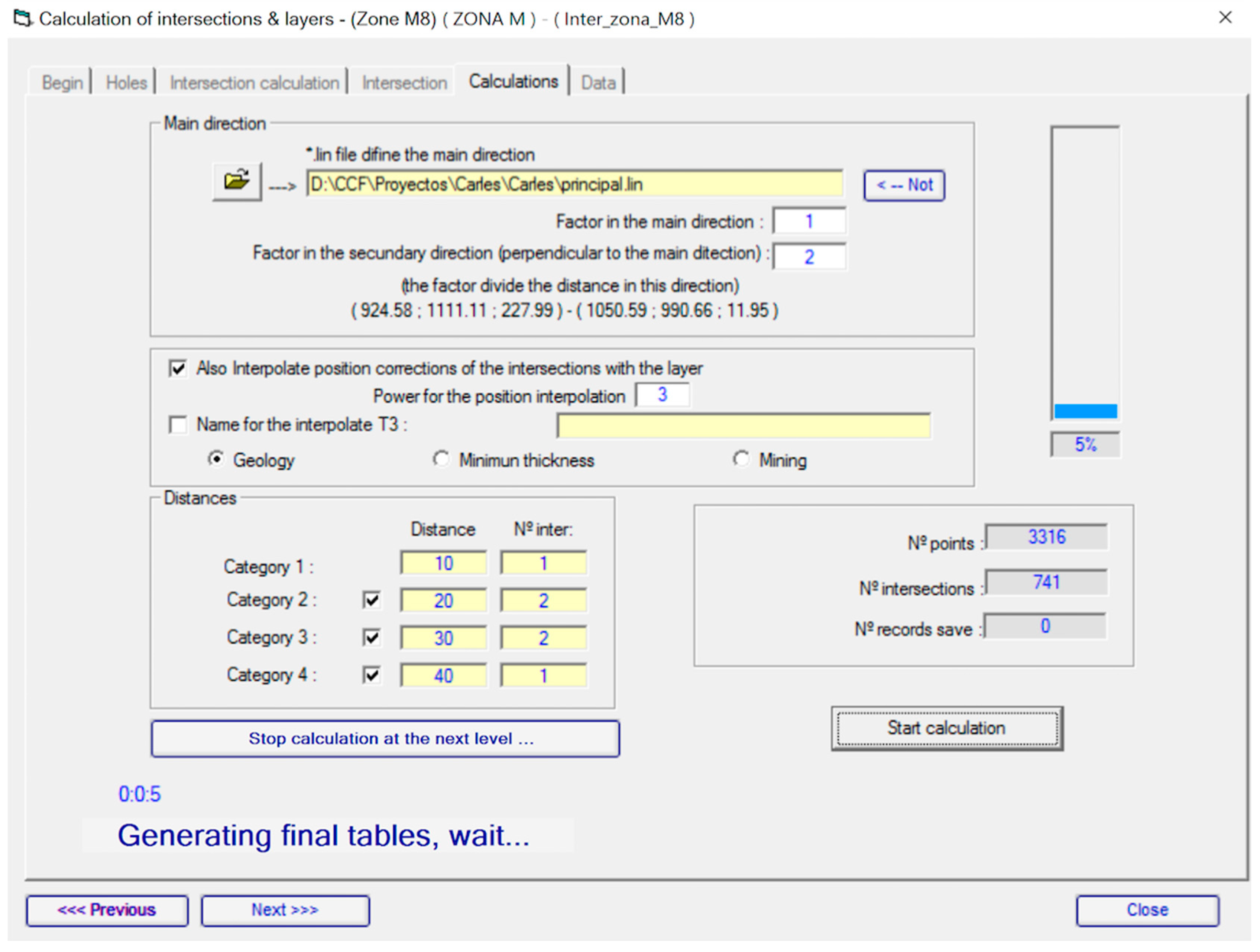
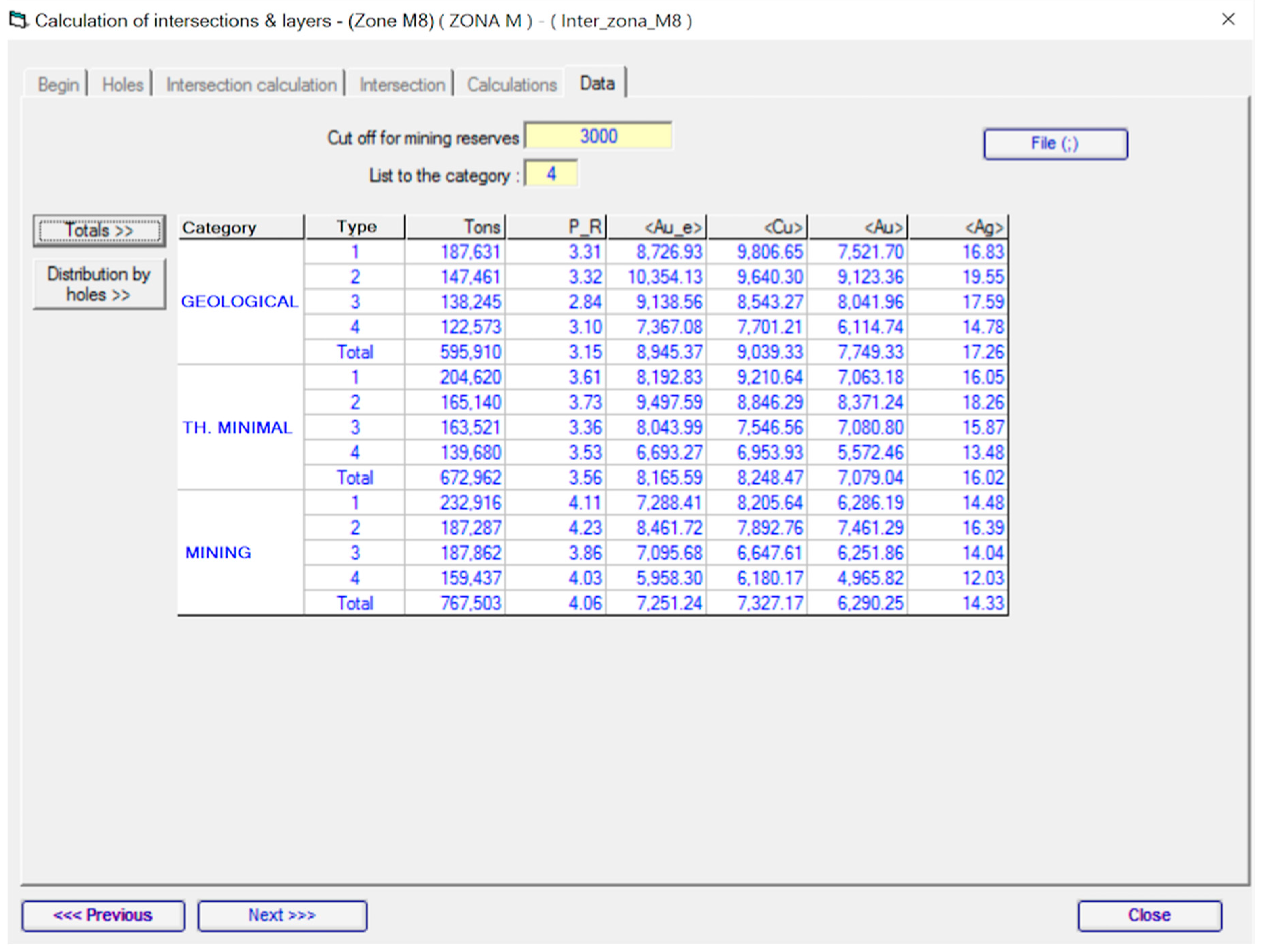
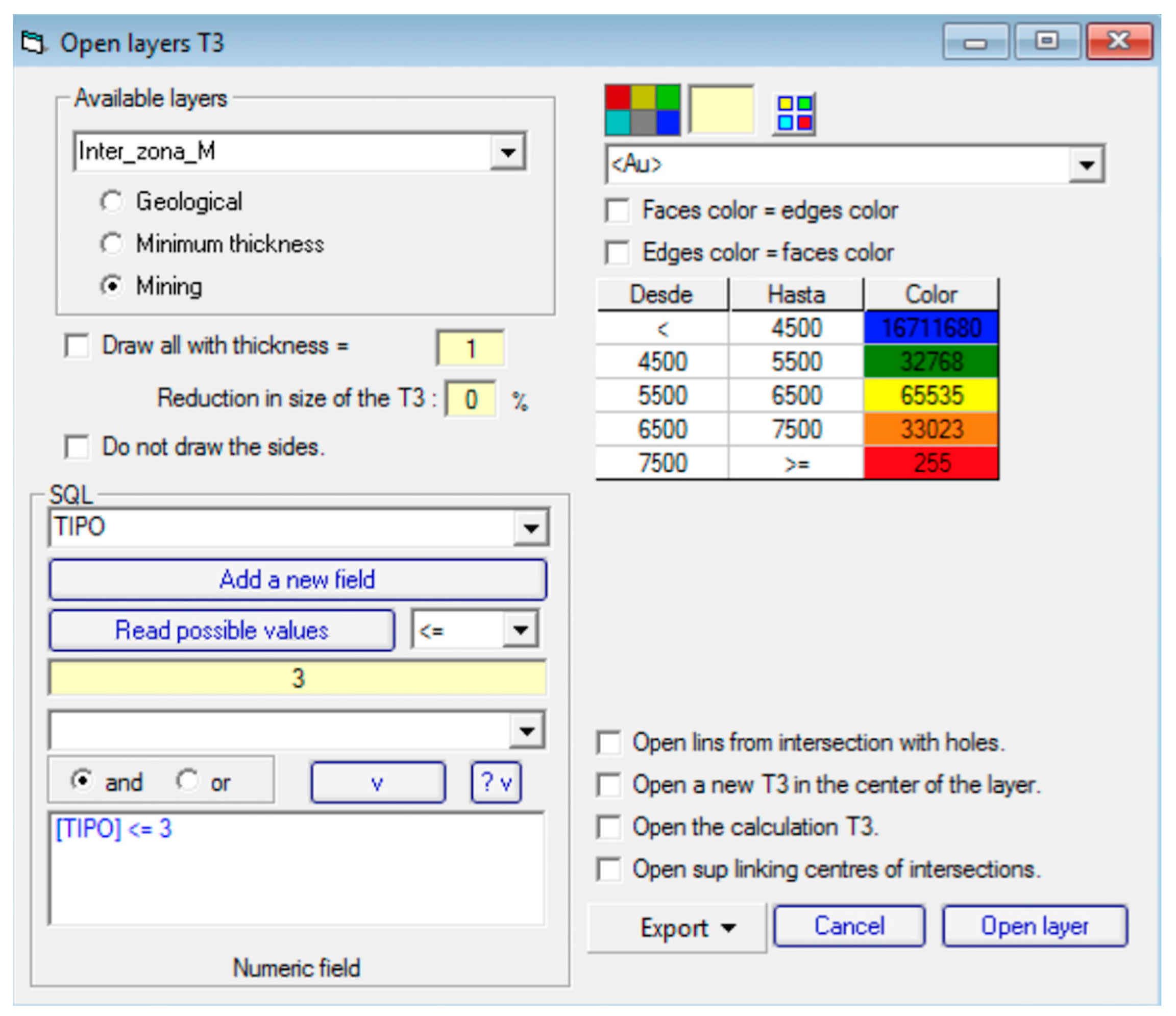
4.8. Definition of the Estimation Categories and Generation of the Calculation Units
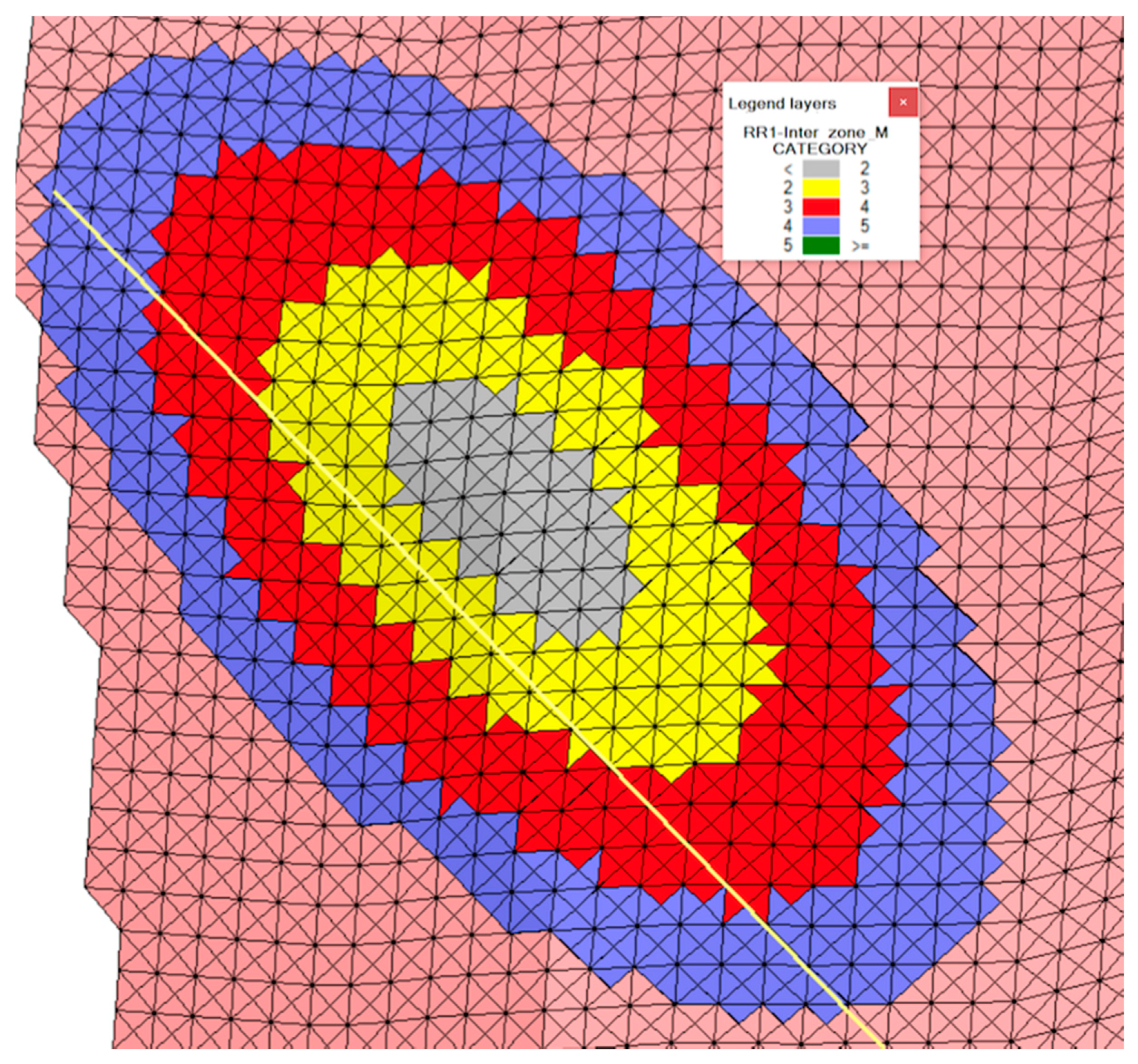
- Category 1: calculation units with an intercept at less than 10 m
- Category 2: calculation units with two intercepts at less than 20 m
- Category 3: calculation units with two intercepts at less than 30 m
- Category 4: calculation units with one intercept at less than 40 m
4.9. Calculation Units Generation and Categories Definition
5. Method Suitability
- Any change in the calculation parameters does not need the calculation units to be redefined.
- When defining the calculation geometry units, these can be separately prepared for subsequent exploitation and scheduling, even exporting them to other software.
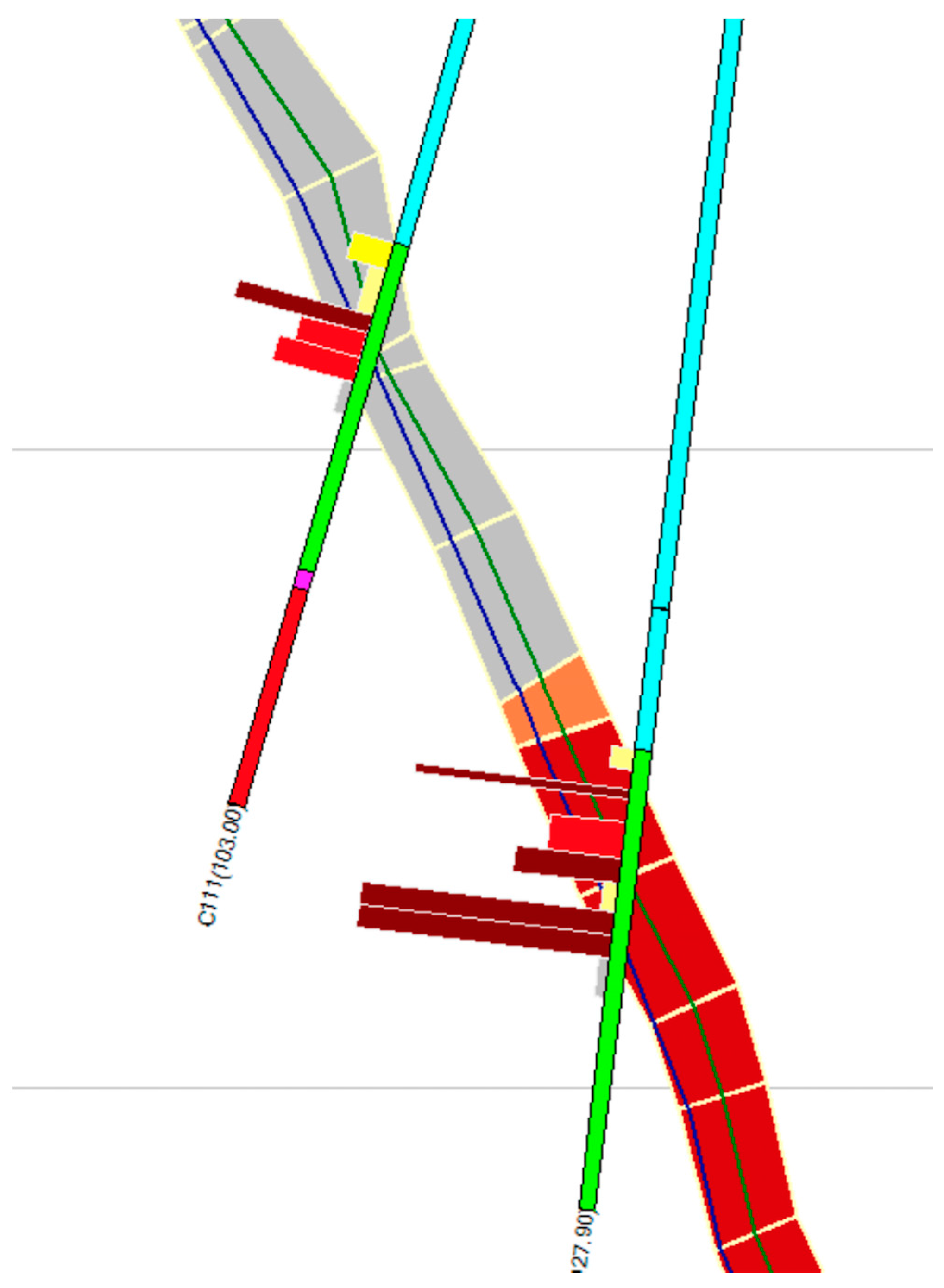
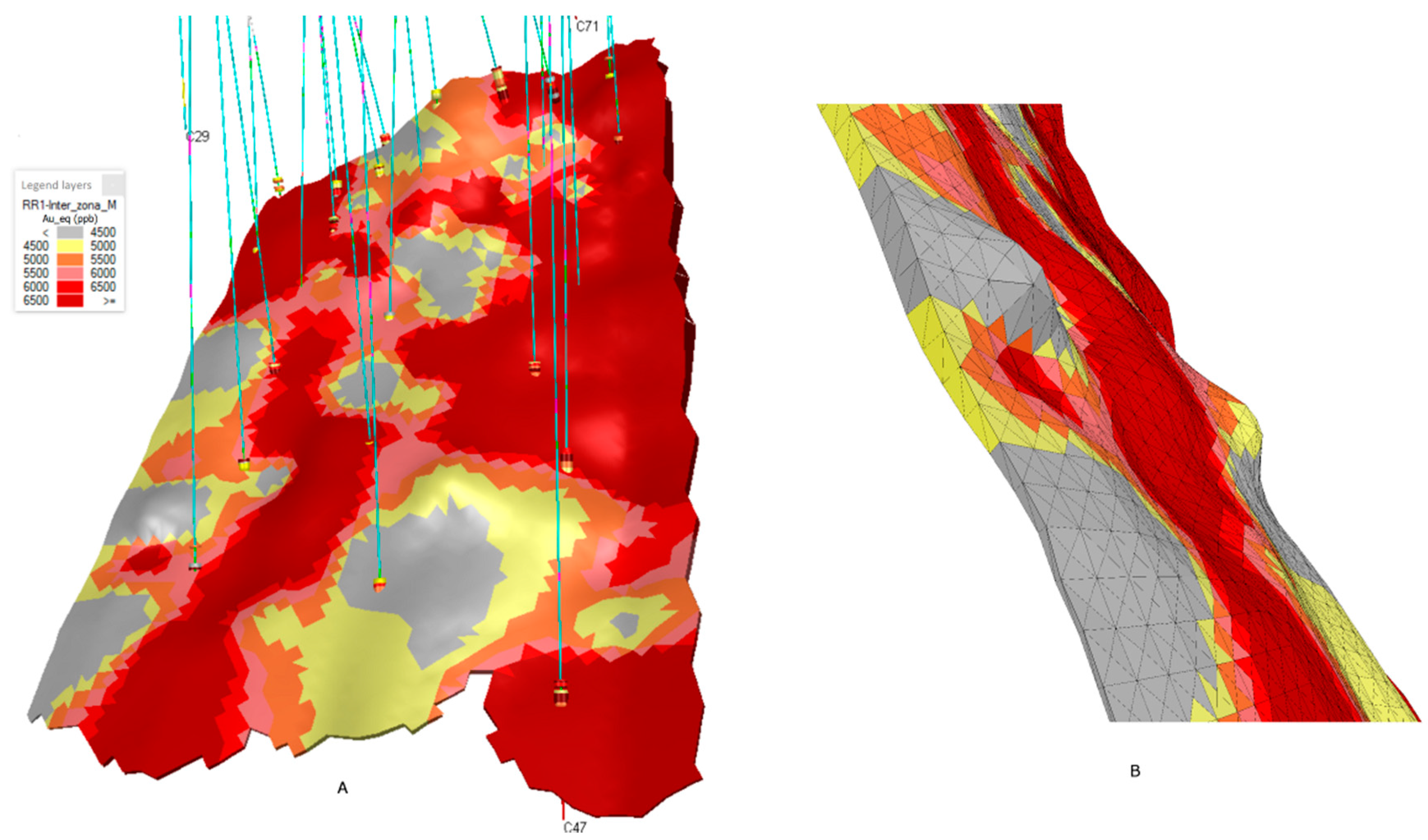
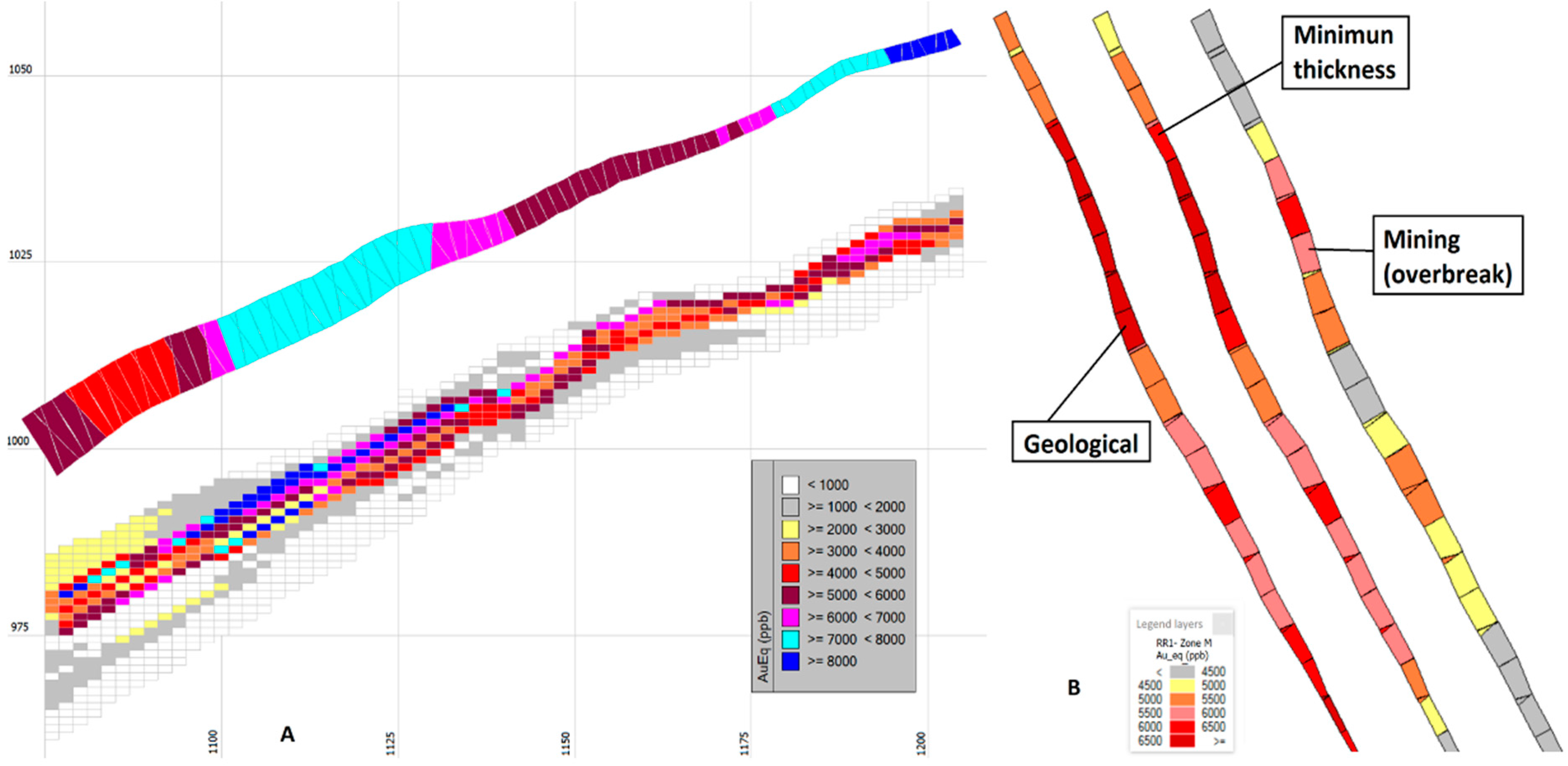
- It provides a fairly accurate representation of the thickness of the seam-shaped structure even in the case of low thickness seams, which is extremely difficult to achieve with traditional block models (Figure 19).
- It interpolates intersections, not samples taken from boreholes.
- Geometrical results closely follow the deposit limits, as opposed to block models that create a stair-shaped profile (see Figure 19).
- It includes the possible internal dilution, as well as the lateral dilution due to mining overbreak.
- A minimum thickness can be defined according to mining technical conditions.
6. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, G.; Zhang, S.; Yan, C.; Song, Y.; Li, D. Mineral potential targeting and resource assessment based on 3D geological modelling in Luanchuan region, China. Comput. Geosci. 2011, 37, 1976–1988. [Google Scholar] [CrossRef]
- Canadian Institute of Mining. CIM Definition Standards on Mineral Resources and Mineral Reserves; CIM Definition Standards (2014); Canadian Institute of Mining, Metallurgy and Petroleum: Quebec, QC, Canada, 2014. [Google Scholar]
- Annels, A.E. Mineral Deposit Evaluation: A Practical Approach; Chapman & Hall: London, UK, 1991. [Google Scholar]
- Clark, I. Practical Geostatistics; Applied Science Publishers Ltd.: London, UK, 1979. [Google Scholar]
- Clark, I.; Harper, W.V. Practical Geostatistics 2000; Ecosse North America Llc.: Columbus, OH, USA, 2001; 342p. [Google Scholar]
- Rendu, J.M. An Introduction to Geostatistical Methods of Mineral Evaluation; South African Institute of Mining and Metallurgy: Johannesburg, South Africa, 1981. [Google Scholar]
- Castañón, C. Nuevo Método de Cálculo de Recursos Geológicos y Reservas Mineras para Yacimientos Tabulares y Aplicación Informática para la Gestión Integral de un Proyecto Minero. Ph.D. Thesis, Universidad de Oviedo, Asturias, Spain, 2006; 200p. [Google Scholar]
- Silva, D.S.F.; Boisvert, J.B. Mineral resource classification: A comparison of new and existing techniques. J. S. Afr. Inst. Min. Metall. 2014, 114, 265–273. [Google Scholar]
- Will Gemcom Produce a Leaped Frog out of Leapfrog? Available online: http://www.orefind.com/blog/orefind_blog/2012/11/14/will-gemcom-produce-a-leaped-frog-out-of-leapfrog- (accessed on 10 February 2017).
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer: London, UK, 2014; p. 332. [Google Scholar]
- Boisvert, J.B.; Deutsch, C.V. Programs for kriging and sequential Gaussian simulation with locally varying anisotropy using non-Euclidean distances. Comput. Geosci. 2011, 37, 495–510. [Google Scholar] [CrossRef]
- Martín-Izard, A.; Fuertes, M.; Cepedal, A.; Maldonado, C.; Pevida, L.R.; Spiering, E.; González, S.; Varela, A. Geochemical characteristisc of the Río Narcea gold belt intrusives and timing of development of the different magmatic-hydrothermal processes based on K/Ar dating. In Gold Exploration and Mining in NW Spain; Arias, D., Martín-Izard, A., Paniagua, A., Eds.; University of Oviedo: Asturias, Spain, 1998; pp. 35–42. [Google Scholar]
- Martín-Izard, A.; Fuertes-Fuente, M.; Cepedal, A.; Moreiras, D.; García-Nieto, J.; Maldonado, C.; Pevida, L.R. The Río Narcea Gold Belt intrusions: Geology, petrology, geochemistry and timing. J. Geochem. Explor. 2000, 71, 103–117. [Google Scholar] [CrossRef]
- Spiering, E.D.; Pevida, L.R.; Maldonado, C.; González, S.; García, J.; Varela, A.; Arias, D.; Martín-Izard, A. The gold belts of western Asturias and Galicia (NW Spain). J. Geochem. Explor. 2000, 71, 89–101. [Google Scholar] [CrossRef]
- Pevida, L.R.; Maldonado, C.; Spiering, E.; González, S.; García, J.; Varela, A.; Martín-Izard, A.; Cepedal, A.; Fuertes, M. Geology and exploration guides along the Río Narcea gold belt. In Gold Exploration and Mining in NW Spain D; Arias, D., Martín-Izard, A., Paniagua, A., Eds.; University of Oviedo: Asturias, Spain, 1998; pp. 27–36. [Google Scholar]
- Martın-Izard, A.; Paniagua, A.; García-Iglesias, J.; Fuertes-Fuente, M.; Boixet, L.L.; Maldonado, C.; Varela, A. The Carlés copper-gold-molybdenum skarn (Asturias, Spain): Geometry, mineral associations and metasomatic evolution. J. Geochem. Explor. 2000, 71, 153–175. [Google Scholar] [CrossRef]
- Castañón, C. Manual de Ayuda del Software Minero RecMin. 2006. Available online: http://recmin.com/WP/?page_id=255 (accessed on 8 May 2017).
- Meinert, L.D. Skarns and skarn deposits. In Ore Deposit Models; Sheahan, P.A., Cherry, M.E., Eds.; Geological Association of Canada: St. John’s, NL, Canada, 1993; Volume II, pp. 117–134. [Google Scholar]
- Bustillo, M.; López-Jimeno, C. Manual de Evaluación y Diseño de Explotaciones Mineras; Entorno Gráfico S.L.: Madrid, Spain, 1997. [Google Scholar]
- The Stanford Geostatistical Modeling Software (SGeMS). Available online: http://sgems.sourceforge.net/ (accessed on 10 February 2017).
- Galera, C.; Bennis, C.; Moretti, I.; Mallet, J.L. Construction of coherent 3D geological blocks. Comput. Geosci. 2003, 29, 971–984. [Google Scholar] [CrossRef]





| Borehole S1 | Borehole S2 | Borehole Sn |
|---|---|---|
| A1: Geological Intercept | A2: Geological Intercept | An: Geological Intercept |
| (L.P)A1: Grade multiplied by thickness | (L.P)A2: Grade multiplied by thickness | (L.P)An: Grade multiplied by thickness |
| PA1: thickness | PA2: thickness | PAn: thickness |
| B1: Minimum Thickness Intercept | B2: Minimum Thickness Intercept | Bn: Minimum Thickness Intercept |
| (L.P)B1: Grade multiplied by thickness | (L.P)B2: Grade multiplied by thickness | (L.P)Bn: Grade multiplied by thickness |
| PB1: thickness | PB2: thickness | PBn: thickness |
| C1: Mining Intercept | C2: Mining Intercept | Cn: Mining Intercept |
| (L.P)C1: Grade multiplied by thickness | (L.P)C2: Grade multiplied by thickness | (L.P)Cn: Grade multiplied by thickness |
| PC1: thickness | PC2: thickness | PCn: thickness |
| NPSID | Dist | % | D.Hole | P_R | <Au> | <Ag> | <Cu> | <As> | <Au_e> |
|---|---|---|---|---|---|---|---|---|---|
| 30038000070 | 23.9 | 36.36% | C1043 | 1.06 | 1975 | 2.4 | 1200 | 253 | 1975.18 |
| 30038000070 | 26.9 | 25.50% | C1041 | 0.98 | 800 | 0.1 | 0 | 3900 | 800.00 |
| 30038000070 | 30.1 | 18.20% | C1042 | 3.03 | 9992 | 6.3 | 5433 | 15114 | 9992.76 |
| 30038000070 | 32.4 | 14.59% | C1012 | 0.59 | 2050 | 0.5 | 570 | 1387 | 2050.08 |
| 30038000070 | 45.3 | 5.34% | C1089 | 0.71 | 4850 | 8.4 | 4000 | 4400 | 4850.60 |
| 30038000070 | - | 100.00% | - | 1.31 | 3299.1 | 2.6 | 1722.1 | 4275.1 | 3299.36 |
| 30038000060 | 19.5 | 59.73% | C1043 | 1.06 | 1975 | 2.4 | 1200 | 253 | 1975.18 |
| 30038000060 | 30.5 | 15.61% | C1041 | 0.98 | 800 | 0.1 | 0 | 3900 | 800.00 |
| 30038000060 | 34.6 | 10.69% | C1042 | 3.03 | 9992 | 6.3 | 5433 | 15114 | 9992.76 |
| 30038000060 | 36.5 | 9.11% | C1012 | 0.59 | 2050 | 0.5 | 570 | 1387 | 2050.08 |
| 30038000060 | 45 | 4.86% | C1089 | 0.71 | 4850 | 8.4 | 4000 | 4400 | 4850.60 |
| 30038000060 | - | 100.00% | - | 1.2 | 2795.3 | 2.6 | 1544 | 2716.1 | 2795.57 |
| 30038000060 | 17.4 | 66.80% | C1043 | 1.06 | 1975 | 2.4 | 1200 | 253 | 1975.18 |
| 30038000060 | 29.5 | 13.71% | C1041 | 0.98 | 800 | 0.1 | 0 | 3900 | 800.00 |
| 30038000060 | 35.9 | 7.61% | C1042 | 0.59 | 2050 | 0.5 | 570 | 1387 | 2050.08 |
| 30038000060 | 36.5 | 7.24% | C1012 | 3.03 | 9992 | 6.3 | 2533 | 15114 | 9992.76 |
| 30038000060 | 42.3 | 4.65% | C1089 | 0.71 | 4850 | 8.4 | 4000 | 4400 | 4850.60 |
| 30038000060 | - | 100% | - | 1.1 | 2562.8 | 2.5 | 1442.1 | 2158.1 | 2563.00 |
| TOTAL | - | - | - | 1.22 | 2885.75 | 2.56 | 1569.37 | 3049.37 | 2885.98 |
| D.Hole | Tons | Au_e | Cu | Au | Ag |
|---|---|---|---|---|---|
| CN1014 | 1.5% | 1.90% | 0% | 2% | 1% |
| CN1015 | 2.9% | 14.90% | 9.7% | 15.4% | 16.6% |
| CN1016 | 1.9% | 2.00% | 1.2% | 2.1% | 1.5% |
| CN1017 | 0.4% | 1.40% | 0.8% | 1.5% | 1.2% |
| CN1018 | 0.2% | 1.30% | 0.9% | 1.3% | 0.8% |
| CN1019 | 0.6% | 0.40% | 0.5% | 0.4% | 1.0% |
| CN1020 | 1.1% | 0.60% | 0.7% | 0.6% | 0.9% |
| CN1021 | 0.7% | 0.90% | 1.0% | 0.9% | 1.4% |
| CN1022 | 0.6% | 0.10% | 0.0% | 0.1% | 0.2% |
| CN1023 | 1.5% | 1.50% | 1.6% | 1.4% | 2.1% |
| CN1024 | 1.2% | 0.70% | 0.0% | 0.8% | 0.0% |
| CN1025 | 0.6% | 0.50% | 0.6% | 0.5% | 0.9% |
| CN1026 | 0.6% | 0.50% | 0.7% | 0.4% | 0.9% |
| CN1027 | 0.9% | 0.60% | 1.1% | 0.6% | 0.8% |
| CN1028 | 0.9% | 0.50% | 0.6% | 0.5% | 0.4% |
| CN1029 | 0.6% | 0.70% | 0.0% | 0.8% | 0.0% |
| CN1030 | 0.7% | 0.10% | 0.0% | 0.1% | 0.1% |
| CN1031 | 0.7% | 0.20% | 0.0% | 0.2% | 0.0% |
| CN1032 | 0.7% | 0.60% | 0.8% | 0.6% | 0.5% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castañón, C.; Arias, D.; Diego, I.; Martin-Izard, A.; Ruiz, Y. Resource and Reserve Calculation in Seam-Shaped Mineral Deposits; A New Approach: “The Pentahedral Method”. Minerals 2017, 7, 72. https://doi.org/10.3390/min7050072
Castañón C, Arias D, Diego I, Martin-Izard A, Ruiz Y. Resource and Reserve Calculation in Seam-Shaped Mineral Deposits; A New Approach: “The Pentahedral Method”. Minerals. 2017; 7(5):72. https://doi.org/10.3390/min7050072
Chicago/Turabian StyleCastañón, César, Daniel Arias, Isidro Diego, Agustin Martin-Izard, and Yhonny Ruiz. 2017. "Resource and Reserve Calculation in Seam-Shaped Mineral Deposits; A New Approach: “The Pentahedral Method”" Minerals 7, no. 5: 72. https://doi.org/10.3390/min7050072
APA StyleCastañón, C., Arias, D., Diego, I., Martin-Izard, A., & Ruiz, Y. (2017). Resource and Reserve Calculation in Seam-Shaped Mineral Deposits; A New Approach: “The Pentahedral Method”. Minerals, 7(5), 72. https://doi.org/10.3390/min7050072