Structural Transition of Inorganic Silica–Carbonate Composites Towards Curved Lifelike Morphologies

Abstract

The self-assembly of alkaline earth carbonates in the presence of silica at high pH leads to a unique class of composite materials displaying a broad variety of self-assembled superstructures with complex morphologies. A detailed understanding of the formation process of these purely inorganic architectures is crucial for their implications in the context of primitive life detection as well as for their use in the synthesis of advanced biomimetic materials. Recently, great efforts have been made to gain insight into the molecular mechanisms driving self-assembly in these systems, resulting in a consistent model for morphogenesis at ambient conditions. In the present work, we build on this knowledge and investigate the influence of temperature, supersaturation, and an added multivalent cation as parameters by which the shape of the forming superstructures can be controlled. In particular, we focus on trumpet- and coral-like structures which quantitatively replace the well-characterised sheets and worm-like braids at elevated temperature and in the presence of additional ions, respectively. The observed morphological changes are discussed in light of the recently proposed formation mechanism with the aim to ultimately understand and control the major physicochemical factors governing the self-assembly process.

1. Introduction

Silica biomorphs are an interesting type of self-assembling inorganic–inorganic composite material with remarkably complex architectures. They form in silica-rich solutions at high pH in the presence of alkaline earth metal cations like barium, strontium, and calcium under ambient conditions [1,2,3,4,5,6]. Upon diffusion of atmospheric carbon dioxide into the system, slow crystallisation of carbonate under the influence of dissolved silicate species results in the spontaneous formation of unusual ultrastructures that consist of uniform elongated carbonate nanocrystals (approximately 200–300 nm long), which maintain long-range co-orientation and are interspersed by certain amounts of amorphous silica; the whole structure is surrounded by a silica skin (typical Si/Ba ratios are 0.1–0.3) [4,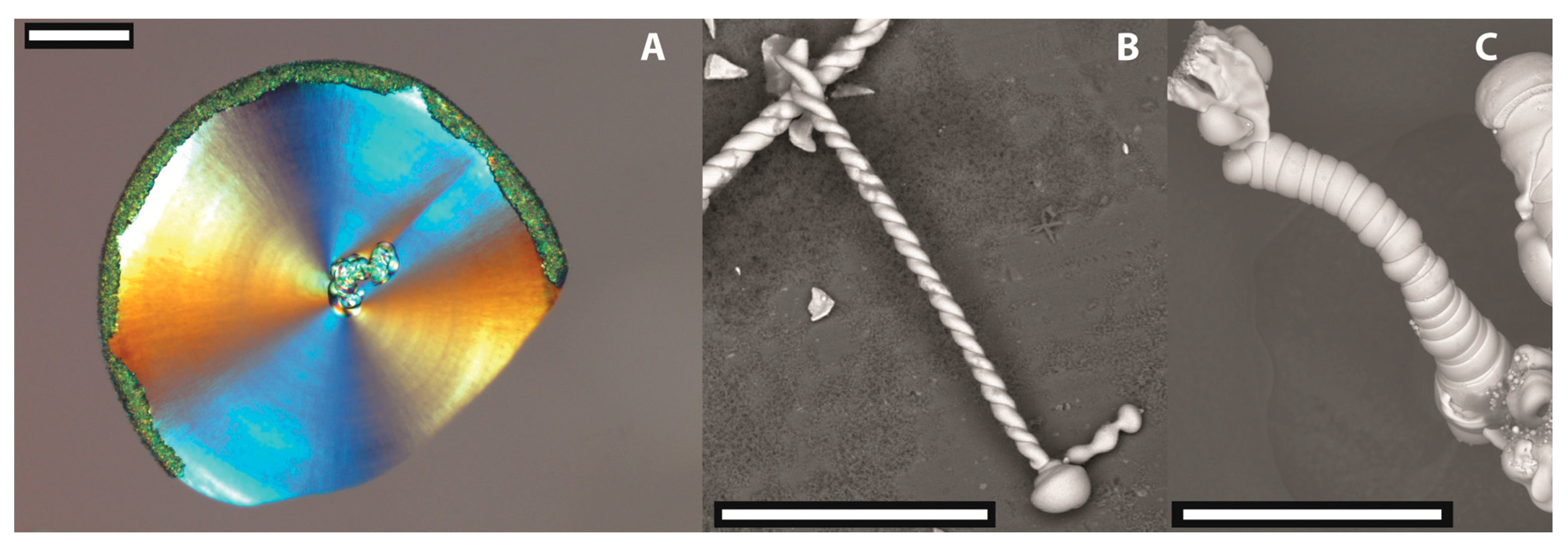7]. On the multimicron scale, these assemblies display intricate morphologies such as flat sheets, helicoids, or tightly wound worms, as shown in Figure 1. While most of the work on silica biomorphs has been carried out with witherite (BaCO₃) as the carbonate phase [4], there is increasing evidence that similar structures can also be obtained with other carbonates, including orthorhombic analogues like strontianite (SrCO₃) [8,9] or aragonite (CaCO₃) [10,11,12].

The mechanisms enabling the structural and morphological complexity observed in this simple inorganic system have been investigated in detail over the past decade, focusing on both the molecular interactions driving self-assembly at the nanoscale and phenomenological aspects determining the final appearance at the micro- and nanoscales [6,13,14,15,16]. With respect to the latter, it was found that growth of biomorphs occurs in two general stages. At the beginning of the crystallisation process, small witherite crystals nucleate and grow in a more or less classical way. With time, oligomeric silica species induce fractal branching at the tips of the carbonate crystal, causing progressive bifurcation and ultimately resulting in closed cauliflowerlike spherulites [2,17,18,19]. At this point, the system passes into the second stage, which is characterised by polycrystalline growth, i.e. numerous nanocrystals are nucleated continuously and/or episodically and co-assemble into aggregates with shapes beyond any constraints of crystallographic symmetry. Typically, the first type of morphologies observed in this stage are flat sheets (Figure 1A), which grow along vessel walls or the solution–air interface. Randomly, these laminar structures start to curl at their rim and assume a new (orthogonal) growth direction along the perimeter of the sheet, which arrests radial advancement and gives birth to more complex three-dimensional shapes. The final morphology is then determined by the interplay of various local parameters, including the relative velocities of growth for different segments as well as their heights. The most common twisted forms obtained at ambient conditions are double helices (Figure 1B) and more tightly scrolled so-called worms (Figure 1C) [2]. In many cases, the carbonate-rich core of the aggregates becomes covered by a layer of amorphous silica, as a result of secondary silica precipitation in the later stages of growth when the bulk pH has been lowered (due to CO₂ uptake) to values where the solubility of silica is noticeably decreased [20].

At the molecular level, the unique behaviour of these inorganic precipitation systems has been ascribed to the pH-mediated coupling of the speciations of carbonate and silicate in solution [2]. As the two components have opposite trends in terms of solubility as a function of pH, it was proposed that they continuously stimulate each other’s mineralisation by periodic changes in the local conditions at actively growing fronts: carbonate crystallisation reduces the pH in the microenvironment and thus increases the local supersaturation of silica, which in turn will precipitate and thereby re-increase the pH-shifting the local carbonate speciation to the side of CO₃²⁻ and hence triggering a new event of carbonate nucleation. This coupled chemistry allows numerous silica-coated carbonate nanocrystals to be produced and integrated into the forming superstructures as building units. Indeed, the postulated local pH-cycling at the growing front could be verified experimentally in recent studies by using pH-sensitive fluorescent dyes [14,16].

Interestingly, most of the observations supporting the mechanisms described above were made for the formation of biomorphs in solution or gels under ambient conditions and within a narrow range of concentrations suitable for the growth of the most striking morphologies. However, it is well known already from early works [21] that the structural variety of silica biomorphs is not at all limited to the forms displayed in Figure 1, but can be significantly expanded by adjusting conditions such as pH, salinity and temperature, or by introducing certain additives that are able to interfere with the growth process [3,6,7,22,23,24,25]. In the present work, we have re-evaluated the role of temperature in biomorph formation, in order to discuss corresponding changes of structure and morphology in light of the current model of morphogenesis. We show that temperature variation is a straightforward means to obtain further interesting ultrastructures, if the conditions are carefully chosen. The resulting narrow distribution of morphologies highlights the possibility of shape control in these systems, which seems crucial for the targeted design of related materials with potential for actual applications [26,27]. Further experiments performed in the presence of added multivalent ions at room temperature expand the range of accessible morphologies and provide support for a morphogenetic scenario in which the relative rates of silica and carbonate mineralisation determine the evolution of the system on the micron scale.

2. Materials and Methods

2.1. Materials and Sample Preparation

Barium chloride dihydrate (>99%), sodium hydroxide (reagent grade, >98%), lanthanum chloride heptahydrate (≥99.9%), and sodium silicate solution (commercial water glass, containing ~10.6% Na₂O and ~26.5% SiO₂, reagent grade, density: 1.39 g/mL) were purchased from Sigma-Aldrich and used without further purification. All solutions were prepared using MilliQ water with a conductivity of 18 µS/cm. Suitable silicate sols were obtained by diluting 1.39 g of water glass in 349 mL of water. The pH of the resulting sol was adjusted to 11.3 (at 25 °C) by adding aliquots of 0.1 M NaOH solution. Crystallisation experiments were carried out in 24-well plates (Linbro) by mixing 1 mL of the dilute silicate solution with 1 mL of BaCl₂ solution at different concentrations (5–500 mM). Optionally, 2 mM LaCl₃ was dissolved in the BaCl₂ solution prior to mixing with the silica sol. Subsequently, the well plates were covered loosely with a lid and stored, respectively, at room temperature (25 °C) or inside a temperature-controlled oven (30–50 °C) or a cooling chamber (5–20 °C) for 12 h in contact with air, to enable diffusion of CO₂ into the systems and slow crystallisation of BaCO₃ under the influence of silica species.

2.2. Analytical Methods

The pH of the mother solutions was measured by a pH meter (Eutech pH 510) before growth. The formed mineral structures were characterised routinely by means of polarised light microscopy (PLM), using a Nikon AZ100 microscope (Nikon Co., Tokyo, Japan) and an Imager M2m from Zeiss (Jena, Germany). In selected cases, scanning electron microscopy (SEM) was performed on a Zeiss EVO15 microscope (Carl Zeiss SMY Ltd., Cambridge, UK). To obtain suitable specimens for the SEM studies, biomorphs were grown on indium tin oxide (ITO) substrates (Osslia), which were placed in Petri dishes with either 35 or 60 mm diameter and covered with 4–8 mL of growth solution.

3. Results and Discussion

In order to investigate the effect of temperature on the formation of silica biomorphs, barium carbonate was crystallised using silica-containing solutions at a fixed composition ([SiO₂] = 17.8 mM and pH = 11.3 (at 25 °C) before mixing with BaCl₂ solution) and varying the temperature between 5 and 50 °C. Figure 2 provides an overview on characteristic structures formed at different temperatures and barium concentrations (i.e., a so-called morphodrome).

Under “standard” conditions (25 °C and 5 mM BaCl₂, Figure 2F), extended flat sheets and helicoids (often intergrown) are observed, as expected and similar to the structures shown in Figure 1. These morphologies can thus be considered as a reference. We note that most of these complex structures emerge from small closed globular particles (or aggregates thereof, as indicated by the arrow in Figure 2F). They form in the fractal regime which has to be very short/fast for such small and discrete morphologies to be observed at the end of the chosen period of growth (12 h).

When the barium concentration is increased to 10 mM (Figure 2J), the total number of aggregates is higher and in particular the sheets grew slightly larger on average. In turn, a Ba²⁺ concentration of 2.5 mM results in fewer, smaller, and less defined structures (Figure 2B), but generally the morphologies are not strongly altered at both higher and lower amounts of cations in the given concentration range. By contrast, lowering the temperature to 5 °C changes the picture fundamentally, as most of the morphologies observed at 2.5 and 5 mM BaCl₂ were isolated globular or cauliflowerlike structures (Figure 2A,E), and only few poorly developed polycrystalline aggregates were formed at 10 mM even after 24 h (such as the small sheet in Figure 2I). This indicates that growth is terminated at the end of the fractal stage in most cases, i.e., the system fails to enter the second stage of dynamic nanocrystal formation and aggregation. In other words, the conditions prevailing in these experiments do not allow for chemically coupled co-precipitation to be initiated and/or maintained. Probably, this behaviour is related to temperature-dependent changes in the kinetics of carbonate and/or silica mineralisation, caused by differences in either diffusive transport of reactants or the relative rates of precipitation. Generally, the following trends and related consequences are expected with increasing temperature:

• Decrease in the solubility of BaCO₃ [28]: higher carbonate supersaturation, higher driving force for carbonate precipitation (thermodynamic factor);
• Decrease in the solubility of CO₂ in water [29]: reduced rate of CO₂ uptake from the atmosphere, slower carbonate precipitation due to diffusion limitation (kinetic factor);
• Acceleration of silica condensation kinetics [30]: reduced rate of silica polymerisation, faster SiO₂ precipitation (kinetic factor);
• Increased solubility of silica [31]: decrease in silica supersaturation, lower driving force for precipitation (thermodynamic factor);
• Increase in the ionic product of water [32]: higher effective pH at the same composition, leading to lower carbonate solubility and higher silica solubility (thermodynamic factor).

Based on these qualitative considerations, it seems reasonable to assume that the growth rates of both silica and carbonate are not sufficiently high to allow for complex ultrastructures to form at lower temperatures. This can be resolved to some extent by increasing the barium concentration (Figure 2I), but the influence of temperature appears to be dominant.

At higher temperatures (35 and 45 °C), there are also regions in the morphodrome where well-developed biomorphs are barely observed. This is particularly true for lower and higher barium concentration (Figure 2C,D,K,L). In the former case (2.5 mM BaCl₂), the slower rate of carbonate formation (lower supersaturation and reduced CO₂ uptake) can probably not supply enough building units to keep the pace of the accelerated silica condensation processes. In turn, at 10 mM BaCl₂ another effect comes into play, namely the electrostatic screening of negative charges on silicate species by dissolved divalent cations like Ba²⁺ [22]. This bridging interaction catalyses silica condensation and—along with the higher temperature—is expected to accelerate silica precipitation kinetics in a way that is less or not suitable for coupling with carbonate formation. As opposed to that, proper conditions for 3D self-assembly are still maintained at the “standard” barium concentration of 5 mM and temperatures up to 45 °C. Here, however, the resulting biomorphs show substantially different morphologies than at room temperature and 5 mM Ba²⁺ ion concentration, with large (>100 µm) trumpetlike forms representing the major population of ultrastructures. When the temperature is increased to 45 °C the biomorphic landscape changes again and highly branched crystal networks are observed, as shown in Figure 2D,H,L. These structures likely derive from a fractal route that shows substantially different branching behaviour than at room temperature. Here, the initial pseudo-hexagonal twinned crystal core transforms into an open star-like architecture that is poorly filled with silica–carbonate composite matter. In some cases, sheet-like domains are formed in between branches, but these structures are often heavily bended and limited in their growth by the mother crystal branches (cf. Figure 2H). This suggests that an increase in temperature changes the branching kinetics, presumably via modulated interactions between growing carbonate surfaces and dissolved silicate species that adsorb specifically on certain witherite faces. One potential scenario is that the accelerated carbonate precipitation gives the silica less time to interfere. Alternatively, the speciation of silica in solution may shift to larger oligomers that show different affinities to interact with specific carbonate faces, thus resulting in a different branching behaviour. In any case, high temperature in combination with high barium concentrations leads to a significant increase in the amount of precipitated matter (probably due to faster carbonate and silica formation). This is shown in Figure 2L, where large networks of tubular filaments and/or twisted ribbons are seen along with various other types of biomorphic morphologies. Interestingly, these forms are much thinner than biomorphs grown at ambient temperature, again indicating important changes in relative growth rates of the components. In summary, the most outstanding feature of the morphodrome established in our study was the formation of biomorphic ultrastructures with trumpetlike appearance. They can sporadically be obtained at temperatures above 30 °C and replace all sheet-like and most twisted morphologies at temperatures above 40 °C.

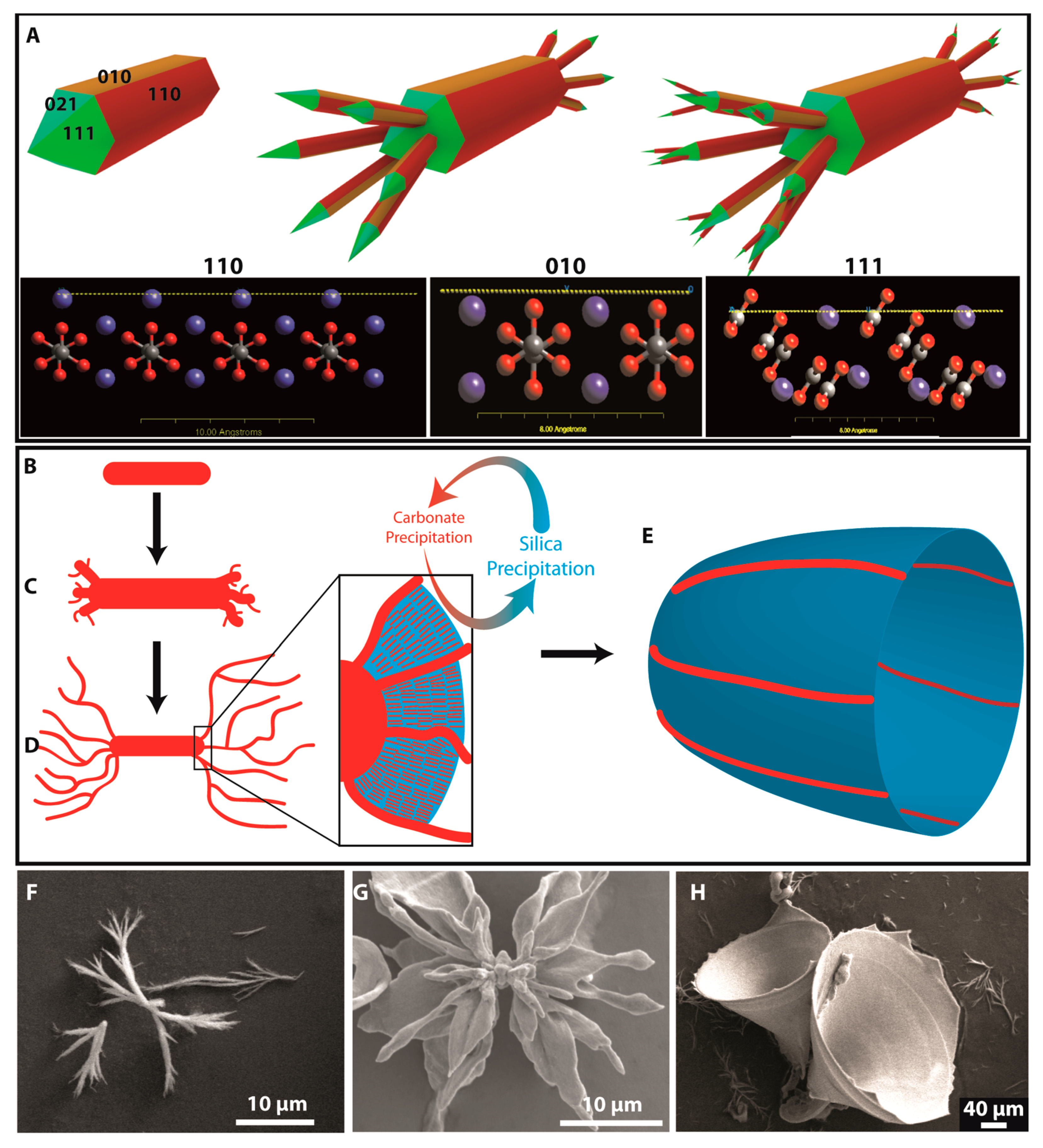
The formation process of the trumpetlike structures was analysed in more detail, in particular with respect to both differences and similarities compared to biomorph growth at room temperature, which leads to twisted (worms and helicoids) and flat sheet-like (as described in previous works [2,3,4] and shown in Figure 1). Figure 3 provides schematic representations of the occurring processes (panels A and B–E) along with selected SEM images showing the relevant stages of growth (panels F–H).

Despite the absence of any of the three “standard” morphologies, the nature of the polycrystalline growth mechanism in the second stage of morphogenesis seems comparable to the corresponding processes at room temperature, based on the characteristic thickness oscillations observed for example in Figure 3H and detailed analysis of the texture of the aggregates at the nanoscale [3,15,16]. Consequently, the main difference leading to distinct final shapes must occur at the beginning of the structure formation. As at ambient conditions, morphogenesis starts with fractal branching of a twinned pseudo-hexagonal witherite crystal due to the poisoning influence of oligomeric silica species (Figure 3A). Closer analysis of the carbonate surfaces suggests that adsorption of silicate species (Bittarello et al. [33]) will mainly occur on the positively charged (110) faces but also on the polar (010) faces (cf. Figure 3A). At higher temperatures, the branching behaviour is different, though, and the first step is a splitting into up to six crystal arms, as silicate-covered (110) and (010) faces are blocked while the remaining (021) and (111) faces can serve for heterogeneous nucleation of the up to six crystal arms in a more or less unhindered fashion, as indicated in Figure 3A. This process repeats itself and produces second-generation branches. Increasing the temperature leads to more ordered and larger branched entities as drawn in Figure 3B–D, compared to the much smaller and heavily bifurcated dumbbell-shaped, spherical or raspberry-like forms observed at room temperature (cf. Figure 1). This suggests that branching at high temperature is more symmetric and of lower dimensionality than at ambient conditions, where a much higher branching density and thus much less symmetric architectures are observed. In other words, branching is more chaotic at low temperature and becomes well-defined at high temperature. This could be related to changes in silica condensation kinetics at higher temperatures, leading to different silica speciation and thus to different affinities of silicate species to adsorb on the different relevant carbonate faces, as already proposed above. That, together with changes in the growth rates of carbonate faces, could explain the different branching behaviour at elevated temperatures [28,30]. Once these open branched structures are formed (Figure 3F), the system enters into the second stage of morphogenesis, where the accelerated kinetics of the precipitation of both components leads to a fortification of the autocatalytic mechanism, which then seems to stay in the tolerant zone for coupled co-precipitation to work. However, the resulting nanocrystals do not assemble into the well-known shapes observed at room temperature, but seem to fill the space in between the large branches formed in the first stage of fractal branching (Figure 3G), leading to selective biomorphic growth from open branched fractals into trumpet-like structures (Figure 3H) according to a mechanism as indicated schematically in Figure 3D,E. Thereby, each structure is unique and shows its own interesting shape, which seems to depend on the orientation of the branches. The pathway to the trumpet structure skips the formation of globular particles and leads directly to 3D architectures of silica–barium carbonate composites with curved surfaces. The dominant effect causing this behaviour could be the increased silica solubility, which allows the system more time to develop in a defined manner throughout the fractal stage. Then, the second stage of morphogenesis is entered before a high degree of branching would lead to closed globular structures. Interestingly, the multiple limbs lead to only one final trumpet structure in most cases, suggesting that the different smaller leaf-like domains fuse to one surface or only the most pronounced leaf develops to the final shape.

During the secondary growth process, the orientation of the growing crystals is crucial. When the experiments are conducted under the same conditions but in petri dishes, where the surface/volume ratio is much higher than in the linbro plates, the reaction leads to trumpet-like structures with wider spreading exhausts. Some examples of these forms are shown in Figure 4A,C.

As it can be noticed, these structures look similar to a marine coccolith element (cf. Figure 4B) [34]. A model of the possible mechanism is presented in Figure 4D. When linbro plates are used, supersaturation is lower and biomorphic aggregates have a narrower shape. Since the petri dish setup favours the availability of CO₂ and therefore the carbonate in the growing front, a higher supersaturation with respect to barium carbonate and a consequently sharper drop of pH (and higher supersaturation with respect to silica) would be explained. This phenomenon is even more evident once the precipitation occurs nearer to the solution/atmosphere interface. It would also explain the spreading of the branches due to a faster (secondary) growth stage. A similar behaviour was already observed in higher concentrated solution and the spreading could be triggered with a CO₂ burst [35]. Therefore, it can be assumed that this sharp saturation gradient explains this behaviour when completely upright structures are forming. When tilted structures form under the influence of the CO₂, biomorphic aggregates develop irregular exhaust orientation as the one shown in Figure 4C. Additionally, a continuum of different morphologies can be detected in Figure 4A,C,F. In Figure 4A a transformation from a sheet over a small ribbon to the final trumpet can be found while C shows a reverse exfoliation from a rolled-up trumpet to a 2D sheet-like structure while Figure 4E demonstrates a continuum of shapes and a transition of a trumpet at elevated temperatures into two helicoidal structures.

Further lifelike morphologies can be produced by increasing the barium concentration (Figure 4G; [Ba²⁺] = 250–500 mM), which shift the formation mechanism as well. [36]. The obtained brain coral-like structures skip the formation of a globular centre, have a nearly perfect spherical shape, and consist of a network of interpenetrating sheet-like units which merge out of the leaf-like parts liked at the seed crystal (similar pathway presented in Figure 3). Their formation is already described by Hyde et al. [36] and reviewed here with consideration of newly obtained knowledge. The formation of these structures follows a similar pathway compared to the trumpets because their formation skips the production of a globular centre. Coral-like architectures can be obtained in a modified way with 5 mM Ba²⁺ ions in solution by using modifiers such as cationic surfactants like CTAB [7] or multivalent ions like La³⁺. Using such modifiers, similar but more homogenous morphologies were obtained and are shown in the SEM micrograph in Figure 4H. The formation is again influenced in the first stage of the formation which is in good accordance with time-resolved experiments with CTAB additions. An addition of CTAB after a few minutes does not lead to coral structures and “standard” biomorphs will be obtained. At first sight, it is comprehensible that an increase of the pure number of multivalent ions like Ba²⁺ (tested before) or La³⁺ has a similar effect on the system despite the effect on silica precipitation, which is in good accordance with the Schulze–Hardy law [37]. A faster silica formation and a reduced colloidal stability by multivalent cations show similarity to the ultrastructures obtained at elevated temperature. Multivalent ions are known as efficient agents to bridge charged colloids or oligomers like silica [38]. Furthermore, these ions will not be free charged ions within this system due to their tendencies to form complexes with hydroxide, carbonate, and silicate ions to reduce their effective charge. In the end it should be noted that La³⁺ as an additive has less effect on the carbonate precipitation rate and that no significant lanthanum adsorption within the BaCO₃ lattice was detected. Additionally, a higher ionic strength depresses the CO₂ uptake rate and its solubility in water, which again leads to a deterioration of the carbonate formation [39]. Therefore, we can assume an extreme of a reduced fractal regime time in the case of coral-like structures. As shown in literature, upon the addition of sodium chloride (note the single charge of Na⁺) to the standard procedure, the process will not enter the second stage at all and the crystal formation stops after the formation of the globular particles formed in the first stage (described by Eiblmeier et al. [22]). A reason for this might be the shifting of the equilibrium of free and sodium-coordinated silicate species to the sodium terminated side [40]. Therefore, less silica is available for the autocatalytic process, which is in line with observations made with decreased silica concentrations, and the resident time in the fractal regime is much longer and globules are formed.

4. Conclusions

The presented work describes the influence of several parameters on biomorph growth and highlights the formation process of reported and unreported lifelike morphologies. The individual impact of the temperature, supersaturation, and ions as additives on carbonate and silica formation is discussed in detail and meaningful, plausible explanations were given for the formation mechanism of the strongly bended morphologies. We showed a linkage between coral- and trumpet-like structures and that a continuum of shapes is possible. Influences of the various and further tuning parameters like the effects of the growth direction and surface/volume ratio were tested. The most exciting growth conditions to lifelike morphologies were highlighted and allow a superior reproducibility.