Abstract
Since the advent of Drinfel’d’s double construction, Hopf algebraic structures have been a centrepiece for many developments in the theory and analysis of integrable quantum systems. An integrable anyonic pairing Hamiltonian will be shown to admit Hopf algebra symmetries for particular values of its coupling parameters. While the integrable structure of the model relates to the well-known six-vertex solution of the Yang–Baxter equation, the Hopf algebra symmetries are not in terms of the quantum algebra Uq(sl(2)). Rather, they are associated with the Drinfel’d doubles of dihedral group algebras D(Dn).
1. Introduction
Integrable quantum systems which admit exact solutions are central in advancing understanding of many-body systems. Classic examples are provided by the Heisenberg spin chain [1], the Bose [2] and Fermi [3] gases with delta-function interactions, the Bardeen–Cooper–Schrieffer pairing Hamiltonian with uniform scattering interactions [4], and the Hubbard model in one dimension [5]. With the development of the Quantum Inverse Scattering Method [6] as a systematic prescription for constructing integrable quantum systems through the Yang–Baxter equation [3,7,8], and solving them through the algebraic Bethe ansatz, it subsequently emerged that Hopf algebraic structures are fundamental in quantum integrability. The works of Jimbo [9] and Drinfel’d [10] were instrumental in formulating the notion of quantum algebras 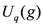 , deformations of the universal enveloping algebras of a Lie algebra g, which have the structure of a quasi-triangular Hopf algebra. The significance of the quasi-triangular structure is that it affords an algebraic solution of the Yang–Baxter equation. Matrix solutions of the Yang–Baxter equation are then generated through representations of these algebras. The simplest example of the two-dimensional loop representation of the untwisted affine quantum algebra
, deformations of the universal enveloping algebras of a Lie algebra g, which have the structure of a quasi-triangular Hopf algebra. The significance of the quasi-triangular structure is that it affords an algebraic solution of the Yang–Baxter equation. Matrix solutions of the Yang–Baxter equation are then generated through representations of these algebras. The simplest example of the two-dimensional loop representation of the untwisted affine quantum algebra  leads to the six-vertex model solution of the Yang–Baxter equation, which establishes integrability of the anisotropic (XXZ) Heisenberg chain. The precise form of six-vertex solution obtained depends on the choice of gradation for
leads to the six-vertex model solution of the Yang–Baxter equation, which establishes integrability of the anisotropic (XXZ) Heisenberg chain. The precise form of six-vertex solution obtained depends on the choice of gradation for  . The principal gradation leads to the symmetric solution, while the homogeneous gradation leads to an asymmetric solution [11]. Only in the latter case is the solution invariant with respect to the action of the non-affine subalgebra
. The principal gradation leads to the symmetric solution, while the homogeneous gradation leads to an asymmetric solution [11]. Only in the latter case is the solution invariant with respect to the action of the non-affine subalgebra 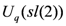 .
.
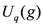 , deformations of the universal enveloping algebras of a Lie algebra g, which have the structure of a quasi-triangular Hopf algebra. The significance of the quasi-triangular structure is that it affords an algebraic solution of the Yang–Baxter equation. Matrix solutions of the Yang–Baxter equation are then generated through representations of these algebras. The simplest example of the two-dimensional loop representation of the untwisted affine quantum algebra
, deformations of the universal enveloping algebras of a Lie algebra g, which have the structure of a quasi-triangular Hopf algebra. The significance of the quasi-triangular structure is that it affords an algebraic solution of the Yang–Baxter equation. Matrix solutions of the Yang–Baxter equation are then generated through representations of these algebras. The simplest example of the two-dimensional loop representation of the untwisted affine quantum algebra  leads to the six-vertex model solution of the Yang–Baxter equation, which establishes integrability of the anisotropic (XXZ) Heisenberg chain. The precise form of six-vertex solution obtained depends on the choice of gradation for
leads to the six-vertex model solution of the Yang–Baxter equation, which establishes integrability of the anisotropic (XXZ) Heisenberg chain. The precise form of six-vertex solution obtained depends on the choice of gradation for  . The principal gradation leads to the symmetric solution, while the homogeneous gradation leads to an asymmetric solution [11]. Only in the latter case is the solution invariant with respect to the action of the non-affine subalgebra
. The principal gradation leads to the symmetric solution, while the homogeneous gradation leads to an asymmetric solution [11]. Only in the latter case is the solution invariant with respect to the action of the non-affine subalgebra 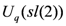 .
.The work of Drinfel’d [10] also provides a means to construct a quasi-triangular Hopf algebra from any Hopf algebra and the dual algebra, through a procedure known as the double construction. The double construction applied to finite group algebras [12] yields a framework in which to develop anyonic models that lead to notions of topological quantum computation [13]. In a series of works [14,15,16], solutions of the Yang–Baxter associated with Drinfel’d doubles of dihedral group algebras, denoted D(Dn), have been studied. In particular, it was found that two-dimensional representations of these algebras belong to the aforementioned six-vertex model solution in the symmetric case. The symmetric solution was employed in [17] to construct an integrable anyonic pairing Hamiltonian, which generalises the pairing Hamiltonian with uniform scattering interactions solved by Richardson [4]. Below, this integrable anyonic pairing Hamiltonian will be shown to admit Hopf algebra symmetries given by D(Dn) for particular values of the coupling parameters.
2. The Integrable Hamiltonian for Anyonic Pairing
Consider a general anyonic pairing Hamiltonian of the reduced Bardeen–Cooper–Schrieffer form, which acts on a Hilbert space  of dimension 4L, given by
of dimension 4L, given by
 of dimension 4L, given by
of dimension 4L, given by 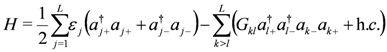
Above, 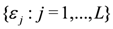 represent single-particle energy levels (two-fold denegerate labelled by
represent single-particle energy levels (two-fold denegerate labelled by 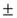 ) and
) and 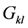 are the pairing interaction coupling parameters of the model. For
are the pairing interaction coupling parameters of the model. For 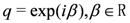 the operators
the operators 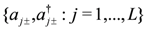 satisfy the relations
satisfy the relations
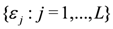 represent single-particle energy levels (two-fold denegerate labelled by
represent single-particle energy levels (two-fold denegerate labelled by 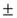 ) and
) and 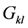 are the pairing interaction coupling parameters of the model. For
are the pairing interaction coupling parameters of the model. For 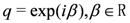 the operators
the operators 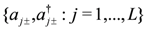 satisfy the relations
satisfy the relations 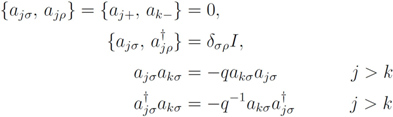
and those relations obtained by taking Hermitian conjugates. Throughout, I is used to denote an identity operator. These types of anyonic operators are considered as q-deformations of fermionic operators, with the usual fermionic commutation relations recovered in the limit 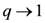 . The anyonic creation and annihilation operators may be realised in terms of the canonical fermionic operators
. The anyonic creation and annihilation operators may be realised in terms of the canonical fermionic operators 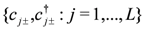 through a generalised Jordan–Wigner transformation
through a generalised Jordan–Wigner transformation
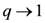 . The anyonic creation and annihilation operators may be realised in terms of the canonical fermionic operators
. The anyonic creation and annihilation operators may be realised in terms of the canonical fermionic operators 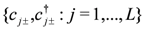 through a generalised Jordan–Wigner transformation
through a generalised Jordan–Wigner transformation 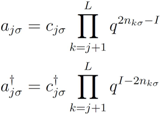
where 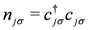 .
.
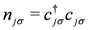 .
.As with the more familiar fermionic pairing Hamiltonians, one of the notable features of Equation (1) is the blocking effect. For any unpaired anyon at level j, the action of the pairing interaction is zero since only paired anyons interact. This means that the Hilbert space can be decoupled into a product of paired and unpaired anyonic states in which the action of the Hamiltonian on the space for the unpaired anyons is automatically diagonal in the natural basis. In view of this property, the pair number operator
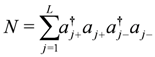
commutes with Equation (1) and thus provides a good quantum number. Below, M will be used to denote the eigenvalues of the pair number operator.
In [17] it was shown that, for a suitable restriction on the coupling parameters, the Hamiltonian is integrable in the sense of the Quantum Inverse Scattering Method and admits an exact solution derived through the algebraic Bethe ansatz. To characterise the integrable manifold of the coupling parameter space, the set of parameters  are introduced with the following constraints imposed:
are introduced with the following constraints imposed:
 are introduced with the following constraints imposed:
are introduced with the following constraints imposed: 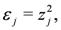
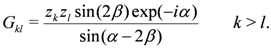
The conserved operators for this integrable model are obtained via the Quantum Inverse Scattering Method in a standard manner. Here, the key steps are noted. A transfer matrix  is constructed as
is constructed as
 is constructed as
is constructed as 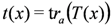
where T(x) is the monodromy matrix and 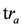 is the partial trace over an auxiliary space labelled by a. The monodromy matrix is required to satisfy the relation
is the partial trace over an auxiliary space labelled by a. The monodromy matrix is required to satisfy the relation
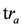 is the partial trace over an auxiliary space labelled by a. The monodromy matrix is required to satisfy the relation
is the partial trace over an auxiliary space labelled by a. The monodromy matrix is required to satisfy the relation 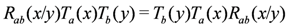
which is an operator equation on 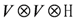 , with the two auxiliary spaces labelled by a and b. Above,
, with the two auxiliary spaces labelled by a and b. Above,
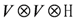 , with the two auxiliary spaces labelled by a and b. Above,
, with the two auxiliary spaces labelled by a and b. Above, 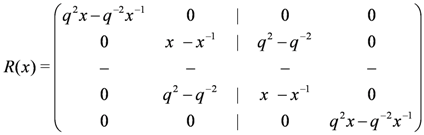
is the six-vertex solution (it is convenient for our purposes to express the deformation parameter as q2 rather than the more familiar q) of the Yang–Baxter equation [3,7,8]
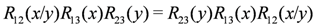
which acts on the three-fold space 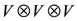 . The subscripts above refer to the spaces on which the operators act, e.g.,
. The subscripts above refer to the spaces on which the operators act, e.g.,
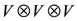 . The subscripts above refer to the spaces on which the operators act, e.g.,
. The subscripts above refer to the spaces on which the operators act, e.g., 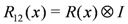
Two important properties of R(x), which will be called upon later, are
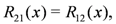
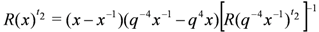
where t2 denotes partial transposition in the second space of the tensor product.
The monodromy matrix is
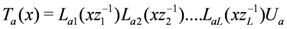
where

and 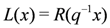 . Bearing in mind the earlier comments regarding the blocking effect, we may write
. Bearing in mind the earlier comments regarding the blocking effect, we may write
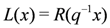 . Bearing in mind the earlier comments regarding the blocking effect, we may write
. Bearing in mind the earlier comments regarding the blocking effect, we may write 
where
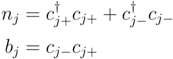
Note that U is defined in a sector-dependent manner in terms of the eigenvalues M of N, which is legitimate since N is conserved.
A consequence of Equation (10), and the diagonal form of U, is that the transfer matrices form a commutative family; i.e.,

The transfer matrices can be expanded in a Laurent series
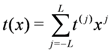
such that, because of Equation (12), the co-efficients commute

Finally it can be verified that the Hamiltonian Equation (1), subject to the constraints of Equations (2,3), is expressible as (the corresponding expression in [17] contains typographical errors, which are corrected here)
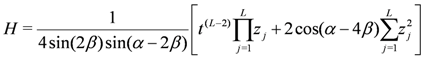
establishing that 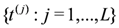 provides a set of Abelian conserved operators for the system. In this sense the system is said to be integrable.
provides a set of Abelian conserved operators for the system. In this sense the system is said to be integrable.
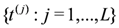 provides a set of Abelian conserved operators for the system. In this sense the system is said to be integrable.
provides a set of Abelian conserved operators for the system. In this sense the system is said to be integrable.In the remainder of this work it will be shown that for certain further restrictions on the coupling parameters there are additional Hopf algebraic symmetries of the system. These non-Abelian symmetries are not related to a quantum algebra 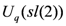 structure, but are realised through the Drinfel’d doubles of dihedral group algebras.
structure, but are realised through the Drinfel’d doubles of dihedral group algebras.
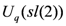 structure, but are realised through the Drinfel’d doubles of dihedral group algebras.
structure, but are realised through the Drinfel’d doubles of dihedral group algebras.3. Drinfel’d Doubles of Dihedral Group Algebras
The dihedral group Dn has two generators 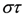 satisfying:
satisfying:
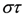 satisfying:
satisfying: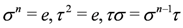
where e denotes the group identity. Considering Dn as a group algebra, the Drinfel’d double [10] of Dn, denoted D(Dn), has basis

where g are the group elements and 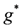 are their dual elements. This gives an algebra of dimension 4n2. Multiplication of dual elements is defined by
are their dual elements. This gives an algebra of dimension 4n2. Multiplication of dual elements is defined by
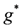 are their dual elements. This gives an algebra of dimension 4n2. Multiplication of dual elements is defined by
are their dual elements. This gives an algebra of dimension 4n2. Multiplication of dual elements is defined by 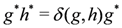
where 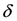 is the Kronecker delta function. The products
is the Kronecker delta function. The products 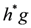 are computed using
are computed using
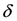 is the Kronecker delta function. The products
is the Kronecker delta function. The products 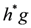 are computed using
are computed using 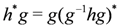
The algebra D(Dn) becomes a Hopf algebra by imposing the following coproduct, antipode and counit respectively:
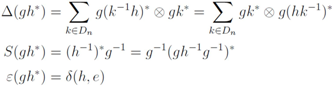
An important property of D(Dn) which will be called upon later is
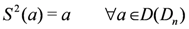
Defining 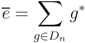 the universal R-matrix is given by
the universal R-matrix is given by
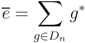 the universal R-matrix is given by
the universal R-matrix is given by 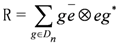
This can be shown to satisfy the relations for a quasi-triangular Hopf algebra as defined in [10]:
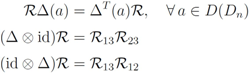
where 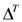 is the opposite coproduct
is the opposite coproduct
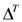 is the opposite coproduct
is the opposite coproduct 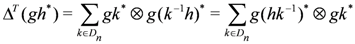
When n is even, D(Dn) admits eight one-dimensional irreducible representations, 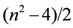 two-dimensional irreducible representations, and eight
two-dimensional irreducible representations, and eight 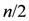 -dimensional irreducible representations. When n is odd, D(Dn) admits two one-dimensional irreducible representations,
-dimensional irreducible representations. When n is odd, D(Dn) admits two one-dimensional irreducible representations, 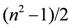 two-dimensional irreducible representations, and two n-dimensional irreducible representations. The explicit irreducible representations are given in [14]. Our interest will be in the two-dimensional irreducible representations. To describe them, let
two-dimensional irreducible representations, and two n-dimensional irreducible representations. The explicit irreducible representations are given in [14]. Our interest will be in the two-dimensional irreducible representations. To describe them, let 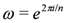 . Then these representations have the form
. Then these representations have the form
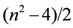 two-dimensional irreducible representations, and eight
two-dimensional irreducible representations, and eight 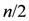 -dimensional irreducible representations. When n is odd, D(Dn) admits two one-dimensional irreducible representations,
-dimensional irreducible representations. When n is odd, D(Dn) admits two one-dimensional irreducible representations, 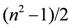 two-dimensional irreducible representations, and two n-dimensional irreducible representations. The explicit irreducible representations are given in [14]. Our interest will be in the two-dimensional irreducible representations. To describe them, let
two-dimensional irreducible representations, and two n-dimensional irreducible representations. The explicit irreducible representations are given in [14]. Our interest will be in the two-dimensional irreducible representations. To describe them, let 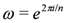 . Then these representations have the form
. Then these representations have the form
for 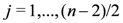 if n is even and
if n is even and 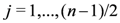 if n is odd,
if n is odd,
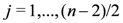 if n is even and
if n is even and 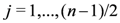 if n is odd,
if n is odd,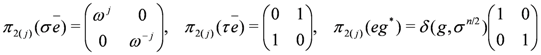
for 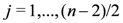 if n is even, and
if n is even, and
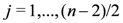 if n is even, and
if n is even, and
for 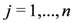 and where
and where 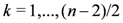 if n is even, and
if n is even, and 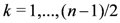 if n is odd.
if n is odd.
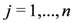 and where
and where 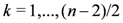 if n is even, and
if n is even, and 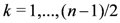 if n is odd.
if n is odd.For any of the above two-dimensional representations 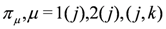 the tensor product representation applied to the universal R-matrix Equation (18) yields the general form
the tensor product representation applied to the universal R-matrix Equation (18) yields the general form
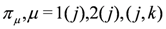 the tensor product representation applied to the universal R-matrix Equation (18) yields the general form
the tensor product representation applied to the universal R-matrix Equation (18) yields the general form 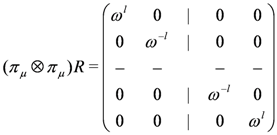
for some 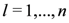 . Choosing
. Choosing 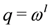 in Equation (6) we then find
in Equation (6) we then find
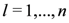 . Choosing
. Choosing 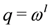 in Equation (6) we then find
in Equation (6) we then find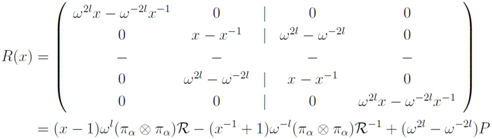
where
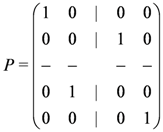
is the permutation operator on the tensor product space. This shows that the Baxterisation of the D(Dn) R-matrix in two-dimensional representations leads to the symmetric six-vertex model at q a root of unity, which was previously reported in [14]. Baxterisation of the D(Dn) R -matrix in higher-dimensional representations lead to the Fateev–Zamolodchikov solution of the Yang–Baxter equation, as discussed in [15,16].
Having identified the relationship Equation (21) between the solution Equation (6) of the Yang–Baxter equation and representations of the universal R-matrix Equation (18) for D(Dn), we can now proceed to determine when D(Dn) is a symmetry algebra of the transfer matrix associated to the Hamiltonian Equation (1) subject to the constraints Equations 2 and 3.
4. Symmetries of the Transfer Matrix and Hamiltonian
First we define
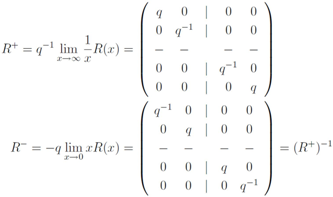
It follows from Equation (7) that
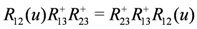
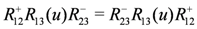
We then define a modified monodromy matrix
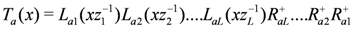
Through use of Equations (7,22,23) it can be shown that this monodromy matrix satisfies a generalised version of Equation (5):
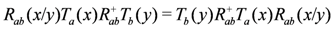
The transfer matrix is again defined by Equation (4). From the results of [18] it is known that Equation (12) still holds by use of Equation (9).
The action of D(Dn) on an L-fold tensor product space is given through iterated use of the co-product action Equation (16):
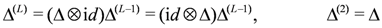
Below, for ease of notation, we will omit the representation symbols  when dealing with tensor product representations obtained through this action. Whenever we have
when dealing with tensor product representations obtained through this action. Whenever we have
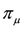 when dealing with tensor product representations obtained through this action. Whenever we have
when dealing with tensor product representations obtained through this action. Whenever we have 
the monodromy matrix Equation (24) commutes with the action of D(Dn) as a consequence of Equations (8–21). From the results of [19], the transfer matrix obtained from Equation (24) also commutes with the action of D(Dn) due to Equation (17).
Observing that we may write
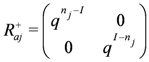
we may simplify Equation (24) as
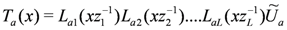
where
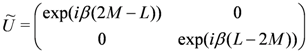
Comparing Equations 11 and 26 and taking note of Equation (25), these matrices are made equal by choosing
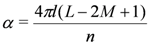
meaning that the transfer matrices obtained from the monodromy matrices Equations 10 and 24 are equal. Thus we have established that the transfer matrix associated to the integrable Hamiltonian Equation (1) subject to the constraints of Equations 2 and 3 commutes with action of the quasi-triangular Hopf algebra D(Dn) whenever Equations 25 and 27 hold.
A crucial point to bear in mind is that the transfer matrices were defined in a sector-dependent manner, where each sector is associated with a fixed number of Cooper pairs. However the D(Dn) action does not preserve sectors, and specifically 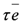 acts as a particle-hole transformation:
acts as a particle-hole transformation:
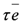 acts as a particle-hole transformation:
acts as a particle-hole transformation: 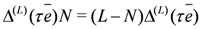
whereas
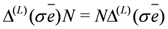
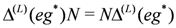
These relations follow from the above two-dimensional matrix representations for which it is seen that representations of 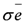 and
and 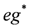 are always diagonal in the basis in which the action of N is diagonal. In the same basis, representations of
are always diagonal in the basis in which the action of N is diagonal. In the same basis, representations of 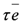 are orthogonal matrices with non-zero off-diagonal entries.
are orthogonal matrices with non-zero off-diagonal entries.
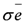 and
and 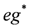 are always diagonal in the basis in which the action of N is diagonal. In the same basis, representations of
are always diagonal in the basis in which the action of N is diagonal. In the same basis, representations of 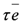 are orthogonal matrices with non-zero off-diagonal entries.
are orthogonal matrices with non-zero off-diagonal entries.Recall that the Hamiltonian is defined through the transfer matrix by Equation (13). Consequently, while D(Dn) is a symmetry of the transfer matrix obtained from Equation (24) in the conventional sense, the interpretation of D(Dn) as a symmetry of the Hamiltonian is more subtle as the choice Equation (27) is sector-dependent and thus α needs to be treated as an operator-valued quantity. From Equation (28) we have for α given by Equation (27) that for each sector where N has eigenvalue M
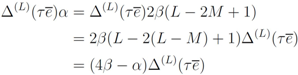
Using Equation (13) we obtain
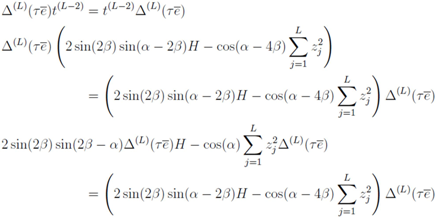
From the trigonometric identity
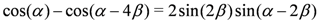
this then leads to the following anti-symmetry relation for the integrable Hamiltonian Equations (1–3) whenever Equations 25 and 27 hold
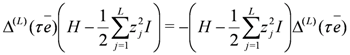
This relation shows how the spectrum of the Hamiltonian maps under a particle-hole transformation 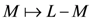 induced by Equation (28). On the other hand,
induced by Equation (28). On the other hand,
 induced by Equation (28). On the other hand,
induced by Equation (28). On the other hand, 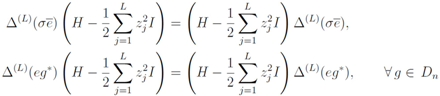
Thus as a result of Equations 29 and 30, the action of 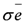 and
and 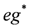 leaves the spectrum of the Hamiltonian invariant in each sector with fixed M.
leaves the spectrum of the Hamiltonian invariant in each sector with fixed M.
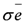 and
and 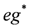 leaves the spectrum of the Hamiltonian invariant in each sector with fixed M.
leaves the spectrum of the Hamiltonian invariant in each sector with fixed M.Finally, if the above procedure is followed using the asymmetric R-matrix
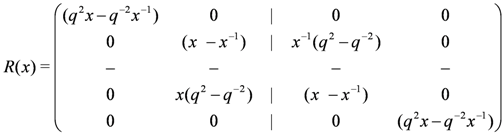
a transfer matrix is obtained which commutes with the co-product action of 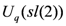 [20,21]. However in this setting the corresponding conserved operator
[20,21]. However in this setting the corresponding conserved operator 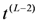 contains additional interaction terms. As a result, an expression analogous to Equation (13) does not yield an operator in the form of Equation (1).
contains additional interaction terms. As a result, an expression analogous to Equation (13) does not yield an operator in the form of Equation (1).
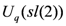 [20,21]. However in this setting the corresponding conserved operator
[20,21]. However in this setting the corresponding conserved operator 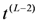 contains additional interaction terms. As a result, an expression analogous to Equation (13) does not yield an operator in the form of Equation (1).
contains additional interaction terms. As a result, an expression analogous to Equation (13) does not yield an operator in the form of Equation (1).5. Conclusions
An analysis of an integrable Hamiltonian for anyonic pairing, as given by Equation (1) subject to Equations 2 and 3, was undertaken. Values of the coupling parameters were identified for which the model admits Hopf algebraic symmetries. In Section 2 the construction of the integrable model was outlined in terms of the Quantum Inverse Scattering Method. This was achieved through the symmetric, six-vertex solution of the Yang–Baxter equation. The Hamiltonian was identified through a conserved operator associated to the corresponding transfer matrix. In Section 3 a description of the quasi-triangular Hopf algebra D(Dn) was presented, including explicit expressions for all irreducible, two-dimensional representations. Through these representations it was established that the symmetric, six-vertex solution of the Yang–Baxter equation is related to representations of the universal R-matrix for D(Dn). These results were utilised in Section 4 to construct a transfer matrix which preserved the D(Dn) symmetry. From this transfer matrix, values of the coupling parameters were identified for which the Hamiltonian Equation (1) subject to Equations 2 and 3 has D(Dn) as a symmetry algebra. However the interpretation of D(Dn) as a symmetry algebra for the Hamiltonian is somewhat unconventional in that both commuting and anti-commuting actions for the generators were found. The anti-commuting action is associated with a particular D(Dn) generator that induces a particle-hole transformation.
Acknowledgments
This work was supported by the Australian Research Council through Discovery Project Topological properties of exactly solvable, two-dimensional quantum systems (DP110101414).
References
- Bethe, H. Zur Theorie der Metalle: I. Eigenwerte und Eigenfunktionen der linearen Atomkette. Zeitschrift für. Physik 1931, 71, 205–226. [Google Scholar] [CrossRef]
- Lieb, E.H.; Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 1963, 130, 1605–1616. [Google Scholar] [CrossRef]
- Yang, C.N. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 1967, 19, 1312–1315. [Google Scholar] [CrossRef]
- Richardson, R.W. A restricted class of exact eigenstates of the pairing-force Hamiltonian. Phys. Lett. 1963, 3, 277–279. [Google Scholar] [CrossRef]
- Lieb, E.H.; Wu, F.Y. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension. Phys. Rev. Lett. 1968, 20, 1445–1448. [Google Scholar] [CrossRef]
- Takhtadzhan, L.A.; Faddeev, L.D. The quantum method of the inverse problem and the Heisenberg XYZ model. Russ. Math. Surveys 1979, 34, 11–68. [Google Scholar] [CrossRef]
- McGuire, J.B. Study of exactly soluble one-dimensional N-body problems. J. Math. Phys. 1964, 5, 622–636. [Google Scholar] [CrossRef]
- Baxter, R.J. Partition function of the eight-vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Jimbo, M. A q-difference analog of U(g) and the Yang–Baxter equation. Lett. Math. Phys. 1985, 10, 63–69. [Google Scholar] [CrossRef]
- Drinfel’d, V.G. Quantum Groups. In Proceedings of the International Congress of Mathematicians; Gleason, A.M., Ed.; American Mathematical Society: Providence, Rhode Island, 1986; pp. 798–820. [Google Scholar]
- Bracken, A.J.; Delius, G.W.; Gould, M.D.; Zhang, Y.-Z. Infinite families of gauge equivalent R-matrices and gradations of quantized affine algebras. Int. J. Mod. Phys. B 1994, 8, 3679–3691. [Google Scholar] [CrossRef]
- Gould, M.D. Quantum double finite group algebras and their representations. Bull. Aust. Math. Soc. 1993, 48, 275–301. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Fault-Tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Dancer, K.A.; Isaac, P.; Links, J. Representations of the quantum doubles of finite group algebras and spectral parameter dependent solutions of the Yang–Baxter equation. J. Math. Phys. 2006, 47, 1–18. [Google Scholar]
- Finch, P.E.; Dancer, K.A.; Isaac, P.; Links, J. Solutions of the Yang–Baxter equation: Descendents of the six-vertex model from the Drinfeld doubles of dihedral group algebras. Nucl. Phys. B 2011, 847, 387–412. [Google Scholar] [CrossRef]
- Finch, P.E. Integrable Hamiltonians with D(Dn) symmetry from the Fateev-Zamolodchikov model. J. Stat. Mech. Theory Exp. 2011. [Google Scholar] [CrossRef]
- Dunning, C.; Ibañez, M.; Links, J.; Sierra, G.; Zhao, S.-Y. Exact solution of the p + ip pairing Hamiltonian and a hierarchy of integrable models. J. Stat. Mech. Theory Exp. 2010. [Google Scholar] [CrossRef]
- Links, J.; Foerster, A. On the construction of integrable closed chains with quantum supersymmetry. J. Phys. A Math. Gen. 1997, 30, 2483–2487. [Google Scholar] [CrossRef]
- Links, J.R.; Gould, M.D. Casimir invariants for Hopf algebras. Rep. Math. Phys. 1992, 31, 91–111. [Google Scholar] [CrossRef]
- Grosse, H.; Pallua, S.; Prester, P.; Raschhofer, E. On a quantum group invariant spin chain with non-local boundary conditions. J. Phys. A Math. Gen. 1994, 27, 4761–4771. [Google Scholar] [CrossRef]
- Karowski, M.; Zapletal, A. Quantum group invariant integrable n-state vertex models with periodic boundary conditions. Nucl. Phys. 1994, 419, 567–588. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).