Surface Pencil Couple with Bertrand Couple as Joint Principal Curves in Galilean 3-Space
Abstract
:1. Introduction
2. Basic Concepts
3. Main Results
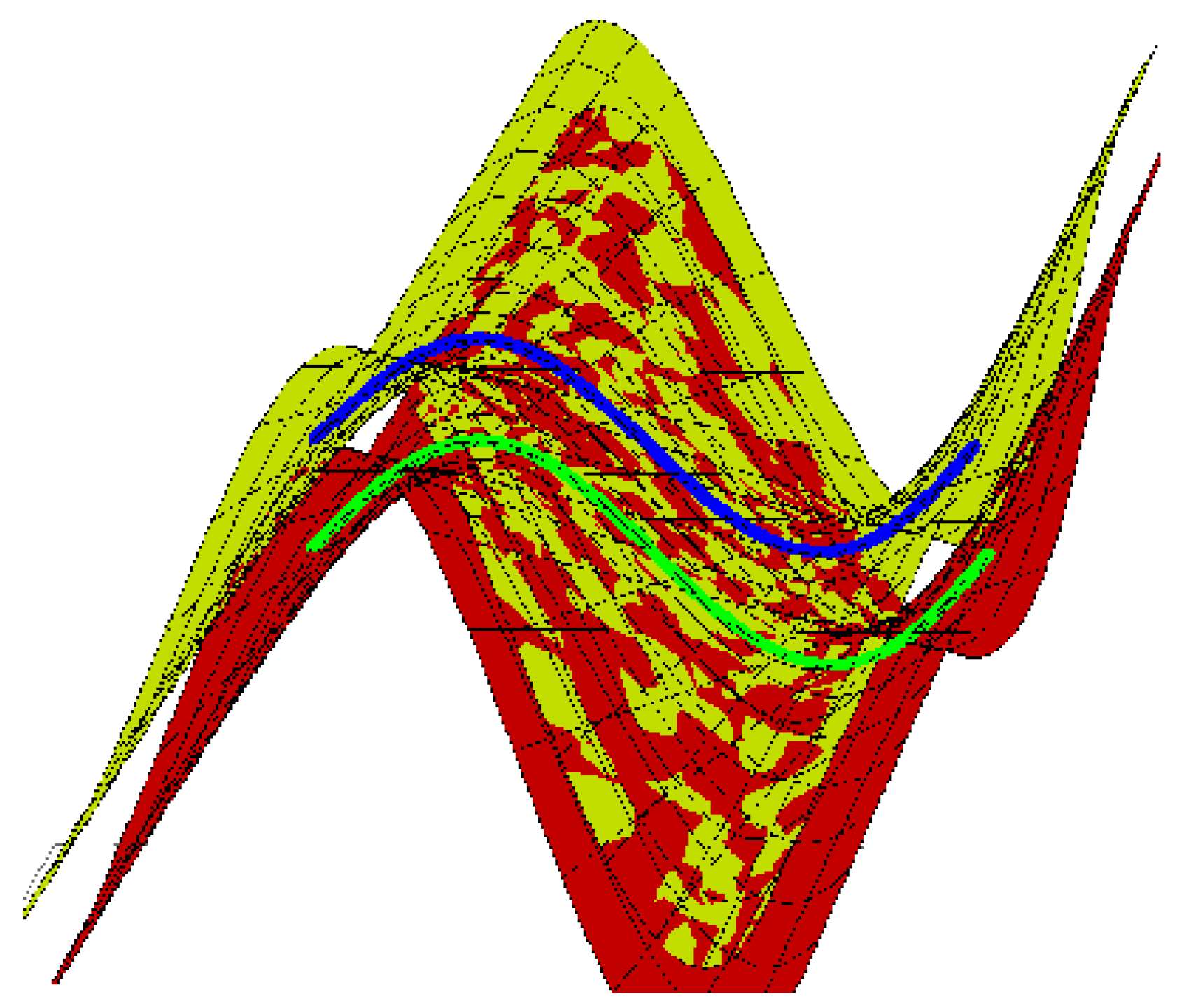
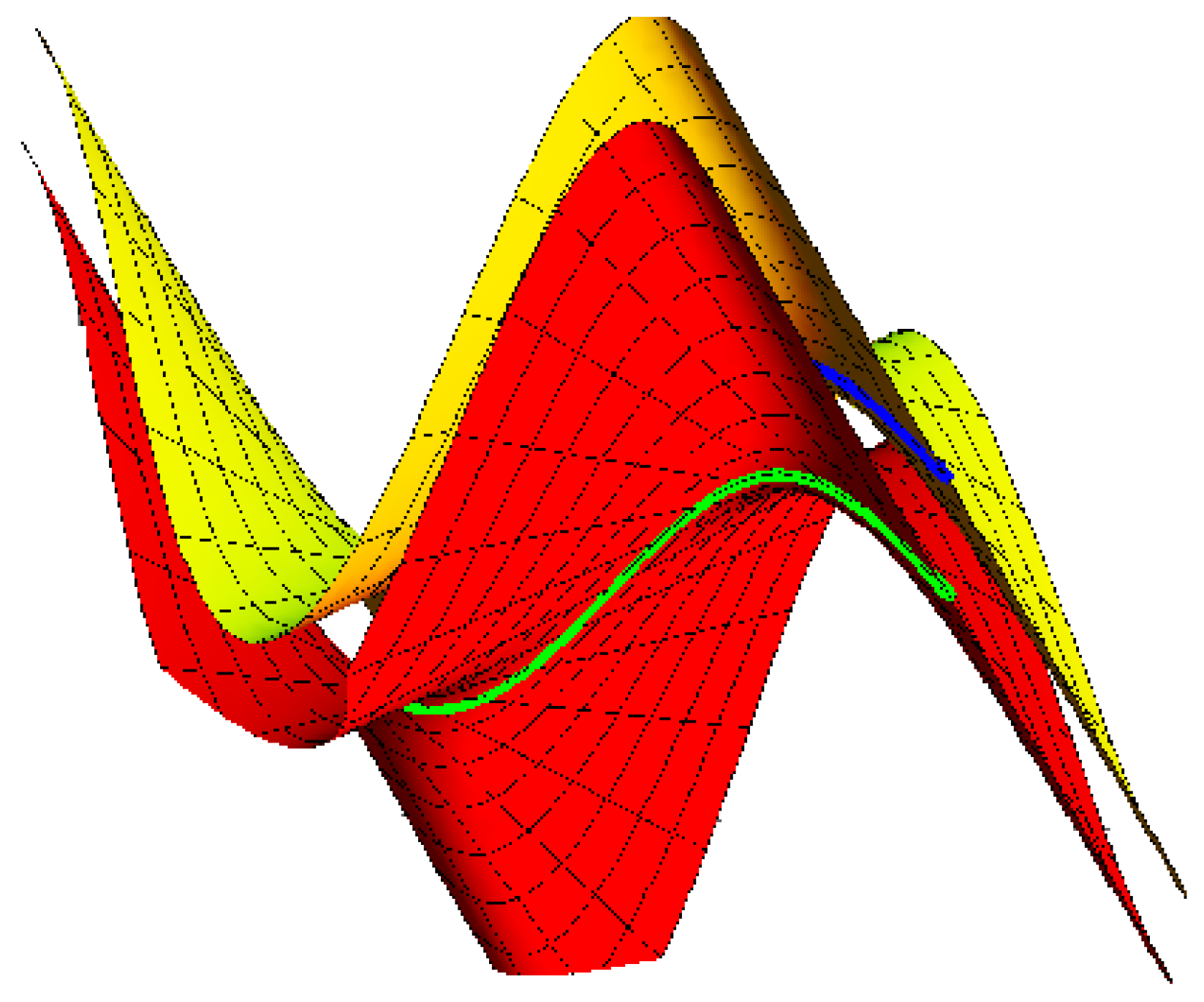
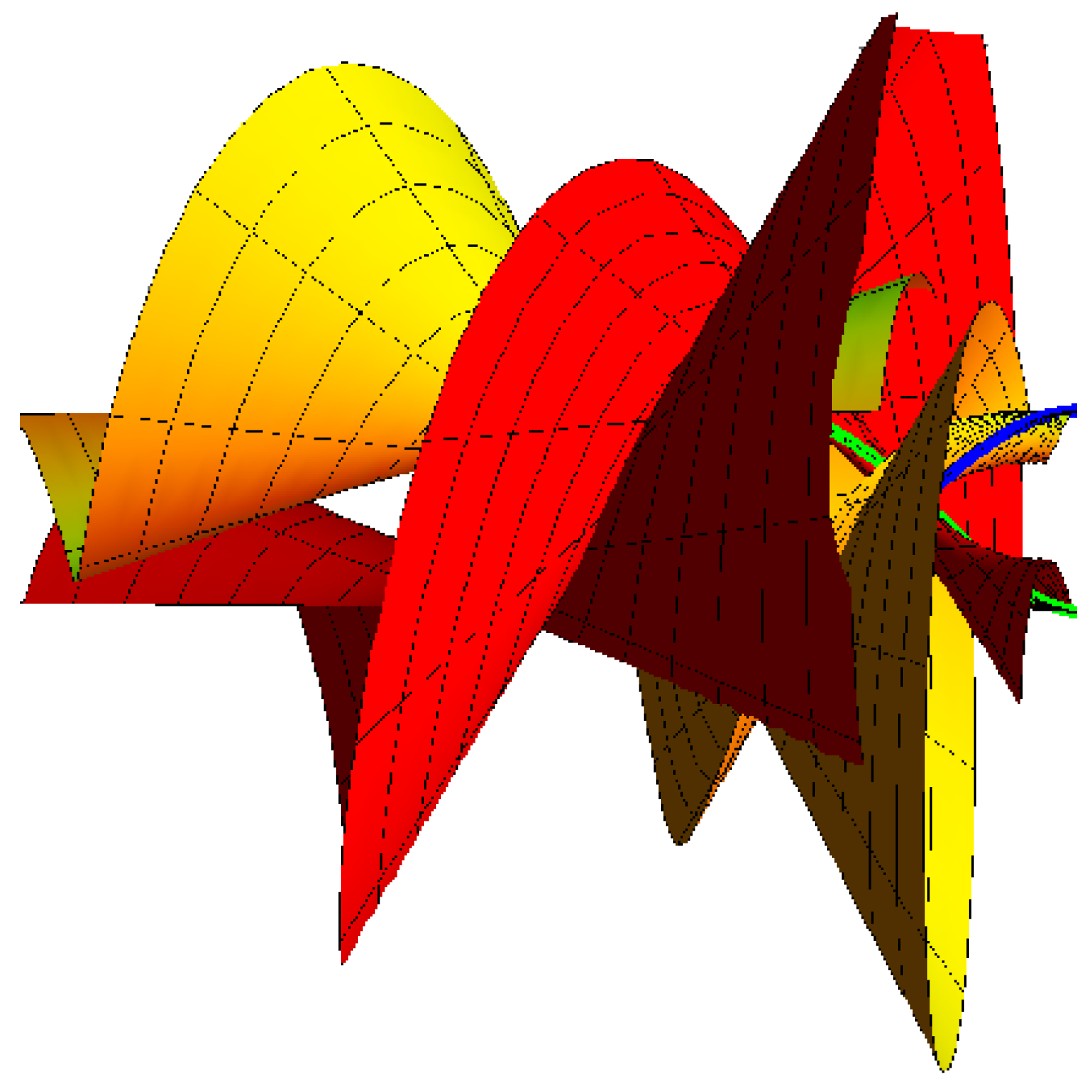
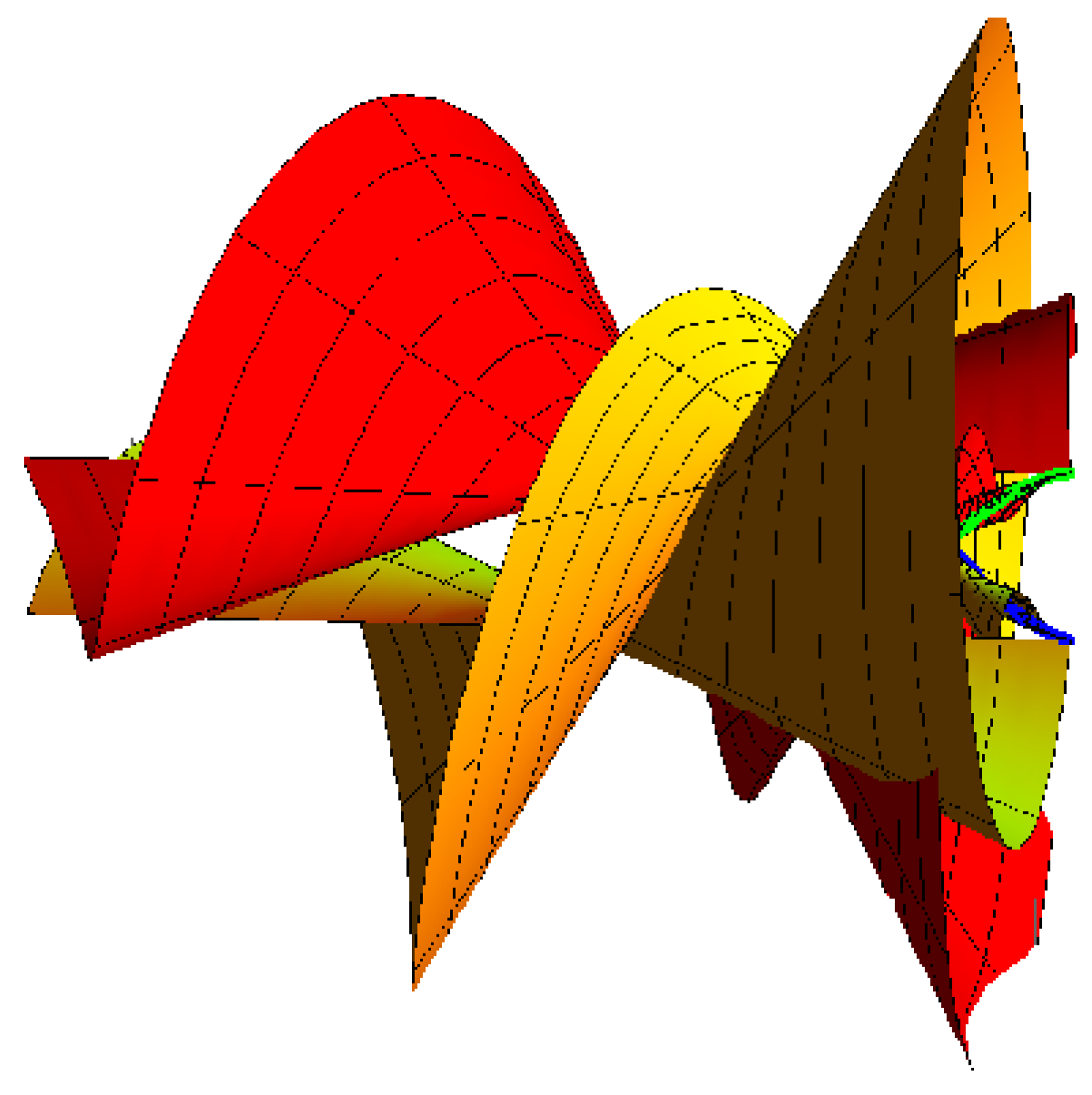
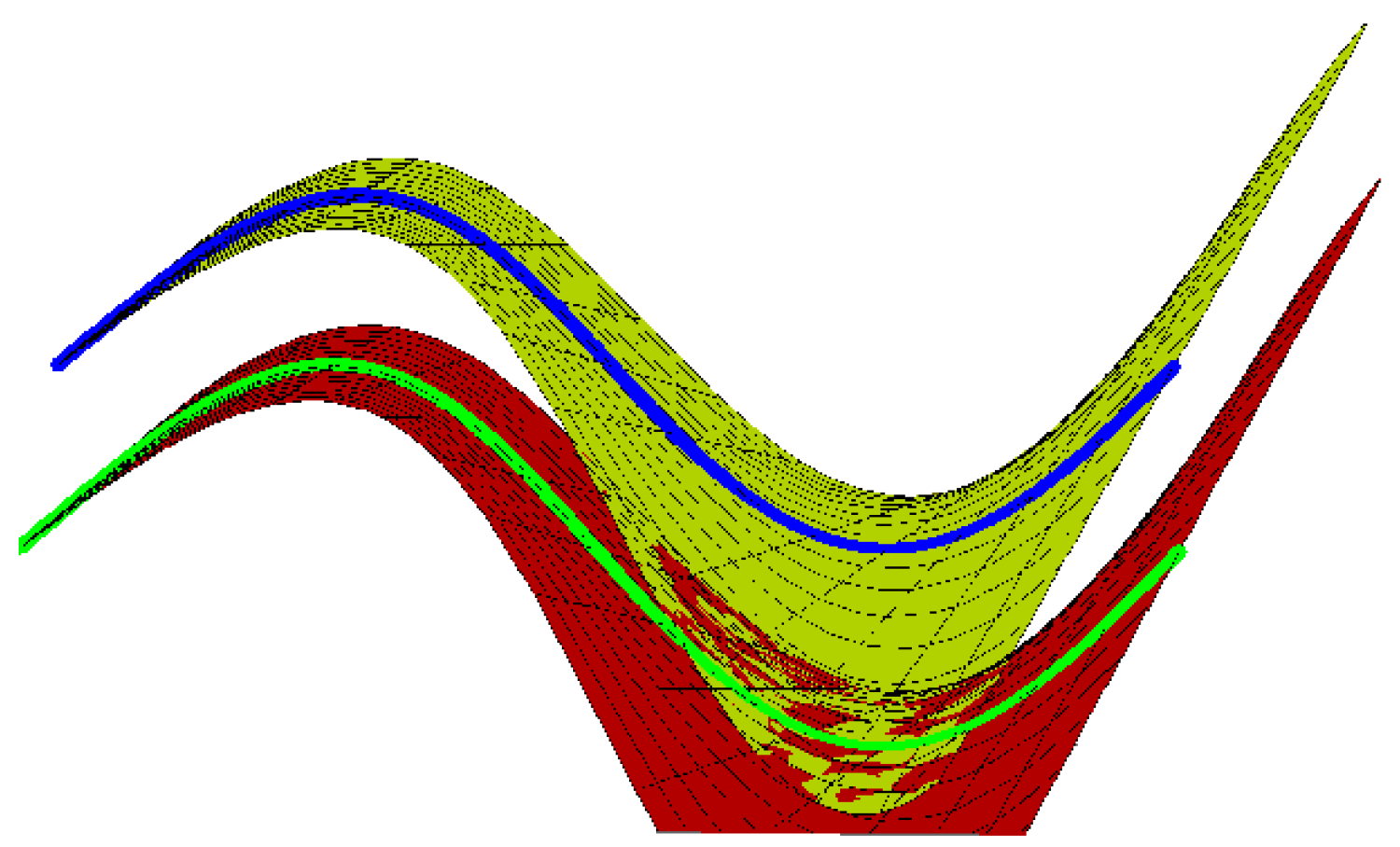
Ruled Surface Pencil Couple with Bertrand Couple as Joint Principal Curves
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Spivak, M. A Comprehensive Introduction to Differential Geometry, 2nd ed.; Publish or Perish: Houston, TX, USA, 1979. [Google Scholar]
- Munchmeyer, F.C. On surface imperfections. In Mathematics of Surfaces II; Martin, R., Ed.; Oxford University Press: Oxford, UK, 1987; pp. 459–474. [Google Scholar]
- Patrikalakis, N.M.; Maekawa, T. Shape Interrogation for Computer Aided Design and Manufacturing; Springer: New York, NY, USA, 2002. [Google Scholar]
- Martin, R.R. Principal patches—A new class of surface patches based on differential geometry. In Eurographics 83, Proceedings of the 4th Ann. European Association for Computer Graphics Conference and Exhibition, Zagreb, Yugoslavia, 31 August–2 September 1983; Ten Hagen, P.J.W., Ed.; North-Holland: Amsterdam, The Netherlands, 1983; pp. 47–55. [Google Scholar]
- Alourdas, P.G.; Hottel, G.R.; Tsohy, S.T. A design and interrogation system for modeling with rational splines. In Proceedings of the Ninth International Symposium on OMAE, Houston, TX, USA; AsME: New York, NY, USA, 1990; pp. 555–565. Volume 1, Part B. [Google Scholar]
- Maekawa, T.; Wolter, F.-E.; Patrikalakis, N.M. Umbilics and lines of curvature for shape interrogation. Comput. Aided Geom. Des. 1996, 13, 133–161. [Google Scholar] [CrossRef]
- Che, W.J.; Paul, J.C. Lines of curvature and umbilical points for implicit surfaces. Comput. Aided Geom. Des. 2007, 24, 395–409. [Google Scholar] [CrossRef]
- Zhang, X.P.; Che, W.J.; Paul, J.C. Computing lines of curvature for implicit surfaces. Comput. Geom. Des. 2009, 26, 923–940. [Google Scholar] [CrossRef]
- Kalogerakis, E.; Nowrouzezahrai, D.; Simari, P.; Singh, K. Extracting lines of curvature from noisy point clouds. Comput.-Aided Des. 2009, 41, 282–292. [Google Scholar] [CrossRef]
- Wang, G.; Tang, K.; Tai, C.H. Parametric representation of a surface pencil with common spatial geodesic. Comput.-Aided Des. 2004, 36, 47–59. [Google Scholar] [CrossRef]
- Kauap, E.; Akyldz, F.K.; Orbay, K. A generalization of surfaces family with common spatial geodesic. Appl. Math. Comput. 2008, 201, 781–789. [Google Scholar]
- Li, C.Y.; Wang, R.H.; Zhu, C.G. Parametric representation of a surface pencil with a common line of curvature. Computer Aided Des. 2011, 43, 1110–1117. [Google Scholar] [CrossRef]
- Li, C.Y.; Wang, R.H.; Zhu, C.G. An approach for designing a developable surface through a given line of curvature. Computer Aided Des. 2013, 45, 621–627. [Google Scholar] [CrossRef]
- Bayram, E.; Guler, F.; Kauap, E. Parametric representation of a surface pencil with a common asymptotic curve. Computer Aided Des. 2012, 44, 637–643. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, G.J. Designing developable surface pencil through given curve as its common asymptotic curve. J. Zhejiang Univ. 2013, 47, 1246–1252. [Google Scholar]
- Atalay, G.; Kasap, E. Surfaces family with common smarandache geodesic curve. J. Uci. Artu. 2017, 4, 651–664. [Google Scholar]
- Atalay, G.; Kasap, E. Surfaces family with common smarandache geodesic curve according to Bishop frame in Euclidean space. Math. Sci. 2016, 4, 164–174. [Google Scholar] [CrossRef]
- Bayram, E.; Mustafa, B. Surface family with a common involute asymptotic curve. Int. J. Geom. Methods Mod. Phys. 2016, 13, 447–459. [Google Scholar]
- Guler, F.; Bayram, E.; Kasap, E. Offset surface pencil with a common asymptotic curve. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850195(1)–1850195(11). [Google Scholar] [CrossRef]
- Atalay, G. Surfaces family with a common Mannheim asymptotic curve. J. Appl. Math. Comput. 2018, 2, 143–154. [Google Scholar]
- Atalay, G. Surfaces family with a common Mannheim geodesic curve. J. Appl. Math. Comput. 2018, 2, 155–165. [Google Scholar]
- Abdel-Baky, R.A.; Alluhaibi, N. Surfaces family with a common geodesic curve in Euclidean 3-upace E3. Inter. J. Math. Anal. 2019, 9, 433–447. [Google Scholar]
- Hobson, M.P.; Efstathiou, G.P.; Lasenby, A.N. General Relativity An Introduction for Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Yaglom, I.M. A Simple Non-Euclidean Geometry and Its Physical Basis; Springer: New York, NY, USA, 1979. [Google Scholar]
- Dede, D. Tubular surfaces in Galilean space. Math. Common. 2013, 18, 209–217. [Google Scholar]
- Dede, D.; Ekici, E.; Coken, A.C. On the parallel surfaces in Galilean space. Hacet. J. Math. Stat. 2013, 42, 605–615. [Google Scholar] [CrossRef]
- Yuzbası, Z.K. On a family of surfaces with joint asymptotic curve in the Galilean space . J. Nonlinear Sci. Appl. 2016, 9, 518–523. [Google Scholar] [CrossRef]
- Yuzbası, Z.K.; Bektas, M. On the conutructios of a surface family with joint geodeuic in Galilean space . Open Phys. 2016, 14, 360–363. [Google Scholar] [CrossRef]
- Jiang, X.; Jiang, P.; Meng, J.; Wang, K. Surface pencil couple interpolating Bertrand couple au joint asymptotic curves in Galilean space. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150114. [Google Scholar] [CrossRef]
- Almoneef, A.A.; Abdel-Baky, R.A. Surface family couple with Bertrand couple au common geodesic curves in Galilean 3-upace . Mathematics 2023, 11, 2391. [Google Scholar]
- Li, Y.; Eren, K.; Ersoy, S. On simultaneous characterizations of partner-ruled surfaces in Minkowski 3-space. AIMS Math. 2023, 8, 22256–22273. [Google Scholar] [CrossRef]
- Li, Y.; Güler, E. A Hypersurfaces of Revolution Family in the Five-Dimensional Pseudo-Euclidean Space . Mathematics 2023, 11, 3427. [Google Scholar]
- Li, Y.; Gupta, M.K.; Sharma, S.; Chaubey, S.K. On Ricci Curvature of a Homogeneous Generalized Matsumoto Finsler Space. Mathematics 2023, 11, 3365. [Google Scholar] [CrossRef]
- Li, Y.; Bhattacharyya, S.; Azami, S.; Saha, A.; Hui, S.K. Harnack Estimation for Nonlinear, Weighted, Heat-Type Equation along Geometric Flow and Applications. Mathematics 2023, 11, 2516. [Google Scholar] [CrossRef]
- Li, Y.; Kumara, H.A.; Siddesha, M.S.; Naik, D.M. Characterization of Ricci Almost Soliton on Lorentzian Manifolds. Symmetry 2023, 15, 1175. [Google Scholar] [CrossRef]
- Li, Y.; Mak, M. Framed Natural Mates of Framed Curves in Euclidean 3-Space. Mathematics 2023, 11, 3571. [Google Scholar]
- Li, Y.; Mofarreh, F.; Abdel-Baky, R.A. Kinematic-geometry of a line trajectory and the invariants of the axodes. Demonstr. Math. 2023, 56, 20220252. [Google Scholar]
- Li, Y.; Patra, D.; Alluhaibi, N.; Mofarreh, F.; Ali, A. Geometric classifications of k-almost Ricci solitons admitting paracontact metrices. Open Math. 2023, 21, 20220610. [Google Scholar] [CrossRef]
- Li, Y.; Güler, E. Hypersurfaces of revolution family supplying in pseudo-Euclidean space. AIMS Math. 2023, 8, 24957–24970. [Google Scholar] [CrossRef]
- Li, Y.; Eren, K.; Ayvacı, K.H.; Ersoy, S. The developable surfaces with pointwise 1-type Gauss map of Frenet type framed base curves in Euclidean 3-space. AIMS Math. 2023, 8, 2226–2239. [Google Scholar] [CrossRef]
- Li, Y.; Ganguly, D. Kenmotsu Metric as Conformal η-Ricci Soliton. Mediterr. J. Math. 2023, 20, 193. [Google Scholar] [CrossRef]
- Li, Y.; Erdoğdu, M.; Yavuz, A. Differential Geometric Approach of Betchow-Da Rios Soliton Equation. Hacet. J. Math. Stat. 2023, 52, 114–125. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Salam, A.A.; Saad, M.K. Primitivoids of curves in Minkowski plane. AIMS Math. 2023, 8, 2386–2406. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Li, Y.; Abdel-Baky, R.A.; Saad, M.K. On the Curvatures of Timelike Circular Surfaces in Lorentz-Minkowski Space. Filomat 2024, 38, 1–15. [Google Scholar]
- Li, Y.; Gezer, A.; Karakaş, E. Some notes on the tangent bundle with a Ricci quarter-symmetric metric connection. AIMS Math. 2023, 8, 17335–17353. [Google Scholar] [CrossRef]
- Al-Jedani, A.; Abdel-Baky, R.A. A surface family with a mutual geodesic curve in Galilean 3-upace . Mathematics 2023, 11, 2971. [Google Scholar] [CrossRef]
- Roschel, O. Die Geometrie des Galileischen Raumes; Habilitationsschrift: Leoben, Austria, 1984. [Google Scholar]
- Divjak, B. Geometrija Pseudogalilejevih Prostora. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 1997. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alluhaibi, N.; Abdel-Baky, R.A. Surface Pencil Couple with Bertrand Couple as Joint Principal Curves in Galilean 3-Space. Axioms 2023, 12, 1022. https://doi.org/10.3390/axioms12111022
Alluhaibi N, Abdel-Baky RA. Surface Pencil Couple with Bertrand Couple as Joint Principal Curves in Galilean 3-Space. Axioms. 2023; 12(11):1022. https://doi.org/10.3390/axioms12111022
Chicago/Turabian StyleAlluhaibi, Nadia, and Rashad A. Abdel-Baky. 2023. "Surface Pencil Couple with Bertrand Couple as Joint Principal Curves in Galilean 3-Space" Axioms 12, no. 11: 1022. https://doi.org/10.3390/axioms12111022





