A Fractional Analysis of Zakharov–Kuznetsov Equations with the Liouville–Caputo Operator
Abstract
:1. Introduction
2. Preliminaries
3. Configuration for HPTM
4. Configuration for YTDM
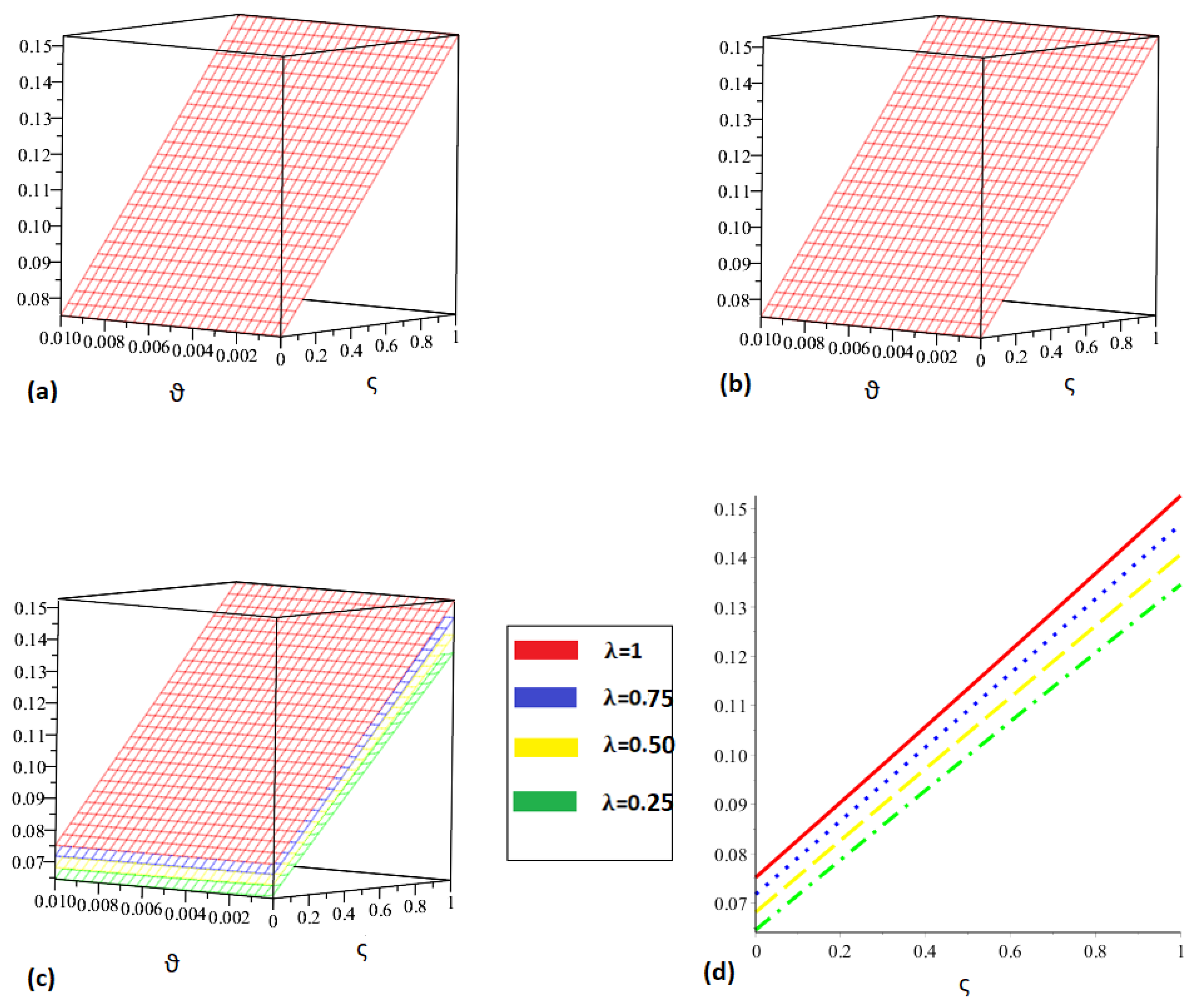
5. Numerical Applications
6. Numerical Simulation Studies
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riemann, G.F.B. Versuch einer allgemeinen Auffassung der Integration und Differentiation, Gesammelte Mathematische Werke; Springer: Leipzig, Germany, 1896. [Google Scholar]
- Liouville, J. Memoire sur quelques questions de geometrie et de mecanique, et sur un nouveau genre de calcul pour resoudre ces questions. J. Ecole Polytech. 1832, 13, 1–69. [Google Scholar]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Sene, N.; Abdelmalek, K. Analysis of the fractional diffusion equations described by Atangana-Baleanu-Caputo fractional derivative. Chaos Solitons Fractals 2019, 127, 158–164. [Google Scholar] [CrossRef]
- Murio, D.A. Stable numerical evaluation of Grünwald-Letnikov fractional derivatives applied to a fractional IHCP. Inverse Probl. Sci. Eng. 2009, 17, 229–243. [Google Scholar] [CrossRef]
- Srivastava, H.M. Some parametric and argument variations of the operators of fractional calculus and related special functions and integral transformations. J. Nonlinear Convex Anal. 2021, 22, 1501–1520. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Legnani, W.; Moschandreou, T.E.; Reyhanoglu, M. Nonlinear Systems: Theoretical Aspects and Recent Applications; IntechOpen: London, UK, 2020. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Nasrolahpour, H. A note on fractional electrodynamics. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2589–2593. [Google Scholar] [CrossRef]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef] [Green Version]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Li, Y.; Liub, F.; Turner, I.W.; Li, T. Time-fractional diffusion equation for signal smoothing. Appl. Math. Comput. 2018, 326, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Al-Smadi, M.; Freihat, A.; Khalil, H.; Momani, S.; Ali Khan, R. Numerical multistep approach for solving fractional partial differential equations. Int. J. Comput. Methods 2017, 14, 1750029. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Y.; Qiu, T. Fractional Processes and Fractional-Order Signal Processing: Techniques and Applications; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of fractional-order regularized long-wave models via a novel transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Rezapour, S.; Etemad, S.; Tellab, B.; Agarwal, P.; Garcia Guirao, J.L. Numerical solutions caused by DGJIM and ADM methods for multi-term fractional BVP involving the generalized ψ-RL-operators. Symmetry 2021, 13, 532. [Google Scholar] [CrossRef]
- Amara, A.; Etemad, S.; Rezapour, S. Approximate solutions for a fractional hybrid initial value problem via the Caputo conformable derivative. Adv. Differ. Equ. 2020, 2020, 608. [Google Scholar] [CrossRef]
- Etemad, S.; Shikongo, A.; Owolabi, K.M.; Tellab, B.; Avci, I.; Rezapour, S.; Agarwal, R.P. A new fractal-fractional version of giving up smoking model: Application of Lagrangian piece-wise interpolation along with asymptotical stability. Mathematics 2022, 10, 4369. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5. [Google Scholar]
- Owyed, S.; Abdou, M.A.; Abdel-Aty, A.H.; Alharbi, W.; Nekhili, R. Numerical and approximate solutions for coupled time fractional nonlinear evolutions equations via reduced differential transform method. Chaos Solitons Fractals 2020, 131, 109474. [Google Scholar] [CrossRef]
- Song, L.; Zhang, H. Application of homotopy analysis method to fractional KdV-Burgers-Kuramoto equation. Phys. Lett. A 2007, 367, 88–94. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A. Solution of the fractional epidemic model by homotopy analysis method. J. King Saud Univ.-Sci. 2013, 25, 73–81. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Vishal, K.; Gupta, P.K.; Yildirim, A. An approximate analytical solution of time-fractional telegraph equation. Appl. Math. Comput. 2011, 217, 7405–7411. [Google Scholar] [CrossRef]
- Jassim, H.K.; Shareef, M.A. On approximate solutions for fractional system of differential equations with Caputo-Fabrizio fractional operator. J. Math. Comput. Sci. 2021, 23, 58–66. [Google Scholar] [CrossRef]
- Mahor, T.C.; Mishra, R.; Jain, R. Analytical solutions of linear fractional partial differential equations using fractional Fourier transform. J. Comput. Appl. Math. 2021, 385, 113202. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 199. [Google Scholar] [CrossRef] [Green Version]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The analysis of fractional-order nonlinear systems of third order KdV and Burgers equations via a novel transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Ganie, A.H.; AlBaidani, M.M.; Khan, A. A Comparative Study of the Fractional Partial Differential Equations via Novel Transform. Symmetry 2023, 15, 1101. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Ganie, A.H.; Houas, M.; AlBaidani, M.M.; Fathima, D. Coupled system of three sequential Caputo fractional differential equations: Existence and stability analysis. Math. Methods Appl. Sci. 2023. early view. [Google Scholar] [CrossRef]
- AL-Smadi, M.H.; Gumah, G.N. On the homotopy analysis method for fractional SEIR epidemic model. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 3809–3820. [Google Scholar] [CrossRef]
- Kolokoltsov, V.N. The probabilistic point of view on the generalized fractional partial differential equations. Fract. Calc. Appl. Anal. 2019, 22, 543–600. [Google Scholar] [CrossRef] [Green Version]
- Martin, O. Stability approach to the fractional variational iteration method used for the dynamic analysis of viscoelastic beams. J. Comput. Appl. Math. 2019, 346, 261–276. [Google Scholar] [CrossRef]
- Khader, M.; Kumar, S.; Abbasbandy, S. Fractional homotopy analysis transforms method for solving a fractional heat-like physical model. Walailak J. Sci. Technol. (WJST) 2016, 13, 337–353. [Google Scholar]
- Haq, F.; Shah, K.; ur Rahman, G.; Shahzad, M. Numerical solution of fractional order smoking model via Laplace Adomian decomposition method. Alex. Eng. J. 2018, 57, 1061–1069. [Google Scholar] [CrossRef]
- Çenesiz, Y.; Tasbozan, O.; Kurt, A. Functional Variable Method for conformable fractional modified KdV-ZK equation and Maccari system. Tbilisi Math. J. 2017, 10, 117–125. [Google Scholar] [CrossRef]
- Zakharov, V.; Kuznetsov, E. On three-dimensional solitons. Sov. Phys. 1974, 39, 285–288. [Google Scholar]
- Monro, S.; Parkes, E.J. The derivation of a modified Zakharov-Kuznetsov equation and the stability of its solutions. J. Plasma Phys. 1999, 62, 305–317. [Google Scholar] [CrossRef]
- Monro, S.; Parkes, E.J. Stability of solitary-wave solutions to a modified Zakharov-Kuznetsov equation. J. Plasma Phys. 2000, 64, 41126. [Google Scholar] [CrossRef]
- Molliq, R.Y.; Noorani, M.S.M.; Hashim, I.; Ahmad, R.R. Approximate solutions of fractional Zakharov-Kuznetsov equations by VIM. J. Comput. Appl. Math. 2009, 233, 103–108. [Google Scholar] [CrossRef] [Green Version]
- Yildirim, A.; Gulkanat, Y. Analytical approach to fractional Zakharov-Kuznetsov equations by He’s homotopy perturbation method. Commun. Theor. Phys. 2010, 53, 1005. [Google Scholar]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Laplace Transform and Applications. In Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2016; pp. 147–178. [Google Scholar]
- Adomian, G. Nonlinear Stochastis System Theory and Applications to Physics Kluwer; Academic Publishers: Cambridge, MA, USA, 1989. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Mishra, N.K.; AlBaidani, M.M.; Khan, A.; Ganie, A.H. Two Novel Computational Techniques for Solving Nonlinear Time-Fractional Lax’s Korteweg-de Vries Equation. Axioms 2023, 12, 400. [Google Scholar] [CrossRef]
- Mishra, N.K.; AlBaidani, M.M.; Khan, A.; Ganie, A.H. Numerical Investigation of Time-Fractional Phi-Four Equation via Novel Transform. Symmetry 2023, 15, 687. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Podlubny, I.; Kacenak, M. Isoclinal matrices and numerical solution of fractional differential equations. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001. [Google Scholar]
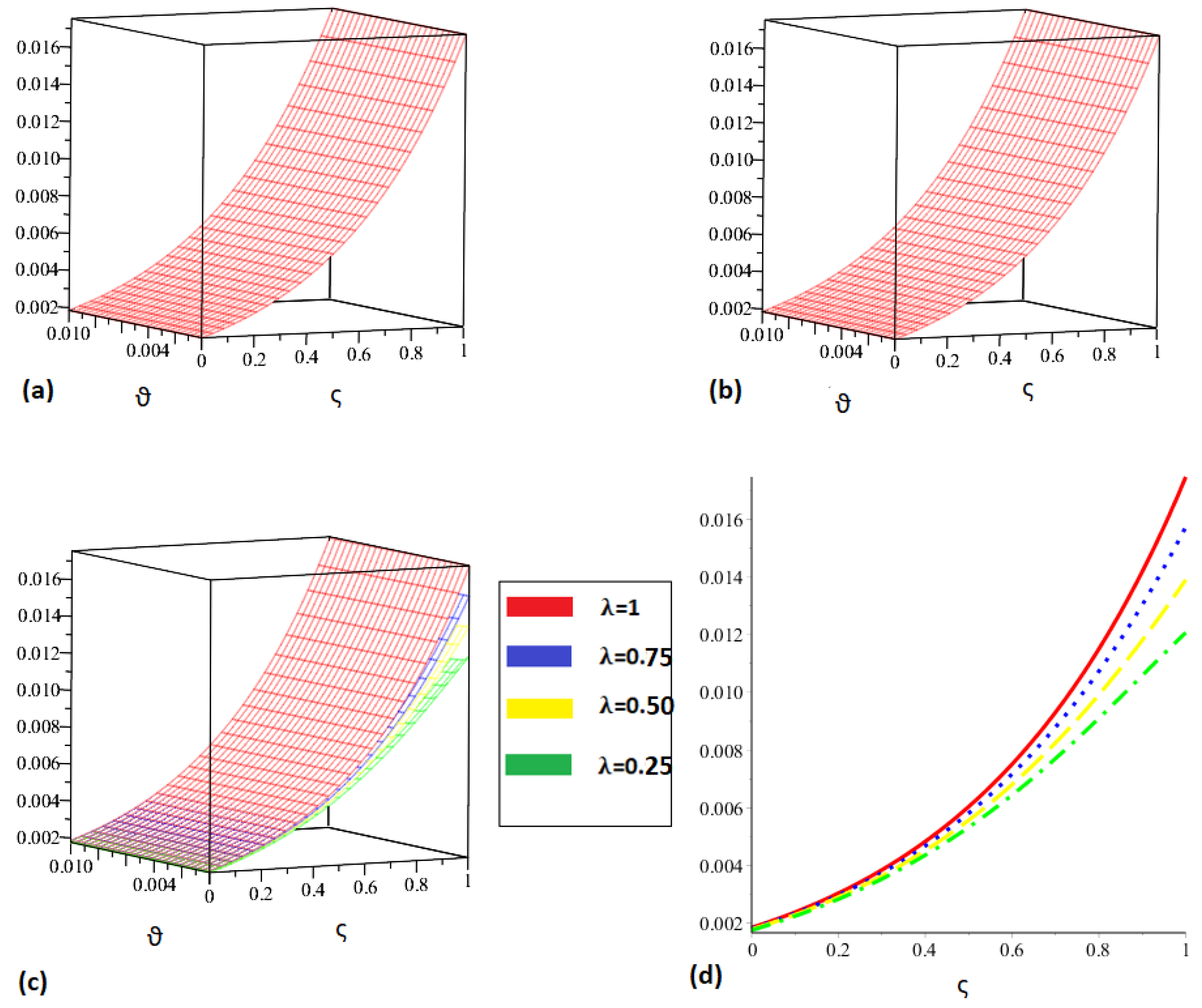
| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | 0.002999 | 0.003012 | 0.003025 | 0.003037 | 0.003037 | |
| 0.4 | 0.004747 | 0.004776 | 0.004805 | 0.004835 | 0.004835 | |
| 0.01 | 0.6 | 0.007327 | 0.007392 | 0.007457 | 0.007524 | 0.007524 |
| 0.8 | 0.011097 | 0.011245 | 0.011392 | 0.011541 | 0.011541 | |
| 1 | 0.016543 | 0.016873 | 0.017203 | 0.017538 | 0.017538 | |
| 0.2 | 0.002999 | 0.003012 | 0.003024 | 0.003037 | 0.003037 | |
| 0.4 | 0.004746 | 0.004775 | 0.004805 | 0.004835 | 0.004835 | |
| 0.02 | 0.6 | 0.007324 | 0.007390 | 0.007456 | 0.007524 | 0.007524 |
| 0.8 | 0.011091 | 0.011240 | 0.011388 | 0.011541 | 0.011541 | |
| 1 | 0.016529 | 0.016863 | 0.017195 | 0.017538 | 0.017538 | |
| 0.2 | 0.002998 | 0.003011 | 0.003024 | 0.003037 | 0.003037 | |
| 0.4 | 0.004745 | 0.004775 | 0.004804 | 0.004835 | 0.004835 | |
| 0.03 | 0.6 | 0.007322 | 0.007388 | 0.007454 | 0.007524 | 0.007524 |
| 0.8 | 0.011086 | 0.011236 | 0.011384 | 0.011541 | 0.011541 | |
| 1 | 0.016517 | 0.016853 | 0.017187 | 0.017538 | 0.017538 | |
| 0.2 | 0.002998 | 0.003011 | 0.003024 | 0.003037 | 0.003037 | |
| 0.4 | 0.004744 | 0.004774 | 0.004803 | 0.004835 | 0.004835 | |
| 0.04 | 0.6 | 0.007319 | 0.007386 | 0.007453 | 0.007524 | 0.007524 |
| 0.8 | 0.011081 | 0.011231 | 0.011381 | 0.011541 | 0.011541 | |
| 1 | 0.016505 | 0.016843 | 0.017179 | 0.017538 | 0.017538 | |
| 0.2 | 0.002997 | 0.003010 | 0.003023 | 0.003037 | 0.003037 | |
| 0.4 | 0.004743 | 0.004773 | 0.004802 | 0.004835 | 0.004835 | |
| 0.05 | 0.6 | 0.004743 | 0.007384 | 0.007451 | 0.007524 | 0.007524 |
| 0.8 | 0.011076 | 0.011227 | 0.011377 | 0.011541 | 0.011541 | |
| 1 | 0.016494 | 0.016834 | 0.017171 | 0.017538 | 0.017538 |
| PIA Error | RPSM Error | Our Method Error | |||
|---|---|---|---|---|---|
| 0.2 | 0.1 | 0.1 | 3.85217 | 3.85217 | 3.8519486000 |
| 0.3 | 0.1 | 0.1 | 5.75911 | 5.75912 | 5.7583616000 |
| 0.4 | 0.1 | 0.1 | 7.65359 | 7.65352 | 7.6517330000 |
| 0.2 | 0.6 | 0.6 | 4.66337 | 4.66389 | 4.6473505000 |
| 0.3 | 0.6 | 0.6 | 6.86056 | 6.86314 | 6.8073230000 |
| 0.4 | 0.6 | 0.6 | 8.98263 | 8.99046 | 8.8581596000 |
| 0.2 | 0.9 | 0.9 | 5.12131 | 5.14241 | 4.9248718000 |
| 0.3 | 0.9 | 0.9 | 7.38186 | 7.48450 | 6.7502883000 |
| 0.4 | 0.9 | 0.9 | 9.57942 | 9.89139 | 8.1510249000 |
| (Approx) | (Exact) | |||||
|---|---|---|---|---|---|---|
| 0.2 | 0.030120 | 0.030147 | 0.030173 | 0.030197 | 0.030197 | |
| 0.4 | 0.035230 | 0.035259 | 0.035288 | 0.035315 | 0.035315 | |
| 0.01 | 0.6 | 0.040377 | 0.040410 | 0.040442 | 0.040473 | 0.040473 |
| 0.8 | 0.045568 | 0.045604 | 0.045641 | 0.045675 | 0.045675 | |
| 1 | 0.050807 | 0.050848 | 0.050889 | 0.050928 | 0.050928 | |
| 0.2 | 0.030119 | 0.030146 | 0.030172 | 0.030195 | 0.030195 | |
| 0.4 | 0.035229 | 0.035258 | 0.035288 | 0.035313 | 0.035313 | |
| 0.02 | 0.6 | 0.040376 | 0.040409 | 0.040441 | 0.040470 | 0.040470 |
| 0.8 | 0.045566 | 0.045603 | 0.045640 | 0.045672 | 0.045672 | |
| 1 | 0.050806 | 0.050847 | 0.050888 | 0.050925 | 0.050925 | |
| 0.2 | 0.030118 | 0.030145 | 0.030172 | 0.030192 | 0.030192 | |
| 0.4 | 0.035228 | 0.035257 | 0.035287 | 0.035310 | 0.035310 | |
| 0.03 | 0.6 | 0.040375 | 0.040408 | 0.040441 | 0.040467 | 0.040467 |
| 0.8 | 0.045565 | 0.045602 | 0.045639 | 0.045670 | 0.045670 | |
| 1 | 0.050804 | 0.050846 | 0.050887 | 0.050923 | 0.050923 | |
| 0.2 | 0.030117 | 0.030144 | 0.030171 | 0.030190 | 0.030190 | |
| 0.4 | 0.035227 | 0.035256 | 0.035286 | 0.035308 | 0.035308 | |
| 0.04 | 0.6 | 0.040374 | 0.040407 | 0.040440 | 0.040465 | 0.040465 |
| 0.8 | 0.045564 | 0.045601 | 0.045638 | 0.045667 | 0.045667 | |
| 1 | 0.050803 | 0.050845 | 0.050886 | 0.050920 | 0.050920 | |
| 0.2 | 0.030116 | 0.030144 | 0.030170 | 0.030187 | 0.030187 | |
| 0.4 | 0.035226 | 0.035256 | 0.035285 | 0.035305 | 0.035305 | |
| 0.05 | 0.6 | 0.040372 | 0.040406 | 0.040439 | 0.040462 | 0.040462 |
| 0.8 | 0.045563 | 0.045600 | 0.045637 | 0.045664 | 0.045664 | |
| 1 | 0.050802 | 0.050843 | 0.050885 | 0.050917 | 0.050917 |
| VIM Error | Our Method Error | |||
|---|---|---|---|---|
| 0.2 | 0.1 | 0.1 | 5.00091 | 4.9951950000 |
| 0.3 | 0.1 | 0.1 | 5.00091 | 7.4927920000 |
| 0.4 | 0.1 | 0.1 | 5.00091 | 9.9903860000 |
| 0.2 | 0.6 | 0.6 | 3.02003 | 5.0898600000 |
| 0.3 | 0.6 | 0.6 | 3.02003 | 7.6348000000 |
| 0.4 | 0.6 | 0.6 | 3.02003 | 1.0179720000 |
| 0.2 | 0.9 | 0.9 | 4.56780 | 5.2122800000 |
| 0.3 | 0.9 | 0.9 | 4.56780 | 7.8184000000 |
| 0.4 | 0.9 | 0.9 | 4.56780 | 1.0424500000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ganie, A.H.; Mofarreh, F.; Khan, A. A Fractional Analysis of Zakharov–Kuznetsov Equations with the Liouville–Caputo Operator. Axioms 2023, 12, 609. https://doi.org/10.3390/axioms12060609
Ganie AH, Mofarreh F, Khan A. A Fractional Analysis of Zakharov–Kuznetsov Equations with the Liouville–Caputo Operator. Axioms. 2023; 12(6):609. https://doi.org/10.3390/axioms12060609
Chicago/Turabian StyleGanie, Abdul Hamid, Fatemah Mofarreh, and Adnan Khan. 2023. "A Fractional Analysis of Zakharov–Kuznetsov Equations with the Liouville–Caputo Operator" Axioms 12, no. 6: 609. https://doi.org/10.3390/axioms12060609






