Symbolic Regression Approaches for the Direct Calculation of Pipe Diameter
Abstract
:1. Introduction
- Unknown pressure drop Δp (head loss Δh)
- 2.
- Unknown flow discharge Q
- 3.
- Unknown pipe diameter D
2. Background of Symbolic Regression
2.1. Theory behind Symbolic Regression
2.2. Software Tools for Symbolic Regression
3. Input Parameters and Analysis of the Error
- Uncertainty of measurement: Some parameters, such as the roughness of the inner surface of pipes ℇ cannot be easily measured [56,57,58,59]. The values of physical roughness measured in dry pipes cannot always be used directly in hydraulic calculations under certain flow conditions due to the existence of a viscose sublayer near the inner wall of the pipe wall (e.g., all types of pipes, new or used, are treated as smooth during laminar flow [60]). Specific values for the absolute roughness ℇ of the inner pipe surface for different materials are given together with Moody’s [4] (Rouse’s [5]) and diagrams for flow friction factor λ; the minimal and maximal values for the parameters used in this article are given in Table 1;
- Empirical nature of used equations: The Colebrook equation is empirical, based on an experiment conducted by Colebrook and White with the flow of air through a set of pipes with different roughnesses of their inner surfaces [2]. It can be disputed whether this equation fits well the physical reality of the turbulent flow friction sufficiently [61,62,63,64]. Anyway, the Colebrook equation is treated as accurate for this study (i.e., the Colebrook equation is considered as an informal standard in hydraulic engineering);
- Error caused by the specific logarithmic structure of the Colebrook equation from which the unknown variable, which is given implicitly, can be evaluated only approximately. In addition, the Colebrook equation in its native form is not suitable for solving the problem of unknown diameter D. For this reason, Section 4.3 of this article proposes a novel, more suitable, relation based on the Colebrook equation.
- Nomograms
- Explicit approximations
4. Solutions for the Unknown Diameter D
4.1. Brute Force of Computing Power
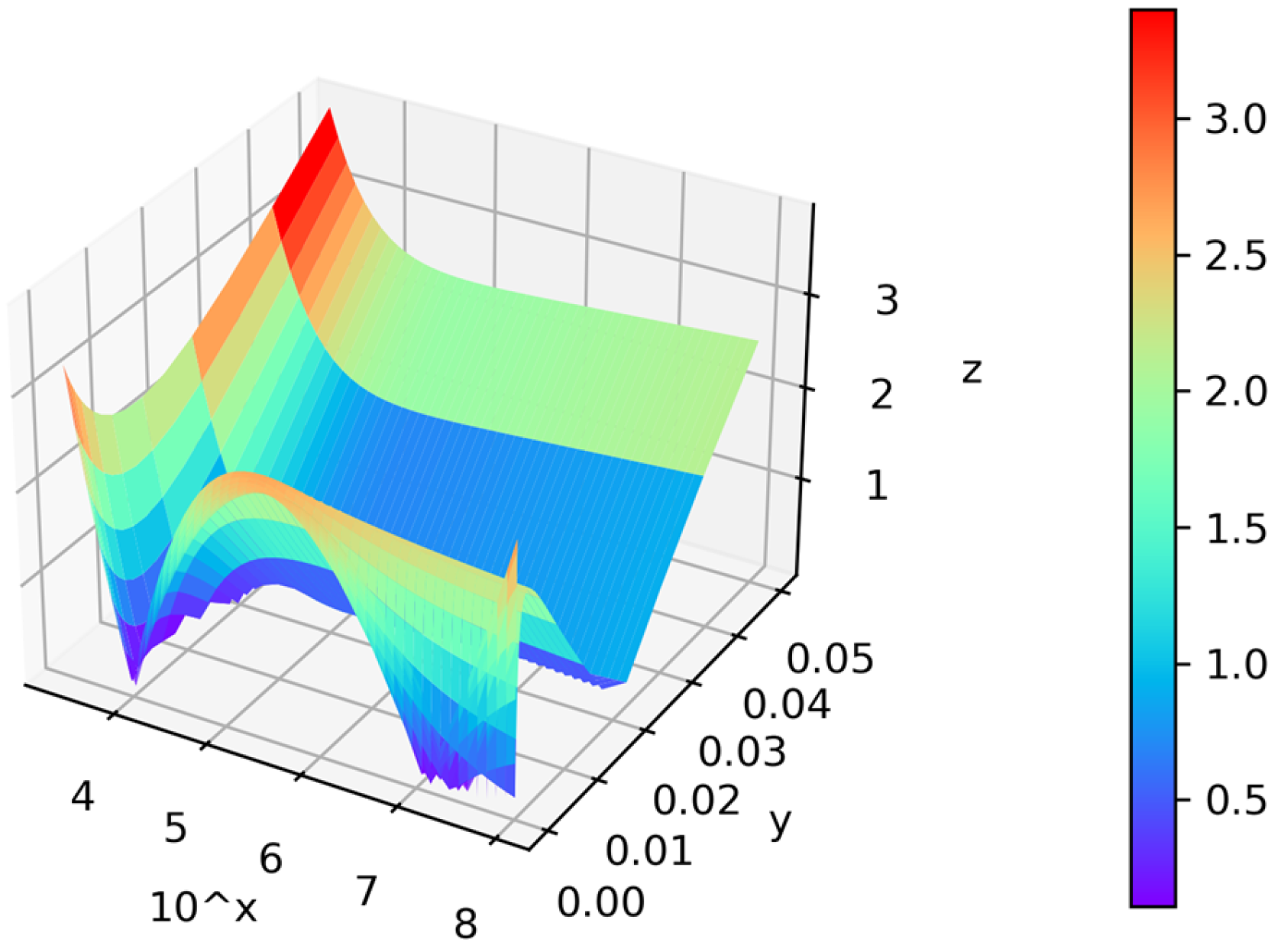
4.1.1. Sensitivity Analysis—Rejection of Viscosity
4.1.2. Symbolic Regression Approximations Discovered by Brute Computing Power
4.2. Method through the Lambert W-Function
4.3. Method Based on New Suitable Dimensionless Groups
5. Conclusions
- Brute force, in which symbolic regression is applied directly to the input data set;
- A method based on the special functions, in which the problem is transformed by the approximation of the Lambert W-function;
- A method based on new suitable dimensionless groups, which eliminates the unknown pipeline diameter from the input.
- A very interesting fact is that both symbolic regression tools, Eureqa and PySR, using raw data and brute force of computing discovered relations without using the viscosity (or temperature t) of the conveying fluid—Equations (4)–(6) are with the relative error relative from 5.9% to 6.7%;
- Equations (7) and (8) leverage also the explicit solution provided by the Lambert W-function function by simplification and keeping the error, as reported by Lamri and Easa [24];
- Equation (10) gives the Colebrook Equation in a form suitable for solving the problem of the unknown diameter of pipe D where the novel approximation is based on the Buckingham-Π theorem through suitable nondimensional numbers Π1 and Π2 in Equation (9). Sobol’s quasi-random sampling [73] is used to provide data to feed the symbolic regression tool. Consequently, symbolic regression was used to construct the novel approximation of the Reynolds number Re in Equation (11). Although the novel approximation is very simple, it is accurate, as the relative error is bounded by 2.68%. On the contrary, references [16,65] report approximations bounded by a relative error larger than 20% when a similar method is used through nomograms.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Δp | the pressure drop in Pa |
| D | the inner diameter of the pipe in m |
| Q | the flow rate in m3/s |
| a dimensionless Darcy flow friction factor | |
| the density of the fluid in kg/m3 | |
| L | the length of the pipe in m |
| the Ludolph’s number; ≈ 3.1415 | |
| the head loss in m | |
| g | acceleration due to gravity in m/s2 (or N/kg); g = 9.81 m/s2 |
| the absolute roughness of the inner pipe surface in m | |
| a dimensionless Reynolds number | |
| V | the velocity of the fluid in m/s |
| the kinematic viscosity of the fluid in m2/s | |
| the dynamic viscosity of the fluid in Pa·s | |
| the density of the fluid in kg/m3 | |
| t | the temperature in °C |
| A and B | auxiliary parameters |
| * | related nondimensional versions of the related parameters |
| s | the index for smooth flow |
| r | index for rough hydraulic flow |
| N, Y, P, K, U, M, Z, and V | auxiliary |
| Π1 | a new-defined dimensionless number |
| a new-defined dimensionless number |
References
- Brown, G.O. The history of the Darcy-Weisbach equation for pipe flow resistance. In Proceedings of the Environmental and Water Resources History Sessions at ASCE Civil Engineering Conference and Exposition, Washington, DC, USA, 3–7 November 2002. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C.M. Experiments with fluid friction in roughened pipes. Proc. R. Soc. A—Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Colebrook, C. Turbulent flow in pipes, with particular reference to transition region between smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–678. [Google Scholar] [CrossRef]
- Rouse, H. Evaluation of boundary roughness. In Proceedings of the Second Hydraulics Conference, Iowa Institute of Hydraulic Research, Iowa City, IA, USA, 1–4 June 1942; pp. 105–116. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. 2017, 10, 4663. Available online: https://sie.scholasticahq.com/article/4663 (accessed on 26 May 2023).
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately. Rev. Int. Metodos Numer. Calc. Diseño Ing. 2020, 36, 41. [Google Scholar] [CrossRef]
- Brkić, D.; Stajić, Z. Excel VBA-based user defined functions for highly precise Colebrook’s pipe flow friction approximations: A comparative overview. Facta Univ. Ser. Mech. Eng. 2021, 19, 253–269. [Google Scholar] [CrossRef]
- Swamee, P.K.; Jain, A.K. Explicit equations for pipe-flow problems. J. Hydraul. Div. 1976, 102, 657–664. [Google Scholar] [CrossRef]
- Brkić, D.; Stajić, Z.; Živković, M. Sizing pipes without iterative calculus: Solutions for head loss, flow discharge and diameter. In Proceedings of the 24th International Carpathian Control Conference, Szilvásvárad, Hungary, 12–14 June 2023. [Google Scholar] [CrossRef]
- Powell, R.W. A diagram for the direct determination of pipe sizes. Civ. Eng. ASCE 1950, 20, 595–596. [Google Scholar]
- Rajaratnam, N. Direct solution for diameter of pipe in rough turbulent flow. Houille Blanche 1960, 46, 714–719. [Google Scholar] [CrossRef]
- Rangu Raju, K.R.; Garde, R.J. Direct solution for problems in pipe friction. Houille Blanche 1966, 52, 917–919. [Google Scholar] [CrossRef]
- Lai, R.Y.; Lee, K.K. Moody diagram for direct pipe diameter calculation. J. Hydraul. Div. 1975, 101, 1377–1380. [Google Scholar] [CrossRef]
- Debler, W. Pipe sizes from modified Moody diagram. J. Hydraul. Div. 1977, 103, 81–85. [Google Scholar] [CrossRef]
- Swamee, P.K.; Rathie, P.N. Exact equations for pipe-flow problems. J. Hydraul. Res. 2007, 45, 131–134. [Google Scholar] [CrossRef]
- Sakkas, J.G. Generalized numerical and nomographic solutions of simple pipe flow problems. Water Util. J. 2014, 7, 51–64. Available online: https://www.ewra.net/wuj/pdf/WUJ_2014_07_06.pdf (accessed on 28 May 2023).
- LaViolette, M. On the history, science, and technology included in the Moody diagram. J. Fluids Eng. 2017, 139, 030801. [Google Scholar] [CrossRef]
- Medina, Y.C.; Fonticiella, O.M.; Morales, O.F. Design and modelation of piping systems by means of use friction factor in the transition turbulent zone. Math. Model. Eng. Probl. 2017, 4, 162–167. [Google Scholar] [CrossRef]
- Yetilmezsoy, K.; Bahramian, M.; Kıyan, E.; Bahramian, M. Development of a new practical formula for pipe-sizing problems within the framework of a hybrid computational strategy. J. Irrig. Drain. Eng. 2021, 147, 04021012. [Google Scholar] [CrossRef]
- Lamri, A.A.; Easa, S.M. Explicit solution for pipe diameter problem using Lambert W-function. J. Irrig. Drain. Eng. 2022, 148, 04022030. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Discussion of “Explicit solution for pipe diameter problem using Lambert W-function”. J. Irrig. Drain. Eng. 2023, 149, 07023016. [Google Scholar] [CrossRef]
- Lohmeier, D.; Cronbach, D.; Drauz, S.R.; Braun, M.; Kneiske, T.M. Pandapipes: An open-source piping grid calculation package for multi-energy grid simulations. Sustainability 2020, 12, 9899. [Google Scholar] [CrossRef]
- Dubčáková, R. Eureqa: Software review. Genet Program Evolvable Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef]
- PySR. Available online: https://astroautomata.com/PySR/options/#loss (accessed on 9 June 2023).
- Cranmer, M. MilesCranmer/PySR v0.2 (v0.2) [Computer software]. Available online: https://doi.org/10.5281/ZENODO.4041459 (accessed on 28 August 2023).
- Wolfram Alfa Simplification. Available online: https://www.wolframalpha.com/input/?i=simplify (accessed on 9 June 2023).
- Stigler, S.M. Gergonne’s 1815 paper on the design and analysis of polynomial regression experiments. Hist. Math. 1974, 1, 431–439. [Google Scholar] [CrossRef]
- Stanton, J.M. Galton, Pearson, and the peas: A brief history of linear regression for statistics instructors. J. Stat. Educ. 2001, 9, 1–12. [Google Scholar] [CrossRef]
- Bethlehem, J. The Rise of Survey Sampling; Statistics Netherlands: The Hague, The Netherlands, 2009; Available online: https://hdl.handle.net/11245/1.312955 (accessed on 22 August 2023).
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Arnastauskaitė, J.; Ruzgas, T.; Bražėnas, M. A New Goodness of Fit Test for Multivariate Normality and Comparative Simulation Study. Mathematics 2021, 9, 3003. [Google Scholar] [CrossRef]
- González-Albornoz, P.; Novoa-Muñoz, F. Goodness-of-Fit Test for the Bivariate Hermite Distribution. Axioms 2023, 12, 7. [Google Scholar] [CrossRef]
- Di Noia, A.; Barabesi, L.; Marcheselli, M.; Pisani, C.; Pratelli, L. Goodness-of-fit test for count distributions with finite second moment. J. Nonparametric Stat. 2023, 35, 19–37. [Google Scholar] [CrossRef]
- Erlemann, R.; Lindqvist, B.H. Conditional Goodness-of-Fit Tests for Discrete Distributions. J. Stat. Theory Pract. 2022, 16, 8. [Google Scholar] [CrossRef]
- Guo, J.; Yang, Y.; Zhang, D.; Wu, W.; Yang, Z.; He, L. A general model for predicting apparent viscosity of crude oil or emulsion in laminar pipeline at high pressures. J. Pet. Sci. Eng. 2018, 160, 12–23. [Google Scholar] [CrossRef]
- Towfighi, S. Symbolic regression by uniform random global search. SN Appl. Sci. 2020, 2, 34. [Google Scholar] [CrossRef]
- Angelis, D.; Sofos, F.; Karakasidis, T.E. Artificial intelligence in physical sciences: Symbolic regression trends and perspectives. Arch. Computat. Methods. Eng. 2023, 30, 3845–3865. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Olhofer, M.; Sendhoff, B. A framework for evolutionary optimization with approximate fitness functions. IEEE Trans. Evol. Comput. 2002, 6, 481–494. [Google Scholar] [CrossRef]
- Luke, S. Two fast tree-creation algorithms for genetic programming. IEEE Trans. Evol. Comput. 2000, 4, 274–283. [Google Scholar] [CrossRef]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing mutation and crossover ratios for genetic algorithms—A review with a new dynamic approach. Information 2019, 10, 390. [Google Scholar] [CrossRef]
- Cranmer, M.; Sanchez Gonzalez, A.; Battaglia, P.; Xu, R.; Cranmer, K.; Spergel, D.; Ho, S. Discovering symbolic models from deep learning with inductive biases. Adv. Neural Inf. Process. Syst. 2020, 33, 17429–17442. [Google Scholar]
- Gholamy, A.; Kreinovich, V. How to use absolute-error-minimizing software to minimize relative error: Practitioner’s guide. Int. Math. Forum 2017, 12, 763–770. Available online: https://scholarworks.utep.edu/cs_techrep/1174/ (accessed on 11 May 2023). [CrossRef]
- Orzechowski, P.; La Cava, W.; Moore, J.H. Where are we now? A large benchmark study of recent symbolic regression methods. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 1183–1190. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Symbolic Regression of Implicit Equations. In Genetic Programming Theory and Practice VII; Genetic and Evolutionary Computation; Riolo, R., O’Reilly, U.M., McConaghy, T., Eds.; Springer: Boston, MA, USA, 2010. [Google Scholar] [CrossRef]
- Cranmer, M.D. Interpretable Machine Learning for the Physical Sciences. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2023. Available online: http://arks.princeton.edu/ark:/88435/dsp01sn00b201q (accessed on 30 July 2023).
- Udrescu, S.M.; Tegmark, M. AI Feynman: A physics-inspired method for symbolic regression. Sci. Adv. 2020, 6, eaay2631. [Google Scholar] [CrossRef] [PubMed]
- Vaddireddy, H. Data Driven Symbolic Regression. Available online: https://github.com/sayin/Data_Driven_Symbolic_Regression (accessed on 8 June 2023).
- Abramovich, S. Using Wolfram Alpha with Elementary Teacher Candidates: From More Than One Correct Answer to More Than One Correct Solution. Mathematics 2021, 9, 2112. [Google Scholar] [CrossRef]
- Lamont, P.A. Common pipe flow formulas compared with the theory of roughness. J.-Am. Water Work. Assoc. 1981, 73, 274–280. [Google Scholar] [CrossRef]
- Zhao, Q.; Wu, W.; Simpson, A.R.; Willis, A. Simpler Is Better—Calibration of Pipe Roughness in Water Distribution Systems. Water 2022, 14, 3276. [Google Scholar] [CrossRef]
- Muzzo, L.E.; Matoba, G.K.; Ribeiro, L.F. Uncertainty of pipe flow friction factor equations. Mech. Res. Commun. 2021, 116, 103764. [Google Scholar] [CrossRef]
- Sharp, W.W.; Walski, T.M. Predicting internal roughness in water mains. J.-Am. Water Work. Assoc. 1988, 80, 34–40. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Basse, N.T. Turbulence intensity and the friction factor for smooth- and rough-wall pipe flow. Fluids 2017, 2, 30. [Google Scholar] [CrossRef]
- Brownlie, W.R. Re-examination of Nikuradse roughness data. J. Hydraul. Div. 1981, 107, 115–119. [Google Scholar] [CrossRef]
- Yen, B.C. Dimensionally homogeneous Manning’s formula. J. Hydraul. Eng. 1992, 118, 1326–1332. [Google Scholar] [CrossRef]
- Diskin, M.H. The limits of applicability of the Hazen-Williams formula. Houille Blanche 1960, 46, 720–726. [Google Scholar] [CrossRef]
- Aiyesimoju, K.O. Accurate, explicit pipe sizing formula for turbulent flows. J. Sci. Technol. 2009, 29, 147–152. [Google Scholar] [CrossRef]
- Huang, S. Reading the Moody chart with a linear interpolation method. Sci. Rep. 2022, 12, 6587. [Google Scholar] [CrossRef]
- Yıldırım, G. Computer-based analysis of explicit approximations to the implicit Colebrook–White equation in turbulent flow friction factor calculation. Adv. Eng. Softw. 2009, 40, 1183–1190. [Google Scholar] [CrossRef]
- Zeghadnia, L.; Robert, J.L.; Achour, B. Explicit solutions for turbulent flow friction factor: A review, assessment and approaches classification. Ain Shams Eng. J. 2019, 10, 243–252. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Symbolic regression-based genetic approximations of the Colebrook equation for flow friction. Water 2018, 10, 1175. [Google Scholar] [CrossRef]
- Hayes, B. Why W? Am. Sci. 2005, 93, 104–108. Available online: https://www.americanscientist.org/article/why-w (accessed on 30 July 2023). [CrossRef]
- ISO 6708:1995—Pipework Components—Definition and Selection of DN (Nominal Size). Available online: https://www.iso.org/standard/21274.html (accessed on 28 May 2023).
- Moran, S. Pump sizing: Bridging the gap between theory and practice. Chem. Eng. Prog. 2016, 112, 38–44. Available online: https://www.aiche.org/sites/default/files/cep/20161238_r.pdf (accessed on 28 May 2023).
- Praks, P.; Brkić, D. Approximate flow friction factor: Estimation of the accuracy using Sobol’s quasi-random sampling. Axioms 2022, 11, 36. [Google Scholar] [CrossRef]
- Vaddireddy, H.; Rasheed, A.; Staples, A.E.; San, O. Feature engineering and symbolic regression methods for detecting hidden physics from sparse sensor observation data. Physics of Fluids 2020, 32, 015113. [Google Scholar] [CrossRef]
- Guimerà, R.; Reichardt, I.; Aguilar-Mogas, A.; Massucci, F.A.; Miranda, M.; Pallarès, J.; Sales-Pardo, M. A Bayesian machine scientist to aid in the solution of challenging scientific problems. Sci. Adv. 2020, 6, eaav6971. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Li, S.; Wu, Q. Why so many published sensitivity analyses are false: A systematic review of sensitivity analysis practices. Environ. Model. Softw. 2019, 114, 29–39. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. 2017, 139, 031401. [Google Scholar] [CrossRef]
- Ruzicka, M.C. On dimensionless numbers. Chem. Eng. Res. Des. 2008, 86, 835–868. [Google Scholar] [CrossRef]
- Polverino, P.; Bove, G.; Sorrentino, M.; Pianese, C.; Beretta, D. Advancements on scaling-up simulation of Proton Exchange Membrane Fuel Cells impedance through Buckingham Pi theorem. Appl. Energy 2019, 249, 245–252. [Google Scholar] [CrossRef]
- Rendón-Castrillón, L.; Ramírez-Carmona, M.; Ocampo-López, C.; Gómez-Arroyave, L. Mathematical model for scaling up bioprocesses using experiment design combined with Buckingham Pi theorem. Appl. Sci. 2021, 11, 11338. [Google Scholar] [CrossRef]
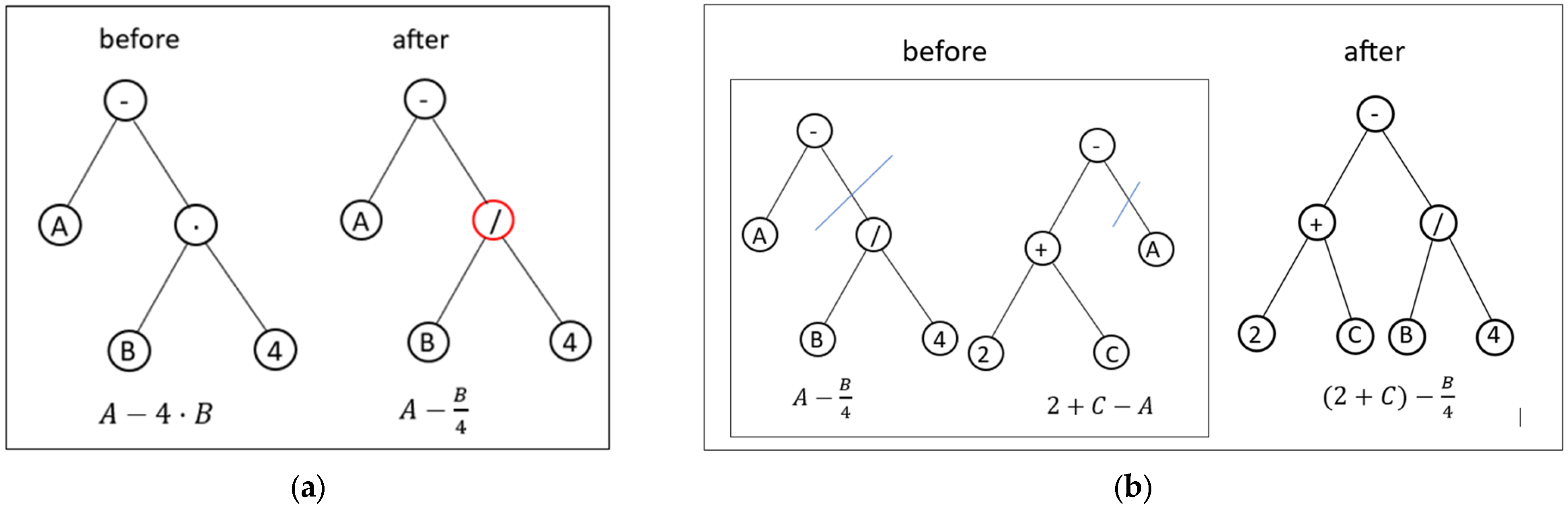
| Flow | Diameter | Hydraulic Slope | Kinematic Viscosity of Water | Absolute Roughness | Relative Roughness | |
|---|---|---|---|---|---|---|
| Q (m3/s) | D (m) | Δh/L (-) | ν (m2/s) | (m) | (-) | |
| Min | 0.001 | 0.01 | 0.0001 | 3.1 × 10−7 | 1.5 × 10−6 | 3 × 10−7 |
| Max | 100 | 5 | 0.1 | 1.5 × 10−6 | 9.1 × 10−3 | 5 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brkić, D.; Praks, P.; Praksová, R.; Kozubek, T. Symbolic Regression Approaches for the Direct Calculation of Pipe Diameter. Axioms 2023, 12, 850. https://doi.org/10.3390/axioms12090850
Brkić D, Praks P, Praksová R, Kozubek T. Symbolic Regression Approaches for the Direct Calculation of Pipe Diameter. Axioms. 2023; 12(9):850. https://doi.org/10.3390/axioms12090850
Chicago/Turabian StyleBrkić, Dejan, Pavel Praks, Renáta Praksová, and Tomáš Kozubek. 2023. "Symbolic Regression Approaches for the Direct Calculation of Pipe Diameter" Axioms 12, no. 9: 850. https://doi.org/10.3390/axioms12090850






