Research on the Optimization of Pricing and the Replenishment Decision-Making Problem Based on LightGBM and Dynamic Programming
Abstract
1. Introduction
2. Basic Assumptions and Data Pre-Processing
2.1. Basic Assumptions
- (1)
- The vegetable items in the annex were sold on the same day and not on the next day;
- (2)
- Vegetables with different supply sources but the same individual item name in the annex were considered to be the same individual item;
- (3)
- The current day’s sales data for a single vegetable item approximated the previous day’s sales data;
- (4)
- Vegetable sales were independent of whether or not they were discounted.
2.2. Data Pre-Processing
2.2.1. Data Consolidation
2.2.2. Outlier Handling
2.2.3. Missing Value Processing
3. Solution to Question One
3.1. Research Ideas
3.2. Preparation
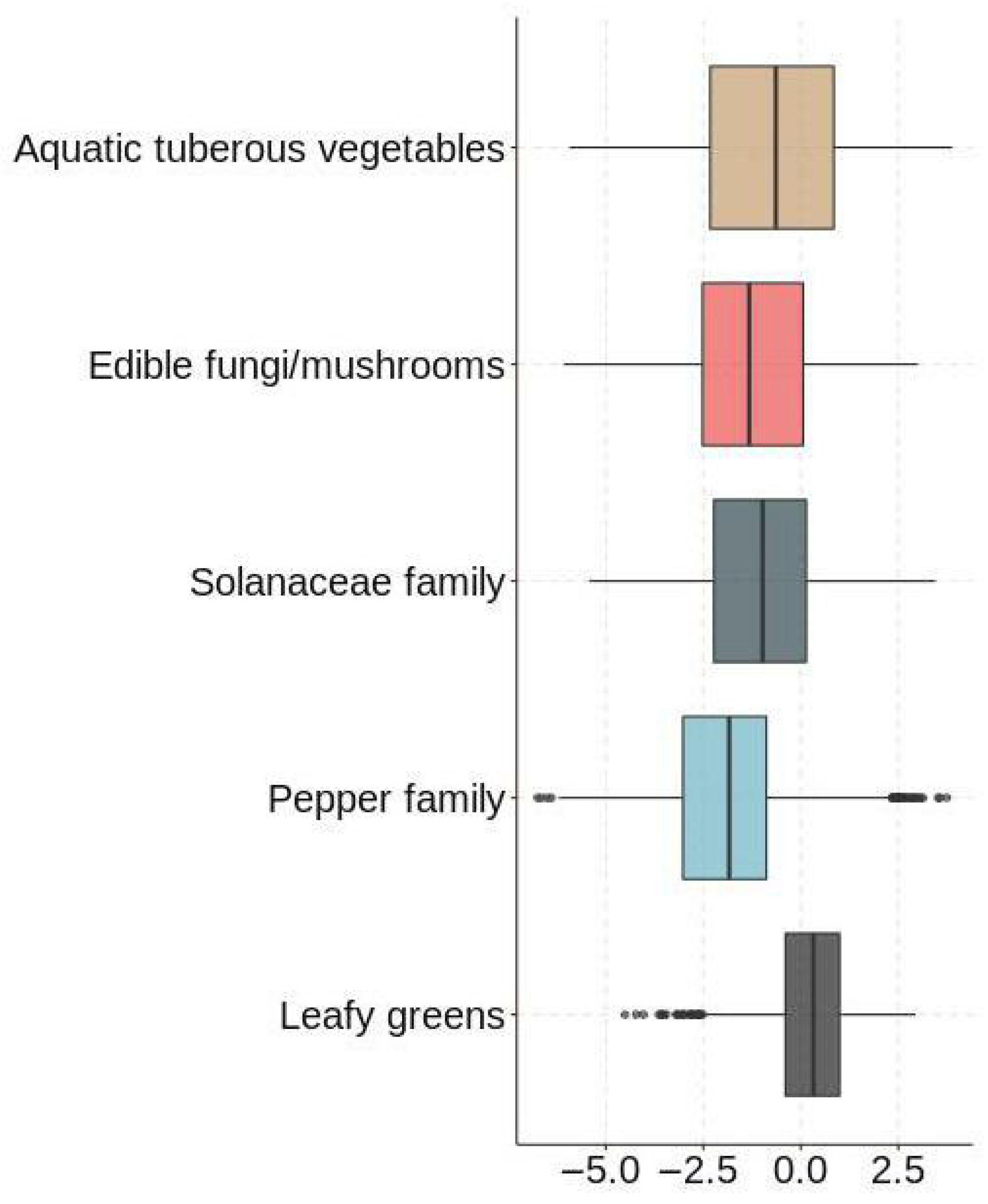
3.2.1. Visualization and Analysis of Data
3.2.2. Statistical Tests
3.3. Modeling and Solving
3.3.1. Establishing and Solving the Category Sales Volume Correlation Model
3.3.2. Establishing and Solving the Single Product Sales Volume Correlation Model
4. Solution to Question Two
4.1. Research Ideas
4.2. Preparation
4.2.1. Calculation of the Average Daily Price of Each Vegetable Category
4.2.2. Preparation of LightGBM Sales Forecasting Model
- (1)
- Lagging characteristics: sales with a lag of 1–14 days;
- (2)
- Sliding characteristics: min/max/median/mean/std of sliding 2–14 day sales volume;
- (3)
- Category coding characteristics: mean and std of sales of each vegetable category;
- (4)
- Category lag characteristics: sales with a lag of 1–14 days of each vegetable category.
- (1)
- The original value of the price: this contained the original features and filled features. The filling strategy was to fill forward and then backward at first, and then to fill with the mode those that were not filled;
- (2)
- Category characteristics: mean and std of sales of each vegetable category;
- (3)
- Price difference characteristics: the difference between the current price and the average of the price;
- (4)
- Price change characteristics: the difference between the current price and the average price from the last week and the previous month.
4.3. Modeling and Solving
4.3.1. Establishing and Solving the Polynomial Fitting Model
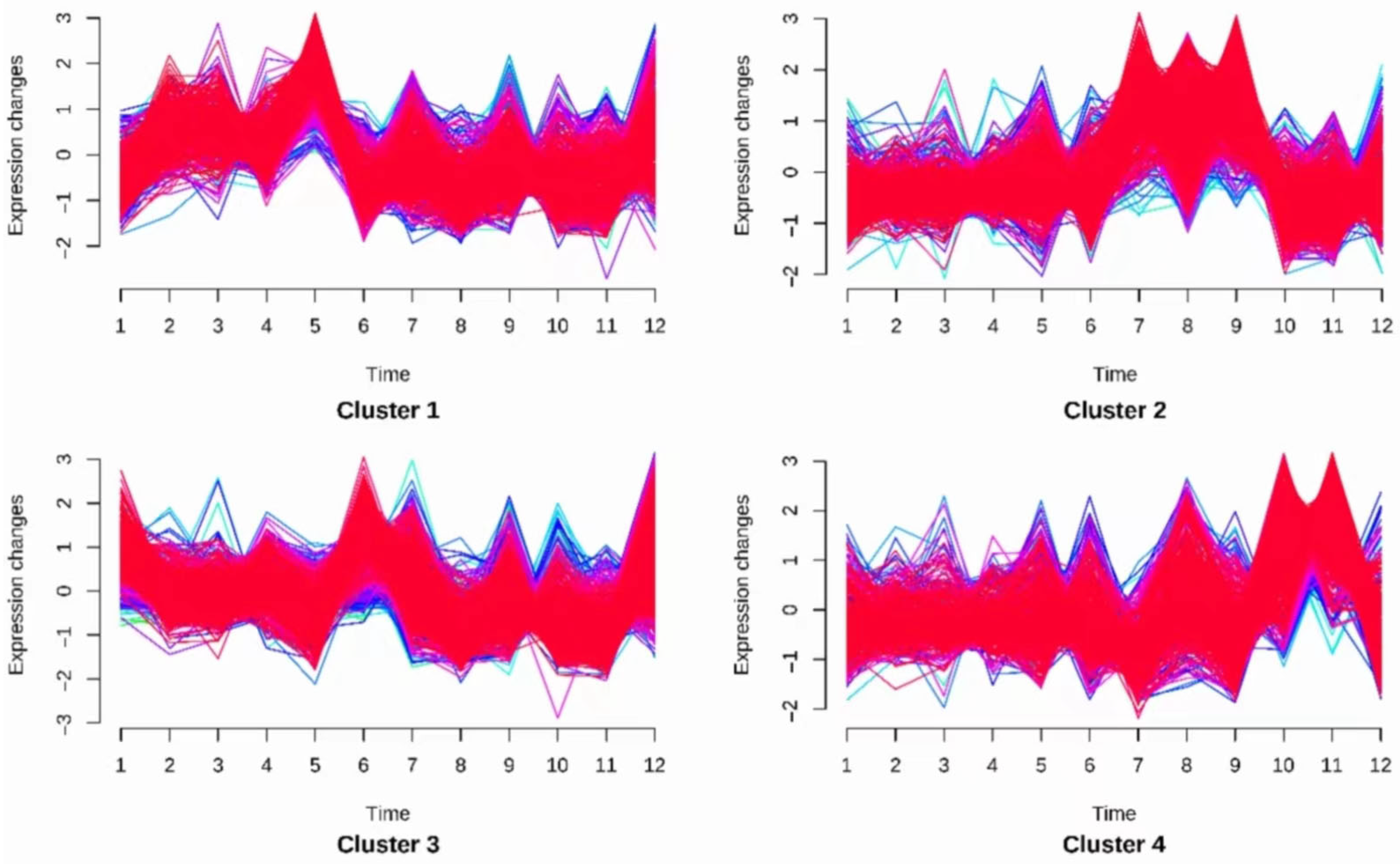
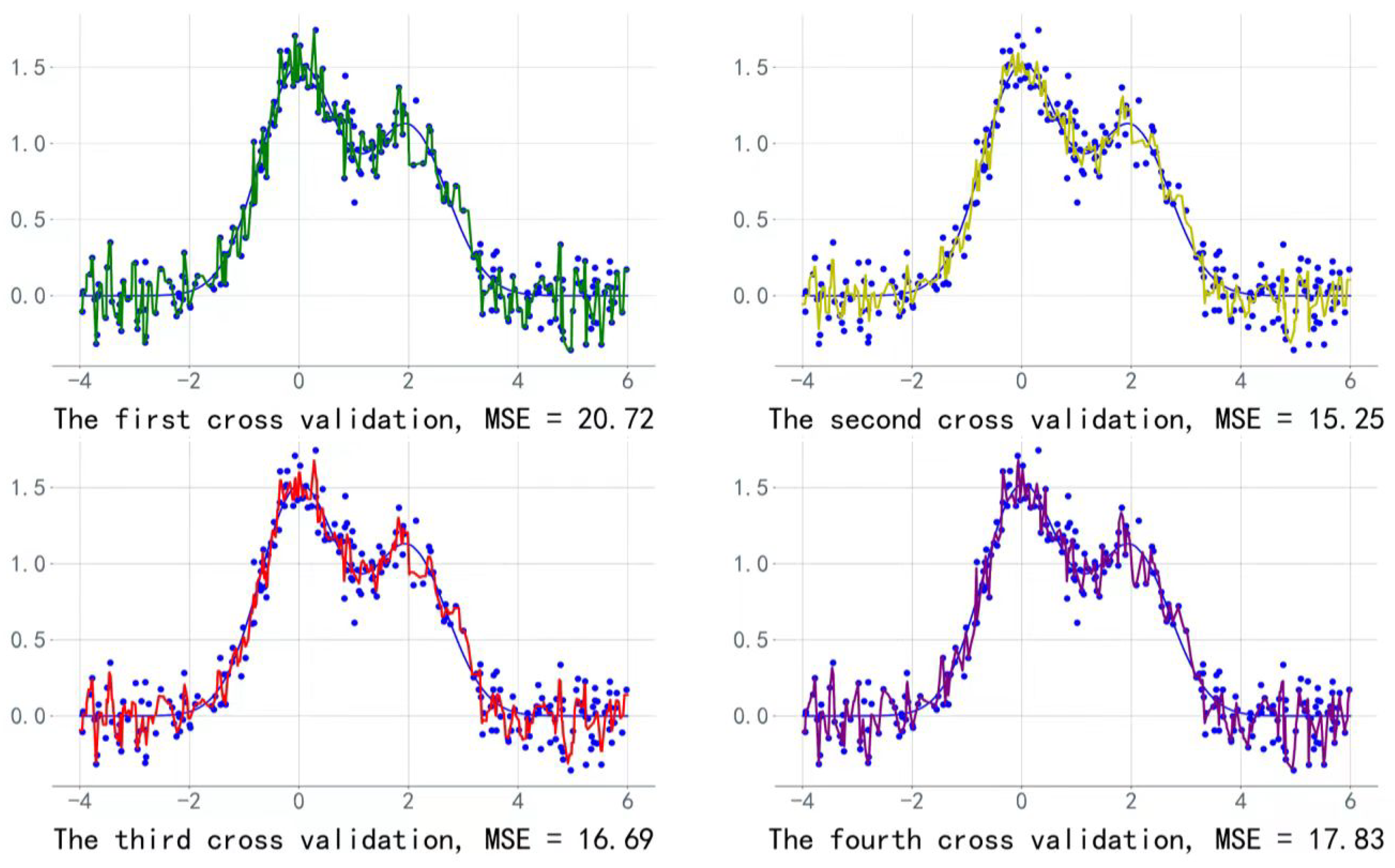
4.3.2. Establishing and Solving the LightGBM Sales Forecasting Model
- (1)
- The training set used the data from the first 713 days and the validation set used the data from the 714-th day; early stop = 50 rounds;
- (2)
- The training set used the data from the first 714 days and the validation set used the data from the 715-th day; early stop = 50 rounds;
- (3)
- The training set used the data from the first 715 days and the validation set used the data from the 716-th day; early stop = 50 rounds;
- (4)
- The training set used the data from the first 716 days and the validation set used the data from the 717-th day; early stop = 50 rounds.
5. Solution to Question Three
5.1. Research Ideas
5.2. Preparation
5.2.1. Preparation of the Dynamic Programming Sales Forecasting Model
5.2.2. Modeling and Solving
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, S.; Zhou, J. Analysis of factors and strategies affecting the efficiency of “agricultural super docking” of bulk vegetables. Shanxi Agric. Econ. 2023, 263–268. [Google Scholar] [CrossRef]
- Li, G. Research on Price Formation and Stabilization Measures of the Whole Vegetable Industry Chain. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. [Google Scholar]
- Wei, D. Research on vegetable revenue insurance risk and pricing in Shandong. Rural Econ. Technol. 2021, 32, 69–70+160. [Google Scholar]
- Zhu, R.; Fan, Z. Dynamic planning model and application of solution for merchandising. J. Shijiazhuang Econ. Coll. 2002, 3, 234–237. [Google Scholar] [CrossRef]
- Yang, P.; Yin, X.; Zhang, G. Cluster analysis of fuzzy C-mean seismic attributes. Pet. Geophys. Explor. 2007, 42, 322–324+242+347+362. [Google Scholar]
- Lu, Y. Research on Dynamic Pricing Problem of High Quality Fresh Vegetables in Supermarkets in China. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2010. [Google Scholar]
- Yan, J.; Li, R. Research on resource allocation of health service stations based on state transfer equation. China Health Econ. 2012, 31, 61–64. [Google Scholar]
- Wang, S. Research on the Formation Problem of Retail Price of Vegetables in Farmers’ Market. Ph.D. Thesis, Huazhong Agricultural University, Wuhan, China, 2014. [Google Scholar]
- Song, J. Research on Optimization of Inventory Management of Vegetable Supply Chain in Shouguang City. Coop. Econ. Sci. Technol. 2015, 138–139. [Google Scholar] [CrossRef]
- Wu, R. Application of state transfer equation in multi-stage decision-making evaluation of emergencies. Decis.-Mak. Explor. 2020, 7, 36–37. [Google Scholar]
- Lu, M.; Zhang, W.; Xu, T. Optimizable replenishment strategy based on dynamic matrix model. Comput. Eng. Appl. 2021, 57, 263–268. [Google Scholar]
- Feng, Z.; Zhang, H. A parameter estimation method for multivariate linear models based on residual vector l1-paradigm minimization with basis tracking. J. Hainan Norm. Univ. Nat. Sci. Ed. 2022, 35, 250–259+267. [Google Scholar]
- Li, Y. Joint Replenishment and Pricing Collaborative Decision Making Considering Investment in Preservation Technology. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2023. [Google Scholar]
- Xie, J.; Zhang, H.; Li, D.; Yu, X.; Deng, J. Optimized deep forest algorithm based on Lightgbm and XGBoost. J. Nanjing Univ. Nat. Sci. 2023, 59, 833–840. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y.; Fang, Y.; Liu, S. Research on Inventory Management Optimization of A Trading Company Based on k-means Clustering Algorithm. China Storage Transp. 2024, 143–144. [Google Scholar] [CrossRef]
- Guo, L.; Guo, Z.; Jia, H.; Fan, R. Identification of residential electricity theft based on Pearson correlation coefficient and SVM. J. Hebei Univ. Nat. Sci. Ed. 2023, 43, 357–363. [Google Scholar]
- Liu, H. Research and application of network intrusion detection method based on deep learning. Comput. Program. Ski. Maint. 2023, 162–165. [Google Scholar] [CrossRef]




| Item Name | Amaranth Greens (Amaranthus) | Yunnan Lettuce | Brussels Sprouts (Brassica oleracea) | Brassica Chinensis | Shanghai Youth |
|---|---|---|---|---|---|
| Product Code | 10290000 | 10290000 | 10290000 | 10290000 | 10290000 |
| 5115762 | 5115779 | 5115786 | 5115793 | 5115823 | |
| Single-Variety Category | Philodendron | Philodendron | Philodendron | Philodendron | Philodendron |
| Date of Sale | 1 July 2020 | 1 July 2020 | 1 July 2020 | 1 July 2020 | 1 July 2020 |
| Daily Sales (kg) | 6.841 | 41.966 | 11.352 | 4.288 | 11.476 |
| Selling Unit Price (CNY/kg) | 6 | 8 | 6 | 16 | 10 |
| Wholesale Price (CNY/kg) | 3.88 | 6.72 | 3.19 | 9.24 | 7.03 |
| Profitability (%) | 54.64 | 19.05 | 88.09 | 73.16 | 42.25 |
| Loss Rate (%) | 18.52 | 15.25 | 13.62 | 7.59 | 14.43 |
| Vegetable Category | Total Sales Volume by Category (kg) | Percentage of Total | Single Vegetables | Total Sales of Individual Products (kg) | Percentage Share | Percentage of Total |
|---|---|---|---|---|---|---|
| Philodendron | 197,395 | 42.15% | Yunnan Lettuce | 30,177 | 15.29% | 6.44% |
| Brassica Pekinensis | 19,100 | 9.68% | 4.08% | |||
| Yunnan Oilseed Rape (Brassica napus) | 19,081 | 9.66% | 4.07% | |||
| Capsicum | 90,561 | 19.34% | Wuhu Green Pepper | 27,628 | 30.51% | 5.9% |
| King Cobra or Chili (Naga Jolokia) | 15,893 | 17.55% | 3.39% | |||
| Chili | 12,185 | 11.87% | 2.61% | |||
| Edible Mushroom | 75,909 | 16.21% | Enoki Mushroom | 23,411 | 30.8% | 5.01% |
| Xixia Shiitake Mushroom | 11,910 | 15.68% | 2.54% | |||
| Agaricus Bisporus (Botany) | 4228 | 5.57% | 0.9% | |||
| Cauliflower (Brassica oleracea var. botrytis) | 41,667 | 8.9% | Broccoli | 27,502.53 | 66.0% | 5.87% |
| Chinese Green Stem with Scattered Flowers | 8339.201 | 20.01% | 1.78% | |||
| Zijiang Qingdian Scattered Flowers | 5811.909 | 13.95% | 1.24% | |||
| Aquatic Rhizomes | 40,466 | 8.64% | Net Lotus Root | 27,105.79 | 66.98% | 5.79% |
| Lotus Root | 6034 | 14.91% | 1.29% | |||
| Lotus Seedling (Pcs) | 2075 | 5.13% | 0.44% | |||
| Eggplant | 22,361 | 4.77% | Purple Eggplant (Solanum melongena L.) | 13,856 | 61.97% | 2.96% |
| Eggplant (Solanum melongena L.) | 3687 | 15.66% | 0.79% | |||
| Long-Term Eggplant | 2493.227 | 11.15% | 0.53% |
| Vegetable Category | Upper Quartile | Average Value | Standard Deviation | Skewness | Kurtosis | S–W Test | p-Value |
|---|---|---|---|---|---|---|---|
| Philodendron | 186.329 | 2035.007 | 3626.467 | 2.507 | 7.096 | 0.628 | 0.988 |
| Capsicum | 368.459 | 2106.073 | 4804.619 | 4.038 | 19.248 | 0.475 | 0.761 |
| Edible Mushroom | 212.171 | 1100.134 | 2467.288 | 4.407 | 22.079 | 0.465 | 0.197 |
| Cauliflower (Brassica oleracea var. botrytis) | 5811.909 | 8333.502 | 11,318.942 | 1.687 | 3.017 | 0.803 | 0.304 |
| Aquatic Rhizomes | 232.403 | 2248.137 | 6369.707 | 3.916 | 15.852 | 0.389 | 0.311 |
| Eggplant | 1047.247 | 2484.639 | 4321.602 | 2.595 | 7.086 | 0.620 | 0.514 |
| Aquatic Rhizomes | Philodendron | Cauliflower (Brassica oleracea var. botrytis) | Eggplant | Capsicum | Edible Mushroom | |
|---|---|---|---|---|---|---|
| Aquatic rhizomes | 1 | 0.637374104 | 0.796073285 | 0.595787529 | 0.808103253 | 0.684693022 |
| Philodendron | 0.637374104 | 1 | 0.713041043 | 0.54202519 | 0.640759134 | 0.542313018 |
| Cauliflower (Brassica oleracea var. botrytis) | 0.796073285 | 0.713041043 | 1 | 0.62882682 | 0.592117531 | 0.506056629 |
| Eggplant | 0.595787529 | 0.54202519 | 0.62882682 | 1 | 0.742529242 | 0.600157973 |
| Capsicum | 0.808103253 | 0.640759134 | 0.592117531 | 0.742529242 | 1 | 0.598800308 |
| Edible Mushroom | 0.684693022 | 0.542313018 | 0.506056629 | 0.600157973 | 0.598800308 | 1 |
| Dates | Aquatic Rhizomes | Philodendron | Cauliflower (Brassica oleracea var. botrytis) | Eggplant | Capsicum | Edible Mushroom |
|---|---|---|---|---|---|---|
| 1 July 2023 | 19.66 | 143.34 | 20.01 | 19.46 | 92.48 | 56.49 |
| 2 July 2023 | 21.82 | 131.05 | 24.49 | 29.69 | 88.75 | 55.61 |
| 3 July 2023 | 21.78 | 122.72 | 22.32 | 25.73 | 83.63 | 54.62 |
| 4 July 2023 | 25.10 | 112.13 | 26.64 | 28.91 | 76.74 | 53.47 |
| 5 July 2023 | 22.71 | 135.93 | 25.02 | 19.80 | 83.03 | 43.74 |
| 6 July 2023 | 26.69 | 118.42 | 28.44 | 26.72 | 81.63 | 51.71 |
| 7 July 2023 | 29.64 | 132.63 | 31.36 | 26.81 | 88.37 | 51.92 |
| Dates | Aquatic Rhizomes | Philodendron | Cauliflower (Brassica oleracea var. botrytis) | Eggplant | Capsicum | Edible Mushroom |
|---|---|---|---|---|---|---|
| 1 July 2023 | 19.9 | 5.1 | 13.7 | 7.4 | 5.9 | 6.5 |
| 2 July 2023 | 19.0 | 5.2 | 15.2 | 7.5 | 5.7 | 5.5 |
| 3 July 2023 | 18.6 | 5.1 | 15.1 | 6.7 | 6.0 | 5.8 |
| 4 July 2023 | 18.5 | 5.7 | 15.2 | 6.4 | 6.5 | 5.9 |
| 5 July 2023 | 18.2 | 5.3 | 15.1 | 8.0 | 6.3 | 5.8 |
| 6 July 2023 | 17.1 | 5.2 | 13.2 | 7.8 | 6.3 | 5.5 |
| 7 July 2023 | 18.7 | 5.0 | 13.7 | 7.5 | 6.2 | 4.7 |
| Single Vegetables | Replenishment (kg) | Sales Price (USD/kg) | Single Vegetables | Replenishment (kg) | Sales Price (USD/kg) |
|---|---|---|---|---|---|
| Shanghai Youth | 3.86 | 4.12 | Yunnan Oilseed Rape (Brassica campestris L.) | 21.29 | 2.86 |
| Yunnan Lettuce | 2.92 | 5.73 | Agaricus bisporus (Box) | 10.00 | 3.40 |
| Baby Chinese Cabbage (Mini-Sized Variety) | 10.43 | 4.73 | Small Wrinkled Skin (Portions) | 11.29 | 1.54 |
| Millet Peppers (Servings) | 21.43 | 2.14 | Baby Bok Choy | 4.90 | 2.83 |
| Snow Fungus (Tremella fuciformis) | 5.93 | 3.21 | Net Lotus Root | 6.03 | 10.75 |
| Honghu Lotus Roots | 4.03 | 18.00 | Seafood Mushroom (Pack) | 8.86 | 1.95 |
| Brussels Sprouts (Brassica oleracea var. botrytis) | 13.30 | 2.32 | Purple Eggplant (Solanum melongena L.) | 10.90 | 3.75 |
| Sweet Potato Tip | 4.51 | 3.20 | Wuhu Green Pepper | 14.23 | 3.38 |
| Amaranth Greens (Genus Amaranthus) | 8.92 | 2.32 | Spinach (Servings) | 9.80 | 4.10 |
| King Cobra or Chili (Naga Jolokia) | 6.84 | 7.52 | Screw Peppers (Servings) | 11.29 | 3.28 |
| Broccoli | 12.56 | 7.82 | Xixia Shiitake Mushroom | 4.62 | 15.60 |
| Golden Needle Mushroom (Box) | 16.14 | 1.45 | Long-Term Eggplant | 4.21 | 6.98 |
| Eggplant (Solanum melongena L.) | 3.12 | 4.05 | Cucumber | 3.00 | 11.54 |
| Zijiang Qingdian Scattered Flowers | 6.30 | 9.36 | Yunnan Lettuce (Servings) | 32.29 | 3.60 |
| Cabbage (Common in Chinese Medicine) | 7.49 | 2.53 | Fresh Fungus (Portions) | 4.00 | 1.30 |
| Ginger, Garlic, and Millet Pepper Combo | 7.00 | 2.44 | |||
| Maximum Profit: USD 1239.86 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, W.; Wu, C.; Wu, T.; Chen, F. Research on the Optimization of Pricing and the Replenishment Decision-Making Problem Based on LightGBM and Dynamic Programming. Axioms 2024, 13, 257. https://doi.org/10.3390/axioms13040257
Tao W, Wu C, Wu T, Chen F. Research on the Optimization of Pricing and the Replenishment Decision-Making Problem Based on LightGBM and Dynamic Programming. Axioms. 2024; 13(4):257. https://doi.org/10.3390/axioms13040257
Chicago/Turabian StyleTao, Wenyue, Chaoran Wu, Ting Wu, and Fuyuan Chen. 2024. "Research on the Optimization of Pricing and the Replenishment Decision-Making Problem Based on LightGBM and Dynamic Programming" Axioms 13, no. 4: 257. https://doi.org/10.3390/axioms13040257
APA StyleTao, W., Wu, C., Wu, T., & Chen, F. (2024). Research on the Optimization of Pricing and the Replenishment Decision-Making Problem Based on LightGBM and Dynamic Programming. Axioms, 13(4), 257. https://doi.org/10.3390/axioms13040257





